Obsah
1. Modely provádějící klasifikaci v balíčku scikit-learn
2. Otestování naučeného modelu s využitím tréninkových dat: skryté nebezpečí
3. Využití funkce metrics.accuracy_score pro zjištění kvality modelu
4. Proč náš model odpovídá ve 100% případů korektně?
5. Porovnání vhodnosti různých modelů pro klasifikaci dat
6. Porovnání různých modelů: první, ne zcela korektní, varianta
7. Rozdělení datové sady na data určená pro trénink a data určená pro ověření modelu
8. Analýza výsledků modelu KNN pro k=1
9. Náhodné rozdělení datové sady na tréninkovou a testovací část
10. Náhodné rozdělení datové sady funkcí shuffle
11. Úplný kód upraveného skriptu
12. Náhodné rozdělení datové sady funkcí train_test_split
13. Úplný kód upraveného skriptu
14. Porovnání různých modelů: druhá, již korektní, varianta
15. Analýza změřených výsledků
16. Opakované měření předpovědí modelů
17. Proč se výsledky odlišují?
18. Zajištění stabilních výsledků s využitím parametru random_state
19. Repositář s demonstračními příklady
1. Modely provádějící klasifikaci v balíčku scikit-learn
Minulý týden na stránkách Roota vyšel článek se základními informacemi o knihovně scikit-learn používané při datové analýze. Ukázali jsme si v něm standardní datovou sadu, která obsahuje informace o rozměrech květů různých druhů kosatců (Iris data set). Tuto datovou sadu využijeme i dnes při tréninku modelů provádějících takzvanou klasifikaci – takové modely pro zadaná (neznámá) data odpoví, do které kategorie tato data patří, což v našem konkrétním případě znamená hodnotu 0, 1 nebo 2 (druh kosatce).
Připomeňme si, že trénink modelu v knihovně scikit-learn probíhá, nezávisle na zvoleném modelu, stále stejným způsobem:
- Import třídy se zvoleným modelem
- Konstrukce modelu (vytvoření jeho instance) se specifikací hyperparametrů (liší se podle typu modelu)
- Trénink modelu metodou fit, které se předají trénovací data i očekávané odpovědi
- Otestování modelu – zda dokáže predikovat výsledky pro odlišná data (tedy nikoli pro trénovací data)
Dnes si vysvětlíme i předvedeme zejména to, proč je datovou sadu nutné rozdělit na trénovací a testovací (validační) část. Ale taktéž se zmíníme i o problému přetrénování modelu (overfitting, overtraining).
A v praxi taktéž musíme získat odpovědi na tyto otázky:
- Který model použít?
- Jaké má mít zvolený model hyperparametry?
- Jak změřit kvalitu modelu pro neznámá data, na která není model natrénován?
2. Otestování naučeného modelu s využitím tréninkových dat: skryté nebezpečí
První úkol, který musíme při tréninku modelů s učitelem vyřešit, je otestování, jak dobře dokáže model odhadovat výsledky pro předaná data. V případě, že máme k dispozici data i s odpověďmi (tedy v našem případě se bude jednat o rozměry květů i druh rostliny), může se nabízet následující postup:
- Model natrénujeme s využitím celé sady dat, která máme k dispozici (čím větší množství dat, tím lépe bude model naučen, ne?)
- Model následně otestujeme nad touto sadou dat, protože dokážeme porovnat odpovědi modelu se správnými odpověďmi (když už tato data ,máme k dispozici, proč je nepoužít znovu, ne?)
Zde se ovšem skrývají minimálně dva problémy, takže si je pojďme ilustrovat. Natrénujeme model KNN (k-nearest neighbors algorithm) pro k=1. Následně tomuto modelu předáme trénovací data znovu a zjistíme, jak se jeho odpovědi odlišují od správných odpovědí. Celá funkce následujícího skriptu je podrobně popsána v komentářích:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=1)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X, y)
# očekávané výsledky
expexted_labels = iris.target
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(iris.data)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print("Odhadů Korektních Přesnost")
print(f"{total:5} {same:5} {100.0*same/total:4.1f}%")
# finito
3. Využití funkce metrics.accuracy_score pro zjištění kvality modelu
Namísto ručního počítání správných odpovědí modelu v programové smyčce:
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
můžeme použít funkci accuracy_score z modulu sklearn.metrics, které se předají korektní odpovědi a skutečné odpovědi modelu. Výsledkem je hodnota odpovídající kvalitě odpovědí (0-model se vždy mýlí, 1-model se nikdy nemýlí):
Help on function accuracy_score in module sklearn.metrics._classification:
accuracy_score(y_true, y_pred, *, normalize=True, sample_weight=None)
Accuracy classification score.
In multilabel classification, this function computes subset accuracy:
the set of labels predicted for a sample must *exactly* match the
corresponding set of labels in y_true.
Read more in the :ref:`User Guide <accuracy_score>`.
Parameters
----------
y_true : 1d array-like, or label indicator array / sparse matrix
Ground truth (correct) labels.
y_pred : 1d array-like, or label indicator array / sparse matrix
Predicted labels, as returned by a classifier.
normalize : bool, default=True
If ``False``, return the number of correctly classified samples.
Otherwise, return the fraction of correctly classified samples.
sample_weight : array-like of shape (n_samples,), default=None
Sample weights.
Celý skript se tedy zkrátí, protože nebude nutné ručně zjišťovat, kdy se model mýlí a kdy nikoli:
from sklearn.datasets import load_iris from sklearn.neighbors import KNeighborsClassifier from sklearn import metrics import numpy as np # nacteni datove sady iris = load_iris() # konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=1) # X je matice (feature matrix) X = iris.data # y je vektor (response vector) y = iris.target # trening modelu (se vsemi dostupnymi daty) classifier.fit(X, y) # očekávané výsledky expexted_labels = iris.target # výsledky modelu (predikované výsledky) predicted_labels = classifier.predict(iris.data) # jak je náš model úspěšný? print(metrics.accuracy_score(expexted_labels, predicted_labels)) # finito
4. Proč náš model odpovídá ve 100% případů korektně?
Podívejme se nyní na výsledky, které oba skripty vypočítají. První skript vypíše:
Odhadů Korektních Přesnost 150 150 100.0%
Druhý skript je stručnější, nicméně nám dodá stejnou informaci o 100% úspěšnosti:
1.0
Proč tomu tak je? Je KNN (pro k=1) skutečně tak dobrý, vlastně i lepší než neuronové sítě atd.? Samozřejmě nikoli, „pouze“ jsme tento model použili nekorektně. KNN se totiž naučí tak, že si zapamatuje všechna vstupní data, které považuje za body v N-rozměrném prostoru (v našem konkrétním případě čtyřrozměrném). A následně pro neznámý vstup zjistí, který známý bod je tomuto vstupu nejblíže. Pro k>1 pak zjišťuje nejbližších k sousedů a vrátí jejich majoritní hodnotu, ostatně proto se za k volí spíše liché číslo, aby se model vždy mohl rozhodnout:
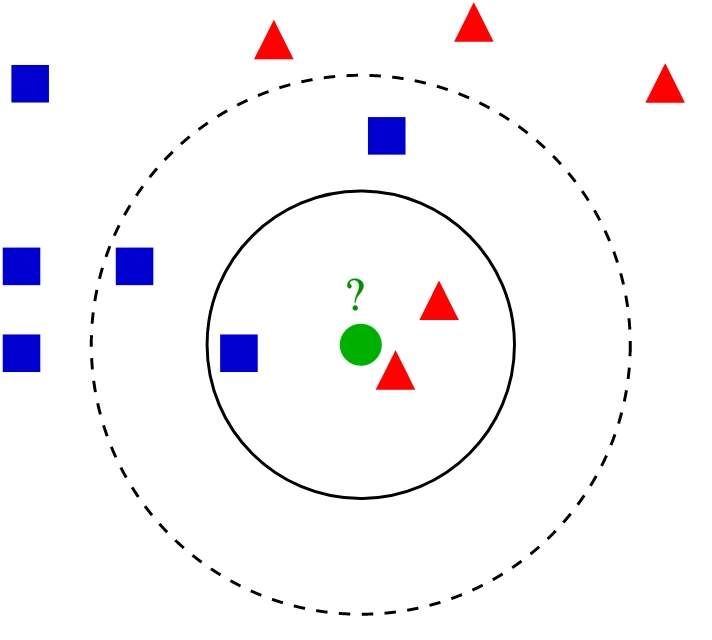
Obrázek 1: Pro k=1 bude pro neznámý bod označený otazníkem vrácena hodnota odpovídající červené barvě. Taktéž pro k=3. Ovšem pokud použijeme model s k=5, bude vrácena hodnota odpovídající modré barvě, protože z pěti bodů nejbližších k neznámému bodu jsou tři modré a jen dva červené.
My jsme modelu při učení předali 150 čtyřrozměrných bodů, které si model zapamatoval (pro každý bod souřadnice i jeho hodnotu=odpověď). A poté jsme mu předali ty samé body jako neznámá data, pro které měl najít odpověď. Ovšem pro k=1 je to snadné, protože nejbližší body (tedy ty samé body) již model zná! Takže není divu, že odpovědi byly v tomto případě vždy na 100% úspěšné.
5. Porovnání vhodnosti různých modelů pro klasifikaci dat
Ve scikit-learnu je nabízeno velké množství modelů, přičemž mnoho z nich je možné nakonfigurovat s využitím takzvaných hyperparametrů, což si ostatně ihned ukážeme. Některé z těchto modelů jsou popsány v článku Comprehensive Guide to Classification Models in Scikit-Learn. Nabízí se tedy otázka, jakým způsobem je vlastně možné jednotlivé modely (nebo jejich parametrizované varianty) porovnat z různých hledisek. Jedním z hledisek je porozumění modelu, tj. analýza, jakým „dovednostem“ se model naučil (některým modelům lze porozumět lépe, jiným, typicky těm sofistikovanějším, hůře). Ovšem důležité je i porovnání vhodnosti modelů pro klasifikaci konkrétních dat, protože model se vybírá mj. i v závislosti na datech, která chceme analyzovat.
6. Porovnání různých modelů: první, ne zcela korektní, varianta
V dalším skriptu se pokusíme o porovnání čtyř typů modelů. První dva modely využívají nám již známý KNN, přičemž první model má k=1 (nalezne nejbližšího souseda) a druhý k=5 (bude tedy vybírat majoritní výsledek z pěti nejbližších sousedů). A další dva modely jsou založeny na logistické regresi a taktéž mají nastaveny rozdílný hyperparametr, konkrétně hyperparametr max_iter. Každý z těchto modelů je nejdříve natrénován (stejnými daty) a posléze ho předáme do funkce score, v níž dojde ke zjištění míry správnosti odpovědí modelů:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# trening modelu (se vsemi dostupnymi daty)
knn_1_classifier.fit(X, y)
knn_2_classifier.fit(X, y)
lr_classifier_1.fit(X, y)
lr_classifier_2.fit(X, y)
def score(model):
# očekávané výsledky
expexted_labels = iris.target
# výsledky modelu (predikované výsledky)
predicted_labels = model.predict(iris.data)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
# finito
Změřené výsledky budou vypadat následovně:
KNN classifier with K=1: 100.00% KNN classifier with K=5: 96.67% LogisticRegression with max_iter=1: 33.33% LogisticRegression with max_iter=1000: 97.33%
7. Rozdělení datové sady na data určená pro trénink a data určená pro ověření modelu
Nyní již víme, proč je tak důležité nepoužít celou datovou sadu pouze pro trénink. V takovém případě nám totiž nezbudou žádná data, na kterých bychom si ověřili kvalitu modelu. Datovou sadu musíme vhodně rozdělit tak, aby bylo možné model na jedné straně natrénovat a na druhé straně musíme mít dostatek údajů pro jeho ověření. V našem konkrétním případě, kdy máme k dispozici 150 záznamů, tedy můžeme volit velikost trénovací množiny od 1 do 149; z toho je odvozena velikost množiny druhé. Skript pro naučení a otestování modelu tedy nepatrně upravíme tak, že hodnotou for_training (1 až 149) zvolíme, kolik záznamů bude použito pro trénink modelu. Potom vstupní množinu rozdělíme na dvě nestejně velké části. Nejprve získáme data pro trénink, a to následujícím způsobem:
# X je matice (feature matrix)
X = iris.data[:for_training]
# y je vektor (response vector)
y = iris.target[:for_training]
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X, y)
Následně získáme data pro ověření modelu:
# očekávané výsledky
expexted_labels = iris.target[for_training:]
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(iris.data[for_training:])
Celý skript je upraven tak, že trénink a ověření modelu je součástí funkce train_and_predict, kterou voláme s měnící se hodnotou argumentu training_set_size:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
# nacteni datove sady
iris = load_iris()
def train_and_predict(training_set_size):
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=1)
# počet vzorků pro trénink
for_training = training_set_size
# X je matice (feature matrix)
X = iris.data[:for_training]
# y je vektor (response vector)
y = iris.target[:for_training]
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X, y)
# očekávané výsledky
expexted_labels = iris.target[for_training:]
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(iris.data[for_training:])
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print(f"{for_training:7} {total:5} {same:5} {100.0*same/total:4.1f}%")
print("Pro trénink Odhadů Korektních Přesnost")
for training_size in np.arange(10, len(iris.data)-10, 10):
train_and_predict(int(training_size))
# finito
8. Analýza výsledků modelu KNN pro k=1
Podívejme se nyní na výsledky ověření modelu KNN pro k=1, a to pro různou velikost trénovacích dat:
Pro trénink Odhadů Korektních Přesnost
10 140 40 28.6%
20 130 30 23.1%
30 120 20 16.7%
40 110 10 9.1%
50 100 0 0.0%
60 90 40 44.4%
70 80 30 37.5%
80 70 20 28.6%
90 60 10 16.7%
100 50 0 0.0%
110 40 29 72.5%
120 30 25 83.3%
130 20 19 95.0%
Tyto výsledky jsou „zvláštní“, protože pro n=50 a n=100 je odhad modelu zcela špatný. Ovšem proč tomu tak je? Vždyť například pro n=100 už by měl být model docela dobře naučen a ostatně pro n=110 už dává v 72% dobré výsledky. Ovšem připomeňme si, že v předchozí kapitole bylo napsáno: „datovou sadu musíme vhodně rozdělit tak, aby bylo možné model …“. My jsme ovšem datovou sadu nerozdělili vhodně, ale pouze jsme ji v určitém indexu rozřízli (split) na dvě nestejně velké části. Problém je v tom, že u datové sady Iris jsou záznamy seřazeny, a to podle druhu rostliny – pro každý druh je k dispozici přesně 50 záznamů. To si ostatně můžeme velmi snadno ověřit:
# nacteni datove sady
iris = load_iris()
# druhy rostlin z datove sady v numericke podobe
print("Targets:")
print(iris["target"])
Výsledky budou vypadat následovně – sekvence padesáti nul, sekvence padesáti jedniček a konečně sekvence padesáti dvojek:
Targets: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
Pokud jsme tedy zvolili n=50, vybraly se pro trénink záznamy pro první druh rostliny a model logicky pořád odpovídal „výsledkem je druh 0“, protože se nic dalšího nenaučil. A pro n=100 se model natrénoval na druhy 0 a 1 (a to se stoprocentní úspěšností), ovšem ověřovali jsme ho jen na rostlinách druhu 2, o kterých model nic nevěděl a proto odpovídal 0 nebo 1.
9. Náhodné rozdělení datové sady na tréninkovou a testovací část
Problém, se kterým jsme se setkali v předchozí kapitole, je možné vyřešit relativně snadným způsobem. Musíme původní datovou sadu rozdělit na tréninkovou a testovací část náhodně, tedy nikoli zvolením dvou intervalů od:do. To lze provést hned několika způsoby. Nejdříve si ukážeme způsob založený na použití funkce nazvané shuffle z balíčku sklearn.utils a posléze použití funkce train_test_split z balíčku sklearn.model_selection. První způsob je více názorný (je tedy zřejmé, co se děje uvnitř), druhý způsob je jednodušší na použití, takže smysl má znát oba tyto způsoby.
10. Náhodné rozdělení datové sady funkcí shuffle
Funkce shuffle je samozřejmě popsána v nápovědě:
shuffle(*arrays, random_state=None, n_samples=None)
Shuffle arrays or sparse matrices in a consistent way.
This is a convenience alias to ``resample(*arrays, replace=False)`` to do
random permutations of the collections.
Parameters
----------
*arrays : sequence of indexable data-structures
Indexable data-structures can be arrays, lists, dataframes or scipy
sparse matrices with consistent first dimension.
random_state : int, RandomState instance or None, default=None
Determines random number generation for shuffling
the data.
Pass an int for reproducible results across multiple function calls.
See :term:`Glossary <random_state>`.
n_samples : int, default=None
Number of samples to generate. If left to None this is
automatically set to the first dimension of the arrays. It should
not be larger than the length of arrays.
Použijeme ji tak, že nejdříve datovou sadou „zamícháme“ a teprve poté z ní přečteme jak vstupní hodnoty (jak rozměry květů, tak i očekávané druhy rostlin). Pouze musíme zařídit, aby se obě tyto datové struktury (což jsou obecně n-rozměrná pole) zamíchaly současně, tedy aby zůstala zachována vazba rozměry:druh rostliny:
# kopie poli (abychom nemenili puvodni data)
data = np.copy(iris.data)
targets = np.copy(iris.target)
# zamichani obou poli se zarucenim, ze bude zachovan vztah data:target
data, targets = shuffle(data, targets)
Poté je již možné rozdělení zamíchané datové sady na obě požadované části, tedy část trénovací a testovací:
# X je matice (feature matrix)
X = data[:for_training]
# y je vektor (response vector)
y = targets[:for_training]
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X, y)
# očekávané výsledky
expexted_labels = targets[for_training:]
Výsledky budou již mnohem lepší, jak je to ostatně patrné z následující tabulky (i když naprosto přesné odpovědi pro n=100 si vyžádají další průzkum):
Pro trénink Odhadů Korektních Přesnost
10 140 135 96.4%
20 130 122 93.8%
30 120 112 93.3%
40 110 104 94.5%
50 100 92 92.0%
60 90 86 95.6%
70 80 79 98.8%
80 70 69 98.6%
90 60 56 93.3%
100 50 50 100.0%
110 40 37 92.5%
120 30 28 93.3%
130 20 20 100.0%
11. Úplný kód upraveného skriptu
Celý skript po výše popsané úpravě vypadá následovně:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.utils import shuffle
import numpy as np
# nacteni datove sady
iris = load_iris()
def train_and_predict(training_set_size):
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=1)
# počet vzorků pro trénink
for_training = training_set_size
# kopie poli (abychom nemenili puvodni data)
data = np.copy(iris.data)
targets = np.copy(iris.target)
# zamichani obou poli se zarucenim, ze bude zachovan vztah data:target
data, targets = shuffle(data, targets)
# X je matice (feature matrix)
X = data[:for_training]
# y je vektor (response vector)
y = targets[:for_training]
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X, y)
# očekávané výsledky
expexted_labels = targets[for_training:]
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(data[for_training:])
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print(f"{for_training:7} {total:5} {same:5} {100.0*same/total:4.1f}%")
print("Pro trénink Odhadů Korektních Přesnost")
for training_size in np.arange(10, len(iris.data)-10, 10):
train_and_predict(int(training_size))
# finito
12. Náhodné rozdělení datové sady funkcí train_test_split
Z praktického hlediska je výhodnější namísto použití funkce shuffle zavolat funkci nazvanou train_test_split, která je definovaná v balíčku sklearn.model_selection. Tato funkce ve svém prvním parametru akceptuje přímo datovou sadu (nemusíme se tedy snažit o ruční získání naměřených dat a očekávaných výsledků), dále velikost testovacích a trénovacích dat (buď jako celé číslo, což je počet záznamů nebo hodnotu typu float, což bude zlomek od 0 do 1, nepovinnou hodnotu, která zamezí různým výsledkům pro několik volání této funkce a dále parametr povolující zamíchání dat (ve výchozím nastavení je povolen):
train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
Split arrays or matrices into random train and test subsets.
Quick utility that wraps input validation,
``next(ShuffleSplit().split(X, y))``, and application to input data
into a single call for splitting (and optionally subsampling) data into a
one-liner.
Read more in the :ref:`User Guide <cross_validation>`.
Parameters
----------
*arrays : sequence of indexables with same length / shape[0]
Allowed inputs are lists, numpy arrays, scipy-sparse
matrices or pandas dataframes.
test_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion
of the dataset to include in the test split. If int, represents the
absolute number of test samples. If None, the value is set to the
complement of the train size. If ``train_size`` is also None, it will
be set to 0.25.
train_size : float or int, default=None
If float, should be between 0.0 and 1.0 and represent the
proportion of the dataset to include in the train split. If
int, represents the absolute number of train samples. If None,
the value is automatically set to the complement of the test size.
random_state : int, RandomState instance or None, default=None
Controls the shuffling applied to the data before applying the split.
Pass an int for reproducible output across multiple function calls.
See :term:`Glossary <random_state>`.
shuffle : bool, default=True
Whether or not to shuffle the data before splitting. If shuffle=False
then stratify must be None.
stratify : array-like, default=None
If not None, data is split in a stratified fashion, using this as
the class labels.
Read more in the :ref:`User Guide <stratification>`.
Konkrétně tuto funkci použijeme následujícím způsobem:
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1.0-training_set_size)
Výsledné hodnoty X_train a X_test jsou dvourozměrná pole se čtyřmi sloupci (rozměry květů), zatímco hodnoty y_train a y_test jsou jednorozměrné vektory s hodnotami 0..3 (druhy rostlin). Počet řádků matic, resp. počet hodnot ve vektorech samozřejmě závisí na test_size a bude se pohybovat od 0 do 150.
Výsledky:
Pro trénink Odhadů Korektních Přesnost 0.05 143 123 86.0% 0.10 135 123 91.1% 0.15 128 118 92.2% 0.20 120 117 97.5% 0.25 113 104 92.0% 0.30 105 100 95.2% 0.35 98 93 94.9% 0.40 91 85 93.4% 0.45 83 79 95.2% 0.50 75 71 94.7% 0.55 68 66 97.1% 0.60 60 58 96.7% 0.65 53 51 96.2% 0.70 46 45 97.8% 0.75 38 35 92.1% 0.80 31 31 100.0% 0.85 23 22 95.7% 0.90 15 14 93.3% 0.95 8 7 87.5%
Druhý běh (random_state totiž není nastaven, takže budeme mít odlišné výsledky):
Pro trénink Odhadů Korektních Přesnost 0.05 143 82 57.3% 0.10 135 130 96.3% 0.15 128 123 96.1% 0.20 120 111 92.5% 0.25 113 109 96.5% 0.30 105 100 95.2% 0.35 98 91 92.9% 0.40 91 86 94.5% 0.45 83 80 96.4% 0.50 75 75 100.0% 0.55 68 66 97.1% 0.60 60 57 95.0% 0.65 53 50 94.3% 0.70 46 46 100.0% 0.75 38 38 100.0% 0.80 31 31 100.0% 0.85 23 22 95.7% 0.90 15 15 100.0% 0.95 8 8 100.0%
13. Úplný kód upraveného skriptu
Opět si ověřme, jak bude vypadat skript po úpravách popsaných v předchozí kapitole.
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
import numpy as np
# nacteni datove sady
iris = load_iris()
def train_and_predict(training_set_size):
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=1)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1.0-training_set_size)
#print(len(X_train), len(X_test))
# trening modelu (se vsemi dostupnymi daty)
classifier.fit(X_train, y_train)
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print(f"{test_size:4.2f} {total:5} {same:5} {100.0*same/total:4.1f}%")
print("Pro trénink Odhadů Korektních Přesnost")
for test_size in np.linspace(0.05, 0.95, 19):
train_and_predict(test_size)
# finito
14. Porovnání různých modelů: druhá, již korektní, varianta
Nyní si již můžeme zopakovat porovnání různých modelů podle přesnosti jejich odhadu. Zopakujeme si tedy úkol ze šesté kapitoly, nyní ovšem s korektně naučenými a otestovanými modely – již nebude docházet k tomu, že pro otestování modelu použijeme trénovací data a navíc bude testovací sada rozdělena náhodně, takže se zamezí tomu, aby se model naučil pouze omezený počet odpovědí. Připomeňme si, že první dva modely využívají nám již známý KNN, přičemž první model má k=1 (nalezne nejbližšího souseda) a druhý k=5 (bude tedy vybírat majoritní výsledek z pěti nejbližších sousedů). A další dva modely jsou založeny na logistické regresi a taktéž mají nastaveny rozdílný hyperparametr, konkrétně hyperparametr max_iter,
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
# trening modelu (se vsemi dostupnymi daty)
knn_1_classifier.fit(X_train, y_train)
knn_2_classifier.fit(X_train, y_train)
lr_classifier_1.fit(X_train, y_train)
lr_classifier_2.fit(X_train, y_train)
def score(model):
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = model.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
# finito
15. Analýza změřených výsledků
Podívejme se na výsledky, které byly získány s využitím skriptu z předchozí kapitoly. Nyní již dostáváme korektní hodnoty a z nich je patrné, že KNN pro k=1 nemusí být tím nejlépe zvoleným a nakonfigurovaným modelem, protože lépe vychází KNN pro k=5. Tento jev, kdy „chytřejší“ model je ve skutečnosti v praxi horší, souvisí s problematikou takzvaného přetrénování (overtraining), ke které se ještě vrátíme. Nejedná se ve skutečnosti o nic složitého, pouze o fakt, že model je příliš navázán na trénovací data a nedokáže tak dobře generalizovat pro obecná data, jako model, který se spíše naučil základní trendy v datech. To je mimochodem jeden z důvodů, proč nebudeme dostávat stoprocentně přesné modely. A dále je zajímavé, že model s logistickou regresí, i když je interně mnohem jednodušší než KNN (pamatuje si menší stavový vektor) vlastně ve výsledku nevychází vůbec špatně, ovšem pro korektně nastavené hyperparametry:
KNN classifier with K=1: 96.67% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 28.33% LogisticRegression with max_iter=1000: 95.00%
16. Opakované měření předpovědí modelů
V předchozím textu jsme pracovali s výsledky testování modelů. Ovšem co se stane ve chvíli, kdy budeme trénink a testování spouštět opakovaně? Projeví se zde náhodný faktor použitý při rozdělení datové sady na tréninkovou a testovací část? Nebo se jedná o takový „detail“, který nemá na výsledky žádný vliv? Otestujme si to:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
for i in range(10):
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
# trening modelu (se vsemi dostupnymi daty)
knn_1_classifier.fit(X_train, y_train)
knn_2_classifier.fit(X_train, y_train)
lr_classifier_1.fit(X_train, y_train)
lr_classifier_2.fit(X_train, y_train)
def score(model):
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = model.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
print("-" * 50)
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
# finito
17. Proč se výsledky odlišují?
Jak je ze skriptu patrné, je každý trénink a ověření spuštěn 10×. Pokaždé přitom můžeme dostat odlišné výsledky, a to v závislosti na tom, jak konkrétně byla původní datová sada rozdělena na tréninkovou a testovací část. Dat je totiž velmi málo (pouze 150), takže se může stát, že se například model trénuje s mnoha vzorky druhu číslo 2 a mnohem méně vzorky druhů 0 a 1 (a naopak). Z toho následně plynou rozdíly měření, které dosahují jednotek procent, což už je dosti velká odchylka. Taktéž si povšimněte, že se nám jednou povedlo dosáhnout stoprocentní úspěšnosti předpovědi KNN pro k=5:
-------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 96.67% LogisticRegression with max_iter=1: 36.67% LogisticRegression with max_iter=1000: 98.33% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 95.00% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 95.00% -------------------------------------------------- KNN classifier with K=1: 91.67% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 36.67% LogisticRegression with max_iter=1000: 96.67% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 93.33% LogisticRegression with max_iter=1: 36.67% LogisticRegression with max_iter=1000: 93.33% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 100.00% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 98.33% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 100.00% LogisticRegression with max_iter=1: 61.67% LogisticRegression with max_iter=1000: 98.33% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 96.67% LogisticRegression with max_iter=1: 35.00% LogisticRegression with max_iter=1000: 95.00% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 95.00% LogisticRegression with max_iter=1: 31.67% LogisticRegression with max_iter=1000: 96.67% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 21.67% LogisticRegression with max_iter=1000: 96.67% -------------------------------------------------- KNN classifier with K=1: 96.67% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 51.67% LogisticRegression with max_iter=1000: 95.00%
18. Zajištění stabilních výsledků s využitím parametru random_state
Jak však dosáhnout stabilních výsledků, například proto, že skript bude testován na CI nebo bude někdo jiný chtít ověřit námi prezentované výsledky? V takových případech budeme stále potřebovat, aby se původní datová sada rozdělila náhodně, ale aby tato „náhodnost“ byla vždy stejná, nezávisle na tom, kolikrát skript spustíme. To je možné v případě, pokud funkci train_test_split předáme parametr random_state s libovolnou, ale konstantní hodnotou. Ověřme si to na dnešním posledním příkladu:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
for i in range(10):
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)
# trening modelu (se vsemi dostupnymi daty)
knn_1_classifier.fit(X_train, y_train)
knn_2_classifier.fit(X_train, y_train)
lr_classifier_1.fit(X_train, y_train)
lr_classifier_2.fit(X_train, y_train)
def score(model):
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = model.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
print("-" * 50)
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
# finito
Nyní dostaneme tyto výsledky, které by měly být shodné i na vašem počítači:
-------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00% -------------------------------------------------- KNN classifier with K=1: 98.33% KNN classifier with K=5: 98.33% LogisticRegression with max_iter=1: 30.00% LogisticRegression with max_iter=1000: 100.00%
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/





































