Obsah
1. Balíček scikit-learn: trénink a předpovědi modelů provádějících regresní analýzu
2. Polynomická regrese nad údaji o souřadnicích bloků
3. Polynomická regrese s údaji, v nichž se vyskytují extrémní hodnoty
4. Preprocessing a filtering dat: odstranění mezních případů
5. Trénink modelu provádějícího regresní analýzu
6. Ukázka natrénování a predikce modelu s využitím všech dostupných údajů
7. Rozdělení dat na tréninkovou a testovací část
8. Ukázka natrénování a predikce modelu po rozdělení dat
9. Trénink modelu s vyloučením určitého atributu nebo atributů
10. Ukázka natrénování a predikce modelu po rozdělení dat a odstranění zvoleného atributu
11. Který atribut či atributy odstranit?
12. Skript, který odstraní vybraný atribut a poté provede otestování modelu s vyjádřením skóre
13. Chování modelu při opakovaném tréninku s náhodně vybranými daty
14. Zjištění, který atribut způsobuje špatné výsledky modelu
15. Graficky znázorněné výsledky měření
16. Výpočet základních statistických údajů o atributech
17. Vypočtené výsledky a identifikace problémových atributů
18. Výsledky získané po normalizaci hodnot
19. Repositář s demonstračními příklady
1. Balíček scikit-learn: trénink a předpovědi modelů provádějících regresní analýzu
V dnešním článku o nástroji scikit-learn úzce navážeme na předchozí část. Dnes totiž dokončíme popis problematiky modelů provádějících regresní analýzu, což jsou modely odlišné od modelů provádějících klasifikaci. Nejdříve si ukážeme, jakým způsobem je možné tyto modely natrénovat. Poté si řekneme, jakým způsobem lze zjistit, které atributy způsobují špatné předpovědi modelu i to, jak detekovat ty atributy, které způsobují nestabilitu předpovědí. Jak je v tomto seriálu zvykem, použijeme namísto čistě teoretického popisu množství demonstračních příkladů. Na tento článek posléze navážeme, protože při výběru modelů a nastavování jejich hyperparametrů je většinou nutné ověřit, který model (a parametry) jsou nejlepší. K tomuto účelu se používá takzvaná křížová validace (cross-validaton nebo též jen crossvalidation).
2. Polynomická regrese nad údaji o souřadnicích bloků
Na předchozí článek o modelech provádějících regresní analýzu dnes navážeme. Nejprve si ukážeme, jakým způsobem lze proložit informace o souřadnicích obytných bloků úsečkou nebo nějakým polynomem. Jedná se o postupný přechod ke skutečnému tréninku modelu. Povšimněte si, že hodnoty je potřeba seřadit podle hodnot zobrazených na x-ové ose, protože jinak by docházelo k problémům při zobrazení pospojovaných vrcholů v korelačním diagramu:
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# serazeni dat (pro pekne grafy)
data = data[data[:,6].argsort()]
FIRST_DIM = 6
SECOND_DIM = 7
x = data[:, FIRST_DIM]
y = data[:, SECOND_DIM]
for degree in range(1, 11):
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(x.reshape(-1, 1))
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=1)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title(f"Degree={degree}")
# osy
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig(f"84_{degree}.png")
# zobrazeni diagramu
plt.show()
Výsledné proložení bude vypadat následovně:
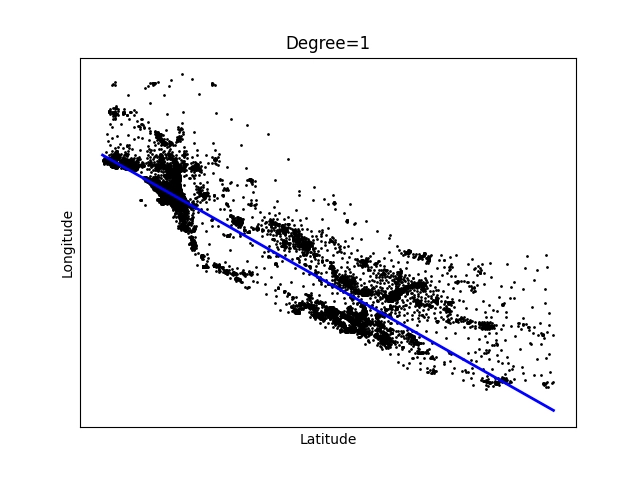
Obrázek 1: Polynom stupně 1 – úsečka.
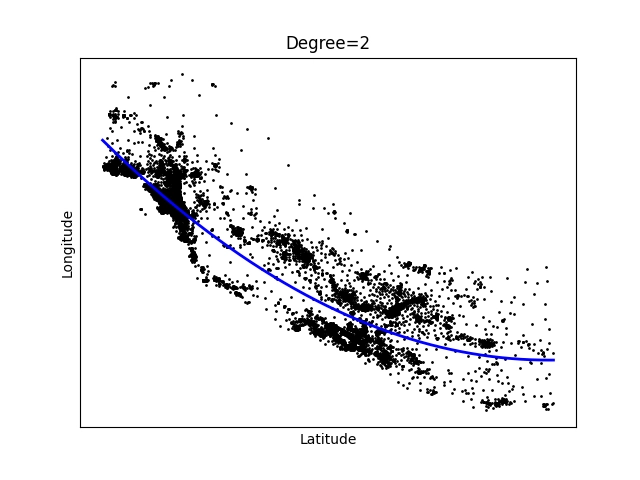
Obrázek 2: Polynom stupně 2.
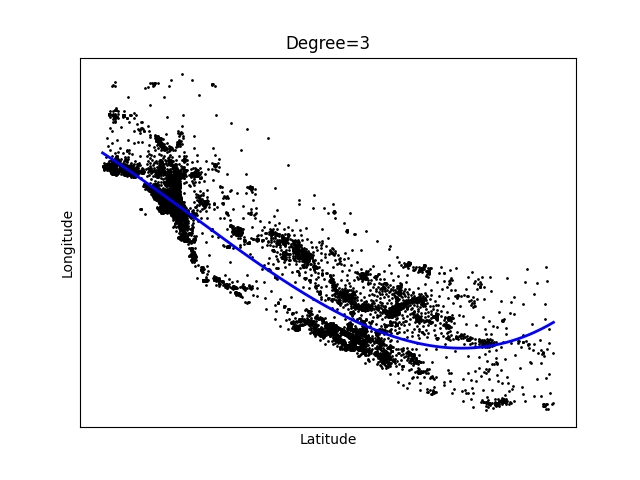
Obrázek 3: Polynom stupně 3.
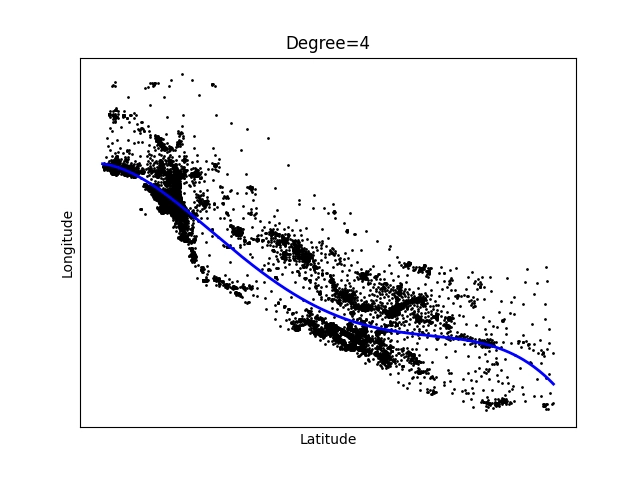
Obrázek 4: Polynom stupně 4.
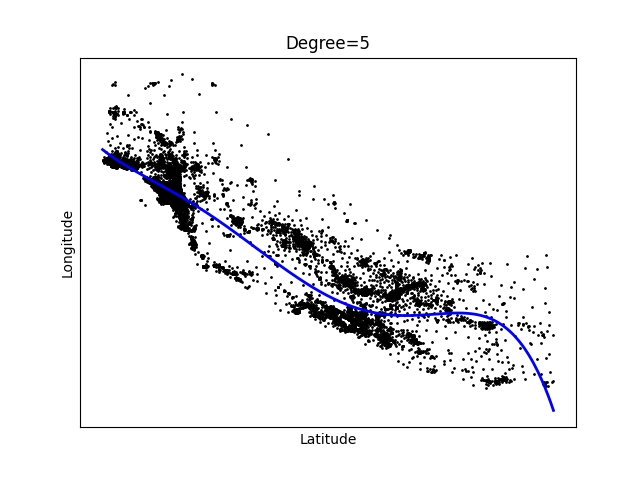
Obrázek 5: Polynom stupně 5.
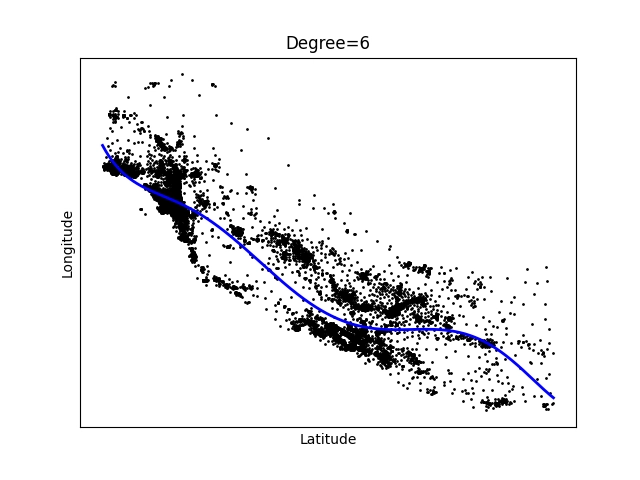
Obrázek 6: Polynom stupně 6.
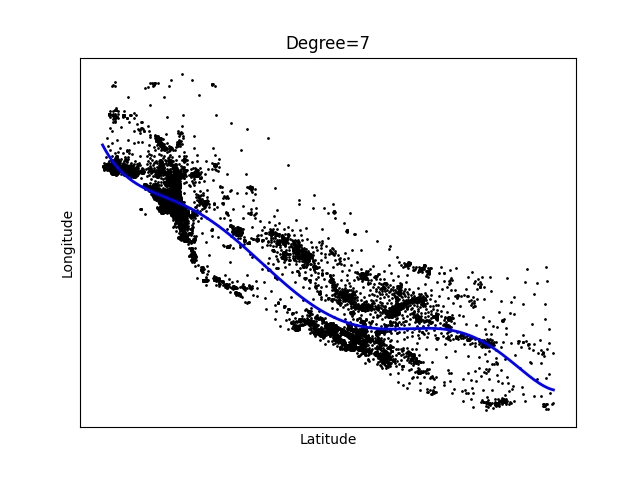
Obrázek 7: Polynom stupně 7.
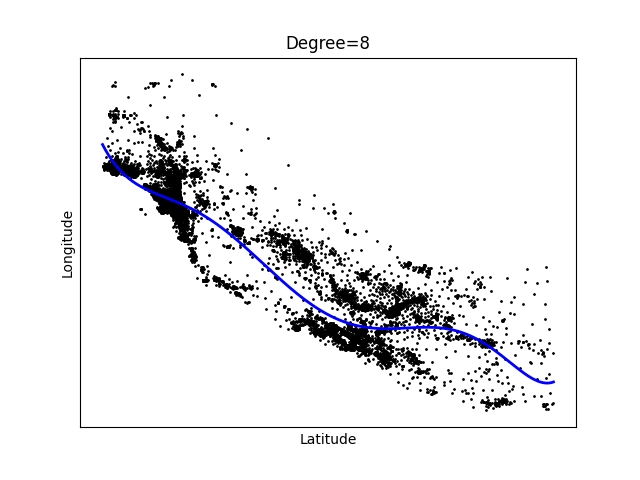
Obrázek 8: Polynom stupně 8.
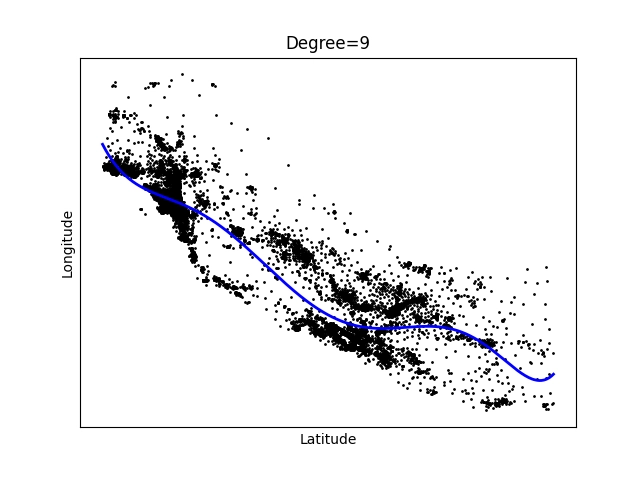
Obrázek 9: Polynom stupně 9.
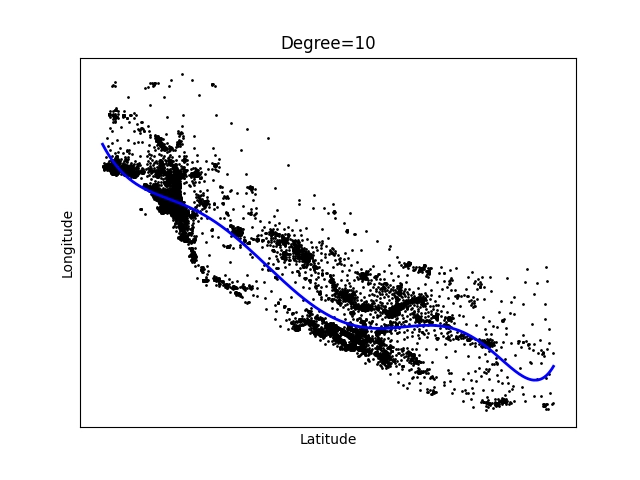
Obrázek 10: Polynom stupně 10.
3. Polynomická regrese s údaji, v nichž se vyskytují extrémní hodnoty
Pokusme se nyní demonstrační příklad z úvodní kapitoly nepatrně poupravit, a to tak, že budeme polynomem n-tého stupně prokládat body představující vztah mezi počtem místností v bloku a počtem ložnic. Zdánlivě se jedná o triviální úlohu, ovšem (jak ještě uvidíme dále), mají některé bloky významně větší množství místností, než většina ostatních bloků a proto máme pro tyto extrémní případy jen malé množství hodnot. Výsledky nebudou dokonalé, o čemž se lze velmi snadno přesvědčit:
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# serazeni dat (pro pekne grafy)
data = data[data[:,2].argsort()]
FIRST_DIM = 2
SECOND_DIM = 3
x = data[:, FIRST_DIM]
y = data[:, SECOND_DIM]
for degree in range(1, 11):
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(x.reshape(-1, 1))
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=1)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title(f"Degree={degree}")
# osy
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig(f"84_{degree}.png")
# zobrazeni diagramu
plt.show()
A takto vypadají vypočtené výsledky. Je z nich patrné, že pro oblast v pravém horním rohu máme k dispozici tak málo hodnot, že proložení nebude příliš úspěšné:
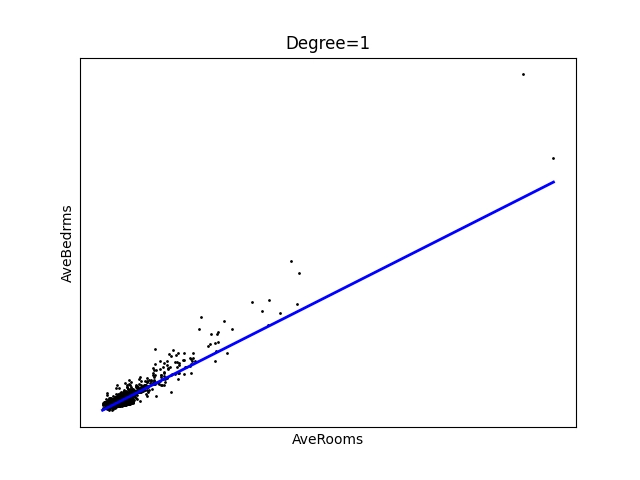
Obrázek 11: Polynom stupně 1 – úsečka.
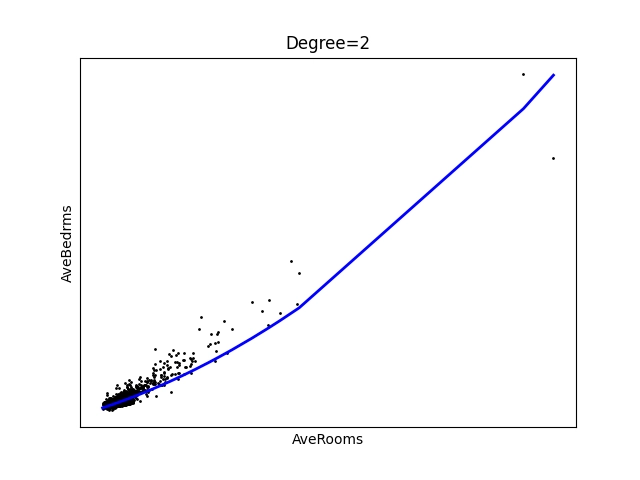
Obrázek 12: Polynom stupně 2.
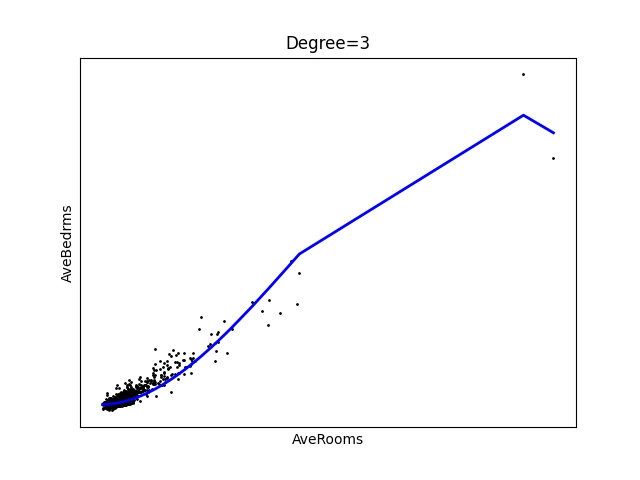
Obrázek 13: Polynom stupně 3.
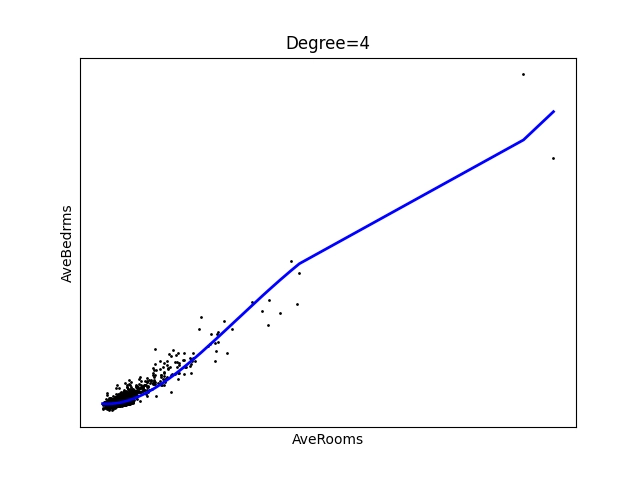
Obrázek 14: Polynom stupně 4.
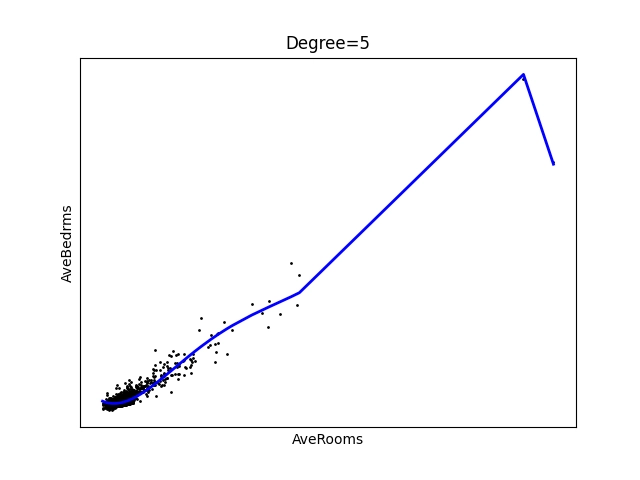
Obrázek 15: Polynom stupně 5.
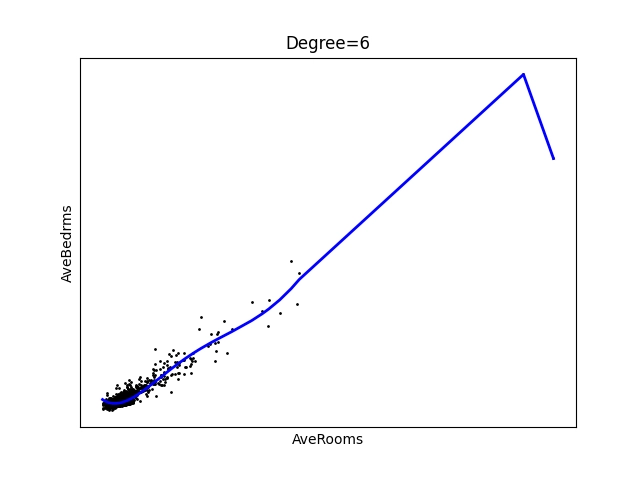
Obrázek 16: Polynom stupně 6.
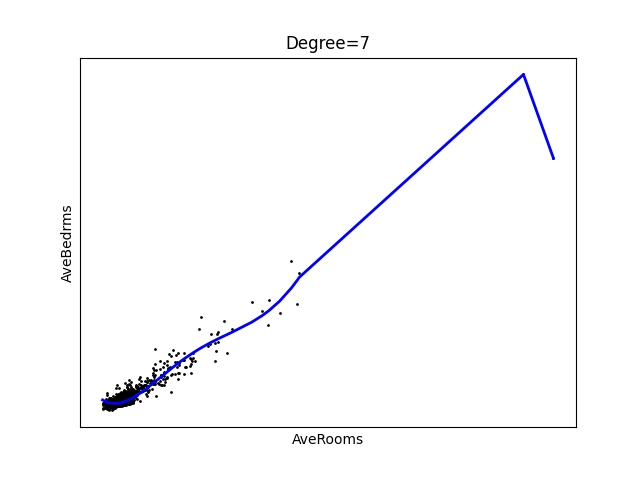
Obrázek 17: Polynom stupně 7.
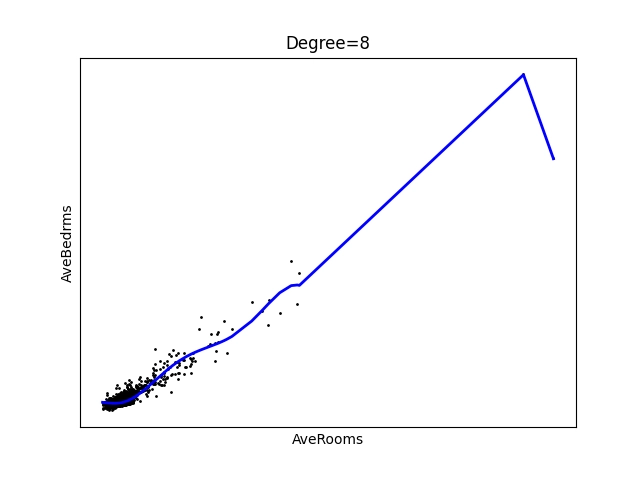
Obrázek 18: Polynom stupně 8.
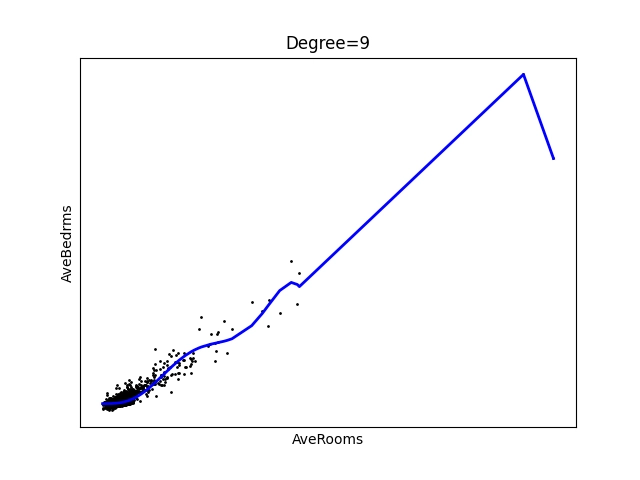
Obrázek 19: Polynom stupně 9.
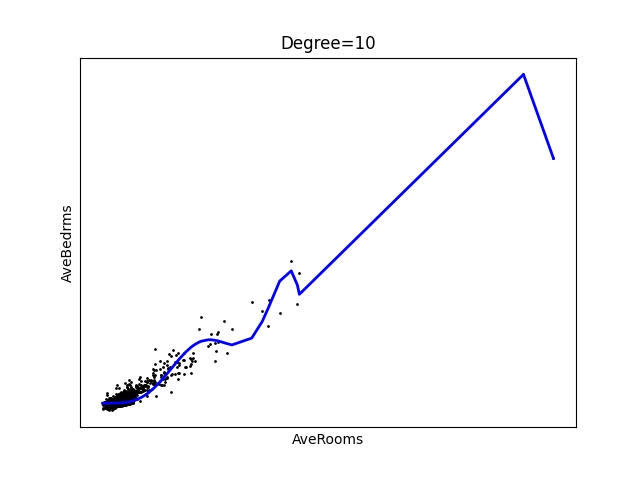
Obrázek 20: Polynom stupně 10.
4. Preprocessing a filtering dat: odstranění mezních případů
V některých případech, což může být konkrétně právě problém s hodnotami místností (a ložnic) v obytných blocích, může být výhodné provést nějakou formu preprocessingu a filteringu dat. Pomoci nám může přímo nástroj scikit-learn, ovšem pokusme se o filtering sami. Bude to prozatím velmi jednoduché, protože odstraníme 30 posledních hodnot (po jejich seřazení), což právě představuje ony mezní případy. Otázkou zůstává, jestli je zvolená hodnota 30 ideální, příliš malá nebo naopak příliš velká. To nám do určité míry napoví grafy:
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import fetch_california_housing
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# serazeni dat (pro pekne grafy)
data = data[data[:,2].argsort()]
data = data[:-30]
FIRST_DIM = 2
SECOND_DIM = 3
x = data[:, FIRST_DIM]
y = data[:, SECOND_DIM]
for degree in range(1, 11):
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(x.reshape(-1, 1))
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=1)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title(f"Degree={degree}")
# osy
plt.xlabel(housings.feature_names[FIRST_DIM])
plt.ylabel(housings.feature_names[SECOND_DIM])
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig(f"84_{degree}.png")
# zobrazeni diagramu
plt.show()
Opět se podíváme na výsledné grafy. Z nich jsou patrné dvě věci – korelace v tomto případě není tak zřejmá, jako tomu bylo v úvodní kapitole a odstranění mezních hodnot skutečně částečně pomohlo:
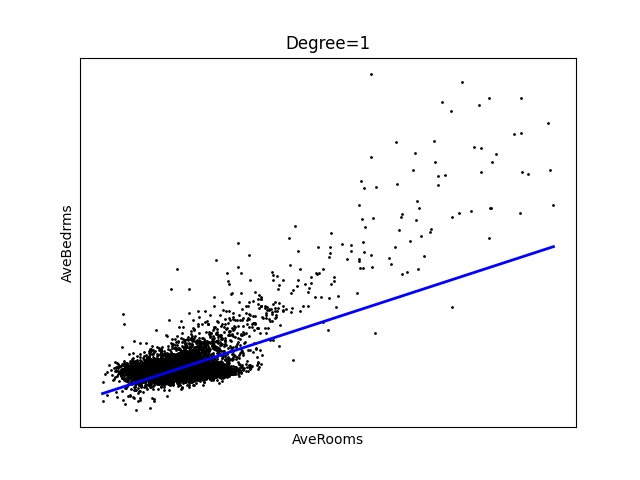
Obrázek 21: Polynom stupně 1 – úsečka.
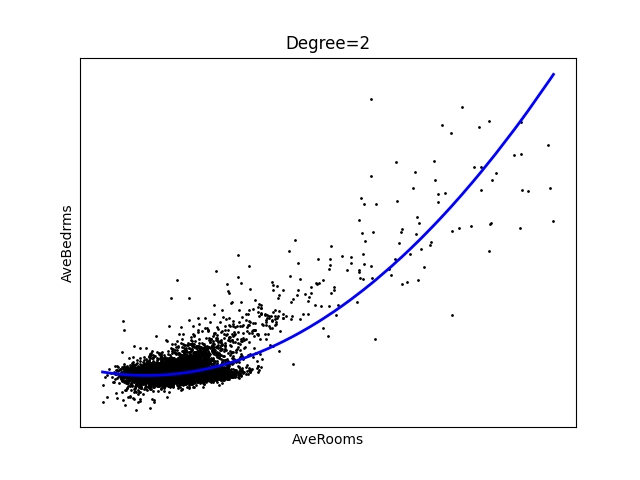
Obrázek 22: Polynom stupně 2.
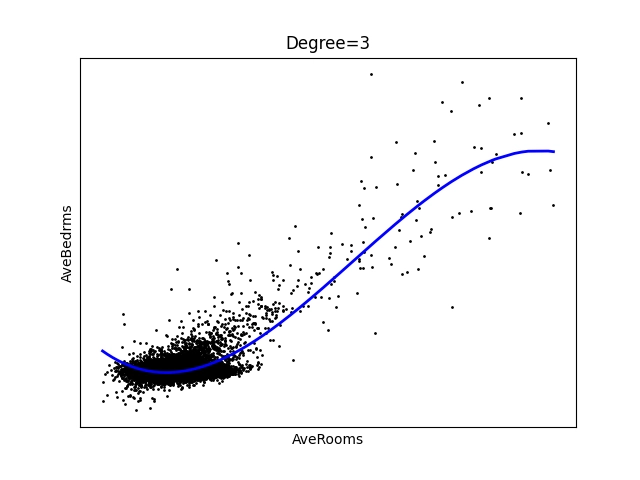
Obrázek 23: Polynom stupně 3.
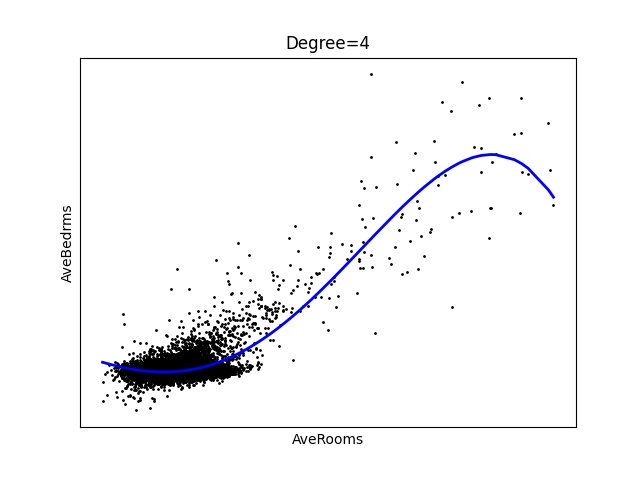
Obrázek 24: Polynom stupně 4.
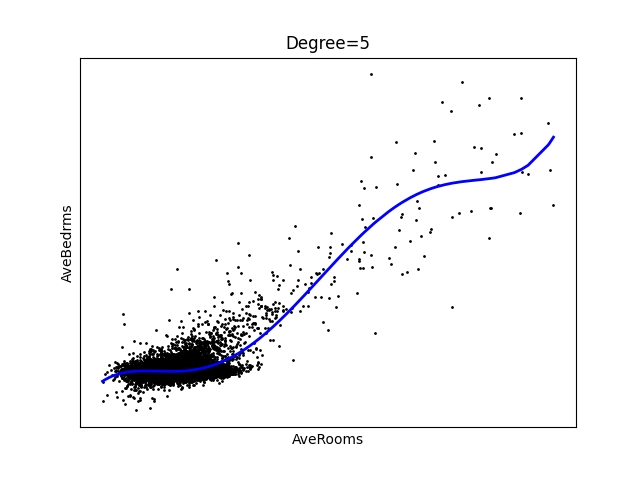
Obrázek 25: Polynom stupně 5.
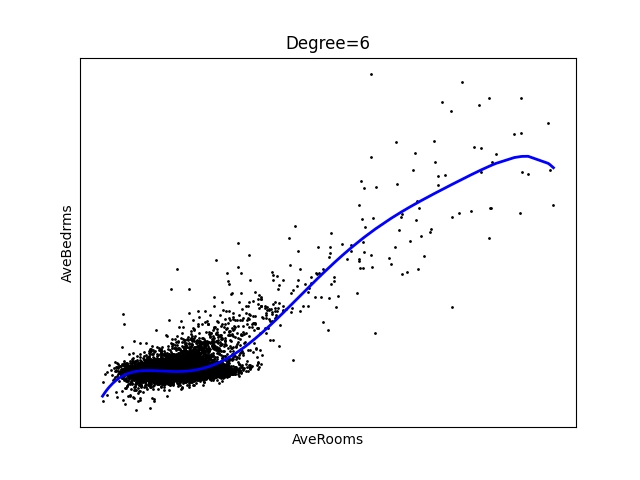
Obrázek 26: Polynom stupně 6.
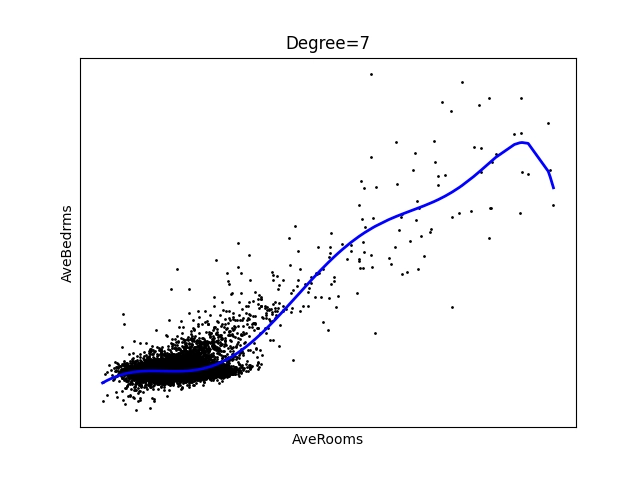
Obrázek 27: Polynom stupně 7.
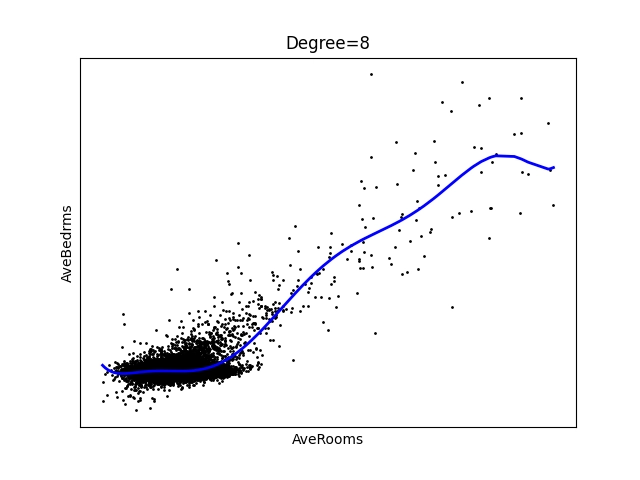
Obrázek 28: Polynom stupně 8.
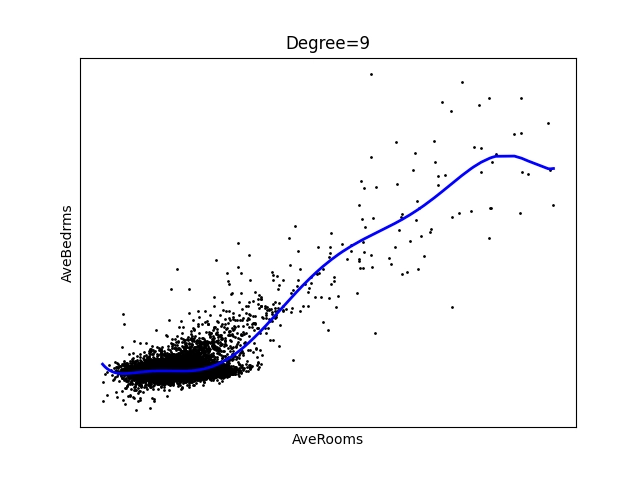
Obrázek 29: Polynom stupně 9.
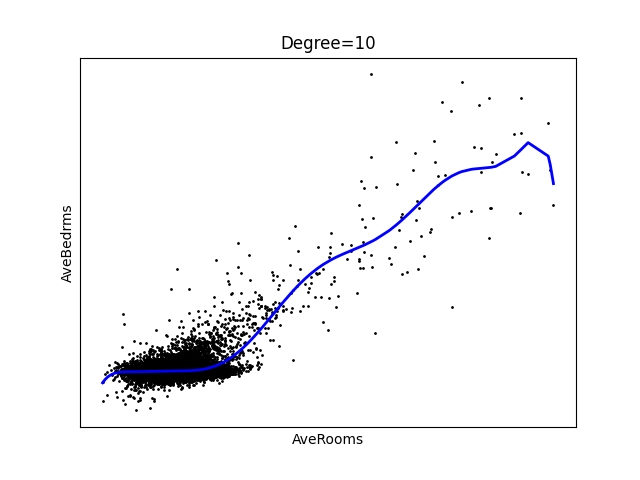
Obrázek 30: Polynom stupně 10.
5. Trénink modelu provádějícího regresní analýzu
Nyní se konečně dostáváme k ústřední části dnešního článku, a to konkrétně k tomu, jakým způsobem lze natrénovat model provádějící regresní analýzu a jak lze zjistit, které atributy jsou pro tento účel vhodné a které naopak nikoli (prakticky vždy je nutné experimentovat a vybrat nějakou rozumnou „střední cestu“). Přípravu na trénink modelu již dobře známe – postačí si připravit n-rozměrné pole s atributy a jednorozměrný vektor s očekávanými výsledky, což je v našem případě cena domů. Tyto údaje jsou dostupné v původní datové sadě, takže:
# nacteni datove sady housings = fetch_california_housing() # precteni dat z datove sady # urcenych pro trenink, validaci atd. data = housings["data"] # ceny bloku targets = housings["target"]
Jak je zvykem, pojmenujeme matici s atributy X (velké písmeno) a vektor s očekávanými výsledky se bude jmenovat y (malé písmeno):
# trening bude proveden se VSEMI zaznamy # testovani taktez (prozatim) X = data y = targets
V posledním kroku model natrénujeme a využijeme (alespoň nyní) všechna dostupná data:
# konstrukce modelu lr = linear_model.LinearRegression() # trénink modelu lr.fit(X, y)
6. Ukázka natrénování a predikce modelu s využitím všech dostupných údajů
Jak bude vypadat predikce takového modelu, jeho MSE (Mean Squared Error) a vypočtené skóre? To zjistíme velmi snadno, protože již tyto kroky známe:
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# trening bude proveden se VSEMI zaznamy
# testovani taktez (prozatim)
X = data
y = targets
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y, y_pred))
Výsledky budou vypadat následovně:
Coefficients: [ 4.36693293e-01 9.43577803e-03 -1.07322041e-01 6.45065694e-01 -3.97638942e-06 -3.78654265e-03 -4.21314378e-01 -4.34513755e-01] Intercept: -36.94192020718441 Mean squared error: 0.52 Coefficient of determination: 0.61
Jak tyto výsledky interpretovat?
- Koeficientů je osm, což je korektní, protože se zpracovává osm atributů a model při tréninku našel osm reálných koeficientů, které mu umožnily proložit všemi atributy vhodný „lineární objekt“ s minimálním MSE (v tomto případě jde vlastně o hyperrovinu v osmidimenzionálním prostoru!).
- Posun je roven přibližně –37 jednotkám, takže ona hyperrovina je posunuta (což je ovšem při více rozměrech matoucí, proto je dobré si vynutit vycentrování při tréninku).
- Skóre je relativně dobré, ale už vzdálenější od ideální hodnoty 1.0. To znamená, že závislost, kterou jsme se snažili zjistit, není ve skutečnosti čistě lineární, popř. menší přesnost způsobuje nějaký „nelineární“ atribut.
7. Rozdělení dat na tréninkovou a testovací část
Jak již dobře víme, musí být korektní trénink modelu prováděn pouze s částí dat, přičemž zbylá část bude použita pro otestování, jak dobře či špatně byl model natrénován. Celý postup opět dobře známe, takže jen krátce – pro rozdělení dat použijeme funkci train_test_split, které určíme, kolik údajů (relativně) se má použít pro testování; zbytek bude pochopitelně použit pro trénink:
from sklearn.model_selection import train_test_split
Samotné rozdělení dat je snadné:
# rozdeleni dat na treninkovou a testovaci mnozinu X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
Konkrétní rozměry polí pro trénink a testování:
print("Array sizes:")
print(f"x_train: {len(X_train)}")
print(f"y_train: {len(y_train)}")
print(f"x_test: {len(X_test)}")
print(f"y_test: {len(y_test)}")
Výsledky:
Array sizes: x_train: 8256 y_train: 8256 x_test: 12384 y_test: 12384
8. Ukázka natrénování a predikce modelu po rozdělení dat
Opět se podívejme, jak dopadne natrénování a následné otestování predikce modelu ve chvíli, kdy data rozdělíme na trénovací a testovací část:
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# X je matice, y je vektor
X = data
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
Výsledky budou v tomto případě nepatrně horší, což je však očekávané, protože nyní model neměl při tréninku k dispozici všechny údaje a naopak při testování dostával k ohodnocení dříve neznámé záznamy:
Coefficients: [ 4.44247517e-01 9.78922329e-03 -1.10983616e-01 5.92399058e-01 -1.66083700e-06 -4.66414487e-03 -4.10094011e-01 -4.23896551e-01] Intercept: -36.03496303337858 Mean squared error: 0.53 Coefficient of determination: 0.60
9. Trénink modelu s vyloučením určitého atributu nebo atributů
Datová sada California housings obsahuje celkem osm atributů, zvaných taktéž proměnné (oboje označení je v kontextu IT poněkud matoucí):
- MedInc median income in block group
- HouseAge median house age in block group
- AveRooms average number of rooms per household
- AveBedrms average number of bedrooms per household
- Population block group population
- AveOccup average number of household members
- Latitude block group latitude
- Longitude block group longitude
Při tréninku interně tak jednoduchého modelu, jakým je i model pro lineární regresi, se může stát, že nějaký atribut ve skutečnosti předpovědi (a tím pádem i skóre) modelu zhorší, protože pro n atributů celé „naučení modelu“ spočívá v nalezení osmi reálných hodnot. To může být málo pro atribut či atributy, které jsou náhodné či do značné míry nelineární. A právě z tohoto důvodu se můžeme pokusit o odstranění těchto atributů z procesu učení. Z n-rozměrného pole odstraníme n-tý sloupec následovně:
# ceny bloku targets = housings["target"] X = np.delete(data, n, axis=1) # smazat jeden sloupec
kde za n dosadíme index příslušeného sloupce nebo vektor indexů sloupců.
10. Ukázka natrénování a predikce modelu po rozdělení dat a odstranění zvoleného atributu
Opět si vyzkoušejme, jak dobře či špatně bude model natrénován, pokud z procesu učení nějaký atribut odstraníme. Zde se konkrétně bude jednat o první sloupec s indexem 0:
import numpy as np
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# X je matice, y je vektor
X = np.delete(data, 0, axis=1) # smazat jeden sloupec
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
Výsledky ukazují, že v tomto konkrétním případě jsme situaci značně zhoršili, protože se zvýšila MSE a snížilo skóre!:
Coefficients: [ 5.37611342e-03 3.58845604e-01 -1.37584051e+00 2.14637514e-05 -1.67202994e-01 -7.42206013e-01 -7.27320486e-01] Intercept: -58.5715835183449 Mean squared error: 5.73 Coefficient of determination: -3.34
11. Který atribut či atributy odstranit?
Jak ale zjistíme, který atribut nebo dokonce které atributy je vhodné z datové sady odstranit, aby model predikoval lepší výsledky? Můžeme se například pokusit postupně odstraňovat všechny kombinace atributů a zjišťovat výsledek tréninku modelu atd. A nebo ještě lépe – můžeme použít takzvanou crossvalidaci, což je velmi důležité téma, kterému bude věnován navazující článek. Prozatím si ovšem ukažme velmi jednoduchý přístup, v němž vždy odstraníme jediný atribut (sloupec) a následně provedeme trénink a testování modelu:
# nacteni datove sady
housings = fetch_california_housing()
# jmena promennych/atributu
names = housings["feature_names"]
for column_to_delete in range(len(names)):
# X je matice, y je vektor
X = np.delete(data, column_to_delete, axis=1) # smazat jeden vybrany sloupec
y = targets
...
...
...
následuje běžný trénink modelu, jeho otestování a zjištění MSE a skóre
...
...
...
12. Skript, který odstraní vybraný atribut a poté provede otestování modelu s vyjádřením skóre
Úplný skript, jenž vždy z datové sady odstraní jeden z atributů (tedy celý sloupec) a následně provede trénink i otestování modelu, může vypadat následovně (ideální bude skript rozšířit tak, aby dokázal pracovat i s kombinacemi atributů):
import numpy as np
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# jmena promennych/atributu
names = housings["feature_names"]
print("Ignored attribute\tMSE\tr2 score")
for column_to_delete in range(len(names)):
# X je matice, y je vektor
X = np.delete(data, column_to_delete, axis=1) # smazat jeden vybrany sloupec
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
#print("Coefficients: \n", lr.coef_)
#print("Intercept: \n", lr.intercept_)
column = names[column_to_delete]
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
print(f"{column:16}\t{mse:0.3f}\t{score:0.3f}")
Výsledky mohou vypadat takto:
Ignored attribute MSE r2 score MedInc 0.805 0.392 HouseAge 0.535 0.601 AveRooms 0.536 0.596 AveBedrms 0.541 0.598 Population 0.525 0.605 AveOccup 0.539 0.596 Latitude 0.617 0.535 Longitude 0.619 0.538
13. Chování modelu při opakovaném tréninku s náhodně vybranými daty
Připomeňme si, že náš model natrénovaný nad osmi atributy, měl MSE rovno 0,53 a skóre 0,6:
Mean squared error: 0.53 Coefficient of determination: 0.60
To jsou relativně dobré hodnoty, ovšem bude chování modelu konzistentní i ve chvíli, kdy budeme trénink opakovat? Vyzkoušejme si to – provedeme celkem 200 natrénování modelu s opakovaným testováním, přičemž víme, že funkce train_test_split vybírá data pro trénink a testování náhodně:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# jmena promennych/atributu
names = housings["feature_names"]
print("MSE\tr2 score")
# X je matice, y je vektor
X = data
y = targets
mses = []
r2_scores = []
MEASUREMENTS = 200
for i in range(MEASUREMENTS):
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
#print("Coefficients: \n", lr.coef_)
#print("Intercept: \n", lr.intercept_)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mses.append(mse)
r2_scores.append(r2)
print(f"{mse:0.3f}\t{r2:0.3f}")
plt.plot(range(MEASUREMENTS), mses, range(MEASUREMENTS), r2_scores)
# titulek grafu
plt.title(f"Mode prediction")
plt.legend(["MSE", "R2 score"])
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig(f"93.png")
# zobrazeni diagramu
plt.show()
Numerické výsledky naznačují, že v některých případech má model výrazně menší skóre:
MSE r2 score 0.520 0.605 0.525 0.605 0.527 0.601 0.523 0.608 0.520 0.610 0.549 0.594 0.594 0.552 0.527 0.604 0.537 0.599 0.538 0.600 0.533 0.597 1.381 -0.038 0.527 0.600 0.530 0.606 0.533 0.598 0.530 0.604 0.533 0.607 0.536 0.605 0.532 0.602 0.530 0.605 0.527 0.598 0.510 0.613 0.538 0.589 0.523 0.605 0.520 0.606 0.521 0.606 0.525 0.597 0.518 0.609 0.528 0.599 0.524 0.601 0.529 0.601 2.998 -1.306 0.535 0.602 0.531 0.604 0.529 0.605 0.524 0.603 0.518 0.616 0.539 0.599 0.623 0.541 0.525 0.608 0.532 0.599 0.525 0.605 0.541 0.599 0.524 0.603 0.526 0.604 1.898 -0.411 0.527 0.605 0.630 0.523 0.526 0.606 0.526 0.603 0.524 0.610 0.630 0.531 3.950 -1.943 0.648 0.514 5.817 -3.349 0.520 0.611 0.525 0.605 0.592 0.554 0.545 0.595 0.530 0.605 1.694 -0.262 0.526 0.605 0.545 0.596 0.525 0.601 0.614 0.544 0.522 0.608 0.521 0.607 0.535 0.596 2.867 -1.131 3.662 -1.777 0.524 0.609 0.533 0.602 0.530 0.604 0.533 0.593 0.532 0.602 0.593 0.551 0.651 0.510 0.643 0.516 0.544 0.593 3.178 -1.413 0.639 0.517 0.529 0.600 0.530 0.605 0.533 0.602 0.532 0.604 0.522 0.607 0.521 0.603 0.521 0.609 0.532 0.599 0.525 0.604 0.529 0.601 0.540 0.596 0.521 0.602 0.525 0.604 0.603 0.551 0.519 0.607 0.620 0.531 0.524 0.605 0.522 0.612 0.510 0.611 0.521 0.610 0.611 0.542 0.528 0.604 0.611 0.541 0.519 0.614 0.522 0.609 2.062 -0.532 2.612 -0.950 0.529 0.599 0.527 0.608 0.521 0.613 0.531 0.603 0.525 0.607 0.539 0.594 0.535 0.595 2.300 -0.719 0.528 0.605 0.526 0.605 0.529 0.603 0.520 0.612 0.522 0.608 0.524 0.607 1.792 -0.355 0.531 0.602 0.612 0.537 0.514 0.614 0.529 0.604 0.529 0.599 0.526 0.602 0.612 0.545 4.819 -2.612 0.520 0.611 0.524 0.607 14.495 -9.852 0.519 0.606 0.527 0.604 0.531 0.601 0.527 0.607 0.526 0.602 0.524 0.603 13.456 -9.121 0.624 0.532 0.532 0.598 10.395 -6.754 3.510 -1.613 0.533 0.592 0.531 0.601 0.527 0.605 4.240 -2.155 0.524 0.602 0.522 0.604 0.526 0.609 2.633 -0.987 0.517 0.615 0.647 0.515 2.295 -0.715 0.610 0.548 0.530 0.599 0.628 0.531 0.527 0.607 0.531 0.602 0.524 0.602 0.530 0.603 0.536 0.603 0.520 0.614 0.523 0.609 0.622 0.539 0.521 0.604 0.533 0.604 0.548 0.595 0.538 0.595 9.867 -6.412 0.533 0.600 0.528 0.596 0.528 0.604 0.535 0.601 3.044 -1.312 0.629 0.525 2.402 -0.823 0.520 0.608 0.531 0.603 0.532 0.605 0.514 0.608 0.522 0.602 3.210 -1.418 2.814 -1.115 0.527 0.604 0.526 0.602 0.532 0.596 0.510 0.612 0.524 0.605 2.094 -0.579 0.520 0.604 0.534 0.596 0.526 0.610 1.825 -0.353 0.523 0.604 0.536 0.598 0.539 0.600 0.521 0.608
Ještě více je tento problém patrný při grafickém znázornění chyby (MSE) i skóre:
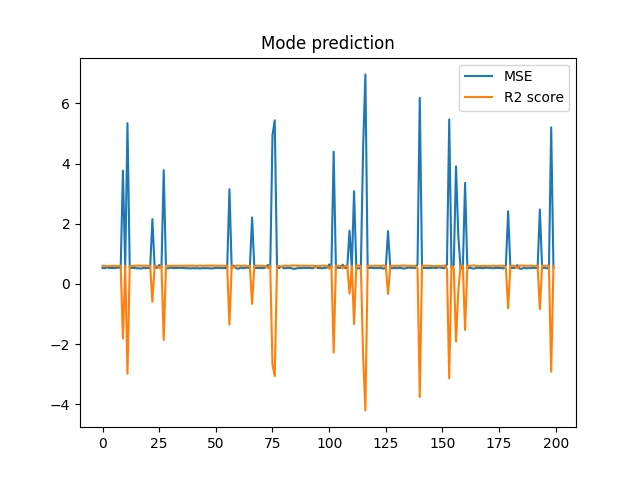
Obrázek 31: V některých případech má model výrazně horší skóre.
14. Zjištění, který atribut způsobuje špatné výsledky modelu
Předchozí demonstrační skript nyní upravíme, a to takovým způsobem, že postupně vždy odstraníme jeden z atributů a následně provedeme opakovaný trénink a následné otestování modelu. V případě, že bude odstraněn onen hledaný „problémový“ atribut, projeví se to tak, že graf s MSE a skóre modelu bude obsahovat průběh bez nežádoucích výchylek (jedná se o výchylky špatným směrem, tedy k vyšší MSE a nižšímu skóre):
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# jmena promennych/atributu
names = housings["feature_names"]
print("Ignored attribute\tMSE\tr2 score")
MEASUREMENTS = 200
for column_to_delete in range(len(names)):
# X je matice, y je vektor
X = np.delete(data, column_to_delete, axis=1) # smazat jeden vybrany sloupec
y = targets
column = names[column_to_delete]
mses = []
r2_scores = []
for i in range(MEASUREMENTS):
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
#print("Coefficients: \n", lr.coef_)
#print("Intercept: \n", lr.intercept_)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mses.append(mse)
r2_scores.append(r2)
print(f"{column:16}\t{mse:0.3f}\t{r2:0.3f}")
plt.plot(range(MEASUREMENTS), mses, range(MEASUREMENTS), r2_scores)
# titulek grafu
plt.title(f"Mode prediction without column {column}")
plt.legend(["MSE", "R2 score"])
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig(f"94_{column}.png")
# zobrazeni diagramu
plt.show()
15. Graficky znázorněné výsledky měření
Podívejme se nejprve na graficky znázorněné výsledky měření; poté se je pokusíme nějakým způsobem interpretovat:
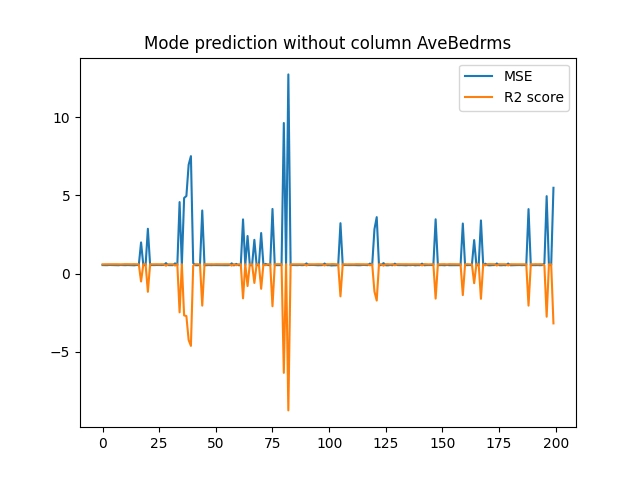
Obrázek 31: Výsledky měření při vyloučení atributu „AveBedrms“.
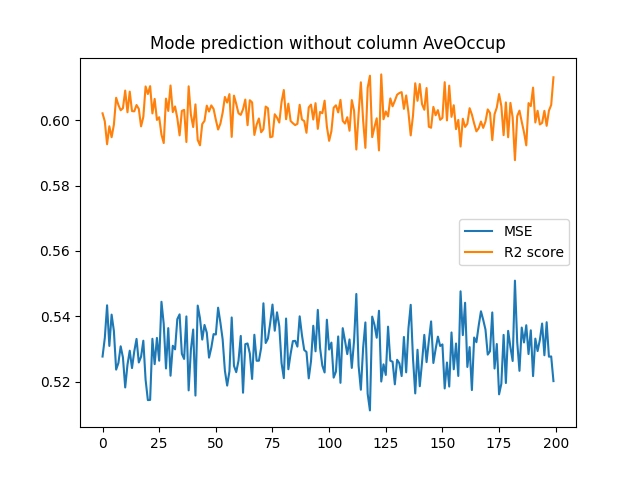
Obrázek 32: Výsledky měření při vyloučení atributu „AveOccup“.
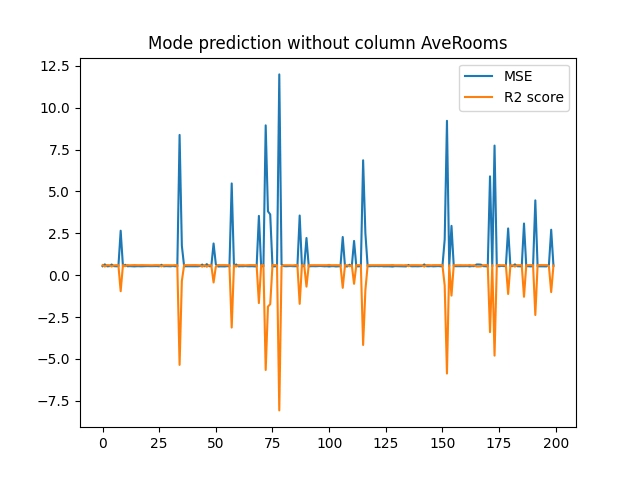
Obrázek 33: Výsledky měření při vyloučení atributu „AveRooms“.
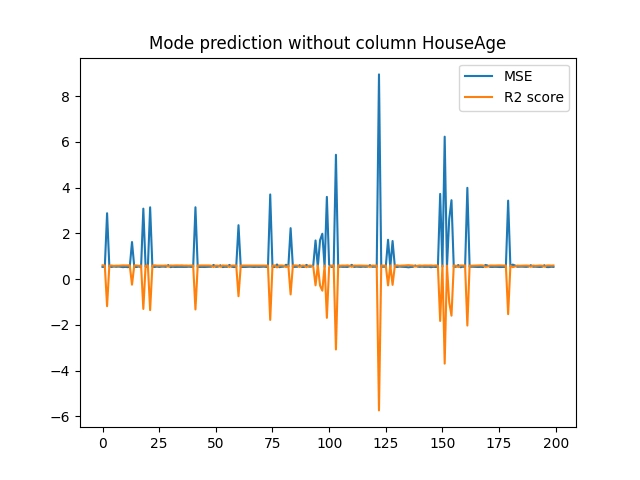
Obrázek 34: Výsledky měření při vyloučení atributu „HouseAge“.
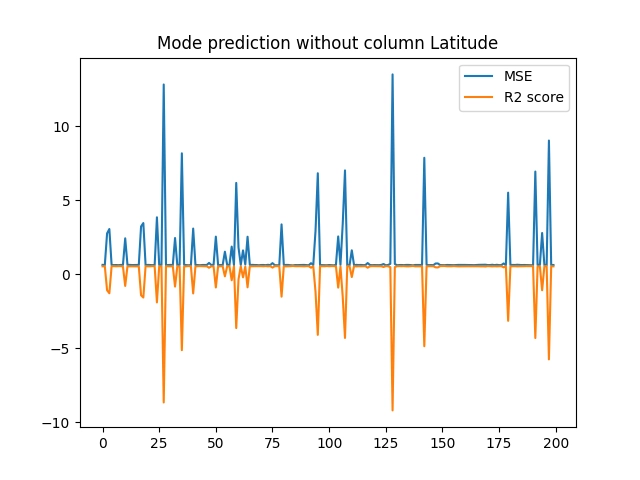
Obrázek 35: Výsledky měření při vyloučení atributu „Latitude“.
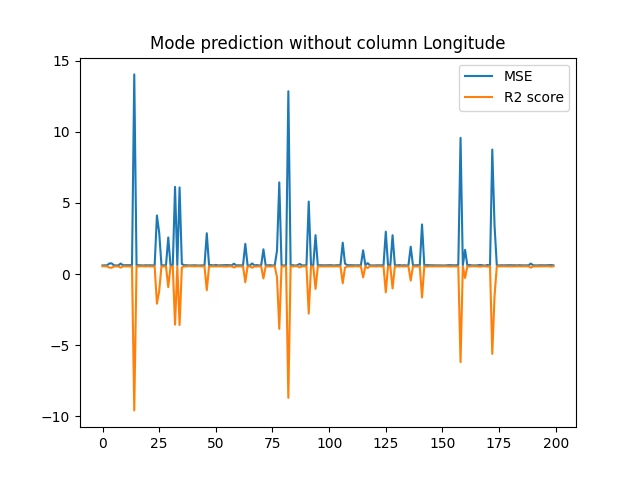
Obrázek 36: Výsledky měření při vyloučení atributu „Longitude“.
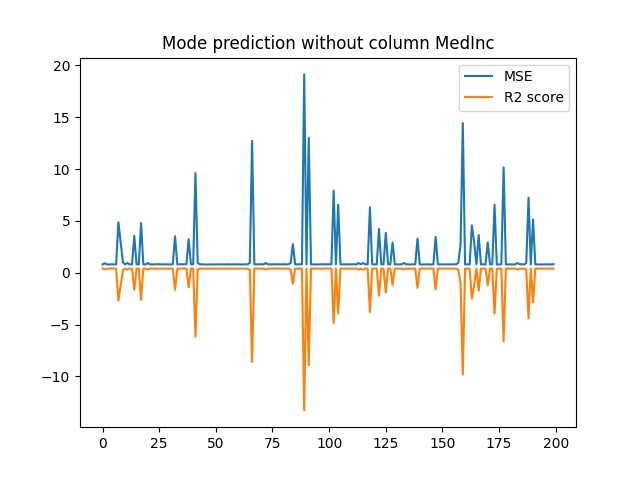
Obrázek 37: Výsledky měření při vyloučení atributu „MedInc“.
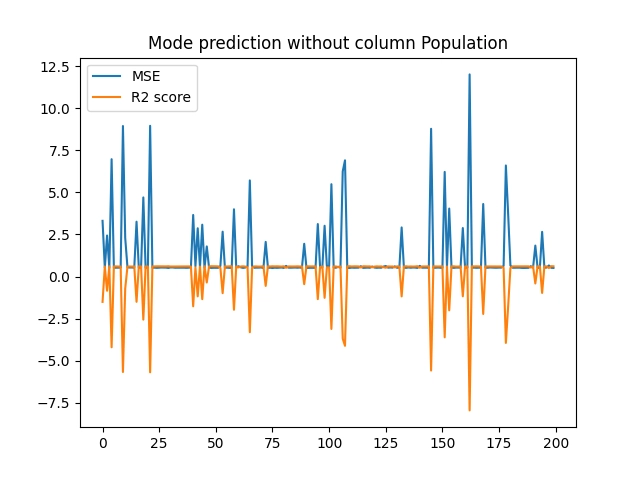
Obrázek 38: Výsledky měření při vyloučení atributu „Population“.
Ze zobrazených výsledků je patrné, že po odstranění atributu „AveOccup“ se již při tréninku modelu nebudou uplatňovat náhodné velké chyby. Zdá se tedy, že právě tento atribut je vhodné z datové sady odstranit, resp. přesněji řečeno ho nepoužívat při tréninku modelu. A nutno říci, že máme štěstí – odstranit je nutné jen jediný atribut, přičemž se nemusíme zabývat jejich kombinacemi.
16. Výpočet základních statistických údajů o atributech
Pokusme se o zobrazení histogramu pro jednotlivé atributy (resp. přesněji řečeno pro jejich hodnoty). Každý atribut je představován vektorem 26000 hodnot, takže je to snadné:
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# vykresleni sady histogramu do mrizky
fig, axes = plt.subplots(nrows=4, ncols=2)
fig.set_figheight(15)
fig.set_figwidth(15)
# vykresleni jednotlivych histogramu do mrizky
for i in range(8):
column = data[:, i]
feature = housings.feature_names[i]
ax = axes[i//2][i%2]
# modifikace zpusobu vypoctu a zobrazeni histogrami
ax.hist(column, bins=100, histtype="step")
ax.set(xlabel=feature)
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("95.png")
# zobrazeni diagramu
plt.show()
Výsledky:
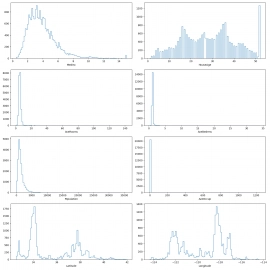
Obrázek 39: Histogramy pro všechny atributy z datové sady.
Alternativně si můžeme pro jednotlivé atributy vypočítat základní statistické údaje, zejména minimum, maximum, průměr a směrodatnou odchylku. Tyto údaje nám naznačí, které atributy budou při tréninku modelu „problémové“. Výpočet je snadný, protože potřebné metody a funkce nám poskytuje přímo knihovna Numpy:
import numpy as np
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
data = housings["data"]
print("Feature Min Max Avg Std")
for i in range(8):
column = data[:, i]
feature = housings.feature_names[i]
print(f"{feature:12} {column.min():10.3f} {column.max():10.3f} {np.mean(column):10.3f} {np.std(column):10.3f}")
17. Vypočtené výsledky a identifikace problémových atributů
Nyní se podívejme na výsledky získané po spuštění předchozího skriptu. Zejména nás bude zajímat údaj o směrodatné odchylce, který je nejvyšší pro atribut Population. Navíc pouze jen několik bloků má velmi vysokou hodnotu AveOccup, což znamená, že právě tento atribut může způsobit to, že model bude natrénován na jiné parametry lineární regrese a bude v některých případech velmi chybový (což uvidíme po normalizaci):
Feature Min Max Avg Std MedInc 0.500 15.000 3.871 1.900 HouseAge 1.000 52.000 28.639 12.585 AveRooms 0.846 141.909 5.429 2.474 AveBedrms 0.333 34.067 1.097 0.474 Population 3.000 35682.000 1425.477 1132.435 AveOccup 0.692 1243.333 3.071 10.386 Latitude 32.540 41.950 35.632 2.136 Longitude -124.350 -114.310 -119.570 2.003
18. Výsledky získané po normalizaci hodnot
Jednotlivé hodnoty z předchozí tabulky samozřejmě není možné přímo porovnávat, protože každý atribut je reprezentován v odlišných jednotkách a má i jiná měřítka. Porovnávání by bylo možné pouze po normalizaci hodnot v jednotlivých sloupcích, takže si ji proveďme, a to opět s využitím funkcí a tříd nabízených knihovnou Scikit-learn, zde konkrétně pomocí třídy MinMaxScaler:
import numpy as np
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from sklearn import preprocessing as pre
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
data = housings["data"]
print("Feature Min Max Avg Std")
for i in range(8):
column = data[:, i]
column = pre.MinMaxScaler().fit_transform(column.reshape(-1,1))
feature = housings.feature_names[i]
print(f"{feature:12} {column.min():10.3f} {column.max():10.3f} {np.mean(column):10.3f} {np.std(column):10.3f}")
Nyní je problémový atribut AveOccup jasně rozeznatelný:
Feature Min Max Avg Std MedInc 0.000 1.000 0.232 0.131 HouseAge 0.000 1.000 0.542 0.247 AveRooms 0.000 1.000 0.032 0.018 AveBedrms 0.000 1.000 0.023 0.014 Population 0.000 1.000 0.040 0.032 AveOccup 0.000 1.000 0.002 0.008 <----- Latitude 0.000 1.000 0.329 0.227 Longitude 0.000 1.000 0.476 0.200
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/




































