Evoluční algoritmy patří mezi globálně optimalizační algoritmy. Cílem je prohledat prostor a najít optimální řešení – tedy takové řešení, které maximalizuje nebo minimalizuje známou funkci. Je-li prostor možných řešení omezený a malý, lze jednotlivá řešení vyhodnotit hrubou silou a vybrat z nich to nejlepší.
Ovšem ve většině případů velikost prostoru možných řešení roste velmi rychle s velikostí problému. U takových problémů prohledávat celý prostor řešení je nemožné a tudíž je i nemožné najít optimální řešení v krátkém čase. Evoluční algoritmy tento problém řeší.
Kdy jsou evoluční algoritmy vhodné?
Tímto způsobem je vhodné řešit obecně obtížné problémy, u kterých je velký prostor řešení. Dále je tímto způsobem možné řešit obtížně formulovatelné problémy. Např. víme, jak by měl vypadat výstup, ale nevíme, jakým způsobem takový výstup dostat. Příkladem může být např. návrh elektronických schémat. Víme, jaký požadujeme od schématu výstup, ale nevíme, jak zapojit součástky, abychom tento výstup dostali.
Možností, jaké součástky a jak je ve schématu zapojit, je neomezeně mnoho. Evoluční algoritmy dokážou prohledat různé možnosti a najít nejvhodnější zapojení. Tímto způsobem se např. podařilo nalézt patentovaná schémata a v mnoha případech dokonce i schémata s lepšími vlastnostmi než patentované. Evoluční algoritmy jsou schopné také najít více optimálních řešení, jsou schopny najít celočíselná řešení i reálná.
Nevýhody evolučních algoritmů
U obtížných problémů jsou tyto algoritmy schopny najít pouze přibližná řešení. I když složitost roste pouze lineárně s velikosti populace a počtem generací, výpočet nemusí být rychlý vzhledem k tomu, že vyhodnotit řešení bývá časově náročné.
Základní principy
Každé možné řešení je reprezentováno jedincem v populaci. Populace je tedy množina jedinců – množina různých řešení. Postupem času se populace vyvíjí. Špatní jedinci vymírají, objevují se lepší jedinci, kteří je nahrazují. Počkáme-li dostatečně dlouho, populace bude tvořena dobrými jedinci, kteří reprezentují správná řešení problému.
Aby byla evoluce funkční, jsou nezbytné tři věci. Za prvé je nezbytné umět ze dvou existujících řešení vytvořit nové „zprůměrované“, této operaci se říká křížení. Za druhé je nezbytné umět vytvořené řešení náhodně pozměnit, této operaci se říká mutace. A za třetí je nezbytné pro vybraného jedince vybrat vhodného jedince ke křížení, této operaci se říká selekce nebo přirozený výběr.
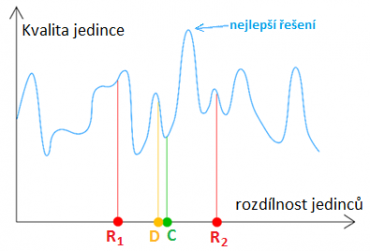
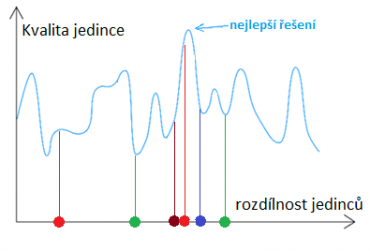
Nyní se podívejme na graf níže. Na vodorovné ose je rozdílnost jedinců (jejich genetický kód). Rozdílní jedinci jsou od sebe dále. Na svislé ose je jejich kvalita. Každý jedinec tak má jednoznačně přiřazenou svoji kvalitu. V grafu je také vyznačeno nejlepší možné řešení, jedná se o globální maximum celého prostoru. Jedinec R1 si vybere jedince R2, se kterým se chce zkřížit. Jejich zkřížením by měl vzniknout „zprůměrovaný“ jedinec mezi nimi C. Ten však nahodile zmutuje (posune se některým směrem) a vznikne tak v populaci nový potomek D se svojí kvalitou. Míra mutace je základním parametrem evolučních algoritmů, což si dále ukážeme.
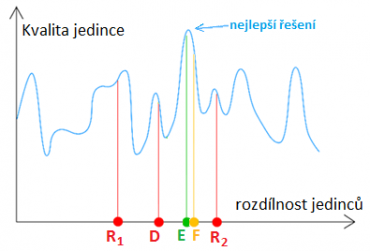
V následující generaci se proces opakuje. Dejme tomu, že jedinec D se chce zkřížit s jedincem R2. Zkřížením by vznikl jedinec E, náhodnou mutací se však toto řešení posune a vznikne nový jedinec v populaci F se svojí kvalitou. Zapojíme-li do tohoto procesu selekci, aby si jedinci vybírali ke křížení kvalitnější partnery, bude celá populace konvergovat k optimálnímu řešení. Špatní jedinci budou mít nižší pravděpodobnost, že si najdou partnera ke křížení a předají své geny.
V přírodě se za kvalitu považuje schopnost přežít. Jedinci si vybírají ke křížení takové partnery, kteří mají vyšší šanci přežít. Vlivem změny životního prostředí se uvedená křivka znázorňující kvalitu deformuje. Náhlá změna životního prostředí tak může vést k tomu, že kvalitní populace se v novém prostředí stane nekvalitní a vyhyne, anebo se populace, která již dosáhla maxima a dlouhou dobu se příliš nevyvíjela, náhle přesune k novému optimálnímu maximu. Nové druhy proto vznikají často při náhlých změnách životního prostředí. Kvalitu jedinců obvykle označujeme pojmem fitness.
Rychlost konvergence a parametry evoluce
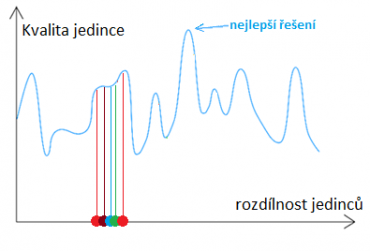
Cílem je v rychlém čase dosáhnout optimálního řešení. Přitom však může docházet ke dvěma nežádoucím jevům. Za prvé populace může uvíznout v lokálním maximu – nikoliv globálním. Tato situace je znázorněna na obrázku níže. Všichni jedinci v populaci jsou si geneticky velmi blízcí a pokrývají pouze rozsah odpovídající lokálnímu maximu. Dostat se z této pasti a nalézt globální maximum bude velmi obtížné, protože vlivem křížení mohou vznikat pouze „zprůměrovaní“ jedinci mezi svými rodiči.
Jedinou cestou jak se dostat z této pasti je vysoká mutace, která populaci rozšíří, přidá nové geny a posune nové potomky mimo tuto past. K tomuto nežádoucímu jevu dochází, nastavíme-li míru mutace příliš nízkou. V přírodě se tento problém řeší tak, že při křížení geneticky blízkých jedinců je zvýšena pravděpodobnost mutace. Jsou-li rodiče vzájemně příbuzní, míra mutace potomků je vyšší. Je nezbytné zajistit v populaci heterogenitu, protože vývoje lze dosáhnout pouze v heterogenní populaci!
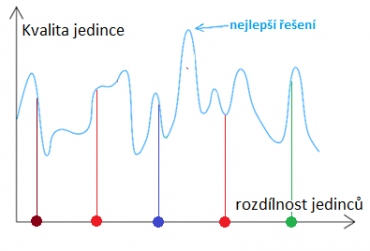
Druhým problémem je nahodilé nebo uniformní rozmístění populace. Najít optimální řešení bude opět velmi obtížné, je totiž málo pravděpodobné, že vznikne dobrý jedinec. Tato situace je znázorněna na obrázku níže. K tomuto jevu dochází, pokud je mutace příliš vysoká.
Optimální situace je znázorněna na dalším obrázku. Hustota populace směrem k maximu roste, vzdálenějších jedinců je méně. Pravděpodobnost, že nastane v genu mutace obvykle volíme mezi 2 – 4 %.
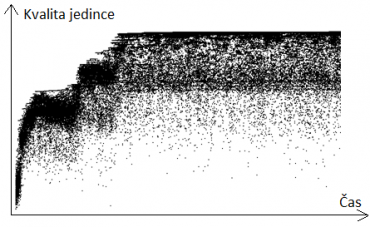
Nyní se podívejme na jiný graf, který znázorňuje typický vývoj populace v čase. Na vodorovné ose je čas, na svislé ose je kvalita jedinců. Každý bod v grafu znázorňuje jedince. Populaci v konkrétním čase získáme svislým řezem v grafu. Na začátku jsou v populaci nekvalitní jedinci. Postupem času se populace vyvíjí. V okamžiku, když se objeví nový kvalitnější jedinec, zbytek populace k němu zkonverguje. Populace se často vyvíjí skokově. Pokud po delší dobu nedochází ke zlepšení populace, signalizuje to, že populace uvízla v lokálním extrému.
Reprezentace řešení
Volba jak řešení reprezentovat často závisí na samotném problému. Pro některé problémy je vhodné řešení reprezentovat jako binární řetězec, u jiných problémů jako pole reálných hodnot, jako textové řetězce či celé grafy. Této reprezentaci jedinců se říká genotyp.
V příštím díle
V příštím díle si vyzkoušíme naprogramovat evoluční algoritmus v Javě a zkusíme pomocí něj vyřešit jednoduchý problém.