Reprezentace řešení
V různých problémech se hodí řešení reprezentovat různými způsoby. Řešení reprezentujeme chromozomem, který může být zadán jako:
- vektor binárních čísel (posloupnost jedniček a nul)
- vektor reálných čísel (viz příklad v minulém dílu)
- grafy či jiné objekty
Celý vektor, který reprezentuje řešení, se nazývá chromozom. Chromozom se skládá z genů, které mohou nabývat různých hodnot. Konkrétní hodnota genu se označuje jako alela. Viz obrázek níže.

Velikost genotypu může být i proměnlivá. V minulém díle jsme hledali tři kružnice, délku genotypu jsme proto zvolili 9. Úlohu lze ale formulovat i tak, aby algoritmus nalezl všechny kružnice, kterých může být libovolný počet. Mutace i křížení by v takovém případě musely být vhodně navrženy, aby pracovaly s různě velkými chromozomy.
Způsoby křížení
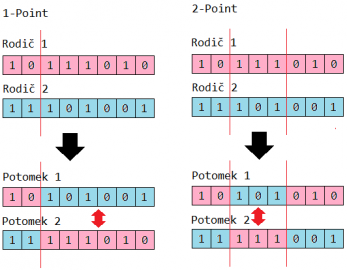
Jedním z nejčastějších způsobů křížení je metoda označovaná jako simple crossover. Většinou se provádí s jedním či se dvěma body, které se v chromozomu náhodně vyberou a geny se mezi těmito body vzájemně prohodí. Tento způsob křížení ilustruje následující obrázek.
Dalším způsobem je arithmetic crossover. Hodnota v potomkovi je dána aritmetickou operací nad alelami obou rodičů. V případě binárních genů lze použít operátory AND, OR, XOR, v případě genů s reálnými čísly se dá také použít average crossover, který hodnoty potomků vypočte jako střední hodnotu aritmetickou či geometrickou.
V minulém díle jsme použili křížení uniform crossover, při kterém se hodnota každého genu (alela) vybírá nahodile z prvního či z druhého rodiče.
Mutace
Při mutaci by mělo platit, že k velkým změnám dochází s menší pravděpodobnosti než k malým změnám. Způsob mutace závisí na způsobu reprezentace. Máme-li binární chromozom, mutaci lze provádět náhodným invertováním bitů. V případě chromozomu s reálnými čísly lze k hodnotám genů přičítat nahodilé hodnoty dané např. normálním rozdělením. Pokud reprezentujeme řešení grafem, mutací může být např. přidání uzlu, hrany, změna pořadí apod.
U některých úloh (např. kódujeme-li permutaci) se hodí mutaci realizovat jako přehození hodnot dvou genů.
Způsoby selekce
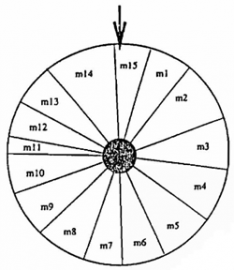
Představte si ruletu rozdělenou na různé díly. Velikost každého dílu odpovídá hodnotě fitness jedince (viz obrázek níže). Když roztočíme ruletu, je vyšší šance, že bude vybrán větší díl. Tento způsob selekce se nazývá Roulette wheel selection. Jedinci s vyšším fitness mají vyšší šanci, že budou vybráni ke křížení a předají své geny.
Předchozí způsob selekce ale bude mít problémy, když se fitness jedinců výrazně odlišuje. Např. jestliže jeden nejlepší jedinec má tak vysokou fitness, že jemu odpovídající díl zabírá téměř veškerý prostor rulety a na ostatní jedince zbývá málo prostoru, pak ke křížení bude vybírán téměř vždy právě tento jedinec a ostatní budou mít velmi nízkou šanci. V takových případech je vhodné použít tzv. Rank selection. Jedinci se seřadí podle svého fitness a ruleta je rozdělena na základě pořadí jedince. Nejhorší jedinec dostane na ruletě 1 díl, druhý nejhorší jedinec 2 díly až nejlepší jedinec dostane na ruletě N dílů, kde N je velikost populace. Horší jedinci tak dostanou větší šanci, že budou vybráni ke křížení.
Jiným typem selekce inspirovaným z přírody je Tournament selection. Pokaždé se vybere několik náhodných jedinců (kandidátů ke křížení). Tento počet se označuje pojmem „tournament size“. Nejlepší jedinec z této omezené skupiny vyhrává a je vybrán ke křížení. Tlak selekce lze pak snadno ovlivňovat volbou hodnoty tournament size. Nastavíme-li hodnotu vysokou (v limitním případě velikost celé populace), bude tlak na selekci vysoký – pouze jedinci s vysokou fitness budou moci předávat geny. Naopak nastavíme-li hodnotu nízkou (v limitním případě 1), špatní jedinci budou mít téměř stejnou šanci, že budou vybráni jako dobří jedinci.
Stagnace
Jsou-li hodnoty fitness vysoké, může se stát, že poměr fitness mezi nejhorším a nejlepším jedincem bude blízký jedné (např. 900:1000 = 0.9). Používáme-li selekci Roulette wheel selection, všichni jedinci budou mít na ruletě téměř stejné díly a dobří jedinci se tak nebudou moci prosadit mezi ostatními. Tento problém se dá řešit lineární transformací fitness, nová hodnota fitness je pak dána vztahem: f'=a*f+b, kde a a b jsou vhodné parametry. V minulém díle jsme např. fitness transformovali tak, že jsme od hodnoty fitness odečetli fitness nejhoršího jedince. Tento problém se ale dá vyřešit i použitím jiného typu selekce – Rank selection.
Proměnlivá mutace
V obtížně optimalizovatelných úlohách se hodí hodnotu mutace v průběhu algoritmu měnit. Je vhodné např. pravděpodobnost mutace přizpůsobit korelaci mezi jedinci. Jsou-li oba jedinci geneticky podobní, lze míru mutace po jejich křížení zvýšit, aby se v populaci zvýšila heterogenita.
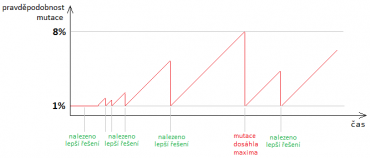
Další zajímavou strategií je zvolit minimální a maximální hodnotu mutace (např. 1 % a 8 %). V první generaci začít s nejnižší mutací a v každé následující generaci mutaci zvýšit. Mutace se znova vrátí na nejnižší hodnotu v případě, že v nové generaci je nalezen lepší jedinec než v předchozí anebo v případě, že mutace dosáhla své maximální hodnoty.
Průběh mutace je znázorněn na grafu níže. V případě, že se lepší řešení daří nalézat, mutace je nízká. Pokud se delší dobu nedaří nalézt lepší řešení (populace uvízla v lokálním extrému), mutace výrazně poroste. Pokud se podaří nalézt lepší řešení, míra mutace opět klesne na minimum. Jestliže i přesto se nepodaří nalézt lepší řešení, mutace po dosažení maxima také klesne na minimum. Tím, že mutace byla po delší dobu vysoká, se do populace dostalo mnoho nových genů, populace je více heterogenní a algoritmus tak snadněji najde globální optimum.
V příštím díle
Příště se seznámíme s neuronovými sítěmi. Zjistíme k čemu jsou dobré, které typy úloh lze s jejich pomocí řešit. Zjistíme, jak neuronové sítě fungují, jak se učí a jakým způsobem si v sobě uchovávají naučené informace.