Biologické algoritmy (4) - Neuronové sítě

Neurony v přírodě

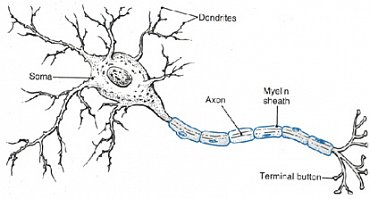
Na úvod se pro zajímavost seznámíme s neurony v přírodě. Neurony jsou buňky v živých organismech, které umožňují vést signály a reagovat na ně.

Neurony mají několik dendritů, které přijímají signál z okolí a jeden výběžek, tzv. axon, kterým jsou schopny samy signál vyslat. Samotný axon je na konci také rozvětven. Rychlost přenosu je v rozmezí 5 – 125 m/s.

Nervová soustava člověka obsahuje cca 10¹¹ – 10¹² neuronů. S rostoucím věkem počet neuronů ubývá. Neurony mohou mít desítky, ale některé dokonce i stovky tisíc dendritů, kterými jsou vzájemně propojeny. Odumře-li velká část neuronů, tuto ztrátu lze částečně nahradit zvětšením počtu spojů – dendritů.

Činnost neuronů se dá shrnout takto: Pomocí dendritů neurony zachycují signály. Tyto signály se šíří dovnitř buňky, kde vzniká potenciál. Je-li tento potenciál dostatečně velký, neuron je schopen sám vyslat signál dál.

Umělý neuron

Seznámíme se s modelem neuronu McCulloch-Pitts (MCP). Tento neuron má několik vstupů x1 - xn a jeden výstup.

Činnost neuronu lze popsat matematicky:

1. Zachycení signálu a vedení dovnitř neuronu, kde vznikne potenciál P:
   P = w1*x1 + w2*x2 + ... + wn*xn
2. Jestliže je potenciál dostatečně velký, neuron vyšle signál y:
   y = 1, jestliže P > w0, jinak  y = 0.

Podmínku že P > w₀ lze přepsat pomocí aktivační funkce f(P). Celou činnost neuronu pak lze zapsat jedním matematickým vztahem, kde w0 bude záporné číslo představující práh, jejž musí potenciál překonat:

y = f(w0 + w1*x1 + w2*x2 + ... + wn*xn)

Aktivační funkce se může lišit, měla by ale být nelineární. Takovou aktivační funkcí může být např. funkce Sigmoid nebo hyperbolický tangens. Příklad funkce Sigmoid je znázorněn na grafu.

Z grafu lze vyčíst, že pokud je potenciál (po odečtení prahu w0) nízký, výstupem neuronu bude 0. Je-li ale potenciál dostatečně vysoký, výstupem neuronu bude  1.

Z matematických vztahů je vidět, že to, co ovlivňuje výsledek, jsou v konečném důsledku váhy w0 - wn. Tyto váhy představují jakousi propustnost signálu – tedy ovlivňují kolik zachyceného signálu se dostane do neuronu, kde zvýší potenciál. Naučené informace si neurony uchovávají právě v různém nastavení hodnot těchto váh.

Neuronové sítě se dají využívat v mnoha disciplinách. Dají se používat pro rozpoznávání (tváří, písmen a číslic, objektů a čehokoliv jiného). Dají se také používat pro řízení, kdy na základě vstupů neuronová sít vyhodnotí výstup a tím se dá povel k provedení činnosti. Neuronové sítě také umí hledat shodu mezi neznámými objekty – tzv. učení bez učitele, nebo aproximovat neznámou funkci na základě vzorků.

Geometrická interpretace činnosti neuronů

Nyní se podíváme na jednoduchý příklad. Chceme například rozpoznávat pohlaví neznámého člověka na základě znalosti jeho výšky a délky vlasů. Jedná se tedy o úlohu klasifikace, kdy neznámé osobě přiřadíme třídu MUŽ nebo ŽENA na základě dvou změřených parametrů: výška a délka vlasů.

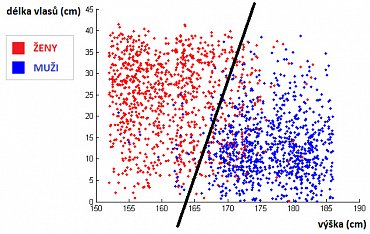
Uděláme-li si anketu mezi náhodnými osobami, ve které budeme u lidí zjišťovat pohlaví, výšku a délku vlasů, lze potom snadno nakreslit graf, který bude vypadat jako ten na obrázku dole.

Z grafu je vidět, že muži jsou vysocí s krátkými vlasy, naopak ženy jsou nižší s delšími vlasy. V takovém grafu by bylo vhodné proložit přímku, která oddělí muže a ženy. Když se nyní objeví neznámá osoba a zjistíme-li u ní její výšku a délku vlasů, lze vytvořit v takovém grafu bod, který odpovídá této neznámé osobě. Padne-li tento bod před přímku – prohlásíme, že neznámá osoba je žena, avšak padne-li bod za proloženou přímku, neznámou osobu lze klasifikovat jako muže. Tento způsob klasifikace samozřejmě není stoprocentní, ale ve většině případech bude klasifikovat správně.

Tento příklad jsme si uvedli pro lepší pochopení toho, co jsou neuronové sítě. Každý neuron totiž je schopen rozpoznávat úplně stejným způsobem, který jsme si popsali. Učení neuronu není nic jiného, než určení pozice a natočení této myšlené přímky, která rozděluje prostor na dva podprostory.

Možná si ze střední školy vzpomenete na rovnici přímky v rovině: ax+by+c=0, popř. rovnici roviny v prostoru: ax+by+cz+d=0. Připomíná vám to něco? Je to analogický vztah jako uvedený potenciál neuronu: P = w0 + w1*x1 + w2*x2 + ... + wn*xn. Je-li tento potenciál dostatečně velký, bod leží v jednom podprostoru, je-li však potenciál malý, bod leží v druhém podprostoru.

Často je parametrů, na základě kterých klasifikujeme, více. Pokud bychom chtěli určovat pohlaví přesněji, mohli bychom měřit více údajů než pouze výšku a délku vlasů. V takovém případě bude prostor mít více než dvě dimenze, obecně N dimenzí. Každý neuron, který má N vstupů, rozděluje N-dimenzionální prostor na dva podprostory. Výstup neuronu (hodnota 0 nebo 1) tak určuje, ve kterém z těchto dvou podprostoru bod leží.

Učení neuronu probíhá tak, že se aktualizují váhy (propustnosti) w0 až wN a tím se uvedená přímka (obecně podprostor prostoru) přizpůsobuje vzorkům, na kterých se neuron učí.

Neuronové sítě kombinují funkce jednotlivých neuronů v ní. Celá síť pak je schopna rozpoznávat nejenom dvě třídy, ale libovolný počet tříd a je schopna řešit složitější problémy, ve kterých nestačí prostor rozdělit na dva podprostory.

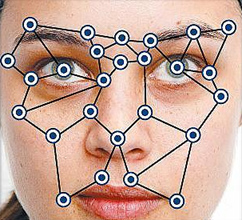
Neuronové sítě lze obdobně využít i pro složitější úlohy – např. rozpoznávání tváří. Místo výšky a délky vlasů lze jako vstupní parametry použít délky mezi detekovanými body na tváři – viz obrázek níže.

Příště

V příštím dílu se seznámíme s celými sítěmi neuronů. Zjistíme, jak se neurony zapojují a jak jsou schopny rozlišovat mezi více než dvěma třídami.