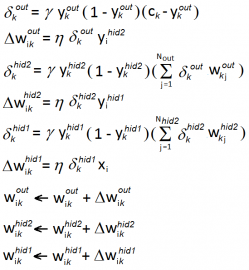Biologické algoritmy (5) - Neuronové sítě

Feed forward sítě

Neuron je schopen rozdělit prostor možných řešení pouze na dva poloprostory (viz minulý díl). V běžných složitějších úlohách je to však nedostatečné a tak musí být sestavena celá síť neuronů.

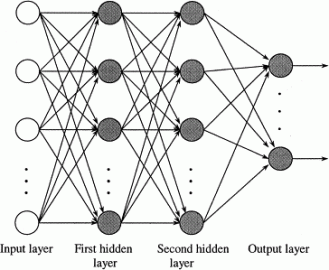
Jedním z nejpoužívanějších zapojení neuronů je tzv. feed-forward zapojení – několik vrstev neuronů je vzájemně propojených každý s každým. Příklad je uveden na obrázku níže.

Každý neuron v síti řeší pouze část celého problému. Výsledek je tvořen kompozicí příspěvků od všech neuronů v síti. Když se nad tím zamyslíme, takový přístup je v přírodě velmi výhodný. Přestane-li některý neuron fungovat (po vypití většího množství alkoholu :)), výsledek výpočtu neuronové sítě sice nebude tak přesný, ale v zásadě řešení bude správné. Celková naučená informace je tak rozprostřena mezi mnoha neurony.

Na uvedeném obrázku vidíme vstupní vrstvu, první skrytou vrstvu, druhou skrytou vrstvu a výstupní vrstvu. Vstupní vrstva pouze přeposílá signál na všechny neurony, neprovádí se žádný výpočet. V ostatních vrstvách pracují podle schématu popsaného v minulém dílu – sečtou se váhované vstupy, což tvoří potenciál, a je-li potenciál dostatečně velký, neuron na výstupu vyšle signál.

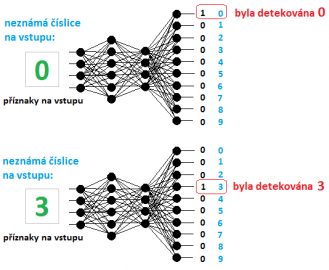
Na příkladu v minulém díle bylo naznačeno, jak by se řešilo rozpoznávání pohlaví. Potřebovali jsme pouze rozlišovat dvě třídy – muž a žena. Jiným příkladem by mohlo být rozlišení číslic od 0 do 9. V této úloze bychom potřebovali rozlišovat celkem 10 tříd. Neuronová síť by v takovém případě měla 10 neuronů ve výstupní vrstvě. Pokud je detekována číslice 0 – 9, pouze jeden výstupní neuron odpovídající detekované číslici vyšle signál.

Na obrázku níže vidíme příklad sítě. Na vstupu jsou zjištěné příznaky o neznámých číslicích. V prvním případě je detekována číslice 0, ve druhém případě číslice 3. Tímto způsobem je možné detekovat libovolný počet tříd. Hodnoty na výstupu samozřejmě nemusejí být diskrétní, jak je to uvedeno na obrázku, nicméně stačí ze všech hodnot vybrat maximum a to odpovídá detekované třídě.

Geometrická interpretace činnosti neuronové sítě

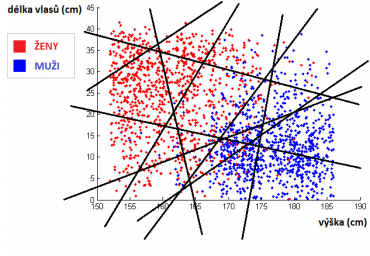
Každý neuron rozděluje prostor na dva poloprostory. První skrytá vrstva, která obsahuje několik neuronů, tak rozdělí prostor na několik různých polorovin – viz obrázek níže. Každá přímka odpovídá jednomu neuronu v první skryté vrstvě.

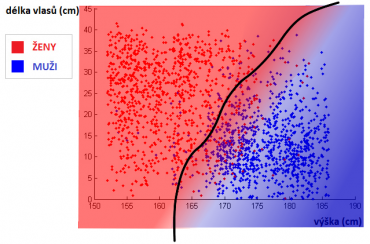
Takové rozdělení umožňuje prostor dobře zmapovat a najít odlišné polygonální oblasti. Výstup z první skryté vrstvy určuje oblast, ve které neznámý bod leží. Zvětšením množství neuronů se tak zvyšuje množství těchto polygonálních oblastí a tudíž i rozlišovací schopnost – prostor lze popsat více detailně. Pomocí druhé skryté vrstvy se celý problém transformuje do nového prostoru, kde na vstupu již nejsou příznaky, ale příslušnosti k těmto polygonálním oblastem – druhá vrstva tak může zpřesnit rozdělení prostoru „vyhlazením“. Třídy nyní mohou být od sebe odděleny křivkami, nikoliv pouze přímkou, což zpřesňuje výsledek.

Učení – Backpropagation

Nejčastěji používaným algoritmem k učení neuronových sítí je algoritmus Backpropagation. Ten pracuje tak, že vyhodnocené řešení se porovná s očekávaným a tím se zjistí, o kolik se neuronová síť „spletla“. Zpětně se na základě toho vypočítává, o kolik se mají změnit váhy neuronů, aby se tato odchylka od správného řešení co nejvíce snížila. Výsledek učení si lze představit tak, že se uvedená křivka na obrázku výše přizpůsobuje datům.

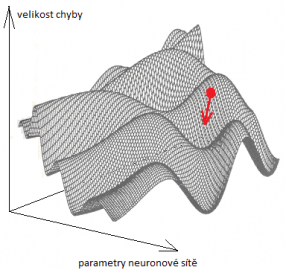
Představme si graf jako na obrázku níže. Svislá osa odpovídá velikosti chyby, zbylé osy parametrům sítě. Pro různou volbu parametrů sítě je tak přesně dána chyba, které se dopustíme. Cílem učení je najít globální minimum – tedy takové nastavení parametrů sítě, aby chyba byla minimální.

Na začátku učení se zvolí náhodné nastavení parametrů. Takovou náhodnou neuronovou síť lze zanést jako bod do výše uvedeného grafu. Výpočtem lze zjistit směr, ve kterém chyba z tohoto vneseného bodu klesá nejrychleji – nejstrmější propast. Směr této nejstrmější propasti je naznačen červenou šipkou. Tato červená šipka reprezentuje vektor, který nazýváme gradient. Postupně ve směru šipky – gradientu – posouváme myšlený bod (nastavení parametrů neuronové sítě), dokud se nedostaneme do místa s nejnižší chybou.

Algoritmus, který zde byl polopaticky v pár větách popsán, se dá přesně vyjádřit matematicky, což je pro implementaci nezbytné.

Uvedeme si nyní vztahy, pomocí kterých se váhy aktualizují. Jejich odvození vyžaduje hlubší znalost vyšší matematiky, čímž nechci čtenáře zatěžovat.

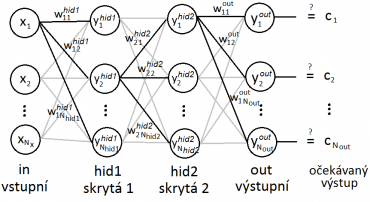
Uvažujme síť se dvěma skrytými vrstvami jako na schématu níže.

Hodnoty x1 - xNx jsou příznaky na vstupu, na základě kterých klasifikujeme. Parametry ykvrstva jsou výstupy jednotlivých neuronů. A parametry wikvrstva jsou váhy mezi spojeními neuronů (váhy dentritů neuronů ve vrstvě vrstva). Nakonec c1 - cNout jsou očekávané výstupy, které by v ideálním případě, pokud je síť dobře naučená, měly být shodné s výstupy sítě  y1out - yNoutout.

Postup algoritmu Backpropagation je následující:

1. inicializujeme všechny váhy wjk nahodile v rozsahu –1 až 1.
2. Vezmeme další vzorek z trénovací sady dat x1 - xNx, u které známe výsledek c1 - cNout a necháme síť tento vstup vyhodnotit, čímž zjistíme hodnoty  yk.
3. Na základě vzorců uvedených níže vypočteme nové hodnoty vah  wjk.
4. Pokračujeme krokem 2. dokud neprojdeme všechny vzorky, popř. lze stejné vzorky procházet i vícekrát.

Symbol η je parametr rychlosti učení. Většinou se volí okolo hodnoty 0.1. Vyšší hodnota umožní rychleji se učit avšak na úkor kvality. Parametr γ odpovídá použité aktivační funkci Sigmoid. Jeho hodnota ovlivňuje strmost této aktivační funkce. Většinou se volí γ =  1.0.

Trocha matematiky na závěr snad nikoho neodradilo, nicméně pro implementaci jsou tyto základy nezbytné, což si vyzkoušíme v příštím dílu.

Příště

Příště naprogramujeme v jazyce Java algoritmus neuronové sítě včetně učení pomocí Backpropagace. Tuto síť vyzkoušíme na praktickém příkladu – rozpoznávání scény na fotografiích. Vstupem bude libovolná fotografie a program rozhodne, jestli je na fotografii vyfocena scéna z přírody, v místnosti, noční scéna nebo jestli na fotografii je sken stránky.