Obsah
1. Cesty a základní geometrické tvary v SVG
2. Obecná struktura souborů typu SVG
3. Vytváření cest
4. Absolutní a relativní pohyb, úsečkové segmenty cest
5. Segmenty cest sestrojené z Bézierových křivek
6. Segmenty cest sestrojené z částí eliptických oblouků
7. Obsah dalšího pokračování tohoto seriálu
1. Cesty v souborech typu Scalable Vector Graphics
V předchozí části tohoto seriálu jsme si řekli, že se při tvorbě výkresů ukládaných do formátu SVG (Scalable Vector Graphics) pro reprezentaci jednotlivých grafických objektů používají nejčastěji cesty (paths), základní geometrické tvary (obdélníky, kružnice atd.) a grafické entity představující text. Kromě těchto údajů, které nesou prakticky veškeré informace o geometrii kresby, je možné do souborů typu SVG ukládat i další informace – animace objektů, jejich styly, způsob výplně objektů, odkazy, neviditelné textové popisky objektů atd. Dnes si popíšeme způsob tvorby cest a základních geometrických tvarů. Před podrobnějším popisem vytváření cest se však podívejme na to, jak vypadá obecná struktura všech souborů typu SVG.
2. Obecná struktura souborů typu SVG
Soubory typu SVG obsahují informace o vektorové kresbě uložené ve specializovaném značkovacím jazyku založeném na XML (eXtensible Markup Language). Volba XML syntaxe, a tím i textového formátu, pro ukládání grafických dat může na první pohled vypadat nevhodně, protože XML soubory jsou známé svým velkým objemem a pomalým zpracováním. Za to však většinou může nešťastné použití XML (například relační databáze uložená do XML opravdu bude mít mnohem větší objem než specializovaný binární formát, či alespoň „ploché“ textové soubory). Sice je pravda, že XML i jiný typ formátu založeného na textově zapsaných datech většinou vede k tvorbě objemnějších souborů, v některých případech však tomu může být přesně naopak (to je případ zápisu cest v SVG, které jsou i v textové podobě vyjádřeny velmi úsporně a mnohdy překonávají i naivně navržené binární formáty).
Soubory typu SVG musí dodržovat, podobně jako i další typy souborů založených na XML, několik základních pravidel. Ta na jedné straně slouží ke sjednocenému způsobu zápisu souborů, na druhé straně dovolují vytváření a používaní obecných knihoven pro práci s XML i jeho aplikacemi včetně SVG (například se jedná o knihovny založené na SAX či DOM). Základních pravidel pro vytváření korektních (well-formed) XML souborů je několik, my se s nimi budeme seznamovat postupně, především při vysvětlování zápisu jednotlivých grafických i negrafických informací do SVG. Podrobnější (mnohdy až příliš podrobné) informace o XML je možné najít na adrese http://www.w3.org/XML/, popř. na adrese http://www.ucc.ie/xml/#FAQ-VALIDWF (well-formed XML).
Nejprve si řekněme, jak vypadá základní struktura prakticky každého SVG souboru. Jako v každém jiném XML dokument i v SVG musí být na prvním řádku uveden takzvaný prolog, ve kterém je uvedena použitá verze XML (prozatím 1.0) a většinou také použité kódování znaků (implicitně je předpokládáno UTF-8) či informace o tom, zda dokument obsahuje reference na externí entity. Na následujícím řádku bývá dobrým zvykem uvedení odkazu na externí DTD (Document Type Declaration). Jmenný prostor SVG má identifikaci http://www.w3.org/2000/svg (ta bude použita u značky <svg>), veřejný identifikátor PUBLIC „-W3CDTD SVG 1.0EN“ a systémový identifikátor http:www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd.
Samotný dokument s kresbou je celý obsažen ve značce <svg>, která může mít uvedeno několik atributů. Typicky zde bývá umístěna minimálně informace o velikosti obrázku, umístění obdélníku s pohledem na obrázek (view box) a jmenném prostoru pro značky SVG a popř. i jmenném prostoru pro značky Xlink (použité pro vytváření jednosměrných i oboustranných vazeb). Uvedením atributu xmlns se jmenným prostorem odpovídajícím SVG je umožněno, aby se všechny značky SVG mohly uvádět bez prefixu, který by celý zápis dokumentu prodloužil a také znepřehlednil. Pokud budeme brát v úvahu všechny výše uvedené informace o prologu, DTD a značce <svg>, můžeme zkonstruovat kostru použitelnou u prakticky každého SVG dokumentu:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN"
"http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg width="100"
height="100"
viewBox="0 0 100 100"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
</svg>
3. Vytváření cest
V předchozí kapitole jsme si řekli, že všechny značky reprezentující uloženou kresbu musí být umístěny uvnitř „obalové“ značky <svg>. Každá cesta je představována značkou <path>, která může mít nastaveno velké množství atributů ovlivňujících tvar, styl či animaci cesty. Nejdůležitější atributy této značky jsou vypsány v následující tabulce:
| Atribut | Význam |
|---|---|
| d | vlastní geometrie cesty, bude podrobněji vysvětleno dále |
| class | třída, do které cesta spadá, může být použito například jako selektor pro styl |
| style | styl, kterým má být cesta vykreslena |
| id | identifikace cesty, může být použito například při programově řízené animaci či při změně vlastností cesty pomocí DOM |
| transform | lineární transformace aplikovaná na všechny specifikované vrcholy |
Hodnota atributu d (data či definition), která je představována řetězcem obsahujícím znaky se speciálním významem a numerické údaje, má velký význam, protože je pomocí ní zapsána celá geometrie cesty, tj. koncové body úsečkových segmentů, parametry Bézierových kvadratických i kubických křivek, parametry eliptických oblouků atd. Všechny údaje, které se vztahují k souřadnicím, jsou zapisovány pomocí absolutního či relativního pohybu grafického kurzoru. Jedná se o obdobu příkazů moveto, lineto a curveto, které již známe z popisu grafického metaformátu PostScript. Význam konkrétních údajů je popsán v následujících třech kapitolách.
4. Absolutní a relativní pohyb, úsečkové segmenty cest
Cesta může být složena z několika segmentů, přičemž každý segment je představován úsečkou, Bézierovou křivkou nebo eliptickým obloukem (kruhový oblouk je podmnožinou obecnějšího oblouku eliptického). Úsečkové segmenty jsou popsány třemi příkazy: moveto (posun grafického kurzoru bez kreslení), lineto (posun grafického kurzoru s kreslením) a closepath (posun grafického kurzoru zpět na začátek cesty).
Příkazy pro posun grafického kurzoru mohou používat absolutní nebo relativní souřadnice, existují i varianty pro posun pouze v horizontálním či vertikálním směru (to je výhodné z hlediska celkové velikosti výsledného řetězce). Relativní souřadnice pracují s předchozími souřadnicemi grafického kurzoru, ke kterým jsou přičteny zapsané číselné údaje, tj. je proveden výpočet:
xnew=xold+Δx
ynew=yold+Δy
Samotný zápis všech příkazů je zkrácen na pouhý jeden znak, přičemž při jejich zápisu záleží na velikosti písmen. Příkazy moveto a lineto obsahují parametry reprezentující souřadnice vrcholů úseček, tyto parametry jsou odděleny buď bílým znakem (nebo i několika bílými znaky), nebo dokonce nemusí být použity žádné oddělovače, pokud je konec číselné hodnoty možné zjistit z nečíselného znaku, který za ní následuje (například se může jednat o znaménko dalšího čísla či jméno následujícího příkazu) – řetězec s popisem cesty tedy může být dokonce kratší než odpovídající binární zápis. V tabulce níže jsou vypsány všechny příkazy pro tvorbu úsečkových segmentů cesty:
| Příkaz | Parametry | Popis |
|---|---|---|
| M | (x y)+ | absolutní pohyb na souřadnice [x, y] bez kreslení. Pokud je uvedeno více párů [x, y], všechny následující páry jsou považovány za parametry příkazu lineto |
| m | (x y)+ | relativní pohyb o souřadnice [x, y] bez kreslení. Pokud je uvedeno více párů [x, y], všechny následující páry jsou považovány za parametry příkazu lineto |
| L | (x y)+ | absolutní pohyb na souřadnice [x, y] s kreslením úsečkového segmentu. Je možné zapsat libovolné množství párů [x, y], výsledkem jejich vykreslení je lomená čára. |
| l | (x y)+ | relativní pohyb o souřadnice [x, y] s kreslením úsečkového segmentu. Je možné zapsat libovolné množství párů [x, y], výsledkem jejich vykreslení je lomená čára. |
| H | x+ | horizontální posun na absolutní souřadnici x s kreslením (vykreslení vodorovné úsečky). Je možné zapsat i více souřadnic, většinou to však nemá smysl (záleží však na nastaveném stylu cesty). |
| h | x+ | relativní posun o hodnotu x v horizontálním směru (vykreslení vodorovné úsečky) |
| V | y+ | vertikální posun na absolutní souřadnici y s kreslením (vykreslení svislé úsečky) |
| v | y+ | relativní posun o hodnotu y ve vertikálním směru (vykreslení svislé úsečky) |
| Z | (nejsou) | uzavření cesty úsečkovým segmentem |
| z | (nejsou) | má stejný význam jako příkaz Z |
Ukažme si použití výše uvedených příkazů na jednoduchém příkladu. Bude se jednat o vektorový obrázek známého domečku kresleného jedním tahem. Celý domek je vykreslen jednou cestou, jejíž barva je nastavena na černou barvu a výplň na konstantní oranžovou barvu (vzhledem k tomu, že se hrany domku protínají, není vykreslen celý jeho vnitřek; podrobnosti o nastavení výplně budou uvedeny v další části tohoto seriálu). Celý soubor s domečkem má následující obsah:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg width="200"
height="200"
viewBox="0 0 200 200"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<path stroke="black" fill="orange"
d="M 50 150 h 100 l -100 -100 v 100 l 100 -100 h -100 l 50 -50 l 50 50 v 100" />
</svg> 
Mezery mezi číselnými hodnotami při zápisu geometrie cesty je možné vynechat všude tam, kde nedojde ke sloučení dvou numerických hodnot do hodnoty jediné. Například řetězec „M 50 150 l –100 –100“ lze zapsat jako „M50 150l-100–100“, protože jak znaky pro tvorbu cesty, tak i znaménko minus jasně oddělují jednotlivá čísla od sebe. Zkrácený zápis cesty je použit v následujícím příkladu, který obsahuje stejný domek jako příklad předešlý:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg width="200"
height="200"
viewBox="0 0 200 200"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<path stroke="black" fill="orange"
d="M50 150h100l-100-100v100l100-100h-100l50-50l50 50v100" />
</svg>
5. Segmenty cest sestrojené z Bézierových křivek
Cesta může obsahovat i segmenty složené z Bézierových křivek. V SVG jsou podporovány jak Bézierovy kvadratické křivky, tak i Bézierovy křivky kubické. Kvadratické křivky jsou specifikovány trojicí řídicích bodů, zatímco křivky kubické potřebují pro zadání svého tvaru čtyři řídicí body. Bézierova křivka obecně prochází pouze svým prvním a posledním bodem (kotvicí body), ostatní body „pouze“ ovlivňují výsledný tvar křivky – jde tedy o aproximační křivky, i když je lze po programových výpočtech použít i pro interpolaci. Ve speciálních případech však křivka může procházet i dalšími (řídicími) body, například tehdy, když všechny body leží na jedné přímce.
Pomocí prvního bodu (kotvicího) a druhého bodu (řídicího) se určuje tečný vektor na začátku křivky. Předposlední bod (řídicí) a poslední bod (kotvicí) zase určují tečný vektor na konci křivky. Této vlastnosti se velmi často využívá při hladkém navazování Bézierových křivek. Samozřejmě je také možné hladce navázat Bézierovu křivku na úsečku či kruhový oblouk.

V SVG se Bézierovy křivky zadávají pomocí čtyř variant příkazů, přičemž každá varianta existuje ve své absolutní a relativní podobě podle toho, jakým způsobem jsou zadávány souřadnice řídicích bodů. Celkem je tedy vyhrazeno osm znaků umožňujících různé způsoby zápisu křivek. Tyto znaky jsou spolu se svým významem popsány v následující tabulce:
| Příkaz | Parametry | Popis |
|---|---|---|
| Q | (x1 y1 x y)+ | kvadratická Bézierova křivka zadaná trojicí řídicích bodů s absolutními souřadnicemi. Konec aktuálně vytvářené cesty je chápán jako první řídicí bod, druhý řídicí bod má souřadnice [x1, y1] a třetí řídicí bod má souřadnice [x, y]. Po vytvoření křivky se konec cesty přesune do bodu [x, y]. Čtveřici souřadnice je možné opakovat, potom je vytvořeno více Bézierových křivek. |
| q | (x1 y1 x y)+ | má stejný význam jako příkaz Q s tím rozdílem, že souřadnice řídicích bodů jsou zadány relativně (vůči předchozím souřadnicím). |
| T | (x y)+ | kvadratická Bézierova křivka vedoucí od konce vytvářené cesty do zadaného bodu se souřadnicemi [x, y]. Řídicí bod této křivky není zadán, protože je dopočítán z pozice řídicího bodu předchozí kvadratické Bézierovy křivky tak, aby na sebe křivky hladce navazovaly (to znamená, že před příkazem T by měl být příkaz Q, q, T či t). |
| t | (x y)+ | má stejný význam jako příkaz T s tím rozdílem, že souřadnice koncového bodu Bézierovy kvadratické křivky jsou zadány relativně vůči koncovému bodu cesty. |
| C | (x1 y1 x2 y2 x y)+ | kubická Bézierova křivka zadaná čtyřmi řídicími body, přičemž konec aktuálně vytvářené cesty je počátečním bodem této křivky a jejím koncovým bodem je [x, y]. Souřadnice řídicích bodů jsou zadány absolutně. |
| c | (x1 y1 x2 y2 x y)+ | má stejný význam jako příkaz C s tím rozdílem, že souřadnice řídicích bodů jsou zadány relativně (vůči předchozím souřadnicím). |
| S | (x2 y2 x y)+ | tento příkaz je podobný příkazu T, ovšem s tím rozdílem, že se vytvoří kubická Bézierova křivka. První řídicí bod křivky je automaticky vypočítán ze druhého řídicího bodu předchozí kubické Bézierovy křivky, tak, aby na sebe křivky hladce navazovaly. To znamená, že před tímto příkazem by měl předcházet příkaz C či S. Norma neurčuje, že by se měly dopočítat návaznosti kvadratických a kubických křivek, proto kombinace příkazů Q a S nemusí dát očekávané výsledky (podobně není možné automaticky navázat kruhový oblouk na křivku). |
| s | (x2 y2 x y)+ | podobné příkazu S, ale všechny souřadnice řídicích bodů jsou zadány relativně. |
Příkazy T, t, S a s sice na první pohled vypadají složitě a možná i nadbytečně, ale mohou být velmi užitečné, protože není nutné zajišťovat hladkou návaznost Bézierových křivek na sebe (výpočet řídicích bodů je ponechán na aplikaci, která SVG soubor zpracovává). Podobným způsobem jsou ostatně dopočítávány řídicí body i v popisu fontů ve formátu True Type (TTF), ve kterých jsou kvůli rychlému vykreslování použity kvadratické Bézierovy křivky.
V následujícím demonstračním příkladu je ukázán způsob zápisu příkazů Q a T použitých k vytvoření dvou na sebe hladce navazujících Bézierových kvadratických křivek. První křivka má své řídicí body specifikovány pomocí příkazů M (začátek a současně i dočasný konec cesty) a Q (řídicí bod a koncový bod křivky), druhá křivka používá příkaz T s pouze jedním bodem, který určuje poslední vrchol cesty:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg width="200"
height="200"
viewBox="0 0 200 200"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<path stroke="black" stroke-width="5" fill="none"
d="M 0 100 Q 50 0 100 100 T 200 100" />
</svg> 
6. Segmenty cest sestrojené z částí eliptických oblouků
Kvadratické ani kubické Bézierovy křivky nemohou geometricky přesně nahradit kruhové a eliptické oblouky (k tomuto účelu by bylo nutné použít racionální křivky, například NURBS), proto byl do repertoáru příkazů pro vytváření cest přidány i příkazy A a a, které slouží pro přidání segmentu vytvořeného z eliptického oblouku do konstruované. Kruhový oblouk je samozřejmě speciálním případem eliptického oblouku, stejně jako elipsa či kruh – pro vytvoření všech těchto tvarů si tedy vystačíme s pouhými dvěma příkazy, které se od sebe odlišují pouze tím, zda jsou souřadnice koncového bodu eliptického oblouku zadány absolutně či relativně. Tyto příkazy vyžadují celkem sedm číselných parametrů, jejichž význam je uveden v následující tabulce:
| Pořadí parametru | Název parametru | Význam |
|---|---|---|
| 1 | rx | první poloměr elipsy |
| 2 | ry | druhý poloměr elipsy |
| 3 | x-axis-rotation | rotace elipsy v souřadném systému |
| 4 | large-arc-flag | příznak, zda se má vykreslit oblouk větší než 180° |
| 5 | sweep-flag | příznak rozhodující, který ze dvou zbývajících možných oblouků se má vykreslit |
| 6 | x | x-ová souřadnice koncového bodu eliptického oblouku |
| 7 | y | y-ová souřadnice koncového bodu eliptického oblouku |
Eliptický oblouk se začíná vykreslovat v bodě, kterým končí vytvářená cesta, a končí v bodě zadaném souřadnicemi [x, y] (jedná se o poslední dva parametry příkazu A a a). Těmito dvěma body prochází elipsa o poloměrech (rx, ry) a úhlu natočení zadaném parametrem x-axis-rotation. To však pro jednoznačnou specifikaci oblouku nestačí, protože daným podmínkám (dva body, dva poloměry a úhel natočení) většinou odpovídají dvě elipsy a navíc na každé této elipse leží dva oblouky začínající v koncovém bodě cesty a končící v bodě [x, y].
Z tohoto důvodu je nutné zadat hodnotu dvou pravdivostních příznaků, pomocí kterých se rozliší, který ze čtyř oblouků se má skutečně vykreslit. Prvním příznakem large-arc-flag se určuje, zda se má vykreslit oblouk větší než 180° či menší než 180° (tedy kratší). Pokud by oba oblouky měly přesně 180°, budou obě elipsy shodné. Druhým příznakem sweep-flag je určeno, která elipsa (ze dvou možných) se má pro vytvoření oblouku zvolit.
V určitém ohledu je tvorba eliptického oblouku složitější než tvorba úsečkového segmentu nebo Bézierovy křivky. Všechny parametry jsou před vykreslením kontrolovány na správný rozsah a smysl. Pokud je koncový a počáteční bod oblouku shodný, není oblouk vykreslen (jako by v cestě vůbec nebyl uveden). V případě, že je jeden z poloměrů nulový, je místo eliptického oblouku vykreslena úsečka z počátečního do koncového bodu.
Záporné poloměry jsou automaticky převedeny na poloměry kladné. Poloměry také mohou být zvětšeny v případě, že jsou koncové body oblouku od sebe příliš vzdáleny a elipsu by nebylo možné pro zadané poloměry vytvořit. Celý kruh či elipsu je možné vykreslit nadvakrát (pomocí dvou symetrických eliptických oblouků), pokaždé se nastaví jiná hodnota příznaku sweep-flag.
Vliv obou příznaků je ukázán na následujícím příkladu, ve kterém jsou vykresleny čtyři eliptické oblouky, které se liší nastavením příznaků large-arc-flag a sweep-flag. Kromě toho jsou vykresleny dvě kružnice, každá pomocí dvojice eliptických oblouků. Také si všimněte způsobu zápisu poznámek do souborů ve formátu XML:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg width="300"
height="200"
viewBox="0 0 300 200"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<!-- ctyri ruzne elipticke oblouky vedouci pres dva shodne body -->
<path stroke="red" stroke-width="6" fill="none"
d="M 80 50 a 80, 60 0 0,0 100, 80" />
<path stroke="green" stroke-width="6" fill="none"
d="M 80 50 a 80, 60 0 1,0 100, 80" />
<path stroke="blue" stroke-width="6" fill="none"
d="M 80 50 a 80, 60 0 0,1 100, 80" />
<path stroke="orange" stroke-width="6" fill="none"
d="M 80 50 a 80, 60 0 1,1 100, 80" />
<!-- ukazka vytvoreni kruznice pomoci dvou oblouku -->
<path stroke="black" stroke-width="1" fill="none"
d="M 70 50 A 10 10 0 0 0 90 50
M 70 50 A 10 10 0 0 1 90 50"/>
<path stroke="black" stroke-width="1" fill="none"
d="M 170 130 A 10 10 0 0 0 190 130
M 170 130 A 10 10 0 0 1 190 130"/>
</svg> 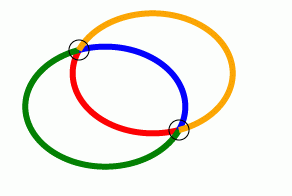
7. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování seriálu o grafických formátech a metaformátech si podrobněji popíšeme vlastnosti vytvářených cest i základních geometrických tvarů, například způsob zápisu barvy cesty či její výplně, seskupování geometrických tvarů do uzlů a specifikace vlastností pro tyto uzly apod.







































