Obsah
1. Číselné hodnoty s neomezeným rozsahem a přesností v programovacím jazyku Go
2. Datový typ big.Int – celá čísla s neomezeným rozsahem
3. Aritmetické operace prováděné s hodnotami typu big.Int
4. Výpočet faktoriálu s využitím datového typu big.Int
5. Zjednodušený faktoriál s využitím datového typu big.Int
6. Převod hodnoty typu big.Int na text s volitelnou bází
7. Konstrukce hodnoty typu big.Int z řetězce
8. Interní struktura hodnot typu big.Int
9. Přímý přístup k internímu datovému bloku hodnoty typu big.Int
10. Konstrukce hodnoty big.Int na základě specifikace obsahu bajtů interní datové struktury
11. Datový typ big.Rat – zlomky s libovolným rozsahem a přesností
12. Konstrukce zlomků s jejich automatickým zjednodušením
13. Zlomky s nulovou hodnotou jmenovatele
14. Výsledek operace, která vede ke zlomku s nulovým jmenovatelem
17. Převod zlomků na hodnoty jiných typů
19. Repositář s demonstračními příklady
1. Číselné hodnoty s neomezeným rozsahem a přesností v programovacím jazyku Go
Jak již bylo napsáno v perexu tohoto článku, existují oblasti (příkladem je šifrování), v nichž se využívají takové numerické hodnoty, které není vhodné či dokonce vůbec možné reprezentovat s využitím základních (primitivních) datových typů, mezi něž typicky patří celočíselný typ či typy (různé varianty int) a typy numerických hodnot s plovoucí řádovou čárkou (různé varianty float). Z tohoto důvodu se v některých vyšších programovacích jazycích setkáme s podporou takových datových typů, které umožňují reprezentovat celočíselné hodnoty s libovolným rozsahem (to je případ Pythonu a jeho typu int), popř. hodnoty s desetinnou tečkou, které budou mít jak neomezený rozsah, tak i neomezenou (či volitelnou) přesnost (podporováno v Clojure i mnoha implementacích Scheme a LISPu). To ovšem není vše, protože se mnohdy setkáme i s datovým typem zlomek, kde jak čitatel, tak i jmenovatel mají neomezený rozsah (opět podporováno v Clojure, Scheme, LISPu a dalších vysokoúrovňových programovacích jazycích).
V dnešním článku se zaměříme na „neomezené“ numerické hodnoty a operaci pro práci s nimi, které jsou součástí ekosystému jazyka Go. Ovšem již na tomto místě je pravděpodobně dobré upozornit na to, že podpora dále popsaných numerických typů je v jazyku Go striktně omezena na definici několika struktur a taktéž funkcí a metod určených pro práci s těmito strukturami. Jinými slovy to znamená – v žádném případě se nejedná o integrální součást jazyka a tudíž například není možné sčítat dva zlomky s využitím standardního operátoru + nebo je porovnávat operátorem <. V tomto ohledu jsme narazili na omezení sémantiky programovacího jazyka Go (tento jazyk neumožňuje přetěžovat operátory, nelze definovat nové typy literálů/konstant a neexistuje zde podpora maker – tedy alespoň prozatím).
2. Datový typ big.Int – celá čísla s neomezeným rozsahem
Připomeňme si, že v programovacím jazyku Go mají vývojáři k dispozici několik základních datových typů určených pro práci s celými čísly, ať již se znaménkem, nebo bez znaménka. Jedná se o tyto typy, přičemž int a uint jsou systémově závislé aliasy:
| Identifikátor | Typ | Stručný popis |
|---|---|---|
| int | datový typ | odpovídá buď typu int32 nebo int64 |
| int8 | datový typ | osmibitové celé číslo se znaménkem |
| int16 | datový typ | šestnáctibitové celé číslo se znaménkem |
| int32 | datový typ | 32bitové celé číslo se znaménkem |
| int64 | datový typ | 64bitové celé číslo se znaménkem |
| uint | datový typ | odpovídá buď typu uint32 nebo uint64 |
| uint8 | datový typ | osmibitové celé číslo bez znaménka |
| uint16 | datový typ | 16bitové celé číslo bez znaménka |
| uint32 | datový typ | 32bitové celé číslo bez znaménka |
| uint64 | datový typ | 64bitové celé číslo bez znaménka |
Práce s hodnotami těchto typů je většinou velmi rychlá, a to z toho důvodu, že současné mikroprocesory operaci s celými čísly typicky provedou přímo v aritmeticko-logické jednotce v několika strojových cyklech (které se navíc překrývají s dalšími instrukcemi díky instrukční pipeline). Ovšem mohou nastat situace, kdy nám ani rozsah typu int64 nebo uint64 nebude dostačovat (a typ long long není k dispozici). V tomto případě je možné využít možnosti poskytované standardním balíčkem math/big, v němž se mj. nachází i specifikace nového typu Int. Podívejme se nyní na způsob konstrukce hodnoty big.Int z celých čísel a z převodu hodnoty big.Int na textovou reprezentaci. Hodnota 10 ve volání metody big.Int.Text určuje bázi, tj. o jakou číselnou soustavu se jedná (k této problematice se ještě později vrátíme):
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
var y big.Int
x.SetInt64(1)
y.SetInt64(2)
fmt.Println(x.Text(10))
fmt.Println(y.Text(10))
}
Po překladu a spuštění tohoto demonstračního příkladu by se na standardním výstupu měly objevit tyto dva řádky:
1 2
3. Aritmetické operace prováděné s hodnotami typu big.Int
Pro datový typ big.Int jsou realizovány metody, které nahrazují základní aritmetické a bitové operace, a dokonce i vybrané algoritmy (výpočet GCD apod.). Pokud se zaměříme pouze na aritmetické operace, jedná se o tyto metody:
| Metoda | Nahrazuje operátor |
|---|---|
| func (z *Int) Add(x, y *Int) *Int | součet hodnot x a y |
| func (z *Int) Sub(x, y *Int) *Int | rozdíl hodnot x a y |
| func (z *Int) Mul(x, y *Int) *Int | součin hodnot x a y |
| func (z *Int) Div(x, y *Int) *Int | podíl hodnot x a y |
| func (z *Int) MulRange(a, b int64) *Int | součin všech hodnot od a do b (včetně) |
| func (z *Int) DivMod(x, y, m *Int) (*Int, *Int) | realizace euklidovského dělení a výpočtu zbytku po dělení |
| func (z *Int) Mod(x, y *Int) *Int | realizace operace modulo (pro modulární aritmetiku) |
| func (z *Int) ModSqrt(x, p *Int) *Int | druhá odmocnina modulo p |
| func (z *Int) Rem(x, y *Int) *Int | výpočet zbytku po dělení |
| func (z *Int) Quo(x, y *Int) *Int | dělení se zaokrouhlením k nule |
| func (z *Int) QuoRem(x, y, r *Int) (*Int, *Int) | výpočet q = x/y a r = x – y*q |
| func (z *Int) Abs(x *Int) *Int | výpočet absolutní hodnoty x |
| func (z *Int) Sqrt(x *Int) *Int | výpočet druhé odmocniny; pád (panic) pro záporný vstup |
Vyzkoušejme si nyní tu nejjednodušší operaci, tedy součet dvou hodnot typu big.Int. Povšimněte si, že je tato operace realizována metodou, která akceptuje dva ukazatele na big.Int, což jsou oba sčítance a výsledek operace je jak vrácen (pro zřetězení), tak i dosazen do příjemce:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
var y big.Int
x.SetInt64(1)
y.SetInt64(2)
var z big.Int
z.Add(&x, &y)
fmt.Println(x.Text(10))
fmt.Println(y.Text(10))
fmt.Println(z.Text(10))
}
Zkusme si tento demonstrační příklad přeložit a spustit:
1 2 3
V dalším demonstračním příkladu použijeme operaci součinu; budeme konkrétně počítat mocniny dvojky, a to bez omezeného rozsahu výsledků:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetInt64(2)
var z big.Int
z.SetInt64(1)
for i := 0; i < 100; i++ {
z.Mul(&z, &x)
fmt.Println(z.Text(10))
}
}
Opět se podívejme na výsledek (celý výpis je zkrácený):
2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768 65536 131072 262144 ... ... ... 1152921504606846976 2305843009213693952 4611686018427387904 9223372036854775808 18446744073709551616 36893488147419103232 73786976294838206464 147573952589676412928 295147905179352825856 590295810358705651712 1180591620717411303424 2361183241434822606848 4722366482869645213696 9444732965739290427392 18889465931478580854784 37778931862957161709568 75557863725914323419136 151115727451828646838272 302231454903657293676544 604462909807314587353088 1208925819614629174706176 2417851639229258349412352 4835703278458516698824704 9671406556917033397649408 19342813113834066795298816 38685626227668133590597632 77371252455336267181195264 154742504910672534362390528 309485009821345068724781056 618970019642690137449562112 1237940039285380274899124224 2475880078570760549798248448 4951760157141521099596496896 9903520314283042199192993792 19807040628566084398385987584 39614081257132168796771975168 79228162514264337593543950336 158456325028528675187087900672 316912650057057350374175801344 633825300114114700748351602688 1267650600228229401496703205376
4. Výpočet faktoriálu s využitím datového typu big.Int
S celými čísly o prakticky neomezeném rozsahu můžeme provádět všechny základní aritmetické operace; pouze nesmíme zapomenout na to, že se nezapisují s využitím operátorů +, -, *, / a %, ale příslušnými metodami popsanými na stránce https://golang.org/pkg/math/big/#Int. Taktéž porovnání dvou hodnot se neprovádí standardní šesticí relačních operátorů, ale metodou Int.Cmp. Pro zajímavost si ukažme, jakým způsobem je možné implementovat funkci pro výpočet faktoriálu pro libovolné kladné n:
package main
import (
"fmt"
"math/big"
)
func factorial(n *big.Int) *big.Int {
one := big.NewInt(1)
if n.Cmp(big.NewInt(0)) <= 0 {
return one
}
return one.Mul(n, factorial(one.Sub(n, one)))
}
func main() {
for n := int64(1); n < 80; n++ {
f := factorial(big.NewInt(n))
fmt.Printf("%3d! = %s\n", n, f.Text(10))
}
}
Z výsledků je patrné, že skutečně nejsme omezení klasickými datovými typy uint64 atd.:
1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200 15! = 1307674368000 16! = 20922789888000 17! = 355687428096000 18! = 6402373705728000 19! = 121645100408832000 20! = 2432902008176640000 21! = 51090942171709440000 22! = 1124000727777607680000 23! = 25852016738884976640000 24! = 620448401733239439360000 25! = 15511210043330985984000000 26! = 403291461126605635584000000 27! = 10888869450418352160768000000 28! = 304888344611713860501504000000 29! = 8841761993739701954543616000000 30! = 265252859812191058636308480000000 31! = 8222838654177922817725562880000000 32! = 263130836933693530167218012160000000 33! = 8683317618811886495518194401280000000 34! = 295232799039604140847618609643520000000 35! = 10333147966386144929666651337523200000000 36! = 371993326789901217467999448150835200000000 37! = 13763753091226345046315979581580902400000000 38! = 523022617466601111760007224100074291200000000 39! = 20397882081197443358640281739902897356800000000 40! = 815915283247897734345611269596115894272000000000 41! = 33452526613163807108170062053440751665152000000000 42! = 1405006117752879898543142606244511569936384000000000 43! = 60415263063373835637355132068513997507264512000000000 44! = 2658271574788448768043625811014615890319638528000000000 45! = 119622220865480194561963161495657715064383733760000000000 46! = 5502622159812088949850305428800254892961651752960000000000 47! = 258623241511168180642964355153611979969197632389120000000000 48! = 12413915592536072670862289047373375038521486354677760000000000 49! = 608281864034267560872252163321295376887552831379210240000000000 50! = 30414093201713378043612608166064768844377641568960512000000000000 51! = 1551118753287382280224243016469303211063259720016986112000000000000 52! = 80658175170943878571660636856403766975289505440883277824000000000000 53! = 4274883284060025564298013753389399649690343788366813724672000000000000 54! = 230843697339241380472092742683027581083278564571807941132288000000000000 55! = 12696403353658275925965100847566516959580321051449436762275840000000000000 56! = 710998587804863451854045647463724949736497978881168458687447040000000000000 57! = 40526919504877216755680601905432322134980384796226602145184481280000000000000 58! = 2350561331282878571829474910515074683828862318181142924420699914240000000000000 59! = 138683118545689835737939019720389406345902876772687432540821294940160000000000000 60! = 8320987112741390144276341183223364380754172606361245952449277696409600000000000000 61! = 507580213877224798800856812176625227226004528988036003099405939480985600000000000000 62! = 31469973260387937525653122354950764088012280797258232192163168247821107200000000000000 63! = 1982608315404440064116146708361898137544773690227268628106279599612729753600000000000000 64! = 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000 65! = 8247650592082470666723170306785496252186258551345437492922123134388955774976000000000000000 66! = 544344939077443064003729240247842752644293064388798874532860126869671081148416000000000000000 67! = 36471110918188685288249859096605464427167635314049524593701628500267962436943872000000000000000 68! = 2480035542436830599600990418569171581047399201355367672371710738018221445712183296000000000000000 69! = 171122452428141311372468338881272839092270544893520369393648040923257279754140647424000000000000000 70! = 11978571669969891796072783721689098736458938142546425857555362864628009582789845319680000000000000000 71! = 850478588567862317521167644239926010288584608120796235886430763388588680378079017697280000000000000000 72! = 61234458376886086861524070385274672740778091784697328983823014963978384987221689274204160000000000000000 73! = 4470115461512684340891257138125051110076800700282905015819080092370422104067183317016903680000000000000000 74! = 330788544151938641225953028221253782145683251820934971170611926835411235700971565459250872320000000000000000 75! = 24809140811395398091946477116594033660926243886570122837795894512655842677572867409443815424000000000000000000 76! = 1885494701666050254987932260861146558230394535379329335672487982961844043495537923117729972224000000000000000000 77! = 145183092028285869634070784086308284983740379224208358846781574688061991349156420080065207861248000000000000000000 78! = 11324281178206297831457521158732046228731749579488251990048962825668835325234200766245086213177344000000000000000000 79! = 894618213078297528685144171539831652069808216779571907213868063227837990693501860533361810841010176000000000000000000
5. big.Int na text s volitelnou bází
Ve skutečnosti ovšem nemusíme explicitně psát celou programovou smyčku pro výpočet faktoriálu, protože lze využít metodu MulRange, o níž jsme se zmínili ve třetí kapitole. Následující příklad ukazuje rozdíly (hint: nejsou žádné) ve vypočtených výsledcích:
package main
import (
"fmt"
"log"
"math/big"
)
func factorial(n *big.Int) *big.Int {
one := big.NewInt(1)
if n.Cmp(big.NewInt(0)) <= 0 {
return one
}
return one.Mul(n, factorial(one.Sub(n, one)))
}
func main() {
for n := int64(1); n < 31; n++ {
f1 := factorial(big.NewInt(n))
var f2 big.Int
f2.MulRange(1, n)
fmt.Printf("%3d! = %s = %s\n", n, f1.Text(10), f2.Text(10))
if f1.Cmp(&f2) != 0 {
log.Panic("Different results detected!")
}
}
}
Vypočtené a zobrazené výsledky ukazují, že oba algoritmy produkují shodné hodnoty pro shodné vstupy:
1! = 1 = 1 2! = 2 = 2 3! = 6 = 6 4! = 24 = 24 5! = 120 = 120 6! = 720 = 720 7! = 5040 = 5040 8! = 40320 = 40320 9! = 362880 = 362880 10! = 3628800 = 3628800 11! = 39916800 = 39916800 12! = 479001600 = 479001600 13! = 6227020800 = 6227020800 14! = 87178291200 = 87178291200 15! = 1307674368000 = 1307674368000 16! = 20922789888000 = 20922789888000 17! = 355687428096000 = 355687428096000 18! = 6402373705728000 = 6402373705728000 19! = 121645100408832000 = 121645100408832000 20! = 2432902008176640000 = 2432902008176640000 21! = 51090942171709440000 = 51090942171709440000 22! = 1124000727777607680000 = 1124000727777607680000 23! = 25852016738884976640000 = 25852016738884976640000 24! = 620448401733239439360000 = 620448401733239439360000 25! = 15511210043330985984000000 = 15511210043330985984000000 26! = 403291461126605635584000000 = 403291461126605635584000000 27! = 10888869450418352160768000000 = 10888869450418352160768000000 28! = 304888344611713860501504000000 = 304888344611713860501504000000 29! = 8841761993739701954543616000000 = 8841761993739701954543616000000 30! = 265252859812191058636308480000000 = 265252859812191058636308480000000
6. Převod hodnoty typu big.Int na text s volitelnou bází
V demonstračních příkladech jsme se již setkali s použitím metody big.Int.Text určené pro převod numerické hodnoty na řetězec, tj. na tisknutelný text. Této metodě se předává báze, což je základ číselné soustavy, která se má pro tisk hodnoty použít. Podporovány jsou soustavy se základy 2 až 62. Je tedy podporována dvojková, osmičková, desítková i šestnáctková soustava (pokud máme jmenovat ty nejpoužívanější báze). Soustavy se základem vyšším než 10 používají jak numerické cifry, tak i znaky malé abecedy a poté i abecedy velké. Jednotlivé cifry jsou tedy reprezentovány těmito znaky:
0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
Můžeme si to snadno otestovat – necháme i vytisknout jednu hodnotu 100000000000 (desítkově), ovšem postupně s použitím všech podporovaných bází:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetInt64(10000000000)
for base := 2; base <= 62; base++ {
fmt.Println(base, x.Text(base))
}
}
Výsledek by měl vypadat následovně:
2 1001010100000010111110010000000000 3 221210220202122010101 4 21110002332100000 5 130440000000000 6 4332142412144 7 502544411644 8 112402762000 9 27726678111 10 10000000000 11 4271815011 12 1b30b91054 13 c349ba483 14 6ac162c24 15 3d7dace6a 16 2540be400 17 1764g6422 18 g603fb9a 19 b3abb909 20 7g500000 21 5bcaikk4 22 40487b0c 23 2lcfd6fg 24 247kjf2g 25 1fo00000 26 169gphag 27 plokh3a 28 kl17a14 29 gnfiqc6 30 dlfkb3a 31 b893q85 32 9a0np00 33 7oh8of1 34 6g35112 35 5fdv5ap 36 4ldqpds 37 3x7qoxa 38 3c7wbss 39 2wwm1Bg 40 2hqa000 41 24czqE1 42 1ylsqa4 43 1p103zn 44 1gs0Fbc 45 198tgra 46 12piFGg 47 HseAcl 48 DbClBg 49 zjwtdw 50 w00000 51 sO7E6j 52 qfzAIg 53 nMisEf 54 lG2vfa 55 jLJa6J 56 i8Knsw 57 gziF6s 58 fdCzz6 59 dWfrGp 60 cPAhKE 61 bPexBe 62 aUKYOA
7. Konstrukce hodnoty typu big.Int z řetězce
Hodnoty přesahující rozsah int64 a uint64 z pochopitelných důvodů není možné použít při konstrukci hodnoty typu big.Int. Pokud ovšem takto velké hodnoty existují například v textových souborech atd., můžeme namísto konstruktoru big.Int.NewInt použít metodu big.Int.SetString. Této metodě se předává řetězec obsahující celočíselnou hodnotu a ve druhém parametru bázi, v níž je hodnota reprezentována (dvojková, osmičková, desítková, šestnáctková atd. soustava). V případě, že je báze nastavena na nulu, je informace o soustavě získána přímo ze vstupního řetězce, který tak může obsahovat klasické „bázové prefixy“ typu „0“ (osmičková) „0ד (šestnáctková) atd.
Metodu big.Int.SetString si můžeme otestovat velmi snadno:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetString("42", 10)
fmt.Println(x.Text(10))
x.SetString("1000000000000000000000000000", 10)
fmt.Println(x.Text(10))
x.SetString("1000000000000000000000000000", 2)
fmt.Println(x.Text(10))
x.SetString("0xcafebabe", 0)
fmt.Println(x.Text(10))
}
Z výsledků je patrné, jak se například liší chápání hodnoty „1000000000000000000000000000“ ve chvíli, kdy je použita desítková soustava a kdy soustava dvojková:
42 1000000000000000000000000000 134217728 3405691582
8. Interní struktura hodnot typu big.Int
Interní struktura typu big.Int v jazyce Go je sice odlišná od typu long v Pythonu, ale z pohledu programátora jsou si oba typy nápadně podobné – nulová hodnota je uložena velmi efektivním způsobem a kapacita obsazené paměti roste společně s velikostí uložené numerické hodnoty. Zajímavé a především poučné je, že v Go můžeme zjistit, jaká je interní struktura celočíselné hodnoty s neomezeným rozsahem a současně můžeme tuto interní strukturu modifikovat. Jedná se o nízkoúrovňovou operaci, kterou se sice nedoporučuje používat mimo vlastní knihovnu/balíček big.Int, ovšem žádná reálná omezení zde ve skutečnosti neexistují.
Nejdříve si ukažme, jakým způsobem můžeme získat obsah paměťového bloku, v němž je uložena nějaká hodnota typu big.Int. Pro tento účel lze použít metodu nazvanou Bytes, jejíž hlavička je následující a která vrátí strukturu hodnoty bez znaménka:
func (x *Int) Bytes() []byte
Podívejme se nyní na způsob zjištění, jak jsou uloženy hodnoty typu big.Int. Pokusíme se přitom zjistit informaci o několika hodnotách s různým rozsahem:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetInt64(0)
fmt.Println(x.Bytes())
x.SetInt64(1)
fmt.Println(x.Bytes())
x.SetInt64(100)
fmt.Println(x.Bytes())
x.SetInt64(1000)
fmt.Println(x.Bytes())
x.SetInt64(100000000)
fmt.Println(x.Bytes())
x.SetInt64(100000000)
x.Mul(&x, &x)
fmt.Println(x.Bytes())
}
Zobrazené výsledky:
[] [1] [100] [3 232] [5 245 225 0] [35 134 242 111 193 0 0]
Původní hodnotu přitom můžeme velmi snadno zrekonstruovat:
[]: 0 (z definice) [1]: 1 [100]: 100 [3 232]: 3*256 + 232 = 768 + 232 = 1000 [5 245 225 0]: 5*256*256*256 + 245*256*256 + 225*256 + 0 = 83886080 + 16056320 + 57600 = 100000000
9. Přímý přístup k internímu datovému bloku hodnoty typu big.Int
Datový typ big.Int obsahuje i metodu Bits s následující hlavičkou:
func (x *Int) Bits() []Word
Užitečné (a potenciálně i nebezpečné) je, že řez (slice) vrácený metodou bit.Int.Bits() nevznikl kopií paměťového bloku s hodnotou typu big.Int, ale jedná se skutečně o totožný blok, v němž je tato hodnota uložena. Co to znamená? Modifikací obsahu pole, které jsme získali, můžeme měnit i hodnotu typu big.Int, což je užitečné při implementaci dalších matematických operací. Ostatně můžeme si to velmi snadno vyzkoušet na tomto demonstračním příkladu:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetInt64(100000000000)
x.Mul(&x, &x)
fmt.Println(x.Text(10))
fmt.Println(x.Bits())
fmt.Println()
words := x.Bits()
words[0] = 1
words[1] = 0
fmt.Println(x.Text(10))
fmt.Println(x.Bits())
fmt.Println()
words[0] = 0
words[1] = 1
fmt.Println(x.Text(10))
fmt.Println(x.Bits())
fmt.Println()
words[0] = 1000
words[1] = 1000
fmt.Println(x.Text(10))
fmt.Println(x.Bits())
}
A takto vypadají „velká celá čísla“ vypočtená a vypsaná tímto demonstračním příkladem:
10000000000000000000000 [1864712049423024128 542] 1 [1 0] 18446744073709551616 [0 1] 18446744073709551617000 [1000 1000]
10. Konstrukce hodnoty big.Int na základě specifikace obsahu bajtů interní datové struktury
Knihovna big navíc programátorům umožňuje konstrukci celočíselné hodnoty typu big.Int specifikací hodnot jednotlivých bajtů (tedy nikoli slov). K tomuto účelu se používá metoda nazvaná big.Int.SetBytes, která má následující hlavičku:
func (z *Int) SetBytes(buf []byte) *Int
Díky této metodě můžeme opět sledovat, jakým způsobem jsou vlastně hodnoty typu big.Int interně reprezentovány. Vyzkoušíme si to na následujícím příkladu, v němž postupně do předávaného řezu přidáváme další a další bajty, z nichž ovšem pouze ten nejvyšší je nenulový. Postupně by tedy měly vznikat hodnoty 0, 256, 65536, tedy celočíselné mocniny základu 256 atd.:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Int
x.SetInt64(0)
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0, 0, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
x.SetBytes([]byte{1, 0, 0, 0, 0, 0, 0, 0, 0})
fmt.Println(x.Bytes())
fmt.Println(x.Text(10))
fmt.Println()
}
A takto vypadají zobrazené výsledky:
[] 0 [] 0 [1 0] 256 [1 0 0] 65536 [1 0 0 0] 16777216 [1 0 0 0 0] 4294967296 [1 0 0 0 0 0] 1099511627776 [1 0 0 0 0 0 0] 281474976710656 [1 0 0 0 0 0 0 0] 72057594037927936 [1 0 0 0 0 0 0 0 0] 18446744073709551616
11. Datový typ big.Rat – zlomky s libovolným rozsahem a přesností
Druhým datovým typem, který programátorům umožňuje pracovat s číselnými hodnotami, s neomezeným rozsahem a přesností, jsou zlomky (ratio). Zlomek je v operační paměti uložen ve formě dvojice celočíselných hodnot s neomezeným rozsahem, pro které platí všechny vlastnosti, s nimiž jsme se seznámili v předchozím textu. A i pro zlomky má programátor k dispozici funkce a metody realizující základní aritmetické a relační operace, které je možné při práci s nimi použít. Navíc se zlomky automaticky zjednodušují a na konci výpočtu je možné výsledky převést na hodnotu typu float32 nebo float64 (samozřejmě jen v situaci, kdy je to možné a obecně se ztrátou přesnosti), popř. je možné kdykoli přečíst hodnotu čitatele a/nebo jmenovatele a pracovat s nimi samostatně.
Zlomky jsou v základní knihovně jazyka Go představovány datovým typem big.Rat neboli „velká krysa“ ;-)
12. Konstrukce zlomků s jejich automatickým zjednodušením
Zlomky, tedy přesněji hodnoty typu big.Rat lze zkonstruovat funkcí NewRat, které se předají hodnoty čitatele a jmenovatele reprezentované jako int64:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewRat(1, 2)
y := big.NewRat(1, 3)
z := big.NewRat(2, 1)
w := big.NewRat(4, 2)
fmt.Println(x.String())
fmt.Println(y.String())
fmt.Println(z.String())
fmt.Println(w.String())
}
Alternativně je možné použít metodu nazvanou SetFrac, které se opět předají hodnoty čitatele a jmenovatele:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
var y big.Rat
var z big.Rat
var w big.Rat
x.SetFrac64(1, 2)
y.SetFrac64(1, 3)
z.SetFrac64(2, 1)
w.SetFrac64(4, 2)
fmt.Println(x.String())
fmt.Println(y.String())
fmt.Println(z.String())
fmt.Println(w.String())
}
Povšimněte si, že zlomky jsou při konstrukci zjednodušeny, což je patrné na zlomku 4/2 (poslední zobrazený výsledek):
1/2 1/3 2/1 2/1
13. Zlomky s nulovou hodnotou jmenovatele
Zajímavé bude zjistit, jakým způsobem se vlastně pracuje se zlomky, v jejichž jmenovateli je nulová hodnota (což může být výsledek nějaké operace). Nejprve si vyzkoušejme, jak Go (resp. přesněji řečeno runtime kód realizovaný v balíčku big) reaguje na pokus o konstrukci zlomku s nulovým jmenovatelem:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
x.SetFrac64(1, 0)
fmt.Println(x.String())
}
Překlad výše uvedeného programu sice proběhne bez problémů, ovšem při jeho spuštění dojde k běhové (runtime) chybě:
panic: division by zero
goroutine 1 [running]:
math/big.(*Rat).SetFrac64(0x100c000006228?, 0x7fe041ec2428?, 0x7fe041eb9108?)
/opt/go/src/math/big/rat.go:321 +0xc7
main.main()
/home/ptisnovs/src/go-root/article_A8/18_rationals_div_zero.go:11 +0x45
exit status 2
14. Výsledek operace, která vede ke zlomku s nulovým jmenovatelem
Taktéž si vyzkoušejme, co se stane ve chvíli, kdy se pokusíme o výpočet zlomku, v jehož jmenovateli bude uložena nula. Takovou operací je výpočet převrácené hodnoty realizovaný metodou Inv:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
x.SetFrac64(0, 1)
fmt.Println(x.String())
x.Inv(&x)
fmt.Println(x.String())
}
Po překladu a spuštění tohoto demonstračního příkladu se nejdříve korektně zobrazí zlomek 0/1, ovšem operace výpočtu převrácené hodnoty zhavaruje:
0/1
panic: division by zero
goroutine 1 [running]:
math/big.(*Rat).Inv(0x4cac28?, 0xc000012018?)
/opt/go/src/math/big/rat.go:383 +0xb9
main.main()
/home/ptisnovs/src/go-root/article_A8/19_rationals_div_zero.go:15 +0xb2
exit status 2
15. Operace se zlomky
Se zlomky je možné provádět podobné operace (kupodivu však ne všechny), jako s hodnotami typu big.Int. Příkladem může být jednoduchý součet zlomků. Po této operaci pochopitelně opět následuje zjednodušení zlomku, pokud je ho možné provést:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
var y big.Rat
var z big.Rat
x.SetFrac64(1, 2)
y.SetFrac64(1, 3)
z.Add(&x, &y)
fmt.Println(x.String())
fmt.Println(y.String())
fmt.Println(z.String())
}
Výsledek pravděpodobně nikoho nepřekvapí:
1/2 1/3 5/6
Samozřejmě je možné provádět i další operace, například kombinovat součin se součtem (což je v této konkrétní variantě operace typu MAC – multiply-accumulate):
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
var y big.Rat
var z big.Rat
x.SetFrac64(1, 2)
y.SetFrac64(1, 1)
z.SetFrac64(1, 1)
for i := 0; i < 10; i++ {
z.Mul(&z, &x)
z.Add(&z, &y)
fmt.Println(z.String())
}
}
Vypočtené a zobrazené výsledky:
3/2 7/4 15/8 31/16 63/32 127/64 255/128 511/256 1023/512 2047/1024
16. Výpočet hodnoty π
Zkusme si nyní provést nějaký výpočet, v němž by se zlomky skutečně používaly. Pro jednoduchost jsem vybral jeden z dnes již nepoužívaných výpočtů hodnoty π z nekonečné řady. Jedná se o takzvaný Wallis product, což je forma řady, která vypadá následovně:
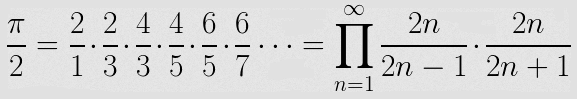
Tento výpočet je možné realizovat různými způsoby (ani se nemusí použít zlomky), ovšem jeho nejprimitivnější podoba může být následující:
package main
import (
"fmt"
"math"
"math/big"
)
func main() {
var result big.Rat
result.SetFrac64(2, 1)
for n := int64(1); n < 40; n++ {
m := 4 * n * n
var item big.Rat
item.SetFrac64(m, m-1)
result.Mul(&result, &item)
f, _ := result.Float64()
absError := math.Pi - f
relError := 100.0 * absError / math.Pi
fmt.Println(f, "\t", absError, "\t", relError, "\t", result.String())
}
}
Po překladu a spuštění tohoto příkladu se bude vypisovat jak postupně vznikající zlomek (výsledek postupně počítané nekonečně řady), tak i hodnota tohoto zlomku přepočtená na typ float64 a navíc i absolutní a relativní chyba vypočtená vůči konstantě :
2.6666666666666665 0.4749259869231266 15.11736368432249 8/3 2.8444444444444446 0.29714820914534856 9.458521263277312 128/45 2.9257142857142857 0.2158783678755074 6.871621870799526 512/175 2.972154195011338 0.1694384585784552 5.3933936465264996 32768/11025 3.002175954556907 0.139416699032886 4.437771360127774 131072/43659 3.023170192001361 0.11842246158843217 3.7695040269818167 2097152/693693 3.0386736288834193 0.10291902470637382 3.276014304043259 8388608/2760615 3.050589996055511 0.09100265753428216 2.8967045562159837 2147483648/703956825 3.0600345471268904 0.08155810646290274 2.5960751585572055 8589934592/2807136475 3.067703806643499 0.07388884694629416 2.3519550461726424 137438953472/44801898141 ... ... ... 3.119547206305518 0.022045447284275266 0.7017283815928417 43556142965880123323311949751266331066368/13962328532115305028016447297397521123911 3.12014908691642 0.021443566673373216 0.6825699267175955 2787593149816327892691964784081045188247552/893416651629057110619867238795201876360873 3.120718977160606 0.02087367642918725 0.6644297568411868 11150372599265311570767859136324180752990208/3573014001219202104195597613151008234533075 3.121259361399075 0.020333292190718222 0.6472287922969278 178405961588244985132285746181186892047843328/57158326473797485184846471512318760538583125 3.1217724732454335 0.019820180344359617 0.6308959349555315 713623846352979940529142984724747568191373312/228595726456351152123222278901666680050099375
Z předchozího zdrojového kódu je pravděpodobně zřejmé, že ve výpočtu nemůžeme pokračovat donekonečna. Je tomu tak proto, že i když se akumulace hodnot provádí se zlomky (což je v pořádku), tak počitadlo smyčky není reprezentováno typem, který může nabývat libovolně velké hodnoty a tak i výpočty s počitadlem trpí stejným problémem. Ostatně si můžeme relativně snadno otestovat, kdy dojde k situaci, v níž již vypočtené výsledky přestanou být platné:
package main
import (
"fmt"
"math"
"math/big"
)
func main() {
var result big.Rat
result.SetFrac64(2, 1)
for n := int64(1); n < math.MaxInt64; n++ {
m := 4 * n * n
var item big.Rat
item.SetFrac64(m, m-1)
result.Mul(&result, &item)
f, _ := result.Float64()
absError := math.Pi - f
relError := 100.0 * absError / math.Pi
fmt.Println(f, "\t", absError, "\t", relError)
}
}
Jedno z možných řešení výše zmíněného problému by mohlo vypadat následovně:
package main
import (
"fmt"
"math"
"math/big"
)
func main() {
var result big.Rat
result.SetFrac64(2, 1)
one := big.NewInt(1)
limit := big.NewInt(1000)
for n := big.NewInt(1); n.Cmp(limit) <= 0; n.Add(n, one) {
m := big.NewInt(4)
m.Mul(m, n)
m.Mul(m, n)
mn := big.NewInt(0)
mn.Sub(m, one)
var item big.Rat
item.SetFrac(m, mn)
result.Mul(&result, &item)
f, _ := result.Float64()
absError := math.Pi - f
relError := 100.0 * absError / math.Pi
fmt.Println(f, "\t", absError, "\t", relError, "\t", result.String())
}
}
17. Převod zlomků na hodnoty jiných typů
Metodami Num a Denom lze získat čitatel i jmenovatel zlomku. Vrací se přitom hodnoty s neomezenou přesností, tedy hodnoty typu big.Int, s nimiž jsme se seznámili výše:
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
var y big.Rat
var z big.Rat
x.SetFrac64(1, 2)
y.SetFrac64(1, 1)
z.SetFrac64(1, 1)
for i := 0; i < 10; i++ {
z.Mul(&z, &x)
z.Add(&z, &y)
numerator := z.Num()
denominator := z.Denom()
fmt.Println(numerator, denominator)
}
}
Výsledky:
3 2 7 4 15 8 31 16 63 32 127 64 255 128 511 256 1023 512 2047 1024
A konečně metodou Float64 se vrátí hodnota typu float64 (primitivní datový typ Go), která je vypočtena podílem čitatele a jmenovatele (může se tedy vrátit i nekonečná hodnota):
package main
import (
"fmt"
"math/big"
)
func main() {
var x big.Rat
var y big.Rat
var z big.Rat
x.SetFrac64(1, 2)
y.SetFrac64(1, 1)
z.SetFrac64(1, 1)
for i := 0; i < 10; i++ {
z.Mul(&z, &x)
z.Add(&z, &y)
fmt.Println(z.Float64())
}
}
18. Obsah navazujícího článku
Prozatím jsme si popsali pouze dva datové typy realizované ve standardní knihovně big: big.Int a big.Rat. Zbývá nám popis posledního typu, který je programátorům ve standardní knihovně nabízený. Jedná se o typ pojmenovaný big.Float, jenž programátorům umožňuje pracovat s „neomezenými“ hodnotami s plovoucí řádovou čárkou. To ovšem není vše, protože i pro programovací jazyk Go (podobně jako pro mnoho dalších programovacích jazyků) vznikla i implementace numerického typu s poněkud záhadným jménem Posit. S těmito dvěma koncepty se seznámíme v navazující části seriálu o programovacím jazyku Go.
19. Repositář s demonstračními příklady
Zdrojové kódy všech dnes použitých demonstračních příkladů naprogramovaných v jazyku Go byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/go-root. V případě, že nebudete chtít klonovat celý repositář, můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- Balíček big pro jazyk Go
https://pkg.go.dev/math/big - Zdrojové kódu pro balíček big
https://cs.opensource.google/go/go/+/master:src/math/big/ - Arbitrary-precision arithmetic
https://en.wikipedia.org/wiki/Arbitrary-precision_arithmetic - Floating-point error mitigation
https://en.wikipedia.org/wiki/Floating-point_error_mitigation - Beating Floating Point at its Own Game: Posit Arithmetic
http://www.johngustafson.net/pdfs/BeatingFloatingPoint.pdf - Unum (number format)
https://en.wikipedia.org/wiki/Unum_(number_format) - The GNU MPFR Library
https://www.mpfr.org/ - GMP: Arithmetic without limitations
https://gmplib.org/ - GNU MP 6.2.1 manual
https://gmplib.org/manual/index - Anatomy of a posit number
https://www.johndcook.com/blog/2018/04/11/anatomy-of-a-posit-number/ - Better floating point: posits in plain language
http://loyc.net/2019/unum-posits.html - Posits, a New Kind of Number, Improves the Math of AI: The first posit-based processor core gave a ten-thousandfold accuracy boost
https://spectrum.ieee.org/floating-point-numbers-posits-processor - Posit Standard Document (2022)
https://posithub.org/khub_widget - Standard for Posit™ Arithmetic (2022)
https://posithub.org/docs/posit_standard-2.pdf - Posit Calculator
https://posithub.org/widget/calculator/ - SoftPosit
https://gitlab.com/cerlane/SoftPosit - PySigmoid
https://github.com/mightymercado/PySigmoid - sgpositpy
https://github.com/xman/sgpositpy - SoftPosit.jl
https://github.com/milankl/SoftPosit.jl - SigmoidNumbers.jl
https://github.com/MohHizzani/SigmoidNumbers.jl