Obsah
1. Práce s hodnotami typu big.Float
2. Konstrukce hodnoty typu big.Float, základní aritmetické operace a zobrazení hodnoty
3. Zvýšení počtu cifer zobrazených za desetinnou čárkou (tečkou)
4. Zobrazení velkých hodnot bez použití exponentu
5. Zobrazení malých hodnot bez použití exponentu
6. Zobrazení numerických hodnot ve tvaru s exponentem
7. Výpis hodnoty s využitím mantisy zapsané v hexadecimálním kódu
9. Převody mezi typem big.Float a zlomky
10. Převod mezi typem big.Float a typy float64 a float32
11. Přesnost hodnot typu big.Float
12. Výpočty, jejichž výsledek je roven kladnému nebo zápornému nekonečnu
13. Povolené operace s nekonečny
14. Zakázané operace s nekonečny
16. Zachycení nepovolené operace s nekonečny
17. Příloha: „numerická věž“ ve vysokoúrovňových programovacích jazycích
18. Repositář s demonstračními příklady
1. Práce s hodnotami typu big.Float
Na úvodní článek o datových typech nabízejících programátorům v Go možnost uložení numerických hodnot s neomezeným rozsahem a/nebo přesností dnes navážeme. Zatímco minule jsme se zabývali datovým typem big.Int určeným pro reprezentaci celých čísel s neomezenou přesností i typem big.Rat představujících zlomky (opět prakticky bez omezení hodnoty čitatele a jmenovatele), dnes se budeme věnovat poslednímu typu z knihovny big. Tento typ se jmenuje big.Float a nabízí programátorům možnost práce s hodnotami, které mají jak prakticky neomezený rozsah, tak i volitelnou (a opět prakticky neomezenou) přesnost. Navíc je možné v tomto datovém typu zachytit i hodnoty ∞ a -∞, s nimiž je možné dále pracovat (pochopitelně jen do té míry, jak nám to povoluje matematika).
2. Konstrukce hodnoty typu big.Float, základní aritmetické operace a zobrazení hodnoty
I když se interní reprezentace hodnot typu big.Float odlišuje od interní reprezentace celých čísel a zlomků, tedy hodnot typu big.Int či big.Rat, jsou základní operace prakticky totožné, takže popis bude oproti předchozímu článku stručnější. Nejprve si ukážeme, jak lze převést hodnotu primitivního typu float64 na big.Float, provést aritmetickou operaci součtu a následně vytisknout výsledek. Konkrétní parametry metody Text budou uvedeny později:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(0.1)
for i := 0; i < 20; i++ {
x.Add(x, y)
fmt.Println(x.Text('f', 10))
}
}
Výsledkem činnosti tohoto demonstračního příkladu by měla být sekvence hodnot vytištěná na konzoli, přičemž počet desetinných míst (cifer) bude roven deseti:
1.1000000000 1.2000000000 1.3000000000 1.4000000000 1.5000000000 1.6000000000 1.7000000000 1.8000000000 1.9000000000 2.0000000000 2.1000000000 2.2000000000 2.3000000000 2.4000000000 2.5000000000 2.6000000000 2.7000000000 2.8000000000 2.9000000000 3.0000000000
3. Zvýšení počtu cifer zobrazených za desetinnou čárkou (tečkou)
Vzhledem k tomu, že hodnoty typu big.Float mohou mít prakticky neomezenou přesnost, asi nebude větším překvapením, že je možné zvýšit počet cifer zobrazených za desetinnou čárkou (přesněji řečeno tečkou) při převodu numerické hodnoty na řetězec metodou Text. Počet cifer je uvedený jako druhý parametr této metody, což je ukázáno na dalším demonstračním příkladu, v němž počet cifer nastavíme na osmdesát (což je u typů float32 či float64 utopie – tyto cifry už nenesou žádnou informaci):
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(0.5)
for i := 1; i < 82; i++ {
fmt.Println(x.Text('f', 80))
x.Mul(x, y)
}
}
Výsledek je kvůli jeho délce zkrácený:
1.00000000000000000000000000000000000000000000000000000000000000000000000000000000 0.50000000000000000000000000000000000000000000000000000000000000000000000000000000 0.25000000000000000000000000000000000000000000000000000000000000000000000000000000 0.12500000000000000000000000000000000000000000000000000000000000000000000000000000 0.06250000000000000000000000000000000000000000000000000000000000000000000000000000 0.03125000000000000000000000000000000000000000000000000000000000000000000000000000 ... ... ... 0.00000000000000000000000661744490042422139897126953655970282852649688720703125000 0.00000000000000000000000330872245021211069948563476827985141426324844360351562500 0.00000000000000000000000165436122510605534974281738413992570713162422180175781250 0.00000000000000000000000082718061255302767487140869206996285356581211090087890625
4. Zobrazení velkých hodnot bez použití exponentu
Konkrétní způsob zobrazení numerické hodnoty závisí v první řadě na prvním parametru metody Text, kterým se udává formát numerických hodnot. Dostupné jsou následující formáty:
| Formát | Způsob zobrazení | Příklad |
|---|---|---|
| f | bez exponentu | -ddddd.dddd |
| e | s desítkovým exponentem (minimálně jedna cifra exponentu) | -d.dddde±dd |
| E | s desítkovým exponentem (minimálně jedna cifra exponentu) | -d.ddddE±dd |
| g | formát „f“ nebo „e“ podle konkrétní hodnoty | viz výše (ovšem udává se počet všech cifer) |
| G | formát „F“ nebo „E“ podle konkrétní hodnoty | viz výše (ovšem udává se počet všech cifer) |
| x | hexadecimální mantisa, exponent bude mocninou dvojky | –0×d.dddddp±dd |
| p | hexadecimální mantisa, exponent bude mocninou dvojky | –0×.dddp±dd |
| b | desítková mantisa, exponent bude mocninou dvojky | -ddddddp±dd |
Vyzkoušejme si nyní použití formátu „f“ (tedy hodnota je zobrazená bez exponentu) v případě, že počet cifer za desetinnou čárkou/tečkou je nulový:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(99)
for i := 0; i < 40; i++ {
x.Mul(x, y)
fmt.Println(x.Text('f', 0))
}
}
Výsledek (nyní nezkrácený) by měl v tomto případě vypadat následovně:
99 9801 970299 96059601 9509900499 941480149401 93206534790699 9227446944279200 913517247483640832 90438207500880445440 8953382542587163836416 886384871716129238679552 87752102299896794226622464 8687458127689782216118763520 860058354641288373425059921920 85145777109487544324743816544256 8429431933839266852120840818917376 834513761450087363019731019944165376 82616862383558650267118944281560088576 8179069375972306130881718374652897656832 809727868221258357732174542905062205685760 80163058953904576641772755194238486550937600 7936142836436553721360802878344310916894425088 785678140807218793061707480391498750838483976192 77782135939914659864071933241904922766697872490496 7700431458051551752311463790804452893403788372606976 762342714347103590248135020666744013851798541879476224 75471928720363251946671106106388406871738329470443978752 7471720943315961528937081328671280708838571980543808765952 739700373388280233178668298783375180554490387289514891542528 73230336965439745493168643020861442160752121787685016908595200 7249803359578534449866267867987232271459539633506022851029762048 717730532598274941228294902879697277151875910759039675026529845248 71055322727229220491106662433579045148537325278934513439342013186048 7034476949995693163852959145337513235593607391744650747094042283081728 696413218049573594104027678936525501515173615926845935206266864536649728 68944908586907783168146445598460077406778525061023478292239216455863762944 6825545950103870797284771000488139744374229755763313827230611096619962073088 675729049060283181613245576645491150479693176020803826018379604257898045112320 66897175856968030043197640124285497432582076754008063827611983920792316420292608
5. Zobrazení malých hodnot bez použití exponentu
Formát zobrazení hodnot „f“ dokáže adaptivně řešit situaci, kdy zobrazovaná hodnota obsahuje velký počet cifer před desetinnou tečkou/čárkou, což jsme ostatně mohli vidět v předchozí kapitole. Ovšem jak je tomu v případě malých hodnot, přesněji řečeno hodnot blízkých nule? V tomto případě není formát „f“ flexibilní, protože zobrazí jen tolik desetinných cifer, aby to odpovídalo druhému parametru (dokonce ani nepomůže tento parametr nastavit na nulu tak, jak je tomu v některých jiných knihovnách).
Toto chování si můžeme velmi snadno otestovat:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(1 / 99.0)
for i := 0; i < 30; i++ {
x.Mul(x, y)
fmt.Println(x.Text('f', 50))
}
}
Povšimněte si, že v posledních řádcích se sice zobrazuje nula, i když interně se stále jedná o nenulovou hodnotu:
0.01010101010101010186870151841276310733519494533539 0.00010203040506070810337999749117798842235060874373 0.00000103061015212836478327669553767265142596443184 0.00000001041020355685217041371556028579378749832074 0.00000000010515357128133506708648264691105295338958 0.00000000000106215728567005135200201172774860398766 0.00000000000001072886147141466139615915720313629145 0.00000000000000010837233809509759571190792398804885 0.00000000000000000109467008176866265687314861272268 0.00000000000000000001105727355321881591655694310982 0.00000000000000000000011168963185069513140340290478 0.00000000000000000000000112817809950197109106624877 0.00000000000000000000000001139573837880778953785515 0.00000000000000000000000000011510846847280595447488 0.00000000000000000000000000000116271180275561578139 0.00000000000000000000000000000001174456366419813980 0.00000000000000000000000000000000011863195620402162 0.00000000000000000000000000000000000119830258791941 0.00000000000000000000000000000000000001210406654464 0.00000000000000000000000000000000000000012226329843 0.00000000000000000000000000000000000000000123498281 0.00000000000000000000000000000000000000000001247457 0.00000000000000000000000000000000000000000000012601 0.00000000000000000000000000000000000000000000000127 0.00000000000000000000000000000000000000000000000001 0.00000000000000000000000000000000000000000000000000 0.00000000000000000000000000000000000000000000000000 0.00000000000000000000000000000000000000000000000000 0.00000000000000000000000000000000000000000000000000 0.00000000000000000000000000000000000000000000000000
6. Zobrazení numerických hodnot ve tvaru s exponentem
Hodnoty datového typu big.Float je možné zobrazit i ve tvaru, v němž se kromě mantisy použije i exponent. Pro tento účel se používá formát „e“. Prozatím ovšem není k dispozici „inženýrská“ notace, v níž je exponent omezen na kladné a záporné násobky trojky (a tedy lze exponent „číst“ formou předpon kilo, mega, … mili, mikro). Exponent může mít jakoukoli hodnotu a druhým parametrem metody Text se určuje počet cifer za desetinou čárkou/tečkou. Předchozí dva demonstrační příklady si nyní upravíme tak, aby používaly formát „e“. Nejdříve příklad s (poměrně) velkými hodnotami:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(99)
for i := 0; i < 60; i++ {
x.Mul(x, y)
fmt.Println(x.Text('e', 10))
}
}
Výsledek bude vypadat následovně. Mimochodem si povšimněte, že nelze takto snadno omezit celkovou šířku sloupce, protože exponent může bez problémů překročit možnosti dvouciferných hodnot:
9.9000000000e+01 9.8010000000e+03 9.7029900000e+05 9.6059601000e+07 9.5099004990e+09 9.4148014940e+11 9.3206534791e+13 9.2274469443e+15 9.1351724748e+17 9.0438207501e+19 8.9533825426e+21 8.8638487172e+23 8.7752102300e+25 8.6874581277e+27 8.6005835464e+29 8.5145777109e+31 8.4294319338e+33 8.3451376145e+35 8.2616862384e+37 8.1790693760e+39 8.0972786822e+41 8.0163058954e+43 7.9361428364e+45 7.8567814081e+47 7.7782135940e+49 7.7004314581e+51 7.6234271435e+53 7.5471928720e+55 7.4717209433e+57 7.3970037339e+59 7.3230336965e+61 7.2498033596e+63 7.1773053260e+65 7.1055322727e+67 7.0344769500e+69 6.9641321805e+71 6.8944908587e+73 6.8255459501e+75 6.7572904906e+77 6.6897175857e+79 ... ... ... 6.1729014094e+95 6.1111723953e+97 6.0500606714e+99 5.9895600647e+101 5.9296644640e+103 5.8703678194e+105 5.8116641412e+107 5.7535474998e+109 5.6960120248e+111 5.6390519045e+113 5.5826613855e+115 5.5268347716e+117 5.4715664239e+119
Podobný demonstrační příklad, ale upravený naopak pro velmi malé hodnoty:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(1 / 99.0)
for i := 0; i < 30; i++ {
x.Mul(x, y)
fmt.Println(x.Text('e', 50))
}
}
Výsledek zobrazený na ploše terminálu:
1.01010101010101018687015184127631073351949453353882e-02 1.02030405060708103379997491177988422350608743727207e-04 1.03061015212836478327669553767265142596443183720112e-06 1.04102035568521704137155602857937874983207393597695e-08 1.05153571281335067086482646911052953389575925768895e-10 1.06215728567005135200201172774860398765640889795492e-12 1.07288614714146613961591572031362914498280741737446e-14 1.08372338095097595711907923988048848980467063669603e-16 1.09467008176866265687314861272267768275942672214472e-18 1.10572735532188159165569431098221261470511653137192e-20 1.11689631850695131403402904782766569004062642114308e-22 1.12817809950197109106624876927407880129500670696404e-24 1.13957383788077895378551491936699546789480855019861e-26 1.15108468472805954474884831669452610195845846835442e-28 1.16271180275561578138574437875301650648307831152748e-30 1.17445636641981398002962852135635944637689815387324e-32 1.18631956204021618895988628179697254388923229872658e-34 1.19830258791941031043953905422304809202567728322527e-36 1.21040665446405094517715640383304949986194361712221e-38 1.22263298430712221421998208845701468241634598727641e-40 1.23498281243143670392733257136953536731326930847497e-42 1.24745738629438053667535332723086755429005166172476e-44 1.26005796595391992455606458322901570918635686054018e-46 1.27278582419587884672086711467371926627233132926519e-48 1.28564224666250410857860323594852539901536777432393e-50 1.29862853198232756224292774640884031731177810970770e-52 1.31174599190134118563999093717256689123717650994598e-54 1.32499595141549631862017541936709472932642748898189e-56 1.33837974890454192356802427082629490266114944105221e-58 1.35189873626721417307818973576258972473012190788000e-60
7. Výpis hodnoty s využitím mantisy zapsané v hexadecimálním kódu
V některých oblastech (ale například i v céčku) se můžeme setkat s tím, že mantisa je zapsána v hexadecimálním kódu; typicky tak, že před šestnáctkovou tečkou je uvedena jednička (normalizace) a za mantisou je zapsán exponent ve formě mocniny čísla 2. Předností tohoto formátu je fakt, že překladač může číslo načíst a interně reprezentovat s předem známou přesností; ostatně i zdrojový kód používající tyto konstanty je velmi dobře přenositelný. Tento de facto standardní formát lze využít i společně s hodnotami big.Float, pokud se při tisku těchto hodnot použije formát „x“:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1)
y := big.NewFloat(1 / 99.0)
for i := 0; i < 30; i++ {
x.Mul(x, y)
fmt.Println(x.Text('x', 50))
}
}
Ve výsledném výpisu je patrný jak prefix 0×, tak i fakt, že před šestnáctkovou tečkou je zapsána jednička a exponent je uvozen znakem „p“ a nikoli „e“:
0x1.4afd6a052bf5b0000000000000000000000000000000000000p-07 0x1.abf250300f7690000000000000000000000000000000000000p-14 0x1.14a6fd8916ed00000000000000000000000000000000000000p-20 0x1.65b11e6e03c870000000000000000000000000000000000000p-27 0x1.ce786567741550000000000000000000000000000000000000p-34 0x1.2af87f9d625110000000000000000000000000000000000000p-40 0x1.828c47e7ee4f00000000000000000000000000000000000000p-47 0x1.f3c77969ee4c50000000000000000000000000000000000000p-54 0x1.4316eed01dee20000000000000000000000000000000000000p-60 0x1.a1bb6350501250000000000000000000000000000000000000p-67 0x1.0e0c889b5a8d30000000000000000000000000000000000000p-73 0x1.5d277a51e970c0000000000000000000000000000000000000p-80 0x1.c36e844ae03f10000000000000000000000000000000000000p-87 0x1.23d5aadb1242a0000000000000000000000000000000000000p-93 0x1.795251449e12f0000000000000000000000000000000000000p-100 0x1.e7d99f6079a190000000000000000000000000000000000000p-107 0x1.3b60b9c76b1320000000000000000000000000000000000000p-113 0x1.97c2e0af161390000000000000000000000000000000000000p-120 0x1.079a6d0c56ad00000000000000000000000000000000000000p-126 0x1.54d2015af15bd0000000000000000000000000000000000000p-133 0x1.b8a816706930f0000000000000000000000000000000000000p-140 0x1.1cde70c4ca7790000000000000000000000000000000000000p-146 0x1.7050bb2cfb6eb0000000000000000000000000000000000000p-153 0x1.dc34a999d5e480000000000000000000000000000000000000p-160 0x1.33d9a3f1abe3f0000000000000000000000000000000000000p-166 0x1.8e074aeae36a00000000000000000000000000000000000000p-173 0x1.014fb44f716630000000000000000000000000000000000000p-179 0x1.4caf74c3ce1790000000000000000000000000000000000000p-186 0x1.ae237fb22c1430000000000000000000000000000000000000p-193 0x1.1611c6ea21aad0000000000000000000000000000000000000p-199
8. Výpočet hodnoty π podruhé
Minule jsme si ukázali výpočet konstanty π založený na dnes již nepoužívané nekonečné řady prvků, které se nesčítají, ale násobí. Jedná se o takzvaný Wallis product, což je forma řady, která vypadá následovně:
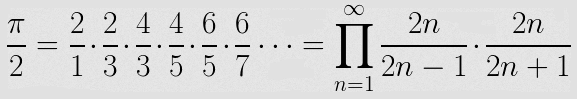
Následující výpočet byl upraven takovým způsobem, že se v něm společně používají všechny tři datové typy z balíčku big, tedy jak big.Int a big.Rat, tak i dnes popisovaný typ big.Float. „Velká celá čísla“ zde vystupují v roli počitadla smyčky, zlomky pro výpočet jednoho členu řady a čísla s plovoucí řádovou čárkou pro akumulaci výsledků:
package main
import (
"fmt"
"math/big"
)
func main() {
result := big.NewFloat(2.0)
one := big.NewInt(1)
limit := big.NewInt(200)
for n := big.NewInt(1); n.Cmp(limit) <= 0; n.Add(n, one) {
m := big.NewInt(4)
m.Mul(m, n)
m.Mul(m, n)
mn := big.NewInt(0)
mn.Sub(m, one)
var item big.Rat
item.SetFrac(m, mn)
var itemFloat big.Float
itemFloat.SetRat(&item)
result.Mul(result, &itemFloat)
fmt.Println(result.Text('f', 50))
}
}
Pro úplnost se podívejme na vypočtené výsledky:
2.66666666666666651863693004997912794351577758789062 2.84444444444444410891037477995269000530242919921875 2.92571428571428526765885180793702602386474609375000 2.97215419501133748525489863823167979717254638671875 3.00217595455690666739201333257369697093963623046875 3.02317019200136050116611841076519340276718139648438 ... ... ... 3.13757784361778702120204798120539635419845581054688 3.13759826218207127368486908380873501300811767578125 3.13761847410761740562179511471185833215713500976562 3.13763848251544885670227813534438610076904296875000 3.13765829046405153590626468940172344446182250976562 3.13767790095093257463076952262781560420989990234375
9. Převody mezi typem big.Float a zlomky
Hodnotu typu big.Float můžeme zavoláním metody big.Float.Rat převést na zlomek, tj. přesněji řečeno na hodnotu typu big.Rat, o němž jsme se zmínili v předchozím článku. Kromě vlastního zlomku se vrátí i příznak určující, zda zlomek reprezentuje přesně původní hodnotu nebo se jedná o aproximaci. Tento příznak může mít tři hodnoty s jasným významem – Below, Exact a Above. Vyzkoušejme si nyní, jak převod na zlomky vypadá:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(2.0)
y := big.NewFloat(0.1)
for i := 0; i < 10; i++ {
var ratio big.Rat
_, accuracy := x.Rat(&ratio)
fmt.Println(accuracy, ratio.String())
x.Mul(x, y)
}
}
Podle očekávání budou zlomky v mnoha případech obsahovat poměrně velké hodnoty v čitateli a jmenovateli, což je způsobeno snahou interního algoritmu o přesné vyjádření původní hodnoty s plovoucí řádovou čárkou:
Exact 2/1 Exact 3602879701896397/18014398509481984 Exact 1441151880758559/72057594037927936 Exact 4611686018427389/2305843009213693952 Exact 7378697629483823/36893488147419103232 Exact 5902958103587059/295147905179352825856 Exact 4722366482869647/2361183241434822606848 Exact 1888946593147859/9444732965739290427392 Exact 6044629098073149/302231454903657293676544 Exact 4835703278458519/2417851639229258349412352
10. Převod mezi typem big.Float a typy float64 a float32
Pokusit se můžeme i o převod hodnoty s prakticky neomezenou přesností a rozsahem na primitivní datový typ float64 či float32. Při tomto typu převodu pochopitelně obecně dojde ke ztrátě přesnosti a navíc může být výsledkem kladné či záporné nekonečno ve chvíli, kdy převáděná hodnota přesahuje rozsah obou zmíněných primitivních datových typů (pro velmi malá čísla bude naopak výsledkem kladná nebo záporná nula). Ostatně si to můžeme snadno ukázat na demonstračních příkladech. Začneme převodem na typ float64, přičemž získáme jak převedenou hodnotu, tak i již zmíněný příznak o přesnosti převedené hodnoty:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(2.0)
y := big.NewFloat(0.1)
for i := 0; i < 20; i++ {
value, accuracy := x.Float64()
fmt.Println(accuracy, value)
x.Mul(x, y)
}
}
Převedené hodnoty vypsané na standardní výstup:
Exact 2 Exact 0.2 Exact 0.020000000000000004 Exact 0.0020000000000000005 Exact 0.00020000000000000006 Exact 2.000000000000001e-05 Exact 2.0000000000000008e-06 Exact 2.000000000000001e-07 Exact 2.000000000000001e-08 Exact 2.000000000000001e-09 Exact 2.000000000000001e-10 Exact 2.0000000000000012e-11 Exact 2.000000000000001e-12 Exact 2.0000000000000013e-13 Exact 2.0000000000000016e-14 Exact 2.0000000000000017e-15 Exact 2.000000000000002e-16 Exact 2.000000000000002e-17 Exact 2.000000000000002e-18 Exact 2.000000000000002e-19
Mnohem zajímavější je převod na typ float32, kdy již pravidelně dochází ke ztrátě přesnosti a vrácená hodnota je pod či nad převáděnou hodnotou:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(2.0)
y := big.NewFloat(0.1)
for i := 0; i < 20; i++ {
value, accuracy := x.Float32()
fmt.Println(accuracy, value)
x.Mul(x, y)
}
}
Výsledky:
Exact 2 Above 0.2 Below 0.02 Above 0.002 Below 0.0002 Below 2e-05 Below 2e-06 Above 2e-07 Below 2e-08 Below 2e-09 Above 2e-10 Below 2e-11 Below 2e-12 Below 2e-13 Below 2e-14 Above 2e-15 Above 2e-16 Below 2e-17 Above 2e-18 Below 2e-19
11. Přesnost hodnot typu big.Float
Přesnost (precision) hodnot typu big.Float je možné řídit. Pro tento účel existuje metoda nazvaná SetPrec, které se předává počet bitů mantisy. Existuje teoretický maximální možný počet bitů mantisy, který je roven konstantě:
MaxPrec = math.MaxUint32
V praxi však bude maximální prakticky použitelný počet bitů mantisy menší.
Při změně přesnosti, přesněji při snižování počtu bitů mantisy, se provádí zaokrouhlování podle nastavené konfigurace (viz další text). Ukažme si nyní, jak se bude postupně měnit přesnost zaznamenané hodnoty π (resp. přiblížení k této hodnotě), pokud budeme počet bitů mantisy snižovat od 35 bitů k jednomu bitu:
package main
import (
"fmt"
"math/big"
)
func main() {
result := big.NewFloat(2.0)
one := big.NewInt(1)
limit := big.NewInt(10000)
for n := big.NewInt(1); n.Cmp(limit) <= 0; n.Add(n, one) {
m := big.NewInt(4)
m.Mul(m, n)
m.Mul(m, n)
mn := big.NewInt(0)
mn.Sub(m, one)
var item big.Rat
item.SetFrac(m, mn)
var itemFloat big.Float
itemFloat.SetRat(&item)
result.Mul(result, &itemFloat)
}
for precision := uint(35); precision != 0; precision-- {
result.SetPrec(precision)
fmt.Println(result.Text('f', 31))
}
}
Výsledky:
3.1415141186444088816642761230469 3.1415141187608242034912109375000 3.1415141187608242034912109375000 3.1415141187608242034912109375000 3.1415141187608242034912109375000 3.1415141187608242034912109375000 3.1415141224861145019531250000000 3.1415141224861145019531250000000 3.1415141224861145019531250000000 3.1415141224861145019531250000000 3.1415140628814697265625000000000 3.1415140628814697265625000000000 3.1415138244628906250000000000000 3.1415138244628906250000000000000 3.1415138244628906250000000000000 3.1415138244628906250000000000000 3.1415100097656250000000000000000 3.1415100097656250000000000000000 3.1415100097656250000000000000000 3.1414794921875000000000000000000 3.1414794921875000000000000000000 3.1416015625000000000000000000000 3.1416015625000000000000000000000 3.1416015625000000000000000000000 3.1406250000000000000000000000000 3.1406250000000000000000000000000 3.1406250000000000000000000000000 3.1406250000000000000000000000000 3.1250000000000000000000000000000 3.1250000000000000000000000000000 3.1250000000000000000000000000000 3.0000000000000000000000000000000 3.0000000000000000000000000000000 3.0000000000000000000000000000000 4.0000000000000000000000000000000
Počet bitů mantisy můžeme snížit až na 0, takže se zachová jen znaménko a normalizovaný bit mantisy (rozlišují se hodnoty 0, nekonečno apod., nic víc):
package main
import (
"fmt"
"math/big"
)
func main() {
result := big.NewFloat(2.0)
one := big.NewInt(1)
limit := big.NewInt(200)
for n := big.NewInt(1); n.Cmp(limit) <= 0; n.Add(n, one) {
m := big.NewInt(4)
m.Mul(m, n)
m.Mul(m, n)
mn := big.NewInt(0)
mn.Sub(m, one)
var item big.Rat
item.SetFrac(m, mn)
var itemFloat big.Float
itemFloat.SetRat(&item)
result.Mul(result, &itemFloat)
}
result.SetPrec(0)
fmt.Println(result.Text('f', 31))
}
Nyní bude výsledek podle předpokladů vypadat takto:
0.0000000000000000000000000000000
12. Výpočty, jejichž výsledek je roven kladnému nebo zápornému nekonečnu
U datového typu big.Float může nastat situace, kdy je výsledek nějakého výpočtu roven kladnému nebo zápornému nekonečnu. Jedná se o zcela legální hodnoty (na rozdíl od zlomků popisovaných minule) a mnoho operací s nekonečny je zcela legální. Příkladem výpočtu, jehož výsledkem je nekonečno, je podíl dvou hodnot, jenž je realizovaný metodou Quo.
Pokusme se například provést výpočet 1,0/0, jehož výsledkem by mělo být kladné nekonečno. Navíc metodou IsInf otestujeme, zda je hodnota nekonečná či nikoli (tato metoda je tedy klasickým predikátem):
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(0.0)
var result big.Float
result.Quo(x, y)
fmt.Println(result.Text('f', 31))
fmt.Println()
fmt.Println(x.IsInf())
fmt.Println(y.IsInf())
fmt.Println(result.IsInf())
}
Výsledek:
+Inf false false true
Podobně můžeme získat záporné nekonečno:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(-1.0)
y := big.NewFloat(0.0)
var result big.Float
result.Quo(x, y)
fmt.Println(result.Text('f', 31))
fmt.Println()
fmt.Println(x.IsInf())
fmt.Println(y.IsInf())
fmt.Println(result.IsInf())
}
S výsledkem:
-Inf false false true
13. Povolené operace s nekonečny
S hodnotami ∞ a -∞ je možné provádět některé aritmetické a popř. relační operace. Nejprve si ukažme ty operace, které jsou zcela legální a jejich provedením získáme korektní výsledek. K nekonečnům je možné přičíst jakoukoli hodnotu, popř. jakoukoli hodnotu odečíst (až na jednu výjimku popsanou níže). Taktéž je možné nekonečno vynásobit nějakou nenulovou hodnotou, přičemž znaménko této hodnoty určuje, zda výsledkem bude kladné nebo záporné nekonečno. Podívejme se na příklad, který některé tyto operace obsahuje:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(-1.0)
z := big.NewFloat(0.0)
var positiveInfinity big.Float
positiveInfinity.Quo(x, z)
fmt.Println(positiveInfinity.Text('f', 31))
var negativeInfinity big.Float
negativeInfinity.Quo(y, z)
fmt.Println(negativeInfinity.Text('f', 31))
var infMultiplyBy1 big.Float
infMultiplyBy1.Mul(&positiveInfinity, x)
fmt.Println(infMultiplyBy1.Text('f', 31))
var infMultiplyByMinus1 big.Float
infMultiplyByMinus1.Mul(&positiveInfinity, y)
fmt.Println(infMultiplyByMinus1.Text('f', 31))
var infMultiplyByNegativeInf big.Float
infMultiplyByNegativeInf.Mul(&positiveInfinity, &negativeInfinity)
fmt.Println(infMultiplyByNegativeInf.Text('f', 31))
}
V tomto příkladu provádíme operace:
- ∞×1 = ∞
- ∞×-1 = -∞
- ∞×-∞ = -∞
Otestujme, zda vypočtené výsledky skutečně odpovídají očekávání:
+Inf -Inf +Inf -Inf -Inf
První dva řádky jsou výpisy vypočtených nekonečen, další tři řádky pak výsledky všech tří výše uvedených výrazů.
14. Zakázané operace s nekonečny
Některé aritmetické operace s kladným či záporným nekonečnem však není možné provést a při snaze o vyčíslení takové operace dojde k pádu aplikace (zavolá se panic). Jednou z nepodporovaných operací je snaha o součet kladného a záporného nekonečna. Výsledkem v tomto případě není nula, jak by se mohlo při mechanické aplikaci pouček zdát, ale jedná se o nedefinovanou operaci:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(-1.0)
z := big.NewFloat(0.0)
var positiveInfinity big.Float
positiveInfinity.Quo(x, z)
fmt.Println(positiveInfinity.Text('f', 31))
var negativeInfinity big.Float
negativeInfinity.Quo(y, z)
fmt.Println(negativeInfinity.Text('f', 31))
var added big.Float
added.Add(&positiveInfinity, &negativeInfinity)
fmt.Println(added.Text('f', 31))
}
Pokus o vyčíslení operace added.Add(&positiveInfinity, &negativeInfinity) povede k pádu aplikace:
+Inf
-Inf
panic: addition of infinities with opposite signs
goroutine 1 [running]:
math/big.(*Float).Add(0x4ce2f8?, 0xc000012018?, 0xc00007ce60?)
/opt/go/src/math/big/float.go:1490 +0x185
main.main()
/home/ptisnovs/src/go-root/article_A9/17_inf_operations.go:22 +0x25a
exit status 2
Podobně není definována operace součinu nekonečna s nulou (či naopak), o čemž se opět můžeme velmi snadno přesvědčit:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(-1.0)
z := big.NewFloat(0.0)
var positiveInfinity big.Float
positiveInfinity.Quo(x, z)
fmt.Println(positiveInfinity.Text('f', 31))
var negativeInfinity big.Float
negativeInfinity.Quo(y, z)
fmt.Println(negativeInfinity.Text('f', 31))
var infMultiplyBy0 big.Float
infMultiplyBy0.Mul(&positiveInfinity, z)
fmt.Println(infMultiplyBy0.Text('f', 31))
}
Výsledek opět nebude příliš potěšující:
+Inf
-Inf
panic: multiplication of zero with infinity
goroutine 1 [running]:
math/big.(*Float).Mul(0x4ce288?, 0xc000012018?, 0xc00007ce60?)
/opt/go/src/math/big/float.go:1608 +0xd7
main.main()
/home/ptisnovs/src/go-root/article_A9/18_inf_operations.go:22 +0x257
exit status 2
15. Operace 0/0 a ∞/∞
Mezi další dvojici nepovolených (resp. přesněji řečeno nedefinovaných) operací patří 0/0 a ∞/∞, o čemž se můžeme velmi snadno přesvědčit:
package main
import (
"fmt"
"math/big"
)
func main() {
x := big.NewFloat(0.0)
var divideZeroByZero big.Float
divideZeroByZero.Quo(x, x)
fmt.Println(x.Text('f', 31))
}
S výsledkem/pádem:
panic: division of zero by zero or infinity by infinity
goroutine 1 [running]:
math/big.(*Float).Quo(0x7f293cf9d5b8?, 0xc00006c011?, 0xc000068058?)
/opt/go/src/math/big/float.go:1653 +0xd8
main.main()
/home/ptisnovs/src/go-root/article_A9/20_div_by_zero.go:12 +0x6f
exit status 2
16. Zachycení nepovolené operace
Pro úplnost si ukažme, jakým způsobem lze zachytit operace, které nejsou definovány. Jedná se o standardní způsob zachycení panic, který sice není příliš elegantní (a už vůbec ne snadno čitelný), ovšem v současné verzi programovacího jazyka Go si s ním budeme muset vystačit:
package main
import (
"fmt"
"log"
"math/big"
)
func main() {
x := big.NewFloat(1.0)
y := big.NewFloat(-1.0)
z := big.NewFloat(0.0)
var positiveInfinity big.Float
positiveInfinity.Quo(x, z)
fmt.Println(positiveInfinity.Text('f', 31))
var negativeInfinity big.Float
negativeInfinity.Quo(y, z)
fmt.Println(negativeInfinity.Text('f', 31))
defer func() {
if recover() != nil {
log.Fatal("Improper operation")
}
}()
var infMultiplyBy0 big.Float
infMultiplyBy0.Mul(&positiveInfinity, z)
fmt.Println(infMultiplyBy0.Text('f', 31))
}
Povšimněte si, že v tomto případě se řízení dostalo do podmíněného bloku uvnitř anonymní funkce zavolané při opouštění funkce main – jinými slovy jsme tedy zachytili výjimku, která by jinak vedla k pádu aplikace:
+Inf -Inf 2023/04/25 17:32:21 Improper operation exit status 1
17. Příloha: „numerická věž“ ve vysokoúrovňových programovacích jazycích
S takzvanou „numerickou věží“ jsme se již na tomto serveru setkali při popisu možností mnoha existujících dialektů programovacího jazyka Scheme. Připomeňme si ve stručnosti, že se jedná o hierarchii datových typů reprezentujících různé typy čísel. Na vrcholu této hierarchie typicky stojí obecný typ number, pod ním leží komplexní čísla, dále čísla reálná, čísla racionální (zlomky) a nakonec čísla celá:
| # | Typ | Význam |
|---|---|---|
| 1 | number | libovolná obecná čísla |
| 2 | complex | komplexní čísla |
| 3 | real | reálná čísla |
| 4 | rational | zlomky (racionální čísla) |
| 5 | integer | celá čísla |
Převody mezi numerickými typy jsou ve Scheme a od něho odvozených jazycích prováděny automaticky na základě vyhodnocovaného výrazu. Například v následujícím výrazu bylo nutné vyhodnotit výsledek jako komplexní číslo, protože jsme se snažili vypočítat druhou odmocninu ze záporného čísla:
(sqrt (/ 3.14159 (- (expt 2 32)))) 0+2.704548801180264e-05i
Výše uvedená numerická věž může být rozšířena o další typy, což je případ programovacího jazyka Kawa, jenž tento koncept rozšiřuje o numerický typ kvaternion a taktéž (což je asi nejzajímavější a poměrně unikátní) o typ quantity, tedy o dvojice hodnota+jednotka:
| Typ | Význam |
|---|---|
| number | libovolná obecná čísla |
| quantity | numerická hodnota i s uvedenou jednotkou (viz další text) |
| quaternion | kvaterniony |
| complex | komplexní čísla |
| real | reálná čísla |
| rational | zlomky (racionální čísla) |
| integer | celá čísla |
18. Repositář s demonstračními příklady
Zdrojové kódy všech minule i dnes použitých demonstračních příkladů naprogramovaných v jazyku Go byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/go-root. V případě, že nebudete chtít klonovat celý repositář, můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
19. Odkazy na Internetu
- Balíček big pro jazyk Go
https://pkg.go.dev/math/big - Zdrojové kódu pro balíček big
https://cs.opensource.google/go/go/+/master:src/math/big/ - Arbitrary-precision arithmetic
https://en.wikipedia.org/wiki/Arbitrary-precision_arithmetic - Floating-point error mitigation
https://en.wikipedia.org/wiki/Floating-point_error_mitigation - Beating Floating Point at its Own Game: Posit Arithmetic
http://www.johngustafson.net/pdfs/BeatingFloatingPoint.pdf - Unum (number format)
https://en.wikipedia.org/wiki/Unum_(number_format) - The GNU MPFR Library
https://www.mpfr.org/ - GMP: Arithmetic without limitations
https://gmplib.org/ - GNU MP 6.2.1 manual
https://gmplib.org/manual/index - Anatomy of a posit number
https://www.johndcook.com/blog/2018/04/11/anatomy-of-a-posit-number/ - Better floating point: posits in plain language
http://loyc.net/2019/unum-posits.html - Posits, a New Kind of Number, Improves the Math of AI: The first posit-based processor core gave a ten-thousandfold accuracy boost
https://spectrum.ieee.org/floating-point-numbers-posits-processor - Posit Standard Document (2022)
https://posithub.org/khub_widget - Standard for Posit™ Arithmetic (2022)
https://posithub.org/docs/posit_standard-2.pdf - Posit Calculator
https://posithub.org/widget/calculator/ - SoftPosit
https://gitlab.com/cerlane/SoftPosit - PySigmoid
https://github.com/mightymercado/PySigmoid - sgpositpy
https://github.com/xman/sgpositpy - SoftPosit.jl
https://github.com/milankl/SoftPosit.jl - SigmoidNumbers.jl
https://github.com/MohHizzani/SigmoidNumbers.jl - How many digits can float8, float16, float32, float64, and float128 contain?
https://stackoverflow.com/questions/56514892/how-many-digits-can-float8-float16-float32-float64-and-float128-contain - 15. Floating Point Arithmetic: Issues and Limitations (Python documentation)
https://docs.python.org/3/tutorial/floatingpoint.html - Number limits, overflow, and roundoff
https://www.khanacademy.org/computing/computers-and-internet/xcae6f4a7ff015e7d:digital-information/xcae6f4a7ff015e7d:limitations-of-storing-numbers/a/number-limits-overflow-and-roundoff - The upper and lower limits of IEEE-754 standard
https://math.stackexchange.com/questions/2607697/the-upper-and-lower-limits-of-ieee-754-standard





































