Základní vlastnosti typu numeric
Čísla jsou interně uložena jako celočíselné násobky zlomku 1/65536, z čehož mohou plynout zaokrouhlovací nepřesnosti. S těmi musíme počítat např. v logických hodnoceních, kdy výsledkem složitějšího výpočtu nemusí být očekávané celé číslo, ale číslo s platnými číslicemi za desetinnou čárkou. K témuž může dojít i při použití proměnné typu numeric jako řídící proměnné cyklů (viz další díly). Na tuto skutečnost je nutno dávat pozor, zejména v případech, kdy se do hodnoty logické proměnné promítá porovnání testované proměnné s nějakou konkrétní hodnotou. Numeric je jediný typ proměnné, kterou nemusíme nijak deklarovat. Všechny dosud nedeklarované proměnné metapost automaticky považuje za proměnné tohoto typu. Z toho mohou plynout různá zdánlivě nesmyslná chybová hlášení, pokud se překlepneme při deklaraci (nebo použití) v názvu proměnné.
Přidělenou hodnotou může být konkrétní číslo, matematický vztah mezi konkrétními čísly, jiná proměnná typu numeric či matematický vztah mezi proměnnými a čísly v libovolné kombinaci. V některých případech po nás metapost vyžaduje umístění složitějších vztahů do závorek, jinak dává na jevo svou nelibost dosti málo srozumitelnými chybovými hlášeními.
Ukázka programu a výpisu z jeho chodu. Ve výpisu jsou opět (jako v minulém díle) pro lepší srozumitelnost vloženy v hranatých závorkách názvy vypisovaných proměnných.
a=5; b=10; c=b/a; d=c*b; e=a-d; f=2b; % definujeme proměnné g=infinity; show a; show b; show c; show d; show e; show f; % vypisujeme jejich hodnoty show g; h=1/infinity; show h; end; This is MetaPost, Version 0.641 (Web2C 7.4.5) >> 5 [a] >> 10 [b] >> 2 [c] >> 20 [d] >> -15 [e] >> 20 [f] >> 4095.99998 [g] >> 0.00024 [h]
Vidíme, že proměnné typu numeric můžeme definovat přímo hodnotami nebo matematickými vztahy (+ – * /), případně lze použít - jako unární operátor (a zadat hodotu jako d=-a;). Povšiměte si také definice proměnné f ve výše uvedeném příkladě, kdy je zadána jako f=2b;, není tedy nutno uvádět znaménko násobení *, protože jména proměnných v metapostu nemohou obsahovat číslice, je tento zápis jednoznačný. Příkaz f=ab; by už jednoznačný nebyl, protože proměnná ab by mohla existovat a systém se ji bude snažit najít. V lepším případě program skončí chybovým hlášením, v horším takovou proměnnou najde a výsledkem bude „záhadné“ chování programu.
Konstanty, operátory a funkce
Konstanta infinity
Datový typ numeric má vestavěno pojmenování nejvyšší přípustné hodnoty jako infinity. Jejím převrácením zase získáme nejnižší možné číslo. Při překročení těchto hodnot dojde k přetečení/podtečení proměnné a chybovému hlášení (a to i při mezivýpočtech).
Operátory
Výše byly uvedeny operátory triviálních matematických výpočtů. K nim lze dodat, že operátor – užíváme nejen pro odečítání, ale i pro negaci. (Platí, že -a=-1*a.) Operátor ** užíváme pro umocňování (jako v perlu nebo pythonu). Pro nematematiky: Umocňujeme-li na (1/n)-tou, je výsledek totožný s n-tou odmocninou.
Další operátory jsou pro pythagorejský součet a rozdíl:A++B je zkratka pro druhou odmocninu součtu druhých mocnin A a B, A+-+B pro druhou odmocninu jejich rozdílu.
Funkce
- abs absolutní hodnota
- round zaokrouhlení (jak známe z matematiky)
- ceiling zaokrouhlení nahoru (nejbližší vyšší celé číslo)
- floor zaokrouhlení dolů (nejbližší nižší celé číslo)
- div výsledek celočíselného dělení čísla před operátorem číslem za operátorem
- mod zbytek po celočíselném dělení A mod B
- cosd kosinus úhlu zadaného ve stupních
- sind sinus úhlu zadaného ve stupních
- mlog a mexp logaritmická a exponenciální funkce; nikoli standardní, ale je použito násobení / dělení 256, nicméně mexp(mlog(n)); vrací jako výsledek n
- sqrt druhá odmocnina
- normaldeviate náhodné číslo, čísla jsou rozložena podle Gaussovy křivky, jejich průměr je 0 a směrodatná odchylka 1, zadává se bez argumentu a=normaldeviate;
- uniformdeviate náhodné číslo z intervalu 0 – argument syntaxe: a=uniformdeviate (argument); přičemž argument je číslo nebo proměnná typu numeric
Dále jsou v systému zabudována dvě funkcím podobná makra decr aincr. Snižují, resp. zvyšují hodnotu proměnné o 1, ale musejí být uplatněny v syntaxi c:=incr©;, takže se nedají použít ve stylu céčkového nebo perlového příkazu c++;
Grafické jednotky
Při grafické presentaci čísel metapost potřebuje číslo doplnit délkovou jednotkou. Není-li zadána, tedy pokoušíme-li se graficky prezentovat „holé“ číslo numeric, je implicitně doplněn jako grafická jednotka tiskový bod.
Přehled metapostem akceptovaných délkových jednotek uvádí následující tabulka:
| Jednotka | Délka v mm | Další vztahy |
| bp | 0.35278 | 1/72 palce |
| dd | 0.37607 | Didôtův bod, tradiční kontinentální typografie |
| mm | 1 | milimetr |
| pc | 4.21753 | pica = 12 pt |
| cc | 4.15279 | cicero = 12 dd |
| cm | 10 | centimetr |
| in | 25.40004 | palec |
Názvy zde uvedených jednotek by neměly být používány jako názvy proměnných.
Nejmenší vnitřně reprezentovanou jednotkou je 1/65536 pt (scaled point, sp), ta však není uživatelsky dostupná. Pokud ovšem uživatel zadá jednotku (1/infinity)*pt, pak ji má o délce cca 84.4 nm, což je za hranicí zobrazitelnosti ve viditelném světle (vzhledem k jeho vlnové délce). Nic tedy nebrání tomu použít metapost (a, pochopitelně, celý TeX) k vytváření obrázků a nápisů pozorovatelných pouze pod největším technicky možným zvětšením ve světelné mikroskopii. Pouze zařízení musí být schopné takovéto předlohy realizovat v praxi.
Nejčastěji bývá zadána na počátku obrázku (nebo celého metapostového programu) jednotka tradičně označovaná jako u, tedy něco jako:
u:=5mm;
Všechny délkové míry na obrázku se poté vyjadřují jako násobky nebo zlomky této základní jednotky. Nic nám pochopitelně nebrání definovat kdekoli v programu bod nebo jiný objekt o souřadnicích jako x=35mm; y=4.7cm;. Nicméně centrální definice délkové jednotky má tu výhodu, že zásahem do jediného místa v programu můžeme upravit měřítko obrázku.
Vztah k u zadáváme jen jednou (a je třeba to ohlídat).
a=25u; b=.7a;
U proměnné b už vztah k u zadávat nemusíme, protože ten byl zadán u definice proměnné a. Metapost by v takovém případě neohlásil žádnou chybu, ale proměnná b by byla škálována v u2.
Demonstrace funkcí pro náhodná čísla
Na závěr alespoň jeden kreslící kód a k němu příslušné obrázky:
Kód produkuje dva obrázky. Příkazy draw kreslí osy, mezi for a endfor jsou cykly. Draw bude důkladně probrán v příštím díle, na podmínky, cykly a další prvky řízení chodu programů se dostane po probrání všech datových typů. Kód v příkladu vyprodukuje dva obrázky, z nichž jeden obsahuje kolečky zobrazené náhodné body vypočtené z funkce normaldeviate,

druhý obsahuje body vykreslené jako čtverečky, jejichž souřadnice byly vypočteny funkcí uniformdeviate.
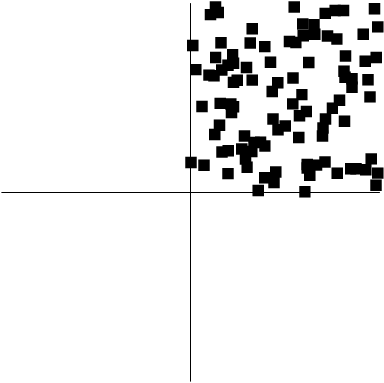
Povšiměte si, že tato funkce daleko pravidelněji pokrývá prostor vymezený pro body.
Třetí obrázek je vlastně první z ukázkového kódu, jenom těch cyklů nebylo sto, ale tisíc. Ukazuje lépe než ten první, že funkce normaldeviate má tendenci vytvářet vyšší hustotu bodů kolem středu souřadnic (0,0) a že s vyšším počtem opakování můžeme s vyšší pravděpodobností narazit i na body vzdálenější od tohoto středu.

Pokud si program opíšete a spustíte, povšimněte si (třeba přejmenováním již vygenerovaných obrázků), že náhodná čísla vycházející z těchto funkcí jsou pokaždé jiná. To mj. znesnadňuje až znemožňuje použití těchto funkcí u obrázků určených ke tvorbě animací.
Příště
V příštím díle se konečně dostaneme k datovým typům, které odpovídají reálně zobrazitelným grafickým prvkům. Probereme datový typ pair a začneme velice náročný a rozsáhlý datový typ path.





































