Obsah
1. Datová analýza s využitím nástroje scikit-learn: první kroky
2. Datová kolekce s rozměry květů kosatců (Iris Data Set)
5. Tvar dat – počet záznamů a počet proměnných
6. Jména atributů, vztah mezi numerickou hodnotou s druhem rostliny a jejím jménem
7. Korelační diagram pro dvojici vybraných proměnných
8. Příprava pro tvorbu složitějších grafů
9. Mřížka obsahující více korelačních diagramů
10. Zobrazení základního histogramu pro data v sadě Iris
11. Analýza hlavních komponent (PCA)
14. Výsledky shlukové analýzy pro různé kombinace atributů
15. Vizualizace chybných „klasifikací“ provedených shlukovou analýzou
19. Repositář s demonstračními příklady
1. Datová analýza s využitím nástroje scikit-learn: první kroky
V oblasti datové analýzy se používá velké množství různých nástrojů. Některé tyto nástroje jsou založeny na programovacím jazyku R, další nástroje pak používají programovací jazyk Python. A právě v ekosystému jazyka Python se můžeme velmi často setkat s balíčkem scikit-learn, který podporuje velké množství různých modelů, trénink modelů s učitelem i bez učitele (supervised learning, unsupervised learning), modely mohou být použity pro klasifikaci i regresi (viz navazující články s podrobnějšími informacemi a ukázkami) atd.

Obrázek 1: Logo projektu Scikit-learn.
V neposlední řadě balíček scikit-learn umožňuje velmi dobrou kooperaci s knihovnami NumPy, Pandas (velmi pravděpodobně i Polars), Xarray i Matplotlib. A pochopitelně je možné scikit-learn provozovat v Jupyter Notebooku. O všech těchto technologiích jsme si na stránkách Roota již psali (vlastně včetně samotného Scikit-learn, i když se jednalo jen o útržkové informace), takže bude zajímavé zjistit, jak lze tyto nástroje a knihovny použít společně ve složitějších analýzách.

Obrázek 2: Logo projektu NumPy.
Ve stručnosti: knihovny Pandas či Polars (popř. Xarray) použijeme pro načítání vstupních dat a jejich prvotní filtraci, transformaci, popř. normalizaci. Matplotlib bude použit pro vizualizaci jak vstupních dat, tak i výsledků modelů. Knihovna Scikit-learn nabízí prakticky veškerou funkcionalitu při tvorbě modelů (ovšem například i clustering) a NumPy se používá interně, protože prakticky všechna data jsou uložena ve formě n-dimenzionálních polí (takže je dobré znát alespoň základní operace, které NumPy nabízí).

Obrázek 3: Logo projektu Matplotlib.
Začneme velmi jednoduchými příklady, které navíc budou (alespoň dnes) využívat datovou sadu dostupnou přímo přes podbalíčky samotného scikit-learnu. To znamená, že si dnes vystačíme se scikit-learnem, knihovnou Numpy (což je závislý balíček) a knihovnou Matplotlib (dtto).

Obrázek 4: Logo projektu Pandas.
2. Datová kolekce s rozměry květů kosatců (Iris Data Set)
Ve scikit-learn nalezneme několik předpřipravených datových kolekcí, na kterých si můžeme vyzkoušet základní vlastnosti tohoto nástroje. Jednou z těchto datových kolekcí je i známá kolekce obsahující rozměry květů různých druhů kosatců. Tato datová kolekce se nazývá buď Iris (flower) data set nebo též Fisher's Iris data set a používá se velmi často při výuce, při testování různých modelů atd. Iris data set obsahuje informace o celkem 150 rostlinách, konkrétně rozměry jejich květů (viz první obrázek) doplněné o konkrétní druh kosatce.

Obrázek 5: Čtyři rozměry, které jsou u každé rostliny změřeny a uloženy do datové sady. Žádné další informace o rostlinách nemáme, tedy například ani informace o barvě, tvaru listů atd. Musíme si vystačit s málem, což ovšem poměrně dobře odráží celou problematiku datové analýzy: jsou dostupné pouze některé informace, typicky ty, o nichž věříme, že nám pomohou při klasifikaci nebo regresi.
Každá z rostlin, jejichž základní rozměry jsou v datové sadě uloženy, je druhu Iris Setosa, Iris Versicolour (psáno též Versicolor) nebo Iris Virginica, viz též seznam druhů kosatců.

Obrázek 6: Iris Setosa (Zdroj: Wikipedia).

Obrázek 7: Iris Versicolor (Zdroj: Wikipedia).

Obrázek 8: Iris Virginica (Zdroj: Wikipedia).
3. Načtení datové kolekce
Vyzkoušejme si nyní načtení výše zmíněné datové kolekce. Je to snadné. Na prvním místě je nutné si říci, že scikit-learn není jediným balíčkem, ale sada hierarchicky uspořádaných balíčků, což může být zpočátku poněkud matoucí, ale rozdělení je logické a pomáhá v orientaci ve scikit-learnu. Předpřipravené datové sady nalezneme v balíčku nazvaném sklearn.datasets. Sem pochopitelně patří i Iris data set, pro který je definována funkce load_iris, kterou si můžeme naimporotvat. Po zavolání této funkce se datová sada skutečně načte a vrátí se jako návratový typ funkce:
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# jakeho typu je vlastne datova sada?
print(type(iris))
print("-" * 100)
# dostupne atributy a metody
print(dir(iris))
Povšimněte si, jakého typu je vrácená hodnota, protože se jedná o datový typ, ke kterému se později ještě vrátíme. Tato hodnota neobsahuje pouze „čistá data“, ale i další informace o metainformace, o čemž nás informuje třetí řádek ve výpisu:
---------------------------------------------------------------------------------------------------- ['DESCR', 'data', 'data_module', 'feature_names', 'filename', 'frame', 'target', 'target_names']
help(load_iris)
Zobrazí se:
Load and return the iris dataset (classification).
The iris dataset is a classic and very easy multi-class classification
dataset.
================= ==============
Classes 3
Samples per class 50
Samples total 150
Dimensionality 4
Features real, positive
================= ==============
Read more in the :ref:`User Guide <iris_dataset>`.
4. Metadata o datové kolekci
V předchozím textu jsme si kromě jiného řekli, že datové kolekce obsahují kromě „čistých dat“ i další informace a metainformace. Zobrazme si tedy popis datové kolekce, který je uložen v atributu DESCR (a přistupujeme k němu pomocí tečkové notace), ovšem stejně tak můžeme tento atribut přečíst tak, jakoby datová sada byla slovník (potom je popis uložen pod klíčem „DESCR“). Ve druhém demonstračním příkladu použijeme druhý způsob, ovšem výsledek je naprosto stejný, jako kdybychom přečetli atribut DESCR:
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
print(dir(iris))
print("-" * 100)
# podrobny popis datove sady
print(iris["DESCR"])
Z výsledků je patrné, že popis datové kolekce je velmi podrobný, což je jen dobře:
['DESCR', 'data', 'data_module', 'feature_names', 'filename', 'frame', 'target', 'target_names']
----------------------------------------------------------------------------------------------------
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
|details-start|
**References**
|details-split|
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
|details-end|
5. Tvar dat – počet záznamů a počet proměnných
Samotné rozměry květů kosatců jsou dostupné v atributu data, popř. pod klíčem „data“, pokud budeme k datové sadě přistupovat tak, jakoby se jednalo o slovník. Rozměry květů jsou uloženy formou n-dimenzionálního pole knihovny NumPy, což je datová struktura, se kterou jsme se již na Rootu několikrát setkali. V tomto konkrétním případě bude pole dvourozměrné, takže si ho můžeme představit jako matici se 150 řádky (počet rostlin) a čtyřmi sloupci (čtyři rozměry květů):
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
print(dir(iris))
print("-" * 100)
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris["data"]
print("Feature data:")
print(data)
print("-" * 100)
# typ a "tvar" n-dimenzionalniho pole
print("Data type:")
print(type(data))
print()
print("Data shape:")
print(data.shape)
Nejprve se vypíšou seznamy atributů, což již známe:
['DESCR', 'data', 'data_module', 'feature_names', 'filename', 'frame', 'target', 'target_names'] ----------------------------------------------------------------------------------------------------
a následně se vypíše vlastní pole uložené v atributu data nebo pod klíčem „data“:
Feature data: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] [5.4 3.7 1.5 0.2] [4.8 3.4 1.6 0.2] [4.8 3. 1.4 0.1] [4.3 3. 1.1 0.1] [5.8 4. 1.2 0.2] [5.7 4.4 1.5 0.4] [5.4 3.9 1.3 0.4] [5.1 3.5 1.4 0.3] [5.7 3.8 1.7 0.3] [5.1 3.8 1.5 0.3] [5.4 3.4 1.7 0.2] [5.1 3.7 1.5 0.4] [4.6 3.6 1. 0.2] [5.1 3.3 1.7 0.5] [4.8 3.4 1.9 0.2] [5. 3. 1.6 0.2] [5. 3.4 1.6 0.4] [5.2 3.5 1.5 0.2] [5.2 3.4 1.4 0.2] [4.7 3.2 1.6 0.2] [4.8 3.1 1.6 0.2] [5.4 3.4 1.5 0.4] [5.2 4.1 1.5 0.1] [5.5 4.2 1.4 0.2] [4.9 3.1 1.5 0.2] [5. 3.2 1.2 0.2] [5.5 3.5 1.3 0.2] [4.9 3.6 1.4 0.1] [4.4 3. 1.3 0.2] [5.1 3.4 1.5 0.2] [5. 3.5 1.3 0.3] [4.5 2.3 1.3 0.3] [4.4 3.2 1.3 0.2] [5. 3.5 1.6 0.6] [5.1 3.8 1.9 0.4] [4.8 3. 1.4 0.3] [5.1 3.8 1.6 0.2] [4.6 3.2 1.4 0.2] [5.3 3.7 1.5 0.2] [5. 3.3 1.4 0.2] [7. 3.2 4.7 1.4] [6.4 3.2 4.5 1.5] [6.9 3.1 4.9 1.5] [5.5 2.3 4. 1.3] [6.5 2.8 4.6 1.5] [5.7 2.8 4.5 1.3] [6.3 3.3 4.7 1.6] [4.9 2.4 3.3 1. ] [6.6 2.9 4.6 1.3] [5.2 2.7 3.9 1.4] [5. 2. 3.5 1. ] [5.9 3. 4.2 1.5] [6. 2.2 4. 1. ] [6.1 2.9 4.7 1.4] [5.6 2.9 3.6 1.3] [6.7 3.1 4.4 1.4] [5.6 3. 4.5 1.5] [5.8 2.7 4.1 1. ] [6.2 2.2 4.5 1.5] [5.6 2.5 3.9 1.1] [5.9 3.2 4.8 1.8] [6.1 2.8 4. 1.3] [6.3 2.5 4.9 1.5] [6.1 2.8 4.7 1.2] [6.4 2.9 4.3 1.3] [6.6 3. 4.4 1.4] [6.8 2.8 4.8 1.4] [6.7 3. 5. 1.7] [6. 2.9 4.5 1.5] [5.7 2.6 3.5 1. ] [5.5 2.4 3.8 1.1] [5.5 2.4 3.7 1. ] [5.8 2.7 3.9 1.2] [6. 2.7 5.1 1.6] [5.4 3. 4.5 1.5] [6. 3.4 4.5 1.6] [6.7 3.1 4.7 1.5] [6.3 2.3 4.4 1.3] [5.6 3. 4.1 1.3] [5.5 2.5 4. 1.3] [5.5 2.6 4.4 1.2] [6.1 3. 4.6 1.4] [5.8 2.6 4. 1.2] [5. 2.3 3.3 1. ] [5.6 2.7 4.2 1.3] [5.7 3. 4.2 1.2] [5.7 2.9 4.2 1.3] [6.2 2.9 4.3 1.3] [5.1 2.5 3. 1.1] [5.7 2.8 4.1 1.3] [6.3 3.3 6. 2.5] [5.8 2.7 5.1 1.9] [7.1 3. 5.9 2.1] [6.3 2.9 5.6 1.8] [6.5 3. 5.8 2.2] [7.6 3. 6.6 2.1] [4.9 2.5 4.5 1.7] [7.3 2.9 6.3 1.8] [6.7 2.5 5.8 1.8] [7.2 3.6 6.1 2.5] [6.5 3.2 5.1 2. ] [6.4 2.7 5.3 1.9] [6.8 3. 5.5 2.1] [5.7 2.5 5. 2. ] [5.8 2.8 5.1 2.4] [6.4 3.2 5.3 2.3] [6.5 3. 5.5 1.8] [7.7 3.8 6.7 2.2] [7.7 2.6 6.9 2.3] [6. 2.2 5. 1.5] [6.9 3.2 5.7 2.3] [5.6 2.8 4.9 2. ] [7.7 2.8 6.7 2. ] [6.3 2.7 4.9 1.8] [6.7 3.3 5.7 2.1] [7.2 3.2 6. 1.8] [6.2 2.8 4.8 1.8] [6.1 3. 4.9 1.8] [6.4 2.8 5.6 2.1] [7.2 3. 5.8 1.6] [7.4 2.8 6.1 1.9] [7.9 3.8 6.4 2. ] [6.4 2.8 5.6 2.2] [6.3 2.8 5.1 1.5] [6.1 2.6 5.6 1.4] [7.7 3. 6.1 2.3] [6.3 3.4 5.6 2.4] [6.4 3.1 5.5 1.8] [6. 3. 4.8 1.8] [6.9 3.1 5.4 2.1] [6.7 3.1 5.6 2.4] [6.9 3.1 5.1 2.3] [5.8 2.7 5.1 1.9] [6.8 3.2 5.9 2.3] [6.7 3.3 5.7 2.5] [6.7 3. 5.2 2.3] [6.3 2.5 5. 1.9] [6.5 3. 5.2 2. ] [6.2 3.4 5.4 2.3] [5.9 3. 5.1 1.8]] ----------------------------------------------------------------------------------------------------
Na konci běhu skriptu se zobrazí typ dat (tedy n-rozměrného pole) a jeho tvar (shape):
Data type: <class 'numpy.ndarray'> Data shape: (150, 4)
6. Jména atributů, vztah mezi numerickou hodnotou s druhem rostliny a jejím jménem
Jednotlivé atributy, což jsou v našem konkrétním případě rozměry květů, jsou pojmenovány, přičemž tato jména nalezneme v atributu objektu typu Bunch, který se jmenuje feature_names, popř. pod stejně pojmenovaným klíčem. Jedná se o pole obsahující čtveřici řetězců obsahujících jak měřenou veličinu, tak i její jednotku.
Datová sada, kterou zkoumáme, ovšem obsahuje nejenom rozměry květů, ale i druh rostliny, což jsou hodnoty, které později použijeme při trénování modelů (protože druh rostliny je vlastně odpovědí, kterou hledáme). Vzhledem k tomu, že většina modelů, s nimiž se dále seznámíme, zpracovává a produkuje numerické hodnoty, jsou i druhy rostlin zakódovány, konkrétně do celočíselné hodnoty 0–2, která odpovídá druhům [‚setosa‘ ‚versicolor‘ ‚virginica‘]. Ony celočíselné hodnoty nalezneme v atributu targets (vektor o velikosti 150 prvků) a převod mezi hodnotami 0–2 a jmény druhů najdeme v atributu target_names (vektor jmen):
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
print(dir(iris))
print("-" * 100)
# jmena atributu
print("Feature names:")
print(iris["feature_names"])
print("-" * 100)
# vazba mezi numerickou hodnotou a lidskym vyjadrenim hodnoty
# atributu
print("Target names:")
print(iris["target_names"])
print("-" * 100)
# druhy rostlin z datove sady v numericke podobe
print("Targets:")
print(iris["target"])
Povšimněte si, že prakticky všechny informace jsou reprezentovány formou vektoru, matice, nebo vícerozměrného pole:
['DESCR', 'data', 'data_module', 'feature_names', 'filename', 'frame', 'target', 'target_names'] ---------------------------------------------------------------------------------------------------- Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] ---------------------------------------------------------------------------------------------------- Target names: ['setosa' 'versicolor' 'virginica'] ---------------------------------------------------------------------------------------------------- Targets: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
7. Korelační diagram pro dvojici vybraných proměnných
Nyní tedy alespoň rámcově víme, s jakou datovou sadou budeme pracovat. Naším úkolem (který dnes ovšem ještě nevyřešíme k plné spokojenosti) bude navržení takového postupu (algoritmu, modelu, funkce atd.), který dokáže na základě čtyř rozměrů květů odpovědět, o jaký druh kosatce se jedná, tj. zda tyto rozměry odpovídají květům Iris Setosa, Iris Versicolour nebo Iris Virginica.
Existuje ovšem vůbec nějaký vztah mezi rozměry květů a druhem rostliny? Pokusme se prozatím zjistit nějakými jednoduchými prostředky základní struktury (vzory atd.) v dostupných datech. Sice nezískáme všechny odpovědi, ale použijeme postupy, které nám však ukážou, jak lze kombinovat scikit-learn, knihovnu NumPy, knihovnu Pandas a konečně knihovnu Matplotlib.
Můžeme začít klasickým korelačním diagramem a zjistit, jaký je vztah (například) mezi dvěma prvními rozměry (sepal length, sepal width). To je pro knihovnu Matplotlib snadný úkol. Užitečné je ovšem vědět, jak z pole (matice) s rozměry květů získat první a druhý sloupec. Navíc jednotlivé body korelačního diagramu obarvíme podle druhu rostliny (tuto informaci máme k dispozici):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# vykresleni korelacniho diagramu pro dvojici vybranych atributu
# první sloupec: x-ové souřadnice
# druhý sloupec: y-ové souřadnice
plt.scatter(data[:, 0], data[:, 1], c=iris.target)
plt.title("Classes")
# popisky os
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
# ulozeni diagramu do souboru
plt.savefig("50.png")
# zobrazeni diagramu
plt.show()
A takto vypadá výsledek:
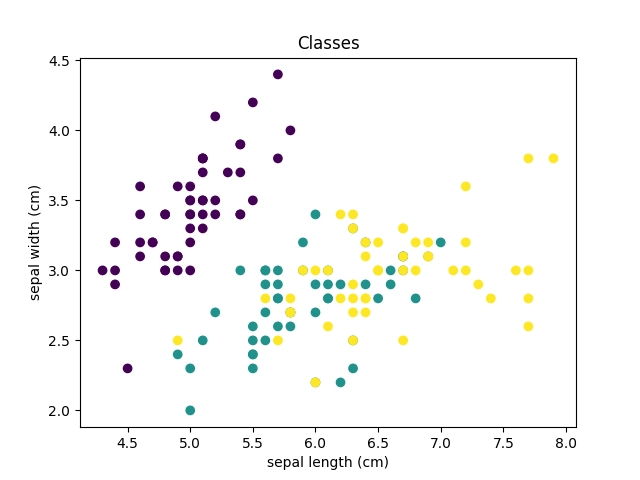
Obrázek 9: Korelační diagram pro atributy sepal_width a sepal_height.
8. Příprava pro tvorbu složitějších grafů
Skript z předchozí kapitoly sice skutečně vykreslil korelační diagram (a navíc velmi snadno), ovšem zvolený postup není ve skutečnosti příliš flexibilní. V praxi totiž velmi často potřebujeme tvořit složitější grafy, které například obsahují více průběhů, více grafů v mřížce, je nutné nastavit rozměry grafů atd. atd. V takovém případě je výhodnější nejprve zavolat funkci plt.subplots, která vrátí dvojici objektů využitelných pro všechny tyto operace. První vrácený objekt je typu Figure (prozatím ho budeme ignorovat) a druhý je typu Axes, což je objekt nebo pole objektů představujících jednotlivé grafy v obrázku (Figure). Nenechte se zmást tímto jménem, protože se v žádném případě nejedná pouze o osy grafu.
Do grafu navíc můžeme vložit popisky os a taktéž legendu, v našem případě názvy druhů kosatců:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# vykresleni korelacniho diagramu pro dvojici vybranych atributu
_, ax = plt.subplots()
# první sloupec: x-ové souřadnice
# druhý sloupec: y-ové souřadnice
scatter = ax.scatter(data[:, 0], data[:, 1], c=iris.target)
# popisky os
ax.set(xlabel=iris.feature_names[0], ylabel=iris.feature_names[1])
# pridani legendy do diagramu
ax.legend(scatter.legend_elements()[0], iris.target_names, loc="upper right", title="Classes")
# ulozeni diagramu do souboru
plt.savefig("51.png")
# zobrazeni diagramu
plt.show()
Výsledek by měl být podobný, jako v příkladu z předchozí kapitoly:
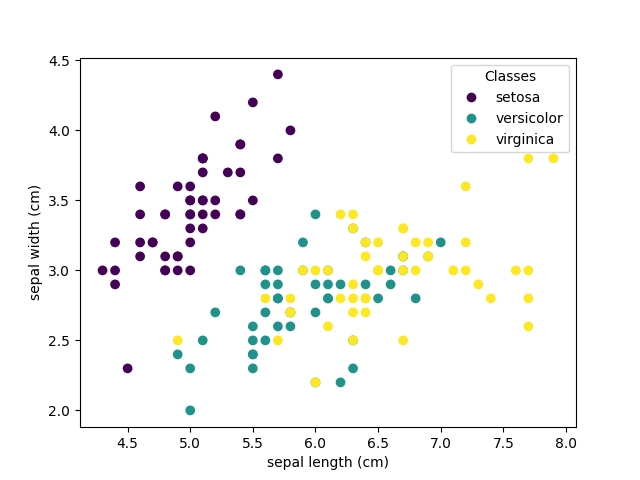
Obrázek 10: Korelační diagram pro atributy sepal_width a sepal_height.
9. Mřížka obsahující více korelačních diagramů
Korelační diagram nám může prozradit vztah či vztahy mezi naměřenými či jinak získanými daty a požadovanou odpovědí, resp. kategorií (tedy v našem případě o tom, o jaký druh rostliny se jedná). Ovšem prakticky můžeme zobrazovat pouze dvourozměrné či trojrozměrné korelační diagramy, zatímco máme k dispozici čtyři různé rozměry květů. V takovém případě si můžeme pomoci tím, že namísto jednoho korelačního diagramu jich nakreslíme větší množství – pro každou kombinaci naměřených hodnot.
Necháme si tedy vytvořit mřížku grafů o rozměrech 4×4 a do této mřížky jednotlivé varianty korelačního diagramu vložíme. Na diagonále bude vynechané místo, protože vztah mezi jednou a tou samou veličinou by vedl k diagramu, na kterém by byly body jen na diagonále a takový graf nepotřebujeme:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# vykresleni mrizky korelacnich diagramu
fig, axes = plt.subplots(nrows=4, ncols=4)
# rozmery grafu
fig.set_figheight(15)
fig.set_figwidth(15)
# vyplneni mrizky
for row in range(4):
for column in range(4):
ax = axes[row][column]
if row == column:
# na diagonale jsou prazdna mista
fig.delaxes(ax)
continue
# pridat korelacni diagram do mrizky
scatter = ax.scatter(data[:, row], data[:, column], c=iris.target)
# popisky os
ax.set(xlabel=iris.feature_names[row], ylabel=iris.feature_names[column])
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("52.png")
# zobrazeni diagramu
plt.show()
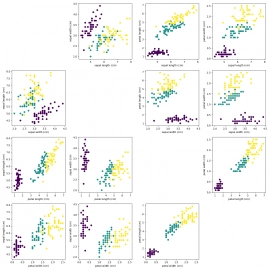
Obrázek 11: Mřížka korelačních diagramů.
10. Zobrazení základního histogramu pro data v sadě Iris
Dalším prostředkem pro prvotní průzkum dat, která jsme nějakým způsobem získali, může být výpočet základních statistických veličin, tedy maxima, minima, průměru, mediánu, směrodatné odchylky atd. Ovšem nesmíme zapomenout na histogramy, které je většinou velmi jednoduché interpretovat (náhodnost hodnot, odhad průměru a mediánu, míru směrodatné odchylky atd.). Histogramy jsou pochopitelně podporovány i knihovnou Matplotlib, takže si ukažme, jakým způsobem lze zobrazit histogram pro každý změřený rozměr květu pro všechny rostliny v datové sadě. Měří se celkem čtyři rozměry, takže získáme i čtyři histogramy (opět použijeme mřížku grafů):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# vykresleni sady histogramu do mrizky
fig, axes = plt.subplots(nrows=2, ncols=2)
fig.set_figheight(15)
fig.set_figwidth(15)
# vykresleni jednotlivych histogramu do mrizky
for i in range(4):
ax = axes[i//2][i%2]
ax.hist(data[:, i], bins=20)
ax.set(xlabel=iris.feature_names[i])
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("53.png")
# zobrazeni diagramu
plt.show()
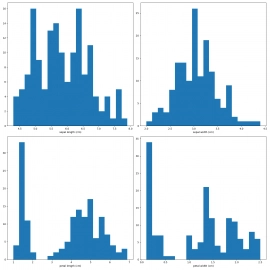
Obrázek 12: Mřížka s histogramy.
Zobrazení histogramů, stejně jako i dalších typů grafů, lze různým způsobem modifikovat, takže již jen krátce (změna počtu intervalů i způsobu zobrazení):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# vykresleni sady histogramu do mrizky
fig, axes = plt.subplots(nrows=2, ncols=2)
fig.set_figheight(15)
fig.set_figwidth(15)
# vykresleni jednotlivych histogramu do mrizky
for i in range(4):
ax = axes[i//2][i%2]
# modifikace zpusobu vypoctu a zobrazeni histogrami
ax.hist(data[:, i], bins=50, histtype="step")
ax.set(xlabel=iris.feature_names[i])
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("54.png")
# zobrazeni diagramu
plt.show()
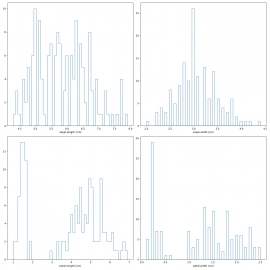
Obrázek 13: Mřížka s histogramy.
11. Analýza hlavních komponent (PCA)
Nyní již nastává okamžik, abychom se pokusili v datech (tedy rozměrech květů) nalézt nějakou strukturu závisející na kombinaci všech rozměrů. V takovém případě nám již běžné 2D korelační diagramy nebo histogramy přestanou dostačovat. Jednou z dalších technologií, ke které se ještě podrobněji vrátíme, je takzvaná analýza hlavních komponent neboli Principal Component Analysis, zkráceně pak PCA. Jedná se o algoritmus, který se pokusí vstupní data vhodným způsobem transformovat (bez ztráty informace) do jiné souřadné soustavy (v 2D případě by se tedy jednalo o rotaci, zkosení, teoreticky i zrcadlení) tak, aby bylo posléze možné snížit počet rozměrů, a to s nejmenší možnou ztrátou informace.
Původní data představují body ve čtyřrozměrném prostoru a vyloučením jedné nebo dvou dimenzí přijdeme o důležité informace (výsledkem jsou pak korelační diagramy, které již známe). Pokud ovšem nejdříve provedeme transformaci do jiné čtyřrozměrné souřadné soustavy tak, že jedna z dimenzí ponese menší množství informací, můžeme tuto dimenzi odstranit a stále být schopni data analyzovat bez větší chyby. Takže si ukažme snížení počtu dimenzí přes PCA ze čtyř na tři:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# Principal component analysis
reduced = PCA(n_components=3).fit_transform(data)
# vykresleni vysledku do matice s diagramy
fig, axes = plt.subplots(nrows=2, ncols=2)
fig.set_figheight(15)
fig.set_figwidth(15)
# graf v matici
ax = axes[0][0]
scatter = ax.scatter(reduced[:, 0], reduced[:, 1], c=iris.target)
# graf v matici
ax = axes[1][0]
scatter = ax.scatter(reduced[:, 0], reduced[:, 2], c=iris.target)
# graf v matici
ax = axes[1][1]
scatter = ax.scatter(reduced[:, 1], reduced[:, 2], c=iris.target)
# prazdne misto v matici
ax = axes[0][1]
fig.delaxes(ax)
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni diagramu do souboru
plt.savefig("55.png")
# zobrazeni diagramu
plt.show()
Výsledkem PCA jsou v tomto případě body v 3D, které již zobrazíme na trojici korelačních diagramů:
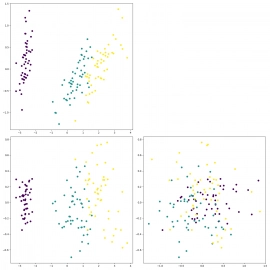
Obrázek 14: Výsledek PCA (z 4D bodů na 3D body zobrazené na trojici korelačních diagramů).
12. Zobrazení PCA v 3D grafu
Díky PCA dokážeme získat body v 2D nebo 3D prostoru. Pokusme se tedy o zobrazení bodů v 3D prostoru přímo 3D grafem. Jedná se o pouhopouhé rozšíření korelačních diagramů o jednu dimenzi. Nicméně z výsledku je patrné, že vstupní data skutečně mají nějakou interní strukturu související s druhem rostlin, protože stejně zbarvené body jsou sdruženy a částečně odděleny od ostatních dvou skupin:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
# Principal component analysis
reduced = PCA(n_components=3).fit_transform(data)
# vykresleni korelacniho grafu ve 3D
fig = plt.figure(1)
ax = fig.add_subplot(111, projection="3d", elev=-150, azim=110)
ax.scatter(
reduced[:, 0],
reduced[:, 1],
reduced[:, 2],
c=iris.target,
s=40,
)
# zbavit se prazdneho mista okolo bunek mrizky
plt.tight_layout()
# ulozeni grafu do souboru
plt.savefig("56.png")
# zobrazeni grafu
plt.show()
Výsledek bude v tomto případě vypadat následovně:
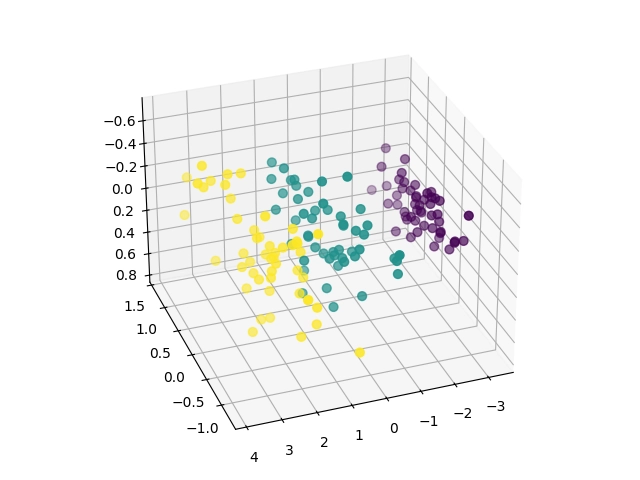
Obrázek 15: Výsledek PCA (z 4D bodů na 3D body zobrazené v 3D diagramu.
13. Základní shluková analýza
Jedním z velmi užitečných nástrojů, které v knihovně scikit-learn nalezneme, je podpora pro provádění takzvané shlukové analýzy (cluster analysis, clustering). Jedná se o proces, který se používá jako vstup pro klasifikaci objektů ve chvíli, kdy nemáme k dispozici trénovací data i s očekávanými výsledky a tudíž nemůžeme provádět učení s učitelem – supervised learning.
Zjednodušeně řečeno se používá k rozdělení vstupních dat (či již nějakým způsobem upravených dat) do skupin, přičemž se očekává, že data, která budou náležet do stejné skupiny, budou představovat objekty (i když možná by bylo lepší říci informace) s podobnými vlastnostmi. V našem konkrétním případě budeme chtít rozdělit body v 4D prostoru (= rozměry květů) do tří oblastí, přičemž každá oblast by mohla odpovídat jednomu druhu rostliny. Zda se nám to povede či nikoli, si posléze zverifikujeme.
Pokusme se tedy rozdělit body do tří clusterů se zobrazením prvních dvou sad souřadnic ve formě korelačního diagramu (což již známe). Body budou obarveny podle toho, do kterého clusteru byly přiděleny. Taktéž si necháme zobrazit středy clusterů:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
plt.figure(1)
colors = ["#4444cc", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
# clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init="auto").fit(data)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
plt.scatter(data[selector, 0], data[selector, 1], c=color, marker=".", s=20)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=100)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig("57.png")
# vykreslení na obrazovku
plt.show()
Výsledný korelační diagram by měl vypadat takto:
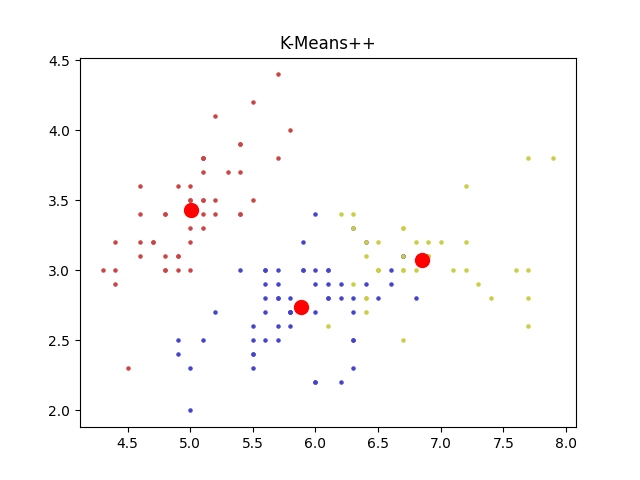
Obrázek 16: Výsledky shlukové analýzy pro první dva rozměry květů.
14. Výsledky shlukové analýzy pro různé kombinace atributů
Skript z předchozí kapitoly vykreslil pouze jednu kombinaci rozměrů, konkrétně první a druhý rozměr květů (což odpovídá atributům nazvaným sepal length a sepal width). Ovšem výsledkem shlukové analýzy je rozdělení původních bodů v 4D prostoru, takže si snadno můžeme zobrazit i další varianty korelačních diagramů a zjistit, zda nám některá kombinace napoví, jak dobré či naopak špatné rozdělení do tří clusterů je:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# nacteni datove sady
data = iris.data
# mrizka s diagramy/grafy
fig, axes = plt.subplots(nrows=2, ncols=2)
fig.set_figheight(15)
fig.set_figwidth(15)
plt.figure(1)
colors = ["#4444cc", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
# clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init="auto").fit(data)
def draw_kmeans(col, row, serie1, serie2):
ax = axes[col][row]
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
ax.scatter(data[selector, serie1], data[selector, serie2], c=color, marker=".", s=50)
ax.scatter(kmeans.cluster_centers_[:, serie1], kmeans.cluster_centers_[:, serie2], c="red", s=100)
ax.set(xlabel=iris.feature_names[serie1], ylabel=iris.feature_names[serie2])
draw_kmeans(0, 0, 0, 1)
draw_kmeans(0, 1, 0, 2)
draw_kmeans(1, 0, 1, 2)
draw_kmeans(1, 1, 1, 3)
plt.tight_layout()
# uložení grafu do souboru
plt.savefig("58.png")
# vykreslení na obrazovku
plt.show()
Výsledek by měl v tomto případě vypadat následovně:
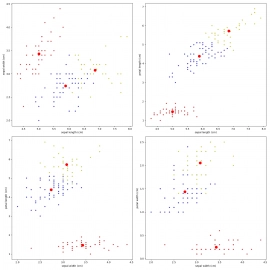
Obrázek 17: Výsledky shlukové analýzy pro různé kombinace měřených rozměrů květů.
15. Vizualizace chybných „klasifikací“ provedených shlukovou analýzou
Pokusme se nyní zjistit, jak se liší rozdělení květů provedených standardním algoritmem shlukové analýzy od skutečným druhů rostlin. Jak budeme postupovat? Shluková analýza nám všechny body rozdělí do třech skupin, tedy do skupin, které můžeme označit indexy 0, 1 a 2. A přímo ve zdrojové datové sadě máme informaci o tom, kterého druhu je každý květ. A i tato informace je, jak již ostatně víme (viz též šestou kapitolu) reprezentována hodnotami 0, 1 a 2. Můžeme tedy pro každý květ s indexem 0..149 tyto dvě hodnoty porovnat a vykreslit zelený bod v případě, že dojde ke shodě a červený bod v případě, že ke shodě nedojde.
Ovšem pozor – parametry shlukové analýzy byly schválně nastaveny tak, aby takové snadné porovnání bylo možné provést. Problém spočívá v tom, že nám vlastně nic nezaručuje, že cluster číslo 0 skutečně odpovídá druhu rostliny číslo 0 atd. (mapování může být odlišné). Ovšem dnes si ještě nebudeme moc komplikovat život a použijeme takové nastavení, které nám zaručí, že 0==0, 1==1 a 2==2:
kmeans = SpectralClustering(n_clusters=3, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(data)
Skript z této kapitoly vykreslí trojici grafů, přičemž poslední graf vizualizuje chybně zařazené rostliny. A nutno říci, že výsledky nejsou tak špatné, s ohledem na to, že se jedná o učení bez učitele:
# vizualizace chybne "predpovedi" clusteringu
ax = axes[2]
colors = []
for i in range(len(targets)):
t = targets[i]
k = kmeans.labels_[i]
color = "#cc4444"
# cislo clusteru odpovida druhu rostliny
if t == k:
color = "#44cc44"
colors.append(color)
ax.scatter(data[:, 0], data[:, 1], c=colors)
Celý skript vypadá následovně:
import matplotlib.pyplot as plt
import numpy
from sklearn.cluster import KMeans
from sklearn.cluster import SpectralClustering
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = iris.data
targets = iris.target
# clustering
# kmeans = KMeans(n_clusters=3, random_state=0, n_init="auto").fit(data)
kmeans = SpectralClustering(n_clusters=3, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(data)
# vykresleni mrizky korelacnich diagramu
fig, axes = plt.subplots(nrows=3, ncols=1)
fig.set_figheight(15)
fig.set_figwidth(10)
# korektni druhy z datove sady
ax = axes[0]
scatter = ax.scatter(data[:, 0], data[:, 1], c=iris.target)
colors = ["#4444cc", "#cc4444", "#cccc44"]
# rozdeleni do clusteru provedene algoritmem
ax = axes[1]
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
ax.scatter(data[selector, 0], data[selector, 1], c=color)
# vizualizace chybne "predpovedi" clusteringu
ax = axes[2]
colors = []
for i in range(len(targets)):
t = targets[i]
k = kmeans.labels_[i]
color = "#cc4444"
# cislo clusteru odpovida druhu rostliny
if t == k:
color = "#44cc44"
colors.append(color)
ax.scatter(data[:, 0], data[:, 1], c=colors)
plt.tight_layout()
# uložení grafu do souboru
plt.savefig("59.png")
# vykreslení na obrazovku
plt.show()
Výsledky:
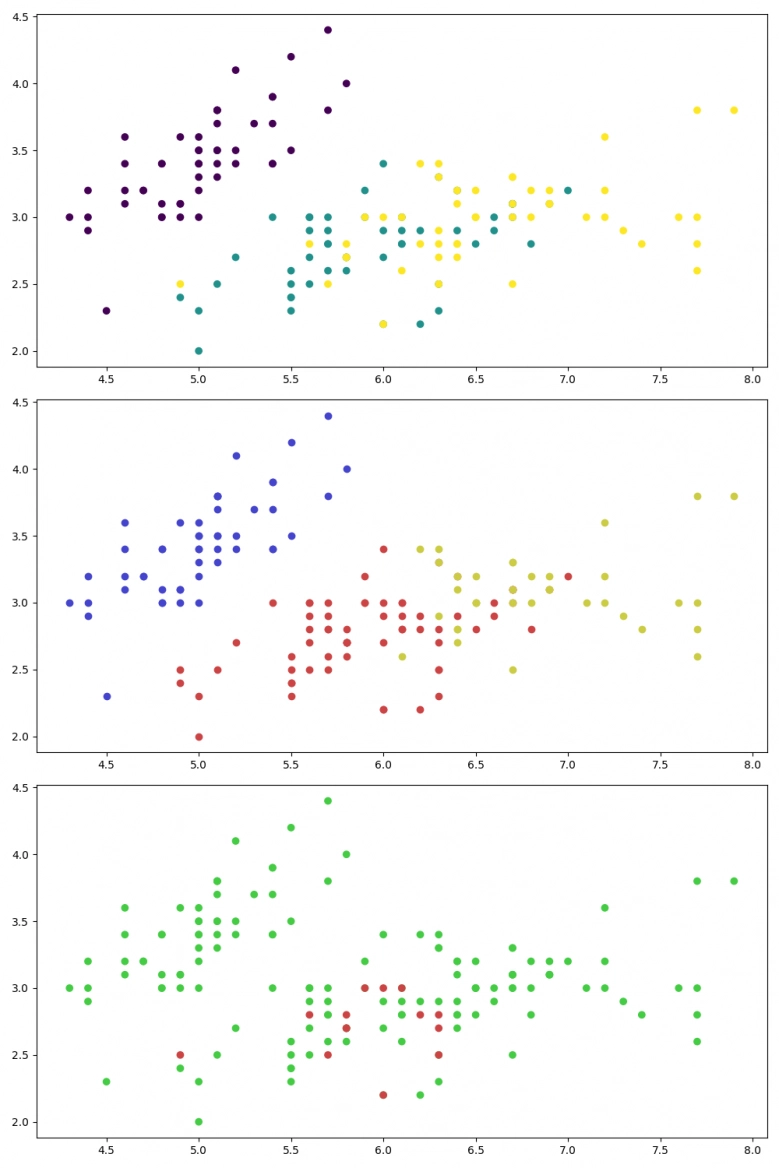
Obrázek 18: Výsledky shlukové analýzy s obarvením bodů podle toho, zda bod (rozměry jednoho květu) byly zařazeny do správného clusteru.
16. Trénink modelu s učitelem
Knihovna scikit-learn obsahuje i mnoho modelů, které je možné natrénovat s tzv. učitelem (supervised learning). Jedná se o modely, kterým se předloží trénovací data (tedy v našem případě rozměry jednotlivých květů) společně s informací o tom, jakého typu je daná rostlina. Model se tedy může natrénovat na základě očekávaných odpovědí.
Nejprve si připravíme potřebné vstupy. Je jím matice s rozměry květů (matice = velké písmeno) a vektor s druhy rostlin (očekávané odpovědi):
# X je matice (feature matrix) X = iris.data # y je vektor (response vector) y = iris.target
Dále model zkonstruujeme (vybereme si KNeighborsClassifier, více info příště) a natrénujeme ho předáním vstupních dat i očekávaných odpovědí:
# konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=1) # trening modelu (se vsemi dostupnymi daty) classifier.fit(X, y)
A nakonec modelu předáme neznámé rozměry (na které nebyl natrénován) a zjistíme, o jaké druhy rostlin se podle mínění modelu jedná. Klasifikace pro jednu rostlinu (i s převodem předpovědi na jméno druhu):
# parametry jedne rostliny unknown = [[3, 5, 4, 2]] print(unknown) # predikce modelu pro jednu sadu dat prediction = classifier.predict(unknown) print(prediction) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[prediction])
Klasifikace pro více rostlin:
# parametry vice rostlin unknown = [[3, 5, 4, 2], [5, 4, 3, 2]] print(unknown) # predikce modelu pro vice sad dat predictions = classifier.predict(unknown) print(predictions) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[predictions])
Předpovědi (klasifikace) modelu:
[[3, 5, 4, 2]] [2] ['virginica'] [[3, 5, 4, 2], [5, 4, 3, 2]] [2 1] ['virginica' 'versicolor']
Celý skript vypadá následovně:
from sklearn.datasets import load_iris from sklearn.neighbors import KNeighborsClassifier # nacteni datove sady iris = load_iris() # X je matice (feature matrix) X = iris.data # y je vektor (response vector) y = iris.target # konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=1) # trening modelu (se vsemi dostupnymi daty) classifier.fit(X, y) # parametry jedne rostliny unknown = [[3, 5, 4, 2]] print(unknown) # predikce modelu pro jednu sadu dat prediction = classifier.predict(unknown) print(prediction) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[prediction]) print() # parametry vice rostlin unknown = [[3, 5, 4, 2], [5, 4, 3, 2]] print(unknown) # predikce modelu pro vice sad dat predictions = classifier.predict(unknown) print(predictions) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[predictions])
17. Ladění parametrů modelu
Model, který jsme použili, tedy KNeighborsClassifier, je možné různými způsoby nakonfigurovat předáním takzvaných hyperparametrů do konstruktoru. Tyto parametry, společně s jejich poměrně podrobným popisem, lze zjistit v nápovědě, kterou má scikit-learn dosti kvalitní:
$ help(KNeighborsClassifier)
| Parameters
| ----------
| n_neighbors : int, default=5
| Number of neighbors to use by default for :meth:`kneighbors` queries.
|
| weights : {'uniform', 'distance'}, callable or None, default='uniform'
| Weight function used in prediction. Possible values:
|
| - 'uniform' : uniform weights. All points in each neighborhood
| are weighted equally.
| - 'distance' : weight points by the inverse of their distance.
| in this case, closer neighbors of a query point will have a
| greater influence than neighbors which are further away.
| - [callable] : a user-defined function which accepts an
| array of distances, and returns an array of the same shape
| containing the weights.
|
| Refer to the example entitled
| :ref:`sphx_glr_auto_examples_neighbors_plot_classification.py`
| showing the impact of the `weights` parameter on the decision
| boundary.
|
| algorithm : {'auto', 'ball_tree', 'kd_tree', 'brute'}, default='auto'
| Algorithm used to compute the nearest neighbors:
|
| - 'ball_tree' will use :class:`BallTree`
| - 'kd_tree' will use :class:`KDTree`
| - 'brute' will use a brute-force search.
| - 'auto' will attempt to decide the most appropriate algorithm
| based on the values passed to :meth:`fit` method.
|
| Note: fitting on sparse input will override the setting of
| this parameter, using brute force.
|
| leaf_size : int, default=30
| Leaf size passed to BallTree or KDTree. This can affect the
| speed of the construction and query, as well as the memory
| required to store the tree. The optimal value depends on the
| nature of the problem.
|
| p : float, default=2
| Power parameter for the Minkowski metric. When p = 1, this is equivalent
| to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2.
| For arbitrary p, minkowski_distance (l_p) is used. This parameter is expected
| to be positive.
|
| metric : str or callable, default='minkowski'
| Metric to use for distance computation. Default is "minkowski", which
| results in the standard Euclidean distance when p = 2. See the
| documentation of `scipy.spatial.distance
| <https://docs.scipy.org/doc/scipy/reference/spatial.distance.html>`_ and
| the metrics listed in
| :class:`~sklearn.metrics.pairwise.distance_metrics` for valid metric
| values.
|
| If metric is "precomputed", X is assumed to be a distance matrix and
| must be square during fit. X may be a :term:`sparse graph`, in which
| case only "nonzero" elements may be considered neighbors.
|
| If metric is a callable function, it takes two arrays representing 1D
| vectors as inputs and must return one value indicating the distance
| between those vectors. This works for Scipy's metrics, but is less
| efficient than passing the metric name as a string.
|
| metric_params : dict, default=None
| Additional keyword arguments for the metric function.
...
...
...
Předání odlišných parametrů může pochopitelně odlišit i predikce modelu. Zkusme tedy namísto volání:
# konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=1)
Použít odlišný hyperparametr n_neighbors:
# konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=5)
Výsledky budou v takovém případě ovšem zcela jiné (pouze poslední druh je odhadnutý stejně):
[[3, 5, 4, 2]] [1] ['versicolor'] [[3, 5, 4, 2], [5, 4, 3, 2]] [1 1] ['versicolor' 'versicolor']
Celý skript, který vypsal výše uvedené výsledky:
from sklearn.datasets import load_iris from sklearn.neighbors import KNeighborsClassifier # nacteni datove sady iris = load_iris() # X je matice (feature matrix) X = iris.data # y je vektor (response vector) y = iris.target # konstrukce klasifikatoru # (s hyperparametrem) classifier = KNeighborsClassifier(n_neighbors=5) # trening modelu (se vsemi dostupnymi daty) classifier.fit(X, y) # parametry jedne rostliny unknown = [[3, 5, 4, 2]] print(unknown) # predikce modelu pro jednu sadu dat prediction = classifier.predict(unknown) print(prediction) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[prediction]) print() # parametry vice rostlin unknown = [[3, 5, 4, 2], [5, 4, 3, 2]] print(unknown) # predikce modelu pro vice sad dat predictions = classifier.predict(unknown) print(predictions) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[predictions])
18. Použití odlišného modelu
Viděli jsme, že stejný model s odlišnými hyperparamery dává odlišné výsledky, takže asi nepřekvapí, že pokud použijeme zcela odlišný model, taktéž dostaneme odlišné výsledky. Například můžeme použít model LogisticRegression, který bude podrobněji popsán příště:
# konstrukce klasifikatoru # (s hyperparametrem) classifier = LogisticRegression(max_iter=1000) classifier.fit(X, y)
Nyní budou odpovědi modelu na neznámé vstupy odlišné od předchozího modelu:
[[3, 5, 4, 2]] [0] ['setosa'] [[3, 5, 4, 2], [5, 4, 3, 2]] [0 0] ['setosa' 'setosa']
Celý skript vypadá následovně (prakticky se nezměnil, až na odlišný model):
from sklearn.datasets import load_iris from sklearn.linear_model import LogisticRegression # nacteni datove sady iris = load_iris() # X je matice (feature matrix) X = iris.data # y je vektor (response vector) y = iris.target # konstrukce klasifikatoru # (s hyperparametrem) classifier = LogisticRegression(max_iter=1000) # trening modelu (se vsemi dostupnymi daty) classifier.fit(X, y) # parametry jedne rostliny unknown = [[3, 5, 4, 2]] print(unknown) # predikce modelu pro jednu sadu dat prediction = classifier.predict(unknown) print(prediction) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[prediction]) print() # parametry vice rostlin unknown = [[3, 5, 4, 2], [5, 4, 3, 2]] print(unknown) # predikce modelu pro vice sad dat predictions = classifier.predict(unknown) print(predictions) # model predikuje hodnoty 0-3, ty si prevedeme na druhy rostlin print(iris.target_names[predictions])
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/



































