Obsah
1. Datový typ Decimal v programovacím jazyku Python
2. Základní numerické datové typy programovacího jazyka Python
3. Další numerické datové typy dostupné v knihovnách
4. Od typu float k typu Decimal
6. Přepis počítané programové smyčky
10. Hodnoty, které nelze uložit přesně
14. Nastavení přesnosti výpočtů i uložení výsledků
15. Změna zaokrouhlovacího režimu
16. Zachytávání výjimek při výpočtech
17. Určení maximálního exponentu a reakce na přetečení hodnoty
18. Příloha: „numerická věž“ v programovacích jazycích
19. Repositář s demonstračními příklady
1. Datový typ Decimal v programovacím jazyku Python
Na úterní článek o numerických datových typech Decimal32, Decimal64 a Decimal128 dnes alespoň částečně navážeme. Budeme se totiž zabývat tím, jakým způsobem je dekadický formát s plovoucí řádovou čárkou realizován v programovacím jazyku Python. Již v základní knihovně Pythonu totiž nalezneme standardní modul nazvaný příznačně Decimal, který obsahuje implementaci dekadického formátu s plovoucí řádovou čárkou. Ovšem již na úvod je nutné poznamenat, že se v tomto případě nejedná o formáty Decimal32/64/128 tak, jak jsou popsány v normě IEEE 754–2008, protože interní struktura hodnot typu Decimal je odlišná. Ovšem základní myšlenka zůstává zachována – je použit formát s plovoucí řádovou čárkou (tečkou) a exponentem s desítkovou bází, který navíc dokáže pracovat s nekonečny atd.
2. Základní numerické datové typy programovacího jazyka Python
Připomeňme si, že v programovacím jazyku Python existují tři základní numerické datové typy, které jsou „vhodně“ pojmenovány takovým způsobem, že mohou mnohé programátory poměrně úspěšně zmást. Jedná se o datové typy int, float a complex. Numerický datový typ int umožňuje práci s celočíselnými typy s prakticky neomezeným rozsahem, na rozdíl od podobně pojmenovaného typu v jiných jazycích (C, C++, Java, Go, …), kde se jedná o celočíselný typ s předem specifikovaným omezeným rozsahem (například 32bitů či 64bitů). Druhý standardní numerický datový typ se v Pythonu jmenuje float, což může být opět matoucí, protože interně se jedná o céčkovský typ double. A konečně numerický typ complex sestává z dvojice hodnot typu float, které reprezentují reálnou a imaginární složku komplexního čísla. Komplexní jednotka se v Pythonu zapisuje znakem j a nikoli i:
>>> type(10)
<class 'int'>
>>> type(10**10000000)
<class 'int'>
>>> type(3.14)
<class 'float'>
>>> type(1+2j)
<class 'complex'>
>>> type(1+2i)
File "<stdin>", line 1
type(1+2i)
SyntaxError: invalid decimal literal
3. Další numerické datové typy dostupné v knihovnách
Kromě základní trojice typů popsaných v předchozí kapitole je však možné ve standardní knihovně Pythonu nalézt realizaci dvou dalších numerických datových typů. Jedná se o typ nazvaný Decimal a o typ Fraction (pozor, je umístěný v modulu fractions, tedy s „s“ na konci). V dnešním článku nás bude primárně zajímat především typ Decimal, i když si ukážeme, že typ Fraction je s Decimal v některých ohledech poměrně úzce propojen.
V některých oblastech IT je ovšem nutné pracovat i s dalšími numerickými datovými typy. V takovém případě může být vhodné využít například možnosti nabízené knihovnou NumPy, v níž nalezneme podporu pro tyto datové typy, a to včetně typu half (precision), se kterým se začínám setkávat poměrně často (popř. i s typem bfloat16):
╔════════════╤═══════════════════════════╤═══════════════════════════════╗ ║ Formát │ Popis │ Rozsah ║ ╟────────────┼───────────────────────────┼───────────────────────────────╢ ║ bool │ uloženo po bajtech │ True/False ║ ╟────────────┼───────────────────────────┼───────────────────────────────╢ ║ int8 │ celočíselný se znaménkem │ -128..127 ║ ║ int16 │ celočíselný se znaménkem │ -32768..32767 ║ ║ int32 │ celočíselný se znaménkem │ -2147483648..2147483647 ║ ║ int64 │ celočíselný se znaménkem │ -9223372036854775808.. ║ ║ │ │ 9223372036854775807 ║ ╟────────────┼───────────────────────────┼───────────────────────────────╢ ║ uint8 │ celočíselný bez znaménka │ 0..255 ║ ║ uint16 │ celočíselný bez znaménka │ 0..65535 ║ ║ uint32 │ celočíselný bez znaménka │ 0..4294967295 ║ ║ uint64 │ celočíselný bez znaménka │ 0..18446744073709551615 ║ ╟────────────┼───────────────────────────┼───────────────────────────────╢ ║ float16 │ plovoucí řádová čárka │ poloviční přesnost (half) ║ ║ float32 │ plovoucí řádová čárka │ jednoduchá přesnost (single) ║ ║ float64 │ plovoucí řádová čárka │ dvojitá přesnost (double) ║ ╟────────────┼───────────────────────────┼───────────────────────────────╢ ║ complex64 │ komplexní číslo (dvojice) │ 2×float32 ║ ║ complex128 │ komplexní číslo (dvojice) │ 2×float64 ║ ╚════════════╧═══════════════════════════╧═══════════════════════════════╝
4. Od typu float k typu Decimal
Datový typ Decimal, kterému se budeme dnes věnovat, je postaven na podobném principu, jako v úterním článku popsané typy Decimal32, Decimal64 či Decimal128. Jedná se tedy o vhodným způsobem uložené hodnoty s plovoucí řádovou čárkou, přičemž základem exponentu je hodnota 10 a nikoli dnes obvyklejší hodnota 2. Navíc není typ Decimal omezen pouze na podporu HW (tedy na FPU jednotku), takže umožňuje specifikovat jak způsoby zaokrouhlení, tak i přesnost (počet cifer), chování při dělení nulou atd. To jsou v praxi poměrně užitečné vlastnosti a ještě se k nim vrátíme v dalším textu.
Připomeňme si nejdříve, s jakými problémy se setkáme při použití datového typu (formátu) float, což je interně ve skutečnosti typ double:
x = 0.1 y = 0.1 z = 0.1 print(x+y+z-0.3)
V ideálním světě by měl tento skript vypsat nulu, ovšem ve skutečnosti dostaneme:
5.551115123125783e-17
To je sice hodnota, která je z určitého pohledu blízká nule, ale o nulu se nejedná.
Stejně tak i v Pythonu narazíme na problém při implementaci počítané programové smyčky s testem na koncovou hodnotu realizovaným porovnáním dvou hodnot typu float (ve skutečnosti se s takto zapsaným kódem často nesetkáme, což je ostatně jen dobře):
x = 0
while x != 1.0:
x += 0.1
print(x)
Tento skript neskončí po deseti iteracích, ale bude pokračovat dále:
.1 0.2 0.30000000000000004 0.4 0.5 0.6 0.7 0.7999999999999999 0.8999999999999999 0.9999999999999999 1.0999999999999999 1.2 1.3 1.4000000000000001 1.5000000000000002 1.6000000000000003 1.7000000000000004 1.8000000000000005 1.9000000000000006 2.0000000000000004 ... ... ...
Chyba se navíc bude akumulovat:
... ... ... 113638.50000212675 113638.60000212675 113638.70000212676 113638.80000212677 ... ... ...
5. Konstruktory typu Decimal
Datový typ Decimal umožňuje přesnou reprezentaci „problematických“ hodnot 0,1, 0,2 atd. Pokusme se tedy první příklad (tedy ve skutečnosti výpočet výrazu 0,1+0,1+0,1–0,3) přepsat tak, aby se použily hodnoty typu Decimal a nikoli float. Hodnoty typu Decimal se vytváří konstruktorem nazvaným taktéž Decimal:
from decimal import Decimal x = Decimal(0.1) y = Decimal(0.1) z = Decimal(0.1) print(x+y+z-Decimal(0.3))
Pokud ovšem očekáváme, že se vypíše nula, budeme překvapeni:
2.775557561565156540423631668E-17
Proč tomu tak je? Hodnoty 0,1 atd. samozřejmě lze typem Decimal reprezentovat zcela přesně, ovšem je nutné je nějakým způsobem získat v přesné podobě. A zápis Decimal(0.1) znamená „zkonstruuj hodnotu Decimal z float hodnoty 0,1“. Jenže již víme, že typ float nedokáže 0,1 reprezentovat přesně, takže sice provedeme přesné uložení i přesný výpočet, ovšem s nepřesnými vstupními daty (což je ovšem obvyklé i v jiných oblastech, než jenom v IT). Příklad si tedy upravme do takové podoby, že zkonstruujeme dekadický formát s plovoucí řádovou čárkou ze zápisu numerické hodnoty reprezentované řetězcem (i to je totiž možné a někdy se tomuto postupu nevyhneme):
from decimal import Decimal
x = Decimal("0.1")
y = Decimal("0.1")
z = Decimal("0.1")
print(x+y+z-Decimal("0.3"))
Nyní se po spuštění vypíše „přesná nula“, tedy skript se chová podle očekávání:
0.0
6. Přepis počítané programové smyčky
Podobným způsobem můžeme postupovat i při realizaci počítané programové smyčky. První (nekorektní) varianta bude vypadat následovně:
from decimal import Decimal
x = Decimal(0)
step = Decimal(0.1)
while x != Decimal("1.0"):
x += step
print(x)
Jedná se o (prakticky) nekonečnou smyčku, která zcela jistě u hodnoty 1.0 neskončí:
... ... ... 52110.30000000000289270478638 52110.40000000000289271033750 52110.50000000000289271588862 52110.60000000000289272143974 52110.70000000000289272699086 52110.80000000000289273254198 52110.90000000000289273809310 ... ... ...
Korektní zápis, v němž se vyhneme hodnotám typu float, by měl vypadat takto:
from decimal import Decimal
x = Decimal(0)
step = Decimal("0.1")
while x != Decimal("1.0"):
x += step
print(x)
Nyní bude vše funkční přesně podle předpokladů:
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
7. Výpočet hodnoty π
Zkusme si nyní provést nějaký výpočet, v němž by se do jisté míry využila konfigurovatelná přesnost hodnot uložených v typu Decimal. Pro jednoduchost jsem vybral jeden z dnes již nepoužívaných výpočtů hodnoty π z nekonečné řady (nepoužívaný proto, že konverguje velmi pomalu, což ovšem pro nás bude výhoda). Jedná se o takzvaný Wallis product, což je forma řady, která vypadá následovně:
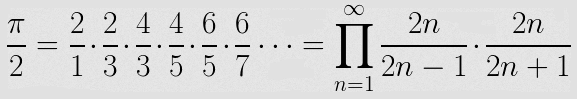
První realizace tohoto výpočtu bude založena na standardním numerickém datovém typu float, tedy na hodnotách s plovoucí čárkou a exponentem, jehož báze je rovna 2:
from math import pi
result = 2
for n in range(1, 1000):
m = 4 * n * n
u = m / (m-1)
result *= u
abs_error = pi - result
rel_error = 100.0 * abs_error / pi
print(result, "\t", abs_error, "\t", rel_error)
Po spuštění tohoto skriptu se bude vypisovat jak postupně se zpřesňující výsledek počítané nekonečně řady, tak i absolutní a relativní chyba vypočtená vůči konstantě π (ovšem typu float). Prvních 100 výsledků vypadá takto:
2.6666666666666665 0.4749259869231266 15.11736368432249 2.844444444444444 0.297148209145349 9.458521263277328 2.9257142857142853 0.21587836787550785 6.87162187079954 2.972154195011337 0.16943845857845607 5.393393646526529 3.0021759545569062 0.1394166990328869 4.437771360127803 3.0231701920013605 0.11842246158843261 3.769504026981831 3.038673628883419 0.10291902470637426 3.276014304043273 3.0505899960555105 0.0910026575342826 2.896704556215998 3.06003454712689 0.08155810646290318 2.5960751585572193 3.0677038066434985 0.0738888469462946 2.3519550461726566 3.074055160280442 0.06753749330935133 2.1497851808438146 3.0794013431678864 0.06219131042190673 1.9796108942017927 3.083963419231839 0.057629234357954306 1.8343955029339434 3.087902069831113 0.05369058375868008 1.7090243605366735 3.09133688859622 0.050255764993573315 1.5996906835183655 3.0943587232869296 0.04723393030286349 1.503502697871758 3.09703782174865 0.04455483184114328 1.4182243452292251 3.0994293567461395 0.04216329684365361 1.3420994219436762 3.101577263438271 0.04001539015152211 1.2737294284730982 3.103516961539233 0.03807569205056005 1.2119869202982834 3.105277322833356 0.036315330756437 1.1559528799808176 3.1068821173154406 0.0347105362743525 1.1048706850867482 3.108351092311807 0.033241561277986165 1.058111758696728 3.1097007888347385 0.031891864755054566 1.0151495840370264 3.110945166901499 0.0306474866882942 0.9755397999570167 3.1120960900117107 0.02949656357808239 0.9389047795352351 3.1131637044508227 0.028428949138970427 0.9049215564750451 3.1141567391252885 0.027435914464504663 0.8733122810544696 3.115082744697434 0.026509908892359046 0.8438366082269468 3.1159482858879586 0.025644367701834536 0.8162855764426229 3.1167590973076535 0.02483355628213957 0.7904766473706606 3.1175202106403295 0.024072442949463646 0.7662496575409568 3.1182360591387543 0.02335659445103877 0.7434634921351108 3.1189105640185164 0.02268208957127671 0.7219933349843635 3.119547206305518 0.022045447284275266 0.7017283815928417 3.12014908691642 0.021443566673373216 0.6825699267175955 3.120718977160606 0.02087367642918725 0.6644297568411868 3.1212593613990753 0.020333292190717778 0.6472287922969135 3.121772473245434 0.019820180344359173 0.6308959349555173 3.1222603264214372 0.019332327168355867 0.6153670860627161 3.1227247411658103 0.01886791242398278 0.6005843056203689 3.1231673669264293 0.01842528666336385 0.5864950900719064 3.1235897019320986 0.0180029516576945 0.5730517493133022 3.123993110133304 0.017599543456489286 0.5602108674521783 3.1243788359155156 0.017213817674277543 0.5479328344687809 3.124748016919405 0.01684463667038827 0.5361814381358597 3.125101695246164 0.016490958343629014 0.5249235073422185 3.125440827280374 0.016151826309418915 0.5141285994211491 3.1257662923253897 0.0158263612644034 0.50376872527758 3.126078900215411 0.015513753374382322 0.49381810708830354 3.1263793980429813 0.015213255546811855 0.4842529641590604 3.1266684761195456 0.014924177470247546 0.47505132319411897 3.126946773269178 0.014645880320615312 0.466192849791648 3.127214881540915 0.014377772048878246 0.4576586984454921 3.1274733504128496 0.014119303176943543 0.4494313787247333 3.1277226905508084 0.01386996303898469 0.44149463563126 3.1279633771757065 0.013629276414086622 0.43383334241353355 3.1281958530863103 0.013396800503482797 0.4264334043490559 3.1284205313778486 0.013172122211944526 0.4192816722083043 3.1286377978915914 0.012954855698201762 0.4123658642822035 3.1288480134259524 0.012744640163840693 0.40567449600054983 3.129051515735769 0.012541137854024331 0.3991968162929714 3.1292486213430593 0.01234403224673386 0.3929227499506897 3.129439627179679 0.012153026410114176 0.38684284533920454 3.1296248120798023 0.011967841509990862 0.3809482268910837 3.129804438138006 0.01178821545178721 0.37523055187683896 3.129978751946869 0.011613901642923974 0.36968197101088696 3.130147985726374 0.011444667863419244 0.36429509250162667 3.130312358355987 0.011280295233806026 0.35906294919923526 3.1304720763190645 0.011120577270728571 0.3539789685343661 3.13062733456815 0.010965319021642994 0.34903694497481363 3.1307783173187924 0.010814336271000702 0.34423101475754725 3.1309251987786713 0.010667454811121857 0.33955563267989286 3.131068143818108 0.010524509771685064 0.33500555075652655 3.131207308587378 0.010385345002414947 0.3305757985698101 3.1313428410856936 0.01024981250409951 0.32626166515851096 3.1314748816862035 0.010117771903589645 0.3220586823065175 3.131603563620935 0.009989089968858167 0.31796260910668883 3.131729013429196 0.009863640160597154 0.31396941768775466 3.131851351372609 0.009741302217184167 0.31007528000337997 3.1319706918196375 0.009621961770155618 0.306276555592302 3.1320871436021926 0.009505509987600469 0.3025697802271991 3.1322008103466525 0.009391843243140574 0.298951655378008 3.132311790781417 0.009280862808376256 0.2954190384221622 3.1324201790229056 0.009172474566887523 0.2919689335409682 3.132526064841755 0.009066588748038118 0.2885984832463251 3.132629533910784 0.00896311967900898 0.28530496048770426 3.132730668036172 0.008861985553620944 0.28208576129354795 3.1328295453731676 0.008763108216625515 0.27893839790503083 3.132926240627508 0.008666412962285097 0.27586049236466975 3.133020825243655 0.008571828346138233 0.27284977052462517 3.133113367580835 0.008479286008958198 0.26990405644312926 3.133203933077802 0.008388720511991021 0.2670212671399492 3.1332925844071484 0.008300069182644698 0.26419940768452227 3.133379381619936 0.008213271969857328 0.2614365665921804 3.133464382281348 0.008128271308445179 0.25873091150621563 3.1335476415980024 0.008045011991790751 0.25608068514541454 3.1336292125375205 0.007963441052272646 0.25348420149802325 3.1337091459408963 0.007883507648896781 0.25093984224493776
Přepis do podoby využívající typ Decimal může vypadat následovně (nejedná se o nejideálnější způsob, protože neustále vytváříme nové objekty):
from decimal import Decimal
from math import pi
result = Decimal(2)
for n in range(1, 1000):
m = Decimal(4 * n * n)
u = m / (m-1)
result *= u
abs_error = Decimal(pi) - result
rel_error = Decimal(100.0) * abs_error / Decimal(pi)
print(result, "\t", abs_error, "\t", rel_error)
Opět si vypišme prvních 100 výsledků:
2.666666666666666666666666666 0.4749259869231264493312968025 15.11736368432248428105764000 2.844444444444444444444444445 0.2971482091453486715535190235 9.458521263277316566461482623 2.925714285714285714285714288 0.2158783678755074017122491805 6.871621870799525611217524929 2.972154195011337868480725626 0.1694384585784552475172378425 5.393393646526502208220977703 3.002175954556906937859318814 0.1394166990328861781386446545 4.437771360127780008304017886 3.023170192001360832529663701 0.1184224615884322834682997675 3.769504026981820427942507516 3.038673628883419093209303002 0.1029190247063740227886604665 3.276014304043265660906315248 3.050589996055510932790515956 0.09100265753428218320744751254 2.896704556215984349772614491 3.060034547126890223604108884 0.08155810646290289239385458454 2.596075158557210307511848612 3.067703806643498971031688105 0.07388884694629414496627536354 2.351955046172641912292580039 3.074055160280442033083513547 0.06753749330935108291444992154 2.149785180843806802380142291 3.079401343167886280097571832 0.06219131042190683590039163654 1.979610894201796031601672956 3.083963419231838704216234900 0.05762923435795441178172856854 1.834395502933946840537379182 3.087902069831113083148822684 0.05369058375868003284914078454 1.709024360536672187715587841 3.091336888596219994253548848 0.05025576499357312174441462054 1.599690683518359253552868850 3.094358723286929886721049874 0.04723393030286322927691359454 1.503502697871749634054875541 3.097037821748650172337258576 0.04455483184114294366070489254 1.418224345229214352352758525 3.099429356746139477489642560 0.04216329684365363850832090854 1.342099421943677066138359093 3.101577263438271244279309673 0.04001539015152187171865379554 1.273729428473090563758690563 3.103516961539233265069978411 0.03807569205055985092798505754 1.211986920298276986875487695 3.105277322833356483030880270 0.03631533075643663296708319854 1.155952879980805788342802227 3.106882117315440904985934989 0.03471053627435221101202847954 1.104870685086739021308354047 3.108351092311807543711696659 0.03324156127798557228626680954 1.058111758696709110680131090 3.109700788834739288194419932 0.03189186475505382780354353654 1.015149584037002948765532783 3.110945166901499888149679804 0.03064748668829322784828366454 0.9755397999569857430627578833 3.112096090011711319850808062 0.02949656357808179614715540654 0.9389047795352162224349601430 3.113163704450823399205816916 0.02842894913896971679214655254 0.9049215564750224715678709208 3.114156739125289371581959122 0.02743591446450374441600434654 0.8733122810544403415747506356 3.115082744697434863515227620 0.02650990889235825248273584854 0.8438366082269215905612432796 3.115948285887959296653186839 0.02564436770183381934477662954 0.8162855764426000905864061564 3.116759097307654315986169714 0.02483355628213880001179375454 0.7904766473706361561837484279 3.117520210640330177845995396 0.02407244294946293815196807254 0.7662496575409342358311681616 3.118236059138755052743319391 0.02335659445103806325464407754 0.7434634921350882965052969970 3.118910564018516842717955626 0.02268208957127627328000784254 0.7219933349843496177894210411 3.119547206305517968834044207 0.02204544728427514716391926154 0.7017283815928379520653527282 3.120149086916420056036211687 0.02144356667337305996175178154 0.6825699267175905737037986486 3.120718977160605703535031086 0.02087367642918741246293238254 0.6644297568411919601099546061 3.121259361399075072488024164 0.02033329219071804350993930454 0.6472287922969220366398438068 3.121772473245433625023366596 0.01982018034435949097459687254 0.6308959349555274816565526958 3.122260326421436974550640135 0.01933232716835614144732333354 0.6153670860627247824038032430 3.122724741165810236037260785 0.01886791242398287996070268354 0.6005843056203720715280638599 3.123167366926429061017563728 0.01842528666336405498039974054 0.5864950900719128755070189269 3.123589701932098625461244263 0.01800295165769449053671920554 0.5730517493133019103786223420 3.123993110133303855814526099 0.01759954345648926018343736954 0.5602108674521774498220393954 3.124378835915515647869818670 0.01721381767427746812814479854 0.5479328344687785335916185823 3.124748016919404991559747750 0.01684463667038812443821571854 0.5361814381358550760155335160 3.125101695246164403556528706 0.01649095834362871244143476254 0.5249235073422088796460955512 3.125440827280374513638303695 0.01615182630941860235965977354 0.5141285994211391247768222204 3.125766292325389652086042768 0.01582636126440346391192070054 0.5037687252775820216970321930 3.126078900215411193205363304 0.01551375337438192279260016454 0.4938181070882908507821104145 3.126379398042981645112813593 0.01521325554681147088514987554 0.4842529641590481602938649400 3.126668476119545952245972429 0.01492417747024716375199103954 0.4750513231941067870308315545 3.126946773269178310586181240 0.01464588032061480541178222854 0.4661928497916318521654136838 3.127214881540915357513265712 0.01437777204887775848469775654 0.4576586984454766289683087291 3.127473350412850303819366486 0.01411930317694281217859698254 0.4494313787247100760820345200 3.127722690550808754772393621 0.01386996303898436122556984754 0.4414946356312495570735104366 3.127963377175706854715046362 0.01362927641408626128291710654 0.4338333424135220656966019552 3.128195853086310771984070150 0.01339680050348234401389331854 0.4264334043490414653298755285 3.128420531377848968548889805 0.01317212221194414744907366354 0.4192816722082922763235787755 3.128637797891591440176679853 0.01295485569820167582128361554 0.4123658642822007624876403921 3.128848013425952227077182217 0.01274464016384088892078125154 0.4056744960005560806870953089 3.129051515735768549173252276 0.01254113785402456682471119254 0.3991968162929788810825872044 3.129248621343058991286586024 0.01234403224673412471137744454 0.3929227499506981238467498927 3.129439627179678844731699043 0.01215302641011427126626442554 0.3868428453392075969666819329 3.129624812079801909933470255 0.01196784150999120606449321354 0.3809482268910946439870361717 3.129804438138005422641381263 0.01178821545178769335658220554 0.3752305518768543348923903778 3.129978751946868580838130992 0.01161390164292453515983247654 0.3696819710109048419564333907 3.130147985726373683221523159 0.01144466786341943277644030954 0.3642950925016326551406429883 3.130312358355986999068985300 0.01128029523380611692897816854 0.3590629491992381601900122975 3.130472076319064502359922031 0.01112057727072861363804143754 0.3539789685343674646524945585 3.130627334568150405474654955 0.01096531902164271052330851354 0.3490369449748046202079501808 3.130778317318792708363754287 0.01081433627100040763420918154 0.3442310147575379119668220467 3.130925198778671610203227134 0.01066745481112150579473633454 0.3395556326798816857370292939 3.131068143818108156411974941 0.01052450977168495958598852754 0.3350055507565232362865310681 3.131207308587378706576711683 0.01038534500241440942125178554 0.3305757985697930048645250706 3.131342841085694396257990163 0.01024981250409871973997330554 0.3262616651584858063623766116 3.131474881686204018623423770 0.01011777190358909737453969854 0.3220586823065000794303235811 3.131603563620935319384410966 0.009989089968857796613552502544 0.3179626091066770467645923551 3.131729013429196383171591371 0.009863640160596732826372097544 0.3139694176877412889248600854 3.131851351372609375725330641 0.009741302217183740272632827544 0.3100752800033664204256579858 3.131970691819638016100886993 0.009621961770155099897076475544 0.3062765555922854985196421029 3.132087143602193124411580463 0.009505509987599991586383005544 0.3025697802271838917339391842 3.132200810346653374570332472 0.009391843243139741427630996544 0.2989516553779814669069289524 3.132311790781417455404211590 0.009280862808375660593751878544 0.2954190384221432491932523927 3.132420179022906137277473786 0.009172474566886978720489682544 0.2919689335409508945529255147 3.132526064841755574661690311 0.009066588748037541336273157544 0.2885984832463067053528630935 3.132629533910784204077864109 0.008963119679008911920099359544 0.2853049604877021242366071549 3.132730668036172768539658392 0.008861985553620347458305076544 0.2820857612935290072753233763 3.132829545373168513032558044 0.008763108216624602965405424544 0.2789383979050018327340007369 3.132926240627508868244540900 0.008666412962284247753422568544 0.2758604923646427167684689059 3.133020825243655579257077340 0.008571828346137536740886128544 0.2728497705246030054716893178 3.133113367580836015103459178 0.008479286008957100894504290544 0.2699040564430943539580420030 3.133203933077803231059958774 0.008388720511989884938004694544 0.2670212671399130588100135593 3.133292584407149291191556542 0.008300069182643824806406926544 0.2641994076844944444608867570 3.133379381619936547051585671 0.008213271969856568946377797544 0.2614365665921562770447384371 3.133464382281348258972673256 0.008128271308444857025290212544 0.2587309115062053820084430413 3.133547641598002473088761277 0.008045011991790642909202191544 0.2560806851454110736620104263 3.133629212537520838375058004 0.007963441052272277622905464544 0.2534842014980115008668434813 3.133709145940896537195004822 0.007883507648896578802958646544 0.2509398422449313287244274752
8. Problém zastavení výpočtů
Zkusme si nyní předchozí výpočet nepatrně upravit do takové podoby, že výpočet přibližné hodnoty π ukončíme ve chvíli, kdy je absolutní chyba menší než zadaná hodnota ε. Mohlo by se zdát, že zde nemůže dojít k žádným podstatným problémům, takže si to otestujme; nejprve ve variantě založené na typu float:
from math import pi
result = 2
n = 1
while True:
m = 4 * n * n
u = m / (m-1)
result *= u
abs_error = pi - result
n += 1
if abs(abs_error) < 0.00000001:
rel_error = 100.0 * abs_error / pi
print(result, "\t", abs_error, "\t", rel_error)
break
Tento výpočet ovšem nemusí nikdy skončit, což znamená, že vypočtená absolutní chyba nikdy nebude menší než nastavená hodnota ε=0.00000001. U typu float si tedy musíme dát pozor i na to, o kolik řádů se liší hodnoty, s nimiž provádíme výpočty (zde konkrétně není problém ve výpočtu chyby, ale podílu m/m-1. Konkrétně se výpočet „zasekne“ na absolutní chybě:
1.0523530935557801e-08
Pokusme se tedy výpočet upravit do podoby využívající výpočty s hodnotami Decimal:
from decimal import Decimal
from math import pi
result = Decimal(2)
n = Decimal(1)
while True:
m = Decimal(4 * n * n)
u = m / (m-1)
result *= u
abs_error = Decimal(pi) - result
n += 1
if abs(abs_error) < 0.00000001:
rel_error = Decimal(100.0) * abs_error / Decimal(pi)
print(result, "\t", abs_error, "\t", rel_error)
break
Tento výpočet relativně rychle (v řádu minut) skončí s následujícími výsledky:
vypočtená hodnota absolutní chyba relativní chyba (v %) 3.141592643589793147458504120 9.999999968539459348544185162E-9 3.183098851823705725414918062E-7
9. Výpočet harmonické řady
Vyzkoušejme si nyní další vlastnosti formátů float a Decimal na jednoduchém testu – výpočtu součtu harmonické řady. Ta je divergentní, což bylo ostatně dokázáno již ve čtrnáctém století. Ovšem při naivním výpočtu této řady se ukazují některé nepříjemné vlastnosti hodnot s plovoucí řádovou čárkou. Ve výpočtu zjišťujeme, kdy je již další přičítaný člen z důvodu velkého dynamického rozsahu (mezisoučet versus hodnota n-tého prvku) považován za tak malou hodnotu (relativně k prvnímu operandu) že již může být výpočet ukončen:
n = 1
h1 = 0.0
h2 = 0.0
while True:
h2 = h1 + 1.0 / n;
if n % 1000000 == 0:
print(n, h1, h2, h2 - h1)
if h1 == h2:
break
h1 = h2
n += 1
print(h1, h2, n)
Tento výpočet skutečně skončí, ovšem po provedení velkého množství iterací.
Úprava pro typ Decimal je (zdánlivě) triviální, ovšem navíc ještě bude možné měnit přesnost výpočtů, což si ukážeme v navazujících kapitolách:
from decimal import Decimal
n = Decimal(1)
h1 = Decimal(0.0)
h2 = Decimal(0.0)
one = Decimal(1.0)
while True:
h2 = h1 + one / n;
if n % 1000000 == 0:
print(n, h1, h2, h2 - h1)
if h1 == h2:
break
h1 = h2
n += 1
print(h1, h2, n)
10. Hodnoty, které nelze uložit přesně
I když je typ Decimal vhodný pro uložení často používaných hodnot s desetinnou řádovou čárkou (tečkou), pochopitelně nedokáže reprezentovat či přesně uložit všechny hodnoty. Je tomu tak z toho důvodu, že množina reprezentovatelná typem Decimal je spočetná, zatímco množina reálných čísel je nespočetná. Jednotlivé reprezentace, resp. formáty se od sebe liší především tím, kterou podmnožinu z nespočetné množiny reálných čísel mohou reprezentovat přesně.
Příkladem hodnot, které nelze uložit přesně, jsou některé zlomky, například známý 1/3 či 1/7. Podíl 1/3, který bude znovu vynásoben hodnotou 3, již nedá kýžený výsledek 1,0:
from decimal import Decimal x = Decimal(1) y = Decimal(3) z = x/y print(z) print(z*Decimal(3))
Výsledek nebude příznivý:
0.3333333333333333333333333333 0.9999999999999999999999999999
Dalším příkladem jsou iracionální čísla, například odmocnina ze dvou. Pokusme se zobrazit hodnotu odmocniny a současně i výsledek zpětného výpočtu čtverce (což by měla být přesná dvojka):
from decimal import Decimal, getcontext
x = Decimal(2)
for precision in range(1, 30):
getcontext().prec = precision
z = x.sqrt()
y = x.sqrt()
print(f"{z:<30} {y*y:<30}")
V závislosti na poslední cifře je čtverec vypočítán přesně nebo nepřesně:
1 1 1.4 2.0 1.41 1.99 1.414 1.999 1.4142 2.0000 1.41421 1.99999 1.414214 2.000001 1.4142136 2.0000001 1.41421356 1.99999999 1.414213562 1.999999999 1.4142135624 2.0000000001 1.41421356237 1.99999999999 1.414213562373 2.000000000000 1.4142135623731 2.0000000000000 1.41421356237310 2.00000000000001 1.414213562373095 2.000000000000000 1.4142135623730950 1.9999999999999999 1.41421356237309505 2.00000000000000000 1.414213562373095049 2.000000000000000001 1.4142135623730950488 2.0000000000000000000 1.41421356237309504880 2.00000000000000000000 1.414213562373095048802 2.000000000000000000001 1.4142135623730950488017 2.0000000000000000000000 1.41421356237309504880169 2.00000000000000000000000 1.414213562373095048801689 2.000000000000000000000001 1.4142135623730950488016887 1.9999999999999999999999999 1.41421356237309504880168872 1.99999999999999999999999999 1.414213562373095048801688724 1.999999999999999999999999999 1.4142135623730950488016887242 2.0000000000000000000000000000
11. Dělení nulou
Hodnotu typu Decimal lze podělit nulou. V závislosti na takzvaném kontextu buď tato operace vede k vyhození výjimky, nebo se vypočte kladné, popř. záporné nekonečno. Ukažme si tedy všechny případy, které mohou nastat.
Dělení nulou s vyhozením výjimky:
from decimal import Decimal x = Decimal(1) y = Decimal(0) z = x/y print(z)
Výsledek:
Traceback (most recent call last):
File "div_by_zero_A.py", line 5, in <module>
z = x/y
decimal.DivisionByZero: [<class 'decimal.DivisionByZero'>]
Dělení kladnou nulou bez vyhození výjimky. Nutno nastavit kontext:
from decimal import Decimal, ExtendedContext, setcontext setcontext(ExtendedContext) x = Decimal(1) y = Decimal(0) z = x/y print(z)
Výsledek:
Infinity
Dělení zápornou nulou bez vyhození výjimky:
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal(1)
y = Decimal("-0")
z = x/y
print(z)
Výsledek:
-Infinity
12. Operace 0/0 a 00
Výsledkem dělení nulou je většinou kladné či záporné nekonečno, ovšem v některých specifických případech není výsledek definován. V těchto případech se vrací hodnota NaN (Not a Number), která je opět typu Decimal. Ukažme si to na jednoduchém příkladu:
from decimal import Decimal, ExtendedContext, setcontext setcontext(ExtendedContext) x = Decimal(0) y = Decimal(0) z = x/y print(z)
Tento skript po svém spuštění vypíše:
NaN
Podobně je možné vypočítat hodnotu xy, a to konkrétně s využitím přetíženého operátoru **:
from decimal import Decimal, ExtendedContext, setcontext setcontext(ExtendedContext) x = Decimal(2) y = Decimal(100) z = x**y print(z)
S výsledkem:
1.26765060E+30
Ovšem operace 00 není dobře definována (má se vrátit nula nebo jednička?) a proto i výsledkem této operace ne hodnota NaN:
from decimal import Decimal, ExtendedContext, setcontext setcontext(ExtendedContext) x = Decimal(0) y = Decimal(0) z = x**y print(z)
Zkusme si tento skript spustit:
NaN
13. Operace s nekonečny
Datový typ Decimal podporuje i práci s hodnotami kladné nekonečno a záporné nekonečno. Je však zapotřebí si uvědomit, že tyto hodnoty vlastně neleží na běžné číselné ose (používá se zde pojem rozšířená reálná čísla) a taktéž nemůžeme s nekonečny pracovat stejně, jako s jinými číselnými hodnotami. Typicky totiž zobecňujeme operace s běžnými čísly tak, že namísto konkrétních čísel použijeme obecnější symboly (například x), pro které platí nějaká pravidla, například x-x=0, x/x=1 atd. Při práci s nekonečny tyto vztahy většinou neplatí, což ostatně uvidíme i v další čtveřici demonstračních příkladů.
Pokusme se například k nekonečnu přičíst nějakou hodnotu:
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal("inf")
y = Decimal(1)
z = x+y
print(z)
Výsledkem bude v tomto případě opět nekonečno:
Infinity
Dvě nekonečna můžeme i sečíst:
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal("inf")
y = Decimal("inf")
z = x+y
print(z)
Výsledkem bude opět, jak již zajisté očekáváte, nekonečno (tedy jakoby platilo x+x=x):
Infinity
Některé operace s nekonečny ovšem vrací NaN (tedy „nečíslo“). Například rozdíl dvou nekonečen není nula, ale právě NaN:
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal("inf")
y = Decimal("inf")
z = x-y
print(z)
Výsledek:
NaN
Podobně podíl dvou nekonečen není 1, ale opět (ne)hodnota NaN:
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal("inf")
y = Decimal("inf")
z = x/y
print(z)
Výsledek:
NaN
Vynásobení nekonečna nulou vrací (nepřekvapivě) opět nehodnotu NaN
from decimal import Decimal, ExtendedContext, setcontext
setcontext(ExtendedContext)
x = Decimal("inf")
y = Decimal("0")
z = x*y
print(z)
Výsledkem je:
NaN
14. Nastavení přesnosti výpočtů i uložení výsledků
U dekadických formátů Decimal32, Decimal64 a Decimal128, které jsme si popsali minule, byla přesnost přímo určena způsobem uložení čísla do 32bitového, 64bitového či 128bitového slova. Ovšem v případě typu Decimal v Pythonu je tomu jinak – zde si totiž můžeme přesnost řídit podle potřeb (a zaplatit za to spotřebou paměti a pomalými výpočty). Například je možné nastavit přesnost (tedy vlastně počet uložených cifer) na 100 a vypočítat přibližnou hodnotu 1/3:
from decimal import Decimal, getcontext getcontext().prec = 100 x = Decimal(1) y = Decimal(3) z = x/y print(z*Decimal(3))
Výsledek vypsaný na obrazovku by měl vypadat následovně:
0.9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
Přesnost lze řídit, a to i za běhu programu:
from decimal import Decimal, getcontext
x = Decimal(1)
y = Decimal(3)
for precision in range(1, 30):
getcontext().prec = precision
z = x/y
print(z*Decimal(3))
Výsledky:
0.9 0.99 0.999 0.9999 0.99999 0.999999 0.9999999 0.99999999 0.999999999 0.9999999999 0.99999999999 0.999999999999 0.9999999999999 0.99999999999999 0.999999999999999 0.9999999999999999 0.99999999999999999 0.999999999999999999 0.9999999999999999999 0.99999999999999999999 0.999999999999999999999 0.9999999999999999999999 0.99999999999999999999999 0.999999999999999999999999 0.9999999999999999999999999 0.99999999999999999999999999 0.999999999999999999999999999 0.9999999999999999999999999999 0.99999999999999999999999999999
15. Změna zaokrouhlovacího režimu
Popsat si musíme ještě jednu důležitou vlastnost datového typu Decimal. Jedná se o možnost výběru zaokrouhlovacího režimu při provádění operací, které vedou ke vzniku hodnoty, která se nevejde do stanoveného počtu cifer. K dispozici jsou následující zaokrouhlovací režimy, jež je možné zvolit pro kontext:
ROUND_CEILING, ROUND_DOWN, ROUND_FLOOR, ROUND_HALF_DOWN, ROUND_HALF_EVEN, ROUND_HALF_UP, ROUND_UP, ROUND_05UP,
Podívejme se na funkci jednotlivých režimů při výpočtu hodnoty 1/7 (která je vždy nepřesná) pro různé zaokrouhlovací režimy a různou uživatelem zadanou přesnost. Ve skriptu budeme postupně jednotlivými režimy procházet a vypisovat hodnotu 1/7 (resp. přesněji řečeno výsledek operace 1/7) pro různé přesnosti:
from decimal import Decimal, getcontext
from decimal import (
ROUND_CEILING,
ROUND_DOWN,
ROUND_FLOOR,
ROUND_HALF_DOWN,
ROUND_HALF_EVEN,
ROUND_HALF_UP,
ROUND_UP,
ROUND_05UP,
)
x = Decimal(1)
y = Decimal(7)
roundings = (
ROUND_CEILING,
ROUND_DOWN,
ROUND_FLOOR,
ROUND_HALF_DOWN,
ROUND_HALF_EVEN,
ROUND_HALF_UP,
ROUND_UP,
ROUND_05UP,
)
for round_mode in roundings:
getcontext().rounding = round_mode
print(round_mode)
for i in range(1, 10):
z = (x / y).quantize(Decimal(10) ** -i)
print(z)
print()
Tento skript po svém spuštění vypíše:
ROUND_CEILING 0.2 0.15 0.143 0.1429 0.14286 0.142858 0.1428572 0.14285715 0.142857143 ROUND_DOWN 0.1 0.14 0.142 0.1428 0.14285 0.142857 0.1428571 0.14285714 0.142857142 ROUND_FLOOR 0.1 0.14 0.142 0.1428 0.14285 0.142857 0.1428571 0.14285714 0.142857142 ROUND_HALF_DOWN 0.1 0.14 0.143 0.1429 0.14286 0.142857 0.1428571 0.14285714 0.142857143 ROUND_HALF_EVEN 0.1 0.14 0.143 0.1429 0.14286 0.142857 0.1428571 0.14285714 0.142857143 ROUND_HALF_UP 0.1 0.14 0.143 0.1429 0.14286 0.142857 0.1428571 0.14285714 0.142857143 ROUND_UP 0.2 0.15 0.143 0.1429 0.14286 0.142858 0.1428572 0.14285715 0.142857143 ROUND_05UP 0.1 0.14 0.142 0.1428 0.14286 0.142857 0.1428571 0.14285714 0.142857142
Pro porovnání je pravděpodobně lepší si výsledky zobrazit vedle sebe a porovnávat tak jednotlivé řádky:
ROUND_CEILING ROUND_DOWN ROUND_FLOOR ROUND_HALF_DOWN ROUND_HALF_EVEN ROUND_HALF_UP ROUND_UP ROUND_05UP 0.2 0.1 0.1 0.1 0.1 0.1 0.2 0.1 0.15 0.14 0.14 0.14 0.14 0.14 0.15 0.14 0.143 0.142 0.142 0.143 0.143 0.143 0.143 0.142 0.1429 0.1428 0.1428 0.1429 0.1429 0.1429 0.1429 0.1428 0.14286 0.14285 0.14285 0.14286 0.14286 0.14286 0.14286 0.14286 0.142858 0.142857 0.142857 0.142857 0.142857 0.142857 0.142858 0.142857 0.1428572 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428572 0.1428571 0.14285715 0.14285714 0.14285714 0.14285714 0.14285714 0.14285714 0.14285715 0.14285714 0.142857143 0.142857142 0.142857142 0.142857143 0.142857143 0.142857143 0.142857143 0.142857142
16. Zachytávání výjimek při výpočtech
Poslední vlastností datového typu Decimal, kterou se dnes budeme zabývat, jsou takzvané „pasti“. Jedná se vlastně o určení toho, jak se má systém zachovat v případě, že dojde k dělení nulou, že výsledkem nějaké operace je nenormalizovaná hodnota, že došlo k zaokrouhlení výsledku (a tím pádem ke ztrátě přesnosti) atd. Systém (resp. právě aktuální kontext) buď bude tyto potenciální problémy ignorovat, nebo naopak vyhodí výjimku. Záleží tedy jen na programátorovi, které potenciální problémy bude chtít ignorovat a na které naopak bude chtít reagovat.
Nejprve se podívejme na to, jakým způsobem lze vypsat výchozí stav všech „pastí“. Je to jednoduché, protože i stav pastí je uložen v kontextech a jedná se o slovník, kde klíčem je třída s daným typem výjimky a hodnotou je pravdivostní hodnota True či False:
from decimal import Decimal, getcontext
c = getcontext()
for trap, state in c.traps.items():
print(trap, state)
Povšimněte si, že ve výchozím nastavení dojde k vyhození výjimky při provedení neplatné operace, dále při dělení nulou (to jsme ostatně již viděli) a taktéž při přetečení výsledku:
<class 'decimal.InvalidOperation'> True <class 'decimal.FloatOperation'> False <class 'decimal.DivisionByZero'> True <class 'decimal.Overflow'> True <class 'decimal.Underflow'> False <class 'decimal.Subnormal'> False <class 'decimal.Inexact'> False <class 'decimal.Rounded'> False <class 'decimal.Clamped'> False
Jaké má povolená past důsledky již víme. Týká se to například dělení nulou:
from decimal import Decimal, getcontext
c = getcontext()
for trap, state in c.traps.items():
print(trap, state)
x = Decimal(1)
y = Decimal(0)
z = x/y
print(z)
Dělení nulou v tomto případě vyhodí výjimku:
<class 'decimal.InvalidOperation'> True
<class 'decimal.FloatOperation'> False
<class 'decimal.DivisionByZero'> True
<class 'decimal.Overflow'> True
<class 'decimal.Underflow'> False
<class 'decimal.Subnormal'> False
<class 'decimal.Inexact'> False
<class 'decimal.Rounded'> False
<class 'decimal.Clamped'> False
Traceback (most recent call last):
File "/home/ptisnovs/src/most-popular-python-libs/decimal/traps_B.py", line 10, in
z = x/y
~^~
decimal.DivisionByZero: [<class 'decimal.DivisionByZero'>]
Tuto konkrétní past, tedy detekci dělení nulou s vyhozením výjimky, můžeme snadno zakázat:
from decimal import Decimal, getcontext, DivisionByZero
c = getcontext()
c.traps[DivisionByZero] = False
for trap, state in c.traps.items():
print(trap, state)
x = Decimal(1)
y = Decimal(0)
z = x/y
print(z)
Tento skript již nezhavaruje a vypíše na konci hodnotu Infinity:
<class 'decimal.InvalidOperation'> True <class 'decimal.FloatOperation'> False <class 'decimal.DivisionByZero'> False <class 'decimal.Overflow'> True <class 'decimal.Underflow'> False <class 'decimal.Subnormal'> False <class 'decimal.Inexact'> False <class 'decimal.Rounded'> False <class 'decimal.Clamped'> False Infinity
Naopak si můžeme nějakou past povolit. Například se to může týkat detekce operace, která vede k uložení nepřesné hodnoty. Příkladem může být výpočet podílu 1/7, jenž nebude uložen zcela přesně:
from decimal import Decimal, getcontext, Rounded
c = getcontext()
c.traps[Rounded] = True
for trap, state in c.traps.items():
print(trap, state)
x = Decimal(1)
y = Decimal(2)
z = x/y
print(z)
x = Decimal(1)
y = Decimal(7)
z = x/y
print(z)
Povšimněte si, že při výpočtu druhého podílu došlo k vyhození výjimky typu decimal.Rounded:
<class 'decimal.InvalidOperation'> True
<class 'decimal.FloatOperation'> False
<class 'decimal.DivisionByZero'> True
<class 'decimal.Overflow'> True
<class 'decimal.Underflow'> False
<class 'decimal.Subnormal'> False
<class 'decimal.Inexact'> False
<class 'decimal.Rounded'> True
<class 'decimal.Clamped'> False
0.5
Traceback (most recent call last):
File "/home/ptisnovs/src/most-popular-python-libs/decimal/traps_D.py", line 17, in
z = x/y
~^~
decimal.Rounded: [<class 'decimal.Rounded'>]
17. Určení maximálního exponentu a reakce na přetečení hodnoty
Můžeme si i určit maximální (desítkový) exponent s vyhozením výjimky, pokud hodnota překročí tento exponent:
from decimal import Decimal, getcontext, Rounded
c = getcontext()
c.traps[Rounded] = True
c.Emax = 5
x = Decimal(1)
y = Decimal(2)
for i in range(20):
x *= y
print(x)
Výsledek:
2
4
8
16
32
64
128
256
512
1024
2048
4096
8192
16384
32768
65536
131072
262144
524288
Traceback (most recent call last):
File "/home/ptisnovs/src/most-popular-python-libs/decimal/traps_E.py", line 11, in <module>
x *= y
decimal.Overflow: [<class 'decimal.Overflow'>, <class 'decimal.Rounded'>]
V případě, že naopak past na přetečení zakážeme, bude výsledkem přetečení nekonečno:
from decimal import Decimal, getcontext, Overflow
c = getcontext()
c.traps[Overflow] = False
c.Emax = 5
x = Decimal(1)
y = Decimal(2)
for i in range(20):
x *= y
print(x)
Výsledek nyní bude vypadat odlišně:
2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768 65536 131072 262144 524288 Infinity
18. Příloha: „numerická věž“ v programovacích jazycích
S takzvanou „numerickou věží“ jsme se již na tomto serveru setkali, a to například při popisu možností mnoha existujících dialektů programovacího jazyka Scheme. Připomeňme si ve stručnosti, že se jedná o hierarchii datových typů reprezentujících různé typy (resp. přesněji řečeno množiny) čísel. Na vrcholu této hierarchie typicky stojí obecný typ number, pod ním leží komplexní čísla, dále čísla reálná, čísla racionální (zlomky) a nakonec čísla celá (nebo jen celá kladná či čísla přirozená):
| # | Typ | Význam |
|---|---|---|
| 1 | number | libovolná obecná čísla |
| 2 | complex | komplexní čísla |
| 3 | real | reálná čísla |
| 4 | rational | zlomky (racionální čísla) |
| 5 | integer | celá čísla |
Výše uvedená numerická věž může být rozšířena o další typy, což je případ programovacího jazyka Kawa, jenž tento koncept rozšiřuje o numerický typ kvaternion a taktéž (což je asi nejzajímavější a poměrně unikátní) o typ quantity, tedy o dvojice hodnota+jednotka (to je koncept, který možná čeká na své „znovuobjevení“):
| Typ | Význam |
|---|---|
| number | libovolná obecná čísla |
| quantity | numerická hodnota i s uvedenou jednotkou (viz další text) |
| quaternion | kvaterniony |
| complex | komplexní čísla |
| real | reálná čísla |
| rational | zlomky (racionální čísla) |
| integer | celá čísla |
19. Repositář s demonstračními příklady
Zdrojové kódy všech prozatím popsaných demonstračních příkladů určených pro programovací jazyk Python 3 a knihovnu libcst byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/most-popular-python-libs:
20. Odkazy na Internetu
- decimal — Decimal fixed point and floating point arithmetic
https://docs.python.org/3/library/decimal.html - An Essential Guide to Python Decimal By Examples
https://www.pythontutorial.net/advanced-python/python-decimal/ - Extended real number line
https://en.wikipedia.org/wiki/Extended_real_number_line - mathematical operations with infinity
https://math.stackexchange.com/questions/3969017/mathematical-operations-with-infinity - GCC: 6.14 Decimal Floating Types
https://gcc.gnu.org/onlinedocs/gcc/Decimal-Float.html - Routines for decimal floating point emulation
https://gcc.gnu.org/onlinedocs/gccint/Decimal-float-library-routines.html - Representation of hexadecimal floating point
https://www.ibm.com/docs/en/hla-and-tf/1.6?topic=lq-representation-hexadecimal-floating-point - Decimal floating point
https://en.wikipedia.org/wiki/Decimal_floating_point - Hexadecimal Floating-Point Constants
https://www.exploringbinary.com/hexadecimal-floating-point-constants/ - Norma IEEE 754 a příbuzní: formáty plovoucí řádové tečky
https://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/ - decimal32 floating-point format
https://en.wikipedia.org/wiki/Decimal32_floating-point_format - decimal64 floating-point format
https://en.wikipedia.org/wiki/Decimal64_floating-point_format - decimal128 floating-point format
https://en.wikipedia.org/wiki/Decimal128_floating-point_format - IEEE-754 Floating-Point Conversion
http://babbage.cs.qc.cuny.edu/IEEE-754.old/32bit.html - Small Float Formats
https://www.khronos.org/opengl/wiki/Small_Float_Formats - Binary-coded decimal
https://en.wikipedia.org/wiki/Binary-coded_decimal - Chen–Ho encoding
https://en.wikipedia.org/wiki/Chen%E2%80%93Ho_encoding - Densely packed decimal
https://en.wikipedia.org/wiki/Densely_packed_decimal - A Summary of Chen-Ho Decimal Data encoding
http://speleotrove.com/decimal/chen-ho.html - Art of Assembly language programming: The 80×87 Floating Point Coprocessors
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–3.html - Art of Assembly language programming: The FPU Instruction Set
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–4.html - INTEL 80387 PROGRAMMER'S REFERENCE MANUAL
http://www.ragestorm.net/downloads/387intel.txt - Floating-Point Formats
http://www.quadibloc.com/comp/cp0201.htm - IBM Floating Point Architecture
http://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - Extended Binary Coded Decimal Interchange Code
http://en.wikipedia.org/wiki/EBCDIC - ASCII/EBCDIC Conversion Table
http://docs.hp.com/en/32212–90008/apcs01.html - EBCDIC
http://www.hansenb.pdx.edu/DMKB/dict/tutorials/ebcdic.php - EBCDIC tables
http://home.mnet-online.de/wzwz.de/temp/ebcdic/cc_en.htm - 36-bit
http://en.wikipedia.org/wiki/36-bit_word_length - 36bit.org
http://www.36bit.org/ - How did the Apple II do floating point?
https://groups.google.com/forum/#!topic/comp.emulators.apple2/qSBiG2TAlRg - IBM Floating Point Architecture
https://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - The Arithmetic Subroutines
http://www.users.waitrose.com/~thunor/mmcoyzx81/chapter17.html - ZX Floating point to Decimal code in BASIC
http://www.sinclairzxworld.com/viewtopic.php?t=1422 - Floating Point Arithmetic Package
http://www.retrocomputing.net/parts/atari/800/docs/atari_os/atari_os_user_manual08.htm - Turbo Pascal Real
http://www.shikadi.net/moddingwiki/Turbo_Pascal_Real - THE FLOATING POINT ARITHMETIC PACKAGE
http://www.atarimax.com/freenet/freenet_material/5.8-BitComputersSupportArea/7.TechnicalResourceCenter/showarticle.php?14 - The Most Expensive One-byte Mistake: Did Ken, Dennis, and Brian choose wrong with NUL-terminated text strings?
http://queue.acm.org/detail.cfm?id=2010365