Obsah
1. Dokončení problematiky tvorby jednoduchých grafů ve frameworku Torch
3. Zobrazení 3D grafu funkce typu [x,y,z]=f(t)
5. Operace typu gather provedená nad vektorem
6. Operace typu gather provedená nad maticí
7. Operace nad vektory a maticemi, násobení vektorů, lineární interpolace a další operace z BLAS
8. Vynásobení komponent tenzoru (vektoru, matice) skalární hodnotou
9. Vynásobení odpovídajících si komponent tenzoru
16. Příklad aplikace lineární transformace: otáčení bodu či vektoru v ploše
17. Lineární interpolace mezi dvěma tenzory
18. Další operace dostupné v knihovně BLAS
19. Repositář s demonstračními příklady
1. Dokončení problematiky tvorby jednoduchých grafů ve frameworku Torch
V předchozí části seriálu o frameworku Torch jsme si mj. ukázali, jakým způsobem je možné vykreslit graf funkce dvou nezávislých proměnných. Připomeňme si, že se pro tyto účely používá metoda nazvaná gnuplot.splot (surface plot), které se předá (dvourozměrná) matice s hodnotami funkce. Graf je automaticky upraven takovým způsobem, aby se vykreslila lokální maxima i minima funkce; navíc se implicitně pod funkcí zobrazuje i kontura („vrstevnice“) s důležitými hodnotami. Celý příklad, který vykreslí průběh jednoduché funkce dvou nezávislých proměnných, je možné zapsat následovně:
require("gnuplot")
GRID=40
v = torch.range(0, GRID*GRID)
v = v - 12
m = v:resize(GRID, GRID)
m = torch.sin(m*4.0*math.pi/90.0/GRID)
gnuplot.pngfigure("plot7.png")
gnuplot.title("splot")
gnuplot.splot(m)
gnuplot.plotflush()
gnuplot.close()
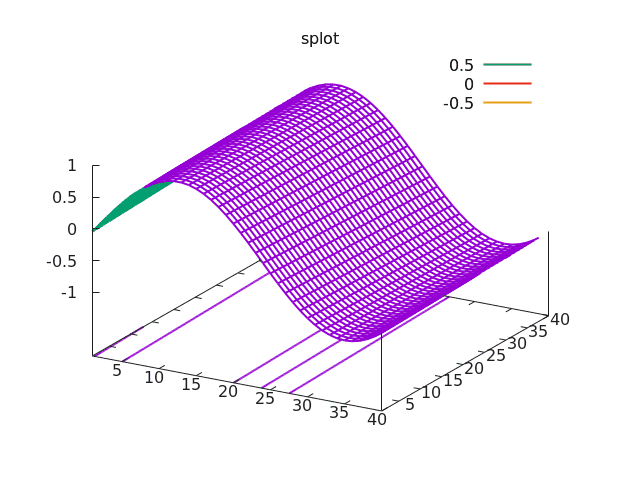
Obrázek 1: Graf vykreslený předchozím demonstračním příkladem.
2. Zobrazení kontur 2D funkce
V některých případech však nemusí být zobrazení plochy představující funkci dostatečně názorné; navíc se v 3D grafu mohou některé důležité hodnoty ztratit (představme si funkci s mnoha lokálními minimy a maximy). V takovém případě lze namísto metody gnuplot.splot použít metodu gnuplot.imagesc. Tato metoda zobrazí funkci dvou nezávislých proměnných odlišně – formou běžného rastrového obrázku, v němž barva jednotlivých oblastí odpovídá hodnotě funkce v daném místě. Nejjednodušší je situace ve chvíli, kdy do druhého parametru metody gnuplot.imagesc předáme řetězec „gray“. Potom je rastrový obrázek zobrazen ve stupních šedi, přičemž nejmenší hodnotě odpovídá černá barva a nejvyšší hodnotě barva bílá:
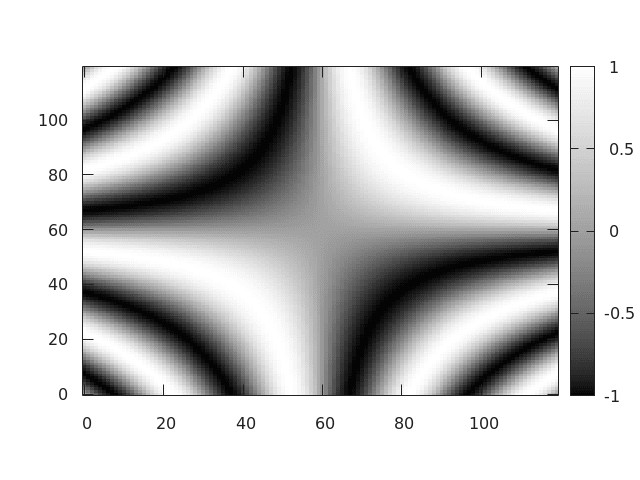
Obrázek 2: Funkce dvou nezávislých proměnných zobrazená formou rastrového obrázku ve stupních šedi.
Obrázek číslo 2 byl vykreslen tímto kódem (funkce ger bude popsána níže):
require("gnuplot")
x = torch.linspace(-1,1,120)
xy = torch.ger(x,x)
z = torch.sin(xy*4.0*math.pi)
gnuplot.pngfigure("plot9.png")
gnuplot.imagesc(z, 'gray')
gnuplot.plotflush()
gnuplot.close()
Alternativně je možné obrázek obarvit barvami z palety s gradientními přechody:
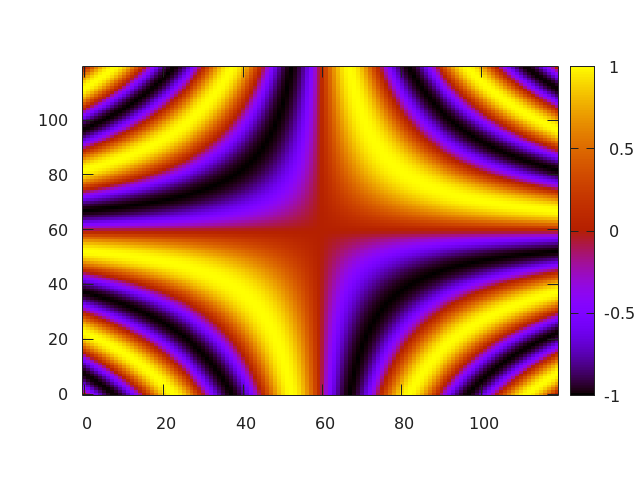
Obrázek 3: Funkce dvou nezávislých proměnných zobrazená formou rastrového obrázku ve falešných barvách.
Třetí obrázek byl vykreslen s využitím tohoto kódu:
require("gnuplot")
x = torch.linspace(-1,1,120)
xy = torch.ger(x,x)
z = torch.sin(xy*4.0*math.pi)
gnuplot.pngfigure("plot10.png")
gnuplot.imagesc(z, 'color')
gnuplot.plotflush()
gnuplot.close()
3. Zobrazení 3D grafu funkce typu [x,y,z]=f(t)
Poslední typ grafu, s nímž se dnes seznámíme, je trojrozměrný graf, v němž se typicky zobrazuje funkce typu [x,y,z]=f(t) popř. složitější funkce [xn, yn, zn]=f(xn-1, yn-1, zn-1). O zobrazení průběhů těchto funkcí se stará metoda gnuplot.scatter3. Po zavolání této metody, které se předá trojice vektorů představujících souřadnice vykreslovaných bodů, se automaticky zjistí potřebné rozsahy na všech třech osách, což je dobře patrné ze čtvrtého screenshotu. Podívejme se tedy, jakým způsobem je možné zobrazit trojrozměrnou spirálu (helix). Je to snadné, protože se použije funkce [x,y,z]=[cos(t), sin(y), t]:
require("gnuplot")
t = torch.linspace(-3 * math.pi, 3 * math.pi, 250)
x = t:clone():cos()
y = t:clone():sin()
gnuplot.pngfigure("plot11.png")
gnuplot.scatter3(x, y, t)
gnuplot.plotflush()
gnuplot.close()
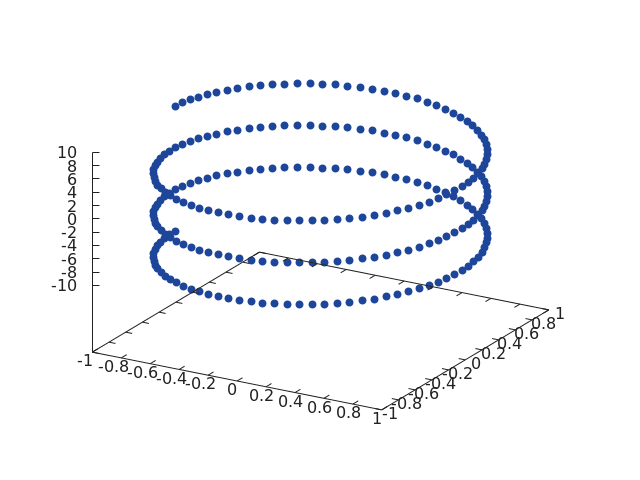
Obrázek 4: Šroubovice (helix) vykreslená demonstračním příkladem.
4. Lorenzův atraktor
Poměrně vděčným příkladem funkce zobrazené v 3D prostoru je dynamický systém s takzvaným podivným atraktorem, který je nazvaný Lorenzův atraktor podle svého objevitele. Tento systém sestávající ze tří dynamických rovnic použil Edward Lorenz v roce 1963 při simulaci vývoje počasí (resp. ve velmi zjednodušeném modelu počasí). Na tomto systému byla také numericky a analyticky ověřena velká citlivost na počáteční podmínky (někdy také nazývaná „motýlí efekt“). Pro upřesnění je však nutné říci, že při simulaci na počítači vlastně získáme atraktor, jenž je periodický. Je to z toho důvodu, že pro zobrazení číselných hodnot je použito konečného počtu bitů, z toho nutně vyplývá, že se po určitém počtu kroků (který je však obrovský, takže tento jev mnohdy nezaregistrujeme) začne dráha Lorenzova atraktoru překrývat. V matematicky přesném modelu však tato situace nenastane, každá smyčka funkce bude mít unikátní tvar a dráhy se nebudou překrývat, pouze protínat. Diferenciální rovnice Lorenzova atraktoru mají po převodu na diferenční tvar následující formát:
dx/dt = σ (y-x)
dy/dt = x(ρ – z) – y
dz/dt = xy – Βz
Takže pro iterativní (samozřejmě že nepřesný) výpočet můžeme pracovat s následujícími vztahy, které pro dostatečně malé dt vedou k výpočtu bodů tvořících Lorenzův atraktor:
xn+1=xn+(σ (y-x)) dt
yn+1=yn+(x(ρ – z) – y) dt
zn+1=zn+(xy – Βz) dt
Podívejme se nyní na způsob implementace této funkce:
-- funkce pro výpočet dalšího bodu Lorenzova atraktoru
function lorenz(x, y, z, s, r, b)
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
end
A výpočtu sekvence bodů ležících na atraktoru:
-- krok (změna času)
dt = 0.01
-- celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
-- prozatím prázdné vektory připravená pro výpočet
x = torch.zeros(n)
y = torch.zeros(n)
z = torch.zeros(n)
-- počáteční hodnoty
x[1], y[1], z[1] = 0., 1., 1.05
-- vlastní výpočet atraktoru
for i=1, n-1 do
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i], 10, 28, 2.667)
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
end
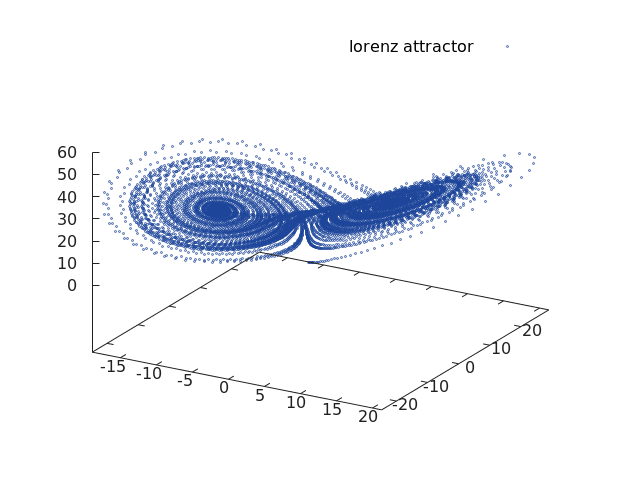
Obrázek 5: Lorenzův atraktor vykreslený přes framework Torch.
Celý příklad i se zobrazením atraktoru lze naprogramovat například takto:
require("gnuplot")
-- funkce pro výpočet dalšího bodu Lorenzova atraktoru
function lorenz(x, y, z, s, r, b)
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
end
-- krok (změna času)
dt = 0.01
-- celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
-- prozatím prázdné vektory připravená pro výpočet
x = torch.zeros(n)
y = torch.zeros(n)
z = torch.zeros(n)
-- počáteční hodnoty
x[1], y[1], z[1] = 0., 1., 1.05
-- vlastní výpočet atraktoru
for i=1, n-1 do
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i], 10, 28, 2.667)
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
end
-- vykreslení grafu
gnuplot.pngfigure("plot12.png")
gnuplot.raw("set pointsize 0.1")
gnuplot.scatter3("lorenz attractor", x, y, z)
gnuplot.plotflush()
gnuplot.close()
Poznámka: za povšimnutí též stojí řádek:
gnuplot.raw("set pointsize 0.1")
který přímo (bez dalšího zpracování) volá příkaz gnuplotu – samotná knihovna Torch totiž zdaleka nereflektuje všechny možnosti gnuplotu.
5. Operace typu gather provedená nad vektorem
Velmi užitečná, i když na první pohled možná poněkud komplikovaná, je operace typu gather představovaná metodou tensor:gather. Tato operace může být aplikována například na jednorozměrný vektor; argumentem metody tensor:gather bude další vektor, který musí obsahovat celá čísla (typu int, long atd.). V takovém případě metoda tensor:gather vrátí ty prvky původního vektoru, které leží na zvolených indexech:
v1 = torch.range(10, 100, 10)
print(v1)
indexes = torch.LongTensor({2, 4, 6, 8, 10})
print(indexes)
print(v1:gather(1, indexes))
print(v1:gather(1, indexes):isContiguous())
print("-----------------------")
indexes = torch.range(10, 1, -1):long()
print(indexes)
print(v1:gather(1, indexes))
print(v1:gather(1, indexes):isContiguous())
Podívejme se na zprávy vypisované příkladem. Nejprve se vypíše obsah původního vektoru:
10 20 30 40 50 60 70 80 90 100 [torch.DoubleTensor of size 10]
Dále se vypíše vektor s indexy vybíraných prvků:
2 4 6 8 10 [torch.LongTensor of size 5]
A na konec výsledný vektor s vybranými prvky:
20 40 60 80 100 [torch.DoubleTensor of size 5]
Nový vektor s indexy tentokrát obsahuje hodnoty od 10 do 1:
10 9 8 7 6 5 4 3 2 1 [torch.LongTensor of size 10]
Výsledkem operace gather jsou prvky původního vektoru, ovšem v opačném pořadí:
100 90 80 70 60 50 40 30 20 10 [torch.DoubleTensor of size 10]
6. Operace typu gather provedená nad maticí
Operaci gather lze aplikovat i na matice, její použití je však v tomto případě složitější, protože indexy nyní nemusí tvořit pouhý jednorozměrný vektor, ale mohou mít podobu 2D matice s různým počtem řádků a sloupců. Příklad použití nyní bude komplikovanější, protože si ukážeme různé možnosti, které nám tato operace nabízí. Nejprve vytvoříme zdrojovou matici:
v = torch.range(1, 24) m1 = v:resize(6, 4) print(m1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [torch.DoubleTensor of size 6x4]
Postupně budeme maticí po sloupcích procházet a vybereme vždy první prvek sloupce:
indexes = torch.LongTensor({{1,1,1,1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(1, indexes))
Výsledky:
Indexes: 1 1 1 1 [torch.LongTensor of size 1x4] Result: 1 2 3 4 [torch.DoubleTensor of size 1x4]
Opačný případ – výběr prvních prvků z každého řádku matice:
indexes = torch.LongTensor({{1},{1},{1},{1},{1},{1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(2, indexes))
Výsledky:
Indexes: 1 1 1 1 1 1 [torch.LongTensor of size 6x1] Result: 1 5 9 13 17 21 [torch.DoubleTensor of size 6x1]
Výběr prvního, druhého a třetího řádku tabulky:
indexes = torch.LongTensor({{1,1,1,1}, {2,2,2,2}, {3,3,3,3}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(1, indexes))
Výsledky:
Indexes: 1 1 1 1 2 2 2 2 3 3 3 3 [torch.LongTensor of size 3x4] Result: 1 2 3 4 5 6 7 8 9 10 11 12 [torch.DoubleTensor of size 3x4]
Výběr z prvních dvou řádků zdrojové matice, ovšem napřeskáčku:
indexes = torch.LongTensor({{1,2,1,2}, {2,1,2,1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(1, indexes))
Výsledky:
Indexes: 1 2 1 2 2 1 2 1 [torch.LongTensor of size 2x4] Result: 1 6 3 8 5 2 7 4 [torch.DoubleTensor of size 2x4]
Prohození všech řádků matice:
indexes = torch.LongTensor({{6,6,6,6}, {5,5,5,5}, {4,4,4,4}, {3,3,3,3}, {2,2,2,2}, {1,1,1,1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(1, indexes))
Výsledky:
Indexes: 6 6 6 6 5 5 5 5 4 4 4 4 3 3 3 3 2 2 2 2 1 1 1 1 [torch.LongTensor of size 6x4] Result: 21 22 23 24 17 18 19 20 13 14 15 16 9 10 11 12 5 6 7 8 1 2 3 4 [torch.DoubleTensor of size 6x4]
Získání matice se dvěma sloupci, prvky jsou získány postupně z prvního, druhého, třetího… sloupce původní matice:
indexes = torch.LongTensor({{1,1}, {2,2}, {3,3}, {4,4}, {1,1}, {1,1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(2, indexes))
Výsledky:
Indexes: 1 1 2 2 3 3 4 4 1 1 1 1 [torch.LongTensor of size 6x2] Result: 1 1 6 6 11 11 16 16 17 17 21 21 [torch.DoubleTensor of size 6x2]
Výběr prvního a čtvrtého sloupce, opět na přeskáčku:
indexes = torch.LongTensor({{1,4}, {1,4}, {1,4}, {4,1}, {4,1}, {4,1}})
print("Indexes:")
print(indexes)
print("Result:")
print(m1:gather(2, indexes))
Výsledky:
Indexes: 1 4 1 4 1 4 4 1 4 1 4 1 [torch.LongTensor of size 6x2] Result: 1 4 5 8 9 12 16 13 20 17 24 21 [torch.DoubleTensor of size 6x2]
Vidíme, že tato operace je skutečně velmi flexibilní.
7. Operace nad vektory a maticemi, násobení vektorů, lineární interpolace a další operace z BLAS
V knihovně Torch nalezneme mnoho funkcí, které mohou provádět různé operace nad vektory, maticemi, popř. nad obecnými tenzory. Některé funkce lze použít pro všechny typy tenzorů (vynásobení komponent tenzoru se skalární hodnotou), jiné je však možné aplikovat jen na tenzory s jednou dimenzí (vektorové operace), se dvěma dimenzemi (maticové násobení) či dokonce jen na tenzory s omezeným počtem komponent (vektorový součin). V dalších kapitolách si popíšeme následující operace:
| Operace | Zápis | Popis v kapitole |
|---|---|---|
| Součin tenzoru a skaláru | torch.mul(tenzor, skalár), tenzor:mul(skalár) | 8 |
| Součin odpovídajících si komponent | torch.cmul(tenzor1, tenzor2), tenzor2:cmul(tenzor2) | 9 |
| Skalární součin | torch.dot(vektor1, vektor2), vektor1:dot(vektor2) | 10 |
| Vektorový součin | torch.cross(vektor1, vektor2), vektor1:cross(vektor2) | 11 |
| Vnější součin | gtorch.ger(vektor1, vektor2), vektor1:ger(vektor2) | 12 |
| Součin matice a vektoru | torch.mv(matice, vektor), * | 13 |
| Součin dvou matic | torch.mm(matice1, matice2), * | 14 |
Ze zápisů ve druhém sloupci je patrné, že některé operace jsou dostupné jako běžné funkce i jako metody. Součin matice a vektoru popř. maticový součin je možné zapsat i pomocí přetíženého operátoru *.
8. Vynásobení komponent tenzoru (vektoru, matice) skalární hodnotou
Jednou z nejjednodušších operací, v nichž se vyskytuje součin, je operace sloužící k vynásobení všech komponent vybraného tenzoru (typicky vektoru nebo matice) skalární hodnotou. Tato operace je představována metodou mul, kterou lze volat dvěma způsoby:
v3 = torch.mul(v1, 10) v4 = v2:mul(10)
V prvním případě se vektor (matice, tenzor) v1 nezmění a výsledkem operace je nový tenzor, ovšem v případě druhém dojde k modifikaci komponent původního tenzoru v2. Záleží jen na rozhodnutí uživatele, zda potřebuje zachovat původní tenzor či zda mu nevadí provedení součinu s modifikací původního tenzoru (což je samozřejmě časově i paměťově méně náročné).
Podívejme se na příklad, v němž budeme násobit prvky vektoru [1, 2, 3] konstantou 10:
v1 = torch.Tensor({1,2,3})
v2 = torch.Tensor({1,2,3})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.mul(v1, 10)
v4 = v2:mul(10)
print("Results of vector*scalar")
print(v3)
print(v4)
print("New value of vector 1")
print(v1)
print("New value of vector 2")
print(v2)
Obsah původních vektorů:
Original vector 1 1 2 3 [torch.DoubleTensor of size 3] Original vector 2 1 2 3 [torch.DoubleTensor of size 3]
Výsledek součinu všech prvků vektorů skalární hodnotou:
Results of vector*scalar 10 20 30 [torch.DoubleTensor of size 3] 10 20 30 [torch.DoubleTensor of size 3]
Nový obsah původních vektorů (vidíme, že druhý vektor byl skutečně modifikován):
New value of vector 1 1 2 3 [torch.DoubleTensor of size 3] New value of vector 2 10 20 30 [torch.DoubleTensor of size 3]
9. Vynásobení odpovídajících si komponent tenzoru
Další operace, v níž se provádí součin, spočívá ve vynásobení odpovídajících si komponent tenzoru (tj. v praxi opět vektorů či matic). Tato operace se jmenuje cmul a chová se podobně jako operace mul z předchozí kapitoly. První způsob volání nemění ani jeden ze vstupních vektorů, druhý způsob volání (metody) modifikuje prvky původního vektoru:
v3 = torch.cmul(v1, v2) v4 = v1:cmul(v2)
Opět si vše ukažme na jednoduchém příkladu:
v1 = torch.Tensor({1,2,3})
v2 = torch.Tensor({1,2,3})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.cmul(v1, v2)
v4 = v1:cmul(v2)
print("Results of vector*vector element-wise")
print(v3)
print(v4)
print("New value of vector 1")
print(v1)
print("New value of vector 2")
print(v2)
Obsah původních vektorů:
Original vector 1 1 2 3 [torch.DoubleTensor of size 3] Original vector 2 1 2 3 [torch.DoubleTensor of size 3]
Výsledek součinu prvek po prvku:
Results of vector*vector element-wise 1 4 9 [torch.DoubleTensor of size 3] 1 4 9 [torch.DoubleTensor of size 3]
Nový obsah původních vektorů (vidíme, že druhý vektor byl skutečně modifikován):
New value of vector 1 1 4 9 [torch.DoubleTensor of size 3] New value of vector 2 1 2 3 [torch.DoubleTensor of size 3]
10. Skalární součin vektorů
Další podporovanou operací je klasický skalární součin dvou vektorů neboli anglicky dot product. Tuto operaci je možné zavolat buď pomocí metody dot, nebo alternativně přetíženým operátorem *. Tato operace NEmodifikuje obsah původních vektorů, takže následující tři příkazy provádí prakticky stejný výpočet:
v3 = torch.dot(v1, v2) v4 = v1 * v2 v5 = v1:dot(v2)
Opět si vše ukážeme na příkladu:
v1 = torch.range(1,5)
v2 = torch.range(1,5)
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.dot(v1, v2)
v4 = v1 * v2
v5 = v1:dot(v2)
print("Dot products")
print(v3)
print(v4)
print(v5)
print("New value of vector 1")
print(v1)
print("New value of vector 2")
print(v2)
Původní vektory mají pět prvků:
Original vector 1 1 2 3 4 5 [torch.DoubleTensor of size 5] Original vector 2 1 2 3 4 5 [torch.DoubleTensor of size 5]
Výsledky skalárního součinu jsou ve všech třech případech shodné:
Dot products 55 55 55
Ani jeden vektor se přitom nezměnil:
New value of vector 1 1 2 3 4 5 [torch.DoubleTensor of size 5] New value of vector 2 1 2 3 4 5 [torch.DoubleTensor of size 5]
11. Vektorový součin
V knihovně Torch je samozřejmě podporována i operace vektorového součinu (cross product). Tato operace předpokládá (a taktéž kontroluje), jestli mají oba vstupní vektory tři prvky, protože vektorový součin je definován pro vektory v 3D prostoru (výsledkem je vektor kolmý na oba vstupní vektory). Ukažme si jednoduchý příklad, nejdříve s vektory [1, 0, 1] a [0, 1, 0] pro ověření, zda je výsledkem opravdu kolmý vektor a taktéž pro vektory [1, 2, 3] a [3, 2, 1]. Výsledky si můžete ověřit například zde:
v1 = torch.Tensor({1,0,0})
v2 = torch.Tensor({0,1,0})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.cross(v1, v2)
v4 = v1:cross(v2)
print("Cross products")
print(v3)
print(v4)
print("New value of vector 1")
print(v1)
print("New value of vector 2")
print(v2)
print("----------------------------")
v1 = torch.Tensor({1,2,3})
v2 = torch.Tensor({3,2,1})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.cross(v1, v2)
v4 = v1:cross(v2)
print("Cross products")
print(v3)
print(v4)
print("New value of vector 1")
print(v1)
print("New value of vector 2")
print(v2)
Ověření vektorového součinu [1, 0, 0] × [0, 1, 0]:
Original vector 1 1 0 0 [torch.DoubleTensor of size 3] Original vector 2 0 1 0 [torch.DoubleTensor of size 3] Cross products 0 0 1 [torch.DoubleTensor of size 3] 0 0 1 [torch.DoubleTensor of size 3] New value of vector 1 1 0 0 [torch.DoubleTensor of size 3] New value of vector 2 0 1 0 [torch.DoubleTensor of size 3]
Ověření vektorového součinu [1, 2, 3] × [3, 2, 1]:
Original vector 1 1 2 3 [torch.DoubleTensor of size 3] Original vector 2 3 2 1 [torch.DoubleTensor of size 3] Cross products -4 8 -4 [torch.DoubleTensor of size 3] -4 8 -4 [torch.DoubleTensor of size 3] New value of vector 1 1 2 3 [torch.DoubleTensor of size 3] New value of vector 2 3 2 1 [torch.DoubleTensor of size 3]
12. Vnější součin
Další operace, kterou lze provádět s vektory, je vnější součin (outer product). Vstupními operandy je dvojice vektorů, které mohou mít libovolnou a rozdílnou délku, výsledkem je dvourozměrná matice. Ve skutečnosti se totiž provádí maticové násobení prvního vstupního vektoru s transponovaným druhým vektorem:
m = v1v2T
Poznámka: pokud naopak budeme transponovat první vstupní vektor, bude výsledkem maticového násobení jediné číslo odpovídající skalárnímu součinu:
s = v1Tv2
Poznámka: vektory v1 a v2 jsou považovány za sloupcové vektory, proto je zdánlivě transponován vždy opačný vektor, než nám napovídá intuice.
Vyzkoušejme si nyní provést vnější součin nad dvojicí vektorů [1, 0, 0], [0, 1, 0], dále pak nad dvojicí [1, 2, 4], [1, 2, 3] a konečně nad vektory [1, … 10] a [1, 2, 3]:
v1 = torch.Tensor({1,0,0})
v2 = torch.Tensor({0,1,0})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.ger(v1, v2)
print("Outer products")
print(v3)
print("---------------")
v1 = torch.Tensor({1,2,3})
v2 = torch.Tensor({1,2,3})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.ger(v1, v2)
print("Outer products")
print(v3)
print("---------------")
v1 = torch.range(1,10)
v2 = torch.Tensor({1,2,3})
print("Original vector 1")
print(v1)
print("Original vector 2")
print(v2)
v3 = torch.ger(v1, v2)
print("Outer products")
print(v3)
Ověření vnějšího součinu [1, 0, 0] ⊗ [0, 1, 0]:
Original vector 1 1 0 0 [torch.DoubleTensor of size 3] Original vector 2 0 1 0 [torch.DoubleTensor of size 3] Outer products 0 1 0 0 0 0 0 0 0 [torch.DoubleTensor of size 3x3]
Ověření vnějšího součinu [1, 2, 3] ⊗ [1, 2, 3]:
Original vector 1 1 2 3 [torch.DoubleTensor of size 3] Original vector 2 1 2 3 [torch.DoubleTensor of size 3] Outer products 1 2 3 2 4 6 3 6 9 [torch.DoubleTensor of size 3x3]
První sloupec odpovídá prvkům původního vektoru, druhý sloupec nese hodnoty vynásobené dvěma, třetí pak vynásobené třemi.
Ověření vnějšího součinu [1, 2, 3 … 10] ⊗ [1, 2, 3]:
Original vector 1 1 2 3 4 5 6 7 8 9 10 [torch.DoubleTensor of size 10] Original vector 2 1 2 3 [torch.DoubleTensor of size 3] Outer products 1 2 3 2 4 6 3 6 9 4 8 12 5 10 15 6 12 18 7 14 21 8 16 24 9 18 27 10 20 30 [torch.DoubleTensor of size 10x3]
Na posledním příkladu je jasně patrné, jak je maticové násobení prováděno (jen se nenechte zmást tím, že jednodimenzionální tenzory jsou zobrazeny jako sloupce čísel a nikoli jako řádky).
13. Součin matice a vektoru
Další podporovanou operací je součin matice a vektoru. Ten je možné zapsat buď pomocí funkce torch.mv nebo s využitím přetíženého operátoru *. Počet sloupců matice musí odpovídat počtu prvků vektoru. Výsledkem je vektor s počtem prvků odpovídajícím počtu řádků matice:
m = torch.Tensor({{1, 2},
{3, 4},
{5, 6},
{7, 8}})
v = torch.Tensor({1, 2})
print("Original matrix")
print(m)
print("Original vector")
print(v)
m2 = torch.mv(m, v)
m3 = m * v
print("New matrix")
print(m2)
print(m3)
Původní matice a vektor vstupující do operace:
Original matrix 1 2 3 4 5 6 7 8 [torch.DoubleTensor of size 4x2] Original vector 1 2 [torch.DoubleTensor of size 2]
Výsledek operace je shodný při použití torch.mv i operátoru *. Poslední prvek vznikl výpočtem 7*1 + 8*2:
New matrix 5 11 17 23 [torch.DoubleTensor of size 4] 5 11 17 23 [torch.DoubleTensor of size 4]
14. Součin dvou matic
Pochopitelně následuje operace pro součin dvou matic, která se zapisuje buď funkcí torch.mm nebo s využitím přetíženého operátoru *. U této operace je nutné zajistit, aby počet sloupců první matice odpovídal počtu řádků matice druhé. Pokud má první matice rozměry m×n (m=počet řádků, n=počet sloupců) a druhá rozměry n×p, bude mít výsledná matice rozměry m×p:
m1 = torch.Tensor({{1, 2, 3},
{4, 5, 6},
{7, 8, 9}})
m2 = torch.eye(3,3)
m3 = torch.eye(3,3)
m3[{2 ,2}] = 10
print("Original matrix 1")
print(m1)
print("Original matrix 2")
print(m2)
print("Original matrix 3")
print(m3)
m12 = m1 * m2
print("m1 x m2:")
print(m12)
m13 = m1 * m3
print("m1 x m3:")
print(m13)
Původní trojice matic:
Original matrix 1 1 2 3 4 5 6 7 8 9 [torch.DoubleTensor of size 3x3] Original matrix 2 1 0 0 0 1 0 0 0 1 [torch.DoubleTensor of size 3x3] Original matrix 3 1 0 0 0 10 0 0 0 1 [torch.DoubleTensor of size 3x3]
Výsledek operace m1·m2:
m1 · m2: 1 2 3 4 5 6 7 8 9 [torch.DoubleTensor of size 3x3]
Výsledek operace m1·m3:
m1 · m3: 1 20 3 4 50 6 7 80 9 [torch.DoubleTensor of size 3x3]
15. Lineární transformace
Díky možnosti provést vynásobení vektoru s maticí je možné použít přetížený operátor * i pro aplikaci lineárních transformací, a to jak v ploše, tak i v trojrozměrném prostoru. Mezi lineární transformace patří posun, otáčení, změna měřítka a zkosení. Jestliže máme tři body, které leží na jedné přímce, tak po aplikaci libovolné lineární transformace získáme nové tři body, které také leží na přímce (proto jsou transformace lineární). Všechny lineární transformace lze vyjádřit maticí o rozměrech n × n, kde n je dimenze vektoru či bodu, který transformujeme.
Pokud provádíme lineární transformace v ploše, vyjadřujeme souřadnici dvěma složkami x a y. Lineární transformaci lze zapsat jako výpočet nových souřadnic x' a y':
x' = xa11 + ya12,
y' = xa21 + ya22.
Členy a11, a12, a21 a a22 představují parametry lineární transformace.
Přehlednější je však vektorově/maticový zápis, kdy dvojici [x, y] označíme jako v, dvojici [x', y'] jako v' a hodnoty a11, a12, a21 a a22 zapíšeme jako prvky do matice M o rozměrech 2×2. Potom lze celou lineární transformaci zapsat jedním vztahem:
v' = M * v – v tomto případě jsou v a v' sloupcové vektory.
Pro zadání lineárních transformací v trojrozměrném prostoru by nám měla stačit transformační matice o rozměrech 3×3 prvky. To je skutečně pravda, ale v počítačové grafice často potřebujeme kromě lineárních transformací vyjádřit i perspektivní projekci. Proto se ke třem souřadnicím [x, y, z] přidává ještě čtvrtá souřadnice označovaná w ze slova weight – váha. Bod je potom vyjádřen čtveřicí [x, y, z, 1] a vektor [x, y, z, 0]. Transformační matice je poté zvětšena na rozměry 4×4 prvky. Stejně tak pro 2D plochu rozšíříme vektor na [x, y, z] a transformační matice bude mít 3×3 prvky.
16. Příklad aplikace lineární transformace: otáčení bodu či vektoru v ploše
Ukažme si nyní aplikaci lineární transformace pro otáčení bodu či vektoru v ploše. Matice otáčení bude mít rozměry 3×3 prvky, přičemž poslední sloupec musí obsahovat hodnoty 0, 0, 1 (neprovádí se nelineární perspektivní projekce) a spodní řádek bude mít taktéž hodnoty 0, 0, 1 (neprovádí se posun). Zbývá nám určit prvky podmatice 2×2 prvky. Pro matici otáčení tyto prvky mají následující obsah:
| cos α -sin α | | sin α cos α |
Postupné otáčení bodu [1, 0] o 30° (π/6) lze naprogramovat následovně:
trans_identity = torch.eye(3, 3)
angle = math.pi/6
trans_rotation = torch.Tensor({{math.cos(angle), -math.sin(angle), 0},
{math.sin(angle), math.cos(angle), 0},
{0, 0, 1}})
v = torch.Tensor({1, 0, 1})
print("Original point")
print(v)
v = trans_identity * v
print("After transformation #1")
print(v)
v = trans_rotation * v
print("First rotation by 30")
print(v)
v = trans_rotation * v
print("Second rotation by 30°")
print(v)
print("Third rotation by 30°")
v = trans_rotation * v
print(v)
Výsledky (včetně původního bodu):
Original point 1 0 1 [torch.DoubleTensor of size 3] After transformation #1 1 0 1 [torch.DoubleTensor of size 3] First rotation by 30 0.8660 0.5000 1.0000 [torch.DoubleTensor of size 3] Second rotation by 30° 0.5000 0.8660 1.0000 [torch.DoubleTensor of size 3] Third rotation by 30° 2.7756e-16 1.0000e+00 1.0000e+00 [torch.DoubleTensor of size 3]
Povšimněte si, že bod se skutečně otočil až na souřadnice [0, 1] (ona nula je kvůli kumulativní chybě vyjádřena jako 2,7×10-16).
17. Lineární interpolace mezi dvěma tenzory
Poslední operací, kterou si dnes podrobněji popíšeme, je operace pro provedení lineární interpolace mezi komponentami dvou tenzorů. Typicky se jedná o jednorozměrné vektory či o dvourozměrné matice, ovšem teoreticky není počet dimenzí nijak omezený. Operace pro výpočet nového tenzoru pomocí lineární interpolace je představována metodou nazvanou lerp, což je jméno používané například v počítačové grafice (mj. i proto, že se jedná o jednu ze základních operací prováděných na grafických akcelerátorech). Oba tenzory předávané metodě lerp by měly mít stejný tvar, tj. shodný počet dimenzí i shodnou velikost. Třetím parametrem této metody je váha, která je typicky představována reálným číslem ležícím mezi 0,0 až 1,0. Ve skutečnosti však může být váha jakákoli – záporné číslo i kladné číslo větší než nula (musíte však umět interpretovat výsledky).
Podívejme se nyní na způsob vytvoření nového vektoru s pěti prvky s využitím lineární interpolace mezi vektorem [100, 0, 0, 0, 0] a vektorem [0, 1, 2, 3, 4]. Váha se postupně mění od nuly do jedničky s krokem 0,2:
v1 = torch.Tensor({100, 0, 0, 0, 0})
v2 = torch.range(0, 4)
print("Source vector 1")
print(v1)
print("Source vector 2")
print(v2)
for weight = 0.0, 1.0, 0.2 do
print("Linear interpolation with weight=" .. weight)
vt = torch.lerp(v1, v2, weight)
print(vt)
end
Zdrojové vektory:
Source vector 1 100 0 0 0 0 [torch.DoubleTensor of size 5] Source vector 2 0 1 2 3 4 [torch.DoubleTensor of size 5]
Pokud je váha nastavená na nulu, vrátí se pochopitelně vektor s prvky odpovídajícími prvnímu vektoru:
Linear interpolation with weight=0 100 0 0 0 0 [torch.DoubleTensor of size 5]
Jak se váha postupně zvyšuje, mění se i hodnota prvků výsledného vektoru:
Linear interpolation with weight=0.2 80.0000 0.2000 0.4000 0.6000 0.8000 [torch.DoubleTensor of size 5] Linear interpolation with weight=0.4 60.0000 0.4000 0.8000 1.2000 1.6000 [torch.DoubleTensor of size 5] Linear interpolation with weight=0.6 40.0000 0.6000 1.2000 1.8000 2.4000 [torch.DoubleTensor of size 5] Linear interpolation with weight=0.8 20.0000 0.8000 1.6000 2.4000 3.2000 [torch.DoubleTensor of size 5]
Na konci smyčky, kdy váha dosáhne hodnoty 1, získáme prvky odpovídající druhému vektoru:
Linear interpolation with weight=1 0 1 2 3 4 [torch.DoubleTensor of size 5]
Stejnou operaci můžeme provést i pro 2D matice, pokud je jejich rozměr a tvar shodný:
m1 = torch.zeros(5, 5)
m2 = torch.range(0, 25):resize(5,5)
print("Source matrix 1")
print(m1)
print("Source matrix 2")
print(m2)
for weight = 0.0, 1.0, 0.2 do
print("Linear interpolation with weight=" .. weight)
mt = torch.lerp(m1, m2, weight)
print(mt)
end
Obě zdrojové matice:
Source matrix 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [torch.DoubleTensor of size 5x5] Source matrix 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [torch.DoubleTensor of size 5x5]
Výsledky pro váhu mezi 0 až 1:
Linear interpolation with weight=0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [torch.DoubleTensor of size 5x5] Linear interpolation with weight=0.2 0.0000 0.2000 0.4000 0.6000 0.8000 1.0000 1.2000 1.4000 1.6000 1.8000 2.0000 2.2000 2.4000 2.6000 2.8000 3.0000 3.2000 3.4000 3.6000 3.8000 4.0000 4.2000 4.4000 4.6000 4.8000 [torch.DoubleTensor of size 5x5] Linear interpolation with weight=0.4 0.0000 0.4000 0.8000 1.2000 1.6000 2.0000 2.4000 2.8000 3.2000 3.6000 4.0000 4.4000 4.8000 5.2000 5.6000 6.0000 6.4000 6.8000 7.2000 7.6000 8.0000 8.4000 8.8000 9.2000 9.6000 [torch.DoubleTensor of size 5x5] Linear interpolation with weight=0.6 0.0000 0.6000 1.2000 1.8000 2.4000 3.0000 3.6000 4.2000 4.8000 5.4000 6.0000 6.6000 7.2000 7.8000 8.4000 9.0000 9.6000 10.2000 10.8000 11.4000 12.0000 12.6000 13.2000 13.8000 14.4000 [torch.DoubleTensor of size 5x5] Linear interpolation with weight=0.8 0.0000 0.8000 1.6000 2.4000 3.2000 4.0000 4.8000 5.6000 6.4000 7.2000 8.0000 8.8000 9.6000 10.4000 11.2000 12.0000 12.8000 13.6000 14.4000 15.2000 16.0000 16.8000 17.6000 18.4000 19.2000 [torch.DoubleTensor of size 5x5] Linear interpolation with weight=1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [torch.DoubleTensor of size 5x5]
18. Další operace dostupné v knihovně BLAS
Ve frameworku Torch najdeme i mnoho dalších užitečných operací, o nichž se dnes (alespoň prozatím) zmíníme pouze ve stručnosti:
| Metoda | Stručný popis |
|---|---|
| torch.clamp | ořezání všech komponent tak, aby byly v rozsahu min_value, max_value |
| torch.addcmul | sekvence operací * a + aplikovaná postupně na všechny prvky tenzorů |
| torch.addcdiv | sekvence operací / a + aplikovaná postupně na všechny prvky tenzorů |
| torch.addmv | kombinace operací add a mv (viz předchozí kapitoly) |
| torch.addmm | kombinace operací add a mm (viz předchozí kapitoly) |
| torch.min | vrátí komponentu s nejmenší hodnotou |
| torch.max | vrátí komponentu s největší hodnotou |
| torch.mean | vrátí průměr vypočtený ze všech komponent |
| torch.median | vrátí medián vypočtený ze všech komponent |
| torch.sum | vypočte sumu prvků |
| torch.std | vypočte standardní odchylku |
| torch.var | vypočte rozptyl |
| torch.mode | vrátí prvek, který se v tenzoru vyskytuje nejčastěji |
| torch.sort | setřídění prvků (lze určit osu atd.) |
| torch.bitand | bitová operace AND všech komponent tenzoru se zadanou hodnotou (skalárem) |
| torch.cbitand | bitový operace AND všech komponent tenzoru s hodnotami přečtenými z dalšího tenzoru |
| torch.bitor | bitová operace OR všech komponent tenzoru se zadanou hodnotou (skalárem) |
| torch.cbitor | bitový operace OR všech komponent tenzoru s hodnotami přečtenými z dalšího tenzoru |
| torch.bitxor | bitová operace XOR všech komponent tenzoru se zadanou hodnotou (skalárem) |
| torch.cbitxor | bitový operace XOR všech komponent tenzoru s hodnotami přečtenými z dalšího tenzoru |
| torch.lshift | bitový posun komponent tenzoru o zadanou hodnotu (skalár) |
| torch.clshift | bitový posun komponent tenzoru o hodnoty přečtené z dalšího tenzoru |
| torch.rshift | bitový posun komponent tenzoru o zadanou hodnotu (skalár) |
| torch.crshift | bitový posun komponent tenzoru o hodnoty přečtené z dalšího tenzoru |
19. Repositář s demonstračními příklady
Všechny demonstrační příklady, které jsme si popsali v předchozích kapitolách, najdete v GIT repositáři dostupném na adrese https://github.com/tisnik/torch-examples.git. Následují odkazy na zdrojové kódy jednotlivých příkladů:
20. Odkazy na Internetu
- Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Lorenzův atraktor
http://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Dot product (Wikipedia)
https://en.wikipedia.org/wiki/Dot_product - Cross product (Wikipedia)
https://en.wikipedia.org/wiki/Cross_product - Outer product
https://en.wikipedia.org/wiki/Outer_product - Linear interpolation
https://en.wikipedia.org/wiki/Linear_interpolation - Matrix multiplication
https://en.wikipedia.org/wiki/Matrix_multiplication - Demos for gnuplot version 5.2
http://gnuplot.info/demo/ - Plotting with Torch7
http://www.lighting-torch.com/2015/08/24/plotting-with-torch7/ - Plotting Package Manual with Gnuplot
https://github.com/torch/gnuplot/blob/master/README.md - An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors - Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor - Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor? - BLAS (Basic Linear Algebra Subprograms)
http://www.netlib.org/blas/ - Basic Linear Algebra Subprograms (Wikipedia)
https://en.wikipedia.org/wiki/Basic_Linear_Algebra_Subprograms - Helix
https://en.wikipedia.org/wiki/Helix - Comparison of deep learning software
https://en.wikipedia.org/wiki/Comparison_of_deep_learning_software - TensorFlow
https://www.tensorflow.org/ - Caffe2 (A New Lightweight, Modular, and Scalable Deep Learning Framework)
https://caffe2.ai/ - PyTorch
http://pytorch.org/ - Seriál o programovacím jazyku Lua
http://www.root.cz/serialy/programovaci-jazyk-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (2)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-2/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (3)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-3/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (4)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-4/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (5 – tabulky a pole)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-5-tabulky-a-pole/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (6 – překlad programových smyček do mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-6-preklad-programovych-smycek-do-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (7 – dokončení popisu mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-7-dokonceni-popisu-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (8 – základní vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-8-zakladni-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (9 – další vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-9-dalsi-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (10 – JIT překlad do nativního kódu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-10-jit-preklad-do-nativniho-kodu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (11 – JIT překlad do nativního kódu procesorů s architekturami x86 a ARM)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-11-jit-preklad-do-nativniho-kodu-procesoru-s-architekturami-x86-a-arm/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (12 – překlad operací s reálnými čísly)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-12-preklad-operaci-s-realnymi-cisly/ - Lua Profiler (GitHub)
https://github.com/luaforge/luaprofiler - Lua Profiler (LuaForge)
http://luaforge.net/projects/luaprofiler/ - ctrace
http://webserver2.tecgraf.puc-rio.br/~lhf/ftp/lua/ - The Lua VM, on the Web
https://kripken.github.io/lua.vm.js/lua.vm.js.html - Lua.vm.js REPL
https://kripken.github.io/lua.vm.js/repl.html - lua2js
https://www.npmjs.com/package/lua2js - lua2js na GitHubu
https://github.com/basicer/lua2js-dist - Lua (programming language)
http://en.wikipedia.org/wiki/Lua_(programming_language) - LuaJIT 2.0 SSA IRhttp://wiki.luajit.org/SSA-IR-2.0
- The LuaJIT Project
http://luajit.org/index.html - LuaJIT FAQ
http://luajit.org/faq.html - LuaJIT Performance Comparison
http://luajit.org/performance.html - LuaJIT 2.0 intellectual property disclosure and research opportunities
http://article.gmane.org/gmane.comp.lang.lua.general/58908 - LuaJIT Wiki
http://wiki.luajit.org/Home - LuaJIT 2.0 Bytecode Instructions
http://wiki.luajit.org/Bytecode-2.0 - Programming in Lua (first edition)
http://www.lua.org/pil/contents.html - Lua 5.2 sources
http://www.lua.org/source/5.2/ - REPL
https://en.wikipedia.org/wiki/Read%E2%80%93eval%E2%80%93print_loop - The LLVM Compiler Infrastructure
http://llvm.org/ProjectsWithLLVM/ - clang: a C language family frontend for LLVM
http://clang.llvm.org/ - LLVM Backend („Fastcomp“)
http://kripken.github.io/emscripten-site/docs/building_from_source/LLVM-Backend.html#llvm-backend - Lambda the Ultimate: Coroutines in Lua,
http://lambda-the-ultimate.org/node/438 - Coroutines Tutorial,
http://lua-users.org/wiki/CoroutinesTutorial - Lua Coroutines Versus Python Generators,
http://lua-users.org/wiki/LuaCoroutinesVersusPythonGenerators