Obsah
1. Serializace a deserializace tenzorů
2. Serializace a deserializace dalších typů objektů
3. Uložení hodnot elementů tenzorů bez dalších metainformací
4. Funkce aplikované na všechny elementy tenzorů
5. Operátory aplikované postupně na všechny elementy tenzorů
6. Tvorba grafů v knihovně Torch
8. Jednoduchý graf zobrazený přímo na desktopu uživatele
9. Export grafu do rastrového obrázku (PNG)
11. Zobrazení průběhů dvou funkcí
12. Export grafu do vektorového formátu SVG
14. Trojrozměrný graf funkce z=f(x,y) – drátový model
15. Repositář s demonstračními příklady
1. Serializace a deserializace tenzorů
V první části článku se budeme zabývat problematikou serializace a deserializace různých typů objektů, především samozřejmě tenzorů. Knihovna Torch umožňuje zapsat obsah tenzoru do souboru, který může být buď čistě textový (ASCII) nebo binární. S binárními soubory se sice pracuje mnohem rychleji, což poznáte u rozměrnějších tenzorů, ovšem nemusí být přenositelné na architektury s jiným pořadím bajtů ve slovech. Navíc mohou být tyto soubory větší než čistě textové soubory (to je ovšem závislé na povaze ukládaných dat).
Pro serializaci se používá třída DataFile odvozená od abstraktní třídy File. Pokud budeme chtít uložit tenzor do souboru s textovým formátem, postačuje po zavolání konstruktoru použít metodu ascii() pro specifikaci formátu (lze vynechat, protože se jedná o výchozí volbu) a následně na výsledném objektu metodu writeObject. Na konci by se měl soubor zavřít (i když se zavře automaticky po opuštění Torche):
local fout = torch.DiskFile(test.asc", "w"):ascii() fout:writeObject(tensor) fout:close()
Zápis souboru do binárního souboru probíhá prakticky stejně, jen se zamění volání metody ascii za binary:
local fout = torch.DiskFile(test.bin", "w"):binary() fout:writeObject(tensor) fout:close()
Vyzkoušejme si nyní uložit několik tenzorů různé velikosti a tvaru do textových i binárních souborů. Uložení je implementováno v následující funkci:
function writeTensor(filename, tensor)
local fout = torch.DiskFile(filename .. ".asc", "w"):ascii()
fout:writeObject(tensor)
fout:close()
local fout = torch.DiskFile(filename .. ".bin", "w"):binary()
fout:writeObject(tensor)
fout:close()
end
Nyní můžeme tuto funkci zavolat pro různé tenzory:
s1 = torch.Tensor(1)
s1[1] = 42
print(s1)
writeTensor("scalar_1", s1)
s2 = torch.Tensor({42})
print(s2)
writeTensor("scalar_2", s2)
v1 = torch.Tensor(3)
v1[1] = 10
v1[2] = 20
v1[3] = 30
print(v1)
writeTensor("vector1", v1)
v2 = torch.Tensor({10,20,30})
print(v2)
writeTensor("vector2", v2)
m = torch.Tensor({{10,20,30}, {40,50,60}, {70,80,90}})
print(m2)
writeTensor("matrix", m)
v = torch.range(1, 24)
q = v:resize(3, 2, 2, 2)
print(q)
writeTensor("tensor_3", q)
Podívejme se nejprve na velikosti souborů, které vznikly pro různé tenzory:
| Soubor | Velikost |
|---|---|
| scalar1.asc | 78 |
| scalar1.bin | 119 |
| scalar2.asc | 78 |
| scalar2.bin | 119 |
| vector1.asc | 84 |
| vector1.bin | 135 |
| vector2.asc | 84 |
| vector2.bin | 135 |
| matrix.asc | 106 |
| matrix.bin | 199 |
| tensor3.asc | 151 |
| tensor3.bin | 351 |
Ve skutečnosti se serializuje celý objekt představující tenzor. Přesněji řečeno se serializují všechny jeho atributy i atributy vložených objektů. V případě tenzoru se jedná především o interní „storage“, s níž jsme se seznámili v úvodním článku tohoto seriálu. Například první tenzor s jediným prvkem se serializuje do této podoby, kde vlastní (jediná) komponenta je ono poslední číslo:
4 1 3 V 1 18 torch.DoubleTensor 1 1 1 1 4 2 3 V 1 19 torch.DoubleStorage 1 42
Příklad serializace vektoru se třemi prvky. Samotný objekt DoubleStorage evidentně obsahuje dva atributy – počet prvků a jejich hodnoty:
4 1 3 V 1 18 torch.DoubleTensor 1 3 1 1 4 2 3 V 1 19 torch.DoubleStorage 3 10 20 30
Příklad serializace matice 3×3 prvky. Objekt typu DoubleStorage samozřejmě nebere do úvahy tvar tenzoru, protože obsahuje jen pole prvků a jejich počet:
4 1 3 V 1 18 torch.DoubleTensor 2 3 3 3 1 1 4 2 3 V 1 19 torch.DoubleStorage 9 10 20 30 40 50 60 70 80 90
Aby měla serializace tenzorů nějaký význam, musí samozřejmě existovat i opačná cesta, tj. deserializace dat. Ta je taktéž podporována, a to opět objektem DiskFile a jeho metodou readObject. Ukažme si jednoduchý příklad serializace a deserializace tenzoru s výpisem informací o deserializovaném objektu:
function writeTensor(filename, tensor)
local fout = torch.DiskFile(filename, "w")
fout:writeObject(tensor)
fout:close()
end
function readTensor(filename)
local fin = torch.DiskFile(filename, "r")
return fin:readObject(tensor)
-- no fin:close() is needed here
end
function printTensorInfo(tensor)
print("Size:")
print(tensor:size())
print("Elements:")
print(tensor:nElement())
print("Dimensions:")
print(tensor:dim())
print("Stride:")
print(tensor:stride())
print("Storage offset:")
print(tensor:storageOffset())
end
v = torch.range(1, 24)
q = v:resize(3, 2, 2, 2)
print(q)
writeTensor("tensor_3_2.asc", q)
deserialized = readTensor("tensor_3_2.asc")
print(deserialized)
printTensorInfo(q)
printTensorInfo(deserialized)
Zkusme si příklad spustit:
Původní tenzor:
(1,1,.,.) = 1 2 3 4 (2,1,.,.) = 9 10 11 12 (3,1,.,.) = 17 18 19 20 (1,2,.,.) = 5 6 7 8 (2,2,.,.) = 13 14 15 16 (3,2,.,.) = 21 22 23 24 [torch.DoubleTensor of size 3x2x2x2]
Serializovaný a deserializovaný tenzor:
(1,1,.,.) = 1 2 3 4 (2,1,.,.) = 9 10 11 12 (3,1,.,.) = 17 18 19 20 (1,2,.,.) = 5 6 7 8 (2,2,.,.) = 13 14 15 16 (3,2,.,.) = 21 22 23 24 [torch.DoubleTensor of size 3x2x2x2]
Informace o původním tenzoru:
Size: 3 2 2 2 [torch.LongStorage of size 4] Elements: 24 Dimensions: 4 Stride: 8 4 2 1 [torch.LongStorage of size 4] Storage offset: 1
Informace o deserializovaném tenzoru:
Size: 3 2 2 2 [torch.LongStorage of size 4] Elements: 24 Dimensions: 4 Stride: 8 4 2 1 [torch.LongStorage of size 4] Storage offset: 1
Můžeme vidět, že se po deserializaci vytvořil klon původního objektu.
Mimochodem, serializovaný tenzor je v textové podobě reprezentován takto:
4 1 3 V 1 18 torch.DoubleTensor 4 3 2 2 2 8 4 2 1 1 4 2 3 V 1 19 torch.DoubleStorage 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2. Serializace a deserializace dalších typů objektů
Ve skutečnosti je možné s využitím objektu typu DiskFile serializovat prakticky libovolný objekt reprezentovatelný v jazyku Lua. Můžeme si to snadno vyzkoušet. Nejprve si zopakujme funkce určené pro serializaci:
function writeObject(filename, object)
local fout = torch.DiskFile(filename .. ".asc", "w")
fout:writeObject(object)
fout:close()
local fout = torch.DiskFile(filename .. ".bin", "w")
fout:writeObject(object)
fout:close()
end
Nyní se pokusíme serializovat speciální hodnoty nil, true a false, dále řetězec, číslo, prázdnou tabulku, naplněnou tabulku a slovník (což je ovšem taktéž tabulka):
writeObject("nil", nil)
writeObject("true", true)
writeObject("false", false)
answer = 42
writeObject("answer", answer)
writeObject("pi", math.pi)
greeting = "Hello world!"
writeObject("greeting", greeting)
empty_array = {}
writeObject("empty_array", empty_array)
array = {1,2,3}
writeObject("array", array)
array2 = {"xx", "yy", "zz"}
writeObject("array2", array2)
dict = {x=1, y=2, z=3}
writeObject("dict", dict)
Podívejme se nejprve na velikosti souborů, které vznikly pro různé objekty:
| Soubor | Velikost |
|---|---|
| nil.asc | 2 |
| nil.bin | 4 |
| true.asc | 4 |
| true.bin | 8 |
| false.asc | 4 |
| false.bin | 8 |
| answer.asc | 5 |
| answer.bin | 12 |
| pi.asc | 21 |
| pi.bin | 12 |
| greeting.asc | 18 |
| greeting.bin | 20 |
| empty_array.asc | 6 |
| empty_array.bin | 12 |
| array2.asc | 39 |
| array2.bin | 78 |
| array.asc | 30 |
| array.bin | 84 |
| dict.asc | 36 |
| dict.bin | 75 |
Jediným objektem, který je plně reprezentován jen svým typem, je nil. Hodnoty true a false jsou reprezentovány svým typem (jedno číslo) a hodnotou (druhé číslo 0 nebo 1); řetězce jsou reprezentovány typem (číslo), počtem znaků (číslo) a samotnými znaky atd.
3. Uložení hodnot elementů tenzorů bez dalších metainformací
Úplná serializace celých tenzorů sice může být výhodná pro další práci s nimi, ovšem velmi často se setkáme s požadavkem, aby se výsledný tenzor použil například v céčkovém programu či naopak – aby nějaký další nástroj vygeneroval sadu hodnot (celých čísel, reálných čísel), které budou moci být načteny do Torche a tam dále zpracovány. I to je samozřejmě možné, ale musíme se vzdát serializace celých objektů a namísto toho serializovat pouze prvky tenzoru (nezávisle na jeho tvaru).
Celý postup je vlastně jednoduchý – pro daný tenzor získáme storage a do souboru uložíme pouze hodnoty komponent tenzoru. Při načítání potom počet komponent získáme snadno – u binárního souboru je to jeho délka podělená bajtovou šířkou jedné komponenty (například 4 nebo osm bajtů), u textového souboru pak počet mezer a konců řádků (většinou ale délku budete zjišťovat dynamicky). Uložení elementů tenzoru typu IntTensor do textového i binárního souboru může vypadat následovně:
function writeTensorStorage(filename, tensor)
local fout = torch.DiskFile(filename .. ".asc", "w"):ascii()
local elements = tensor:nElement()
local storage = tensor:storage()
local written = fout:writeInt(storage)
fout:close()
print("Written " .. written .. " element(s)")
local fout = torch.DiskFile(filename .. ".bin", "w"):binary()
local elements = tensor:nElement()
local storage = tensor:storage()
local written = fout:writeInt(storage)
fout:close()
print("Written " .. written .. " element(s)")
end
s1 = torch.Tensor(1):int()
s1[1] = 42
print(s1)
writeTensorStorage("scalar_1", s1)
s2 = torch.Tensor({42}):int()
print(s2)
writeTensorStorage("scalar_2", s2)
v1 = torch.Tensor(3):int()
v1[1] = 10
v1[2] = 20
v1[3] = 30
print(v1)
writeTensorStorage("vector1", v1)
v2 = torch.Tensor({10,20,30}):int()
print(v2)
writeTensorStorage("vector2", v2)
m = torch.Tensor({{10,20,30}, {40,50,60}, {70,80,90}}):int()
print(m2)
writeTensorStorage("matrix", m)
v = torch.range(1, 24):int()
q = v:resize(3, 2, 2, 2)
print(q)
writeTensorStorage("tensor_3", q)
Velikosti souborů se nyní razantně zkrátily, neboť se skutečně ukládají jen hodnoty komponent:
| Soubor | Velikost |
|---|---|
| scalar1.asc | 3 |
| scalar1.bin | 4 |
| scalar2.asc | 3 |
| scalar2.bin | 4 |
| vector1.asc | 9 |
| vector1.bin | 12 |
| vector2.asc | 9 |
| vector2.bin | 12 |
| matrix.asc | 27 |
| matrix.bin | 36 |
| tensor3.asc | 63 |
| tensor3.bin | 96 |
Tříprvkový vektor serializovaný do textového souboru:
10 20 30
Tříprvkový vektor serializovaný do binárního souboru:
0000000: 31 30 20 32 30 20 33 30 0a 10 20 30.
Matice 3×3 prvky v textovém souboru:
10 20 30 40 50 60 70 80 90
Matice 3×3 prvky v binárním souboru (prohlíženo přes xxd):
0000000: 0a 00 00 00 14 00 00 00 1e 00 00 00 28 00 00 00 ............(... 0000010: 32 00 00 00 3c 00 00 00 46 00 00 00 50 00 00 00 2...<...F...P... 0000020: 5a 00 00 00 Z...
Komponenty tenzoru čtvrtého řádu v textovém souboru:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Komponenty tenzoru čtvrtého řádu v binárním souboru:
0000000: 01 00 00 00 02 00 00 00 03 00 00 00 04 00 00 00 ................ 0000010: 05 00 00 00 06 00 00 00 07 00 00 00 08 00 00 00 ................ 0000020: 09 00 00 00 0a 00 00 00 0b 00 00 00 0c 00 00 00 ................ 0000030: 0d 00 00 00 0e 00 00 00 0f 00 00 00 10 00 00 00 ................ 0000040: 11 00 00 00 12 00 00 00 13 00 00 00 14 00 00 00 ................ 0000050: 15 00 00 00 16 00 00 00 17 00 00 00 18 00 00 00 ................
Poznámka: povšimněte si, že šířka typu int je v Torchi rovna čtyřem bajtům. Samozřejmě však můžeme použít tenzory takového typu, které budou odpovídat požadavkům dalších aplikací (short, long, …).
4. Funkce aplikované na všechny elementy tenzorů
Ještě předtím, než si vysvětlíme způsob vykreslování grafů, si ukážeme, jakým způsobem je možné na všechny komponenty tenzorů aplikovat vybranou matematickou funkci. Je to velmi jednoduché. Nejprve vytvořme vektor s 25 prvky s hodnotami –12 až 12:
v = torch.range(-12, 13)
Z vektoru vytvoříme matici 5×5 prvků:
mx = v:resize(5, 5) print(mx)
Matice vypadá takto:
-12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 [torch.DoubleTensor of size 5x5]
Z této matice můžeme vytvořit novou matici, přičemž se na každý prvek bude aplikovat funkce abs:
my = torch.abs(mx) print(my)
Nová matice vypadá takto:
12 11 10 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 11 12 [torch.DoubleTensor of size 5x5]
Podobně můžeme postupovat i v případě, kdy budeme chtít vypočítat druhou mocninu všech prvků vektoru:
vx = torch.range(0, 10) print(vx)
Obsah vektoru:
0 1 2 3 4 5 6 7 8 9 10 [torch.DoubleTensor of size 11]
Dále vytvoříme nový vektor obsahující druhé mocniny prvků původního vektoru. Povšimněte si, jakým způsobem se funkci předává druhý parametr:
vy = torch.pow(vx, 2) print(vy)
Obsah nového vektoru:
0 1 4 9 16 25 36 49 64 81 100 [torch.DoubleTensor of size 11]
Poznámka: aplikací funkce se v těchto případech vytvoří nový tenzor; původní tenzor zůstane zachován.
Seznam všech dostupných funkcí aplikovatelných na všechny komponenty tenzorů:
| Funkce |
|---|
| torch.abs |
| torch.sign |
| torch.floor |
| torch.ceil |
| torch.round |
| torch.trunc |
| torch.frac |
| torch.sin |
| torch.cos |
| torch.tan |
| torch.sinh |
| torch.cosh |
| torch.tanh |
| torch.asin |
| torch.acos |
| torch.atan |
| torch.atan2 |
| torch.exp |
| torch.log |
| torch.log1p |
| torch.pow |
| torch.sqrt |
| torch.rsqrt |
| torch.sigmoid |
Většina funkcí akceptuje buď pouze tenzor nebo tenzor a skalární hodnotu. Výjimkou je funkce torch.atan2, která počítá arkus tangens pro podíl komponent dvou tenzorů (ty by měly mít stejný tvar).
5. Operátory aplikované postupně na všechny elementy tenzorů
Pro zpracování tenzorů lze použít i běžné matematické operátory +, -, *, / a % aplikované buď postupně na odpovídající si komponenty dvou tenzorů nebo na komponenty tenzoru a skalární hodnotu:
th> v=torch.Tensor({1,2,3,4})
[0.0002s]
th> v*2
2
4
6
8
[torch.DoubleTensor of size 4]
[0.0005s]
th> 2*v
2
4
6
8
[torch.DoubleTensor of size 4]
[0.0003s]
th> v%2
1
0
1
0
[torch.DoubleTensor of size 4]
[0.0003s]
th> v + 100
101
102
103
104
[torch.DoubleTensor of size 4]
[0.0003s]
Většina operací vyžaduje, aby tenzory měly stejný tvar i velikost:
th> v1=torch.range(1,5)
[0.0001s]
th> v2=torch.range(1,10)
[0.0001s]
th> v1+v2
inconsistent tensor size, expected r_ [5], t [5] and src [10] to have the same number of elements, but got 5, 5 and 10 elements respectively at torch/pkg/torch/lib/TH/generic/THTensorMath.c:887
stack traceback:
[C]: at 0x7f1780e95000
[C]: in function '__add'
[string "_RESULT={v1+v2}"]:1: in main chunk
[C]: in function 'xpcall'
/home/tester/torch/install/share/lua/5.1/trepl/init.lua:661: in function 'repl'
...novs/torch/install/lib/luarocks/rocks/trepl/scm-1/bin/th:204: in main chunk
[C]: at 0x00405780
[0.0003s]
Podívejme se nyní na složitější příklad, který kombinuje naše znalosti z předchozí kapitoly:
vx = torch.range(1, 11) vy = torch.pow(vx-6, 2) print(vx) print(vy)
Původní vektor vx:
1 2 3 4 5 6 7 8 9 10 11 [torch.DoubleTensor of size 11]
Vektor vy získaný aplikací funkce pow(vx-6,2):
25 16 9 4 1 0 1 4 9 16 25 [torch.DoubleTensor of size 11]
Nyní se pokusíme vytvořit vektor hodnot funkce sin x:
vx = torch.range(0, 360, 10) vy = torch.sin(vx/180.0*math.pi) print(vx) print(vy)
Druhá verze vektoru vx s úhly:
0 10 20 30 ... ... ... 330 340 350 360 [torch.DoubleTensor of size 37]
Vektor (tabulka) hodnot funkce sin x:
0.0000 0.1736 0.3420 0.5000 0.6428 0.7660 ... ... ... -0.7660 -0.6428 -0.5000 -0.3420 -0.1736 -0.0000 [torch.DoubleTensor of size 37]
Poznámka: v dokumentaci se sice píše, že prvním operandem musí být tenzor a nikoli skalár, ovšem ve skutečnosti lze použít obě varianty.
6. Tvorba grafů v knihovně Torch
V mnoha případech budeme chtít zobrazit výsledky nějakého výpočtu nebo analýzy formou grafu. Grafický výstup je samozřejmě v knihovně Torch podporován, a to dokonce několika způsoby. Již v základní instalaci je obsaženo rozhraní pro knihovnu gnuplot, což je téma, kterému se budeme (prozatím ve stručnosti) věnovat v navazujících kapitolách. Alternativně je však možné použít backendy gfx.js popř. visdom a vykreslovat grafy s využitím webových technologií. Pro interaktivní tvorbu (nejenom) grafů je pak určen nástroj iTorch, který spojuje možnosti iPythonu s Torchem. Popisem iTorche se budeme věnovat v samostatném článku, protože se jedná o poměrně rozsáhlé téma; navíc nemusí být instalace zcela jednoduchá. Dnes se seznámíme především s vykreslením průběhu funkcí jedné nezávislé proměnné či dvou nezávislých proměnných. Navzorkované hodnoty těchto funkcí jsou reprezentovány vektorem či maticí, tj. pro jejich zpracování je možné použít všech možnosti, které nám knihovna Torch nabízí.
7. Použití knihovny gnuplot
Nástroj gnuplot je určen pro tvorbu plošných (2D) ale i prostorových (3D) grafů, včetně možností vizualizace vektorových polí. Přitom se jedná o program, který je možné v celé své šíři ovládat pouze z příkazové řádky, a to buď s využitím uživatelsky vytvořených skriptů, nebo interaktivním způsobem, tj. postupným zadáváním a následným prováděním příkazů zapsaných na standardní vstup (stdin), což většinou znamená z klávesnice, ale standardní vstup je samozřejmě možné pomocí prostředků operačního systému přesměrovat a použít místo něj například výstup z jiného běžícího procesu. Vývoj této aplikace probíhal velmi dlouho (poprvé jsem se s gnuplotem setkal ještě v dobách kralování DOSu na počítačích s procesorem 386 a pouhými čtyřmi megabyty RAM) a mimo jiné i proto se dnes jedná o jeden z nejvíce propracovaných programů určených pro dávkovou tvorbu grafů (mezi další používané aplikace s podobným zaměřením patří například plotutils, což je taktéž utilita resp. sada utilit šířených pod GNU licencí).
Další předností gnuplotu je – minimálně pro programátory – zabudování poměrně sofistikovaného příkazového jazyka, pomocí kterého je možné zadávat a spouštět makra řídící načtení dat uložených v externím souboru, vytvoření grafu a jeho uložení resp. export do zvoleného formátu atd. gnuplot se také vyznačuje malým počtem interních chyb – to je důležité zejména při dávkovém vytváření mnoha grafů, kdy není možná jejich důsledná kontrola člověkem a musíme se spolehnout na to, že grafy budou po automatickém zpracování korektní. gnuplot je k dispozici pro mnoho platforem, zjednodušeně je možné říci, že tam, kde se rozběhne nějaký překladač ANSI C (dokonce i šestnáctibitový), je možné zprovoznit i gnuplot.
Při popisu dalších vlastností gnuplotu začněme – možná poněkud netypicky – popisem možností exportu vytvořených grafů do některých podporovaných souborových formátů. Při výstupu grafů je možné použít jak rastrové, tak i vektorové grafické souborové formáty. Oba dva typy grafických formátů jsou totiž důležité: rastrovou grafiku využijeme například při publikování grafů na Internetu, vektorová grafika se naopak hodí při přípravě publikací určených pro tisk. Mezi podporované rastrové formáty patří PBM (Portable BitMap), PNG (Portable Network Graphics – vhodné pro web), GIF (pouze s podporou dalších knihoven), JPEG apod. Z vektorových formátů je podporován především PostScript, dále je pak možné provést výstup například do LATEXu, DXF (Drawing Interchange File Format – formát podporovaný prakticky každým CAD systémem) a do SVG (to je ideální pro webové prezentace).
8. Jednoduchý graf zobrazený přímo na desktopu uživatele
Jak již víme z předchozích dvou kapitol, poskytuje framework Torch rozhraní umožňující tvorbu grafů s využitím gnuplotu jako jednoho z podporovaných backendů. Podívejme se tedy na postup vykreslení velmi jednoduchého grafu s průběhem funkce sinus.
Nejprve musíme naimportovat modul gnuplot:
require("gnuplot")
Dále vytvoříme vektor obsahující hodnoty od 0 do 360 s krokem 5:
x = torch.range(0, 360, 5)
Ve třetím kroku z předchozího vektoru x vytvoříme nový vektor s průběhem funkce sinus. Vektor bude obsahovat stejný počet 72 prvků, samozřejmě s jinými hodnotami:
y = torch.sin(x/180.0*math.pi)
Zbývá nám specifikace titulku grafu a jeho vykreslení do samostatného okna na obrazovce:
gnuplot.title("sin x")
gnuplot.figure(1)
gnuplot.plot(x, y)
Metodě gnuplot.figure se předává nepovinný celočíselný identifikátor grafu. Pokud se tento identifikátor neuvede, vykreslí se vždy nové okno s grafem. Metodě gnuplot.plot se předávají hodnoty na x-ové ose i hodnoty, které se mají vynést na y-ovou osu. Nové okno se otevřen až po zavolání této metody (což má význam jen při interaktivní práci).
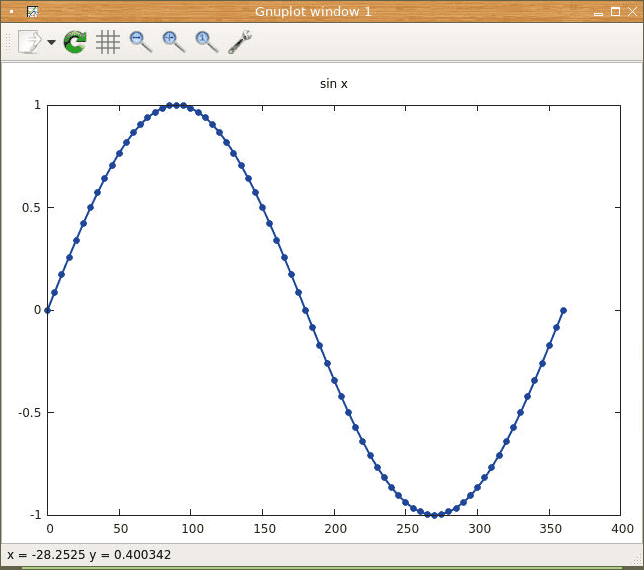
Obrázek 1: Graf zobrazený v samostatném okně na desktopu.
Celý příklad vypadá následovně:
require("gnuplot")
x = torch.range(0, 360, 5)
y = torch.sin(x/180.0*math.pi)
gnuplot.title("sin x")
gnuplot.figure(1)
gnuplot.plot(x, y)
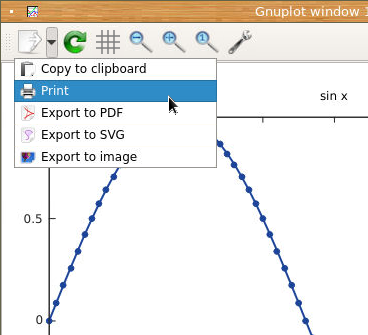
Obrázek 2: V případě potřeby je možné graf uložit do vybraného rastrového nebo vektorového formátu.
9. Export grafu do rastrového obrázku (PNG)
Zobrazení grafu na obrazovce je užitečné při interaktivní práci s Torchem, ovšem ve chvíli, kdy se automaticky či poloautomaticky zpracovává delší skript (například pro různá vstupní data), budeme požadovat export grafu do souboru. Jednou z možností je export grafu do rastrového obrázku ve formátu PNG. To je snadné zajistit; postačuje pouze nahradit volání:
gnuplot.figure(1)
za volání:
gnuplot.pngfigure("plot2.png")
Vzhledem k tomu, že se má graf vykreslit neinteraktivně, je nutné na konec programu přidat volání:
gnuplot.plotflush()
Navíc je ještě vhodné na samotném konci přidat volání metody:
gnuplot.close()
Toto volání zabezpečí uzavření souboru s obrázkem grafu. Soubor se sice korektně uzavře i po doběhnutí celého skriptu, takže je toto volání zdánlivě nadbytečné, ovšem pokud budete vytvářet stovky grafů, mohl by skript zhavarovat kvůli velkému množství současně otevřených souborů.
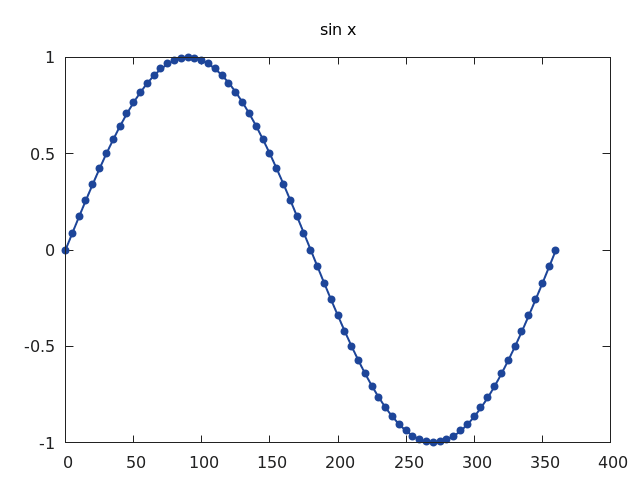
Obrázek 3: Průběh funkce sin x naznačený polyčárou.
Opět se podívejme na to, jak vypadá celý příklad:
require("gnuplot")
x = torch.range(0, 360, 5)
y = torch.sin(x/180.0*math.pi)
gnuplot.pngfigure("plot2.png")
gnuplot.title("sin x")
gnuplot.plot(x, y)
gnuplot.plotflush()
gnuplot.close()
10. Nastavení popisků os
Podobně jako existuje metoda gnuplot.title určená pro nastavení titulku celého grafu, je možné specifikovat popisy os x, y a u některých typů grafů i osy z. Je to velmi snadné:
gnuplot.title("sin x")
gnuplot.xlabel("x")
gnuplot.ylabel("sin x")
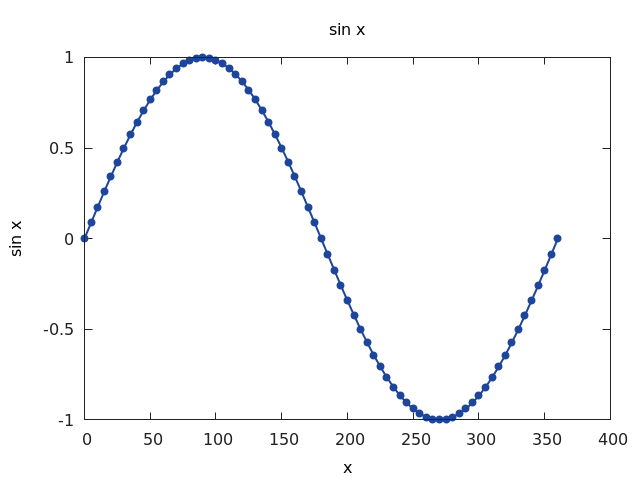
Obrázek 4: Průběh funkce sin x naznačený polyčárou s popiskami horizontální i vertikální osy.
Zdrojový kód skriptu se změní jen nepatrně:
require("gnuplot")
x = torch.range(0, 360, 5)
y = torch.sin(x/180.0*math.pi)
gnuplot.pngfigure("plot3.png")
gnuplot.title("sin x")
gnuplot.xlabel("x")
gnuplot.ylabel("sin x")
gnuplot.plot(x, y)
gnuplot.plotflush()
gnuplot.close()
11. Zobrazení průběhů dvou funkcí
Metoda gnuplot.plot nás neomezuje na zobrazení pouze jediného průběhu funkce. Pokud se například dostaneme do situace, kdy budeme chtít zobrazit průběhy dvou funkcí (nebo i více funkcí) a současně budou mít funkce společnou y-ovou osu (tedy zhruba stejné amplitudy), lze to zařídit velmi jednoduše. Nejprve si průběhy obou funkcí vytvoříme – bude se samozřejmě jednat o vektory obsahující hodnoty funkcí ve zvolených bodech:
x = torch.range(0, 360, 5) y1 = torch.sin(x/180.0*math.pi) y2 = torch.cos(x/180.0*math.pi)
Následně se vykreslení obou funkcí provede takto:
gnuplot.plot({"sin x", x, y1},
{"cos x", x, y2})
Povšimněte si, že předáváme dvojici polí (či tabulek), přičemž prvním prvkem polí je text použitý v legendě, druhý prvek představuje hodnoty na x-ové ose a třetí prvek pak hodnoty samotné funkce, která se má vykreslit.
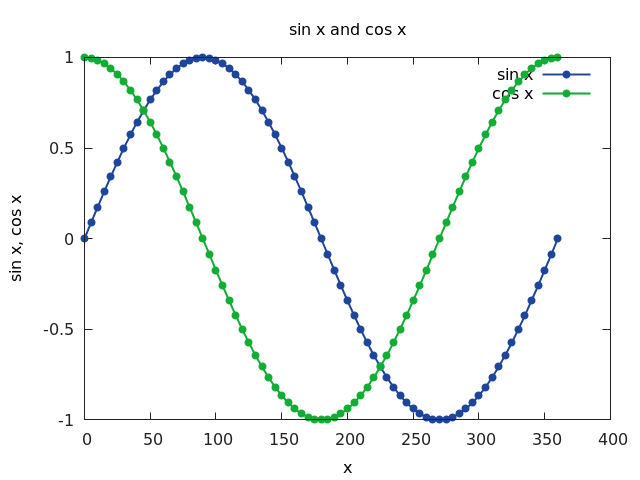
Obrázek 5: Průběhy funkcí sin x a cos x.
Zdrojový kód skriptu bude vypadat takto:
require("gnuplot")
x = torch.range(0, 360, 5)
y1 = torch.sin(x/180.0*math.pi)
y2 = torch.cos(x/180.0*math.pi)
gnuplot.pngfigure("plot4.png")
gnuplot.title("sin x and cos x")
gnuplot.xlabel("x")
gnuplot.ylabel("sin x, cos x")
gnuplot.plot({"sin x", x, y1},
{"cos x", x, y2})
gnuplot.plotflush()
gnuplot.close()
Podobným způsobem si můžeme zobrazit průběh napětí u třífázového napájení:
require("gnuplot")
x = torch.range(0, 360, 5)
y1 = torch.sin(x/180.0*math.pi)
y2 = torch.sin((x+120)/180.0*math.pi)
y3 = torch.sin((x-120)/180.0*math.pi)
gnuplot.pngfigure("plot5.png")
gnuplot.title("Three-phases")
gnuplot.xlabel("x")
gnuplot.ylabel("sin x, cos x")
gnuplot.plot({"phase 1", x, y1},
{"phase 2", x, y2},
{"phase 3", x, y3})
gnuplot.plotflush()
gnuplot.close()
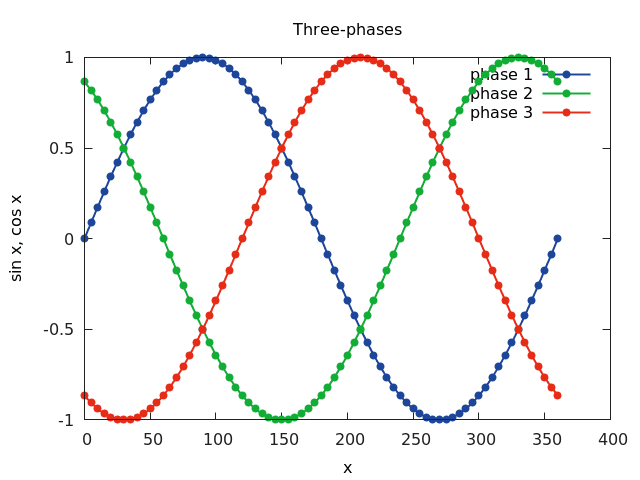
Obrázek 6: Naznačení průběhu napětí u třífázového napájení.
12. Export grafu do vektorového formátu SVG
Volba výstupního formátu obsahujícího vytvořený graf se provádí na základě zavolané metody:
| Metoda | Formát výstupního souboru |
|---|---|
| gnuplot.epsfigure(jméno_výstupního_souboru) | Encapsulated PostScript (varianta PostScriptu) |
| gnuplot.pdffigure(jméno_výstupního_souboru) | |
| gnuplot.pngfigure(jméno_výstupního_souboru) | PNG |
| gnuplot.svgfigure(jméno_výstupního_souboru) | SVG |
Poměrně často se můžeme setkat s požadavkem na vytvoření grafu ve vektorové podobě, který by byl škálovatelný podle typu zařízení, na kterém se graf zobrazuje. Téměř ideálním formátem pro tento požadavek je formát SVG (Scalable Vector Graphics). Graf se do SVG vyexportuje jednoduše:
require("gnuplot")
x = torch.range(0, 360, 5)
y1 = torch.sin(x/180.0*math.pi)
y2 = torch.cos(x/180.0*math.pi)
gnuplot.svgfigure("plot5.svg")
gnuplot.title("sin x and cos x")
gnuplot.xlabel("x")
gnuplot.ylabel("sin x, cos x")
gnuplot.plot({"sin x", x, y1},
{"cos x", x, y2})
gnuplot.plotflush()
gnuplot.close()
13. Jednoduchý sloupcový graf
V dalším příkladu se pokusíme nahradit volání:
gnuplot.plot(x, y)
za:
gnuplot.bar(x, y)
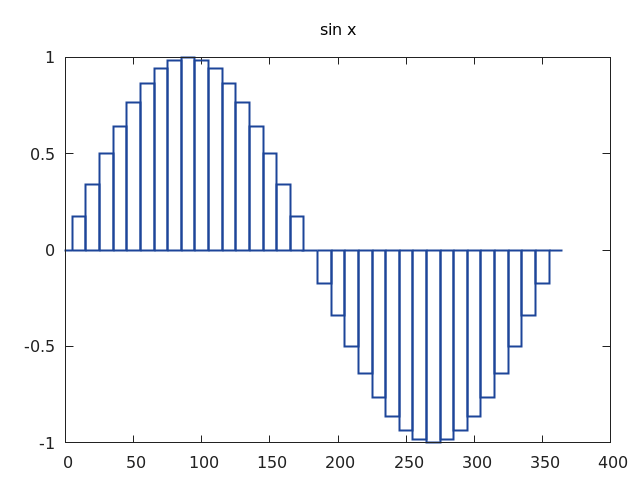
Obrázek 7: Jednoduchý sloupcový graf.
Výsledkem bude graf, v němž se namísto polyčáry spojující jednotlivé hodnoty funkce vykreslí sloupcový graf. Ostatně i z tohoto důvodu jsme zmenšili počet hodnot ze 72 na polovinu (vektory x a y mají jen 36 prvků):
require("gnuplot")
x = torch.range(0, 360, 10)
y = torch.sin(x/180.0*math.pi)
gnuplot.pngfigure("plot6.png")
gnuplot.title("sin x")
gnuplot.bar(x, y)
gnuplot.plotflush()
gnuplot.close()
Poznámka: sloupcový graf je možné zkombinovat s liniovým grafem. Jak se to provádí si ukážeme v navazujícím článku.
14. Trojrozměrný graf funkce z=f(x,y) – drátový model
V této kapitole si stručně vysvětlíme možnosti tvorby grafů funkcí typu z=f(x,y), tj. funkcí se dvěma nezávislými proměnnými.
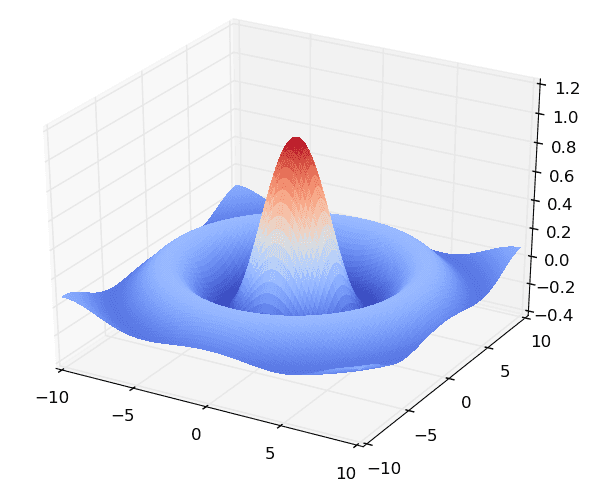
Obrázek 8: Funkce dvou nezávislých proměnných vykreslená „konkurenčním“ frameworkem Matplotlib.
Tyto funkce je možné zobrazit různým způsobem, například ve formě kontur či vyplněné plochy, ovšem zpočátku si ukážeme, jak se vykreslí „pouhý“ drátěný model (wireframe) s průběhem funkce.
require("gnuplot")
GRID=40
v = torch.range(0, GRID*GRID)
v = v - 12
m = v:resize(GRID, GRID)
m = torch.sin(m*4.0*math.pi/90.0/GRID)
gnuplot.pngfigure("plot7.png")
gnuplot.title("splot")
gnuplot.splot(m)
gnuplot.plotflush()
gnuplot.close()
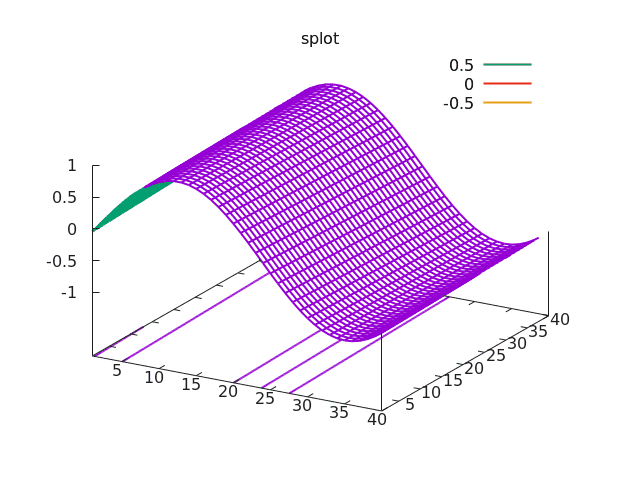
Obrázek 9: Graf vykreslený předchozím demonstračním příkladem.
15. Repositář s demonstračními příklady
Všechny demonstrační příklady, které jsme si popsali v předchozích kapitolách, najdete v GIT repositáři dostupném na adrese https://github.com/tisnik/torch-examples.git. Následují odkazy na zdrojové kódy jednotlivých příkladů:
16. Odkazy na Internetu
- Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Plotting with Torch7
http://www.lighting-torch.com/2015/08/24/plotting-with-torch7/ - Plotting Package Manual with Gnuplot
https://github.com/torch/gnuplot/blob/master/README.md - An Introduction to Tensors
https://math.stackexchange.com/questions/10282/an-introduction-to-tensors - Differences between a matrix and a tensor
https://math.stackexchange.com/questions/412423/differences-between-a-matrix-and-a-tensor - Qualitatively, what is the difference between a matrix and a tensor?
https://math.stackexchange.com/questions/1444412/qualitatively-what-is-the-difference-between-a-matrix-and-a-tensor? - BLAS (Basic Linear Algebra Subprograms)
http://www.netlib.org/blas/ - Basic Linear Algebra Subprograms (Wikipedia)
https://en.wikipedia.org/wiki/Basic_Linear_Algebra_Subprograms - Comparison of deep learning software
https://en.wikipedia.org/wiki/Comparison_of_deep_learning_software - TensorFlow
https://www.tensorflow.org/ - Caffe2 (A New Lightweight, Modular, and Scalable Deep Learning Framework)
https://caffe2.ai/ - PyTorch
http://pytorch.org/ - Seriál o programovacím jazyku Lua
http://www.root.cz/serialy/programovaci-jazyk-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (2)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-2/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (3)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-3/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (4)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-4/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (5 – tabulky a pole)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-5-tabulky-a-pole/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (6 – překlad programových smyček do mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-6-preklad-programovych-smycek-do-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (7 – dokončení popisu mezijazyka LuaJITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-7-dokonceni-popisu-mezijazyka-luajitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (8 – základní vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-8-zakladni-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (9 – další vlastnosti trasovacího JITu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-9-dalsi-vlastnosti-trasovaciho-jitu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (10 – JIT překlad do nativního kódu)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-10-jit-preklad-do-nativniho-kodu/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (11 – JIT překlad do nativního kódu procesorů s architekturami x86 a ARM)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-11-jit-preklad-do-nativniho-kodu-procesoru-s-architekturami-x86-a-arm/ - LuaJIT – Just in Time překladač pro programovací jazyk Lua (12 – překlad operací s reálnými čísly)
http://www.root.cz/clanky/luajit-just-in-time-prekladac-pro-programovaci-jazyk-lua-12-preklad-operaci-s-realnymi-cisly/ - Lua Profiler (GitHub)
https://github.com/luaforge/luaprofiler - Lua Profiler (LuaForge)
http://luaforge.net/projects/luaprofiler/ - ctrace
http://webserver2.tecgraf.puc-rio.br/~lhf/ftp/lua/ - The Lua VM, on the Web
https://kripken.github.io/lua.vm.js/lua.vm.js.html - Lua.vm.js REPL
https://kripken.github.io/lua.vm.js/repl.html - lua2js
https://www.npmjs.com/package/lua2js - lua2js na GitHubu
https://github.com/basicer/lua2js-dist - Lua (programming language)
http://en.wikipedia.org/wiki/Lua_(programming_language) - LuaJIT 2.0 SSA IRhttp://wiki.luajit.org/SSA-IR-2.0
- The LuaJIT Project
http://luajit.org/index.html - LuaJIT FAQ
http://luajit.org/faq.html - LuaJIT Performance Comparison
http://luajit.org/performance.html - LuaJIT 2.0 intellectual property disclosure and research opportunities
http://article.gmane.org/gmane.comp.lang.lua.general/58908 - LuaJIT Wiki
http://wiki.luajit.org/Home - LuaJIT 2.0 Bytecode Instructions
http://wiki.luajit.org/Bytecode-2.0 - Programming in Lua (first edition)
http://www.lua.org/pil/contents.html - Lua 5.2 sources
http://www.lua.org/source/5.2/ - REPL
https://en.wikipedia.org/wiki/Read%E2%80%93eval%E2%80%93print_loop - The LLVM Compiler Infrastructure
http://llvm.org/ProjectsWithLLVM/ - clang: a C language family frontend for LLVM
http://clang.llvm.org/ - LLVM Backend („Fastcomp“)
http://kripken.github.io/emscripten-site/docs/building_from_source/LLVM-Backend.html#llvm-backend - Lambda the Ultimate: Coroutines in Lua,
http://lambda-the-ultimate.org/node/438 - Coroutines Tutorial,
http://lua-users.org/wiki/CoroutinesTutorial - Lua Coroutines Versus Python Generators,
http://lua-users.org/wiki/LuaCoroutinesVersusPythonGenerators