Obsah
1. Programy pro generování fraktálů napsané v assembleru
2. Výpočet Mandelbrotovy množiny pomocí FPU
3. Optimalizace výpočtu Mandelbrotovy množiny na velikost výsledného kódu
4. Fixed point aritmetika
5. Vykreslení Mandelbrotovy množiny s využitím fixed point aritmetiky
6. Mandelbrot is possible
7. Odkazy na další informační zdroje
8. Obsah dalšího pokračování tohoto seriálu
1. Programy pro generování fraktálů napsané v assembleru
Při výpočtech obrázků, na kterých jsou zobrazeny fraktální objekty, se provádí poměrně zdlouhavé a přitom jednoduše naprogramovatelné numerické výpočty, většinou založené na iteraci řešené programovou smyčkou. Není tedy divu, že se mnohdy místo vyššího programovacího jazyka použil pro psaní těchto programů assembler, přesněji jazyk symbolických adres (JSA). Použití assembleru umožnilo programátorům zkrátit dobu trvání výpočtu fraktálu, a to mnohdy až o několik řádů, zejména při přechodu z interpretovaných jazyků. Efekt přechodu z Céčka na assembler není tak výrazný, i když se uvádí, že dobrý programátor dokáže po úpravě assemblerovského zdrojového kódu program urychlit až o 50%. Je to ostatně logické, protože překladač má o řešeném problému k dispozici mnohem méně informací než samotný programátor.
Kromě toho je ručně napsaný a optimalizovaný program v assembleru mnohdy také kratší než tentýž algoritmus pouze přeložený z vyššího programovacího jazyka. Toho lze využít například při tvorbě takzvaných inter, tj. velmi krátkých spustitelných programů, typicky o velikosti pouhých 128, 256, 1024 nebo 4096 bytů (existují ještě 64kB intra, ty se však již dají napsat ve vyšším programovacím jazyce, protože je zde kladen menší důraz na kompaktní kód). V následujících kapitolách si uvedeme některé postupy, které je možné použít právě při tvorbě jednoduchých assemblerovských programů, které mají generovat fraktály. Kvůli jednoduchému přístupu ke grafickým funkcím jsou všechny demonstrační příklady vytvořeny pro operační systém DOS a mikroprocesory řady x86, přičemž jsou samozřejmě spustitelné v DOSBoxu či podobném emulátoru.
Všechny dále popisované demonstrační příklady, tj. jak zdrojové kódy, tak i výsledné spustitelné soubory, můžete získat pod tímto odkazem. Pro překlad (resp. korektnější by bylo slovo „sestavení“) všech demonstračních příkladů byl použit známý Turbo Assembler verze 2.51, linkování (de facto pouze převod z objektového kódu do spustitelného tvaru) pak bylo provedeno programem Turbo Link 4.01; obě dvě zmiňované aplikace vytvořila v minulém století firma Borland International. Po úpravách zdrojového kódu je však možné použít i další assemblery, například dnes oblíbený NASM. Překlad a následný převod objektového kódu demonstračních příkladů do spustitelných programů ve formátu COM byl proveden pomocí příkazů:
tasm /l mandelf1.asm
tlink /t mandelf1.obj
tasm /l mandelf2.asm
tlink /t mandelf2.obj
tasm /l mandelf3.asm
tlink /t mandelf3.obj
tasm /l mandelfx.asm
tlink /t mandelfx.obj
tasm /l julia1.asm
tlink /t julia1.obj
tasm /l julia2.asm
tlink /t julia2.obj
2. Výpočet Mandelbrotovy množiny pomocí FPU
V dnešním prvním demonstračním příkladu je ukázán jeden ze způsobů výpočtu a zobrazení Mandelbrotovy množiny s využitím matematického koprocesoru, který umožňuje provádění operací s hodnotami uloženými ve formátu pohyblivé řádové binární čárky (FP – Floating Point). Výpočet je poměrně přímočarý. Nejprve se nastaví grafický režim 320×200 pixelů s 256 barvami a dvojice registrů ES:DI je naplněna tak, aby ukazovala na počáteční adresu video paměti. Posléze se ve třech do sebe vložených smyčkách (návěstí for_y, for_x a smycka) provádí výpočet barev jednotlivých pixelů.
Po odchodu z těchto smyček (buď po překročení hodnoty bailout nebo dosažení maximálního počtu iterací) je v registru CL uložen počet iterací (čítá se od počáteční hodnoty směrem k nule). Tento údaj je převeden do registru AL a posléze uložen do video paměti. Dvojice registrů ES:DI se při této operaci automaticky nastaví na další pixel. Na konci programu se volají BIOSovské funkce pro čekání na stisk klávesy, zpětné nastavení textového režimu a konečně instrukce retn, která v programech typu COM vlastně znamená ukončení aplikace (DOS totiž na zásobník před spuštěním programu uloží adresu obsluhy jeho korektního ukončení). Celý program má po překladu délku 196 bytů.
; Vykresleni Mandelbrotovy mnoziny s vyuzitim instrukci FPU
; prvni verze
; Autor: Pavel Tisnovsky 19.09.99
model tiny ; pametovy model CS=DS=SS<64kB
p386 ; povoleny instrukce procesoru 386+
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
;*** zacatek data segmentu
dataseg ; zacatek data-segmentu
ypos dd -2.0 ; pozice na vertikalni ose
c4 dd 4.0 ; bailout
min dd -2.5 ; minimalni hodnota na horizontalni ose
posunx dd 0.015 ; posun po horizontalni ose
posuny dd 0.02 ; posun po vertikalni ose
xpos dd ?
p286
udataseg
zx1 dd ? ; hodnota komplexni promenne Z
zy1 dd ? ;
zx2 dd ? ; druha mocnina slozek Z
zy2 dd ? ;
ccx dd ? ; hodnota komplexni konstanty C
ccy dd ?
;*** zacatek kodoveho segmentu
codeseg ; zacatek code-segmentu
org 100h ; zacatek kodu pro programy typu COM
p386
start:
mov al,13h ; graficky mod 13h
int 10h
push 0a000h
pop es ; video segment
xor di,di ; zacatek vykreslovani na obrazovce
for_y: mov si,SLOUPCU ; x
fld ypos
fadd posuny ; ypos+=4.0/200.0
fstp ypos
mov eax,min ; xpos=-2.5
mov xpos,eax
for_x:
fld xpos
fadd posunx ; xpos+=4.0/260.0
fstp xpos
xor eax,eax
mov zx1,eax ; na zacatku iterace vynulovat Z
mov zy1,eax
mov eax,xpos
mov ccx,eax ; nastavit korektne C
mov eax,ypos
mov ccy,eax
mov cl,51 ; maximalni pocet iteraci
smycka:
fld zx1 ;\
fmul zx1 ; > zx2=zx1*zx1
fstp zx2 ;/
fld zy1 ;\
fmul zy1 ; > zy2=zy1*zy1
fstp zy2 ;/
fld zx1 ;\
fmul zy1 ; \
fadd st,st ; > zy1=2*zx1*zy1+cy
fadd ccy ; /
fstp zy1 ;/
fld zx2 ;\
fsub zy2 ; \
fadd ccx ; /` zx1=zx2-zy2+cx
fstp zx1 ;/
fld zx2 ;\
fadd zy2 ; > zx2+zy2>4 ?
fcomp c4 ;/
fstsw ax ; FPU priznaky do AX
sahf ; predani FPU priznaku do priznakoveho registru
jnb short pokr ; pokud jsme prekrocili bailout, konec
loop short smycka
pokr:
xchg ax,cx ; pocet iteraci do AL -> barva pixelu
stosb ; vykreslit bod+posun na dalsi
dec si
for_x_: jnz short for_x ; dalsi radek
cmp di,64000 ; konec obrazku ?
for_y_: jne for_y ; konec smycky for y
xor ax,ax ; cekat na klavesu
int 16h
mov ax,3 ; textovy rezim
int 10h
retn ; finito
end start 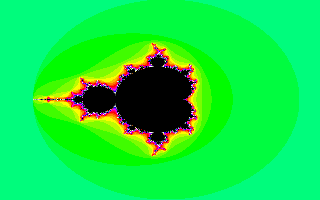
3. Optimalizace výpočtu Mandelbrotovy množiny na velikost výsledného kódu
Výše uvedený příklad je možné optimalizovat, a to jak na velikost výsledného programového kódu, tak i na rychlost provádění celého výpočtu. Nyní si ukážeme, jakým způsobem by mohla probíhat optimalizace na velikost výsledného kódu (přičemž se mimochodem zvýší i jeho rychlost). Největší díl neefektivity předchozího příkladu spočíval v tom, že se všechny mezivýsledky ukládaly ze zásobníku matematického koprocesoru zpět do operační paměti. Všechny instrukce koprocesoru, které mají jako operand uvedenu adresu do paměti, mají délku čtyři byty (v 16bitovém prostředí). Pokud však místo přímé adresy budeme adresovat nepřímo přes registr BX s posunem, zkrátí se délka instrukcí na tři byty. Posun však musí být malý, aby se offset nemusel kódovat na šestnáct bytů.
Toho je (pro větší komfort z programování) dosaženo použitím „maker“ equ, která ve zdrojovém kódu při sestavování programu nahrazují svoji levou stranu za stranu pravou (vlastně se jedná o obdobu direktivy #define z céčka). Dalšího zkrácení programu bylo dosaženo použitím celočíselných konstant pro bailout a minimální hodnotu proměnné x na horizontální ose (ta musela být zaokrouhlena). Matematický koprocesor totiž zpracuje i celočíselné operandy, které si nejprve automaticky převede do interního tvaru (formát extended) a posléze s nimi provede požadovanou operaci. V čem jsou celočíselné konstanty výhodnější? Ve výsledném kódu mohou být zakódovány na šestnácti bitech (integer) a ne na třiceti dvou bitech (float/single). Těmito úpravami se délka přeloženého kódu zmenšila ze 196 bytů na 142 bytů.
; Vykresleni Mandelbrotovy mnoziny s vyuzitim instrukci FPU
; druha verze
; Autor: Pavel Tisnovsky 19.09.99
model tiny ; pametovy model CS=DS=SS<64kB
p386 ; povoleny instrukce procesoru 386+
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
;*** zacatek data segmentu
dataseg ; zacatek data-segmentu
min dw -3 ; minimalni hodnota promenne xpos jako integer
ypos dd -2.0 ; pozice na vertikalni ose
posunx dd 0.015 ; posun po horizontalni ose
posuny dd 0.02 ; posun po vertikalni ose
c4 dw 4 ; bailout jako integer
p286
udataseg
zx1 dd ? ; hodnota komplexni promenne Z
zy1 dd ? ;
ccx dd ? ; hodnota komplexni konstanty C
ccy dd ?
zy2 dd ?
xpos dd ?
; makra - nahrada primeho adresovani adresovanim pres registr BX
minptr equ word ptr [bx-16]
yposptr equ dword ptr [bx-14]
posunxptr equ dword ptr [bx-10]
posunyptr equ dword ptr [bx-6]
c4ptr equ word ptr [bx-2]
zx1ptr equ dword ptr [bx]
zy1ptr equ dword ptr [bx+4]
cxptr equ dword ptr [bx+8]
cyptr equ dword ptr [bx+12]
zy2ptr equ dword ptr [bx+16]
xposptr equ dword ptr [bx+20]
;*** zacatek kodoveho segmentu
codeseg ; zacatek code-segmentu
org 100h ; zacatek kodu pro programy typu COM
p386
start:
mov al,13h ; graficky mod 13h
int 10h
push 0a000h
pop es ; video segment
xor di,di ; zacatek vykreslovani na obrazovce
mov bx, offset zx1 ; inicializace pro relativni adresovani
for_y: mov si,SLOUPCU ; x
fld yposptr
fadd posunyptr ; ypos+=4.0/200.0
fstp yposptr
fild minptr ; xpos=-3
fstp xposptr
for_x:
fld xposptr
fadd posunxptr ; xpos+=4.0/260.0
fst cxptr ; vlozit i do promenne ccx
fst zx1ptr ; zx1=cx (nahrada prvni iterace)
fstp xposptr
fld yposptr
fst zy1ptr ; zy1=cy (nahrada prvni iterace)
fstp cyptr
mov cl,50 ; maximalni pocet iteraci
smycka: ; zasobnik FPU
fld zx1ptr ;\ zx1
fmul st(0),st(0) ; > zx2=zx1*zx1 zx1*zx1
fld st(0) ;/ zx2 zx2
fld zy1ptr ;\ zy1 zx2 zx2
fmul st(0),st(0) ; > zy2=zy1*zy1 zy2 zx2 zx2
fst zy2ptr ;/ zy2 zx2 zx2
fld zx1ptr ;\ zx1 zy2 zy2 zx2 zx2
fmul zy1ptr ; \ zx1*zy1 zy2 zy2 zx2 zx2
fadd st(0),st(0) ; > zy1=2*zx1*zy1+cy 2*zx1*zy1 zy2 zy2 zx2 zx2
fadd cyptr ; / 2*zx1*zy1+ccy zy2 zy2 zx2 zx2
fstp zy1ptr ;/ zy2 zy2 zx2 zx2
fsubp st(1), st(0) ;\ zx2-zy2 zy2 zx2
fadd cxptr ; \ zx2-zy2+ccx zy2 zx2
fstp zx1ptr ; /` zx1=zx2-zy2+cx zy2 zx2
;/
fadd zy2ptr ; zx2+zy2>4 ?
ficomp c4ptr
fstsw ax ; FPU priznaky do AX
sahf ; predani FPU priznaku do priznakoveho registru
jnb short pokr ; pokud jsme prekrocili bailout, konec
loop short smycka
pokr:
xchg ax,cx ; pocet iteraci do AL -> barva pixelu
stosb ; vykreslit bod+posun na dalsi
dec si
for_x_: jnz short for_x ; dalsi radek
cmp di,64000 ; konec obrazku ?
for_y_: jne short for_y ; konec smycky for y
xor ax,ax ; cekat na klavesu
int 16h
mov ax,3 ; textovy rezim
int 10h
retn ; finito
end start 
V úpravách však můžeme dále pokračovat. Zásobník operandů matematického koprocesoru se totiž nechová pouze jako řádný zásobník, ale také jako pole s osmi hodnotami, které je možné indexovat. Jinými slovy – matematické operace nemusí probíhat pouze nad nejvyššími dvěma položkami na zásobníku, ale i s položkami uloženými níže. Tato možnost je využita ve třetí verzi programu pro vykreslení Mandelbrotovy množiny. Před provedením smyček jsou všechny hodnoty, se kterými se počítá, uloženy na zásobník matematického koprocesoru a veškeré výpočty jsou posléze prováděny pouze nad zásobníkem. Vzhledem k tomu, že jsou operace nad zásobníkem zakódovány do dvou bytů, došlo k dalšímu zkrácení přeloženého programového kódu, který dosáhl velikosti přesně 128 bytů, může tedy sloužit jako primitivní intro 128B.
; Vykresleni Mandelbrotovy mnoziny s vyuzitim instrukci FPU
; treti verze
; Autor: Pavel Tisnovsky 19.09.99 00:04:19
model tiny ; pametovy model CS=DS=SS<64kB
p386 ; povoleny instrukce procesoru 386+
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
;*** zacatek data segmentu
dataseg ; zacatek data-segmentu
min dw -3 ; minimalni hodnota promenne xpos
ypos dd -2.0
posunx dd 0.015
posuny dd 0.02
c4 dw 4
p286
udataseg
xpos dd ?
minptr equ word ptr [bx-16]
yposptr equ dword ptr [bx-14]
posunxptr equ dword ptr [bx-10]
posunyptr equ dword ptr [bx-6]
c4ptr equ word ptr [bx-2]
xposptr equ dword ptr [bx]
;*** zacatek kodoveho segmentu
codeseg ; zacatek code-segmentu
org 100h ; zacatek kodu pro programy typu COM
p386
start:
mov al,13h ; graficky mod 13h
int 10h
push 0a000h
pop es ; video segment
xor di,di ; zacatek vykreslovani na obrazovce
mov bx, offset xpos ; inicializace pro relativni adresovani
for_y: mov si,SLOUPCU ; x
fld yposptr
fadd posunyptr ; ypos+=4.0/200.0
fstp yposptr
fild minptr ; xpos=-3
fstp xposptr
for_x:
mov cl,51 ; maximalni pocet iteraci
finit
fldz ; pocatecni hodnota Z zx bailout
fldz ; zy zx bailout
fld xposptr
fadd posunxptr ; xpos+=4.0/260.0
fst xposptr ; cx zy zx bailout
fld yposptr ; cy cx zy zx bailout
fldz ; pocatecni hodnoty ZX2 zy2 cy cx zy zx bailout
fldz ; a ZY2 zx2 zy2 cy cx zy zx bailout
smycka:
fxch st(1) ; pocitame se ZY2
fsubp st(1), st(0) ; ZX2-ZY2
fadd st(0), st(2) ; ZX2-ZY2+CX
fxch st(4) ; ZX1=ZX2-ZY2+CX
fadd st(0), st(0) ; 2*ZX1
fmul st(0), st(3) ; 2*ZX1*ZY1
fadd st(0), st(1) ; ZY1=2*ZX1*ZY1+CY
fst st(3) ; pro dalsi vypocty nechat v ST(0)
fmul st(0), st(0) ; ZY1*ZY1
fld st(4) ; ZX1
fmul st(0), st(0) ; ; ZX1*ZX1
fld st(1) ; pro dalsi vypocty nechat na zasobniku
fadd st(0), st(1) ; ZX2+ZY2
ficomp c4ptr ; ZX2+ZY2>bailout ?
fstsw ax ; FPU priznaky do AX
sahf ; predani FPU priznaku do priznakoveho registru
jnb short pokr ; pokud jsme prekrocili bailout, konec
loop short smycka
pokr:
xchg ax,cx ; pocet iteraci do AL -> barva pixelu
stosb ; vykreslit bod+posun na dalsi
dec si
for_x_: jnz short for_x ; dalsi radek
cmp di,64000 ; konec obrazku ?
for_y_: jne short for_y ; konec smycky for y
xor ax,ax ; cekat na klavesu
int 16h
mov ax,3 ; textovy rezim
int 10h
retn ; finito
end start
4. Fixed point aritmetika
Při návrhu algoritmů pro výpočet fraktálů se – zejména v minulosti – používal formát pevné řádové binární čárky (FX – fixed point). Tento formát je zajímavý především tím, že binární řádová čárka je vždy umístěna na pevném místě, které si stanovil programátor na základě analýzy řešeného problému. Vzhledem k tomu, že je tato skutečnost dopředu známá algoritmu, který provádí zpracování čísel, není zapotřebí spolu s číslem uchovávat i pozici binární tečky, což výrazně snižuje počet bitů, které je zapotřebí rezervovat pro čísla ze zadaného rozsahu. To může znamenat i to, že pro mnoho výpočtů je možné použít pouze šestnáctibitové registry, zatímco nejmenší počet bitů pro FP hodnoty je roven hodnotě třicet dva.
V případě, že není k dispozici specializovaný a současně velmi komplikovaný matematický koprocesor (FPU), je mnohdy mnohem jednodušší a rychlejší implementovat matematické operace v FX formátu. To je případ mnoha jednočipových mikroprocesorů (mikrořadičů), signálových procesorů, ale i specializovaných zařízení obsahujících programovatelné obvody CPLD či FPGA. Dnes sice mají komplikovanější (a dražší) FPGA implementovanou i jednotku FPU, ale mnohdy je výhodnější použít FPGA bez této jednotky a potřebné operace si do tohoto obvodu „vypálit“ po svém. Výpočty v FX formátu jsou v tomto případě mnohem rychlejší, než volání funkcí emulujících jednotlivé operace FPU.
FX formát má však i některé nevýhody. První nevýhoda spočívá v tom, že není příliš podporován, a to ani po programové stránce (podpora v programovacích jazycích), ani výrobci mikroprocesorů pro počítače PC. Absence podpory FX formátu ve vyšších programovacích jazycích nás při práci v assembleru nemusí trápit, potřebné operace si můžeme naimplementovat sami. Jedinou překážkou je omezený počet registrů, zejména u procesorů řady x86. Na této platformě je však možné FX formát využít v instrukční sadě MMX. Použití formátu FX bude ukázáno na demonstračním příkladu v následující kapitole.
5. Vykreslení Mandelbrotovy množiny s využitím fixed point aritmetiky
V dnešním čtvrtém a současně i posledním demonstračním příkladu je ukázáno použití šestnáctibitové fixed point aritmetiky při výpočtu a zobrazení Mandelbrotovy množiny. Příklad je vytvořen tak, aby byl spustitelný i na procesorech, které neobsahují matematický koprocesor, teoreticky by měl dokonce dostačovat procesor Intel 286, protože nejsou použity ani třicetidvoubitové registry. Na tomto příkladu je patrná jedna zajímavá vlastnost platformy x86 – malý počet celočíselných registrů a existence instrukcí, které implicitně používají konkrétní registr (čítače smyček – CX, adresování – SI, DI a BX, aritmetické operace – AX, DX apod.).
Díky pečlivému rozvržení použití všech registrů se celková velikost kódu snížila na pouhých 116 bytů, na druhou stranu můžeme ve výsledném obrázku vidět chyby při výpočtech. Vzhledem k tomu, že počet registrů byl nedostatečný, použil jsem pro uložení mezivýsledků video paměť, která je sice v porovnání s operační pamětí velmi pomalá, její adresování však vedlo ke kratším instrukcím (používají se buňky video paměti umístěné těsně nad vykreslovaným pixelem, ke kterému máme vypočtenou adresu).
; Demonstracni program vykreslujici Mandelbrotovu mnozinu s vyuzitim
; fixed point aritmetiky.
; Autor: Pavel Tisnovsky
model tiny ; pametovy model CS=DS=SS<64kB
p286 ; povoleny instrukce procesoru 286+
P equ 4096 ; poloha desetinne tecky v X-pointu
K equ 3*P/320 ; vzdalenost mezi dvema body v rovine (krok smycky)
K1 equ 3*P/240 ; totez ve smeru y-ove osy
MIN equ -2*P ; minimalni a maximalni hodnota konstant fraktalu
; v komplexni rovine
ITERACI equ 32 ; pocet iteraci
SLOUPCU equ 320 ; pocet sloupcu na obrazovce
; Obsazeni jednotlivych registru
; ch --- pocet iteraci
; cl --- desetinna tecka
; di --- poloha vykreslovaneho bodu
; si --- pocitadlo sloupcu
; bp --- realna cast komplexniho cisla
; bx --- imaginarni cast komplexniho cisla
; ss:[sp] --- pomocna promenna zx3
; es:[di] --- pomocna promenna zy3
codeseg ; zacatek code-segmentu
org 100h ; zacatek kodu pro programy typu COM
start:
mov al,13h ; VGA graficky rezim 13h
int 10h
push 0a000h
pop es ; zacatek obrazove pameti
xor di,di ; zacatek vykreslovani na obrazovce
mov cl,6 ; poloha desetinne tecky v x-pointu
mforx: mov [zx1],MIN ; od -2 (imaginarni osa)
mov si,SLOUPCU ; x
mfory: mov ch,ITERACI ; pocet iteraci
xor ax,ax ; \
mov bp,ax ; /`nastaveni real.casti zacatku
xchg ax,bx ; nastaveni imag.casti cacatku
mrep_: ; *** iteracni smycka ***
mov ax,bp ; \
sar ax,cl ; \
imul ax ; /`ZX3:=ZX2^2 (v X-pointu)
push ax ; /
mov ax,bx ; \
sar ax,cl ; \
imul ax ; /`ZY3:=ZY2^2 (v X-pointu)
mov es:[di],ax ; /
mov ax,bp ; \
sar ax,cl ; /`ZX2 div 256 (pro mul v X-pointu)
sar bx,5 ; /`ZY2 div 256 * 2 (pro mul v X-pointu)
imul bx ; ZY2:=2*ZX2*ZY2
add ax,[zy1] ; ZY2:=2*ZX2*ZY2+CY (u Mandelbrota poc.iter.)
xchg ax,bx
pop ax ; ax=zx3
push ax
sub ax,es:[di]
add ax,[zx1] ; \
mov bp, ax ; /`ZX2:=ZX2^2-ZY2^2+CX
pop ax ; ax=zx3
add ax,es:[di]
dec ch ; pocitadlo iteraci
jz short mpokrac ; konec iteraci ?
cmp ax,4*P ; kontrola na bailout (abs[Z]<4)
jc short mrep_ ; abs[Z]<4 =>dalsi iterace
mpokrac:
xchg al,ch ; al=pocet iteraci
stosb ; vykreslit bod+posun na dalsi
add [zx1],K ; ZY1:=ZY1+K
dec si
jnz short mfory ; Y!=0 ->dalsi radek
add [zy1],K1 ; ZX1:=ZX1+K
cmp di,64000 ; konec obrazku ?
jne short mforx
xor ah,ah ; cekat na klavesu
int 16h
mov ax,3 ; textovy rezim
int 10h
retn ; finito
zy1 dw -1*P-1000 ; poloha v komplexni rovine
zx1 dw ? ;
end start 
6. Mandelbrot is possible
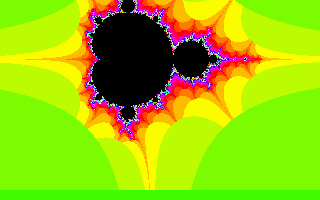
Velmi zajímavé intro, ve kterém se vykresluje Mandelbrotova množina, se jmenuje Mandelbrot is possible (http://downtown.dee.cz). Autorem intra je Dement (známá to postava naší demoscény). V intru je ukázáno zoomování Mandelbrotovy množiny, přičemž je synchronně generována hudba pomocí OPL (Adlib). Vzhledem k tomu, že málokterá zvuková karta ještě OPL nativně podporuje, je vhodné pro spuštění použít například DOSBox. Také si všimněte nekorektního testování ukončení iterační smyčky – v obrázcích se vyskytují „obloučky“, které v klasické Mandelbrotově množině nenajdeme. To je však daň za optimalizaci výpočtů na velikost výsledného kódu.
7. Odkazy na další informační zdroje
- John Bridges:
VGAKIT Version 5.2b - Matthew Hildebrand:
SVGA library - Jidan Al-Eryani:
Floating Point Unit - Randy Yates:
Fixed-Point Arithmetic: An Introduction - Hook Brian:
An Introduction to Fixed Point Math,
Game Design and Review, 2003 - Agner Fog:
How to optimize for the Pentium processor - Randall Hyde:
The Great Debate: Will Compilers Ever Produce Code as Good as an Expert Assembly Language Programmer?" - Randall Hyde:
The Art of ASSEMBLY LANGUAGE PROGRAMMING - Paul Hsieh:
Programming Optimization - Tomáš Papoušek:
Učebnice assembleru - Peter Norton:
Peter Norton's Assembly Language Book for the IBM PC - Software optimization resources:
http://www.agner.org/optimize/ - The PC Game Programmer's Encyclopedia:
http://www.geocities.com/SiliconValley/2151/pcgpe.html - Nasm (Netwide assembler):
http://sourceforge.net/projects/nasm - Intro anapurna:
http://downtown.dee.cz - Intro mandelbrot is possible:
http://downtown.dee.cz - Intro poledne dot com:
http://downtown.dee.cz - QuickMAN – Fast Mandelbrot Generator:
http://sourceforge.net/projects/quickman - A realtime Mandelbrot zoomer in SSE assembly:
http://www.softlab.ntua.gr/~ttsiod/mandelSSE.html - Fractal eXtreme: The Mandelbrot Set:
http://www.cygnus-software.com/gallery/mandelbrot.htm - Assembly Language Programming…:
http://www.magma.ca/~wjr/ - Jeremy Gordon: The Go tools for Windows + Assembler:
http://www.jorgon.freeserve.co.uk/ - sandpile.org: The world's leading source for pure technical IA-32 processor information:
www.sandpile.org - Wikipedia: Fixed-point arithmetic,
http://en.wikipedia.org/wiki/Fixed-point_arithmetic - Wikipedia: Floating point,
http://en.wikipedia.org/wiki/Floating_point - Wikipedia: IEEE floating-point standard,
http://en.wikipedia.org/wiki/IEEE_Floating_Point_Standard
8. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování seriálu si ukážeme způsob naprogramování animovaných Juliových množin, samozřejmě taktéž s využitím assembleru.









































