Hrátky se systémem LÖVE - kolize a odrazy těles II

Obsah

1. Interakce většího množství objektů ve scéně
2. První demonstrační příklad – simulace pádu dominových kostek
3. Detekce kolizí a obalová tělesa
4. Druhý demonstrační příklad – zobrazení obalových těles pro různé tvary
5. Nastavení fyzikálních vlastností těles
6. Třetí demonstrační příklad – změna hmotnosti a pružnosti těles
7. Tvorba a ukládání animací v systému LÖVE
8. Obsah dalšího pokračování seriálu

1. Interakce většího množství objektů ve scéně

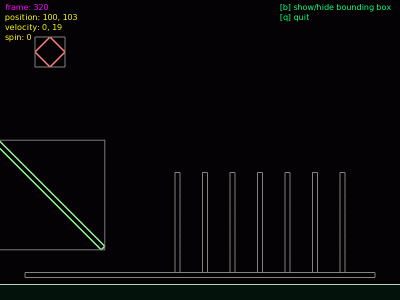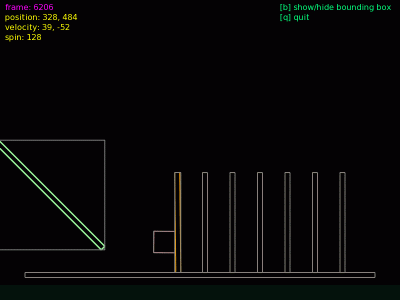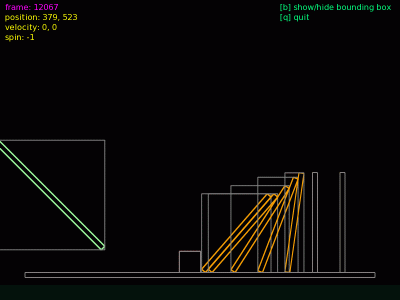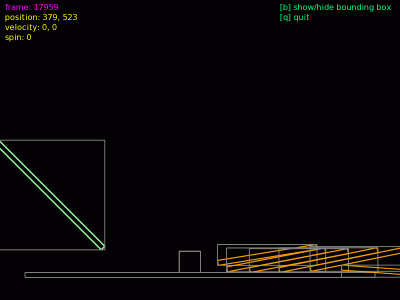
V předchozí části tohoto seriálu jsme si řekli, že s využitím knihovny love.physics je možné simulovat vzájemné interakce (kolize a odrazy) dvojrozměrných těles, vytvářet složitější objekty složené ze vzájemně provázaných základních tvarů (shape) a těles (body) i ovlivňovat trajektorii pohybujících se těles pomocí externích sil, které mohou na tato tělesa různým způsobem působit. Taktéž je možné libovolnou část tělesa navázat ke kurzoru myši, takže se současně s pohybem myši pohybuje i tato část tělesa, která může ovlivnit i části další, s nimiž je spojena pomocí programově vytvořené vazby apod. Pomocí této knihovny je například možné poměrně jednoduše vytvořit hru typu pinball, ve které se bude pohybovat a odrážet kulička na základě fyzikálních zákonů; zkonstruovat lze i systémy typu hmota–pružina (mass and spring) apod. Ve většině reálných simulací se však setkáme s tím, že spolu interaguje větší množství pohybujících se objektů, což je i případ dominových kostek použitých v prvním demonstračním příkladu.

2. První demonstrační příklad – simulace pádu dominových kostek

V dnešním prvním demonstračním příkladu je ukázána simulace míčku narážejícího do kostek domina. Vzhledem k tomu, že se jedná pouze o simulaci prováděnou v dvourozměrném prostoru, je možné kostky domina reprezentovat úzkými obdélníky postavenými na podlaze vytvořené taktéž pomocí obdélníku. Hmotnost i moment setrvačnosti kostek domina je vypočítána automaticky z tvaru tělesa pomocí metody setMassFromSha­pes(). Tatáž metoda je použita i u míčku, jehož tvar odpovídá kruhu. Míček nejprve volným pádem dopadne na šiknou plošku, po níž sklouzne (a částečně se i odvalí, což způsobí jeho rotaci) na podlahu. Posléze následuje náraz do první kostky domina a pád dalších kostek. Zajímavý je způsob vykreslení jednotlivých objektů ve scéně – s výhodou se zde používá metoda love.graphics­.polygon(), která akceptuje dva parametry – styl vykreslovaného polygonu a seznam jeho vrcholů. Není tedy nutné složitě zjišťovat souřadnice jednotlivých vrcholů polygonů (obdélníků) představujících jednotlivá tělesa ani používat jejich rozklad na úsečky – veškeré vykreslení je provedeno jedinou metodou. Kód tohoto demonstračního příkladu má tvar:

-------------------------------------------------
-- Seriál "Programovací jazyk Lua"
--
-- První demonstrační příklad: použití nakloněných
-- "podlah", úzké kvádry v roli kostek domina.
-------------------------------------------------

-- rozměry okna
window = {
    width = 800,
    height = 600
}

-- objekt představující svět, ve kterém se provádí simulace
world = nil

-- počet kostek domina
dominos_count = 5

-- počitadlo snímků
frame = 0

function load()
    -- inicializace grafického režimu
    love.graphics.setMode(window.width, window.height, false, false, 0)

    -- načtení fontu
    local font = love.graphics.newFont(love.default_font, 16)
    love.graphics.setFont(font)

    -- vytvoření "světa" o rozměrech 2000x2000 délkových jednotek
    world = love.physics.newWorld(2000, 2000)
    world:setGravity(0, 50)

    -- podlaha na souřadnicích [0, 0] s nulovou hmotností
    ground_body = love.physics.newBody(world, 0, 0, 0)

    -- obdélník představující podlahu
    ground_shape = love.physics.newRectangleShape(ground_body, 400, 500, 700, 10, 00)

    -- nakloněný plát pro "rozjetí" míčku
    plate_body = love.physics.newBody(world, 0, -100, 0)
    plate_shape = love.physics.newRectangleShape(plate_body, 100, 350, 300, 10, 60)

    -- rastrový obrázek představující těleso - míček
    ball = love.graphics.newImage("green_ball.png")

    -- vytvoření tělesa na zadaných souřadnicích
    ball_body = love.physics.newBody(world, 100, 100)

    -- přiřazení tvaru k tělesu
    ball_shape = love.physics.newCircleShape(ball_body, 31)
    ball_shape:setRestitution(0.6)

    -- výpočet hmotnosti na základě jeho poloměru
    ball_body:setMassFromShapes()

    -- dvě pole - tělesa představující kostky domina a jejich tvary
    domino_bodies = {}
    domino_shapes = {}
    for i = 1, dominos_count do
        domino_bodies[i] = love.physics.newBody(world, 0, 0, 0)
        domino_shapes[i] = love.physics.newRectangleShape(domino_bodies[i], 300+i*75, 400, 16, 200)
        domino_bodies[i]:setMassFromShapes()
    end
end

-- pravidelně volaná callback funkce
function update(dt)
    world:update(dt)
end

-- callback funkce volaná průběžně ve chvíli, kdy je zapotřebí
-- překreslit obsah okna
function draw()
    love.graphics.setColor(160, 160, 160)
    love.graphics.setLineWidth(2)

    -- vykreslení podlahy a nakloněné roviny
    love.graphics.polygon(love.draw_line, ground_shape:getPoints())
    love.graphics.polygon(love.draw_line, plate_shape:getPoints())

    -- vykreslení míčku se správným natočením
    love.graphics.draw(ball, ball_body:getX(), ball_body:getY(), ball_body:getAngle())

    -- vykreslení kostek domina
    love.graphics.setColor(250, 160, 0)
    for i = 1, dominos_count do
        love.graphics.polygon(love.draw_line, domino_shapes[i]:getPoints())
    end

    -- výpis počitadla snímků
    love.graphics.setColor(255, 0, 255)
    love.graphics.draw(string.format("frame: %d", frame), 10, 20)
    frame = frame + 1

    -- výpis informací o pohybujícím se míčku
    love.graphics.setColor(255, 255, 0)

    -- získání aktuálních informací o míčku
    local x, y = ball_body:getPosition()
    local vx, vy = ball_body:getVelocity()
    local spin = ball_body:getSpin()

    -- výpis aktuálních informací o míčku
    love.graphics.draw(string.format("position: %d, %d", x, y), 10, 40)
    love.graphics.draw(string.format("velocity: %d, %d", vx, vy), 10, 60)
    love.graphics.draw(string.format("spin: %d", spin), 10, 80)
end

-- callback funkce volaná ve chvíli, kdy uživatel stlačí nějakou klávesu
function keypressed(key)
    -- klávesou [ESC] nebo [Q] se celá simulace ukončí
    if key == love.key_escape or key == love.key_q then
        love.system.exit()
    end
end

-- finito

Animace 1: Náraz míčku do kostek domina – zdánlivě jednoduchý systém, který je však založený na poměrně složitých algoritmech detekce kolizí a simulace vzájemné interakce těles.

3. Detekce kolizí a obalová tělesa

V mnoha aplikacích, především ve hrách, je nutné zaregistrovat okamžik, ve kterém dojde ke kolizi dvou či více těles. Může se například jednat o střet hráče se stěnou (hry typu Doom), náraz střely do protihráče apod. Samotná detekce kolizí je – i když jsou veškeré výpočty prováděny pouze v dvourozměrné ploše – poměrně výpočetně náročná, proto je také množina tvarů, které je možné navázat na tělesa, omezená na kruhy a (uzavřené) konvexní polygony s maximálně osmi hranami. Každý tvar (shape) je navíc vždy uzavřen do takzvaného „obalového tělesa“ (bounding box), jehož strany jsou rovnoběžné se souřadnými osami a tudíž je detekce kolizí výrazně jednodušší než v případě obecného polygonu či kruhu. Obalový box je možné získat metodou getBoundingBox(), což si taktéž ukážeme v následujícím demonstračním příkladu. Při každé změně pozice i natočení tvaru je velikost obalového tělesa přepočítána tak, aby tvar vždy ležel uvnitř tohoto tělesa a současně byla jeho plocha minimální (jak bude z animací patrné, tato podmínka není vždy splněna). Detekce kolizí probíhá vždy nejprve nad obalovými tělesy a teprve v okamžiku, kdy dojde k jejich prolnutí nastává obecně složitější část výpočtu – detekce kolize samotných tvarů.

Animace 2: Šedou barvou naznačená obalová tělesa míčku, nakloněných rovin i jednotlivých kostek domina. Tato animace byla vytvořena pomocí druhého demonstračního příkladu popsaného v následující kapitole.

4. Druhý demonstrační příklad – zobrazení obalových těles pro různé tvary

V dnešním druhém demonstračním příkladu je ukázáno, jakým způsobem lze získat a zobrazit obalové těleso pro různé tvary. Po spuštění příkladu je možné pomocí klávesy [B] zapínat či vypínat zobrazení obalových těles všech tvarů, které se ve scéně nachází – jak samotného míčku, tak i nakloněné roviny, podlahy a všech dominových kostek (obalová tělesa jsou vykreslena šedou barvou). Navíc je možné změnou globální konstanty shape_type místo kulatého míčku zvolit použití pravidelného čtyřúhelníku (čtverce), šestiúhelníku či osmiúhelníku. Za zmínku stojí použití funkce unpack() pomocí níž se hodnoty uložené v (asociativním) poli transformují do seznamu hodnot. Tímto způsobem je možné připravit parametry pro metodu love.physics.new­PolygonShape(), která vyžaduje, aby po prvním parametru (objektu typu těleso) následovaly souřadnice jednotlivých vrcholů polygonu, tj. hodnoty x1, y1, x2, y2, x3, y3 atd., zatímco v programu jsou tyto hodnoty uložené v asociativním po­li.

Animace 3: U čtvercového tvaru je obalové těleso vypočteno zcela přesně.

Následuje výpis zdrojového kódu druhého demonstračního příkladu:

-------------------------------------------------
-- Seriál "Programovací jazyk Lua"
--
-- Druhý demonstrační příklad: vykreslení obalových
-- boxů a změna tvaru tělesa.
-------------------------------------------------

-- rozměry okna
window = {
    width = 800,
    height = 600
}

-- objekt představující svět, ve kterém se provádí simulace
world = nil

-- počet kostek domina
dominos_count = 7

-- počitadlo snímků
frame = 0

-- příznak zobrazení obalového boxu
draw_bounding_box = false

-- typ pohybujícího se tělesa
-- povolené hodnoty:
--     "ball"
--     "square"
--     "hexagon"
--     "octagon"
shape_type = "octagon"

function load()
    -- inicializace grafického režimu
    love.graphics.setMode(window.width, window.height, false, false, 0)

    -- načtení fontu
    local font = love.graphics.newFont(love.default_font, 16)
    love.graphics.setFont(font)

    -- vytvoření "světa" o rozměrech 2000x2000 délkových jednotek
    world = love.physics.newWorld(2000, 2000)
    world:setGravity(0, 50)

    -- podlaha na souřadnicích [0, 0] s nulovou hmotností
    ground_body = love.physics.newBody(world, 0, 0, 0)

    -- obdélník představující podlahu
    ground_shape = love.physics.newRectangleShape(ground_body, 400, 550, 700, 10, 00)

    -- nakloněný plát pro "rozjetí" míčku
    plate_body = love.physics.newBody(world, 0, -100, 0)
    plate_shape = love.physics.newRectangleShape(plate_body, 100, 490, 300, 10, 45)

    -- rastrový obrázek představující těleso - míček
    ball = love.graphics.newImage("green_ball.png")

    -- vytvoření tělesa na zadaných souřadnicích
    ball_body = love.physics.newBody(world, 100, 100)

    -- přiřazení tvaru k tělesu
    if shape_type=="ball" then
        ball_shape = love.physics.newCircleShape(ball_body, 31)
    end
    if shape_type=="square" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(4)))
    end
    if shape_type=="hexagon" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(6)))
    end
    if shape_type=="octagon" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(8)))
    end
    ball_shape:setRestitution(0.6)

    -- výpočet hmotnosti na základě jeho tvaru
    ball_body:setMassFromShapes()

    -- dvě pole - tělesa představující kostky domina a jejich tvary
    domino_bodies = {}
    domino_shapes = {}
    -- vytvoření kostek domina a výpočet jejich hmotnosti
    for i = 1, dominos_count do
        domino_bodies[i] = love.physics.newBody(world, 0, 0, 0)
        domino_shapes[i] = love.physics.newRectangleShape(domino_bodies[i], 300+i*55, 450, 10, 200)
        domino_bodies[i]:setMassFromShapes()
    end
end

-- vytvoření seznamu bodů tvořících vrcholy pravidelného n-úhelníku
function construct_polygon(n)
    points = {}
    for i=0, n do
        points[i*2] = 30*math.cos(math.rad(i*360/n))
        points[i*2+1] = 30*math.sin(math.rad(i*360/n))
    end
    return points
end

-- pravidelně volaná callback funkce
function update(dt)
    world:update(dt)
end

-- callback funkce volaná průběžně ve chvíli, kdy je zapotřebí
-- překreslit obsah okna
function draw()
    love.graphics.setColor(160, 250, 160)
    love.graphics.setLineWidth(2)

    -- vykreslení podlahy a nakloněné roviny
    love.graphics.polygon(love.draw_line, ground_shape:getPoints())
    love.graphics.polygon(love.draw_line, plate_shape:getPoints())
    if draw_bounding_box then
        love.graphics.setColor(128, 128, 128)
        love.graphics.polygon(love.draw_line, ground_shape:getBoundingBox())
        love.graphics.polygon(love.draw_line, plate_shape:getBoundingBox())
    end

    -- vykreslení míčku či polygonu se správným natočením
    if shape_type=="ball" then
        love.graphics.draw(ball, ball_body:getX(), ball_body:getY(), ball_body:getAngle())
    else
        love.graphics.setColor(250, 128, 128)
        love.graphics.polygon(love.draw_line, ball_shape:getPoints())
    end

    -- vykreslení obalového kvádru v případě, že uživatel stlačil klávesu [B]
    if draw_bounding_box then
        love.graphics.setColor(128, 128, 128)
        love.graphics.polygon(love.draw_line, ball_shape:getBoundingBox())
    end

    -- vykreslení kostek domina
    for i = 1, dominos_count do
        love.graphics.setColor(250, 160, 0)
        love.graphics.polygon(love.draw_line, domino_shapes[i]:getPoints())
        -- vykreslení obalového kvádru v případě, že uživatel stlačil klávesu [B]
        if draw_bounding_box then
            love.graphics.setColor(128, 128, 128)
            love.graphics.polygon(love.draw_line, domino_shapes[i]:getBoundingBox())
        end
    end

    -- výpis počitadla snímků
    love.graphics.setColor(255, 0, 255)
    love.graphics.draw(string.format("frame: %d", frame), 10, 20)
    frame = frame + 1

    -- výpis informací o pohybujícím se míčku či polygonu
    love.graphics.setColor(255, 255, 0)

    -- získání aktuálních informací o míčku
    local x, y = ball_body:getPosition()
    local vx, vy = ball_body:getVelocity()
    local spin = ball_body:getSpin()

    -- výpis aktuálních informací o míčku či polygonu
    love.graphics.draw(string.format("position: %d, %d", x, y), 10, 40)
    love.graphics.draw(string.format("velocity: %d, %d", vx, vy), 10, 60)
    love.graphics.draw(string.format("spin: %d", spin), 10, 80)

    -- výpis nápovědy
    love.graphics.setColor(0, 255, 128)
    love.graphics.draw("[b] show/hide bounding box", 560, 20)
    love.graphics.draw("[q] quit", 560, 40)
end

-- callback funkce volaná ve chvíli, kdy uživatel stlačí nějakou klávesu
function keypressed(key)
    -- klávesou [ESC] nebo [Q] se celá simulace ukončí
    if key == love.key_escape or key == love.key_q then
        love.system.exit()
    end
    -- povolení či zákaz zobrazení obalového boxu
    if key == love.key_b then
        draw_bounding_box = not draw_bounding_box
    end
end

-- finito

Animace 4: Povšimněte si, že u šestiúhelníku dochází ke změně velikosti obalového tělesa na základě jeho rotace. Obalové těleso však není ve všech případech minimální.

Animace 5: I u osmiúhelníku není obalové těleso vždy minimální. Osmiúhelníkový polygon je pro systém LÖVE mezním tvarem – více vrcholů (a tím pádem i hran) již polygon nesmí mít.

5. Nastavení fyzikálních vlastností těles

V předchozí části tohoto seriálu jsme si řekli, že pro každé těleso ve vytvářené scéně je možné nastavit několik důležitých fyzikálních vlastností. Pro korektní výpočet trajektorie těles je nejdůležitější vlastností jejich hmotnost a moment hybnosti, které je možné zcela automaticky změnit buď metodou setMassFromSha­pes() popř. manuálně (na jakékoli hodnoty) s využitím metody setMass(). Metoda setMassFromSha­pes() vyhodnotí tvar tělesa a na základě jeho plochy stanoví celkovou hmotnost i moment hybnosti (v 2D je plocha tělesa úměrná hmotnosti, v 3D by se musel počítat jeho objem). Při použití metody setMass() se kromě hmotnosti a momentu hybnosti zadávají i souřadnice, ve kterých je hmota tělesa soustředěna. To znamená, že například u středově symetrického míčku se jedná o jeho střed, ovšem v případě potřeby může být těžiště posunuto (dokonce i mimo vlastní těleso), což se projeví na vypočtené trajektorii a zejména chování objektů při srážkách.

Mezi další důležité vlastnosti patří pružnost (v tomto případě jsou však výpočty oproti realitě zjednodušeny, neboť se například neuvažuje deformace těles, pouze jejich odrazy od ostatních objektů) specifikovaná pomocí metody setRestitution() a taktéž konstanta, pomocí níž se vypočítá součinitel smykového tření ve chvíli, kdy dojde ke kolizi dvou těles a plochy těles se po sobě začnou posouvat (příkladem může být míček použitý v demonstračních příkladech, který po dopadu na nakloněnou plochu začne po jejím horním povrchu klouzat a tím pádem získává i rotaci). Tuto konstantu lze nastavit pomocí metody setFriction(), ovšem při vzájemném dotyku těles se skutečný součinitel tření vypočítá až na základě konstant zapsaných pro obě tělesa (ostatně i v reálném světě vždy záleží na materiálu obou těles). Všechny výše uvedené vlastnosti se uplatní především při kolizi těles, při volném pohybu v prostoru se počítá především s momentem hybnosti.

Animace 6: Větší pružnost tělesa se projeví až ve chvíli jeho dopadu na nakloněnou rovinu. Zde je koeficient větší než 1, což znamená, že těleso má po odrazu větší rychlost (a tím pádem i kinetickou energii) než při dopadu.

6. Třetí demonstrační příklad – změna hmotnosti a pružnosti těles

V dnešním třetím a současně i posledním demonstračním příkladu je ukázáno, jak se výsledek celé simulace změní v případě, že je nastavena odlišná pružnost tělesa (viz animace číslo 6) popř. jeho hmotnost (animace číslo 7) na hodnotu 200000 jednotek. Při změně hmotnosti tělesa je vhodné nejdříve automaticky vypočítat a následně nastavit jak hmotnost, tak i moment hybnosti pomocí metody setMassFromSha­pes() a posléze vypočítanou hybnost použít při volání metody setMass(). Povšimněte si, že těžiště je umístěno do bodu [0, 0], což v případě symetrického míčku znamená jeho geometrický střed. Pokud se těžiště posune, projeví se to především při prvním odrazu míčku od nakloněné roviny.

Animace 7: Mnohonásobně větší hmotnost tělesa.

-------------------------------------------------
-- Seriál "Programovací jazyk Lua"
--
-- Třetí demonstrační příklad: změna hmotnosti
-- a odrazivosti tělesa.
-------------------------------------------------

-- rozměry okna
window = {
    width = 800,
    height = 600
}

-- objekt představující svět, ve kterém se provádí simulace
world = nil

-- počet kostek domina
dominos_count = 7

-- počitadlo snímků
frame = 0

-- příznak zobrazení obalového boxu
draw_bounding_box = false

-- typ pohybujícího se tělesa
-- povolené hodnoty:
--     "ball"
--     "square"
--     "hexagon"
--     "octagon"
shape_type = "octagon"

-- hmotnost tělesa
body_mass = 200000

-- odrazivost tělesa
body_restitution = 0.6

function load()
    -- inicializace grafického režimu
    love.graphics.setMode(window.width, window.height, false, false, 0)

    -- načtení fontu
    local font = love.graphics.newFont(love.default_font, 16)
    love.graphics.setFont(font)

    -- vytvoření "světa" o rozměrech 2000x2000 délkových jednotek
    world = love.physics.newWorld(2000, 2000)
    world:setGravity(0, 50)

    -- podlaha na souřadnicích [0, 0] s nulovou hmotností
    ground_body = love.physics.newBody(world, 0, 0, 0)

    -- obdélník představující podlahu
    ground_shape = love.physics.newRectangleShape(ground_body, 400, 550, 700, 10, 00)

    -- nakloněný plát pro "rozjetí" míčku
    plate_body = love.physics.newBody(world, 0, -100, 0)
    plate_shape = love.physics.newRectangleShape(plate_body, 100, 490, 300, 10, 45)

    -- rastrový obrázek představující těleso - míček
    ball = love.graphics.newImage("green_ball.png")

    -- vytvoření tělesa na zadaných souřadnicích
    ball_body = love.physics.newBody(world, 100, 100)

    -- přiřazení tvaru k tělesu
    if shape_type=="ball" then
        ball_shape = love.physics.newCircleShape(ball_body, 31)
    end
    if shape_type=="square" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(4)))
    end
    if shape_type=="hexagon" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(6)))
    end
    if shape_type=="octagon" then
        ball_shape = love.physics.newPolygonShape(ball_body, unpack(construct_polygon(8)))
    end
    ball_shape:setRestitution(body_restitution)

    -- výpočet hmotnosti na základě jeho tvaru
    ball_body:setMassFromShapes()
    ball_body:setMass(0, 0, body_mass, ball_body:getInertia())

    -- dvě pole - tělesa představující kostky domina a jejich tvary
    domino_bodies = {}
    domino_shapes = {}
    -- vytvoření kostek domina a výpočet jejich hmotnosti
    for i = 1, dominos_count do
        domino_bodies[i] = love.physics.newBody(world, 0, 0, 0)
        domino_shapes[i] = love.physics.newRectangleShape(domino_bodies[i], 300+i*55, 450, 10, 200)
        domino_bodies[i]:setMassFromShapes()
    end
end

-- vytvoření seznamu bodů tvořících vrcholy pravidelného n-úhelníku
function construct_polygon(n)
    points = {}
    for i=0, n do
        points[i*2] = 30*math.cos(math.rad(i*360/n))
        points[i*2+1] = 30*math.sin(math.rad(i*360/n))
    end
    return points
end

-- pravidelně volaná callback funkce
function update(dt)
    world:update(dt/4)
end

-- callback funkce volaná průběžně ve chvíli, kdy je zapotřebí
-- překreslit obsah okna
function draw()
    love.graphics.setColor(160, 250, 160)
    love.graphics.setLineWidth(2)

    -- vykreslení podlahy a nakloněné roviny
    love.graphics.polygon(love.draw_line, ground_shape:getPoints())
    love.graphics.polygon(love.draw_line, plate_shape:getPoints())
    if draw_bounding_box then
        love.graphics.setColor(128, 128, 128)
        love.graphics.polygon(love.draw_line, ground_shape:getBoundingBox())
        love.graphics.polygon(love.draw_line, plate_shape:getBoundingBox())
    end

    -- vykreslení míčku či polygonu se správným natočením
    if shape_type=="ball" then
        love.graphics.draw(ball, ball_body:getX(), ball_body:getY(), ball_body:getAngle())
    else
        love.graphics.setColor(250, 128, 128)
        love.graphics.polygon(love.draw_line, ball_shape:getPoints())
    end

    -- vykreslení obalového kvádru v případě, že uživatel stlačil klávesu [B]
    if draw_bounding_box then
        love.graphics.setColor(128, 128, 128)
        love.graphics.polygon(love.draw_line, ball_shape:getBoundingBox())
    end

    -- vykreslení kostek domina
    for i = 1, dominos_count do
        love.graphics.setColor(250, 160, 0)
        love.graphics.polygon(love.draw_line, domino_shapes[i]:getPoints())
        -- vykreslení obalového kvádru v případě, že uživatel stlačil klávesu [B]
        if draw_bounding_box then
            love.graphics.setColor(128, 128, 128)
            love.graphics.polygon(love.draw_line, domino_shapes[i]:getBoundingBox())
        end
    end

    -- výpis počitadla snímků
    love.graphics.setColor(255, 0, 255)
    love.graphics.draw(string.format("frame: %d", frame), 10, 20)
    frame = frame + 1

    -- výpis informací o pohybujícím se míčku či polygonu
    love.graphics.setColor(255, 255, 0)

    -- získání aktuálních informací o míčku
    local x, y = ball_body:getPosition()
    local vx, vy = ball_body:getVelocity()
    local spin = ball_body:getSpin()

    -- výpis aktuálních informací o míčku či polygonu
    love.graphics.draw(string.format("position: %d, %d", x, y), 10, 40)
    love.graphics.draw(string.format("velocity: %d, %d", vx, vy), 10, 60)
    love.graphics.draw(string.format("spin: %d", spin), 10, 80)
    love.graphics.draw(string.format("mass: %d", ball_body:getMass()), 10, 100)
    love.graphics.draw(string.format("restitution: %f", body_restitution), 10, 120)

    -- výpis nápovědy
    love.graphics.setColor(0, 255, 128)
    love.graphics.draw("[b] show/hide bounding box", 560, 20)
    love.graphics.draw("[q] quit", 560, 40)
end

-- callback funkce volaná ve chvíli, kdy uživatel stlačí nějakou klávesu
function keypressed(key)
    -- klávesou [ESC] nebo [Q] se celá simulace ukončí
    if key == love.key_escape or key == love.key_q then
        love.system.exit()
    end
    -- povolení či zákaz zobrazení obalového boxu
    if key == love.key_b then
        draw_bounding_box = not draw_bounding_box
    end
end

-- finito

7. Tvorba a ukládání animací v systému LÖVE

Všechny animace použité v tomto článku byly vytvořeny ze screenshotů obrazovky systému LÖVE pomocí utility gifsicle, jejíž zdrojové kódy i binární tvar (mj. i pro MS Windows) lze nalézt na adrese http://www.lcdf­.org/gifsicle/. Každý screenshot byl nejprve zmenšen na polovinu a současně převeden do formátu GIF. Posléze se na zkonvertované obrázky zavolala výše zmíněná utilita gifsicle s následujícími parametry:

gifsicle -l -O --colors=256 *.gif > cesta_k_vyslednemu_obrazku.gif

První parametr zajistil optimalizaci (zmenšení) výsledného souboru, druhý parametr je použit proto, aby všechny obrázky využívaly jednu barvovou paletu, což opět vede ke zmenšení souboru s výslednou animací. Manuálová stránka k této užitečné utilitě, kterou využijeme i v další části seriálu o jazyku Lua, se nachází na adrese http://www.lcdf­.org/gifsicle/man­.html.

8. Obsah dalšího pokračování seriálu

V následující části seriálu o programovacím jazyce Lua a systému LÖVE si na několika demonstračních příkladech ukážeme, jakým způsobem je možné navzájem pospojovat více těles pomocí různých vazeb, například s využitím pružných (elastických) spojů. S použitím těchto vazeb lze například provádět simulace nad systémy typu hmota–pružina (mass and springs), pohybovat částmi objektů pomocí myši, napodobit inverzní kinematiku apod. Podobný systém ostatně tvoří i výpočetní jádro známého programu Sodaplay, jehož zjednodušenou verzi si příště taktéž ukážeme (původní Sodaplay je napsán v Javě – jedná se o klasický applet, my se samozřejmě v tomto seriálu budeme zabývat pouze jazykem Lua).

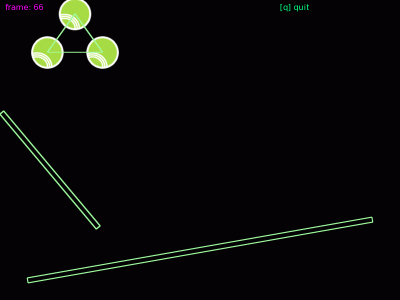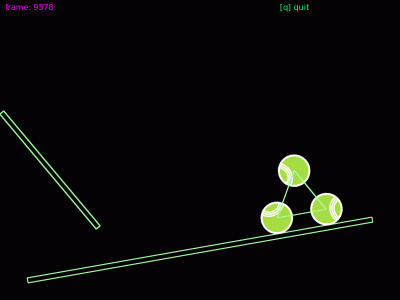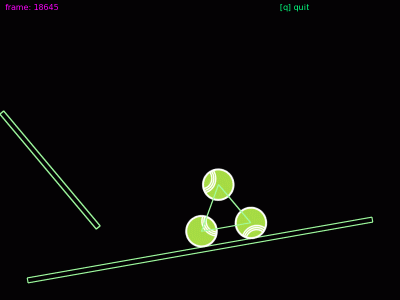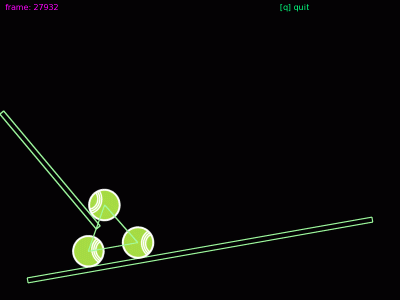
Animace 8: Tři tělesa, která jsou navzájem svázaná pomocí pružných vazeb. Princip tohoto demonstračního příkladu si vysvětlíme příště.