Obsah
1. Implicitní plochy (metaballs) v POV-Rayi
2. Stručná historie vzniku této modelovací techniky
3. Teorie implicitních ploch
4. Od teorie k praxi
5. Konstrukce těles pomocí implicitních ploch
6. Přednosti a zápory implicitních ploch
7. První demonstrační příklad – implicitní plocha vytvořená ze tří prvků kostry
8. Druhý demonstrační příklad – vliv hodnoty threshold na celkový tvar implicitní plochy
9. Obsah následující části seriálu
1. Implicitní plochy (metaballs) v POV-Rayi
Raytracer POV-Ray podporuje modelování složitých těles pomocí takzvaných implicitních ploch. Jedná se o techniku, která byla převzata z jiného raytraceru nazvaného Polyray, ve kterém jsou implicitní plochy použity v mnohem obecnějším pojetí než v POV-Rayi. Při popisu tělesa s využitím implicitních ploch se těleso nepopisuje hranicí (jak je tomu například u polygonálních či parametrických reprezentací) ani vyčíslením obsazeného objemu v prostoru, ale množinou implicitních funkcí spolu se specifikací jejich vzájemné kombinace. Implicitní funkce je určena rovnicí, která každému bodu v prostoru přiřazuje určitou hodnotu. Tuto hodnotu můžeme považovat například za hustotu tělesa či intenzitu síly v daném místě prostoru. V rovnici popisující implicitní plochu vystupují implicitní funkce, jejichž hodnota je závislá na poloze bodu (v Euklidovském trojrozměrném prostoru E3 jde o souřadnice x, y a z). Vlastní vykreslení spočívá ve volbě hranice (threshold), pomocí které je určena izoplocha (isosurface), která je s využitím analytických či numerických metod vykreslena.
Implicitní plochy lze považovat také za určitou alternativu či rozšíření ke konstruktivní geometrii těles (CSG), kterou jsme si popsali v předchozích částech tohoto seriálu. Z tohoto důvodu se také modelování pomocí implicitních ploch někdy označuje jako Implicit Solid Modelling – ISM. Výhodou ISM oproti CSG je poměrně jednoduchý výpočet celkového tělesa, které vzniká sloučením základních primitiv. Zatímco v CSG reprezentaci se musí (často složitě traverzací n-árního stromu) počítat průsečíky jednotlivých základních těles, v ISM reprezentaci se pozice průsečíků nemusí vyčíslit, protože se celkový tvar tělesa vyjadřuje pomocí jednoduché směšovací funkce. Nelze tak sice dosáhnout numericky naprosto přesných výsledků, ale v mnoha praktických aplikacích je kvalita a přesnost vizuálního výsledku více než dostačující.
Implicitní plocha vytvořená pomocí tří prvků kostry (bude vysvětleno dále)
2. Stručná historie vzniku této modelovací techniky
Implicitní plochy původně vyvinul pro účely simulace rozložení elektronové hustoty mezi atomy vodíku známý odborník na počítačovou grafiku J. F. Blinn v roce 1982. Blinn používal pro popis elektronové hustoty exponenciální funkci se záporným exponentem, což je klesající a nezáporná funkce v celém svém definičním oboru <0, ∞ ). Pro praktické aplikace se dnes používají spíše polynomiální funkce nízkého stupně, které mají pro modelování a vykreslování výhodnější vlastnosti než exponenciální funkce. Tato zajímavá technika byla dále rozšiřována a vznikaly tak objekty nazývané Blobby objects, Soft objects, Metaballs a podobně. Jules Bloomenthal (další autor, který se implicitními plochami aktivně zabýval) v roce 1988 zveřejnil poznatek, že všechny tyto objekty patří do stejné kategorie a mohou být proto označeny jediným názvem implicitní plochy.
Existuje několik důvodů, proč se implicitní plochy začaly ve větší míře používat až v poslední dekádě minulého století. Dnes nejpoužívanější parametrická reprezentace těles je vhodná pro přesné modelování tvarů umělých (technických) objektů či artefaktů, u kterých potřebujeme znát souřadnice bodů na povrchu. Je také vhodná pro provádění rychlých geometrických transformací a pro rychlé zobrazování s využitím technických prostředků – grafických akcelerátorů. Implicitní plochy jsou vhodné spíše pro vizuální modelování, kdy neklademe důraz na rozměrovou přesnost, ale spíše na celkový vzhled objektu. Reprezentace těles pomocí implicitních ploch umožňuje popsat kompaktním a jednoduchým způsobem i velmi složité objekty z reálného světa, jejichž popis parametrickými plochami či dokonce trojúhelníkovými sítěmi by byl velmi náročný, a to jak z hlediska doby a pracnosti vytváření modelu, tak i z hlediska paměťového prostoru potřebného pro popis tohoto tělesa.
Model vytvořený především z (jediné) implicitní plochy
3. Teorie implicitních ploch
Implicitní plocha se konstruuje pomocí takzvané kostry (skeleton). Kostra se skládá z jednodušších částí nazývaných prvky kostry, kde každý prvek odpovídá jedné implicitní funkci. Prvky kostry jsou ve své nejjednodušší podobě vyjádřeny svým středem a intenzitou, kterou působí na své okolí. Tato intenzita je největší ve středu prvku kostry a se vzrůstající vzdáleností od tohoto středu se snižuje. V původní definici funkce pro vyjádření intenzity byla intenzita v každém bodě prostoru kladná (a tedy nenulová), protože pro popis intenzity se používala exponenciální funkce. Pro urychlení výpočtů se zavádí jistá zjednodušení, která zaručí, že od určité vzdálenosti od středu prvku kostry bude intenzita nulová. Definici implicitní plochy lze rozšířit tak, že k prvku kostry povolíme přiřazovat zápornou intenzitu, což nám dovolí jednoduše modelovat i děravé objekty nebo objekty vzniklé odebíráním hmoty od základního tvaru.
Pro algoritmy pracující s implicitními plochami je důležité vyjádřit hranici tělesa. Proto je definována globální proměnná T (označení T je odvozeno od slova threshold – hranice hodnot, práh), která určuje mez, kde se nachází hranice (obálka) implicitní plochy. Je-li intenzita v určitém bodě v prostoru větší než zadaná mez, leží bod uvnitř tělesa, je-li naopak intenzita menší než mez, leží bod vně tělesa. Body, jejichž intenzita je rovna proměnné T, leží přesně na povrchu implicitní plochy – tvoří izoplochu. Pro osamocené body, které tvoří prvky kostry, nabývá obálka implicitní plochy tvar kružnice v ploše a koule v prostoru, pro úsečky má obálka tvar válce s polokulovitými základnami atd.
Implicitní plochy jsou dle Blinna definovány implicitní rovnicí:
D(x,y,z)=∑i=0n bi e-airi2=T
přičemž platí následující vztahy:
ri2=(x-xi)2+(y-yi)2+(z-zi)2
ai=-ln(Tbi-1)/Ri2
bi=Te-Bi
Význam jednotlivých konstant a proměnných v předchozích rovnicích:
- [xi,yi,zi] jsou souřadnice středu i-tého prvku kostry
- ai určuje rychlost změny intenzity se změnou vzdálenosti od středu prvku kostry
- bi odpovídá intenzitě i-tého prvku kostry
- Ri je poloměr osamoceného prvku kostry
- B je takzvaná míra prolínání (blobinnes)
- T je takzvaný práh (threshold)
Každý prvek kostry je tedy podle těchto rovnic plně určen svým středem [xi,yi,zi], poloměrem Ri a intenzitou odpovídající členu bi. Jak již bylo napsáno výše, nemusí mít prvek kostry intenzitu pouze kladnou, protože je dovoleno používat i záporné hodnoty. Potom se tento prvek od výsledného tělesa odečítá. Vykreslíme-li pouze izoplochu jednoho bodového prvku kostry, zobrazí se jako koule, protože intenzita se od středu prvku kostry zmenšuje do všech stran rovnoměrně a v místě, kde překročí práh T se vykreslí stěna (hranice) implicitní plochy (z předchozích vztahů plyne, že čím větší je zadaná síla, tím větší koule se vykreslí).
Podobný jev nastane, vykreslíme-li skupinu prvků kostry, které jsou od sebe dostatečně vzdáleny. V tomto případě se zobrazí pouze osamocené koule. Jestliže jsou některé prvky kostry dostatečně blízko u sebe (jejich poloměry Ri se překrývají), dojde ke splynutí ploch a výsledný tvar tělesa je podobný kapce. Prvky s kladnou intenzitou se přilepují k sobě, zatímco prvky s intenzitou zápornou do výsledného tělesa vytlačují díry (bude ukázáno na animacích v další kapitole). Celkový tvar tělesa je současně závislý na hodnotách T a Bi, protože povrch tělesa je v tomto případě vlastně izoplocha s konstantní hodnotou D(x,y,z) rovnou prahové hodnotě T.
Složitější model, jehož ústřední část tvoří implicitní plochy
4. Od teorie k praxi
Definice implicitních ploch tak, jak je navrhl J. F. Blinn, je sice z fyzikálního hlediska korektní, ale pro praktické potřeby počítačové grafiky až příliš složitá. V Blinnově definici se totiž vyskytuje exponenciální funkce se záporným koeficientem, která je v celém svém definičním oboru (ve skutečnosti definiční obor omezujeme na rozsah <0,∞)) klesající, přičemž platí:
limx→∞e-x=0
Z této rovnice mimo jiné vyplývá, že funkce nabývá nulové hodnoty až v nekonečnu. Pro urychlení výpočtů je však vhodnější použít nějakou funkci, která prochází nulou (na grafu funkce protíná osu x). Potom lze tuto funkci použít například při testu průsečíku paprsku s koulí, protože body, ve kterých je intenzita nulová, tvoří u samostatného bodového prvku kostry povrch koule (hranice, uvnitř které leží izoplocha izolovaného bodu). Vše, co leží vně této koule, zcela jistě neleží uvnitř implicitní plochy. Prostor uvnitř koule je zapotřebí podrobit další analýze. Tímto způsobem jsme mimo jiné také získali základní obalové těleso pro implicitní plochu. Tento fakt může významně urychlit zobrazování implicitních ploch metodou zpětného sledování paprsku (raytracingem), který je v POV-Rayi použit.

Ukázka vzájemného prolínání dvou bodových prvků kostry při tvorbě izoplochy. V dolní části animace jsou zobrazeny dva bodové prvky kostry spolu s poloměrem dosahu jejich sil. Při vzájemném přibližování dochází ke sčítání sil a „slévání“ obou tvarů. V horní části je zobrazen průběh sil v řezu procházejícím přes oba bodové prvky kostry se silou=0,7, přičemž je na grafu zvýrazněna prahová hodnota threshold=0,5. Body, ve kterých graf překročí prahovou hodnotu, tvoří izoplochu – lze se o tom přesvědčit spuštěním kolmice z grafu do spodní části obrázku.
Při aproximaci exponenciální funkce a s požadavkem na průchod funkce nulou, lze s výhodou použít polynomů. Přesnější aproximaci lze provést polynomem šestého stupně. Jeho nevýhodou jsou poměrně složité výpočty, které se mohou projevit například při vykreslování implicitních ploch sníženou rychlostí vykreslování. Tvar tohoto polynomu je následující:
Di(ri)=-4/9(ri6/Ri6) + 17/9(ri4/Ri4) – 22/9(ri2/Ri2) + 1
kde:
- Ri je poloměr prvku kostry
- ri je vzdálenost vyšetřovaného bodu v prostoru od středu prvku kostry
- Di(ri) je výsledná intenzita v daném bodě
Tato funkce je pro ri>Ri nulová. Při výpočtu intenzity tedy nemusíme vyšetřovat všechny body v prostoru, ale pouze ty, které leží ve vzdálenosti menší než Ri. Mezi další výhodné vlastnosti této funkce patří to, že má pro ri=0 a ri=Ri nulové derivace a že je symetrická pro hodnotu r=(Ri/2).
Pro urychlení výpočtů se v praxi nejvíce používá aproximace polynomem stupně čtyři. Tento polynom je dostatečně jednoduchý pro provádění většiny potřebných výpočtů a také jeho tvar je uspokojivý – aproximace exponenciální funkce tímto polynomem je pro účely počítačové grafiky dostačující. Průběh funkce se značně podobá výše uvedené funkci definované polynomem šestého stupně, ale pro hodnotu r=(R/2) není symetrický.
Tvar polynomu vychází z rovnice:
Di(ri)=(1-(ri/Ri)2)2
Po rozepsání mocniny:
Di(ri)=12-2(ri/Ri)2+(ri/Ri)4
A po zjednodušení rovnice dostaneme výsledek:
Di(ri)=(ri4/Ri4)-2(ri2/Ri2)+1
kde platí opět:
- Ri je poloměr prvku kostry
- ri je vzdálenost vyšetřovaného bodu v prostoru od středu implicitní plochy
- Di(ri) je výsledná intenzita v daném bodě
Hodnoty výše uvedené funkce pro některé významné body:
| ri | Fi |
|---|---|
| 0 | 0–0+1=1 |
| R/2 | 1/8–2/4+1=5/8 |
| R | 1–2+1=0 |
Z těchto hodnot můžeme vidět, že tato polynomická funkce není v bodě ri=R/2 symetrická, což však pro běžnou vizualizaci není podstatné.

Ukázka vzájemného prolínání dvou bodových prvků kostry při zvýšení sil obou bodových prvků kostry na hodnotu 1,0
5. Konstrukce těles pomocí implicitních ploch
Základní tvary prvků kostry jsou definovány jako osamocené body tvořící středy pomyslných koulí. Je však možné použít i jiné tvary, například úsečku, plochu a kružnici. Jejich použití je podobné jako v případě bodových prvků kostry, pouze se liší tvarem vykreslené implicitní plochy:
- Úsečkový prvek kostry je zadán úsečkou (většinou dvěma koncovými body úsečky) a intenzitou. Při vykreslení samostatného prvku se okolo úsečky vytvoří válec se zaoblenými podstavami, které mají tvar polokoule. Při interakci více prvků opět dochází k „lepení“ jednotlivých prvků k sobě. Výška válce závisí na délce úsečky, jeho poloměr (a poloměr polokoulí, které válec z obou stran uzavírají) je závislý na zadané intenzitě. Kombinace bodových a úsečkových prvků kostry bude vysvětlena v navazující části tohoto seriálu.
- Plošný prvek kostry je zadán plochou (většinou jedním bodem ležícím v ploše a normálovým vektorem) a intenzitou. Při vykreslení samostatného prvku se zobrazí dvě roviny, jejichž vzdálenost od roviny je opět závislá na zadané intenzitě. Pomocí plošného prvku kostry a prvku bodového lze jednoduše vytvořit například hrbolatou plochu. Stačí k plošnému prvku přidávat bodové prvky se střídavě kladnou a zápornou intenzitou.
- Kružnicový prvek kostry je zadán kružnicí (například souřadnicí středu kružnice, poloměrem kružnice a normálovým vektorem) a intenzitou. Při vykreslení samostatného prvku vznikne toroid (anuloid). Tento prvek lze opět kombinovat s jinými typy prvků pro získání potřebného výsledného tvaru.
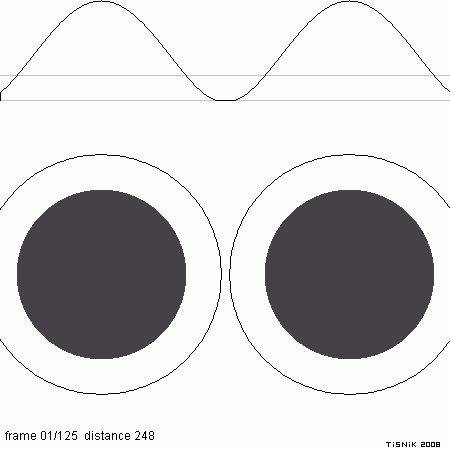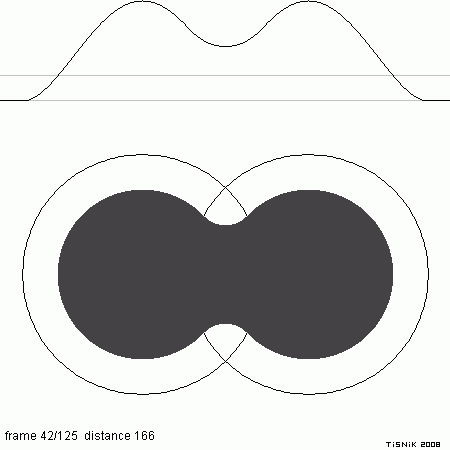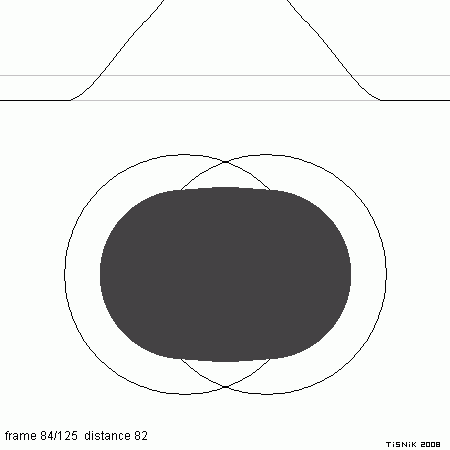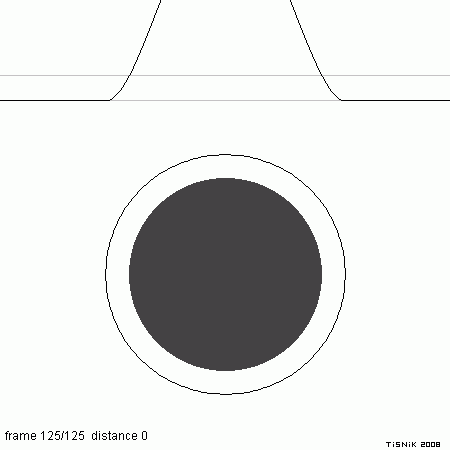
Ukázka vzájemného prolínání dvou bodových prvků kostry při zvýšení sil obou bodových prvků kostry na hodnotu 2,0
6. Přednosti a zápory implicitních ploch
Mezi velké výhody popisu těles implicitními plochami patří malá paměťová náročnost při práci s daty i při ukládání dat. I velmi složité a zaoblené objekty lze reprezentovat s využitím malého množství paměti (jak externí paměti při ukládání dat, tak interní paměti při vytváření, editaci a zobrazování těles), neboť je zapotřebí ukládat pouze parametry implicitních funkcí, což je několik reálných čísel. Také modelování těles je poměrně jednoduché a intuitivní. Modelování probíhá tak, že se k dosud vytvořenému tělesu přilepují či naopak odebírají kousky hmoty. To je pro mnoho konstruktérů velmi intuitivní postup, na rozdíl od většiny současných CAD systémů, kde se tělesa vytvářejí šablonováním nebo volnou deformací těles (free form deformation).
Mezi nevýhody patří především fakt, že přímo z parametrů implicitní plochy nelze jednoduše vypočítat souřadnice bodů na této ploše. Vizualizační algoritmy pro zobrazování implicitních ploch tedy musejí nejdříve najít povrch těchto ploch a teprve poté provést vykreslení. To je časově náročné, proto při dnešním stavu výpočetní techniky není možné vykreslovat složitější implicitní plochy v reálném čase (jednoduchá tělesa samozřejmě v reálném čase vykreslit lze, ale pro vykreslení komplikovanějších tvarů nebo celých scén je výpočetní výkon současných mikroprocesorů zatím nedostatečný). Praktická rada: při nastavování komplexních scén, ve kterých se používají implicitní plochy je vhodné pro první náhledy snižovat kvalitu výsledného obrázku pomocí přepínače +q1 a teprve po „doladění“ zvýšit kvalitu na maximum.
Implicitní plochy lze vykreslovat algoritmem vrhání paprsku (raycastingem) nebo jeho rekurzivní formou – metodou zpětného sledování paprsku (raytracingem). Další možností je převod do jiné reprezentace, nejčastěji na voxely nebo na síť trojúhelníků (v dnešní době se intenzivně studují efektivní algoritmy pro převod implicitně zadaných ploch na NURBS plochy či jiné parametrické plochy). Obě metody převodu jsou však časově i paměťově náročné, neboť po převodu ztrácíme výhody popisu tělesa pomocí parametrů implicitních funkcí. Pro rychlé náhledy na tělesa zkonstruovaná z implicitních ploch lze použít metodu vykreslování obrysových hran (vrstevnic). Nic podobného však v POV-Rayi nečekejte – bude se používat starý dobrý a velmi kvalitní raytracing.
Izoplochy jednotlivých prvků kostry se navzájem „přitahují“, i když se nemusí spojit
7. První demonstrační příklad – implicitní plocha vytvořená ze tří prvků kostry
V dnešním prvním demonstračním příkladu si ukážeme, jakým způsobem se implicitní plochy (metaballs, blobs) zapisují do scén určených pro vykreslení v POV-Rayi. Každá implicitní plocha je reprezentována jedním uzlem či blokem nazvaným blob. Velmi důležitým parametrem je hodnota threshold, která globálně ovlivňuje tvar celého objektu. Dále již následují specifikace jednotlivých prvků kostry. V prvních demonstračních příkladech jsou použity pouze bodové prvky kostry, které se zapisují následovně:
component síla, poloměr, <souřadnice středu prvku kostry> V prvním příkladu je implicitní plocha vytvořena ze tří prvků kostry, které se vlivem vhodně zvolené hodnoty threshold, jejich síly, poloměru a samozřejmě souřadnic středů vzájemně prolínají tak, jak je vidět na následujícím obrázku:
Obrázek vytvořený za použití prvního demonstračního příkladu
Zdrojový kód tohoto demonstračního příkladu má tvar:
// ------------------------------------------------------------
// Jednoduchá scéna s jednou implicitní plochou vymodelovanou
// pomocí tří prvků kostry.
//
// rendering lze spustit příkazem:
// povray +W800 +H600 +B100 +FN +D +Iblobs1.pov +Oblobs1.png
// (pro náhled postačí zadat povray blobs1.pov)
// ------------------------------------------------------------
#include "colors.inc"
global_settings {
assumed_gamma 2.2
}
camera {
location <0, 0, -2.5> // umístění kamery
right 4/3 * x // vektor směřující doprava
up y // a nahoru
look_at <0, 0, 0> // bod, na který se kamera zaměřila
}
light_source { // první světelný zdroj
<2, 10, -10> // pozice světelného zdroje
color red 0.7 green 0.7 blue 0.7 // barva světelného zdroje
}
light_source { // druhý světelný zdroj
<0, 0, -10000> // pozice světelného zdroje
color red 0.7 green 0.7 blue 0.7 // barva světelného zdroje
shadowless
}
plane { // rovina tvořící pozadí scény
<0, 0, 1>, 2 // posun a orientace roviny
hollow on
pigment { // procedurální textura
agate
agate_turb 0.3
}
finish { // optické vlastnosti materiálu povrchu
ambient 0.1
diffuse 0.4
}
}
blob {
threshold 0.6 // hraniční hodnota
component 1.0, 1.0, < 0.750, 0, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, <-0.375, 0.64952, 0> // druhý prvek kostry
component 1.0, 1.0, <-0.375, -0.64952, 0> // třetí prvek kostry
texture {
pigment {
color red 0 green 0 blue 1 // barva materiálu
}
finish { // optické vlastnosti materiálu povrchu
ambient 0.2
diffuse 0.4
specular 0.6
phong 0.6
phong_size 3
reflection 0
}
}
}
// ------------------------------------------------------------
// finito
// ------------------------------------------------------------
8. Druhý demonstrační příklad – vliv hodnoty threshold na celkový tvar implicitní plochy
Ve druhém příkladu je vytvořeno celkem osm implicitních ploch, kde každá z nich je vymodelována pomocí dvou bodových prvků kostry. Všechny parametry těchto ploch, tj. souřadnice, síly i poloměry prvků koster, jsou naprosto stejné, jednotlivé implicitní plochy se odlišují „pouze“ v hraniční hodnotě threshold. Tato hodnota zcela jasně ovlivňuje tvar výsledné plochy, což demonstruje i následující obrázek. Čím nižší je hraniční hodnota, tím více se prvky slévají; vyšší hodnota naopak vede až k jejich separaci na jednotlivé koule.
Obrázek vytvořený za použití druhého demonstračního příkladu
Zdrojový kód druhého demonstračního příkladu má tvar:
// ------------------------------------------------------------
// Jednoduchá scéna s několika implicitními plochami (blobs),
// které se liší pouze hodnotou threshold.
//
// rendering lze spustit příkazem:
// povray +W800 +H600 +B100 +FN +D +Iblobs2.pov +Oblobs2.png
// (pro náhled postačí zadat povray blobs2.pov)
// ------------------------------------------------------------
#include "colors.inc"
global_settings {
assumed_gamma 2.2
}
camera {
orthographic // vypnutí perspektivy
location <0, 0, -1> // umístění kamery
right 5*4/3 * x // vektor směřující doprava
up y*5 // a nahoru
look_at <0, 0, 0> // bod, na který se kamera zaměřila
}
light_source { // první světelný zdroj
<2, 10, -10> // pozice světelného zdroje
color red 0.7 green 0.7 blue 0.7 // barva světelného zdroje
}
light_source { // druhý světelný zdroj
<0, 0, -10000> // pozice světelného zdroje
color red 0.7 green 0.7 blue 0.7 // barva světelného zdroje
shadowless
}
plane { // rovina tvořící pozadí scény
<0, 0, 1>, 2 // posun a orientace roviny
hollow on
pigment { // procedurální textura
agate
agate_turb 0.9
}
finish { // optické vlastnosti materiálu povrchu
ambient 0.1
diffuse 0.4
}
}
#declare Tex =
texture {
pigment {
color red 0.6 green 0.8 blue 1
}
finish {
ambient 0.2 diffuse 0.4 phong 0.5 phong_size 5
}
}
blob {
threshold 0.4 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate <-2.0, -1.2, 0>
}
blob {
threshold 0.5 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate <-0.65, -1.2, 0>
}
blob {
threshold 0.6 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate < 0.65, -1.2, 0>
}
blob {
threshold 0.7 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate < 2.0, -1.2, 0>
}
blob {
threshold 0.75 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate <-2.0, 1.2, 0>
}
blob {
threshold 0.8 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate <-0.65, 1.2, 0>
}
blob {
threshold 0.82 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate < 0.65, 1.2, 0>
}
blob {
threshold 0.9 // hraniční hodnota
component 1.0, 1.0, < 0, -0.6, 0> // prvek kostry: síla, poloměr, souřadnice v prostoru
component 1.0, 1.0, < 0, 0.6, 0> // druhý prvek kostry
texture {Tex}
translate < 2.0, 1.2, 0>
}
// ------------------------------------------------------------
// finito
// ------------------------------------------------------------
9. Obsah následující části seriálu
I v další části seriálu o raytraceru POV-Ray se budeme zabývat implicitními plochami. Ukážeme si jejich další možnosti, především použití odlišných základních prvků kostry a také pokročilejší způsoby modelování s těmito poněkud netradičními objekty, například využití záporných „sil“ při tvorbě povrchů s vytlačenými částmi.
Implicitní plocha, ve které jsou použity bodové a úsečkové prvky kostry













































