Obsah
1. Další možnosti nabízené modulem Geometry pro geometrické konstrukce
5. Měření vzdáleností, úhlů a ploch
6. Úhly v trojúhelnících v Thaletově kružnici
9. Kuželosečka procházející pěti vybranými body
10. Jednoduché animace založené na posunu bodů
11. Animace měření středového a obvodového úhlu
12. Modul CAS Calculator a jeho možnosti
14. Kořeny kvadratické rovnice
15. Zobrazení oblasti, pro kterou platí zadaná podmínka
17. Převod hodnot funkce do tabulky
18. Vytvoření knížky s úkoly a příklady
1. Další možnosti nabízené modulem Geometry pro geometrické konstrukce
V první části dnešního článku o nástroji GeoGebra (viz též úvodní díl o GeoGebře) se budeme zabývat popisem některých dalších možností, které nám nabízí modul Geometry. Připomeňme si, že tento modul slouží primárně pro vytváření různých geometrických konstrukcí, a to včetně klasických eukleidovských konstrukcí, z nichž některé jsou vyučovány i na základních a středních školách (což je ostatně jen dobře – geometrie je jednou z nejnázornějších oblastí matematiky). Všechny zde ukázané postupy lze aplikovat jak v již zmíněném modulu Geometry, tak i v GeoGebra Classic, který vlastně (velmi zjednodušeně řečeno) obsahuje funkce Geometry a Graphing Calculator.
Obrázek 1: Přihlašovací obrazovka nástroje GeoGebra.
Jen pro připomenutí si ukažme, jak lze s využitím eukleidovských konstrukcí a dvou základních nástrojů (pravítka bez délkových značek a kružítka) zkonstruovat kolmici na libovolnou úsečku v libovolně zvoleném bodě. Tuto konstrukci jsme si popsali minule, takže na dalším obrázku je zobrazen jen její výsledek – nová úsečka CD je kolmá na úsečku AB (body C a E leží na zhruba stejném místě, takže se překrývají).
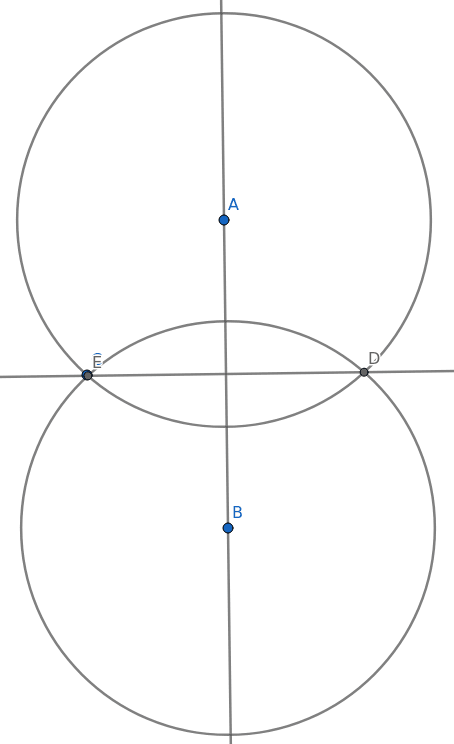
Obrázek 2: Vytvoření kolmice na přímku procházející body A a B.
Nyní si již můžeme ukázat další užitečný nástroj, který sice není klasickou eukleidovskou konstrukcí, ale v případě potřeby je možné operace provedené tímto nástrojem rozložit na řadu dílčích kroků. Tento nástroj umožňuje vytvoření nové přímky nebo úsečky procházející nějakým bodem, která je rovnoběžná s jinou úsečkou. Pro úspěšné provedení této konstrukce je nutné zadat onen bod, kterým bude nová úsečka (rovnoběžka) procházet a poté zadat úsečku nebo segment, se kterou má být nově konstruovaná úsečka rovnoběžná – jinými slovy, nezadává se přímá vzdálenost rovnoběžek. Celá konstrukce je patrná na dalším screenshotu:
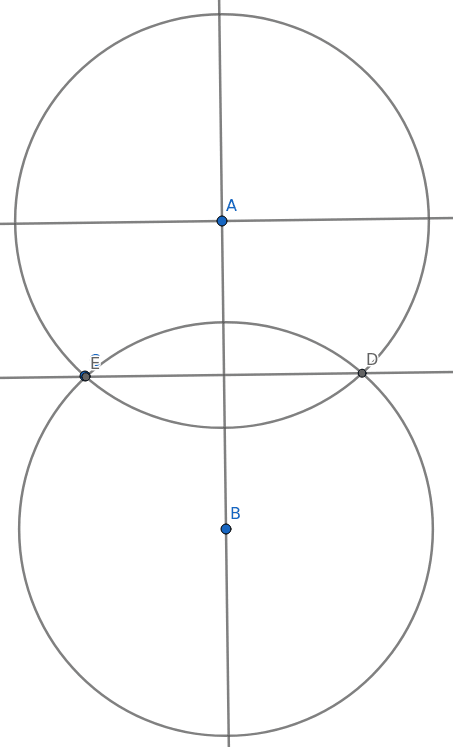
Obrázek 3: Vytvoření přímky procházející bodem A, která je rovnoběžná s přímkou procházející body D a E.
2. Přímka, polopřímka, úsečka
Již v předchozí kapitole jsme se zmínili o úsečkách a přímkách. Ve skutečnosti nástroj GeoGebra poměrně striktně rozlišuje mezi třemi typy lineárních geometrických entit. Jedná se o přímky (zde nazývané line), polopřímky (paprsek, ray) a úsečky (segment). Z hlediska geometrie je pochopitelně toto rozlišování zcela správné a zmiňuji se o něm jen proto, že označení line má v jiných programech odlišný význam – tam se může jednat právě o úsečky a nikoli o přímky.

Obrázek 4: Úsečka (segment) s vrcholy A a B.
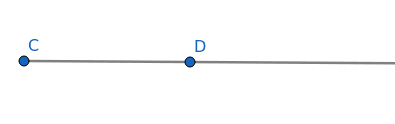
Obrázek 5: Polopřímka (paprsek, ray) z bodu C procházející bodem D.

Obrázek 6: Přímka (line) procházející body E a F.
3. Konstrukce pravého úhlu
S pravým úhlem se setkáme nejen v abstraktní geometrii, ale pochopitelně i v reálném světě, takže je důležité vědět, jakým způsobem lze pravý úhel sestrojit. Můžeme použít hned několik způsobů. Nejprve se zmiňme o nástroji, který dokáže vytvořit kolmici na zadanou úsečku, popř. na přímku nebo polopřímku. Tento nástroj vlastně nahrazuje klasickou eukleidovskou konstrukci, s níž jsme se seznámili minule, takže urychluje provádění některých dalších operací. Kolmice musí být zadaná (specifikovaná) dvěma údaji – bodem, kterým má procházet a úsečkou/přímkou/polopřímkou, na kterou musí být kolmá. Výsledek této operace je zobrazen na sedmém obrázku:
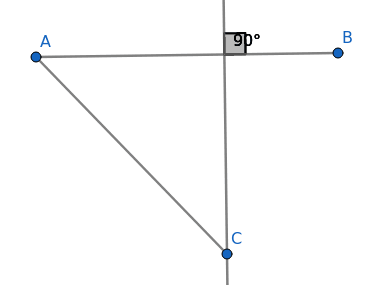
Obrázek 7: Vytvoření přímky procházející bodem C, která je kolmá na úsečku AB.
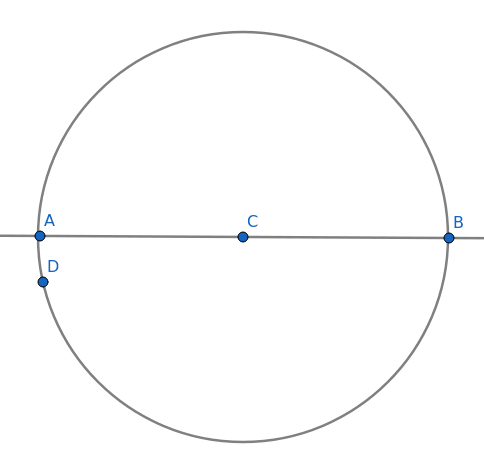
Obrázek 8: Kružnice se středem ležícím na úsečce.
Pravý úhel ale můžeme vytvořit i odlišným způsobem. Klasický způsob spočívá v konstrukci pravého úhlu s využitím Thaletovy věty; výsledek se proto někdy označuje jako Thaletova kružnice. Celá geometrická konstrukce spočívá v konstrukci trojúhelníka, jehož jedna strana půlí střed kružnice opsané tomuto trojúhelníku. Konstrukci můžeme začít vytvořením polopřímky z bodu A. Tato polopřímka bude (kromě dvou limitních případů) protínat kružnici:
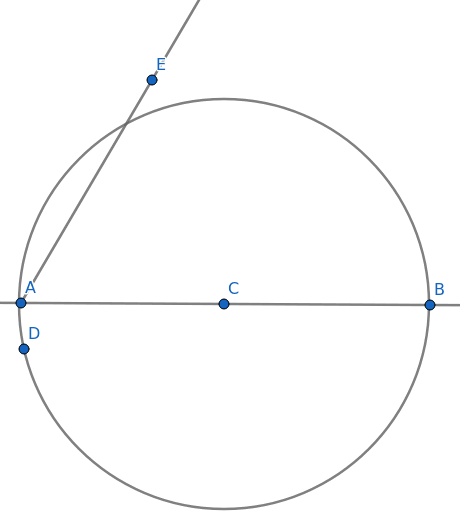
Obrázek 9: Polopřímka neboli paprsek vyslaný z bodu A.
Dále můžeme zkonstruovat další polopřímku, tentokrát z bodu B, ovšem takovým způsobem, aby protínala kružnici ve stejném bodě, jako polopřímka předchozí. Úhel svíraný těmito dvěma polopřímkami je podle Thaletovy věty pravý, a to pro libovolný bod ležící na kružnici:
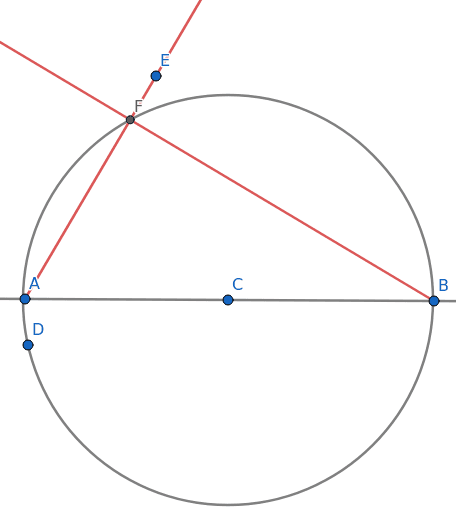
Obrázek 10: Průsečík polopřímky/paprsku s kružnicí a další paprsek, nyní vyslaný do průsečíku.
4. Polygony
Dalšími geometrickými objekty, s nimiž je možné v GeoGebře pracovat, jsou polygony. Ty jsou důležité mj. i proto, že u polygonů lze měřit jejich plochu, což je téma, kterému se budeme podrobněji věnovat v navazující kapitole. A měření plochy nám například umožňuje zjistit platnost Pythagorovy věty i dalších podobně koncipovaných problémů. Nejprve si ukažme konstrukci obecného polygonu. Ten může mít libovolný tvar a libovolný počet vrcholů (prakticky ovšem dávají smysl polygony se třemi, popř. s více vrcholy). U polygonů se specifikují souřadnice jejich vrcholů, přičemž ukončení kreslení polygonu se provede jednoduše – znovu se nakreslí jeho první bod:
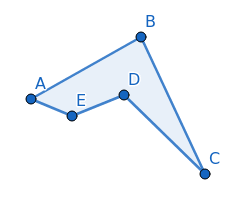
Obrázek 11: Obecný polygon.
Zkonstruovat je možné i pravidelné polygony, a to s libovolným počtem hran a tedy i libovolným počtem vrcholů. To je důležité a potenciálně užitečné, protože s využitím klasických euklidovských konstrukcí nelze všechny pravidelné polygony vytvořit – pouze jejich podmnožinu. Pravidelný polygon je specifikován dvojicí bodů udávajících jednu jeho hranu a poté celkovým počtem vrcholů.
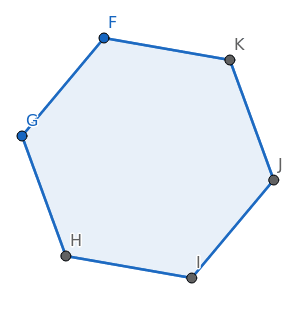
Obrázek 12: Pravidelný polygon se šesti hranami – šestiúhelník.
Při vyšším počtu hran se polygon začne (v daném měřítku a omezeném rozlišení obrazovky) podobat kružnici:
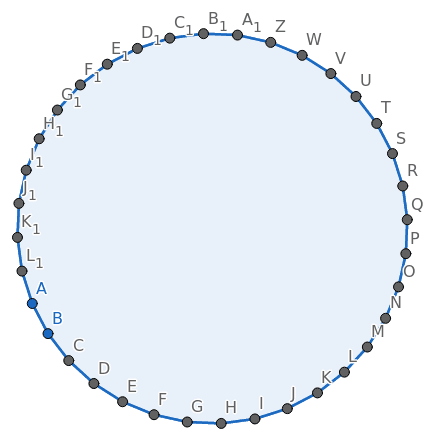
Obrázek 13: Pravidelný polygon s celkem třiceti šesti hranami.
5. Měření vzdáleností, úhlů a ploch
Další užitečná funkcionalita modulu Geometry, popř. modulu Classic spočívá v možnosti měření vzdáleností, úhlů a ploch. Vzdálenosti lze měřit jak mezi dvěma body, tak i na základě vlastností zvolené geometrické entity (typicky úsečky). Zjistit lze například i obvod kružnice, což je ukázáno na dalším screenshotu:
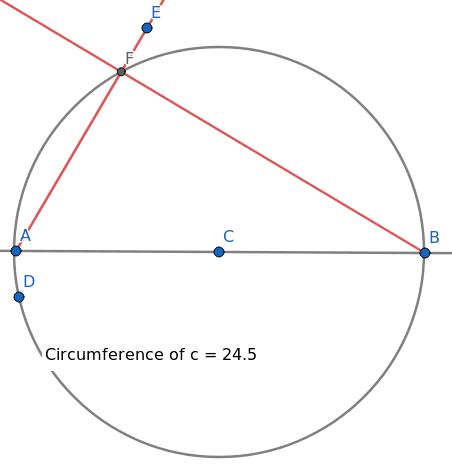
Obrázek 14: Výpočet obvodu kružnice.
Triviální je měření délky hran:
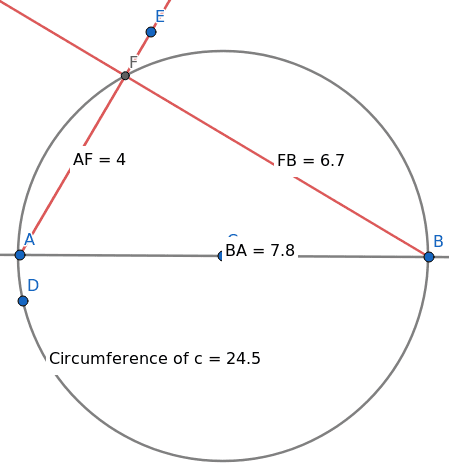
Obrázek 15: Změření délky hran úsečky (segmentu).
Zjistit lze i úhly svírané mezi dvěma geometrickými entitami a popř. i plochu polygonu (u úhlů je nutné správně zvolit obě entity, zejména v případě přímek, které v bodě protnutí tvoří čtyři úhly a nikoli úhel jediný):
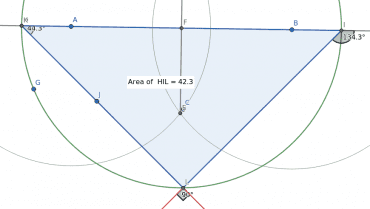
Obrázek 16: Změření úhlů a plochy polygonu.
6. Úhly v trojúhelnících v Thaletově kružnici
Nyní již máme k dispozici všechny potřebné nástroje, abychom mohli ověřit platnost Thaletovy věty, o níž jsme se již zmínili v předchozích kapitolách. Vytvoříme tedy geometrickou konstrukci Thaletovy kružnice a zadáme všechny úhly, které budeme chtít měřit – především pak úhel trojúhelníku sestaveného nad přímkou protínající kružnici a procházející jejím středem. Celou konstrukci již známe – důležité je vytvořit polopřímky IL a KL:
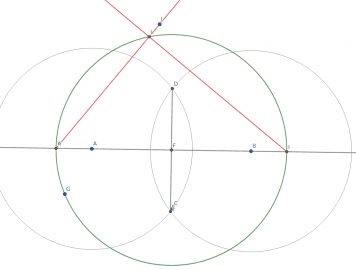
Obrázek 17: Konstrukce trojúhelníku v Thaletově kružnici.
Dále do konstrukce vložíme úhly, jejichž velikost je nutné měřit. V případě průsečíků polopřímek IL a KL je jedno jaký úhel se zvolí, protože protilehlé úhly budou totožné a jejich součet musí dát 360°:
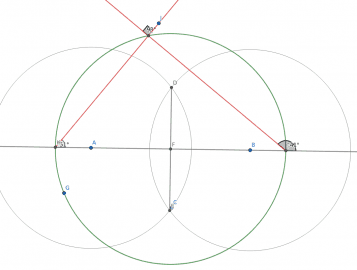
Obrázek 18: Úhel průsečíku paprsků KL a IL je vždy pravý.
Bodem J lze pohybovat a měnit tak pozici průsečíků a tím pádem i tvar trojúhelníku. Úhel však zůstane zachován:
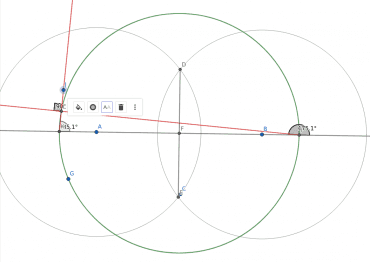
Obrázek 19: Úhel průsečíku paprsků KL a IL je vždy pravý.
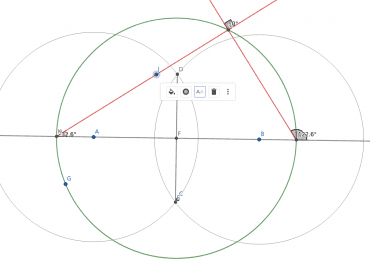
Obrázek 20: Úhel průsečíku paprsků KL a IL je vždy pravý.
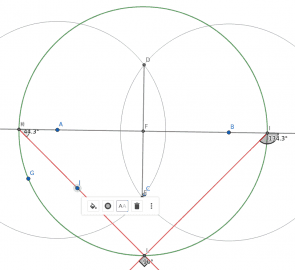
Obrázek 21: Úhel průsečíku paprsků KL a IL je vždy pravý.
Do konstrukce můžeme pro úplnost vložit i úsečku ze středu kružnice a změřit úhly v nově vzniklých trojúhelnících – to je však již téma další kapitoly.
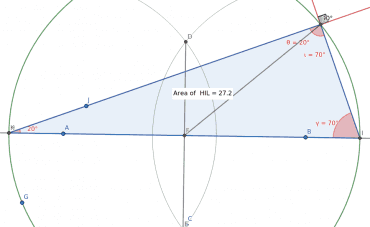
Obrázek 22: Další vztahy mezi úhly v Thaletově kružnici.
7. Středový a obvodový úhel
Další dosti typická školní látka se týká středových a obvodových úhlů trojúhelníků v kružnici, viz též různé úlohy na dané téma https://www.hackmath.net/cz/priklady-ulohy/stredovy-a-obvodovy-uhel. Díky možnosti měření úhlů si můžeme otestovat, jaký je vlastně vztah (a zda vůbec nějaký) mezi středovým a obvodovým úhlem. Podívejme se na následující sekvenci screenshotů s příslušnou geometrickou konstrukcí:

Obrázek 23: Začneme, jak je zvykem, jediným bodem v rovině.
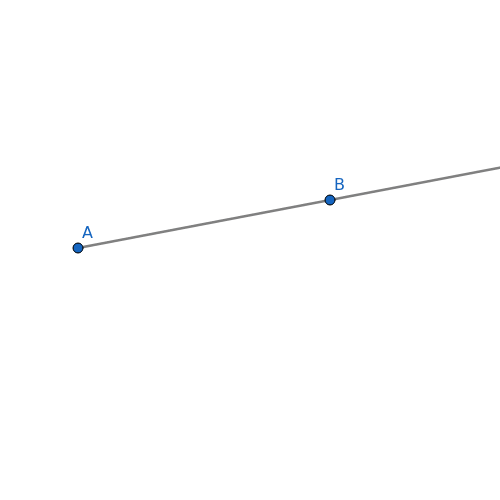
Obrázek 24: Sestrojíme polopřímku začínající v tomto bodě (směr může být libovolný).
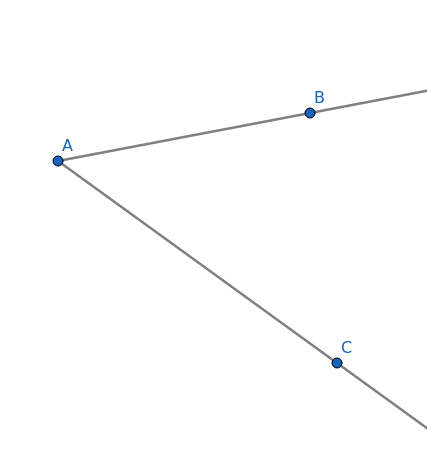
Obrázek 25: Sestrojíme druhou polopřímku, v odlišném směru.
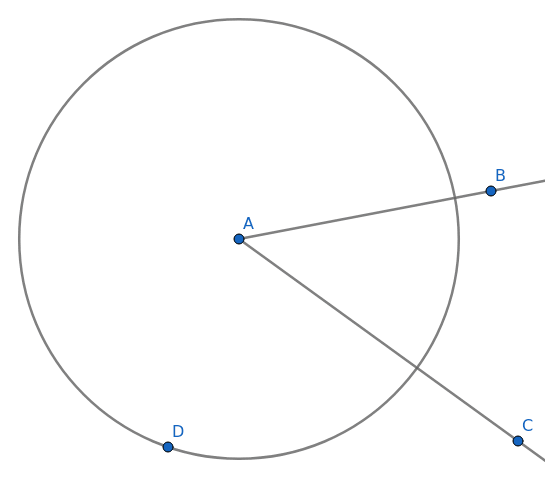
Obrázek 26: Z bodu A bude vycházet i kružnice, v níž budou sestrojeny trojúhelníky.
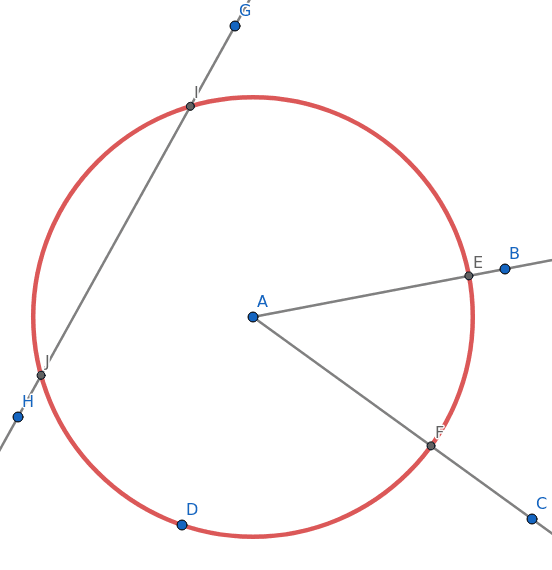
Obrázek 27: Sestrojíme sečnu (přímka či úsečka) a dva body, kde sečna protíná kružnici.
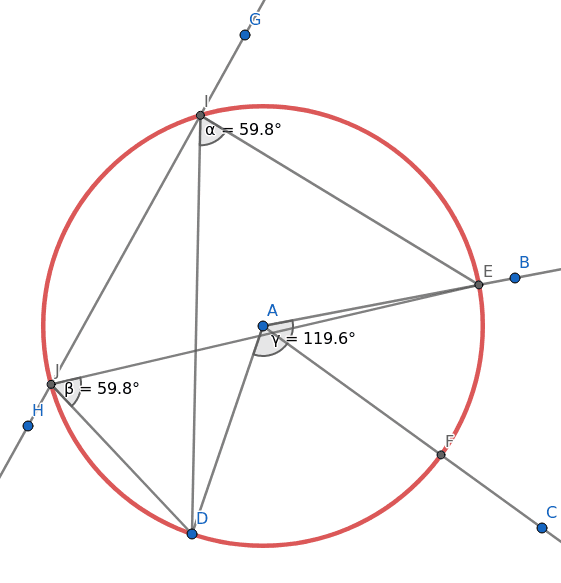
Obrázek 28: Nyní je již možné vytvořit trojúhelníky EID, EJD a ADE a nechat si změřit příslušné středové a obvodové úhly.
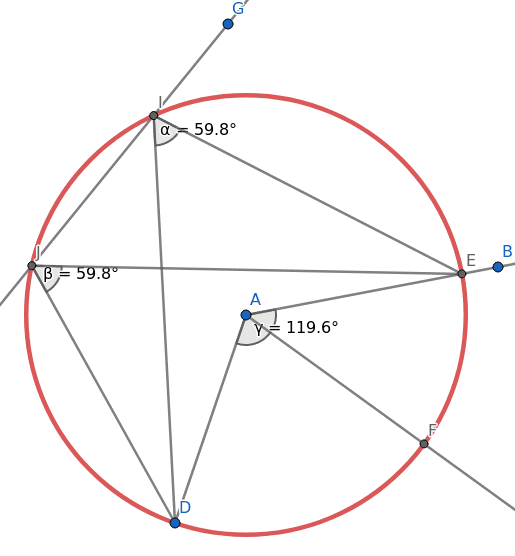
Obrázek 29: Posun sečny nemění úhly žádným způsobem nezmění.
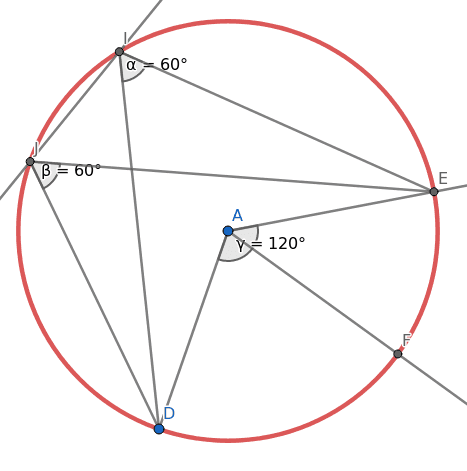
Obrázek 30: Středový úhel má dvojnásobnou velikost oproti úhlům obvodovým.
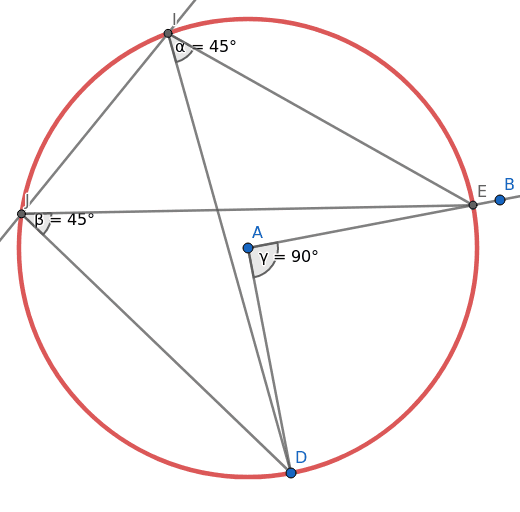
Obrázek 31: A tato podmínka platí i pro jiné hodnoty úhlů.
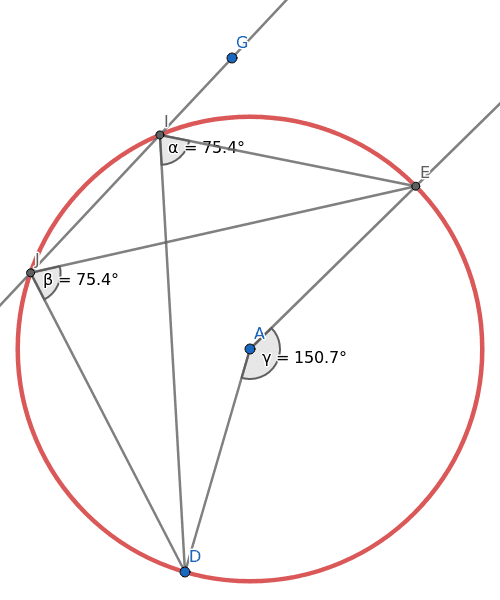
Obrázek 32: Další změna úhlů.
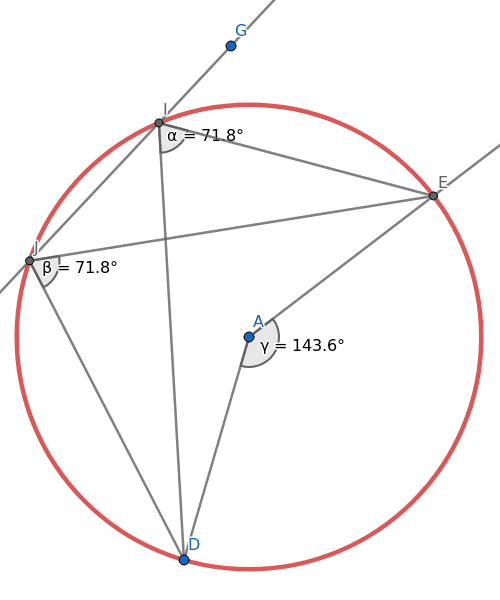
Obrázek 33: A další.
8. Základní kuželosečky
V modulu Geometry nalezneme i nástroje určené pro kreslení všech typů kuželoseček, ovšem způsoby specifikace umístění a tvaru jednotlivých kuželoseček se od sebe odlišují. Nejvíce možností máme u kružnice, což je ovšem pochopitelné, protože ta se v geometrických konstrukcích používá nejčastěji (a nejčastěji ji nalezneme i v reálném světě). Kružnici lze zadat středem a poloměrem, středem a bodem, kterým kružnice prochází, popř. třemi body, kterými kružnice prochází. Kromě kružnic lze zkonstruovat i kruhové oblouky.
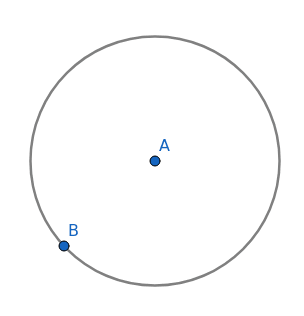
Obrázek 34: Kružnice je při geometrických konstrukcích nejpoužívanější kuželosečkou.
Dále je možné pracovat s elipsami, ovšem možnosti konstrukce elipsy jsou více omezené – musí se specifikovat souřadnice obou ohnisek elipsy a poté bod, kterým elipsa prochází. Způsob konstrukce je patrný z následujícího obrázku:
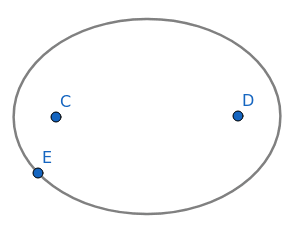
Obrázek 35: Elipsa specifikovaná dvěma ohnisky a bodem na ní ležícím.
Ještě zajímavější je způsob konstrukce paraboly. U ní je nutné specifikovat její ohnisko a taktéž takzvanou řídicí přímku (ta musí být již dopředu nakreslena):
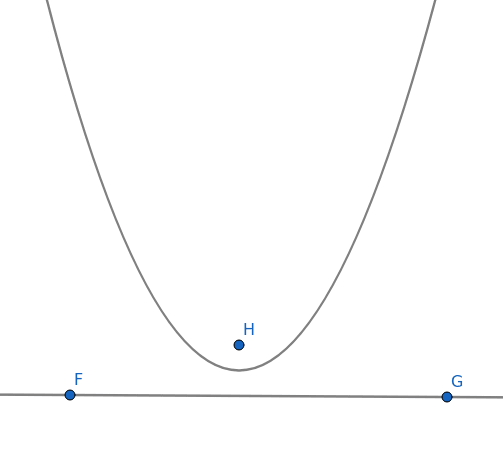
Obrázek 36: Parabola specifikovaná svým ohniskem a řídicí přímkou.
Poslední kuželosečkou je hyperbola. Podobně jako v případě elipsy je i hyperbola zadaná dvojicí ohnisek a bodem, kterým prochází jedna z polovin hyperboly – viz též následující screenshot:
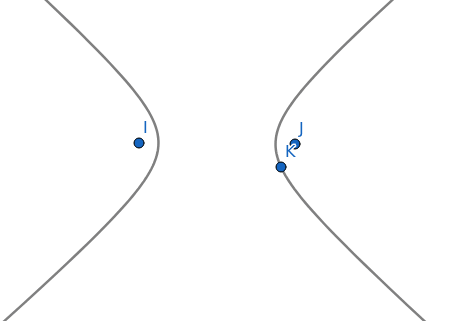
Obrázek 37: Hyperbola specifikovaná ohnisky a bodem na ní ležícím.
9. Kuželosečka procházející pěti vybranými body
Logo celého programu GeoGebra, který si v dnešním článku popisujeme, je tvořeno kuželosečkou specifikovanou pěti body, kterými tato kuželosečka prochází. Může se jednat o kružnici, elipsu, parabolu i hyperbolu – vše v závislosti na vzájemné poloze oněch pěti bodů. Díky existenci tohoto nástroje lze i parabolu nebo hyperbolu zkonstruovat i bez nutnosti znalosti přesné polohy jejich ohnisek:
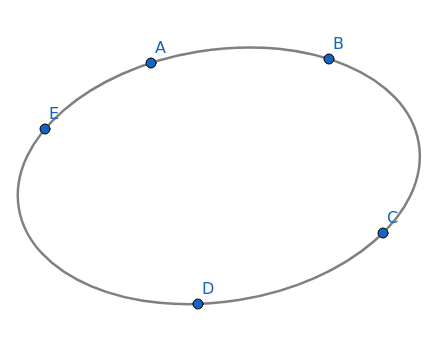
Obrázek 38: Logo programu GeoGebra – kuželosečka procházející pěticí zadaných bodů.
10. Jednoduché animace založené na posunu bodů
V předchozích kapitolách jsme si ukázali, jak lze zkonstruovat kružnici s trojúhelníky pro měření středového a obvodového úhlu. Průběh tohoto měření je možné zautomatizovat, a to například takovým způsobem, že se bude provádět posun bodu B, řekněme ve vertikálním směru. Ukažme si, jak lze tuto animaci vytvořit (jedná se přitom sice o nejjednodušší, nikoli však o nejlepší řešení):
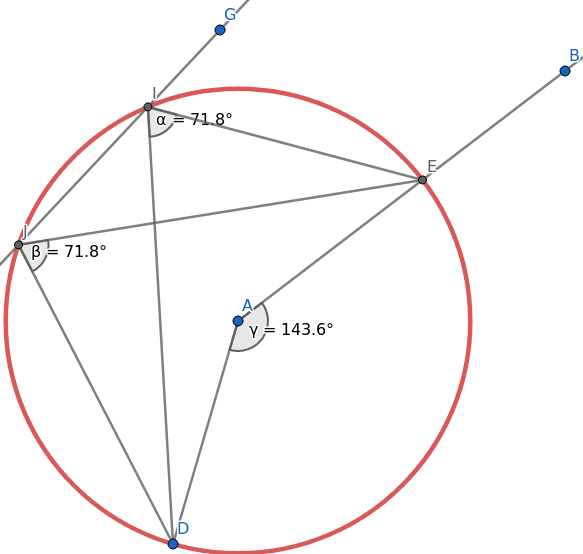
Obrázek 39: Pohybovat budeme s bodem B, který je zde zobrazen v pravém horním rohu.
Levý nástrojový pruh je nutné přepnout do režimu „kalkulačky“. Následně se přidá nová proměnná (klidně na konec celého seznamu) a změní se poloha bodu B tak, aby jedna ze souřadnic byla navázána na hodnotu nové proměnné:
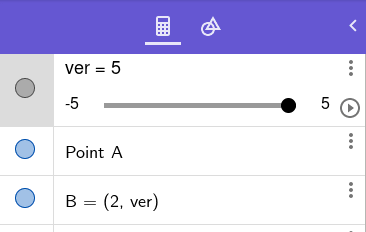
Obrázek 40: Nová proměnná a změna souřadnic bodu B tak, aby obsahovaly tuto proměnnou.
V dalším panelu se v tabu Scripting zadá minimální a maximální hodnota proměnné, přírůstek hodnoty mezi jednotlivými snímky, rychlost celé animace a taktéž způsob, jakým se animace bude opakovat. Nám zde bude postačovat, aby hodnoty vertikální souřadnice oscilovaly mezi –5 a 5:
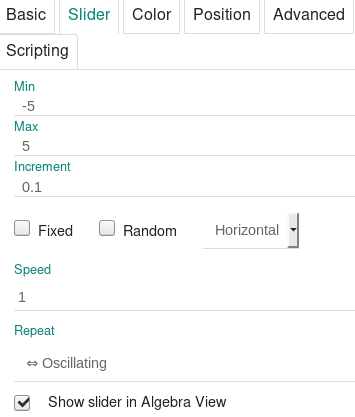
Obrázek 41: Nastavení parametrů animace.
11. Animace měření středového a obvodového úhlu
Druhá animace, kterou si dnes vytvoříme, bude sice stále jednoduchá, ale v mnoha ohledech vylepšená. Budeme v ní opět ukazovat vztah mezi středovým a obvodovým úhlem, tentokrát se ovšem bod B bude pohybovat po kružnici. Nejprve je nutné celou konstrukci přesunout tak, aby střed kružnice ležel v počátku souřadné soustavy. Následně přidáme proměnnou alfa, která bude oscilovat mezi hodnotami 0 a (přibližně) 2π. Tento úhel bude použit při výpočtu souřadnic bodu B, který bude obíhat kružnici:
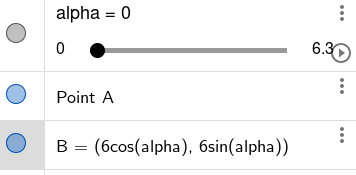
Obrázek 42: Bod B se bude pohybovat po kružnici, úhel se bude postupně měnit.
Samotné nastavení animace a její spuštění se nebude lišit od postupu uvedeného v předchozí kapitole:
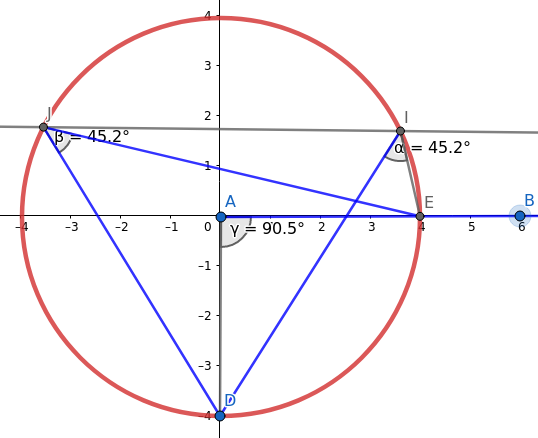
Obrázek 43: Postupná změna úhlu bodu B oproti počátku souřadné soustavy.
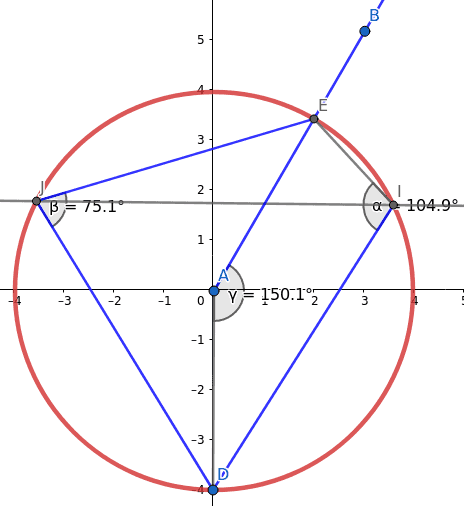
Obrázek 44: Postupná změna úhlu bodu B oproti počátku souřadné soustavy.
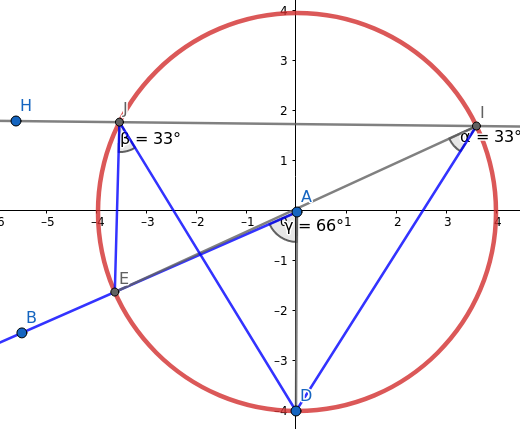
Obrázek 45: Postupná změna úhlu bodu B oproti počátku souřadné soustavy.
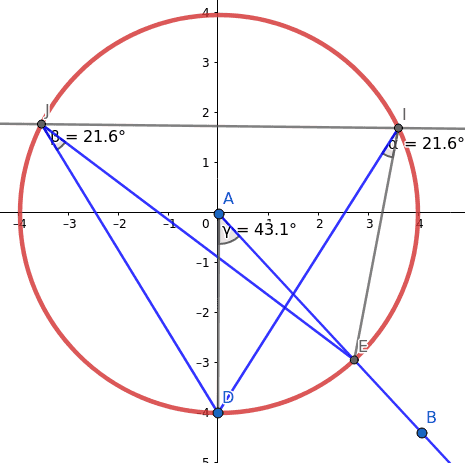
Obrázek 46: Postupná změna úhlu bodu B oproti počátku souřadné soustavy.
12. Modul CAS Calculator a jeho možnosti
Druhý modul, se kterým se dnes alespoň ve stručnosti seznámíme, se jmenuje CAS Calculator. Jedná se o zobecnění Graphing Calculatoru, jehož některé možnosti jsme si popsali v předchozím článku. CAS Calculator nabízí nové funkce, zejména možnost řešení rovnic a taktéž výpočty derivací a integrálů zadaných funkcí (pokud je to v případě integrálů v možnostech tohoto nástroje). Nejprve si však ukážeme funkcionalitu, kterou vlastně již známe – je to možnost zobrazení průběhu uživatelem specifikované funkce v ploše:
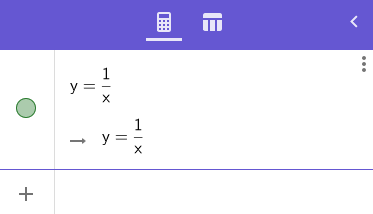
Obrázek 47: Funkce, jejíž průběh se má zobrazit.
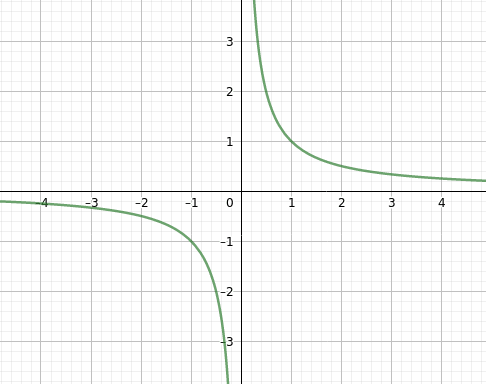
Obrázek 48: Zobrazení průběhu funkce (nástroj nemá problémy s nedefinovanými hodnotami atd.).
13. Příkaz solve
Příkaz, či možná lépe řečeno nástroj solve, slouží například k nalezení kořenů polynomu, průchodů funkce nulou atd. Na následujícím obrázku je ukázáno, jak lze snadno zjistit, pro kterou hodnotu x je hodnota funkce rovna dvěma:
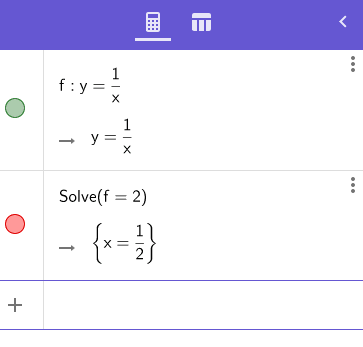
Obrázek 49: Zadání příkazu solve.
Navíc se příslušná hodnota zakreslí i do grafu:
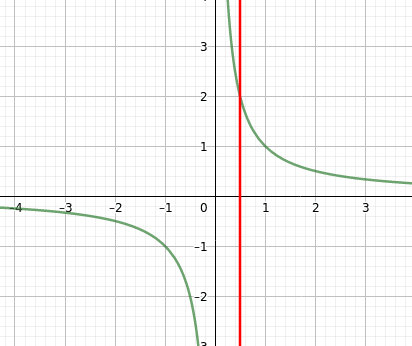
Obrázek 50: Vykreslení výsledku získaného příkazem solve.
14. Kořeny kvadratické rovnice
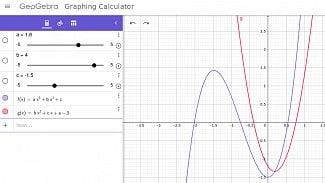
Výsledkem příkazu solve nemusí být pouze jedna hodnota, ale sekvence hodnot (i nekonečná sekvence). Ukažme si tuto vlastnost na výpočtu kořenů kvadratické rovnice, což jsou (nepřesně řečeno) takové hodnoty x, pro které příslušná parabola prochází osou x (tedy kde má funkce nulové hodnoty). Pro reálné kořeny je získání řešení snadné:

Obrázek 51: Výpočet kořenů kvadratické rovnice.
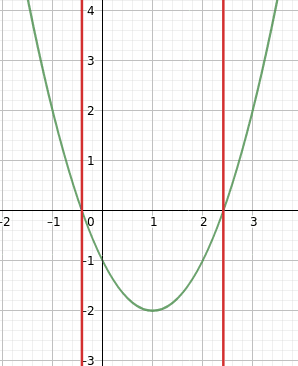
Obrázek 52: Zobrazení kořenů v grafu s průběhem funkce.
15. Zobrazení oblasti, pro kterou platí zadaná podmínka
Jen v rychlosti si ukažme na příkladu ze třinácté kapitoly, že lze snadno zobrazit i oblast nebo oblasti, pro kterou/které platí nějaká zadaná podmínka. Příkladem mohou být takové hodnoty x, pro které je hodnota funkce záporná:

Obrázek 53: Výpočet podmínky – pro které hodnoty x je hodnota funkce záporná.
Výsledek popsaný nerovnicí se zobrazí jako oblast, zde vybarvená zeleně:
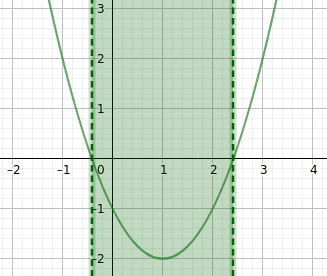
Obrázek 54: Oblast, ve které je hodnota funkce záporná.
16. Řešení s mnoha výsledky, výpočet derivace
Již v předchozím textu jsme si řekli, že některá řešení mohou mít větší množství výsledků, popř. dokonce nekonečně výsledků. Některé z těchto řešení dokáže nástroj CAS Calculator vyřešit přesně, například tehdy, pokud se jedná například o periodickou funkci. Opět si vše ukážeme na příkladě:
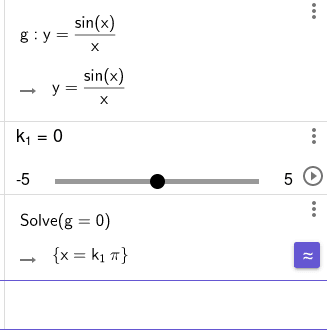
Obrázek 55: Body, v nichž je periodická funkce nulová.
Nakonec si ukažme výpočet derivace se zobrazením významných bodů analyzované funkce (nulová derivace):

Obrázek 56: Výpočet derivace.
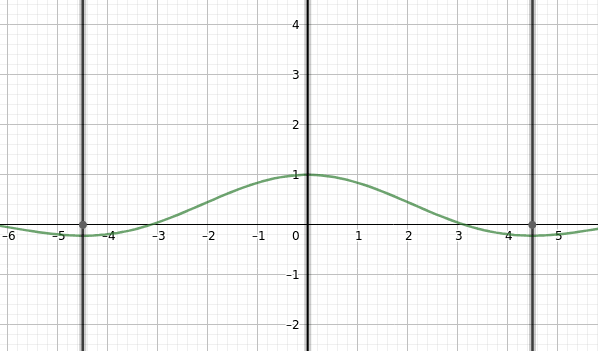
Obrázek 57: Nulové body derivace (lokální minima a maxima).
17. Převod hodnot funkce do tabulky
Hodnoty funkce, přesněji řečeno vybrané hodnoty funkce, lze zobrazit ve formě tabulky. K tomu opět slouží kontextové menu; výsledná tabulka nebo tabulky se zobrazí při stisku příslušné ikony v horním pruhu nástrojového pruhu. Hodnoty z tabulky je možné zkopírovat do dalších nástrojů, například do tabulkového procesoru atd.:

Obrázek 58: Zkoumaná funkce.
Při tvorbě tabulky je nutné specifikovat minimální a maximální hodnotu v prvním sloupci a krok, kterým se nepřímo uvádí počet zobrazených hodnot:

Obrázek 59: Základní parametry tabulky.
Výsledná tabulka je „živý“ objekt, jehož vlastnosti lze kdykoli změnit:
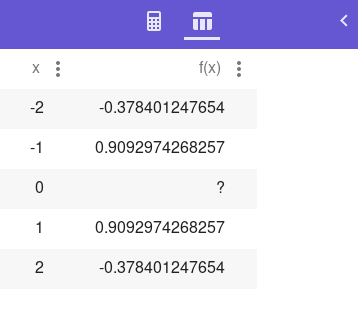
Obrázek 60: Výsledná tabulka (i s nedefinovanou hodnotou).
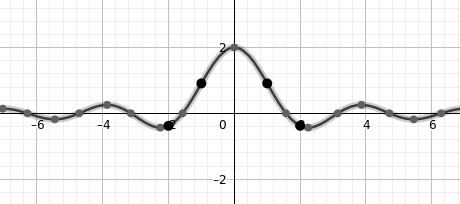
Obrázek 61: Zvýraznění bodů, které mohou být zobrazeny v tabulce.
18. Vytvoření knížky s úkoly a příklady
V navazující části tohoto seriálu si mj. ukážeme, jak lze vytvořit takzvanou knížku s prezentacemi, úlohami a příklady. Jedná se o mnohdy o ideální učební pomůcku – náhradu učebnice a současně i cvičebního sešitu.
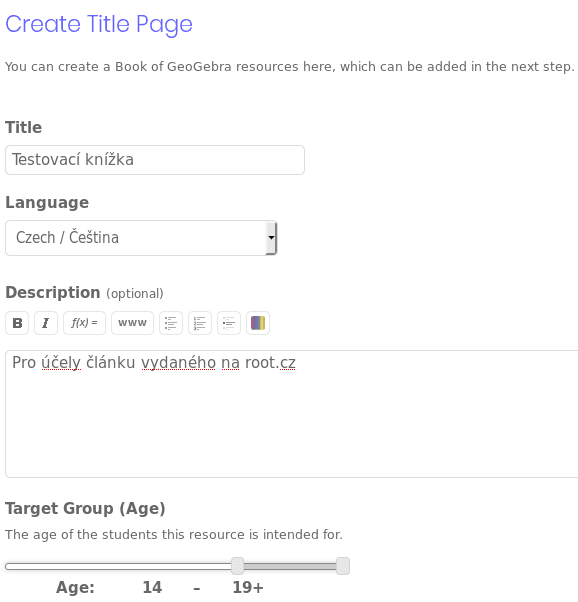
Obrázek 62: Průvodce vytvořením knížky.
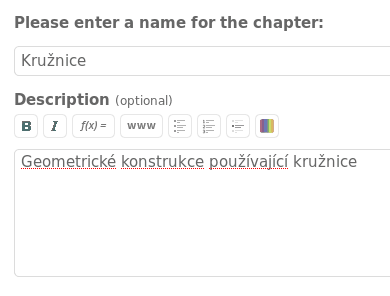
Obrázek 63: Přidání nové kapitoly.
19. Demonstrační příklady
Většina demonstračních příkladů, které byly popsány v předchozích kapitolách, je dostupná i online, a to konkrétně na následujících adresách:
- Konstrukce kolmice na zadanou úsečku
https://www.geogebra.org/m/vfbwtq2t - Konstrukce pravidelného šestiúhelníku
https://www.geogebra.org/m/cd8awnbd - Parametricky zadané kuželosečky
https://www.geogebra.org/m/fktgzemr - Thaletova kružnice
https://www.geogebra.org/m/xye46prn - Thaletova kružnice s měřením úhlů
https://www.geogebra.org/m/tunfkwxk - Všechny kuželosečky
https://www.geogebra.org/m/udcqt5pf - Kuželosečka specifikovaná pěticí bodů
https://www.geogebra.org/m/zbybe3cr - Středový a obvodový úhel
https://www.geogebra.org/m/bew3ddct - První animace středového a obvodového úhlu
https://www.geogebra.org/m/sqfhjtxu - Druhá animace středového a obvodového úhlu
https://www.geogebra.org/m/zfgfggan - Vyřešení rovnice
https://www.geogebra.org/m/vecq5fvj
20. Odkazy na Internetu
- Kružnice
https://matematika.cz/kruznice - Thaletova kružnice
https://matematika.cz/thaletova-kruznice - Středový a obvodový úhel – slovní úlohy a příklady
https://www.hackmath.net/cz/priklady-ulohy/stredovy-a-obvodovy-uhel - Obvodový, Středový úhel, příklad
https://forum.matematika.cz/viewtopic.php?id=46345 - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Euclid's Elements
https://en.wikipedia.org/wiki/Euclid%27s_Elements - Elements v řečtině a angličtině
http://farside.ph.utexas.edu/Books/Euclid/Elements.pdf - Euclid: Elementa
https://www2.hf.uio.no/polyglotta/index.php?page=volume&vid=67 - Elements (HTML + Java applety – dnes nefunční)
https://mathcs.clarku.edu/~djoyce/java/elements/toc.html - Constructible polygon
https://en.wikipedia.org/wiki/Constructible_polygon - Oskulační kružnice elipsy
https://www.geogebra.org/m/pzN24X7c - Oskulační kružnice
https://www.geogebra.org/m/j9kJemN6 - Seriál Fraktály v počítačové grafice
https://www.root.cz/serialy/fraktaly-v-pocitacove-grafice/ - Konstrukce kružítkem (diplomová práce)
https://is.muni.cz/th/tu7mj/Konstrukce_kruzitkem.pdf - ThinkPad T series
https://en.wikipedia.org/wiki/ThinkPad_T_series - Squaring the circle
https://www.itisaturn.com/squaringthecircle - Conic section
https://en.wikipedia.org/wiki/Conic_section - Kuželosečka
https://cs.wikipedia.org/wiki/Ku%C5%BEelose%C4%8Dka - Hyperbola
https://cs.wikipedia.org/wiki/Hyperbola - Thaletova věta
https://cs.wikipedia.org/wiki/Thaletova_v%C4%9Bta - Thales's theorem
https://en.wikipedia.org/wiki/Thales%27s_theorem - Polygon
https://en.wikipedia.org/wiki/Polygon - Five points determine a conic
https://en.wikipedia.org/wiki/Five_points_determine_a_conic