Obsah
1. Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008
2. Reprezentace hodnot v plovoucí řádové čárce na různých typech počítačů a systémů
3. Používané varianty báze, exponentu a mantisy
4. Elektronkové a tranzistorové sálové počítače IBM
5. Rozdělení sálových počítačů IBM podle způsobu jejich použití
6. IBM 704 – sálový počítač určený pro vědeckotechnické výpočty
8. Formát dat zpracovávaných počítači IBM 1400
9. Sovětský elektronkový počítač Strela a jím používaný formát numerických hodnot
10. Slavná architektura IBM/360 a její matematický procesor
12. Příchod osmibitových mikropočítačů
13. Formát FP hodnot v Applesoft BASICu a na ZX Spectru
14. Atari BASIC a jeho neortodoxní reprezentace reálných čísel
15. Vlastnosti formátu použitého v osmibitových Atari
16. Datový typ real v Turbo Pascalu
1. Interní reprezentace numerických hodnot: od skutečného počítačového pravěku po IEEE 754–2008
Reálná čísla (resp. přesněji řečeno samozřejmě podmnožina z této nespočetné množiny) začala být používána už u prvních mechanických a elektromechanických počítačů, což není příliš překvapivé, protože tyto stroje zpočátku skutečně sloužily především pro výpočty; teprve později byly navrženy stroje pro zpracování dat. První moderní (sic) použití reálných čísel nalezneme především u počítače Z1 navrženého v letech 1935 až 1936 Konradem Zusem. Tento počítač používal pro reprezentaci reálných čísel slova o šířce 22 bitů. Později vyvinutý stroj Z4 již využíval slova o šířce 32 bitů.

Obrázek 1: Konrad Zuse u makety svého mechanicko-elektronického počítače Z1.
Další vývoj systémů pro ukládání numerických hodnot byl prováděn především ve společnosti IBM (dalo by se říci, že paralelně s vývojem Fortranu), přičemž právě zde došlo k první unifikaci interní reprezentace reálných čísel s využitím slov rozdělených na tři části, které postupně reprezentují znaménko, mantisu a exponent. Tento systém, který si popíšeme v následující kapitole, se ukázal byl nadčasový, protože je používán dodnes. Ovšem konkrétní způsoby uložení mantisy a exponentu, stejně jako volba takzvané báze, se na různých typech počítačů a nebo operačních systémů, od sebe odlišují, takže se liší i rozsah reprezentovatelných hodnot, přesnost, existence či neexistence speciálních hodnot (+∞, -∞) atd.

Obrázek 2: Hlavní moduly počítače MESM (SSSR) včetně jeho řídicího (operátorského) panelu.
2. Reprezentace hodnot v plovoucí řádové čárce na různých typech počítačů a systémů
Všechny dále popsané formáty (reprezentace) čísel používají systém takzvané plovoucí řádové čárky (anglicky floating point, protože se v angličtině namísto čárky používá tečka). Systém plovoucí řádové čárky je založen na tom, že vybraná podmnožina reálných čísel může být vyjádřena vztahem:
XFP = (-1)s × bexp-bias × m
přičemž význam jednotlivých symbolů ve vztahu je následující:
- XFP značí reprezentovanou numerickou hodnotu z podmnožiny racionálních čísel (ta je zase podmnožinou čísel reálných). Díky vyhrazeným (speciálním) hodnotám je většinou možné rozlišit kladnou a zápornou nulu i kladné a záporné nekonečno, což je jeden z důležitých rozdílů oproti způsobu reprezentace celých čísel. Také se většinou může uložit nečíselná hodnota: NaN – (Not a Number), která je výsledkem některých matematicky nedefinovaných operací, například 0/0 nebo 00.
- b je báze, někdy také nazývaná radix, u normy IEEE 754 je to vždy dvojka, protože výpočty s bází dvě jsou pro číslicové obvody nejjednodušší. V minulosti se však používaly i jiné báze, například 8, 16 nebo i 10, s nimi se však již dnes prakticky nesetkáme (o to relevantnější jsou však v dnešním článku).
- exp je vždy kladná hodnota exponentu posunutého o hodnotu bias
- bias je hodnota, díky které je uložený exponent vždy kladný. Tato hodnota se většinou volí dle vztahu:
bias=2eb-1-1, kde eb je počet bitů vyhrazených pro exponent. Pro specifické účely je však možné zvolit i jinou hodnotu. - m je mantisa, která je u formátů dle normy IEEE 754 vždy kladná
- s je znaménkový bit nabývající hodnoty 0 nebo 1. Pokud je tento bit nulový, je reprezentovaná hodnota XFP kladná, v opačném případě se jedná o zápornou hodnotu. Vzhledem k tomu, že je jeden bit vyhrazen na uložení znaménka, je možné rozlišit kladnou a zápornou nulu (některé systémy bit znaménka používají v negované podobě).

Obrázek 3: Sálový počítač IBM-702 z roku 1953. Jednalo se o jeden z prvních počítačů specializovaných na hromadné zpracování dat, který byl vystavěn s využitím technologie elektronek a katodových (Williamsových) trubic.
3. Používané varianty báze, exponentu a mantisy
Do následující tabulky jsem se pokusil napsat všechny důležité formáty reprezentace exponentu a mantisy současně s uvedením báze. Ta je většinou dvojková, ovšem výjimkou je IBM 360 se šestnáctkovou bází a FP rutiny u osmibitových Atari s desítkovou bází:
| Počítač/norma/systém | Šířka (b) | Báze | Exponent (b) | Mantisa (b) |
|---|---|---|---|---|
| IEEE 754 half | 16 | 2 | 5 | 10+1 |
| IEEE 754 single | 32 | 2 | 8 | 23+1 |
| IEEE 754 double | 64 | 2 | 11 | 52+1 |
| IEEE 754 double extended | 80 | 2 | 15 | 64 |
| IEEE 754 quadruple | 128 | 2 | 15 | 112+1 |
| IEEE 754 octuple | 256 | 2 | 19 | 236+1 |
| IBM řady 7×x | 36 | 2 | 8 | 27 |
| IBM 360 single | 32 | 16 | 7 | 24 |
| IBM 360 double | 64 | 16 | 7 | 56 |
| HP 3000 single | 32 | 2 | 9 | 22 |
| HP 3000 double | 64 | 2 | 9 | 54 |
| CDC 6000, 6600 | 60 | 2 | 11 | 48+1 |
| Cray-1 | 64 | 2 | 15 | 48 |
| Strela | 43 | 2 | 7 | 35 |
| Apple II | 40 | 2 | 8 | 31+1 |
| ZX Spectrum | 40 | 2 | 8 | 31+1 |
| Atari (FP rutiny) | 48 | 10 | 7 | 40 |
| Turbo Pascal real | 48 | 2 | 8 | 39 |
Poznámka: pokud je ve sloupci Mantisa napsána hodnota n+1, znamená to, že hodnoty jsou normalizovány tak, aby první bit mantisy byl vždy jedničkový. V takovém případě tento bit nemusíme nikam zapisovat (víme, že je jednička) a tudíž se mantisa automaticky o tento jeden bit rozšiřuje. To samozřejmě neplatí pro denormalizované hodnoty (blízké nule).
Poznámka2: to, že u normy IEEE 754 se pro exponent používá 8(11) bitů a pro mantisu 23(52) bitů nemusí být ve všech případech ideální řešení, protože někdy vyžadujeme spíše menší rozsah hodnot, ale větší přesnost či naopak.

Obrázek 4: Ovládací panel sálového počítače IBM-702.
4. Elektronkové a tranzistorové sálové počítače IBM
První generace sálových počítačů firmy IBM byla označována tříciferným kódem začínajícím na 7. Celkem se vyrábělo pět typů počítačů této generace – IBM 701, IBM 702, IBM 704, IBM 705 a IBM 709. Číselné označení těchto počítačů respektuje i posloupnost jejich vzniku (rok vzniku počítače), což u dalších řad již není vždy splněno. Procesor těchto počítačů byl sestaven z elektronek a pasivních elektronických součástek. Operační paměť se u modelů 701 a 702 skládala z katodových trubic a u dalších třech modelů pak z magnetické paměti vytvořené ze sítě feritových jader navlečených na adresové a čtecí/zápisové vodiče. Dva modely těchto počítačů byly určeny pro hromadné zpracování dat (tomu byla uzpůsobena především instrukční sada), další dva modely byly optimalizovány spíše pro vědeckotechnické výpočty – viz tabulka zobrazená pod tímto odstavcem.
| Model | Určení | Rok výroby |
|---|---|---|
| 701 | první elektronický počítač firmy IBM | 1952 |
| 702 | hromadné zpracování dat | 1953 |
| 704 | vědeckotechnické výpočty | 1954 |
| 705 | hromadné zpracování dat | 1954 |
| 709 | vědeckotechnické výpočty | 1958 |

Obrázek 5: Elektronky byly v prvních sálových počítačích firmy IBM použity pro konstrukci kombinačních i sekvenčních logických obvodů.
Druhá generace sálových počítačů firmy IBM, jejíž modely jsou označovány čtyřciferným kódem začínajícím opět na sedmičku, se od první generace odlišovala především v použití odlišné technologie elektronických součástek – namísto rozměrných a poruchových elektronek s velkou spotřebou elektrické energie se zde objevují tranzistory. Rozdělení počítačů podle způsobu jejich použití (vědeckotechnické výpočty, hromadné zpracování dat, účetní operace v dekadické soustavě) však zůstává zachováno. Některé modely z druhé generace nejsou v podstatě ničím jiným, než počítači první generace s upravenou součástkovou základnou a několika dalšími vylepšeními (příkladem může být model IBM 705, který byl nahrazen modernějším modelem IBM 7080). V následující tabulce jsou vypsány nejvýznamnější modely druhé generace sálových počítačů firmy IBM (vynechány jsou pouze některé méně často prodávané varianty těchto počítačů):
| Model | Určení | Rok výroby |
|---|---|---|
| 7090 | vědeckotechnické výpočty | 1959 |
| 7094 | vědeckotechnické výpočty | 1962 |
| 7094 II | vědeckotechnické výpočty | 1964 |
| 7040 | vědeckotechnické výpočty | 1963 |
| 7044 | vědeckotechnické výpočty | 1963 |
| 7080 | hromadné zpracování dat | 1961 |
| 7010 | rozšířená verze IBM 1410 | 1962 |
| 7070 | dekadická soustava | 1960 |
| 7072 | dekadická soustava | 1962 |
| 7074 | dekadická soustava | 1961 |

Obrázek 6: Sálový počítač IBM-705.
5. Rozdělení sálových počítačů IBM podle způsobu jejich použití
Nehledě na technologii elektronických součástek používaných při implementaci logických obvodů (elektronky × tranzistory) byly první dvě generace sálových počítačů firmy IBM vyráběny v několika různých řadách, které se od sebe odlišovaly především tím, pro jaký typ úloh byly tyto počítače určeny. Jedná se o odlišný přístup, než na jaký jsme zvyklí dnes, protože v současnosti se setkáváme s prakticky zcela univerzálními počítači (i když výjimky se také najdou, jedná se například o specializované mikrořadiče, zařízení se signálovými procesory atd.). Nicméně na přelomu padesátých a šedesátých let minulého století byli inženýři firmy IBM (a nejenom oni) přesvědčeni o tom, že struktura procesoru (aritmeticko-logické jednotky, řadiče a registrů) a tím pádem i jeho instrukční sada musí být optimalizována s ohledem na to, k jakému účelu je daný model počítače používán, zda pro numerické vědeckotechnické výpočty (tyto počítače byly například používány v misích NASA), účetní operace či pro hromadné zpracování dat.
Instrukční sady sálových počítačů byly navíc poměrně složité (dnes bychom řekli, že se jednalo o architekturu CISC), což sice pomáhalo programátorům při psaní aplikací v assembleru, ale s nástupem překladačů vyšších programovacích jazyků se ukázalo, že mnohé strojové instrukce tyto překladače vůbec nepoužívají a že zjednodušení instrukční sady procesorů může vést k urychlení zpracování instrukcí (například se vynechá nutnost mikroprogramování či dokonce nanoprogramování, zjednoduší se dekodér instrukcí atd.), což je idea, která a mnoho let později vedla ke vzniku procesorů RISC, tj. procesorů se zjednodušenou instrukční sadou. Nicméně v dobách sálových počítačů 7×x a 7×xx se firmy, které si tyto počítače pořizovaly, musely podle plánovaného nasazení těchto strojů rozhodnout, který typ si zakoupí – bližší informace jsou uvedeny v navazujících kapitolách.
6. IBM 704 – sálový počítač určený pro vědeckotechnické výpočty
Typickým představitelem sálových počítačů navržených pro provádění vědeckotechnických výpočtů je model IBM 704. Jedná se o počítač založený na dnes již překonaných technologiích – elektronkách (procesor, tj. jak aritmeticko-logická jednotka, tak i řadič) a feritových pamětech s dobou přístupu 12 mikrosekund. Tento počítač zpracovával numerické hodnoty uložené ve slovech, jejichž šířka byla rovna 36 bitům, přičemž akumulátor (registr používaný jako zdroj i cíl aritmetických operací) byl rozšířen o další dva bity na celkovou šířku 38 bitů. Aritmeticko-logická jednotka tohoto počítače dokázala zpracovávat tři typy hodnot:
- Celá čísla či čísla s pevnou řádovou čárkou. Absolutní hodnota čísla byla uložena v 35 bitech, bit s nejvyšší váhou nesl znaménko uložené či zpracovávané hodnoty (to je zajímavé, bylo tak možné reprezentovat i zápornou nulu, kód byl symetrický).
- Čísla s pohyblivou řádovou čárkou, u kterých byl jeden bit rezervován pro uložení znaménka, osm bitů pro uložení exponentu (posunutého o hodnotu 128) a zbylých 27 bitů bylo použito pro uložení mantisy (v akumulátoru bylo díky dalším dvou bitům možné mantisu uložit v 29 bitech). Formát čísel s pohyblivou řádovou čárkou použitý u tohoto počítače do značné míry připomíná formát „single“ specifikovaný v normě IEEE 754, ovšem s tím rozdílem, že pro mantisu je zde použit větší počet bitů (základem exponentu je v obou případech hodnota 2).
- Alfanumerické znaky uložené po šesticích do slova s délkou 36 bitů. Každý alfanumerický znak je v tomto případě představován šesti bity, tj. rozeznávalo se pouze 64 různých znaků.
Bitově vypadá rozdělení 36bitového slova s FP hodnotou:
| bit | 35 | 34 … 27 | 26 … 0 |
|---|---|---|---|
| význam | s | exponent (8 bitů) | mantisa (27 bitů) |

Obrázek 7: Sálový počítač IBM-704.
7. Počítače série IBM 1400
Firma IBM na začátku šedesátých let minulého století nabízela i počítače, jejichž procesory zpracovávaly řetězce a číselné údaje proměnné délky (reprezentovaná různým způsobem, například v kódu 1 z 10 u děrných štítků a v BCD v případě uložení údajů do operační paměti), což je poměrně podstatný rozdíl oproti moderním mikroprocesorům, které zpracovávají numerické údaje zakódované binárně do slov pevné délky (například 16, 32 či 64 bitů) a zpracování řetězců buď není podporováno vůbec (RISC procesory) nebo pouze několika strojovými instrukcemi (architektura i386). Jedná se o počítače série 1400, které byly i přes výkonnostní rozdíly vzájemně kompatibilní (týká se to jak kompatibility aplikací, tak i kompatibility periferních zařízení):
| Označení modelu | Rok vzniku |
|---|---|
| IBM 1240 | 1963 |
| IBM 1401 | 1959 |
| IBM 1410 | 1960 |
| IBM 1420 | 1962 |
| IBM 1440 | 1962 |
| IBM 1450 | 1968 |
| IBM 1460 | 1963 |
| IBM 7010 | 1962 |

Obrázek 8: Část sálového počítače IBM 1401.
Snaha o dosažení co nejvyšší míry kompatibility s počítači série IBM 1400 šla dokonce tak daleko, že některé mainframy řady IBM System/360, například model 30, bylo možné nakonfigurovat tak, aby dokázaly spouštět aplikace vytvořené pro řadu 1400. Vzhledem k tomu, že procesory počítačů IBM System/360 většinou obsahovaly mikrokód, bylo přepnutí do režimu kompatibility s počítači 1400 poměrně snadné a zůstal přitom zachován relativně vysoký výpočetní výkon. Emulace řady 1400 byla použita i u dalších mainframů firmy IBM, takže aplikace napsané pro IBM 1400 mnohdy beze změny fungovaly i několik desítek let (do některých musel být zásah proveden až kvůli „syndromu“ Y2K, což znamená, že mnohé tyto programy mohly beze změny pracovat i po dobu delší než 35 let!)).

Obrázek 9: Zrekonstruovaný řídicí panel počítače IBM 1401.
8. Formát dat zpracovávaných počítači IBM 1400
V předchozí kapitole jsme si řekli, že počítače série IBM 1400 zpracovávaly řetězce a číselné hodnoty proměnné délky. Jednotlivé číslice byly ukládány v kódu BCD (binary-coded decimal), tj. ve čtyřech bitech označovaných symboly 8, 4, 2 a 1 (tyto symboly samozřejmě odpovídají váze každého bitu). K těmto čtyřem bitům se přidávaly bity označované symboly A a B, jejichž nastavením bylo možné rozšířit repertoár zpracovávaných dat i o znaky a řídicí kódy (u samotných číslic byly bity A i B vždy nulové). K takto vzniklé šestici bitů se navíc automaticky přidával bit C nesoucí informaci o paritě (lichá parita použitá k detekci jednoduché chyby) a bit M, jehož hodnota udávala, zda se jedná o poslední číslici numerické hodnoty či poslední znak řetězce. Výsledný formát bajtů zpracovávaných počítačem IBM 1400 je následující:
C B A 8 4 2 1 M
Celou tabulku hodnot jednotlivých bitů i přiřazení těchto kombinací číslicím a znakům je dostupný na adrese http://en.wikipedia.org/wiki/IBM_1401#Character_and_Op_codes. Povšimněte se, že příznak ukončení numerické hodnoty či řetězce (bit M) je součástí každého bajtu, což je poměrně velký rozdíl oproti formátu řetězců používaných například v céčku (ukončení znakem NUL, tj. nulovým bajtem; podporováno některými mikroprocesory) nebo řetězcům, kterým předchází bajt/slovo s uloženu délkou (některé Basicy, klasický Forth, Pascal atd., taktéž podporováno některými mikroprocesory, viz například prefixový kód REP u architektury i386).

Obrázek 10: Jedno velmi často používané periferní zařízení – řádková tiskárna IBM 1403. Mimochodem: právě tuto tiskárnu můžete vidět ve slavném filmu Dr. Divnoláska (Dr. Strangelove).
9. Sovětský elektronkový počítač Strela a jím používaný formát numerických hodnot
Jedním z prvních poměrně úspěšných počítačů navržených a vyráběných v SSSR byly počítače Strela-1, které byly vytvořeny vývojovým týmem vedeným Y. Bazilevským. Jednalo se o první počítač, který byl v SSSR vyráběn sériově (v průběhu let 1953 až 1956), i když celkový počet vyrobených a následně plně zprovozněných počítačů dosahoval pouze několika jednotek, s velkou pravděpodobností 7 až 10 kusů. Dostupné údaje o počtu vyrobených kusů se od sebe liší, pravděpodobně i z toho důvodu, že některé instalace počítačů Strela neobsahovaly všechny moduly, takže například počet vyrobených procesorových jednotek se odlišuje od počtu bubnových pamětí atd. Po technologické stránce se tyto počítače příliš neodlišovaly od jejich západních kolegů – procesorová jednotka i řadič byly vytvořeny z elektronek a polovodičových diod, využívaly se bubnové paměti, Williamsovy (katodové) trubice, magnetické pásky, děrné štítky atd.

Obrázek 11: Pohled na počítač Strela, z jehož rozměrů je zřejmé, proč se těmto strojům říkalo „sálové počítače“.
Počítače Strela byly určeny především pro numerické výpočty (simulace, vědeckotechnické aplikace, další vývoj výpočetní techniky), čemuž odpovídá i formát údajů, které bylo možné v procesorové jednotce těchto počítačů zpracovávat – jednalo se o číselné hodnoty reprezentované ve formátu plovoucí řádové čárky, které byly uložené ve slovech i poněkud neobvyklé šířce 43 bitů. Pokud vám připadá podivné, že tyto počítače nezpracovávaly slova o šířce, jež je celočíselným násobkem osmi (8 bitů, 16 bitů, 32 bitů, 64 bitů), vzpomeňte si na IBM 704 (1954, tj. současník počítače Strela, dokonce i určení tohoto počítače bylo podobné), jež zpracovávaly operandy o šířce 36 bitů. Bitová šířka zpracovávaných operandů na hodnoty obvyklé dnes se ustálila až o cca 10 let později.
Procesorová jednotka elektronkového počítače Strela pracovala s operandy majícími šířku 43 bitů. Číselné hodnoty mohly být uloženy ve dvou formátech – binárním formátu s pohyblivou řádovou čárkou (FP – floating point) a BCD formátu, taktéž s pohyblivou řádovou čárkou. Největší rozdíl mezi těmito dvěma formáty spočíval v tom, jakým způsobem byly zakódovány číslice mantisy. Buď se jednalo o binární kód: v tomto případě byla mantisa uložena na 35 bitech, což odpovídá 10 až 11 platným desítkovým číslicím. Nebo bylo možné pro uložení mantisy použít kód BCD, což znamenalo, že každá číslice mantisy byla uložena ve čtveřici bitů. Délka mantisy byla v tomto případě rovna 36 bitům, což odpovídá 36/4=9 číslicím. To je sice méně než při použití binárního formátu, ale operace pro vstupy nebo výstupy numerických hodnot se díky použití BCD kódu zjednodušily (ostatně právě z tohoto důvodu se BCD používal i na mnoha kalkulačkách, včetně legendární HP-35). Funkce jednotlivých bitů 43bitových slov zpracovávaných procesorem počítače Strela jsou uvedeny v následující dvojici tabulek:
Binární formát uložení mantisy:
| Bity (pozice) | Význam |
|---|---|
| 0 | znaménko mantisy |
| 1–35 | absolutní hodnota mantisy |
| 36 | znaménko exponentu |
| 37–42 | hodnota exponentu |
| Přesnost | 10–11 desítkových číslic |
| Rozsah | 1.8×10-19 až 1.8×1019 |
BCD formát uložení mantisy:
| Bity (pozice) | Význam |
|---|---|
| 0 | znaménko mantisy |
| 1–36 | mantisa uložená v BCD tvaru – 4 bity na číslici |
| 37 | znaménko exponentu |
| 38–42 | hodnota exponentu |
| Přesnost | 9 desítkových číslic |
| Rozsah | 1.8×10-19 až 1.8×1019 |
10. Slavná architektura IBM/360 a její matematický procesor
V roce 1964 firma IBM oznámila vznik nové série počítačů pojmenované System/360. Číslo „360“ v názvu této série naznačovalo, že se jedná o universální počítače, což znamenalo určitý odklon firmy IBM od návrhu počítačů specializovaných na určitý typ úloh (viz výše popisované počítače specializované buď na hromadné zpracování dat nebo na provádění vědeckotechnických výpočtů). Celá série System/360 původně zahrnovala šest vzájemně kompatibilních modelů, které se však od sebe odlišovaly jak cenou, tak i výpočetním výkonem (mezi nejvýkonnějším a nejméně výkonným modelem dosahoval poměr výpočetní rychlosti hodnoty téměř 25:1).

Obrázek 12 Jeden z prvních modelů počítače série System/360.
Procesory počítačů System/360 zpracovávaly poměrně složité instrukce, protože se jednalo o klasickou architekturu CISC (v té době se věřilo, že komplexní instrukční sada pomůže programátorům překonat sémantickou propast mezi strojovým kódem popř. assemblerem a vyššími programovacími jazyky). Aby i jednodušší modely série System/360 mohly zpracovávat všechny instrukce, používaly jejich procesory mikrokód, pomocí něhož se složitější instrukce rozdělily na sérii jednodušších mikroinstrukcí (ty měly zcela jiný formát, protože se jimi přímo ovládaly jednotlivé bloky v procesoru – ALU, registry, interní sběrnice atd.). Jednalo se o 32bitovou architekturu se šestnácti 32bitovými registry označovanými jmény R0 až R15 a čtyřmi 64bitovými registry určenými pro práci s hodnotami uloženými ve formátu pohyblivé řádové čárky. Kromě pracovních registrů procesor obsahoval i PSW (processor status word), v němž byl uložen i čítač instrukcí PC, příznak práce v superuživatelském režimu atd.

Obrázek 13: Úvodní stránka manuálu k assembleru počítačů System/360.
Výkonný model označovaný IBM System/360 Model 91 byl vybaven i matematickým procesorem se čtyřmi pracovními registry, z nichž každý měl šířku 64 bitů. Pro reprezentaci čísel v pohyblivé řádové čárce se používal formát navržený samotnou firmou IBM s jednoduchou (single) či dvojitou (double) přesností, o kterém se v tomto článku zmiňuji i z toho důvodu, že se dodnes používá například v několika souborových formátech. I když moderní matematické koprocesory na platformě i386 využívají formát numerických hodnot definovaný v IEEE 754, který je v několika ohledech od formátu firmy IBM odlišný (rozdílné šířky mantisy a exponentu, jiná hodnota biasu), je původní „360“ formát zachován například v mainframech IBM System z10, spolu s formátem IEEE 754.
Největším rozdílem IBM System/360 oproti jiným počítačům při práci s FP hodnotami je použitá báze, která není rovna dvěma ale šestnácti. To znamená, že změna exponentu o jedničku znamená změnu uložené hodnoty na šestnáctinásobek či naopak na 1/16. Díky tomu se mohlo pro exponent obětovat pouze sedm bitů, a to při zachování dostatečného rozsahu. Taktéž se lišil algoritmu normalizace hodnot, který vyžadovat, že nejvyšší 4 bity mantisy budou nenulové. To v některých případech snižovalo přesnost (u single na pouhých 21 bitů namísto 24). Zpočátku také nebylo nijak definováno, jak se mají reprezentovat speciální hodnoty typu +∞, -∞ a 0/0 (či jiné NaN).
Rozsah normalizovaných hodnot je 16-65 až zhruba 1663.

Obrázek 14: Částečně zrekonstruovaný ovládací panel počítače IBM System/360 Model 91.
11. Superpočítače Cray
V tomto článku samozřejmě nesmíme zapomenout na superpočítače Cray, které jsou známé především díky špičkovému výpočetnímu výkonu a také astronomickými sumami, za které je bylo možné pořídit :-). Tyto stroje byly optimalizovány pro provádění výpočtů se skalárními hodnotami, vektory i maticemi, což znamená, že se jejich architektura poměrně značně odlišovala od například již zmíněných strojů Connection Machine, které spíše excelovaly při (symbolickém) zpracovávání strukturovaných údajů – seznamů, stromů, grafů atd. Díky tomu, že jedním z cílů počítačů Cray byl co největší výpočetní výkon, umisťovaly se tyto stroje mezi TOP10 nejvýkonnějších počítačů světa.

Obrázek 15: Celkový pohled na superpočítač Cray-1.
Dokonce ještě v roce 2010 byl nejrychlejším (reálně existujícím) počítačem na světě Jaguar neboli Cray XT5 s výpočetním výkonem neuvěřitelných 1.75 PFLOPS (petaflops), který překonal i IBM Roadrunner. Vzhledem k tomu, že počítače Cray zpracovávaly a zpracovávají neuvěřitelné množství numerických dat, může být popis jejich interního formátu FP hodnot užitečný.

Obrázek 16: Cray-1 a jeho duchovní otec a konstruktér.
Počítače Cray-1 používaly pro skalární i vektorové operace numerické hodnoty uložené v systému plovoucí řádové čárky (FP). Tyto hodnoty byly sice uložené v 64 bitech, podobně jako je tomu u formátu double v normě IEEE 754, ovšem význam jednotlivých bitů je poněkud jiný, takže se liší jak rozsah uchovávaných hodnot, tak i počet platných míst, což je patrné z následující tabulky:
| Min | Max | Počet míst | |
|---|---|---|---|
| IEEE single | 1.17E-0038 | 3.40E+0038 | 7 |
| IEEE double | 2.22E-0308 | 1.79E+0308 | 16 |
| Cray single | 3.67E-2466 | 2.73E+2465 | 15 |

Obrázek 17: Detail spodní části superpočítače CRAY-1S. Na pravé straně fotografie je patrný „vstup“ do vnitřního prostoru stroje.
Obsazení bitů v 64bitovém slovu (registru) je u počítačů Cray-1 následující:
1 1 14 48 +-+-+--------------+------------------------------------------------+ |s|t| e | m | +-+-+--------------+------------------------------------------------+
kde:
- s: znaménko mantisy
- t: znaménko exponentu
- e: exponent
- m: mantisa
12. Příchod osmibitových mikropočítačů
O významu osmibitových domácích i osobních mikropočítačů jsme se již zmiňovali minule, a to v kontextu s programovacími jazyky. Osmibitové mikropočítače měly společnou minimálně jednu vlastnost – neobsahovaly žádný matematický koprocesor, takže se veškeré výpočty musely zdlouhavě provádět na osmibitovém CPU (přičemž jen některé CPU obsahovaly násobičku). Na druhou stranu to tvůrcům programového vybavené umožnilo volbu rozličných formátů reprezentace čísel. V dalších kapitolách se seznámíme s formátem používaným Applesoft BASICem na počítačích Apple II, dále s prakticky totožným formátem využívaným na ZX Spectru a nezapomeneme ani na Atari BASIC se zajímavým formátem založeným na desítkové a nikoli dvojkové bázi.

Obrázek 18: Výkonu Crayů v FP operacích osmibitové mikropočítače samozřejmě ani zdaleka nedosahovaly. Tento výpočet Mandelbrotovy množiny v Atari BASICu trval přibližně osm hodin.
13. Formát FP hodnot v Applesoft BASICu a na ZX Spectru
„Before .Net, before math coprocessors, before IEEE-574, Microsoft defined a bit pattern for floating-point numbers.“
Applesoft BASIC na osobních osmibitových mikropočítačích Apple používal formát FP hodnot, který je známý pod jménem MBF neboli Microsoft Binary Format. Tento formát byl navržen Monte Davidoffem pro Altair Basic a později byl portován i do Applesoft Basicu. Ve skutečnosti existoval Microsoft Binary Format ve více variantách, především v 32bitové a 40bitové variantě. Applesoft BASIC využíval právě 40bitovou variantu, v níž je mantisa uložena ve čtyřech bajtech (32 bitech), pro znaménko je vyhrazen další bit a zbývajících sedm bitů je použito pro exponent s biasem (offsetem) nastaveným na 128. Báze je samozřejmě rovna dvěma:
8 1 31 +--------------+-+------------------------------------------------+ | e |s| m | +--------------+-+------------------------------------------------+
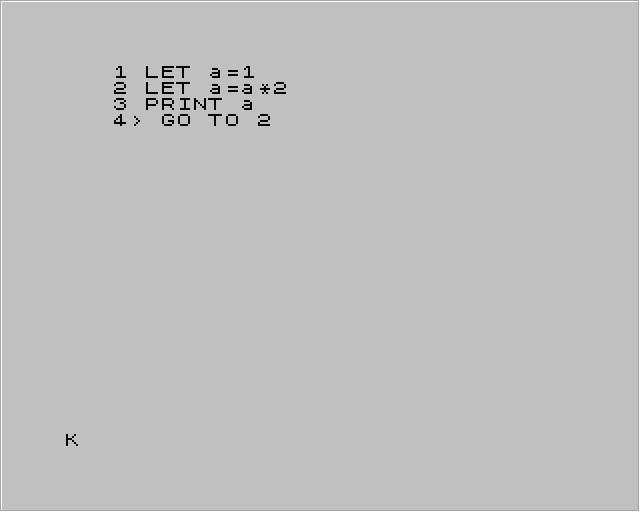
Obrázek 19: Primitivní prográmek pro zjištění, zda dojde k překročení maximální reprezentovatelné hodnoty.
I na ZX Spectru se používal podobný formát numerických hodnot uložených v pěti bajtech (40 bitech), ovšem na těchto počítačích se mantisa normalizovala takovým způsobem, aby její nejvyšší bit byl jedničkový. Nejmenší reprezentovatelná hodnota odlišná od nuly byla přibližně ±4×10-39, nejvyšší hodnota pak cca 1038, což pro většinu výpočtů zcela dostačovalo. Při výpočtech se kontrolovalo překročení maximální hodnoty, což mj. znamená, že neexistovaly speciální hodnoty typu +∞ atd.
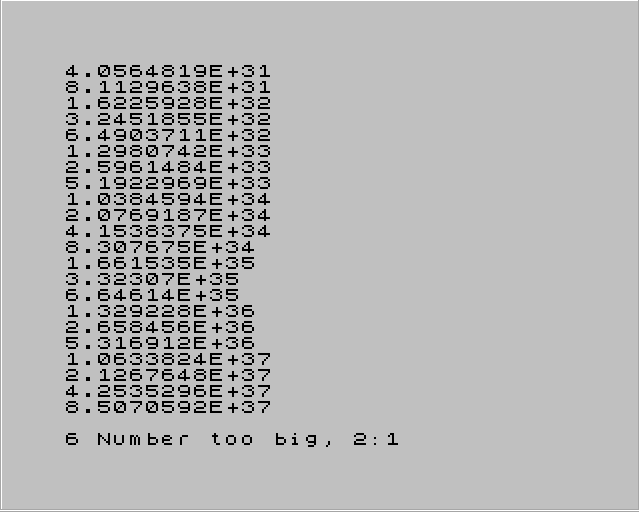
Obrázek 20: Interpret BASICu korektně zjistil, že výpočet přesáhl maximální hodnotu.
Podobně jako u dále popsaného typu real v Turbo Pascalu leží vlastnosti FP hodnot ZX Spectra mezi možnostmi typů single a double podle IEEE 754.

Obrázek 21: Výsledek pokusu o dělení nulou (viz výpis programu).
14. Atari BASIC a jeho neortodoxní reprezentace reálných čísel
V Atari BASICu, přesněji řečeno v subrutinách uložených v ROM, které se staraly o výpočty nad reálnými čísly, se používal formát odlišný od prakticky všech předchozích formátů. Stále se sice jedná o hodnoty s plovoucí řádovou čárkou, ovšem báze není rovna dvěma (většina strojů) ani šestnácti (IBM/360), ale stu! Navíc není mantisa uložená binárně, ale používá se BCD, což konkrétně znamená, že v pěti bajtech je uloženo přesně deset číslic (procesor 6502 dokázal s BCD pracovat nativně). To není úplně špatné řešení, protože ho najdeme například na mnoha kalkulačkách. Zjednodušují se převody řetězců na čísla a naopak, na druhou stranu jsou však veškeré výpočty značně pomalejší a přesnost ani rozsah hodnot není tak vysoký, jako při použití binárního kódu.
Formát uložení FP hodnot tedy vypadá následovně:
| Bajt | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Význam | znaménko+exponent | 2 BCD číslice | 2 BCD číslice | 2 BCD číslice | 2 BCD číslice | 2 BCD číslice |
Povšimněte si faktu, že pro uložení exponentu muselo stačit pouze sedm bitů, což je pro formát používající šest bajtů pro jednu hodnotu, na první pohled poměrně málo, ovšem musíme si uvědomit, že báze je rovna 100 a nikoli 2.
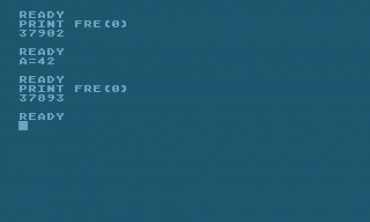
Obrázek 22: Po vytvoření nové proměnné (s reálnou hodnotou) se v paměti alokuje celkem devět bajtů, přičemž šest bajtů zabere vlastní hodnota (viz předchozí tabulku), dva bajty typ a jméno proměnné a jeden bajt její index.
Uložená hodnota se vypočte takto: mantisa×100exponent-64
Pokud je exponent sudý, lze přesně reprezentovat deset číslic (cifer), u lichého exponentu jen devět číslic (cifer). Je to logické, protože změna exponentu o jedničku znamená posun čárky o dvě cifry.
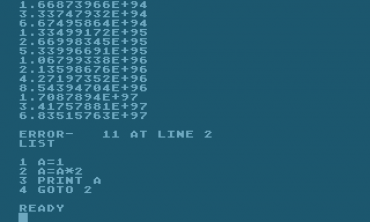
Obrázek 23: V mnoha moderních jazycích dojde při výpočtech k „tichému“ přetečení z nejvyšší hodnoty do nekonečna. V Atari BASICu není možné ∞ reprezentovat a proto je namísto toho hlášena chyba.
15. Vlastnosti formátu použitého v osmibitových Atari
Jaké má toto řešení výhody? Především lze přesně reprezentovat často používané hodnoty 0,1, 0,01 atd. Ostatně podívejme se na to, jak se chová interpret jazyka Lua (používá typ double), interpret Pythonu (taktéž double) a interpret Atari BASICu:
Lua:
> print(0.2 + 0.2 == 0.4) true > print(0.1 + 0.2 == 0.3) false > print(1 + 2 == 3) true
Python:
>>> 0.2 + 0.2 == 0.4 True >>> 0.1 + 0.2 == 0.3 False >>> 1 + 2 == 3 True
Atari BASIC:
PRINT 0.2 + 0.2 = 0.4 1 PRINT 0.1 + 0.2 = 0.3 1 PRINT 1 + 2 = 3 1
Poznámka: v Atari BASICu odpovídá hodnota 1 pravdivostní hodnotě True.
Dále – nebylo možné reprezentovat žádné speciální hodnoty, takže dělení nulou či výpočet 0/0 skončil s chybou:
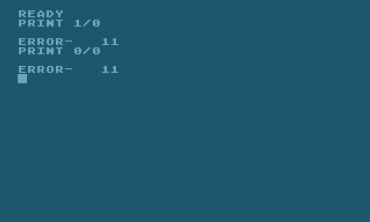
Obrázek 24: Speciální hodnoty není možné reprezentovat.
Pro zajímavost jsou v následující tabulce vypsány adresy těch paměťových buněk, které se používají FP subsystémem operačního systému osmibitových mikropočítačů Atari. Prvních šest oblastí paměti je uloženo v RAM, další oblasti pak v paměti ROM (jedná se o subrutiny):
| Jméno | Adresa | Délka (bajtů) | Význam |
|---|---|---|---|
| FR0 | 0×00D4 | 6 | první FP operand |
| FR1 | 0×00E0 | 6 | druhý FP operand |
| CIX | 0×00F2 | 1 | index do INBUFF |
| INBUFF | 0×00F3 | 2 | ukazatel na buffer používaný při převodu z řetězce na FP |
| FLPTR | 0×00FC | 2 | ukazatel na uživatelský buffer |
| LBUFF | 0×0580 | ? | buffer používaný při převodu na řetězec |
| AFP | 0×D800 | ? | subrutina pro převod řetězce na FP |
| FASC | 0×D8E6 | ? | subrutina pro převod FP na řetězec |
| IFP | 0×D9AA | ? | subrutina pro převod integer na FP |
| FPI | 0×D9D2 | ? | subrutina pro převod FP na integer |
| ZFR0 | 0×DA44 | ? | subrutina pro vymazání FR0 |
| ZF1 | 0×DA46 | ? | subrutina pro vymazání bufferu FP |
| FSUB | 0×DA60 | ? | subrutina pro výpočet FR0 – FR1 |
| FADD | 0×DA66 | ? | subrutina pro výpočet FR0 + FR1 |
| FMUL | 0×DADB | ? | subrutina pro výpočet FR0 * FR1 |
| FDIV | 0×DB28 | ? | subrutina pro výpočet FR0 / FR1 |
| FLD0R | 0×DD89 | ? | subrutina pro načtení FR0 s použitím X,Y jako ukazatelů |
| FLD0P | 0×DD8D | ? | subrutina pro načtení FR0 přes ukazatel FLPTR |
| FLD1R | 0×DD98 | ? | subrutina pro načtení FR1 s použitím X,Y jako ukazatelů |
| FLD1P | 0×DD9C | ? | subrutina pro načtení FR1 přes ukazatel FLPTR |
| FST0R | 0×DDA7 | ? | subrutina pro uložení FR0 na adresu v X,Y |
| FST1P | 0×DDAB | ? | subrutina pro uložení FR0 na adresu v FLPTR |
| FMOVE | 0×DDB6 | ? | subrutina pro převod FR0 do FR1 |
| EXP | 0×DDC0 | ? | subrutina pro výpočet en |
| EXP10 | 0×DDCC | ? | subrutina pro výpočet 10n |
| PLYEVL | 0×DD40 | ? | subrutina pro další výpočty pomocí řady |
| LOG | 0×DECD | ? | subrutina pro výpočet ln FR0 |
| LOG10 | 0×DED1 | ? | subrutina pro výpočet log FR0 |
16. Datový typ real v Turbo Pascalu
Standard programovacího jazyka Pascal uvádí několik základních datových typů, mezi jinými i real. Ovšem není nijak specifikováno, s jakou přesností a rozsahem mají být hodnoty používající tento formát uloženy. V populárním Turbo Pascalu se používal datový typ real, který je někdy známý i pod označením real48, protože pro reprezentaci FP hodnoty skutečně využíval 48 bitů. Tento typ byl navržen ještě předtím, než se na IBM PC rozšířily matematické koprocesory, což mj. znamenalo, že se hodnoty typu real zpracovávaly softwarově. Rozsah a přesnost leží přibližně na polovině cesty mezi typem single/float a double z normy IEEE 754.
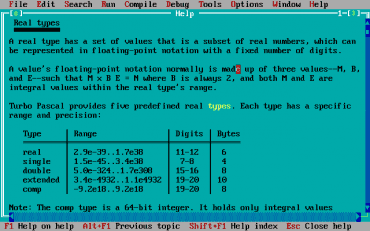
Obrázek 25: Nabídka datových typů pro FP hodnoty nabízená Turbo Pascalem 7.
Formát real48 je celkem jednoduchý – jeden bajt je rezervován pro uložení exponentu posunutého o 129, dalších pět bajtů pak pro uložení mantisy. Pouze v posledním bajtu (nejvyšším – jedná se o little endian) je jeden bit rezervován pro uložení znaménka:
| Bajt | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Význam | exponent | mantisa | mantisa | mantisa | mantisa | znaménko+mantisa |
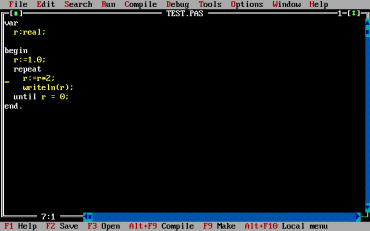
Obrázek 26: Testovací prográmek pro zjištění, jak se testuje překročení maximální hodnoty.
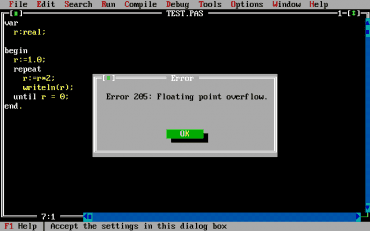
Obrázek 27: Pro typ real testování funguje.
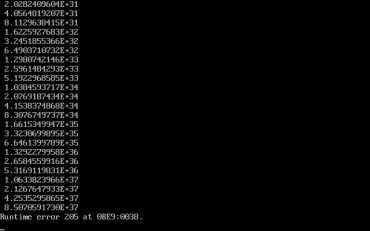
Obrázek 28: Pro typ real testování funguje.
Později byly do Turbo Pascalu přidány i typy single, double a extended, které mohly být zpracovány buď matematickým koprocesorem nebo jeho emulátorem. Dnešní varianty Pascalu, tj. FreePascal a Lazarus, již původní real48 nepoužívají a mapují namísto toho real buď na single (SW emulace) či na double (HW koprocesor).
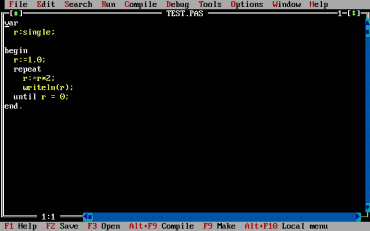
Obrázek 29: Testovací prográmek přepsaný pro použití typu single (podle IEEE 754).
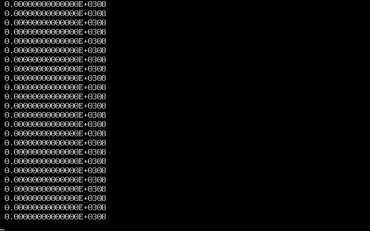
Obrázek 30: Hmm, nekonečná smyčka.
17. Odkazy na Internetu
- Norma IEEE 754 a příbuzní: formáty plovoucí řádové tečky
https://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/ - IEEE-754 Floating-Point Conversion
http://babbage.cs.qc.cuny.edu/IEEE-754.old/32bit.html - Small Float Formats
https://www.khronos.org/opengl/wiki/Small_Float_Formats - Art of Assembly language programming: The 80×87 Floating Point Coprocessors
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–3.html - Art of Assembly language programming: The FPU Instruction Set
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–4.html - INTEL 80387 PROGRAMMER'S REFERENCE MANUAL
http://www.ragestorm.net/downloads/387intel.txt - Floating-Point Formats
http://www.quadibloc.com/comp/cp0201.htm - Mainframe family tree and chronology
http://www-03.ibm.com/ibm/history/exhibits/mainframe/mainframe_FT1.html - 704 Data Processing System
http://www-03.ibm.com/ibm/history/exhibits/mainframe/mainframe_PP704.html - 705 Data Processing System
http://www-03.ibm.com/ibm/history/exhibits/mainframe/mainframe_PP705.html - The IBM 704
http://www.columbia.edu/acis/history/704.html - IBM Mainframe album
http://www-03.ibm.com/ibm/history/exhibits/mainframe/mainframe_album.html - Mainframe computer
http://en.wikipedia.org/wiki/Mainframe_computer - IBM mainframe
http://en.wikipedia.org/wiki/IBM_mainframe - IBM 700/7000 series
http://en.wikipedia.org/wiki/IBM700/7000_series - IBM System/360
http://en.wikipedia.org/wiki/IBM_System/360 - IBM System/370
http://en.wikipedia.org/wiki/IBM_System/370 - IBM Floating Point Architecture
http://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - Extended Binary Coded Decimal Interchange Code
http://en.wikipedia.org/wiki/EBCDIC - ASCII/EBCDIC Conversion Table
http://docs.hp.com/en/32212–90008/apcs01.html - EBCDIC
http://www.hansenb.pdx.edu/DMKB/dict/tutorials/ebcdic.php - EBCDIC tables
http://home.mnet-online.de/wzwz.de/temp/ebcdic/cc_en.htm - The Mainframe Blog
http://mainframe.typepad.com/blog/2006/11/my_personal_mai.html - IBM Tightens Stranglehold Over Mainframe Market Gets Hit with Antitrust Complaint in Europe
http://www.ccianet.org/artmanager/publish/news/IBM_Tightens_Stranglehold_Over_Mainframe_Market_Gets_Hit_with_Antitrust_Complaint_in_Europe.shtml - Lectures in the History of Computing: Mainframes
http://www.computinghistorymuseum.org/teaching/lectures/pptlectures/9-MainframeComputers.ppt - 36-bit
http://en.wikipedia.org/wiki/36-bit_word_length - 36bit.org
http://www.36bit.org/ - Applesoft BASIC
https://en.wikipedia.org/wiki/Applesoft_BASIC - How did the Apple II do floating point?
https://groups.google.com/forum/#!topic/comp.emulators.apple2/qSBiG2TAlRg - IBM Floating Point Architecture
https://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - The Arithmetic Subroutines
http://www.users.waitrose.com/~thunor/mmcoyzx81/chapter17.html - ZX Floating point to Decimal code in BASIC
http://www.sinclairzxworld.com/viewtopic.php?t=1422 - Floating Point Arithmetic Package
http://www.retrocomputing.net/parts/atari/800/docs/atari_os/atari_os_user_manual08.htm - 704 Data Processing System
https://www-03.ibm.com/ibm/history/exhibits/mainframe/mainframe_PP704.html - Turbo Pascal Real
http://www.shikadi.net/moddingwiki/Turbo_Pascal_Real - THE FLOATING POINT ARITHMETIC PACKAGE
http://www.atarimax.com/freenet/freenet_material/5.8-BitComputersSupportArea/7.TechnicalResourceCenter/showarticle.php?14 - Sinclair ZX81 BASIC Programming (by Steven Vickers)
http://www.worldofspectrum.org/ZX81BasicProgramming/ - The Most Expensive One-byte Mistake: Did Ken, Dennis, and Brian choose wrong with NUL-terminated text strings?
http://queue.acm.org/detail.cfm?id=2010365 - UCSD Pascal
https://en.wikipedia.org/wiki/UCSD_Pascal - D Language: Strings
https://dlang.org/spec/arrays.html#strings - The History Behind the Definition of a ‚String‘
https://stackoverflow.com/questions/880195/the-history-behind-the-definition-of-a-string - Libc: Representation of Strings
https://www.gnu.org/software/libc/manual/html_node/Representation-of-Strings.html - ATARI BASIC
http://www.atariarchives.org/dere/chapt10.php - BASIC (Wikipedia EN)
http://en.wikipedia.org/wiki/BASIC - BASIC (Wikipedia CZ)
http://cs.wikipedia.org/wiki/BASIC - Turbo BASIC (Wikipedia CZ)
http://cs.wikipedia.org/wiki/Turbo_BASIC - Sinclair BASIC (Wikipedia CZ)
http://cs.wikipedia.org/wiki/Sinclair_BASIC - More BASIC Computer Games
http://www.atariarchives.org/morebasicgames/ - Dartmouth College Computation Center: 1964 – The original Dartmouth BASIC manual
http://www.bitsavers.org/pdf/dartmouth/BASIC_Oct64.pdf - The Original BASIC
http://www.truebasic.com/ - BASIC – Beginners All-purpose Symbolic Instruction Code
http://hopl.murdoch.edu.au/showlanguage.prx?exp=176 - Universal Coded Character Set
https://en.wikipedia.org/wiki/Universal_Coded_Character_Set - UTF-16
https://en.wikipedia.org/wiki/UTF-16 - PEP 393 – Flexible String Representation
https://www.python.org/dev/peps/pep-0393/ - In-memory size of a Python structure
https://stackoverflow.com/questions/1331471/in-memory-size-of-a-python-structure - What is internal representation of string in Python 3.x
https://stackoverflow.com/questions/1838170/what-is-internal-representation-of-string-in-python-3-x#9079985 - How to profile memory usage in Python
https://www.pluralsight.com/blog/tutorials/how-to-profile-memory-usage-in-python - What's the rationale for null terminated strings?
https://stackoverflow.com/questions/4418708/whats-the-rationale-for-null-terminated-strings - Unicode
https://en.wikipedia.org/wiki/Unicode - The Development of the C Language
https://www.bell-labs.com/usr/dmr/www/chist.html - Borland Pascal Wiki: String operations
http://borlandpascal.wikia.com/wiki/String_operations - Pascal Strings
https://www.tutorialspoint.com/pascal/pascal_strings.htm - PChar – Null terminated strings
https://www.freepascal.org/docs-html/ref/refsu12.html - Comparison of Pascal and C
https://en.wikipedia.org/wiki/Comparison_of_Pascal_and_C - FORTRAN 66
http://fortranwiki.org/fortran/show/FORTRAN+66 - Fortran: strings
https://en.wikibooks.org/wiki/Fortran/strings - Strings in Atari BASIC
http://www.cyberroach.com/analog/an11/strings.htm - String Arrays in Atari BASIC
http://www.atarimagazines.com/compute/issue11/52_1_STRING_ARRAYS_IN_ATARI_BASIC.php - An Atari BASIC Tutorial
http://www.cyberroach.com/analog/an25/basictutorial.htm - Basic Multilingual Plane
https://en.wikipedia.org/wiki/Plane_(Unicode)#Basic_Multilingual_Plane





































