Obsah
2. Překlad a instalace Pythonu bez GILu
3. Je to užitečné v praxi? Role benchmarků
4. Výpočet členů Fibonacciho posloupnosti
5. Výsledky benchmarku pro různý počet vláken
6. Algoritmus bublinkového řazení
7. Výsledky benchmarku při vypnuté i zapnuté volbě „nogil“
8. Složitější výpočty s velkým množstvím numerických operací
9. Paralelní varianta výpočtů z předchozí kapitoly
10. Výsledky benchmarku pro sekvenční i paralelní variantu výpočtů
11. Benchmark s větším množstvím výpočtů, které je možné provádět paralelně
12. Sekvenční a paralelní verze benchmarku
13. Výsledky benchmarku pro sekvenční i paralelní variantu výpočtů
14. Vliv počtu paralelně běžících vláken na čas dokončení výpočtů
17. Repositář s demonstračními příklady
18. Odkazy na články s problematikou souběžnosti a paralelnosti v Pythonu
1. Interpret Pythonu bez GILu
Programovací jazyk Python, resp. přesněji řečeno jeho standardní varianta CPython, nepatří (poněkud eufemisticky řečeno) mezi nejrychlejší interpretry, i když se situace stále zlepšuje (viz například nedávno vydaný článek Rychlost CPythonu 3.11 a 3.12 v porovnání s JIT a AOT překladači). Příčin relativně pomalé interpretace programů psaných v Pythonu je pochopitelně větší množství, a mnohé z nich do značné míry souvisí s vlastnostmi tohoto programovacího jazyka (dynamický typový systém, způsob uložení referencí na hodnoty atd.).
Jedním z nejčastěji citovaných důvodů je existence (ne)slavného GILu, což je zkratka sousloví Global Interpreter Lock(u). Existence GILu, která zajišťuje korektní přístup k hodnotám objektů atd., do značné míry znemožňuje skutečně paralelní běh vícevláknových aplikací. Samozřejmě nám nic nebrání ve vytvoření aplikace s větším množstvím vláken, ale ty poběží spíše souběžně (concurrent) a nikoli skutečně paralelně (parallel), protože běh jednotlivých vláken bude často zastaven právě na zámku (lock).
Není tedy divu, že s příchodem mikroprocesorů s větším množstvím jader se vlastně neustále objevují snahy o odstranění GILu – dalo by se dokonce říct, že je to v ekosystému programovacího jazyka Python evergreen a každý „skutečný programátor“ by měl aspoň jednou v životě napsat do fóra Pythonu, že by bylo dobré GIL odstranit. Neustálé odmítání odstranění GILu vedlo mnohé k tomu, že opakovali mantru „interpret Pythonu musí vždy GIL obsahovat“. To pochopitelně není zcela pravda, protože některé jiné interpretry Pythonu (určené pro běh nad virtuálními stroji atd.) GIL neobsahují.
V současnosti je, většinou ve stavu proof of concept, k dispozici hned několik upravených verzí CPythonu bez GILu (nebo s redukovaným počtem zámků – locků). Jsou však tyto varianty stabilní a přináší nějaké skutečné zrychlení vícevláknových aplikací? Pokusme se o několik srovnání; využijeme přitom variantu CPythonu 3.9 bez GILu, jejíž zdrojové kódy jsou dostupné na adrese https://github.com/colesbury/nogil.
2. Překlad a instalace Pythonu bez GILu
Překlad a instalace vlastní varianty Pythonu (resp. CPythonu) bez GILu je relativně snadná. Nejdříve si ovšem ověřte, že máte nainstalovány všechny potřebné nástroje (git, gcc a Make) i knihovny. Závislosti jsou popsány zde. Nezapomeňte především na knihovnu libssl-dev. Pokud tato knihovna nebude nainstalována, interpret se sice přeloží, ale například pip nebude (logicky) podporovat HTTPs a tím pádem nepůjdou stáhnout balíčky z PyPi (a některé balíčky použijeme v benchmarcích).
Ve druhém kroku naklonujeme repositář s Pythonem s odstraněným GILem:
$ git clone https://github.com/colesbury/nogil Cloning into 'nogil'... remote: Enumerating objects: 917040, done. remote: Counting objects: 100% (917040/917040), done. remote: Compressing objects: 100% (176101/176101), done. remote: Total 917040 (delta 737567), reused 916960 (delta 737528), pack-reused Receiving objects: 100% (917040/917040), 404.58 MiB | 5.21 MiB/s, done. Resolving deltas: 100% (737567/737567), done.
Další kroky jsou již standardní a vlastně se nijak neliší od překladu klasického Pythonu. Zavoláme ./configure s povolením optimalizací:
$ ./configure --enable-optimizations
Pokud vše proběhne v pořádku, zbývají nám pouze provést dva kroky. Prvním z nich je vlastní překlad, ideálně prováděný paralelně. Příklad překladu interpretru Pythonu na systému s osmi jádry:
$ make -j8
A v posledním kroku si můžete (ale striktně nemusíte) nově vzniklý interpret nechat nainstalovat do /usr/local/ příkazem:
$ make install
Nyní se pokusme si nově přeložený (a popř. i nainstalovaný) interpret Pythonu spustit:
$ ./python Python 3.9.10 (heads/nogil:8f9803ddf4, Jan 5 2024, 13:38:23) [nogil, GCC 9.4.0] on linux Type "help", "copyright", "credits" or "license" for more information. >>>
3. Je to užitečné v praxi? Role benchmarků
Neexistence GILu by měla usnadnit paralelní běh vláken vytvořených v jedné instanci interpretru Pythonu. Do jaké míry je to pravda, je samozřejmě nutné si nejprve ověřit v praxi (v IT již totiž známe příklady stovek „vylepšení“, která jsou dobrá jen na papíře nebo spíš v PowerPointové prezentaci, zatímco praxe poněkud pokulhává). Z tohoto důvodu si vyzkoušíme několik benchmarků, které jsou založeny na spuštění a řízení běhu většího množství vláken s využitím třídy ThreadPoolExecutor, se kterou jsme se již na stránkách Rootu setkali a která je popsána zde.
4. Výpočet členů Fibonacciho posloupnosti
Přímo v dokumentaci, která je dostupná na https://github.com/colesbury/nogil, je uveden jednoduchý benchmark, jenž je založen na výpočtu členů Fibonacciho posloupnosti. Zajímavé je, že tento benchmark se vlastně používá pro zjištění hodnoty (resp. přesněji řečeno počtu vláken), která ještě mohou běžet paralelně tak, aby se celková doba výpočtu nezvětšila. Zvýšení počtu vláken tedy v tomto případě nevede ke zrychlení výpočtu jedné úlohy, ale ke zvětšení počtu dokončených úloh (což je vlastně odvozeno od známého Gustafsonova zákona, který v této oblasti nahrazuje Amdahlův zákon zaměřený na snížení celkového času).
Zdrojový kód tohoto benchmarku vypadá následovně (získáno přímo ze stránky https://github.com/colesbury/nogil):
import sys
from concurrent.futures import ThreadPoolExecutor
print(f"nogil={getattr(sys.flags, 'nogil', False)}")
def fib(n):
if n < 2: return 1
return fib(n-1) + fib(n-2)
threads = 8
if len(sys.argv) > 1:
threads = int(sys.argv[1])
with ThreadPoolExecutor(max_workers=threads) as executor:
for _ in range(threads):
executor.submit(lambda: print(fib(34)))
5. Výsledky benchmarku pro různý počet vláken
Na stránkách projektu nogil jsou uvedeny výsledky tohoto benchmarku provedené na počítači s mikroprocesorem Intel Xeon E5–2698 v4, který má dvacet jader. A dosažené výsledky tomu odpovídají.
V mém případě takový luxusní mikroprocesor není k dispozici. Benchmark byl namísto toho spuštěn na mikroprocesoru Intel Core i7–8665U, který má „jen“ čtyři jádra. Tomu budou odpovídat i výsledky benchmarků.
Při spuštění jediného výpočtu bude reálný čas pro dokončení výpočtů dosahovat 0,708 sekundy:
$ time python3.9 fib.py 1
Výsledky:
nogil=True 9227465 real 0m0,708s user 0m0,688s sys 0m0,020s
V případě, že spustíme čtyři výpočty paralelně, bude reálný čas prakticky stejný, konkrétně 0,787 sekundy (user time naproti tomu naznačuje, že běžely čtyři výpočty, každý z nich přibližně oněch 0,7 sekundy):
$ time python3.9 fib.py 4
Výsledky:
nogil=True 9227465 9227465 9227465 9227465 real 0m0,787s user 0m2,856s sys 0m0,013s
U většího počtu výpočtů se již nedosáhne stejného reálného času, protože čtyři fyzická jádra neumožní plně paralelní běh pěti, šesti atd. výpočtů. Je to jasně patrné na výsledcích:
$ time python3.9 fib.py 8
Nyní je již reálný čas přibližně dvojnásobný oproti předchozímu času, což docela dobře odpovídá teorii: osm úloh běžících na čtyřech jádrech:
nogil=True 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 real 0m1,474s user 0m11,178s sys 0m0,020s
A pro jistotu si ještě pusťme stejný výpočet, tentokrát však šestnáctkrát:
$ time python3.9 fib.py 16
nogil=True 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 9227465 real 0m3,177s user 0m23,449s sys 0m0,024s
6. Algoritmus bublinkového řazení
Jako druhý benchmark byl zvolen algoritmus bublinkového řazení, který intenzivně pracuje s operační pamětí. Samozřejmě se jedná o velmi neefektivní algoritmus (což vlastně benchmarky mají být :-). Čistě sekvenční varianta tohoto benchmarku vypadá následovně:
from time import perf_counter
import random
def bubble_sort(size):
a = [random.randrange(0, 10000) for i in range(size)]
t1 = perf_counter()
for i in range(size - 1, 0, -1):
for j in range(0, i):
if a[j] > a[j + 1]:
a[j], a[j + 1] = a[j + 1], a[j]
t2 = perf_counter()
print(f"Sorted in {t2-t1} seconds:")
t1 = perf_counter()
for i in range(100):
bubble_sort(5000)
t2 = perf_counter()
print(f"Total time: {t2-t1} seconds:")
V tomto benchmarku stokrát voláme funkci, která vytvoří pole (realizované seznamem) se 10000 prvky s náhodnou hodnotou. Toto pole je následně seřazeno. Pro úplnost se ještě měří čas seřazení pole a taktéž celkový čas všech výpočtů.
Paralelní či možná lépe řečeno pseudoparalelní varianta benchmarku je prakticky stejná, ovšem oněch sto volání funkce bubble_sort není provedeno sekvenčně, ale využívá se namísto toho již výše zmíněná třída ThreadPoolExecutor. Hodnotou max_workers můžeme omezit počet úloh spouštěných současně:
from concurrent.futures.thread import ThreadPoolExecutor
from time import perf_counter
import random
def bubble_sort(size):
a = [random.randrange(0, 10000) for i in range(size)]
t1 = perf_counter()
for i in range(size - 1, 0, -1):
for j in range(0, i):
if a[j] > a[j + 1]:
a[j], a[j + 1] = a[j + 1], a[j]
t2 = perf_counter()
print(f"Sorted in {t2-t1} seconds:")
t1 = perf_counter()
with ThreadPoolExecutor(max_workers=8) as executor:
for i in range(100):
executor.submit(bubble_sort, 5000)
t2 = perf_counter()
print(f"Total time: {t2-t1} seconds:")
7. Výsledky benchmarku při vypnuté i zapnuté volbě „nogil“
Benchmark, přesněji řečeno dvojice benchmarků, z předchozí kapitoly byl spuštěn v interpretru Pythonu, který jsme přeložili v rámci druhé kapitoly. Benchmark byl spuštěn celkem třikrát, a to konkrétně v těchto variantách:
- Sekvenční varianta benchmarku běžící v jednom vlákně
- Souběžná varianta benchmarku běžící ve více vláknech, ovšem se zapnutým GILem (proměnná prostředí PYTHONGIL=1)
- Souběžná a současně i paralelní varianta benchmarku běžící ve více vláknech a s vypnutým GILem (proměnná prostředí PYTHONGIL=0)
Výsledky jsou zajímavé:
| Varianta | Čas běhu benchmarku |
|---|---|
| sekvenční | 202s |
| souběžná s GILem | 205s |
| paralelní bez GILu | 74s |
Nejprve se podívejme na první dva výsledky, což znamená 202 sekund u sekvenční varianty a 205 sekund u varianty souběžné (zde lze použít i klasický CPython). Časy výpočtu jsou prakticky shodné, i když chování benchmarku v runtime se liší. Zatímco u sekvenčního benchmarku bylo trvale využito jedno jádro procesoru prakticky na 100% a další jádra nebyla využita, u souběžné varianty se sice využívalo více jader, ale jejich využití bylo menší než 100% (pokud lze věřit topu, tak byla jádra využita ze 40%, ale tipuji, že ve skutečnosti to bylo poněkud méně). Zde jsme tedy nic neušetřili i přesto, že jsme použili vícevláknový program – a zde je patrné, že volání pro odstranění GILu má svůj význam!
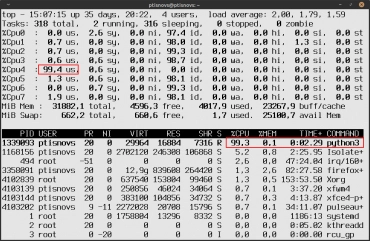
Obrázek 1: Při sekvenčním výpočtu je zatíženo jen jedno jádro mikroprocesoru.
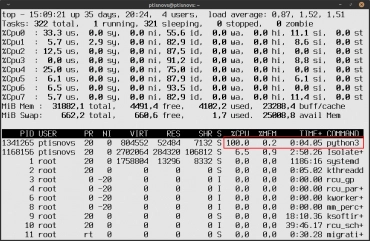
Obrázek 2: Souběžné výpočty sice vytíží více jader (nenulové hodnoty v levém horním rohu), ovšem nelze přesáhnout 100% výkonu (měřeno výkonem jednoho jádra). Celkový čas výpočtu tedy bude srovnatelný se sekvenčním přístupem.
Paralelní běh bez GILu vytížil všechna jádra prakticky na 100%, takže bychom očekávali, že doba běhu benchmarku bude dosahovat 202s/4=50 sekund. Ve skutečnosti je to však o něco více. Díky odstranění GILu a spuštění výpočtu ve více vláknech jsme na mikroprocesoru se čtyřmi fyzickými jádry dosáhli přibližně trojnásobného zrychlení. To není špatné, i když na druhou stranu to ukazuje, že se stále provádí nějaké synchronizace.
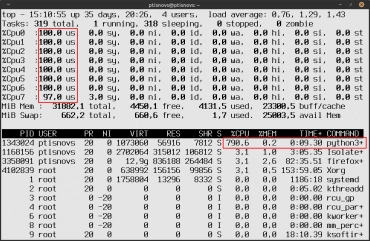
Obrázek 3: Teprve odstranění GILu vede k tomu, že jsou výpočtem vytížena všechna jádra mikroprocesoru (zde se zobrazuje osm jader, ovšem fyzicky se jedná o čtyři jádra).
8. Složitější výpočty s velkým množstvím numerických operací
Větší počet jader mikroprocesoru, které mohou v ideálním případě pracovat paralelně, oceníme především ve chvíli, kdy musíme vykonat nějaké složitější výpočty, neboť takové úlohy typicky nejsou omezeny rychlostí I/O operací a mnohdy ani nemají velké množství čtení a zápisů do operační paměti. Jednou typicky výpočetně náročnou úlohou (kterou jsme v nepatrně pozměněné podobě již použili při testování nástroje Numba a mypyc), je výpočet nějakého fraktálu v komplexní rovině.

Obrázek 4: Jedna varianta fraktálu vykreslená benchmarkem.
Zkusme si tedy nechat vykreslit několik Juliových množin ve větším rozlišení (1024×1024 pixelů) a s využitím většího maximálního počtu iterací (1000). Následující benchmark sekvenčně vypočítá deset obrázků Juliových množin a uloží je na disk:
#!/usr/bin/env python
"""Renderer of the classic Julia fractal."""
from PIL import Image
from time import perf_counter
IMAGE_WIDTH = 1024
IMAGE_HEIGHT = 1024
def julia(cx, cy, zx, zy, maxiter):
c = complex(cx, cy)
z = complex(zx, zy)
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(filename, palette, xmin, ymin, xmax, ymax, cx, cy, maxiter=1000):
"""Recalculate the whole fractal and render the set into given image."""
t1 = perf_counter()
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
width, height = image.size
stepx = (xmax - xmin) / width
stepy = (ymax - ymin) / height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = julia(cx, cy, x1, y1, maxiter)
i = 3 * i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image.save(filename)
t2 = perf_counter()
print("Done", filename, t2-t1)
def main():
import palette_mandmap
recalc_fractal("spiral_1.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.769824999999999998320, -0.109270000000000000000, 1000)
recalc_fractal("spiral_2.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.171119200000000013445, 0.657309400000000000000, 1000)
recalc_fractal("spiral_3.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.207190825000000012496, 0.676656624999999999983, 1000)
recalc_fractal("spiral_4.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.540623850000000003876, 0.523798050000000000019, 1000)
recalc_fractal("julia1.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.0, 1.0, 1000)
recalc_fractal("julia2.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -1.0, 0.0, 500)
recalc_fractal("julia3.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.285, 0.01, 1000)
recalc_fractal("julia4.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.4, 0.6, 1000)
recalc_fractal("julia5.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.835, -0.2321, 1000)
recalc_fractal("julia6.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.4, 0.4, 1000)
if __name__ == "__main__":
t1 = perf_counter()
main()
t2 = perf_counter()
print(f"Rendering time: {t2-t1} seconds")

Obrázek 5: Další varianta fraktálu vykreslená benchmarkem.
9. Paralelní varianta výpočtů z předchozí kapitoly
Výpočet z předchozí kapitoly je možné snadno převést do varianty, ve které se výpočet každého obrázku odehraje v samostatném vláknu. V závislosti na verzi Pythonu (s GILem či bez GILu) potom tato vlákna běží buď souběžně (concurrent) nebo paralelně (parallel). Počet vytvořených vláken lze specifikovat parametrem předávaným do konstruktoru ThreadPoolExecutor:
#!/usr/bin/env python
"""Renderer of the classic Julia fractal."""
from concurrent.futures.thread import ThreadPoolExecutor
from PIL import Image
from time import perf_counter
IMAGE_WIDTH = 1024
IMAGE_HEIGHT = 1024
def julia(cx, cy, zx, zy, maxiter):
c = complex(cx, cy)
z = complex(zx, zy)
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(filename, palette, xmin, ymin, xmax, ymax, cx, cy, maxiter=1000):
"""Recalculate the whole fractal and render the set into given image."""
t1 = perf_counter()
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
width, height = image.size
stepx = (xmax - xmin) / width
stepy = (ymax - ymin) / height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = julia(cx, cy, x1, y1, maxiter)
i = 3 * i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image.save(filename)
t2 = perf_counter()
print("Done", filename, t2-t1)
def main():
import palette_mandmap
with ThreadPoolExecutor(max_workers=10) as executor:
executor.submit(recalc_fractal, "spiral_1.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.769824999999999998320, -0.109270000000000000000, 1000)
executor.submit(recalc_fractal, "spiral_2.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.171119200000000013445, 0.657309400000000000000, 1000)
executor.submit(recalc_fractal, "spiral_3.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.207190825000000012496, 0.676656624999999999983, 1000)
executor.submit(recalc_fractal, "spiral_4.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.540623850000000003876, 0.523798050000000000019, 1000)
executor.submit(recalc_fractal, "julia1.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.0, 1.0, 1000)
executor.submit(recalc_fractal, "julia2.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -1.0, 0.0, 500)
executor.submit(recalc_fractal, "julia3.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.285, 0.01, 1000)
executor.submit(recalc_fractal, "julia4.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.4, 0.6, 1000)
executor.submit(recalc_fractal, "julia5.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, -0.835, -0.2321, 1000)
executor.submit(recalc_fractal, "julia6.png", palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, 0.4, 0.4, 1000)
if __name__ == "__main__":
t1 = perf_counter()
main()
t2 = perf_counter()
print(f"Rendering time: {t2-t1} seconds")

Obrázek 6: Ještě jedna varianta fraktálu vykresleného popisovaným benchmarkem.
10. Výsledky benchmarku pro sekvenční i paralelní variantu výpočtů
Opět se podívejme na výsledky benchmarků získané pro tři varianty spuštění. Tyto varianty již dobře známe:
- Sekvenční varianta benchmarku běžící v jednom vlákně
- Souběžná varianta benchmarku běžící ve více vláknech, ovšem se zapnutým GILem (proměnná prostředí PYTHONGIL=1)
- Souběžná a současně i paralelní varianta benchmarku běžící ve více vláknech a s vypnutým GILem (proměnná prostředí PYTHONGIL=0)
Průběh výpočtů při jejich sekvenčním spouštění vypadá následovně. Časy výpočtů jsou uvedeny v sekundách, stejně jako celkový čas výpočtu:
Done spiral_1.png 5.1859697019681334 Done spiral_2.png 4.786959243938327 Done spiral_3.png 3.4001936549320817 Done spiral_4.png 3.4124309360049665 Done julia1.png 2.20688958466053 Done julia2.png 13.11793684400618 Done julia3.png 3.6973323193378747 Done julia4.png 4.339927026070654 Done julia5.png 2.9289116361178458 Done julia6.png 2.5796306179836392 Rendering time: 45.65670717321336 seconds
Naproti tomu souběžné spuštění (s GILem) nám ukáže zcela odlišné časy výpočtu. Všechny výpočty jsou spuštěny v prakticky stejný okamžik, ovšem tím, že běží souběžně (nikoli plně paralelně), tak trvají mnohem delší dobu. A celkový čas výpočtů je zde taktéž delší (!), pravděpodobně kvůli nutnosti synchronizace vláken přes GIL (samotná práce se zámky není zcela zadarmo):
Done julia6.png 30.125944807194173 Done julia1.png 31.00761267496273 Done julia5.png 30.421344230882823 Done spiral_3.png 32.166233513038605 Done julia3.png 36.28653717506677 Done spiral_4.png 37.24156935699284 Done spiral_2.png 41.884877351112664 Done julia4.png 41.84162455704063 Done spiral_1.png 42.753659673035145 Done julia2.png 49.35199412936345 Rendering time: 49.35429013008252 seconds
A konečně se dostáváme k paralelnímu běhu bez GILu. Čas výpočtů jednotlivých obrázků se zvýšil, protože počet vláken je vyšší, než počet fyzických jader. Ovšem celkový čas se snížil ze 45 sekund na 25 sekund. Teoretická doba výpočtů by měla být 45/4=11 sekund, to je ovšem, jak ukazuje realita, spíše optimistické (a je zde mnoho proměnných, včetně koordinace vláken, přístupy k operační paměti, teplotním managementem procesoru atd.). Taktéž nesmíme zapomenout na to, že jednotlivé výpočty trvají různou dobu a na konci se typicky již čeká na jediné vlákno:
Done julia1.png 11.038880513980985 Done julia6.png 12.374067123048007 Done spiral_4.png 12.891932097729295 Done julia5.png 13.229847213253379 Done spiral_3.png 14.292223097756505 Done julia4.png 15.105731802992523 Done julia3.png 15.142507585231215 Done spiral_2.png 16.04855623608455 Done spiral_1.png 16.921899473760277 Done julia2.png 25.186154996976256 Rendering time: 25.188359602820128 seconds

Obrázek 7: Poslední uvedená varianta fraktálu vykresleného popisovaným benchmarkem.
11. Benchmark s větším množstvím výpočtů, které je možné provádět paralelně
Pojďme ještě dále. Pokusíme se předchozí benchmark upravit do takové podoby, aby se mohlo paralelně provádět ještě větší množství výpočtů. Namísto jednotlivých obrázků tedy budeme tvořit animaci se 72 snímky, což znamená, že teoreticky může současně běžet až 72 vláken. Výsledek po převodu do GIFu (se snížením kvality) by měl vypadat následovně:

Obrázek 8: Výsledná animace po převodu do GIFu.
12. Sekvenční a paralelní verze benchmarku
Nejdříve se podívejme na sekvenční verzi benchmarku. Jedná se o relativně triviální program, který vygeneruje různé hodnoty konstant cx a cy a pro každou dvojici těchto hodnot vykreslí jeden snímek Juliovy množiny. Výsledek lze spojit do animovaného GIFu buď přímo v programu (zde to není ukázáno, ale knihovna PIL/Pillow to podporuje) nebo konverzí na příkazové řádce:
#!/usr/bin/env python
"""Renderer of the classic Julia fractal."""
from PIL import Image
from time import perf_counter
import math
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
def julia(cx, cy, zx, zy, maxiter):
c = complex(cx, cy)
z = complex(zx, zy)
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(filename, palette, xmin, ymin, xmax, ymax, cx, cy, maxiter=1000):
"""Recalculate the whole fractal and render the set into given image."""
t1 = perf_counter()
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
width, height = image.size
stepx = (xmax - xmin) / width
stepy = (ymax - ymin) / height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = julia(cx, cy, x1, y1, maxiter)
i = 3 * i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image.save(filename)
t2 = perf_counter()
# print("Done", filename, t2-t1)
def main():
import palette_mandmap
for angle in range(0, 360, 5):
rad = math.radians(angle)
cx = 1.0 * math.cos(rad)
cy = 1.0 * math.sin(rad)
filename = f"anim_{angle:03d}.png"
# print(filename)
recalc_fractal(filename, palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, cx, cy, 1000)
if __name__ == "__main__":
t1 = perf_counter()
main()
t2 = perf_counter()
print(f"Threads: no Rendering time: {t2-t1} seconds")
Paralelní verze benchmarku umožňuje modifikovat počet workerů (tj. vlastně počet aktivních vláken) z příkazové řádky. Výsledné rastrové obrázky se opět ukládají na disk pro pozdější zpracování, a samozřejmě taktéž pro kontrolu, zda se neliší od předchozího benchmarku – musí být stejné bit po bitu:
#!/usr/bin/env python
"""Renderer of the classic Julia fractal."""
import sys
from concurrent.futures.thread import ThreadPoolExecutor
from PIL import Image
from time import perf_counter
import math
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
def julia(cx, cy, zx, zy, maxiter):
c = complex(cx, cy)
z = complex(zx, zy)
for i in range(0, maxiter):
if abs(z) > 2:
return i
z = z * z + c
return 0
def recalc_fractal(filename, palette, xmin, ymin, xmax, ymax, cx, cy, maxiter=1000):
"""Recalculate the whole fractal and render the set into given image."""
t1 = perf_counter()
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
width, height = image.size
stepx = (xmax - xmin) / width
stepy = (ymax - ymin) / height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
i = julia(cx, cy, x1, y1, maxiter)
i = 3 * i % 256
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
x1 += stepx
y1 += stepy
image.save(filename)
t2 = perf_counter()
# print("Done", filename, t2-t1)
def main(threads):
import palette_mandmap
with ThreadPoolExecutor(max_workers=threads) as executor:
for angle in range(0, 360, 5):
rad = math.radians(angle)
cx = 1.0 * math.cos(rad)
cy = 1.0 * math.sin(rad)
filename = f"anim_{angle:03d}.png"
# print(filename)
executor.submit(recalc_fractal, filename, palette_mandmap.palette, -1.5, -1.5, 1.5, 1.5, cx, cy, 1000)
if __name__ == "__main__":
threads = 8
if len(sys.argv) > 1:
threads = int(sys.argv[1])
t1 = perf_counter()
main(threads)
t2 = perf_counter()
print(f"Threads: {threads} Rendering time: {t2-t1} seconds")
13. Výsledky benchmarku pro sekvenční i paralelní variantu výpočtů
Benchmarky byly tentokrát spuštěny na složitějším mikroprocesoru s výkonnými a méně výkonnými jádry:
12th Gen Intel(R) Core(TM) i7-1270P
Tento procesor se z pohledu operačního systému tváří jako čip se šestnácti jádry.
Opět si nejdříve ukažme tabulky s výsledky pro naše tři známé scénáře (sekvenční, paralelní s GIL a paralelní bez GIL). Nyní ovšem rozšíříme scénář o různý počet workerů a tím pádem i o různý počet skutečně využitých jader:
| Varianta | Čas běhu benchmarku |
|---|---|
| sekvenční | 17,8s |
| souběžná s GILem 8 workerů | 19,5s |
| souběžná s GILem 32 workerů | 18,4s |
| paralelní bez GILu 8 workerů | 7,77s |
| paralelní bez GILu 32 workerů | 8,47s |
Varianta bez GILu je sice opět rychlejší, ale kupodivu pouze dvakrát, i když z výsledků TOP bylo patrné, že jsou všechna jádra plně vytížena. Popravdě řečeno byly výsledky tohoto benchmarku zklamáním, protože jsem očekával mnohem větší zrychlení (navíc na papírově lepším CPU).
14. Vliv počtu paralelně běžících vláken na čas dokončení výpočtů
Zajímavé bude zjistit, u kolika paralelně běžících vláken narazíme na sweet spot, tj. hodnotu, při níž jsou všechny snímky animace vypočteny nejrychleji. Teoreticky by tato hodnota měla odpovídat počtu fyzických jader, což je však u mikroprocesorů kombinujících výkonné a méně výkonné jednotky dosti problematické zjistit. Pokusme se tedy benchmark pustit s různým počtem vláken (samozřejmě se zde bavíme o variantě bez GIL):
for i in `seq 1 8`
do
python3.9 julia_parallel_anim.py $i
done
Výsledky ukazují, že sweet spot je v tomto případě přibližně u sedmi vláken, ovšem rozdíly mezi (například) čtyřmi a sedmi vlákny jsou relativně malé – benchmark tedy příliš neškáluje tak, jak bychom očekávali:
| Počet vláken | Čas výpočtu |
|---|---|
| 1 | 20.33s |
| 2 | 11.72s |
| 3 | 9.31s |
| 4 | 8.38s |
| 5 | 8.68s |
| 6 | 8.85s |
| 7 | 7.77s |
| 8 | 8.65s |
15. Několik pozorování
Zejména u druhého mikroprocesoru použitého pro benchmarky (12th Gen Intel® Core™ i7–1270P) je nutné vypnout režim „energy safe“, protože jinak byl výpočetní čas pro sekvenční zpracování a pro paralelní zpracování prakticky stejný! Tj. v prvním případě pracovalo jen jedno jádro na 100%, ovšem v plné frekvenci a ve druhém případě pracovala všechna jádra sice taktéž na 100%, ale při nižší frekvenci a výsledky se nakonec srovnaly (na druhou stranu je vypnutí „energy safe“ režimu na laptopu velmi nepraktické (větrák pracující i ve chvíli, kdy je load prakticky nulový).
16. Závěrem – vyplatí se to?
V první řadě je nutné poznamenat, že „Python bez GIL“ je stabilní a týden jsem ho dokázal profesionálně používat namísto běžného Pythonu 3.12. Naproti tomu výsledky výpočetně náročných benchmarků ukazují, že urychlení možná neodpovídá očekávání, protože v této oblasti bych skutečně očekával, že urychlení bude zhruba odpovídat počtu jader. Nicméně i pro větší počet fyzických jader procesoru se dosahuje maximálně dvojnásobného až trojnásobného urychlení.
17. Repositář s demonstračními příklady
Všechny demonstrační příklady (resp. jednoduché benchmarky) ukazující vlastnosti Pythonu bez GILu naleznete v repositáři https://github.com/tisnik/most-popular-python-libs. Ideální je mít nainstalován Python bez GILu, protože jen tak se projeví výhody paralelních variant benchmarků. Následují odkazy na jednotlivé příklady/benchmarky:
18. Odkazy na články s problematikou souběžnosti a paralelnosti v Pythonu
Na stránkách Roota jsme se již několikrát setkali s problematikou souběžnosti, paralelnosti a asynchronního běhu v Pythonu. Různé varianty spouštění a řízení více vláken, procesů a asynchronních úloh naleznete v následujících článcích (všechny v článcích uvedené demonstrační příklady by měly být spustitelné i v interpretru Pythonu bez GILu):
- Souběžné a paralelně běžící úlohy naprogramované v Pythonu
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu/ - Souběžné a paralelně běžící úlohy naprogramované v Pythonu (2)
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu-2/ - Souběžné a paralelně běžící úlohy naprogramované v Pythonu – Curio a Trio
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu-curio-a-trio/ - Souběžné a paralelně běžící úlohy naprogramované v Pythonu – knihovna Trio
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu-knihovna-trio/ - Souběžné a paralelně běžící úlohy naprogramované v Pythonu – knihovna Trio (2)
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu-knihovna-trio-2/ - Souběžné a paralelně běžící úlohy naprogramované v Pythonu – závěrečné zhodnocení
https://www.root.cz/clanky/soubezne-a-paralelne-bezici-ulohy-naprogramovane-v-pythonu-zaverecne-zhodnoceni/
19. Odkazy na Internetu
- PEP 684 – A Per-Interpreter GIL
https://peps.python.org/pep-0684/ - What Is the Python Global Interpreter Lock (GIL)?
https://realpython.com/python-gil/ - PEP 703 – Making the Global Interpreter Lock Optional in CPython
https://peps.python.org/pep-0703/ - GlobalInterpreterLock
https://wiki.python.org/moin/GlobalInterpreterLock - What is the Python Global Interpreter Lock (GIL)
https://www.geeksforgeeks.org/what-is-the-python-global-interpreter-lock-gil/ - Python 3.12: More Faster and More Efficient Python
https://medium.com/@HeCanThink/python-3–12-more-faster-and-more-efficient-python-b636f00b047 - Numba
http://numba.pydata.org/ - numba 0.57.0
https://pypi.org/project/numba/ - Pushing Python toward C speeds with SIMD
https://laurenar.net/posts/python-simd/ - Retrieve generated LLVM from Numba
https://stackoverflow.com/questions/25213137/retrieve-generated-llvm-from-numba - Numba documentation
http://numba.pydata.org/numba-doc/latest/index.html - Numba na GitHubu
https://github.com/numba/numba - First Steps with numba
https://numba.pydata.org/numba-doc/0.12.2/tutorial_firststeps.html - Numba and types
https://numba.pydata.org/numba-doc/0.12.2/tutorial_types.html - Just-in-time compilation
https://en.wikipedia.org/wiki/Just-in-time_compilation - Cython (home page)
http://cython.org/ - Cython (wiki)
https://github.com/cython/cython/wiki - Cython (Wikipedia)
https://en.wikipedia.org/wiki/Cython - Cython (GitHub)
https://github.com/cython/cython - PyPy (home page)
https://pypy.org/ - PyPy (dokumentace)
http://doc.pypy.org/en/latest/ - Nuitka
https://github.com/Nuitka/Nuitka - SIMD Autovectorization in Numba
https://tbetcke.github.io/hpc_lecture_notes/simd.html - Does Jython have the GIL?
https://stackoverflow.com/questions/1120354/does-jython-have-the-gil - Let's remove the Global Interpreter Lock
https://www.pypy.org/posts/2017/08/lets-remove-global-interpreter-lock-748023554216649595.html - Global interpreter lock
https://en.wikipedia.org/wiki/Global_interpreter_lock - Rychlost CPythonu 3.11 a 3.12 v porovnání s JIT a AOT překladači
https://www.root.cz/clanky/rychlost-cpythonu-3–11-a-3–12-v-porovnani-s-jit-a-aot-prekladaci-pythonu/