Revoluce v masovém skenování
Zhruba v polovině loňského roku se objevil nový skener ZMap. Nejprve to byl jenom „trochu rychlejší“ nmap bez fíčur nmap-u, i když s celkem zajímavými interními triky, jak reprezentovat stav spojení, aniž bych se informace o něm držely někde implicitně v kernelu nebo user space. Rychlejší značí „full IPv4 scan in 45 minutes“.
Na 30C3 byla o ZMap-u přednáška, mě osobně dost příjemně překvapila (slajdy). Čekal jsem, že se bude točit především jen kolem TCP/IP, nakonec ukázali i dost zajímavých podrobností z kryptosféry. Některé z nich dále vypíchnu.
V aktuální verzi disponuje možností na polo-otevřené (half-SYN) spojení navázat a použít ho i pro „mluvení daným protokolem“ (banner scan), pokud zjistíme, že host žije. Lze tak například posílat ClientHello zprávy SSL/TLS serverům, scrapovat SSH klíče a libovolný další materiál, o který se servery rády podělí. Pokud vaše stávající skenovací infrastruktura nespustí dostatečný počet výstrah u různých IDS/IPS, nebo pokud chcete výsledky skutečně rychle, tak hurá do ZMap-u.
Pro banner ske je potřeba kernelový modul forge-socket , který v jádře zahodí RST paket, pomocí něhož by jádro odpovídalo normálně na nečekaný SYN+ACK od skenovaného stroje. Tudíž bohužel nestačí rychlý server a tlustá linka, ale systém serveru musí běžet na holém železe, nebo na „té správné“ virtualizaci (mnohé VPS to neumožňují). Ne vždy existuje možnost ZMap-em upgradovat „starý“ skenovací systém.
ZMap posílá jen jeden pokus o spojení na jeden cíl, nmap ve výchozím nastavení dva. Přesto ZMap ve výsledku pokryje víc cílů, hlavně při plném IPv4 skenu. Autory to nejprve taky mátlo, pak zjistili, že je to timeoutem – 99 % odpovědí dorazí do sekundy, 99,9 % do cca 8 sekund. Nmap má výchozí timeout příliš krátký pro tento typ skenu. Někdy prostě člověk jenom tak náhodně něco navrhne a je rád, že to funguje ještě mnohem lépe, než původně doufal.
Repozitáře skenů
Hotové výsledky skenů jsou k dispozici ke stažení. Z principu ZMap tady nenajdete skeny, které jdou podle DNS jmen, ale procházení IPv4 prostoru. Důsledkem je, že nebudou vidět X.509 certifikáty strojů, které vyžadují SNI (server name indication).
Kdy získají „krabičky“ dost entropie?
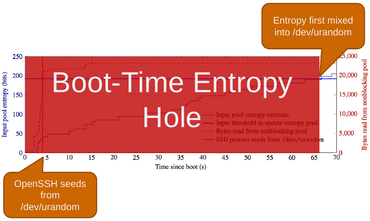
Před dvěma lety jsem psal, jak si různé „krabičky“ (hlavně domácí routříky) vygenerovaly lehce lousknutelné SSL a SSH klíče se slabou entropií kvůli chybějícímu RNG. Mnohem zajímavějším údajem je, jak dlouho trvá, než mají krabičky dost entropie na kvalitnější klíče: 65 sekund, viz graf ze ZMap prezentace níže.
Provětrání ECC klíčů
Protože dat není nikdy dost a RSA s DSA se už probíraly až příliš, vzal si jiný tým na starost rozebrání klíčového materiálu založeného na eliptických křivkách. Skenování SSH a TLS provedli ZMap-em. Další dva zdroje datasetů představovaly bitcoinový blockchain a rakouská e-ID karta.
HW generátory v smartkartách
V případě rakouských e-ID karet se sice nějaké klíče opakovaly, ale po jejich analýze se došlo k tomu, že patří i stejným subjektům, až na občasnou změnu v diakritice apod.
U Tchajwanských „občanských smartkaret“ se už ale ukázal problém s náhodným generátorem a 184 klíčů z více než dvou milionů bylo možné prolomit. Trochu zneklidňující je, že použitý čip AE45C1 měl jak EAL4+, tak FIPS 140–2 level 2 certifikaci. Nicméně to poukazuje na známý fakt, že RNG se testují velmi obtížně a testy odhalí jenom tragicky špatný RNG.
Analýza ECC implementací
Veřejný klíč u ECC se vypočítá jako Q = d * G, kde G je bod na křivce, označený jako „base point“ a sloužící jako generátor cyklické grupy křivky. Celé číslo d je prvek konečného tělesa a označuje privátní klíč. Veřejný klíč Q je také bod na křivce.
U ECC neexistuje paralela k stavu, který nastal u RSA, tedy že by se sdílelo jedno prvočíslo mezi klíči. ECC privátním klíčem je prvek z konečného tělesa. Tím pádem odpadá starost s „masovou faktorizací“ specializovaným algoritmem.
Způsob generování klíčů navádí k vyzkoušení malých hodnot d do 106, které mohly vzniknout slabým RNG. Autoři si hráli ještě víc a vyzkoušeli i hodnoty s nízkou Hammingovou váhou („málo jedničkových bitů“) a „magické hodnoty“ pro jeden specifický automorfizmus křivky secp256k1, která se používá v Bitcoinu. Tento automorfizmus umožňuje urychlit lámání klíče Pollardovou rho metodou. Žádný slabý klíč se takhle naštěstí nenašel.
Nedostatečná entropie ale pořád může způsobit, že se dá ECC privátní klíč lousknout, pokud se opakuje při podpisu per-message-nonce. To se již stalo v případě Android bitcoin pěněženek a dost lidí přišlo o Bitcoiny. Jedním způsobem, jak předejít této zranitelnosti u nových systémů, je použít deterministické schéma podpisů z RFC 6979.
Eliptické křivky v Bitcoinu
Bitcoinové adresy nemusí odpovídat žádnému veřejnému klíči, lze vytvořit transakce, které bitcoiny „zničí“ tím, že je nikdy nebude možné vybrat. Adres tohoto typu není málo, většinou vznikly chybou v implementaci nebo při testování. Několik zajímavých adres bylo nalezeno. Většina nich má na první pohled unikátní tvar, nebo má unikátní tvar HASH160 hodnota, ze které jsou odvozeny (pro aktuální obnosy se podívejte třeba na blockchain.info). Kódování bodů na křivce se řídí podle SEC1. V tabulce níže u posledních dvou veřejných klíčů tři tečky symbolizují 126 nulových hexa číslic.
| HASH160 | Bitcoin adresa | obnos v BTC |
|---|---|---|
| 0000000000000000000000000000000000000000 | 1111111111111111111114oLvT2 | 2.94896715 |
| 0000000000000000000000000000000000000001 | 11111111111111111111BZbvjr | 0.01000000 |
| 0000000000000000000000000000000000000002 | 11111111111111111111HeBAGj | 0.00000001 |
| 0000000000000000000000000000000000000003 | 11111111111111111111QekFQw | 0.00000001 |
| 0000000000000000000000000000000000000004 | 11111111111111111111UpYBrS | 0.00000001 |
| 0000000000000000000000000000000000000005 | 11111111111111111111g4hiWR | 0.00000001 |
| 0000000000000000000000000000000000000006 | 11111111111111111111jGyPM8 | 0.00000001 |
| 0000000000000000000000000000000000000007 | 11111111111111111111o9FmEC | 0.00000001 |
| 0000000000000000000000000000000000000008 | 11111111111111111111ufYVpS | 0.00000001 |
| aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa | 1GZQKjsC97yasxRj1wtYf5rC61AxpR1zmr | 0.00012000 |
| ffffffffffffffffffffffffffffffffffffffff | 1QLbz7JHiBTspS962RLKV8GndWFwi5j6Qr | 0.01000005 |
| 151 dalších ASCII HASH160 hodnot | 1.32340175 |
| veřejný klíč | validní kódování | na křivce | Bitcoin adresa | obnos v BTC |
|---|---|---|---|---|
| ∅ | ✗ | ✗ | 1HT7×U2Ngenf7D4yocz2SAcnNLW7rK8d4E | 68.80080003 |
| 00 | ✓ | ✓ | 1FYMZEHnszCHKTBdFZ2DLrUuk3dGwYKQxh | 2.08000002 |
| 000…0 | ✗ | ✗ | 13VmALKHkCdSN1JULkP6RqW3LcbpWvgryV | 0.00010000 |
| 040…0 | ✓ | ✗ | 16QaFeudRUt8NYy2yzjm3BMvG4×BbAsBFM | 0.01000000 |
Tabulka: Zajímavé Bitcoin adresy
Chtěl bych ale zdůraznit jednu velmi specifickou adresu – 1FYMZEHnszCHKTBdFZ2DLrUuk3dGwYKQxh – přísluší jí veřejný klíč reprezentující speciální bod na křivce – takzvaný bod v nekonečnu. Bod v nekonečnu představuje v grupě eliptické křivky element identity, je validním bodem na křivce.
K bodu v nekonečnu existuje triviální privátní klíč d=0. Ten je v SEC1 a SEC2, kde je křivka secp256k1 definována, zakázán. To ovšem neznamená, že to každá implementace kontroluje. Úpravou implementace lze podpis s tímto klíčem vygenerovat a v některých implementacích podpis projde ověřením bez „ohackování“. Další implementace nepočítají s bodem v nekonečnu vždy správně, ale kvůli zapeklitostem reprezentace bodů by stejně mohlo ověření projít.
Záludnosti NIST křivek
Již před nějakou dobou varoval Bruce Schneier před křivkami, které standardizoval NIST. Šlo především o konstanty, které byly použité v NIST křivkách. Nejprve jsem to pokládal za poněkud přehnané, ale jak si člověk ty standardy pročítá, pak to už tak šíleně nevypadá.
O backdooru v Dual-EC-DRBG se ví už dlouho, nyní si dokonce můžete zahrát na NSA, zvolit si své body a reverznout tento „RNG“. Bohužel je původní článek na blogu nyní rozbitý, ale podstatná textová část je v The Way Back Machine.
Parametry NIST křivek mají ale na křivky jiný vliv, než měly parametry na Dual-EC-DRBG. Bernstein a Lange vytvořili stránku SafeCurves, která hodnotí bezpečnost jednotlivých křivek. „Kompletní executive summary“ odpověď poskytuje sloupec „safe?“, další sloupce hodnotí jednotlivé vlastnosti křivky. Zde pouze připomenu, že NIST křivky a také secp256k1, použitá v Bitcoinu, pochází ze stejného dokumentu – SEC2. Slajdy od těch samých autorů poskytují o trochu víc detailů než SafeCurves stránka.
Poučením z krizového vývoje je: v nových projektech používat některou z „bezpečných“ křivek. Momentálně je hodně populární Curve25519, jsou k ní dostupné implementace a křivka není zatížena patenty. Je již podporovaná v OpenSSH a brzy bude dostupná i v TLS.
Bizarní útoky – twist, fault
Proti světu matematiky stojí svět reálně implementovaných algoritmů. Skutečné implementace trpí postranními kanály, někdy známé implementace bez postranních kanálů vůbec neexistují. Některé z nich jsou popsány i na webu SafeCurves.
U ECC existují dva typy algoritmů, jak počítat křivkové operace: „non-laddering“, která používá celý bod a „laddering“, která používá jen x souřadnici. Non-laddering implementace mají jednu hlavní nevýhodu. Pokud totiž autor nedá pozor, může počítat s bodem mimo křivku a prozradit tím tajné bity privátního klíče. Název tohoto útoku je „fault attack“. Naštěstí Bitcoin algoritmus nedovolí útočníkovi jednoduše zadávat jako vstup do algoritmu libovolné body. Jinak by stačilo asi 13 „fault signatures“ na dopočítání se k privátnímu Bitcoin klíči.
„Crypto is hard“
Kryptografie je těžká jak na pochopení, tak na implementování. Ale už jenom její nasazení v běžných protokolech jako TLS, SSH, OTR značně ztěžuje všudepřítomný odposlech. Je to sice jenom technické řešení, které samo o sobě úplně postačovat nebude, ale je to skvělý začátek.