Obsah
1. Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook (2. část)
2. Specifikace jednotlivých segmentů cesty
3. Šířka obrysů úseček a křivek
4. Styly ukončení křivek i úseček
5. Styl napojení křivek, úseček a uzavřených tvarů
6. Ukázka tří stylů napojení lomených čar
7. Čárkovaná, čerchovaná, tečkovaná atd. čára či segment cesty
8. Změna offsetu čárkovaných atd. čar
9. Vzorek čar při změně směrnice
10. Offset čar při změně směrnice
11. Simulace ručního kreslení na plátno
12. Úsečky na ručně nakresleném plátnu
13. Modifikace atributu roughness
14. Modifikace atributu bowing
15. Změna stylu šraf vyplněných 2D entit
16. Porovnání jmen atributů ve formátu SVG a knihovny ipycanvas
17. Repositář s demonstračními příklady
18. Odkazy na články o Jupyter Notebooku
19. Odkazy na články o formátu SVG
1. Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook (2. část)
Ve druhé části článku o knihovně ipycanvas navážeme na první část, ve které jsme si ukázali základní způsoby použití kreslicího plátna (canvasu). Dnes nejdříve dokončíme popis stylu vykreslení cest (path), resp. přesněji řečeno jednotlivých segmentů, z nichž se cesty skládají. Dále si ukážeme definici vzorku čáry (čárkovaná, čerchovaná, tečkovaná atd.) a nezapomeneme ani na možnost simulace ručního kreslení na plátno, což je varianta zpopularizovaná například serverem xkcd.
Připomeňme si na úvod, jak se knihovna ipycanvas importuje do Jupyter Notebooku, popř. do Jupyter Labu či JupyterLite. V případě JupyterLite je zapotřebí provést přípravné kroky:
# příprava knihovny určené pro instalaci # dalších knihoven do prostředí prohlížeče import micropip
Vlastní instalace v rámci webového prohlížeče:
# instalace knihovny ipycanvas do prostředí prohlížeče
await micropip.install("ipycanvas")
Další kroky jsou již stejné pro všechna tři prostředí:
# nyní je již možné provést import nově nainstalované knihovny import ipycanvas
Vytvoříme kreslicí plátno s nastavenými rozměry a popř. i měřítkem:
# vytvoření kreslicího plátna canvas = ipycanvas.Canvas(width=320, height=240)
Takto jednoduše se plátno vykreslí:
# vložení kreslicího plátna na plochu diáře canvas
Obrázek 1: Vykreslení prázdného plátna na plochu Jupyter Notebooku.
2. Specifikace jednotlivých segmentů cesty
Minule jsme si ukázali, jakým způsobem je možné jediným příkazem vytvořit cestu a dalším příkazem ji zobrazit. Cesta je v tomto případě popsána řetězcem obsahujícím jednotlivé příkazy typu „nakresli úsečku“, „nakresli segment Bézierovy kubiky“ atd.:
# Specifikace jednotlivých segmentů cesty
path1 = ipycanvas.Path2D('M80 80 A 45 45, 0, 0, 0, 125 125 L 125 80 Z')
Vykreslení může vypadat následovně (v tomto konkrétním případě cestu vyplníme) zelenou barvou:
# vykreslení čtveřice cest canvas.fill_style = 'green' canvas.fill(path1)
Existuje však i alternativní (a nutno říci, že i pomalejší) způsob, v němž je každý segment specifikován zvláštním příkazem. Definice cesty začíná zavoláním metody begin_path a končí metodou stroke nebo fill. Mezi těmito příkazy se zadávají jednotlivé segmenty, a to pomocí metod:
- move_to
- line_to
- arc
- arc_to
- ellipse
- quadratic_curve_to
- bezier_curve_to
- rect
- close_path
Podívejme se nyní na jednoduchý příklad použití:
# vykreslení několika úseček na plochu plátna
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
S výsledkem:
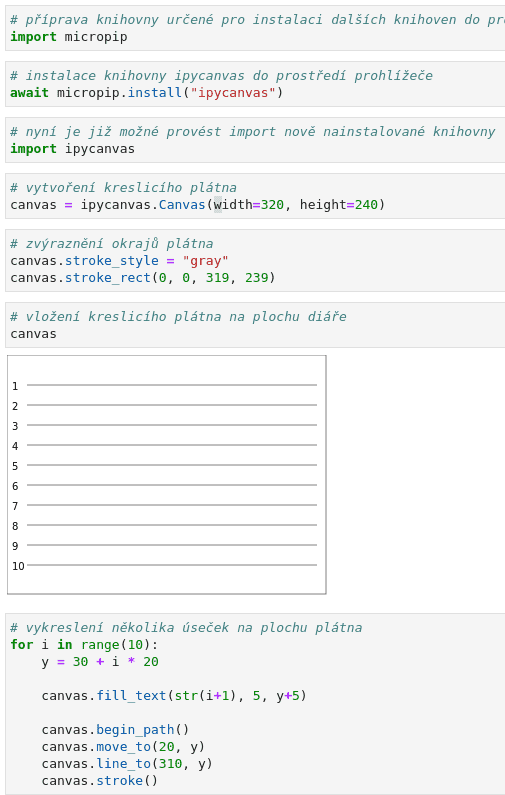
Obrázek 2: Deset cest, z nichž každá je tvořena jediným (liniovým) segmentem.
3. Šířka obrysů úseček a křivek
Implicitní šířka obrysů grafických objektů (a to jak otevřených, tak i uzavřených) je nastavena na jeden pixel. Změnou atributu nazvaného line_width je možné zadat libovolnou tloušťku kreslené stopy. Tato tloušťka je zadána v bezrozměrných jednotkách, jejich převod na pixely či délkové jednotky je proveden až ve chvíli vykreslování. Implicitně je jednotka rovna šířce jednoho pixelu, ale kresby v ipycanvasu je možné v případě potřeby zvětšovat či zmenšovat, takže tato rovnost nemusí vždy platit). Podívejme se nyní na demonstrační příklad, v němž se vykreslí deset úseček (resp. přesněji řečeno deset cest obsahujících jedinou úsečku), přičemž každá úsečka bude mít zadánu odlišnou tloušťku vykreslované stopy:
# vykreslení několika úseček na plochu plátna
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
Výsledek zobrazený v diáři by měl vypadat následovně:
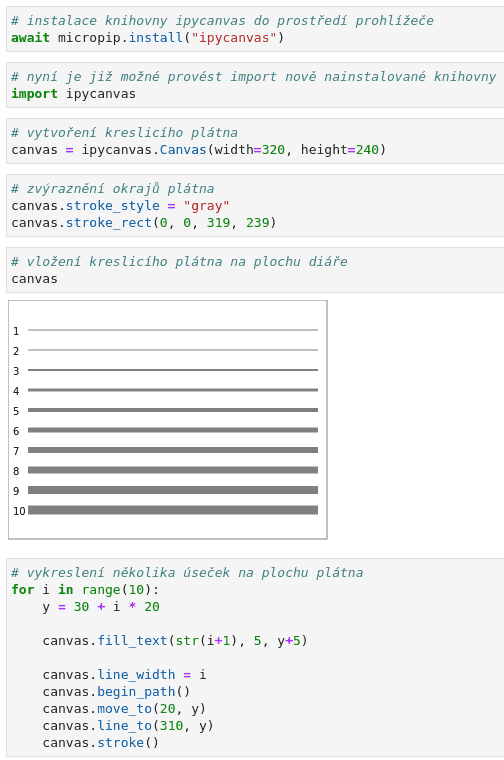
Obrázek 3: Deset úseček, každá s odlišně nastavenou tloušťkou stopy.
4. Styly ukončení křivek i úseček
U otevřených geometrických entit, tj. zejména u cest, úseček a lomených čar, je možné specifikovat i způsob jejich zakončení. Uzavřené tvary, tj. například kružnice, elipsy, obdélníky či obecné mnohoúhelníky, žádný jasně definovaný konec nemají, proto na ně nebude mít nastavení stylu ukončení žádný význam. Je možné specifikovat tři způsoby ukončení, které jsou specifikovány jako hodnota atributu line_cap:
| Hodnota | Význam |
|---|---|
| butt | ukončení cesty kolmým řezem v místě koncových bodů |
| round | ukončení cesty kruhovým obloukem (dochází k prodloužení tvaru) |
| square | ukončení cesty kolmým řezem vzdáleným od koncových bodů o 1/2 šířky cesty (dochází k prodloužení tvaru) |
Vliv všech tří způsobů zakončení na vizuální podobu úseček si opět ukážeme na demonstračních příkladech, ve kterých jsou vykresleny různě orientované úsečky zakončené jedním ze zadaných stylů. Pro vysvětlení rozdílu mezi stylem „butt“ a „square“ jsou vykresleny i osy všech úseček, tj. vlasové čáry, které začínají a končí přesně ve vrcholech „tlustých“ úseček.
Příklad použití hodnoty „butt“:
# zvýraznění začátku a konce úseček
canvas.line_width = 1
canvas.stroke_line(20, 20, 20, 220)
canvas.stroke_line(310, 20, 310, 220)
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "butt"
canvas.stroke_style = "black"
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
Výsledek:
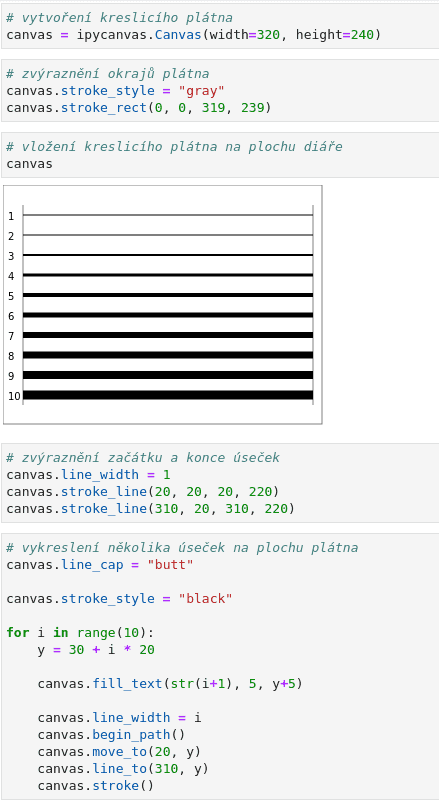
Obrázek 4: Zakončení úseček typu „butt“.
Použití hodnoty „square“:
# zvýraznění začátku a konce úseček
canvas.line_width = 1
canvas.stroke_line(20, 20, 20, 220)
canvas.stroke_line(310, 20, 310, 220)
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "square"
canvas.stroke_style = "black"
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()

Obrázek 5: Zakončení úseček typu „square“.
Použití hodnoty „round“:
# zvýraznění začátku a konce úseček
canvas.line_width = 1
canvas.stroke_line(20, 20, 20, 220)
canvas.stroke_line(310, 20, 310, 220)
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "round"
canvas.stroke_style = "black"
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
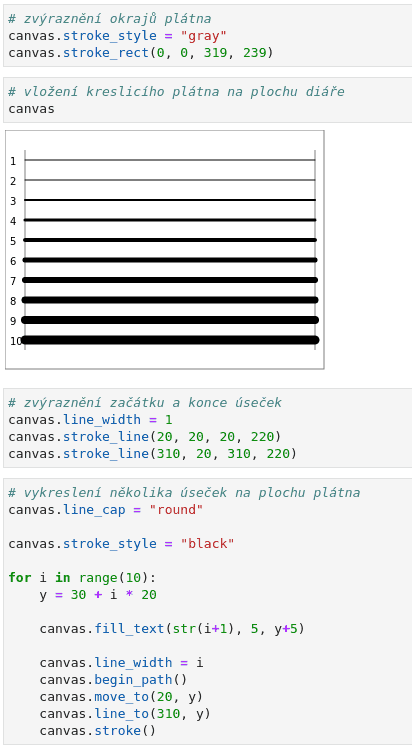
Obrázek 6: Zakončení úseček typu „round“.
5. Styl napojení křivek, úseček a uzavřených tvarů
V předchozí části tohoto seriálu jsme si ukázali, jakým způsobem se vytváří cesty a lomené čáry, popř. mnohoúhelníky. Všechny tyto geometrické tvary mají společnou jednu vlastnost: mohou být složeny z několika na sebe napojených úseček. Ve skutečnosti se samozřejmě nejedná o geometricky chápané úsečky, tj. o nekonečně tenké křivky, ale o úsečky se zadanou šířkou kreslené stopy (viz předchozí kapitoly a význam hodnoty atributu line_width).
Podívejme se, jak vypadá implicitní způsob napojení lomených čar, popř. cest:
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "butt"
canvas.stroke_style = "black"
for i in range(0,10,2):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y-12)
canvas.line_to(310, y)
canvas.line_to(20, y+12)
canvas.stroke()

Obrázek 7: Implicitní způsob napojení lomených čar nebo cest.
V ipycanvasu je možné specifikovat, jak má toto napojení vizuálně vypadat. Úsečky, při jejichž napojení se vytvoří jiný úhel než 180°, lze spojit třemi různými způsoby: buď jsou okraje úseček protaženy až do místa svého protnutí (vzniká tak „špička“), úsečky jsou zakončeny obloukem („kolenem“, nemění se tedy tloušťka cesty), nebo je možné zakončit napojení rovným okrajem tak, aby byla v co největší míře zachována tloušťka cesty. Přímo při vytváření obrázku se tedy můžeme rozhodnout, jak lomené čáry vykreslit. Vše je řízeno hodnotou atributu line_join, který může nabývat hodnot:
| Hodnota | Význam |
|---|---|
| miter | okraje úseček jsou protaženy do místa svého protnutí (vzniká tak „špička“) |
| round | je vykresleno obloukové „koleno“ (je zachována tloušťka cesty, resp. stopy) |
| bevel | napojení je ukončeno rovným okrajem tak, aby byla zachována tloušťka cesty či lomené čáry |
6. Ukázka tří stylů napojení lomených čar
Použití všech tří výše popsaných způsobů napojení je ukázáno v další trojici demonstračních příkladů. Povšimněte si, že není možné specifikovat napojení dvou samostatných úseček zadaných funkcí stroke_line. Vždy je nutné použít buď cestu či lomenou čáru, tj. příkaz begin_path následovaný segmenty cesty a ukončený příkazem end_path. Knihovna ipycanvas totiž každý grafický prvek vykresluje samostatně a na sobě ležící prvky jsou vykreslovány v pořadí, v jakém jsou volány.
Napojení obloukem:
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "butt"
canvas.line_join = "round"
canvas.stroke_style = "black"
for i in range(0,10,2):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y-12)
canvas.line_to(310, y)
canvas.line_to(20, y+12)
canvas.stroke()
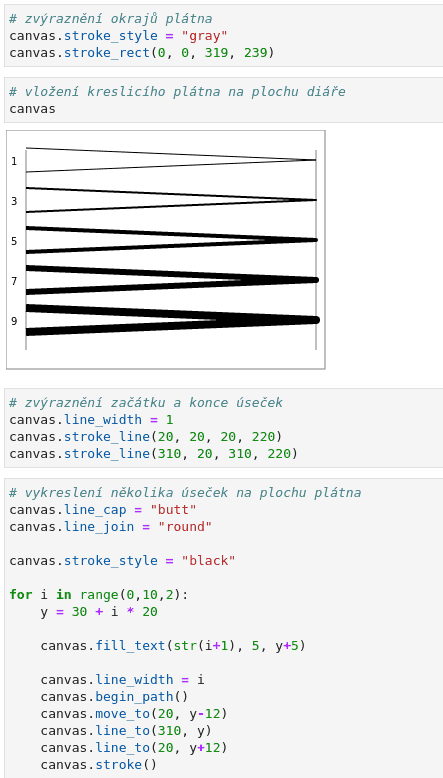
Obrázek 8: Napojení segmentů cesty obloukem.
Napojení rovným okrajem:
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "butt"
canvas.line_join = "bevel"
canvas.stroke_style = "black"
for i in range(0,10,2):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y-12)
canvas.line_to(310, y)
canvas.line_to(20, y+12)
canvas.stroke()

Obrázek 9: Napojení segmentů cesty rovným okrajem.
Protažení napojení do špičky:
# vykreslení několika úseček na plochu plátna
canvas.line_cap = "butt"
canvas.line_join = "miter"
canvas.stroke_style = "black"
for i in range(0,10,2):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_width = i
canvas.begin_path()
canvas.move_to(20, y-12)
canvas.line_to(310, y)
canvas.line_to(20, y+12)
canvas.stroke()
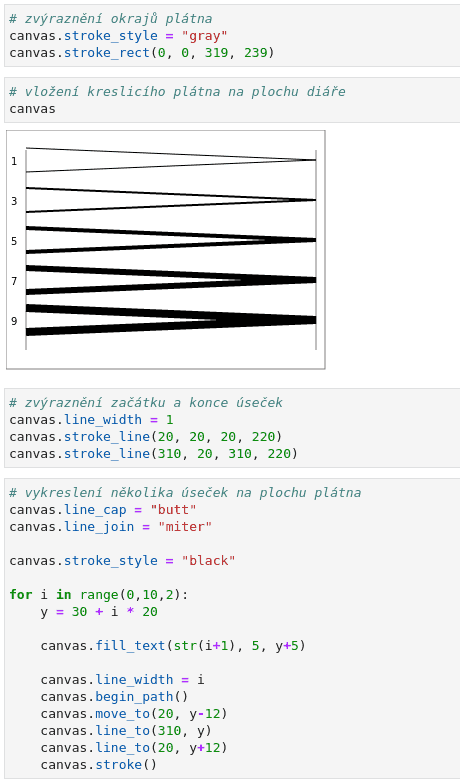
Obrázek 10: Napojení segmentů cesty jejich protažením do špičky.
7. Čárkovaná, čerchovaná, tečkovaná atd. čára či segment cesty
V kresbách vytvořených s využitím knihovny ipycanvas je však možné měnit i další vlastnosti křivek/cest a obrysů základních geometrických tvarů. Zejména se jedná o nastavení typu čáry. Nejprve si řekněme, jakým způsobem je možné měnit vzorek čáry, posléze si ukážeme i vliv parametru offset. Pro tento účel se používá atribut nazvaný set_line_dash, jehož hodnotou je seznam číselných hodnot oddělených čárkami. Hodnoty uložené na lichých místech udávají délku čárek, tj. vykreslovaných částí, hodnoty na sudých místech značí naopak délku mezer mezi čárkami. To znamená, že například zápis [10,1] vede k vytvoření úsečky, křivky či obrysu základního geometrického tvaru, které je složený vždy z čárky dlouhé deset jednotek za kterou následuje mezera o šířce jedné délkové jednotky.
Můžeme si vše otestovat na sadě deseti vzorků:
# vzorek použitý pro vykreslení čar
line_dashes = [
[5, 5],
[5, 10],
[10, 5],
[5, 10, 20],
[10, 20],
[20, 10],
[20, 20],
[1, 10],
[10, 1],
[1, 2, 3],
]
Které budou vybrány pro vykreslení deseti čar, resp. přesněji řečeno segmentů cesty:
# vykreslení několika úseček na plochu plátna
canvas.line_width = 2
canvas.stroke_style = "black"
for i in range(0,10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.set_line_dash(line_dashes[i])
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
Výsledek zobrazený na plátnu by měl vypadat následovně:
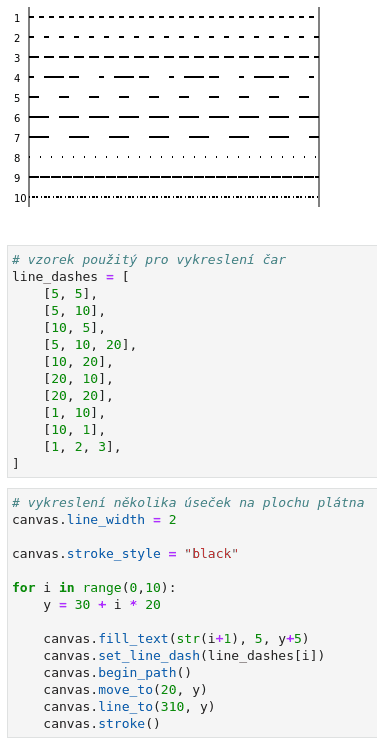
Obrázek 11: Deset segmentů cesty, každý používající odlišný vzorek.
8. Změna offsetu čárkovaných atd. čar
K atributu nastavovanému metodou set_line_dash se vztahuje ještě atribut line_dash_offset, jehož číselná hodnota udává posun začátku vykreslování stylu čáry od skutečného počátku tvaru (cesty, úsečky atd.). Pro jaké účely je možné offset použít? Zejména pro animaci (animovaný typ čáry vyvolává efekt pohybu, čehož je možné využít například pro „rozpohybování“ schématických nákresů), ale také pro zajištění, aby došlo ke korektnímu napojení čar na sebe, tj. že nedojde k napojení jednotlivých segmentů vykreslených mezerou.
Opět si ukažme demonstrační příklad:
# vzorek
line_dash = [20, 10]
# vykreslení několika úseček na plochu plátna
canvas.line_width = 2
# nastavení vzorku
canvas.set_line_dash(line_dash)
canvas.stroke_style = "black"
for i in range(0,10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_dash_offset = i*2
canvas.begin_path()
canvas.move_to(20, y)
canvas.line_to(310, y)
canvas.stroke()
Výsledek by měl vypadat následovně:

Obrázek 12: Změna offsetu u vzorků použitých pro vykreslení úseček.
9. Vzorek čar při změně směrnice
V případě nenulové tloušťky vykreslovaných segmentů a současně při použití vzorků musí knihovna ipycanvas zajistit, aby konce vzorků byly vždy kolmé na vrcholy segmentů. Toto chování si otestujeme na dalším demonstračním příkladu, v němž je vykresleno několik úsečkových segmentů, každý s odlišnou směrnicí:
# vzorek
line_dash = [20, 10]
# vykreslení několika úseček na plochu plátna
canvas.line_width = 5
# nastavení vzorku
canvas.set_line_dash(line_dash)
canvas.stroke_style = "black"
for i in range(0,10):
angle = i * 2 * math.pi/10.0
canvas.fill_text(str(i+1), 5, y+5)
canvas.begin_path()
canvas.move_to(160+10*math.sin(angle), 120+10*math.cos(angle))
canvas.line_to(160+100*math.sin(angle), 120+100*math.cos(angle))
canvas.stroke()
Výsledky:
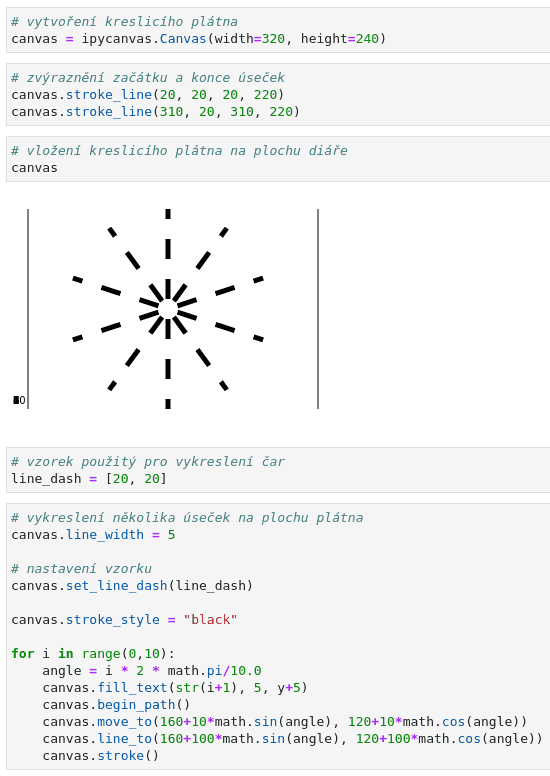
Obrázek 13: Vzorek čar pro segmenty s různou směrnicí.
10. Offset čar při změně směrnice
I offset vzorků by měl být nezávislý na směrnici segmentu. Jinými slovy – offset se počítá od začátku segmentu ve směru jeho směrnice a nikoli například ve směru horizontální či vertikální souřadné osy. Toto chování si opět ověříme na jednoduchém demonstračním příkladu:
# vzorek
line_dash = [20, 10]
# vykreslení několika úseček na plochu plátna
canvas.line_width = 5
# nastavení vzorku
canvas.set_line_dash(line_dash)
canvas.stroke_style = "black"
for i in range(0,20):
angle = i * 2 * math.pi/20.0
canvas.fill_text(str(i+1), 5, y+5)
canvas.line_dash_offset = i*2
canvas.begin_path()
canvas.move_to(160+10*math.sin(angle), 120+10*math.cos(angle))
canvas.line_to(160+100*math.sin(angle), 120+100*math.cos(angle))
canvas.stroke()
Výsledek by při vykreslení na plátno měl vypadat následovně:
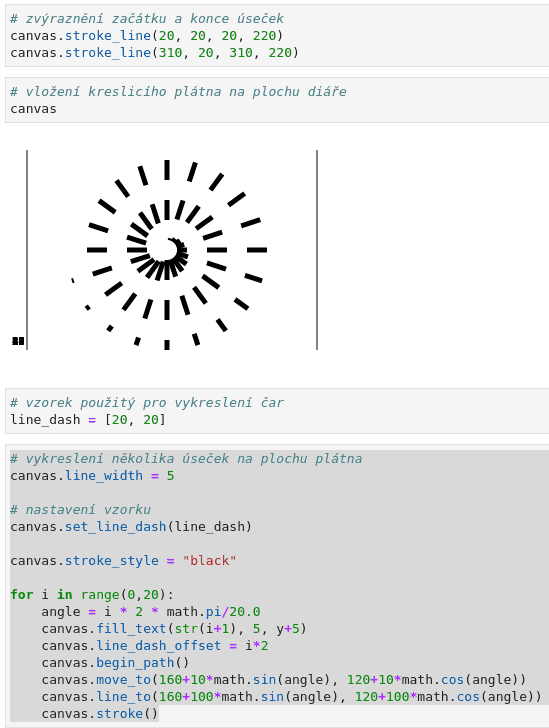
Obrázek 14: Offset čar při změně směrnice úsečkových segmentů.
11. Simulace ručního kreslení na plátno
Knihovna ipycanvas podporuje i simulaci ručního kreslení na plátno, což je styl zpopularizovaný například v xkcd. Přepnutí z naprosto přesného kreslení (se subpixelovou přesností) na ruční kreslení je snadné – namísto kreslicího plátna typu Canvas se zkonstruuje plátno typu RoughCanvas:
# vytvoření kreslicího plátna canvas = ipycanvas.RoughCanvas(width=320, height=240)
Toto plátno podporuje většinu metod a atributů klasického plátna, pouze styl vykreslování bude odlišný:
# zvýraznění začátku a konce úseček canvas.stroke_line(20, 20, 20, 220) canvas.stroke_line(310, 20, 310, 220)
Vykreslení takového plátna na plochu diáře je naprosto stejné, jako v případě objektu typu Canvas:
# vložení kreslicího plátna na plochu diáře canvas
12. Úsečky na ručně nakresleném plátnu
Podívejme se nejdříve, jak vypadají úsečky na ručně nakresleném plátnu (resp. na jeho simulaci). Úsečky je v současné verzi knihovny ipycanvas nutné vykreslit s využitím metody stroke_line a nikoli jako cestu:
# vykreslení několika úseček na plochu plátna
for i in range(10):
y = 30 + i * 20
canvas.fill_text(str(i+1), 5, y+5)
canvas.stroke_line(20, y, 310, y)
Z výsledného screenshotu je patrné, že každá úsečka je vykreslena několikrát a to navíc rozstřeseně, jak je to u ručního kreslení (ne rýsování) poměrně běžné. Navíc je každá úsečka vykreslena odlišně, takže výsledek nepůsobí strojově:
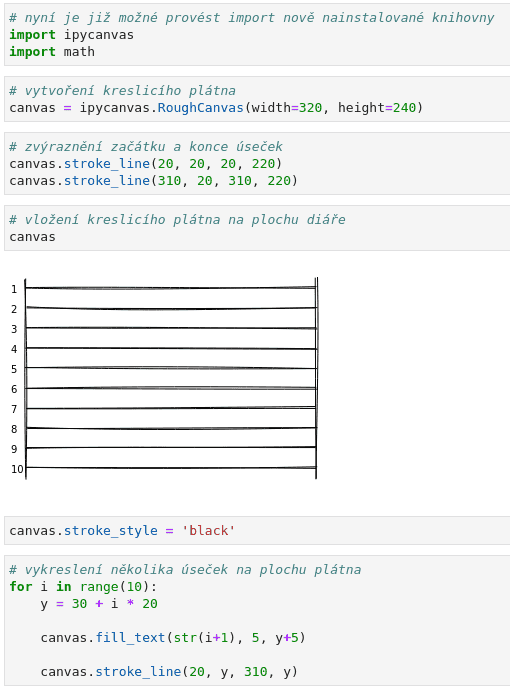
Obrázek 15: Simulace ručně nakreslených úseček..
13. Modifikace atributu roughness
Jeden z parametrů, kterým se řídí simulátor ručního kreslení je parametr nazvaný roughness. Ten určuje nepřesnost napojení na koncové body úsečky i vzdálenost jednotlivých tahů pera. Vyzkoušet si můžeme, jak bude vypadat deset čar, každá s různým nastavením tohoto atributu v rozsahu od nuly do devíti:
# vykreslení několika úseček na plochu plátna
for i in range(10):
y = 30 + i * 20
canvas.roughness = i
canvas.fill_text(str(i+1), 5, y+5)
canvas.stroke_line(20, y, 310, y)
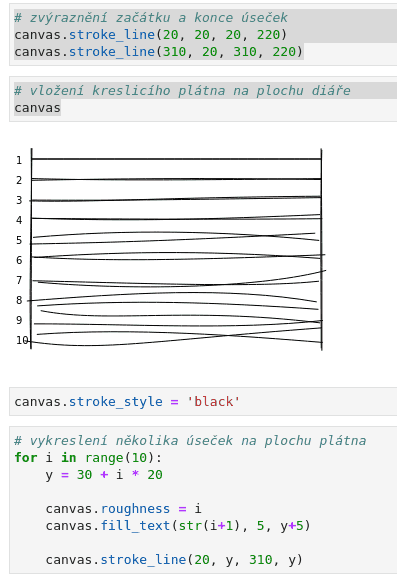
Obrázek 16: Deset čar, každá s různým nastavením atributu roughness v rozsahu od nuly do devíti.
14. Modifikace atributu bowing
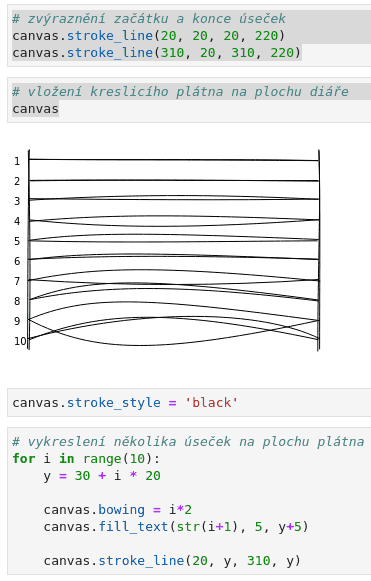
Druhým parametrem, který ovlivňuje simulátor ručního kreslení, je atribut nazvaný bowing. Jak již název tohoto atributu naznačuje, ovlivňuje „rozmáchlost“ nakreslených křivek. Vše je osvětleno v následujícím demonstračním příkladu:
# vykreslení několika úseček na plochu plátna
for i in range(10):
y = 30 + i * 20
canvas.bowing = i*2
canvas.fill_text(str(i+1), 5, y+5)
canvas.stroke_line(20, y, 310, y)
Výsledek může vypadat takto:
 *** image ***
*** image ***
Obrázek 17: Deset čar, každá s různým nastavením atributu bowing v rozsahu od nuly do osmnácti.
15. Změna stylu šraf vyplněných 2D entit
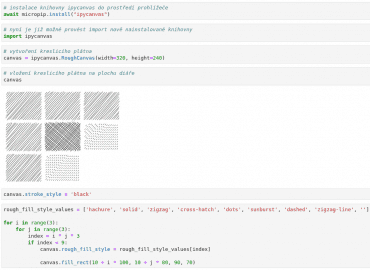
Posledním atributem, o němž se v dnešním článku zmíníme, je atribut nazvaný rough_fill_style. Tímto atributem se určuje vzorek vyplněných 2D entit ve chvíli, kdy je simulováno ruční kreslení. V tomto případě totiž není výplň dokonalá, ale snaží se napodobit kreslení fixou nebo propiskou. Existuje celkem osm typů výplňových vzorků, z nichž všechny jsou použity v dnešním posledním demonstračním příkladu:
rough_fill_style_values = ['hachure', 'solid', 'zigzag', 'cross-hatch', 'dots', 'sunburst', 'dashed', 'zigzag-line', '']
for i in range(3):
for j in range(3):
index = i * j * 3
if index < 9:
canvas.rough_fill_style = rough_fill_style_values[index]
canvas.fill_rect(10 + i * 100, 10 + j * 80, 90, 70)
Výsledky:
 *** image ***
*** image ***
Obrázek 18: Změna stylu šraf vyplněných 2D entit.
16. Porovnání jmen atributů ve formátu SVG a knihovny ipycanvas
Mnoho vlastností a stylů, které je možné specifikovat v knihovně ipycanvas, má svoji obdobu i ve formátu SVG. Pro snazší porovnání jsou tyto atributy vypsány v následující tabulce:
| Atribut v ipycanvas | Odpovídající atribut v SVG |
|---|---|
| line_width | stroke-width |
| stroke_style | stroke |
| fill_style | fill |
| global_alpha | opacity, stroke-opacity, fill-opacity |
| text_align | text-align |
| text_baseline | alignment-baseline |
| line_cap | stroke-linecap |
| line_join | stroke-linejoin |
| set_line_dash | stroke-dasharray |
| line_dash_offset | stroke-dashoffset |
| roughness | × |
| bowing | × |
17. Repositář s demonstračními příklady
Všechny demonstrační příklady (resp. přesněji řečeno diáře), s nimiž jsme se seznámili minule i v předchozích kapitolách, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/jupyter-notebook-examples/). Poslední verze souborů s diáři naleznete pod odkazy uvedenými v tabulce pod tímto odstavcem. Diář by se měl otevřít přímo v rámci stránky GitHubu:
18. Odkazy na články o Jupyter Notebooku
Se samotným nástrojem Jupyter Notebook jsme se již na stránkách Rootu setkali několikrát, a to konkrétně v následujících článcích (přidán je i prozatím předposlední článek o projektu JupyterLite):
- Jupyter Notebook – nástroj pro programátory, výzkumníky i lektory
https://www.root.cz/clanky/jupyter-notebook-nastroj-pro-programatory-vyzkumniky-i-lektory/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib (dokončení)
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib-dokonceni/ - Jupyter Notebook – operace s rastrovými obrázky a UML diagramy, literate programming
https://www.root.cz/clanky/jupyter-notebook-operace-s-rastrovymi-obrazky-a-uml-diagramy-literate-programming/ - Interpret programovacího jazyka Clojure integrovaný do Jupyter Notebooku
https://www.root.cz/clanky/interpret-programovaciho-jazyka-clojure-integrovany-do-jupyter-notebooku/ - Calysto Hy: integrace programovacího jazyka Hy s Jupyter Notebookem
https://www.root.cz/clanky/calysto-hy-integrace-programovaciho-jazyka-hy-s-jupyter-notebookem/ - JupyterLite: nová alternativní architektura Jupyter Notebooku
https://www.root.cz/clanky/jupyterlite-nova-alternativni-architektura-jupyter-notebooku/ - Interaktivní ovládací prvky v Jupyter Notebooku
https://www.root.cz/clanky/interaktivni-ovladaci-prvky-v-jupyter-notebooku/ - Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook
https://www.root.cz/clanky/knihovna-ipycanvas-aneb-kreslici-platno-pro-jupyter-notebook/
19. Odkazy na články o formátu SVG
Některé vlastnosti knihovny ipycanvas jsou odvozeny od vlastností vektorového formátu SVG. Týká se to například způsobu deklarace cest, řešení vyplnění cest, jejichž hrany se protínají atd. Z tohoto důvodu jsou pro úplnost v této příloze doplněny odkazy na již vydané články o tomto velmi užitečném formátu:
- Vektorový grafický formát SVG
https://www.root.cz/clanky/vektorovy-graficky-format-svg/ - Cesty v souborech typu Scalable Vector Graphics
https://www.root.cz/clanky/cesty-v-souborech-typu-scalable-vector-graphics/ - Scalable Vector Graphics a základní geometrické tvary
https://www.root.cz/clanky/scalable-vector-graphics-a-zakladni-geometricke-tvary/ - Vlastnosti cest a základních geometrických tvarů v SVG
https://www.root.cz/clanky/vlastnosti-cest-a-zakladnich-geometrickych-tvaru-v-svg/ - SVG – styly výplní a značky připojované ke křivkám
https://www.root.cz/clanky/svg-styly-vyplni-a-znacky-pripojovane-ke-krivkam/ - Gradientní výplně a textové objekty v SVG
https://www.root.cz/clanky/gradientni-vyplne-a-textove-objekty-v-svg/ - Grafický formát SVG a animace
https://www.root.cz/clanky/graficky-format-svg-a-animace/ - Pokročilejší animace ve formátu SVG
https://www.root.cz/clanky/pokrocilejsi-animace-ve-formatu-svg/ - Podpora skriptování v grafickém formátu SVG
https://www.root.cz/clanky/podpora-skriptovani-v-grafickem-formatu-svg/ - Zpracování událostí při skriptování výkresů SVG
https://www.root.cz/clanky/zpracovani-udalosti-pri-skriptovani-vykresu-svg/
20. Odkazy na Internetu
- ipycanvas: Interactive Canvas in Jupyter
https://ipycanvas.readthedocs.io/en/latest/index.html - ipycanvas na PyPi
https://pypi.org/project/ipycanvas/ - Canvas API
https://developer.mozilla.org/en-US/docs/Web/API/Canvas_API - ipycanvas usage
https://ipycanvas.readthedocs.io/en/latest/usage.html - ipywidgets (dokumentace)
https://ipywidgets.readthedocs.io/en/latest/ - Interactive Widgets
https://github.com/jupyter-widgets/ipywidgets/blob/master/docs/source/examples/Index.ipynb - Notebook interface
https://en.wikipedia.org/wiki/Notebook_interface - Jypyter: open source, interactive data science and scientific computing across over 40 programming languages
https://jupyter.org/ - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - showcase example code: xkcd.py
https://matplotlib.org/xkcd/examples/showcase/xkcd.html - Customising contour plots in matplotlib
https://philbull.wordpress.com/2012/12/27/customising-contour-plots-in-matplotlib/ - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - The IPython Notebook
http://ipython.org/notebook.html - nbviewer: a simple way to share Jupyter Notebooks
https://nbviewer.jupyter.org/ - Back to the Future: Lisp as a Base for a Statistical Computing System
https://www.stat.auckland.ac.nz/~ihaka/downloads/Compstat-2008.pdf - gg4clj: a simple wrapper for using R's ggplot2 in Clojure and Gorilla REPL
https://github.com/JonyEpsilon/gg4clj - Analemma: a Clojure-based SVG DSL and charting library
http://liebke.github.io/analemma/ - Clojupyter: a Jupyter kernel for Clojure
https://github.com/roryk/clojupyter - Incanter is a Clojure-based, R-like platform for statistical computing and graphics.
http://incanter.org/ - Evolution of incanter (Gource Visualization)
https://www.youtube.com/watch?v=TVfL5nPELr4 - Questions tagged [incanter] (na Stack Overflow)
https://stackoverflow.com/questions/tagged/incanter?sort=active - Data Sorcery with Clojure
https://data-sorcery.org/contents/ - What is REPL?
https://pythonprogramminglanguage.com/repl/ - What is a REPL?
https://codewith.mu/en/tutorials/1.0/repl - Programming at the REPL: Introduction
https://clojure.org/guides/repl/introduction - What is REPL? (Quora)
https://www.quora.com/What-is-REPL - Gorilla REPL: interaktivní prostředí pro programovací jazyk Clojure
https://www.root.cz/clanky/gorilla-repl-interaktivni-prostredi-pro-programovaci-jazyk-clojure/ - R Markdown: The Definitive Guide
https://bookdown.org/yihui/rmarkdown/ - Single-page application
https://en.wikipedia.org/wiki/Single-page_application - Video streaming in the Jupyter Notebook
https://towardsdatascience.com/video-streaming-in-the-jupyter-notebook-635bc5809e85 - How IPython and Jupyter Notebook work
https://jupyter.readthedocs.io/en/latest/architecture/how_jupyter_ipython_work.html - Jupyter kernels
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels - Keras: The Python Deep Learning library
https://keras.io/ - TensorFlow
https://www.tensorflow.org/ - PyTorch
https://pytorch.org/ - Seriál Torch: framework pro strojové učení
https://www.root.cz/serialy/torch-framework-pro-strojove-uceni/ - Scikit-learn
https://scikit-learn.org/stable/ - Java Interop (Clojure)
https://clojure.org/reference/java_interop - Obrazy s balíčky Jupyter Notebooku pro Docker
https://hub.docker.com/u/jupyter/#! - Správce balíčků Conda (dokumentace)
https://docs.conda.io/en/latest/ - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02 - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Embedding Matplotlib Animations in Jupyter Notebooks
http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/ - Literate programing, Kolokviální práce Pavla Starého
https://www.fi.muni.cz/usr/jkucera/pv109/starylp.htm - PlantUML (home page)
http://plantuml.sourceforge.net/ - PlantUML (download page)
http://sourceforge.net/projects/plantuml/files/plantuml.jar/download - PlantUML (Language Reference Guide)
http://plantuml.sourceforge.net/PlantUML_Language_Reference_Guide.pdf - Plain-text diagrams take shape in Asciidoctor!
http://asciidoctor.org/news/2014/02/18/plain-text-diagrams-in-asciidoctor/ - Graphviz – Graph Visualization Software
http://www.graphviz.org/ - graphviz (Manual Page)
http://www.root.cz/man/7/graphviz/ - PIL: The friendly PIL fork (home page)
https://python-pillow.org/ - Python Imaging Library (PIL), (home page)
http://www.pythonware.com/products/pil/ - PIL 1.1.6 na PyPi
https://pypi.org/project/PIL/ - Pillow 5.2.0 na PyPi
https://pypi.org/project/Pillow/ - Python Imaging Library na Wikipedii
https://en.wikipedia.org/wiki/Python_Imaging_Library - Pillow na GitHubu
https://github.com/python-pillow/Pillow - Pillow – dokumentace na readthedocs.io
http://pillow.readthedocs.io/en/5.2.x/ - How to use Pillow, a fork of PIL
https://www.pythonforbeginners.com/gui/how-to-use-pillow - await in Python
https://docs.python.org/3/reference/expressions.html#await






































