Obsah
1. Kouzlo datových typů Decimal32, Decimal64 a Decimal128
2. Obecná reprezentace hodnot s plovoucí řádovou čárkou
3. Poněkud nepřehledný svět formátů čísel s plovoucí řádovou čárkou
4. Varianta IEEE 754 single – hodnoty s jednoduchou přesností
5. Varianta IEEE 754 double – hodnoty s dvojnásobnou přesností
6. Denormalizovaná čísla, hodnoty typu NaN a nekonečna
7. Omezení typů single i double
8. Klasický problém: konečná či nekonečná smyčka?
9. Tisk numerických hodnot single a double v hexadecimálním formátu
10. Interní struktura hodnot typu single a double
11. Dekódování numerických hodnot uložených ve formátu single a double
12. Formáty Decimal32, Decimal64 a Decimal128
14. Počítaná smyčka s krokem 0,1 a koncovou hodnotou 1,0 realizovaná s využitím typů Decimal
15. Interní struktura formátu Decimal32
16. Dekódování hodnoty typu Decimal32
17. Rychlost výpočtů: porovnání Decimal se single a double
19. Repositář s demonstračními příklady
1. Kouzlo datových typů Decimal32, Decimal64 a Decimal128
Reprezentace numerických hodnot v paměti počítače s využitím plovoucí řádové čárky se používá již 70 let, protože prvním počítačem podporujících výpočty s těmito hodnotami na úrovni hardware byl mainframe IBM 704 pocházející z roku 1954. Od té do doby vzniklo minimálně několik desítek, ale mnohem pravděpodobněji spíše stovek různých variant uložení čísel. Většinou však mají společný základ: číselná hodnota je uložena jako trojice (znaménko, mantisa, exponent), přičemž se liší jak bitové šířky mantisy a exponentu, tak i základ (báze) pro exponent, forma reprezentace nekonečen a různých „nečísel“ NaN, to, jak jsou číslice uloženy (binárně, BCD, …) apod.
Původní norma IEEE 754 z roku 1985, která definovala mj. i formáty nazvané single (precision) a double (precision), byla brzy implementována v hardware (jednalo se například o matematický koprocesor 8087 atd.) a postupně se stala skutečně celosvětově dodržovaným standardem. Ovšem formáty single a double se nehodí pro bankovní a další finanční aplikace a z tohoto důvodu se v pozdější variantě normy IEEE 754 objevily i datové typy Decimal (32bitový, 64bitový a 128bitový). A právě těmito datovými typy se budeme dnes zabývat, mj. i proto, že byly oficiálně přijaty i do tak konzervativního programovacího jazyka, jakým je C (a podporuje je například GCC).

Obrázek 1: Sálový počítač IBM-704, který na úrovni hardware podporoval výpočty s hodnotami s plovoucí řádovou čárkou (tečkou).
2. Obecná reprezentace hodnot s plovoucí řádovou čárkou
Všechny dále popsané formáty (reprezentace) numerických hodno používají systém takzvané plovoucí řádové čárky (anglicky floating point, protože se v angličtině namísto čárky používá tečka). Systém plovoucí řádové čárky je založen na tom, že vybraná konečná podmnožina reálných čísel může být vyjádřena vztahem:
XFP = (-1)s × bexp-bias × m
přičemž význam jednotlivých symbolů ve vztahu je následující:
- XFP značí reprezentovanou numerickou hodnotu z podmnožiny racionálních čísel (ta je zase podmnožinou čísel reálných). Díky vyhrazeným (speciálním) hodnotám je většinou možné rozlišit kladnou a zápornou nulu i kladné a záporné nekonečno, což je jeden z důležitých rozdílů oproti způsobu reprezentace celých čísel. Také se většinou může nějakým vhodným způsobem uložit nečíselná hodnota: NaN – (Not a Number), která je výsledkem některých matematicky nedefinovaných operací, například 0/0 nebo 00.
- b je báze, někdy také nazývaná radix, u normy IEEE 754 to byla původně dvojka (formáty single, double i extended), protože výpočty s bází dvě jsou pro číslicové obvody nejjednodušší. V minulosti se však používaly i jiné báze, například 8, 16 nebo i 10. S bází 16 se dnes již prakticky nesetkáme, o to relevantnější je však v dnešním článku báze nastavená na desítku.
- exp je vždy kladná hodnota exponentu posunutého o hodnotu bias
- bias je hodnota, díky které je uložený exponent vždy kladný. Tato hodnota se většinou volí dle vztahu:
bias=2eb-1-1, kde eb je počet bitů vyhrazených pro exponent. Pro specifické účely je však možné zvolit i jinou hodnotu. - m je mantisa, která je u formátů dle normy IEEE 754 vždy kladná (protože znaménko je uloženo zvlášť).
- s je znaménkový bit nabývající hodnoty 0 nebo 1. Pokud je tento bit nulový, je reprezentovaná hodnota XFP kladná, v opačném případě se jedná o zápornou hodnotu. Vzhledem k tomu, že je jeden bit vyhrazen na uložení znaménka, je možné rozlišit kladnou a zápornou nulu, kladné i záporné nekonečno atd. (některé systémy bit znaménka používají v negované podobě, to však na principu nic nemění).

Obrázek 2: První čip, který používal formát definovaný v IEEE 754 – Intel 8087.
Zdroj: Wikipedia, Autor: Dirk Oppelt
3. Poněkud nepřehledný svět formátů čísel s plovoucí řádovou čárkou
V následující tabulce jsou pro zajímavost vypsány některé nejčastěji používané či nějakým způsobem (z hlediska historie atd.) zajímavé formáty hodnot s plovoucí řádovou čárkou. Povšimněte si především toho, že báze je většinou dvojková, pouze v některých případech desítková či šestnáctková. Dnes nás budou nejvíce zajímat formáty definované v normě IEEE 754 ve variantě z roku 2008, tedy formáty s bází 2 a 10:
| Počítač/norma/systém | Šířka (b) | Báze | Exponent (b) | Mantisa (b) |
|---|---|---|---|---|
| „microfloat“ | 8 | 2 | 4 | 3+1 |
| IEEE 754 half | 16 | 2 | 5 | 10+1 |
| IEEE 754 single | 32 | 2 | 8 | 23+1 |
| IEEE 754 double | 64 | 2 | 11 | 52+1 |
| IEEE 754 double extended | 80 | 2 | 15 | 64 |
| IEEE 754 quadruple | 128 | 2 | 15 | 112+1 |
| IEEE 754 octuple | 256 | 2 | 19 | 236+1 |
| IEEE 754 decimal32 | 32 | 10 | variabilní | 20 (variabilní) |
| IEEE 754 decimal64 | 64 | 10 | variabilní | 50 (variabilní) |
| IEEE 754 decimal128 | 128 | 10 | variabilní | 110 (variabilní) |
| IBM řady 7×x | 36 | 2 | 8 | 27 |
| IBM 360 single | 32 | 16 | 7 | 24 |
| IBM 360 double | 64 | 16 | 7 | 56 |
| HP 3000 single | 32 | 2 | 9 | 22 |
| HP 3000 double | 64 | 2 | 9 | 54 |
| CDC 6000, 6600 | 60 | 2 | 11 | 48+1 |
| Cray-1 | 64 | 2 | 15 | 48 |
| Strela | 43 | 2 | 7 | 35 |
| Apple II | 40 | 2 | 8 | 31+1 |
| ZX Spectrum | 40 | 2 | 8 | 31+1 |
| Atari (FP rutiny) | 48 | 10 | 7 | 40 |
| Turbo Pascal real | 48 | 2 | 8 | 39 |
Druhá verze normy IEEE 754–2008 již obsahuje specifikaci většího množství formátů; navíc došlo k přejmenování typů single a double na binary32 a binary64 (což nikdo nepoužívá :-):
| Oficiální jméno | Základní | Známo též jako | Znaménko | Exponent | Mantisa | Celkem | Decimálních číslic |
|---|---|---|---|---|---|---|---|
| binary16 | × | half precision | 1b | 5b | 10b | 16b | cca 3,3 |
| binary32 | ✓ | single precision/float | 1b | 8b | 23b | 32b | cca 7,2 |
| binary64 | ✓ | double precision | 1b | 11b | 52b | 64b | cca 15,9 |
| binary128 | ✓ | quadruple precision | 1b | 15b | 112b | 128b | cca 34,0 |
| binary256 | × | octuple precision | 1b | 19b | 236b | 256b | cca 71,3 |
4. Varianta IEEE 754 single – hodnoty s jednoduchou přesností
V dalším textu budeme porovnávat základní vlastnosti typů Decimal s původními formáty float/single a double, takže ještě na chvíli u těchto formátů zůstaneme.
Formát numerických hodnot, který je v programovacích jazycích označován buď jako single či float, je charakteristický tím, že se pro uložení numerické hodnoty používá třiceti dvou bitů (4 byty), což pro mnoho aplikací představuje velmi dobrý poměr mezi rozsahem hodnot, přesností a nároky na úložný prostor, nehledě na to, že mnoho architektur stále používá 32bitové sběrnice (klasické ARMy, …). Oněch 32 bitů je rozděleno do třech částí. V první části (představované nejvyšším bitem) je uloženo znaménko, následuje osm bitů pro uložení posunutého exponentu a za nimi je zbývajících 23 bitů, které slouží pro uložení mantisy. Celé třiceti dvoubitové slovo s FP hodnotou tedy vypadá následovně:
| bit | 31 | 30 29 … 24 23 | 22 21 … 3 2 1 0 |
|---|---|---|---|
| význam | s | exponent (8 bitů) | mantisa (23 bitů) |
Exponent je přitom posunutý o hodnotu bias, která je nastavena na 127, protože je použit výše uvedený vztah:
bias=2eb-1-1
a po dosazení eb=8 (bitů) dostaneme:
bias=28–1-1=27-1=128–1=127
Vzorec pro vyjádření reálné hodnoty vypadá následovně:
Xsingle=(-1)s × 2exp-127 × m
Uložení znaménka číselné hodnoty je jednoduché: pokud je znaménkový bit nastavený na jedničku, jedná se o zápornou hodnotu, v opačném případě jde o hodnotu kladnou. Exponent je uložený v takzvané posunuté formě, tj. jako binárně zakódované celé číslo v rozsahu 0..255. Po vyjádření neposunutého exponentu dostáváme rozsah –127..128, obě krajní hodnoty jsou však použity pro speciální účely, proto dostáváme rozsah exponentů pouze –126..127 pro normalizovaná čísla (krajními hodnotami jsou takové exponenty, které mají všechny bity buď jedničkové nebo naopak nulové).

Obrázek 3: Matematický koprocesor vyráběný firmou Weitek. Tento konkrétní čip je určen pro procesory řady 486 (není kompatibilní s 80487), ovšem Weitek vyráběl koprocesory pro celou řadu dalších architektur, od 8087 přes Motoroly řady 68k až po (micro)SPARC.
Ještě si však musíme říci, jakým způsobem je uložena mantisa. Ta je totiž většinou (až na velmi malá čísla) normalizovaná, což znamená, že se do mantisy ukládají pouze hodnoty v rozsahu <1,0;2,0-ε>. Vzhledem k tomu, že první bit umístěný před binární tečkou je u tohoto rozsahu vždy nastavený na jedničku, není ho zapotřebí ukládat, což znamená, že ušetříme jeden bit z třiceti dvoubitového slova (viz úvodní kapitolu). Pro normalizované hodnoty platí následující vztah:
Xsingle=(-1)s × 2exp-127(1.M)2
kde M je hodnota bitového vektoru mantisy, tj.:
M=m22-1+m21-2+m20-3+…+m1-22+m0-23
Rozsah hodnot, které je možné reprezentovat ve formátu jednoduché přesnosti v normalizovaném tvaru je –3,4×1038 až 3,4×1038. Nejnižší reprezentovatelná (normalizovaná) hodnota je rovna 1,17549×10-38, denormalizovaná pak 1,40129×10-45. Jak jsme k těmto hodnotám došli? Zkuste se podívat na následující vztahy:
| hexadecimální hodnota | výpočet FP | dekadický výsledek | normalizováno |
|---|---|---|---|
| 0×00000001 | 2-126×2-23 | 1,40129×10-45 | ne |
| 0×00800000 | 2-126 | 1,17549×10-38 | ano |
| 0×7F7FFFFF | (2–2-23)×2127 | 3,4×1038 | ano |
5. Varianta IEEE 754 double – hodnoty s dvojnásobnou přesností
Formát s dvojitou přesností (double), který je definovaný taktéž původní normou IEEE 754, se v mnoha ohledech podobá formátu s jednoduchou přesností (single), pouze se zdvojnásobil celkový počet bitů, ve kterých je hodnota uložena, tj. místo 32 bitů se používá 64 bitů. Právě to je hlavní příčinou toho, proč se tento formát nazývá double, ve skutečnosti je totiž přesnost více než dvojnásobná. 64 bitů alokovaných pro FP hodnotu je v tomto případě rozděleno následujícím způsobem:
- 1 bit pro znaménko
- 11 bitů pro exponent
- 52 bitů pro mantisu
Bitově vypadá rozdělení následovně:
| bit | 63 | 62 … 52 | 51 … 0 |
|---|---|---|---|
| význam | s | exponent (11 bitů) | mantisa (52 bitů) |
Exponent je v tomto případě posunutý o hodnotu bias=2047 a vzorec pro výpočet reálné hodnoty vypadá takto:
Xdouble=(-1)s × 2exp-2047 × m
Přičemž hodnotu mantisy je možné pro normalizované hodnoty získat pomocí vztahu:
m=1+m51-1+m50-2+m49-3+…+m0-52
(mx představuje x-tý bit mantisy)
Rozsah hodnot ukládaných ve dvojité přesnosti je –1,7×10308..1,7×10308, nejmenší možná nenulová hodnota je rovna 2,2×10-308.
6. Denormalizovaná čísla, hodnoty typu NaN a nekonečna
Ještě si musíme vysvětlit význam těch exponentů, které mají minimální a maximální hodnotu, tj. jsou buď nulové, nebo mají v případě formátu single hodnotu 255 (obě samozřejmě před posunem). Vše je přehledně uvedeno v následující tabulce:
| s-bit | exponent | mantisa | význam | šestnáctkově |
|---|---|---|---|---|
| 0 | 0<e<255 | >0 | normalizované kladné číslo | |
| 1 | 0<e<255 | >0 | normalizované záporné číslo | |
| 0 | 0 | >0 | denormalizované kladné číslo | |
| 1 | 0 | >0 | denormalizované záporné číslo | |
| 0 | 0 | 0 | kladná nula | 0×00000000 |
| 1 | 0 | 0 | záporná nula | 0×80000000 |
| 0 | 255 | 0 | kladné nekonečno | 0×7F800000 |
| 1 | 255 | 0 | záporné nekonečno | 0×FF800000 |
| 0 | 255 | >0 | NaN – not a number | |
| 1 | 255 | >0 | NaN – not a number |
Pojmem denormalizovaná čísla označujeme takové hodnoty, u kterých není první (explicitně nevyjádřený) bit mantisy roven jedničce, ale naopak nule. Výpočty s těmito velmi malými hodnotami nejsou přesné, zejména při násobení a dělení (a samozřejmě i všech odvozených operacích). Při ukládání denormalizovaných čísel je exponent vždy nastaven na nejnižší hodnotu, tj. na –126 a nejvyšší (explicitně neukládaný) bit mantisy je vždy nulový, nikoli jedničkový, jak je tomu u normalizovaných hodnot.
Hodnota typu NaN vznikne v případě, že je použita operace s nejasným výsledkem, například 0/0 nebo, a to v praxi snad nejčastěji, při odmocňování záporných čísel. Nekonečná hodnota vzniká typicky při dělení nulou (zde je možné zjistit znaménko), nebo při vyjádření funkcí typu log(0) atd.
Minimální a maximální hodnota exponentu má speciální význam i u formátu double:
| s-bit | exponent | mantisa | význam |
|---|---|---|---|
| 0 | 0<e<2047 | >0 | normalizované kladné číslo |
| 1 | 0<e<2047 | >0 | normalizované záporné číslo |
| 0 | 0 | >0 | denormalizované kladné číslo |
| 1 | 0 | >0 | denormalizované záporné číslo |
| 0 | 0 | 0 | kladná nula |
| 1 | 0 | 0 | záporná nula |
| 0 | 2047 | 0 | kladné nekonečno |
| 1 | 2047 | 0 | záporné nekonečno |
| 0 | 2047 | >0 | NaN – not a number |
| 1 | 2047 | >0 | NaN – not a number |
Kromě obou základních formátů (tj. jednoduché i dvojité přesnosti) je v normě IEEE 754 povoleno používat i rozšířené formáty. Na platformě x86 je při výpočtech prováděných v matematickém koprocesoru používán rozšířený formát nazývaný extended či temporary. Tento formát je zajímavý tím, že pro uložení FP hodnot používá 80 bitů a je do něho možné beze ztráty přesnosti uložit 64bitové hodnoty typu integer (což je v mnoha oblastech velmi důležité, protože například převod 64bitový integer → double je vždy doprovázen ztrátou nejnižších číslic!). Osmdesátibitový vektor je rozdělený do třech částí následujícím způsobem:
- 1 bit pro znaménko
- 15 bitů pro exponent (BIAS je roven 16383)
- 64 bitů pro mantisu (maximální hodnota přesahuje 104932)
U tohoto formátu je zajímavá funkce bitu s indexem 63. Podle hodnoty tohoto bitu se rozlišují čísla normalizovaná a nenormalizovaná (tento bit ve skutečnosti nahrazuje implicitně nastavovaný nejvyšší bit mantisy, jak ho známe z předchozích formátů). Všechny možnosti, které mohou při ukládání extended FP formátu nastat, jsou přehledně vypsány v následující tabulce:
| s-bit | exponent | mantisa | m63 | význam |
|---|---|---|---|---|
| 0 | 0<e<32767 | >0 | 1 | normalizované kladné číslo |
| 1 | 0<e<32767 | >0 | 1 | normalizované záporné číslo |
| 0 | 0<e<32767 | >0 | 0 | nenormalizované kladné číslo |
| 1 | 0<e<32767 | >0 | 0 | nenormalizované záporné číslo |
| 0 | 0 | >0 | 0 | denormalizované kladné číslo |
| 1 | 0 | >0 | 0 | denormalizované záporné číslo |
| 0 | 0 | 0 | x | kladná nula |
| 1 | 0 | 0 | x | záporná nula |
| 0 | 32767 | 0 | x | kladné nekonečno |
| 1 | 32767 | 0 | x | záporné nekonečno |
| 0 | 32767 | >0 | x | NaN – not a number |
| 1 | 32767 | >0 | x | NaN – not a number |
Pro normalizované i nenormalizované hodnoty je možné uloženou hodnotu vyjádřit pomocí vzorce (všimněte si, že bit 63 je umístěn před binární tečkou):
Xextended=(-1)s × 2exp-16383 × m
m=m630+m62-1+m61-2+…+m0-63
7. Omezení typů single i double
Největší nevýhodou formátů single a double, s nimiž jsme se seznámili v předchozích kapitolách, je fakt, že zvolený základ exponentu (báze) je sice výhodný z pohledu realizace výpočtů (ať již v SW či HW), ovšem na druhou stranu to způsobuje problémy při práci s hodnotami, s nimiž se běžně setkáváme při výpočtech s měnou (úroky, daně, účetnictví). Zdaleka nejznámější je v tomto ohledu konstanta, kterou můžeme v desítkové soustavě zapsat jako 0,1 (či 0.1). Zatímco v desítkové soustavě je tato konstanta reprezentovatelná konečným počtem cifer (zde konkrétně se jedná o dvě cifry + desetinnou tečku), ve formátech single a double to tak snadné není, protože pro přesnou reprezentaci desítkové hodnoty 0,1 by bylo nutné použít nekonečný rozvoj dvojkových cifer:
0.00011001100110011... (opakující se sekvence 0011)
V případě, že použijeme konečný počet cifer (a to u typů single i double pochopitelně musíme), tak ve skutečnosti uložíme pouze přibližnou hodnotu 0,1, konkrétně hodnotu 0.100000001490116119384765625 s chybou 0.000000001490116119384765625 (v případě typu float). Sice se může stát, že se jedná o malou chybu, ovšem u operací s měnou v takovém případě to může vést k reálným problémům (typickým příkladem může být složený úrok).
Podívejme se na jednoduchý příklad, který navíc ukazuje další vlastnost formátů single a double – zaokrouhlování při výpočtech i zaokrouhlování při výpisu hodnot na obrazovku. Budeme sčítat dvojici desítkových hodnot 0,1 a 0,2 a porovnávat výsledek s konstantou 0,3. Ani jednu z hodnot přitom není možné reprezentovat přesně:
| Původní hodnota | Ve skutečnosti uloženo | Chyba |
|---|---|---|
| 0.1 | 0.100000001490116119384765625 | 0.000000001490116119384765625 |
| 0.2 | 0.20000000298023223876953125 | 0.00000000298023223876953125 |
| 0.3 | 0.300000011920928955078125 | 0.000000011920928955078125 |
Přesto „díky“ nepřesnostem, které jsou zkombinovány se zaokrouhlením atd. dostaneme odlišné výsledky pro single (float) a double:
#include <stdio.h>
int main(void) {
float x = 0.1;
float y = 0.2;
float z = 0.3;
puts(x + y == z ? "rovnost" : "nerovnost");
return 0;
}
Tento program vypíše:
rovnost
Zatímco pro typ double:
#include <stdio.h>
int main(void) {
double x = 0.1;
double y = 0.2;
double z = 0.3;
puts(x + y == z ? "rovnost" : "nerovnost");
return 0;
}
Dostaneme opačný výsledek:
nerovnost
8. Klasický problém: konečná či nekonečná smyčka?
Ještě zákeřnější je chování formátů s plovoucí řádovou čárkou v případech, že s jejich využitím realizujeme počítané programové smyčky, speciálně ve chvíli, kdy testujeme, zda se přesně dosáhne koncové hodnoty počitadla. Problém pochopitelně spočívá především v chápání onoho slova „přesně“, protože přesné obecně nejsou ani výpočty s plovoucí čárkou ani uložené hodnoty.
Opět si toto chování ukažme na známých příkladech. Například si zkusme přeložit a spustit program s touto smyčkou:
#include <stdio.h>
int main(void) {
float x;
for (x=0.0; x!=1.0; x+=0.2) {
printf("%f\n", x);
}
return 0;
}
Z výsledků plyne, že se tento program chová podle očekávání:
0.000000 0.200000 0.400000 0.600000 0.800000
Mohlo by se tedy zdát, že i když nahradíme krok 0,2 za 0,1, nic podstatného se nezmění, pouze se nevypíše pět hodnot, ale hodnot deset:
#include <stdio.h>
int main(void) {
float x;
for (x=0.0; x!=1.0; x+=0.1) {
printf("%f\n", x);
}
return 0;
}
Jak je tomu však v praxi? Program nejprve vypíše prvních deset hodnot podle očekávání:
0.000000 0.100000 0.200000 0.300000 0.400000 0.500000 0.600000 0.700000 0.800000 0.900000
Poté však pokračuje dále (mezní hodnotu smyčky tedy přeskočí, což je matoucí, ovšem jedná se o zaokrouhlení při výpisu hodnoty):
1.100000 1.200000 1.300000 1.400000 1.500000 1.600000 ... ... ...
A po určité chvíli již bude chyba tak velká, že se ve výpisu objeví „divná“ čísla:
... ... ... 7.799995 7.899995 7.999995 ... ... ...
A chyba bude narůstat:
... ... ... 107436.304688 107436.406250 107436.507812 107436.609375 107436.710938 ... ... ...
Mohlo by se tedy zdát, že přechodem ze single (float) na double se problému zbavíme, protože vše by mělo být „přesnější“. Opět si to nejprve otestujme se smyčkou s krokem 0,2:
#include <stdio.h>
int main(void) {
double x;
for (x=0.0; x!=1.0; x+=0.2) {
printf("%f\n", x);
}
return 0;
}
Vše vypadá v pořádku:
0.000000 0.200000 0.400000 0.600000 0.800000
Přejděme tedy na smyčku s krokem 0,1:
#include <stdio.h>
int main(void) {
double x;
for (x=0.0; x!=1.0; x+=0.1) {
printf("%f\n", x);
}
return 0;
}
Nyní opět dojde k problému s „přeskokem“ mezní hodnoty:
0.000000 0.100000 0.200000 0.300000 0.400000 0.500000 0.600000 0.700000 0.800000 0.900000 1.000000 !!!!!!!! 1.100000 1.200000 1.300000 1.400000 1.500000 1.600000 1.700000 1.800000 1.900000 ... ... ... 495457.199956 495457.299956 495457.399956 495457.499956 495457.599956 495457.699956 495457.799956 495457.899956 495457.999956 495458.099956
9. Tisk numerických hodnot single a double v hexadecimálním formátu
Zajímavé bude zjistit, jak vlastně vypadá interní formát numerických hodnot uložených ve formátech single a double. Můžeme se pokusit vypsat si ony 32bitové či 64bitové hodnoty v hexadecimálním formátu (tedy zakódovaná sekvence 32 či 64 bitů), popř. využít „hexadecimální FP formát“, jenž je v céčkové knihovně podporován.
Nejprve si ukažme použití „hexadecimálního FP formátu“, který je zajištěn díky formátovacímu znaku %a:
#include <stdio.h>
int main(void)
{
float values[] = {0.0, 0.1, 0.2, 1.0, 2.0, 10.0, 100.0, 1000.0, 1000.1, 1.0/0.0, -0.0, -0.1, -0.2, -1.0, -1000.0, -1.0/0.0, 0.0/0.0};
int i;
for (i=0; i<sizeof(values)/sizeof(float); i++) {
printf("%9.4f %a\n", values[i], values[i]);
}
return 0;
}
Výsledky zde odhalují, že hodnoty 0,1 atd. nelze reprezentovat zcela přesně:
0.0000 0x0p+0
0.1000 0x1.99999ap-4
0.2000 0x1.99999ap-3
1.0000 0x1p+0
2.0000 0x1p+1
10.0000 0x1.4p+3
100.0000 0x1.9p+6
1000.0000 0x1.f4p+9
1000.1000 0x1.f40cccp+9
inf inf
-0.0000 -0x0p+0
-0.1000 -0x1.99999ap-4
-0.2000 -0x1.99999ap-3
-1.0000 -0x1p+0
-1000.0000 -0x1.f4p+9
-inf -inf
-nan -nan
Totéž lze pochopitelně provést i pro datový typ double:
#include <stdio.h>
int main(void)
{
double values[] = {0.0, 0.1, 0.2, 1.0, 2.0, 10.0, 100.0, 1000.0, 1000.1, 1.0/0.0, -0.0, -0.1, -0.2, -1.0, -1000.0, -1.0/0.0, 0.0/0.0};
int i;
for (i=0; i<sizeof(values)/sizeof(double); i++) {
printf("%9.4f %a\n", values[i], values[i]);
}
return 0;
}
Výsledky odhalují stále stejný problém:
0.0000 0x0p+0
0.1000 0x1.999999999999ap-4
0.2000 0x1.999999999999ap-3
1.0000 0x1p+0
2.0000 0x1p+1
10.0000 0x1.4p+3
100.0000 0x1.9p+6
1000.0000 0x1.f4p+9
1000.1000 0x1.f40cccccccccdp+9
inf inf
-0.0000 -0x0p+0
-0.1000 -0x1.999999999999ap-4
-0.2000 -0x1.999999999999ap-3
-1.0000 -0x1p+0
-1000.0000 -0x1.f4p+9
-inf -inf
-nan -nan
10. Interní struktura hodnot typu single a double
„Hexadecimální výstup“ ve formě, v jaké byl ukázán v předchozí kapitole, však nenapovídá, jak přesně jsou hodnoty typu single a double reprezentovány (resp. uloženy). První náhled na způsob uložení nám dá pouhý převod těchto hodnot na sekvenci osmi či šestnácti hexadecimálních cifer. Toho můžeme dosáhnout v programovacím jazyku C snadno, viz též následující dva příklady.
První příklad převede hodnoty typu float na 32bitové hexadecimální číslo:
#include <stdio.h>
#include <stdint.h>
void print_float_as_hex(float value) {
union {
float f;
uint32_t u;
} f2u = { .f = value };
printf("%f -> %08x\n", value, f2u.u);
}
int main(void) {
float x = 0.1;
float y = 0.2;
float z = 0.3;
print_float_as_hex(x);
print_float_as_hex(y);
print_float_as_hex(z);
return 0;
}
Z výsledků je patrné, že všechny tři „problémové“ numerické hodnoty, s nimiž jsme se již setkali, by pravděpodobně vyžadovaly nekonečný rozvoj. I bez znalosti přesného způsobu uložení je navíc patrné, že se provedlo zaokrouhlení (z C na D, resp. z 9 na A):
0.100000 -> 3dcccccd 0.200000 -> 3e4ccccd 0.300000 -> 3e99999a
Tutéž operaci můžeme provést i pro hodnoty typu double, které převedeme na 64bitové hexadecimální číslo:
#include <stdio.h>
#include <stdint.h>
void print_double_as_hex(double value) {
union {
double f;
uint64_t u;
} f2u = { .f = value };
printf("%f -> %016lx\n", value, f2u.u);
}
int main(void) {
double x = 0.1;
double y = 0.2;
double z = 0.3;
print_double_as_hex(x);
print_double_as_hex(y);
print_double_as_hex(z);
return 0;
}
I zde je jasně patrné zaokrouhlení:
0.100000 -> 3fb999999999999a 0.200000 -> 3fc999999999999a 0.300000 -> 3fd3333333333333
11. Dekódování numerických hodnot uložených ve formátu single a double
Mnohem více informací o uložení single a double však získáme až ve chvíli, kdy se pokusíme o dekódování oněch 32bitových či 64bitových hodnot. Opět se nejdříve podívejme na typ single, který rozděluje 32bitovou hodnotu na jednobitové znaménko, osmibitový exponent s biasem 127 a 23 bitovou mantisou, kde se u normalizovaných hodnot předpokládá, že nejvyšší bit mantisy je jedničkový a proto nemusí být uložen. Navíc víme, že pokud má exponent maximální možnou hodnotu, je uloženo buď nekonečno či „nečíslo“ NaN (rozlišujeme zde podle hodnoty mantisy). Znaménko nekonečna je určeno znaménkovým bitem. Zbytek je již zajištěn bitovými posuny, maskováním bitů a trikem s přičtením jedničky (ten je ovšem nekorektní pro nenormalizované hodnoty):
#include <stdio.h>
void decode_float(float value)
{
const int exponent_bias = 127;
const int mantissa_base = 1 << 23;
const int max_exponent = 255;
const int mantissa_mask = 0x07fffff;
const int mantissa_bits = 23;
const int exponent_bits = 8;
typedef union {
float value;
__uint32_t x;
} IEEE_754_float;
IEEE_754_float f;
f.value = value;
__uint32_t x = f.x;
unsigned int sign = 0x01 & (x >> (mantissa_bits + exponent_bits));
unsigned int exponent = max_exponent & (x >> mantissa_bits);
unsigned int mantissa = mantissa_mask & x;
printf("%+10.4f ", value);
if (exponent == max_exponent) {
if (mantissa == 0) {
printf("%c infinity\n", sign ? '-' : '+');
} else {
puts("NaN");
}
} else {
printf("%c %10.8f x 2^%-2d\n", sign ? '-' : '+',
1.0 + (float) mantissa / mantissa_base, exponent - exponent_bias);
}
}
int main(void)
{
float values[] = {0.0, 0.1, 0.2, 1.0, 2.0, 10.0, 100.0, 1000.0, 1000.1, 1.0/0.0, -0.0, -0.1, -0.2, -1.0, -1000.0, -1.0/0.0, 0.0/0.0};
int i;
for (i=0; i<sizeof(values)/sizeof(float); i++) {
decode_float(values[i]);
}
return 0;
}
Nyní se podívejme, jaké výsledky (interní struktura) se vypíšou pro některé zajímavé hodnoty, které jsou součástí zdrojového kódu:
+0.0000 + 1.00000000 x 2^-127
+0.1000 + 1.60000002 x 2^-4
+0.2000 + 1.60000002 x 2^-3
+1.0000 + 1.00000000 x 2^0
+2.0000 + 1.00000000 x 2^1
+10.0000 + 1.25000000 x 2^3
+100.0000 + 1.56250000 x 2^6
+1000.0000 + 1.95312500 x 2^9
+1000.1000 + 1.95332026 x 2^9
+inf + infinity
-0.0000 - 1.00000000 x 2^-127
-0.1000 - 1.60000002 x 2^-4
-0.2000 - 1.60000002 x 2^-3
-1.0000 - 1.00000000 x 2^0
-1000.0000 - 1.95312500 x 2^9
-inf - infinity
-nan NaN
U hodnoty +0.0 a –0.0 by se ve skutečnosti mělo postupovat sofistikovaněji, protože u nejmenší hodnoty exponentu se jedná o nenormalizovaná čísla.
Naprosto stejným způsobem lze dekódovat hodnoty typu double; pouze se použije větší počet bitů pro exponent (a tím pádem i větší bias) i větší počet bitů pro mantisu:
#include <stdio.h>
void decode_double(double value)
{
const int exponent_bias = 1023;
const __uint64_t mantissa_base = 1L << 52;
const int max_exponent = 2047;
const __uint64_t mantissa_mask = 0x0fffffffffffff;
const int mantissa_bits = 52;
const int exponent_bits = 11;
typedef union {
double value;
__uint64_t x;
} IEEE_754_double;
IEEE_754_double d;
d.value = value;
__uint64_t x = d.x;
unsigned int sign = 0x01 & (x >> (mantissa_bits + exponent_bits));
unsigned int exponent = max_exponent & (x >> mantissa_bits);
__uint64_t mantissa = mantissa_mask & x;
printf("%+10.4f ", value);
if (exponent == max_exponent) {
if (mantissa == 0) {
printf("%c infinity\n", sign ? '-' : '+');
} else {
puts("NaN");
}
} else {
printf("%c %10.8f x 2^%-2d\n", sign ? '-' : '+',
1.0 + (double) mantissa / mantissa_base, exponent - exponent_bias);
}
}
int main(void)
{
double values[] = {0.0, 0.1, 0.2, 1.0, 2.0, 10.0, 100.0, 1000.0, 1000.1, 1.0/0.0, -0.0, -0.1, -0.2, -1.0, -1000.0, -1.0/0.0, 0.0/0.0};
int i;
for (i=0; i<sizeof(values)/sizeof(double); i++) {
decode_double(values[i]);
}
return 0;
}
Výsledky až na větší počet cifer odpovídají předchozímu příkladu:
+0.0000 + 1.00000000 x 2^-1023
+0.1000 + 1.60000000 x 2^-4
+0.2000 + 1.60000000 x 2^-3
+1.0000 + 1.00000000 x 2^0
+2.0000 + 1.00000000 x 2^1
+10.0000 + 1.25000000 x 2^3
+100.0000 + 1.56250000 x 2^6
+1000.0000 + 1.95312500 x 2^9
+1000.1000 + 1.95332031 x 2^9
+inf + infinity
-0.0000 - 1.00000000 x 2^-1023
-0.1000 - 1.60000000 x 2^-4
-0.2000 - 1.60000000 x 2^-3
-1.0000 - 1.00000000 x 2^0
-1000.0000 - 1.95312500 x 2^9
-inf - infinity
-nan NaN
12. Formáty Decimal32, Decimal64 a Decimal128
Víme již, že formáty single i double jsou sice výhodné z hlediska jejich implementace (a proto je najdeme v HW), ovšem způsobují problémy při práci s často používanými desetinnými čísly, a to i při použití malého množství desetinných míst. Jaké je tedy řešení tohoto reálného problému? Zajisté nebude postačovat pouze zvýšit přesnost uložení, tj. přejít z typu double na 96bitová či 128bitová čísla s plovoucí řádovou čárkou a bází=2. Problému desítkové hodnoty 0.1, tedy:
0.110 == 0.000110011001100112... (opakující se sekvence 0011)
se totiž ani vyšším počtem bitů mantisy či exponentu jen tak jednoduše nezbavíme (tedy nikoli při použití konečného počtu cifer), pouze ho odsuneme do pozdější doby.
Skutečné řešení spočívá v tom, že se použijí formáty FP hodnot, u nichž nebude báze exponentu nastavena na konstantu 2, ale na desítku. Realizace výpočtů v počítači (ať již SW či HW) se sice zkomplikuje, ovšem „lidské“ numerické hodnoty, tedy hodnoty, které zapisujeme v desítkové soustavě, bude možné uložit naprosto přesně. A právě z tohoto důvodu vznikly různé „dekadické formáty s plovoucí řádovou tečkou/čárkou“. Tři z těchto formátů byly standardizovány v normě IEEE 754–2008 (druhé číslo je rok vydání upravené normy) a tyto formáty nazvané Decimal32, Decimal64 a Decimal128 můžeme používat i v jazyku C, i když s omezeními (k dispozici jsou prakticky jen výpočty a pomocné specializované funkce, ale již ne realizace v knihovnách math či stdio).
#include <stdint.h>
int main(void) {
_Decimal32 x;
_Decimal64 y;
_Decimal128 z;
return 0;
}
Společné znaky a rozdíly mezi všemi třemi „dekadickými“ formáty:
| Formát | Šířka | Znaménko | Bitové pole s ciframi | Exponent | Bitové pole combination |
|---|---|---|---|---|---|
| Decimal32 | 32 bitů | 1 bit | 20 bitů | 6 bitů | 5 bitů |
| Decimal64 | 64 bitů | 1 bit | 50 bitů | 8 bitů | 5 bitů |
| Decimal128 | 128 bitů | 1 bit | 110 bitů | 12 bitů | 5 bitů |
13. Problém hodnoty 0,1 mizí
Hodnoty 0,1, 0,2 i 0,3 je možné s využitím libovolného typu Decimal uložit zcela přesně a proto všechny tři následující příklady vypíšou (podle očekávání) zprávu „rovnost“:
#include <stdio.h>
int main(void) {
_Decimal32 x = 0.1df;
_Decimal32 y = 0.2df;
_Decimal32 z = 0.3df;
puts(x + y == z ? "rovnost" : "nerovnost");
return 0;
}
#include <stdio.h>
int main(void) {
_Decimal64 x = 0.1dd;
_Decimal64 y = 0.2dd;
_Decimal64 z = 0.3dd;
puts(x + y == z ? "rovnost" : "nerovnost");
return 0;
}
a:
#include <stdio.h>
int main(void) {
_Decimal128 x = 0.1dl;
_Decimal128 y = 0.2dl;
_Decimal128 z = 0.3dl;
puts(x + y == z ? "rovnost" : "nerovnost");
return 0;
}
14. Počítaná smyčka s krokem 0,1 a koncovou hodnotou 1,0 realizovaná s využitím typů Decimal
Při využití datových typů Decimal taktéž zcela odpadá problém s realizací počítané programové smyčky s krokem nastaveným na 0.1 a koncovou hodnotou 1.0 – tyto smyčky vždy korektně skončí. Opět si to pro úplnost ukažme ve všech třech variantách, i když se nyní budeme muset spokojit s výpisem numerických hodnot převedených na float či double, protože libc nemusí podporovat přímý výpis dekadických hodnot s plovoucí řádovou čárkou.
Varianta pro Decimal32:
#include <stdio.h>
#include <stdint.h>
int main(void) {
_Decimal32 x;
for (x=0.0df; x!=1.0df; x+=0.1df) {
printf("%f\n", (float)x);
}
return 0;
}
Výsledky:
0.000000 0.100000 0.200000 0.300000 0.400000 0.500000 0.600000 0.700000 0.800000 0.900000
Varianta pro Decimal64:
#include <stdio.h>
#include <stdint.h>
int main(void) {
_Decimal64 x;
for (x=0.0dd; x!=1.0dd; x+=0.1dd) {
printf("%f\n", (float)x);
}
return 0;
}
Výsledky:
0.000000 0.100000 0.200000 0.300000 0.400000 0.500000 0.600000 0.700000 0.800000 0.900000
Varianta pro Decimal128:
#include <stdio.h>
#include <stdint.h>
int main(void) {
_Decimal128 x;
for (x=0.0dl; x!=1.0dl; x+=0.1dl) {
printf("%f\n", (float)x);
}
return 0;
}
Výsledky:
0.000000 0.100000 0.200000 0.300000 0.400000 0.500000 0.600000 0.700000 0.800000 0.900000
15. Interní struktura formátu Decimal32
Interně vypadají formáty Decimal dosti odlišně od formátů single a double, i když základní myšlenka – rozdělení na znaménko, mantisu a exponent – vlastně zůstává zachována. Nejsložitější je, i když to může znít poněkud paradoxně, formát Decimal32 a proto se zaměřme na jeho popis. 32bitové slovo je zde rozděleno na tři oblasti:
- 1 bitové znaménko
- 11 bitů pro tzv. combination field
- 20 bitů pro tzv. trailing significand field
Oněch 11 bitů combination fieldu se označuje symboly G10, G9, až G0. V případě, že alespoň jeden z bitů G10 a G9 je nastavený na nulu, je hodnota uložena takto:
- Následujících šest bitů obsahuje desítkový exponent s biasem 101
- Nejnižší tři bity se spojí s posledními 20 bity a vytvoří tak mantisu (ta může být uložena dvěma způsoby, ale typicky se setkáme s binární reprezentací
To tedy znamená, že většina běžných numerických hodnot je v 32bitových slovech uložena takto:
s 00eeeeee mmmmmmmmmmmmmmmmmmmmmmm s 01eeeeee mmmmmmmmmmmmmmmmmmmmmmm s 10eeeeee mmmmmmmmmmmmmmmmmmmmmmm
kde s je znaménko, e jsou bity exponentu (před nimi jsou i ony konstantní bity) a m jsou bity mantisy.
V případě, že jak bity G10, tak i G9 jsou nastaveny na jedničku, je kódování odlišné. Nejprve se rozeznávají speciální hodnoty podle bitů G10 až G6:
s 11110xxx xxxxxxxxxxxxxxxxxxxxxxx - kladné nebo záporné nekonečno s 11111xxx xxxxxxxxxxxxxxxxxxxxxxx - not a number (NaN)
Ostatní kombinace bitů (de facto kombinace nezačínající čtyřmi jedničkami) vypadají takto:
s 11EEeeeeee 100mmmmmmmmmmmmmmmmmmmm s 11EEeeeeee 100mmmmmmmmmmmmmmmmmmmm s 10EEeeeeee 100mmmmmmmmmmmmmmmmmmmm
přičemž platí, že kombinace bitů EE nesmí být 11 (ale jen 00, 01 či 10); v opačném případě se jedná o speciální hodnoty.
16. Dekódování hodnoty typu Decimal32
Zkusme si tyto případy (kromě posledního) zanést do prográmku s funkcí, které se předá hodnota typu Decimal32, která je dekódována a následně jsou vypsána jednotlivá bitová pole i (symbolicky) hodnota, která je uložena. Opět připomínám, že prográmek neobsahuje jednu větev, která odpovídá G10=1 a G9=1, přičemž se nebude jednat o speciální hodnotu typu nekonečno či NaN (doplnění je relativně snadné a můžeme ho ponechat jako domácí úkol váženého čtenáře :-). Zdrojový kód popsaného programu bude vypadat následovně:
#include <stdio.h>
void decode_decimal32(_Decimal32 value)
{
const int combination_bits = 11;
const int trailing_bits = 20;
const int combination_mask = 0x7ff;
const int trailing_mask = 0x0fffff;
const int exponent_bias = 101;
typedef union {
_Decimal32 value;
__uint32_t x;
} IEEE_754_decimal32;
IEEE_754_decimal32 d;
d.value = value;
__uint32_t x = d.x;
unsigned int sign = 0x01 & (x >> (combination_bits + trailing_bits));
unsigned int combination = combination_mask & (x >> trailing_bits);
unsigned int trailing = trailing_mask & x;
unsigned int g10 = 0x01 & (combination >> 10);
unsigned int g9 = 0x01 & (combination >> 9);
// hodnota po konverzi
printf("%+10.4f ", (float)value);
// ziskana bitova pole
printf("%d %d %d %03x %05x ", sign, g10, g9, combination, trailing);
// znamenko
printf("%c ", sign ? '-' : '+');
if ((combination & 0x7c0) == 0x780) {
printf("infinity\n");
} else if ((combination & 0x7c0) == 0x7c0) {
printf("NaN\n");
} else if ((g10 == 1) && (g9 == 1)) {
printf("special case\n");
} else {
unsigned int exponent = (combination >> 3) - exponent_bias;
unsigned int mantissa = trailing + ((combination & 0x07) << 20);
printf("%d x 10^%d\n", mantissa, exponent);
}
}
int main(void)
{
_Decimal32 one = 1.0dd;
_Decimal32 three = 3.0dd;
_Decimal32 values[] = {0.0dd, 0.1dd, 0.2dd, 1.0dd, 2.0dd,
10.0dd, 100.0dd, 1000.0dd, 1000.1dd,
one/three, 1.0dd/0.0dd,
-0.0dd, -0.1dd, -0.2dd, -1.0dd,
-1000.0dd, -1.0dd/0.0dd, 0.0dd/0.0dd};
int i;
printf(" value S G10 G9 comb.trailing decoded\n");
for (i=0; i<sizeof(values)/sizeof(_Decimal32); i++) {
decode_decimal32(values[i]);
}
return 0;
}
Výsledky, které tento prográmek vypíše, vypadají následovně:
value S G10 G9 comb.trailing decoded
+0.0000 0 0 1 320 00000 + 0 x 10^-1
+0.1000 0 0 1 320 00001 + 1 x 10^-1
+0.2000 0 0 1 320 00002 + 2 x 10^-1
+1.0000 0 0 1 320 0000a + 10 x 10^-1
+2.0000 0 0 1 320 00014 + 20 x 10^-1
+10.0000 0 0 1 320 00064 + 100 x 10^-1
+100.0000 0 0 1 320 003e8 + 1000 x 10^-1
+1000.0000 0 0 1 320 02710 + 10000 x 10^-1
+1000.1000 0 0 1 320 02711 + 10001 x 10^-1
+0.3333 0 0 1 2f3 2dcd5 + 3333333 x 10^-7
+inf 0 1 1 780 00000 + infinity
-0.0000 1 0 1 320 00000 - 0 x 10^-1
-0.1000 1 0 1 320 00001 - 1 x 10^-1
-0.2000 1 0 1 320 00002 - 2 x 10^-1
-1.0000 1 0 1 320 0000a - 10 x 10^-1
-1000.0000 1 0 1 320 02710 - 10000 x 10^-1
-inf 1 1 1 780 00000 - infinity
+nan 0 1 1 7c0 00000 + NaN
Tyto hodnoty si postupně popišme.
Z výše uvedeného výpisu je patrné, že formát Decimal32 dokáže bez problémů ukládat hodnoty typu 0,1 atd., a to jak hodnoty kladné, tak i záporné (znaménko je opět uloženo ve zvláštním bitu a tedy nemusíme složitě přemýšlet na dvojkovým doplňkem atd.):
value S G10 G9 comb.trailing decoded +0.1000 0 0 1 320 00001 + 1 x 10^-1 +0.2000 0 0 1 320 00002 + 2 x 10^-1 -0.1000 1 0 1 320 00001 - 1 x 10^-1 -0.2000 1 0 1 320 00002 - 2 x 10^-1
Zcela přirozeně (alespoň z pohledu člověka, ne počítače) jsou uloženy i násobky deseti, včetně hodnoty 1 (tedy deset na nultou):
+1.0000 0 0 1 320 0000a + 10 x 10^-1 +10.0000 0 0 1 320 00064 + 100 x 10^-1 +100.0000 0 0 1 320 003e8 + 1000 x 10^-1 +1000.0000 0 0 1 320 02710 + 10000 x 10^-1 -1.0000 1 0 1 320 0000a - 10 x 10^-1 -1000.0000 1 0 1 320 02710 - 10000 x 10^-1
Nula nepatří mezi speciální hodnoty, ale je uložena jako hodnota s mantisou rovnou nule (a teoreticky libovolným exponentem). A jak je dobrým zvykem, rozlišuje se kladná a záporná nula:
value S G10 G9 comb.trailing decoded +0.0000 0 0 1 320 00000 + 0 x 10^-1 -0.0000 1 0 1 320 00000 - 0 x 10^-1
Speciální hodnoty mají nastaveny bity G10 a G9, na rozdíl od běžných hodnot. A samozřejmě odlišíme kladné a záporné nekonečno:
value S G10 G9 comb.trailing decoded
+inf 0 1 1 780 00000 + infinity
-inf 1 1 1 780 00000 - infinity
+nan 0 1 1 7c0 00000 + NaN
Zbývají nám dvě hodnoty 1000,1 a 1/3. První z těchto hodnot je uložena přesně, tedy jako 10001×0,1. Ovšem druhou hodnotu přesně nelze reprezentovat a opět zde dojde k chybě. Povšimněte si navíc, jak málo cifer máme ve formátu Decimal32 k dispozici (zde jen sedm desítkových cifer):
value S G10 G9 comb.trailing decoded +1000.1000 0 0 1 320 02711 + 10001 x 10^-1 +0.3333 0 0 1 2f3 2dcd5 + 3333333 x 10^-7
17. Rychlost výpočtů: porovnání Decimal se single a double
V předchozím textu jsme si popsali ty nejdůležitější vlastnosti datových typů Decimal32 a Decimal64. Prozatím jsme se ovšem nezmínili o tom, jak pomalé či naopak rychlé budou výpočty s numerickými hodnotami uloženými v těchto formátech (a již dopředu prozradím, že výsledky budou překvapivé). Pro porovnání rychlostí výpočtů s typy single (float), double, Decimal32 a Decimal64 použijeme výpočet Mandelbrotový množiny, což je benchmark, který jsem v článcích použil již nejméně desetkrát (v různých podobách a v různých programovacích jazycích).
Výpočet Mandelbrotovy množiny bude naprogramován takovým způsobem, aby jediný zápis algoritmu bylo možné použít pro výpočty s numerickými hodnotami různých typů (přesněji řečeno typů s plovoucí řádovou čárkou, i když teoreticky lze použít i typy s pevnou řádovou čárkou, které však většinou nejsou na mainstreamových platformách přímo podporovány – nalezneme je jen u některých digitálních signálových procesorů). Povšimněte si, že se ve výpočtu (kromě celočíselných počitadel atd.) používá obecný a dopředu neznámý datový typ number, který budeme muset dodefinovat:
void calc_mandelbrot(unsigned int width, unsigned int height, unsigned int maxiter, unsigned char palette[][3])
{
const number_type zero = 0.0;
const number_type two = 2.0;
const number_type three = 3.0;
const number_type bailout = 4.0;
puts("P3");
printf("%d %d\n", width, height);
puts("255");
number_type cy = -1.5;
int y;
for (y=0; y<height; y++) {
number_type cx = -2.0;
int x;
for (x=0; x<width; x++) {
number_type zx = zero;
number_type zy = zero;
unsigned int i = 0;
while (i < maxiter) {
number_type zx2 = zx * zx;
number_type zy2 = zy * zy;
if (zx2 + zy2 > bailout) {
break;
}
zy = two * zx * zy + cy;
zx = zx2 - zy2 + cx;
i++;
}
unsigned char *color = palette[i % 256];
unsigned char r = *color++;
unsigned char g = *color++;
unsigned char b = *color;
printf("%d %d %d\n", r, g, b);
cx += three/width;
}
cy += three/height;
}
}
Výše uvedený výpočet Mandelbrotovy množiny je pro jednoduchost uložen v hlavičkovém souboru, který budeme vkládat do jednotlivých benchmarků. V každém benchmarku ovšem nejprve nadefinujeme datový typ number. Příklad pro benchmark využívající hodnoty typu single (float):
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
typedef float number_type;
#include "mandelbrot.h"
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
Dtto pro benchmark pro typ double:
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
typedef double number_type;
#include "mandelbrot.h"
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
A pro úplnost si uveďme i tři zbývající benchmarky pro typy Decimal32 a Decimal64:
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
typedef _Decimal32 number_type;
#include "mandelbrot.h"
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
typedef _Decimal64 number_type;
#include "mandelbrot.h"
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
a konečně:
#include <stdlib.h>
#include <stdio.h>
#include "palette_mandmap.h"
typedef _Decimal128 number_type;
#include "mandelbrot.h"
int main(int argc, char **argv)
{
if (argc < 4) {
puts("usage: ./mandelbrot width height maxiter");
return 1;
}
int width = atoi(argv[1]);
int height = atoi(argv[2]);
int maxiter = atoi(argv[3]);
calc_mandelbrot(width, height, maxiter, palette);
return 0;
}
Po překladu všech výše uvedených benchmarků (s přepínačem -O3; žádné další přepínače nepoužijeme, ale klidně si vyzkoušejte přidat přepínače pro optimalizace IEEE 754 operací) je spustíme s vhodně zvolenými konstantami width, height a maxiter. Pro jednoduchost budeme postupně měnit pouze hodnotu maxiter od nuly do 1000 s krokem 100.
for i in $(seq 0 100 1000)
do
echo $i >> results.txt
/usr/bin/time -f "%U" -o results.txt -a ./mandelbrot_float 1000 1000 $i > /dev/null
/usr/bin/time -f "%U" -o results.txt -a ./mandelbrot_double 1000 1000 $i > /dev/null
/usr/bin/time -f "%U" -o results.txt -a ./mandelbrot_decimal32 1000 1000 $i > /dev/null
/usr/bin/time -f "%U" -o results.txt -a ./mandelbrot_decimal64 1000 1000 $i > /dev/null
done
Výsledky benchmarků vypsané do textového souboru si převedeme do formátu CSV a ten dále použijeme pro zobrazení grafu:
from toolz.itertoolz import partition
with open("results.txt") as f:
lines = f.read().split("\n")
results = partition(5, lines)
for result in results:
print(",".join(result))
18. Výsledky benchmarků
První výsledky jsou získané pro počítač s mikroprocesorem Intel® Core™ i7–8665U CPU @ 1.90GHz (počet jader nebude hrát žádnou roli):
Iter float double Decimal32 Decimal64 -------------------------------------------- 0 0.12 0.11 0.17 0.15 100 0.16 0.17 5.36 4.09 200 0.23 0.23 9.80 7.12 300 0.29 0.29 14.56 10.43 400 0.37 0.37 19.34 14.06 500 0.43 0.50 23.13 16.70 600 0.46 0.48 25.71 19.66 700 0.50 0.54 29.61 21.44 800 0.58 0.58 35.01 25.15 900 0.61 0.64 37.23 28.01 1000 0.66 0.77 41.00 31.03
V grafické podobě vypadají výsledky takto:
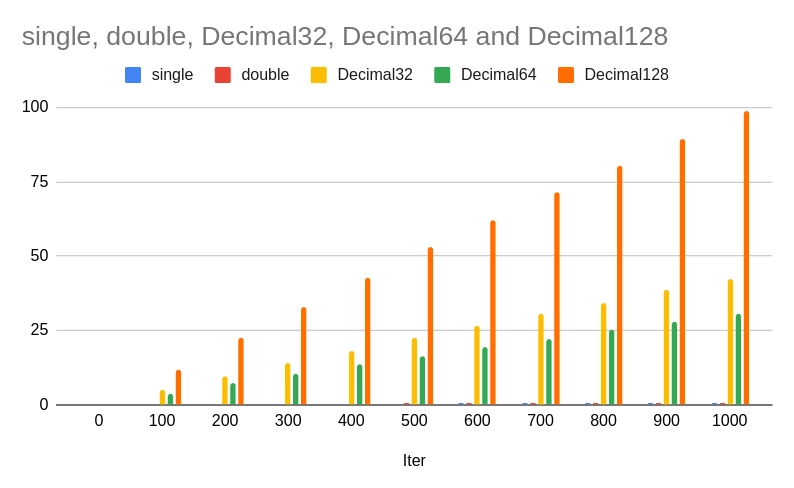
Obrázek 4: Rychlost výpočtů pro všech pět formátů numerických hodnot.
Rychlosti v případě single/float a double jsou tak velké, že příslušné sloupce na grafu nejsou patrné. Proto si porovnejme pouze tyto dvě série hodnot:
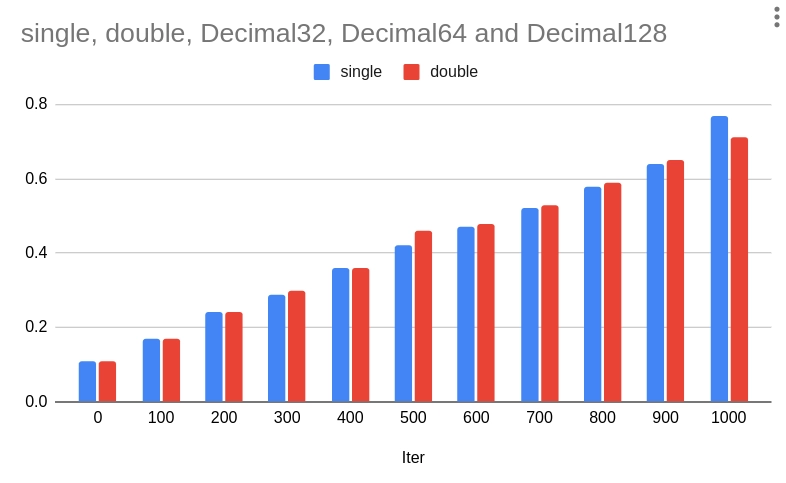
Obrázek 5: Rozdíly mezi rychlostí výpočtů s formáty single/float a double.
Druhé výsledky jsou získané pro počítač s mikroprocesorem 12th Gen Intel® Core™ i7–1270P (počet jader opět nebude hrát žádnou roli):
Iter float double Decimal32 Decimal64 --------------------------------------------- 0 0.07 0.07 0.08 0.07 0.15 100 0.10 0.10 3.08 2.47 7.85 200 0.15 0.14 5.34 4.26 13.58 300 0.17 0.17 7.26 5.94 19.87 400 0.21 0.22 9.07 6.95 25.48 500 0.24 0.25 11.23 9.07 31.06 600 0.28 0.28 13.20 10.64 36.39 700 0.32 0.32 15.17 12.52 41.93 800 0.35 0.35 17.33 13.76 47.07 900 0.38 0.38 19.09 15.54 52.84 1000 0.42 0.41 20.65 16.25 57.95
Opět se podívejme i na grafickou podobu výsledků:
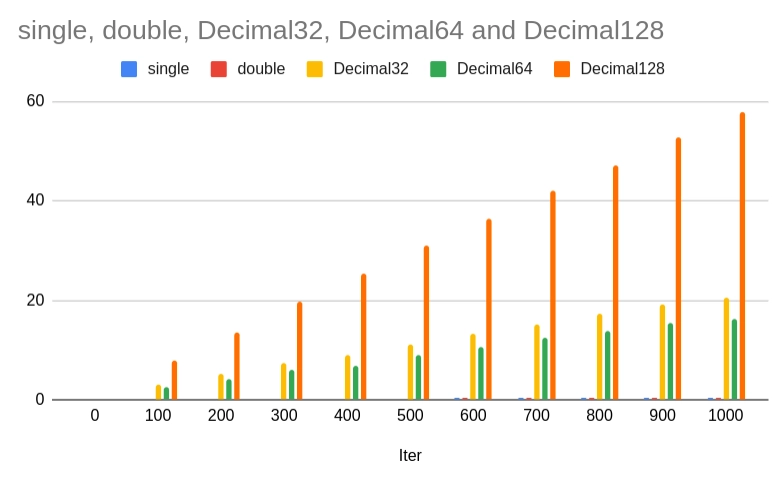
Obrázek 6: Rychlost výpočtů pro všech pět formátů numerických hodnot
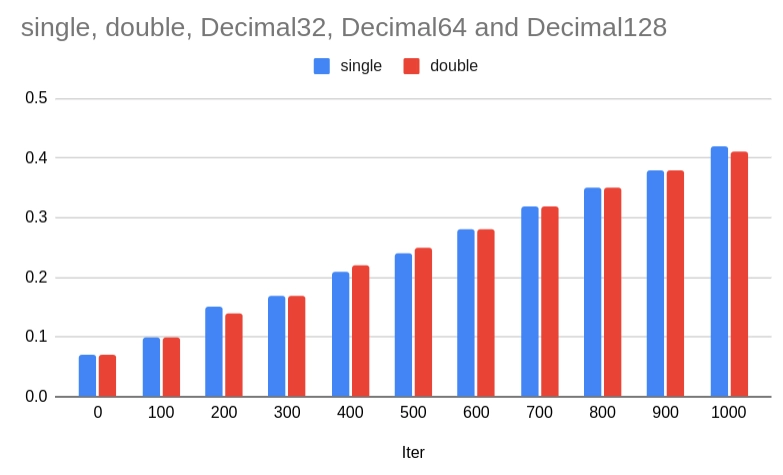
Obrázek 7: Rozdíly mezi rychlostí výpočtů s formáty single/float a double.
Výsledky benchmarků jsou (možná) poněkud překvapivé. Začněme porovnáním rychlostí operací s numerickými hodnotami ve formátech single (float) a double. Zajímavé je, že výpočty s hodnotami s dvojitou přesností jsou prakticky stejně rychlé (někdy i rychlejší), než výpočty s jednoduchou přesností. To do určité míry dává smysl, protože výpočty jsou prováděny stejnou výpočetní jednotkou a navíc překladač GCC neprovedl zásadní „vektorizaci“ kódu, kde by se dalo využít větší délky vektorů s hodnotami single oproti vektorům s hodnotami double. Z tohoto pohledu má typ single výhodu v menší paměťové náročnosti, což se však využije například při zpracování delších signálů, velkých polí atd.
Zajímavější je však fakt, že výpočty s typem Decimal32 jsou pomalejší, než výpočty s typem Decimal64. Zde se již jedná o způsob reprezentace hodnot (Decimal32 je složitější a pravděpodobně vyžaduje více rozeskoků) a možná i o optimalizace určené pro 64bitovou platformu. Nicméně opět platí – pokud není zapotřebí šetřit pamětí RAM (velká pole, tiskové sestavy, účetnictví s miliony položek), pravděpodobně se vyplatí přímo použít Decimal64, i když se jeho dalších předností (rozsah, přesnost) nevyužije.
19. Repositář s demonstračními příklady
Demonstrační příklady popsané v dnešním článku byly uloženy do veřejného Git repositáře, z něhož si je můžete snadno stáhnout a otestovat. Všechny příklady byly otestovány s GCC verze 9.4.0 (to je už trošku vykopávka) a 13.2.1:
| # | Soubor | Stručný popis | Odkaz |
|---|---|---|---|
| 1 | float0_1.c | součet konstant 0,1 a 0,2, porovnání s konstantou 0,3; realizace typem float/single | https://github.com/tisnik/presentations/blob/master/decimal/float0_1.c |
| 2 | float_loop1.c | programová smyčka s krokem 0,2; realizace typem float/single | https://github.com/tisnik/presentations/blob/master/decimal/float_loop1.c |
| 3 | float_loop2.c | programová smyčka s krokem 0,1; realizace typem float/single | https://github.com/tisnik/presentations/blob/master/decimal/float_loop2.c |
| 4 | float_values.c | převod hodnot typu float/single na 32bitovou hexadecimální hodnotou | https://github.com/tisnik/presentations/blob/master/decimal/float_values.c |
| 5 | double0_1.c | součet konstant 0,1 a 0,2, porovnání s konstantou 0,3; realizace typem double | https://github.com/tisnik/presentations/blob/master/decimal/double0_1.c |
| 6 | double_loop1.c | programová smyčka s krokem 0,2; realizace typem double | https://github.com/tisnik/presentations/blob/master/decimal/double_loop1.c |
| 7 | double_loop2.c | programová smyčka s krokem 0,1; realizace typem double | https://github.com/tisnik/presentations/blob/master/decimal/double_loop2.c |
| 8 | double_values.c | převod hodnot typu float/single na 64bitovou hexadecimální hodnotou | https://github.com/tisnik/presentations/blob/master/decimal/double_values.c |
| 9 | hexa_float.c | výpis hodnot typu float/single v hexadecimálním formátu | https://github.com/tisnik/presentations/blob/master/decimal/hexa_float.c |
| 10 | hexa_double.c | výpis hodnot typu double v hexadecimálním formátu | https://github.com/tisnik/presentations/blob/master/decimal/hexa_double.c |
| 11 | decode_float.c | dekódování numerických hodnot typu float/single | https://github.com/tisnik/presentations/blob/master/decimal/decode_float.c |
| 12 | decode_double.c | dekódování numerických hodnot typu double | https://github.com/tisnik/presentations/blob/master/decimal/decode_double.c |
| 13 | decimal32_0_1.c | součet konstant 0,1 a 0,2, porovnání s konstantou 0,3; realizace typem Decimal32 | https://github.com/tisnik/presentations/blob/master/decimal/decimal32_0_1.c |
| 14 | decimal64_0_1.c | součet konstant 0,1 a 0,2, porovnání s konstantou 0,3; realizace typem Decimal64 | https://github.com/tisnik/presentations/blob/master/decimal/decimal64_0_1.c |
| 15 | decimal128_0_1.c | součet konstant 0,1 a 0,2, porovnání s konstantou 0,3; realizace typem Decimal128 | https://github.com/tisnik/presentations/blob/master/decimal/decimal128_0_1.c |
| 16 | decimal32_loop.c | programová smyčka s krokem 0,1; realizace typem Decimal32 | https://github.com/tisnik/presentations/blob/master/decimal/decimal32_loop.c |
| 17 | decimal64_loop.c | programová smyčka s krokem 0,1; realizace typem Decimal64 | https://github.com/tisnik/presentations/blob/master/decimal/decimal64_loop.c |
| 18 | decimal128_loop.c | programová smyčka s krokem 0,1; realizace typem Decimal128 | https://github.com/tisnik/presentations/blob/master/decimal/decimal128_loop.c |
| 19 | decode_decimal32.c | dekódování numerických hodnot typu Decimal32 | https://github.com/tisnik/presentations/blob/master/decimal/decode_decimal32.c |
| 20 | mandelbrot_float.c | benchmark s výpočtem Mandelbrotovy množiny, varianta pro typ float/single | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot_float.c |
| 21 | mandelbrot_double.c | benchmark s výpočtem Mandelbrotovy množiny, varianta pro typ double | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot_double.c |
| 22 | mandelbrot_decimal32.c | benchmark s výpočtem Mandelbrotovy množiny, varianta pro typ Decimal32 | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot_decimal32.c |
| 23 | mandelbrot_decimal64.c | benchmark s výpočtem Mandelbrotovy množiny, varianta pro typ Decimal64 | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot_decimal64.c |
| 24 | mandelbrot_decimal128.c | benchmark s výpočtem Mandelbrotovy množiny, varianta pro typ Decimal128 | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot_decimal128.c |
| 25 | mandelbrot.h | realizace výpočtu Mandelbrotovy množiny nezávislá na použitém datovém typu | https://github.com/tisnik/presentations/blob/master/decimal/mandelbrot.h |
| 26 | palette_mandmap.h | barvová paleta použitá v benchmarku | https://github.com/tisnik/presentations/blob/master/decimal/palette_mandmap.h |
| 27 | bench.sh | spuštění benchmarků | https://github.com/tisnik/presentations/blob/master/decimal/bench.sh |
| 28 | results2csv.py | převod výsledků benchmarků na formát CSV | https://github.com/tisnik/presentations/blob/master/decimal/results2csv.py |
20. Odkazy na Internetu
- GCC: 6.14 Decimal Floating Types
https://gcc.gnu.org/onlinedocs/gcc/Decimal-Float.html - Routines for decimal floating point emulation
https://gcc.gnu.org/onlinedocs/gccint/Decimal-float-library-routines.html - Representation of hexadecimal floating point
https://www.ibm.com/docs/en/hla-and-tf/1.6?topic=lq-representation-hexadecimal-floating-point - Decimal floating point
https://en.wikipedia.org/wiki/Decimal_floating_point - Hexadecimal Floating-Point Constants
https://www.exploringbinary.com/hexadecimal-floating-point-constants/ - Norma IEEE 754 a příbuzní: formáty plovoucí řádové tečky
https://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/ - decimal32 floating-point format
https://en.wikipedia.org/wiki/Decimal32_floating-point_format - decimal64 floating-point format
https://en.wikipedia.org/wiki/Decimal64_floating-point_format - decimal128 floating-point format
https://en.wikipedia.org/wiki/Decimal128_floating-point_format - IEEE-754 Floating-Point Conversion
http://babbage.cs.qc.cuny.edu/IEEE-754.old/32bit.html - Small Float Formats
https://www.khronos.org/opengl/wiki/Small_Float_Formats - Binary-coded decimal
https://en.wikipedia.org/wiki/Binary-coded_decimal - Chen–Ho encoding
https://en.wikipedia.org/wiki/Chen%E2%80%93Ho_encoding - Densely packed decimal
https://en.wikipedia.org/wiki/Densely_packed_decimal - A Summary of Chen-Ho Decimal Data encoding
http://speleotrove.com/decimal/chen-ho.html - Art of Assembly language programming: The 80×87 Floating Point Coprocessors
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–3.html - Art of Assembly language programming: The FPU Instruction Set
https://courses.engr.illinois.edu/ece390/books/artofasm/CH14/CH14–4.html - INTEL 80387 PROGRAMMER'S REFERENCE MANUAL
http://www.ragestorm.net/downloads/387intel.txt - Floating-Point Formats
http://www.quadibloc.com/comp/cp0201.htm - IBM Floating Point Architecture
http://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - Extended Binary Coded Decimal Interchange Code
http://en.wikipedia.org/wiki/EBCDIC - ASCII/EBCDIC Conversion Table
http://docs.hp.com/en/32212–90008/apcs01.html - EBCDIC
http://www.hansenb.pdx.edu/DMKB/dict/tutorials/ebcdic.php - EBCDIC tables
http://home.mnet-online.de/wzwz.de/temp/ebcdic/cc_en.htm - 36-bit
http://en.wikipedia.org/wiki/36-bit_word_length - 36bit.org
http://www.36bit.org/ - How did the Apple II do floating point?
https://groups.google.com/forum/#!topic/comp.emulators.apple2/qSBiG2TAlRg - IBM Floating Point Architecture
https://en.wikipedia.org/wiki/IBM_Floating_Point_Architecture - The Arithmetic Subroutines
http://www.users.waitrose.com/~thunor/mmcoyzx81/chapter17.html - ZX Floating point to Decimal code in BASIC
http://www.sinclairzxworld.com/viewtopic.php?t=1422 - Floating Point Arithmetic Package
http://www.retrocomputing.net/parts/atari/800/docs/atari_os/atari_os_user_manual08.htm - Turbo Pascal Real
http://www.shikadi.net/moddingwiki/Turbo_Pascal_Real - THE FLOATING POINT ARITHMETIC PACKAGE
http://www.atarimax.com/freenet/freenet_material/5.8-BitComputersSupportArea/7.TechnicalResourceCenter/showarticle.php?14 - The Most Expensive One-byte Mistake: Did Ken, Dennis, and Brian choose wrong with NUL-terminated text strings?
http://queue.acm.org/detail.cfm?id=2010365




































