Obsah
1. Křivky určené polynomem – nejpoužívanější křivky v současnosti
2. Interpolační a aproximační křivky
4. Interpolační křivka získaná Lagrangeovou metodou
5. Zákmity interpolační křivky u polynomů vyšších stupňů
9. Použití polynomů vyšších stupňů namísto přímky
10. Aproximace funkce Taylorovou řadou
11. Aproximační parametrické křivky pro počítačovou grafiku
12. Požadované vlastnosti parametrických křivek
14. Bézierova kvadrika – zdaleka nejčastěji používaná křivka
16. B-spline zkonstruovaná z Coonsových oblouků
18. Křivky pro počítačovou animaci
19. Repositář s demonstračními příklady
1. Křivky určené polynomem – nejpoužívanější křivky v současnosti
V současnosti, a to jak v matematice, tak i (a to zejména) v počítačové grafice, se nejčastěji setkáme s křivkami popsanými polynomem, popř. několika křivkami popsanými polynomem, které na sebe hladce navazují. Jedná se jak o křivky popsané explicitní rovnicí ve tvaru y=f(t), tak i o křivky popsané parametricky, tj. bodovou funkcí x=f(t), y=f(t). Použití polynomů je v mnoha ohledech ideální, protože polynomy lze relativně snadno a rychle vypočítat, je zaručen jejich definiční obor, lze zaručit parametrickou a popř. i geometrickou spojitost potřebného stupně a současně lze těmito křivkami aproximovat nebo interpolovat velkou škálu tvarů. Dnes si některé z těchto křivek popíšeme, přičemž se jedná o téma skutečně široké – sahající od interpolace a aproximace modelovaných dat přes vektorové editory a design fontů až k systémům CAD a CAM.
Obrázek 1: Úsečka je nejjednodušší křivkou popsanou polynomem prvního stupně.
2. Interpolační a aproximační křivky
Podle toho, zda křivka reprezentovaná polynomem prochází všemi zadanými body, popř. zda tyto body „pouze“ ovlivňují tvar křivky, rozeznáváme křivky interpolační a aproximační. V případě interpolačních křivek prochází vypočtená křivka předem zadanými (uzlovými) body. Typickou křivkou reprezentovanou polynomem, která do této skupiny náleží, je křivka vytvořená Lagrangeovým polynomem, s nímž se seznámíme v navazujících kapitolách. Naproti tomu u aproximačních křivek platí, že křivka obecně neprochází všemi zadanými uzlovými body. Příkladem takové křivky z oblasti matematiky resp. zpracování reálných dat je aproximační polynom určený metodou nejmenších čtverců. Ovšem do této skupiny patří i křivky používané v počítačové grafice – Bézierova křivka, Coonsův oblouk, B-spline, NURBS atd. Všemi těmito křivkami se pochopitelně budeme v tomto seriálu zabývat.

Obrázek 2: Parabola (tedy kuželosečka) je popsána polynomem druhého stupně.
3. Interpolační polynom
Nejprve si ukážeme interpolační polynom, tj. polynom určující křivku, která bude procházet všemi zadanými body. Konkrétně se jedná o polynom stupně n-1, který má procházet n zadanými body (jedním bodem tedy bude procházet křivka y=k, dvěma body úsečka, třemi body parabola atd.). Problém nalezení koeficientů polynomu je možné řešit takzvanou metodou neurčitých koeficientů. Polynom stupně n-1 má obecně rovnici:
y = cn-1xn-1 + cn-2xn-2 + c1x + c0
V případě, že do této rovnice postupně dosadíme všechny body xn, kterými má polynom procházet, dostaneme pro neznámé koeficienty c soustavu lineárních rovnic, kterou lze vyřešit a tyto koeficienty získat. Metoda neurčitých koeficientů je však pro praktické účely značně nevhodná, a to zvláště tehdy, je-ji počet uzlových bodů větší a soustava je řešena Gaussovou eliminační metodou. Je totiž velmi špatně podmíněna a výsledky jsou z tohoto důvodu poměrně nejisté.
Výhodnější je v tomto případě aplikace Lagrangeova interpolačního polynomu (výsledek bude shodný – interpolační polynom daného minimálního stupně existuje jen jeden – ovšem Langrangeova metoda je numericky stabilní). Ten se na základě zadaných bodů sestaví následujícím způsobem:
Ln(x) = y0l0(x) + y1l1(x) + … + ynln(x)
kde pro li(xj) platí:
li(x) = 1 pro i=j
li(x) = 0 pro i≠j
Tyto podmínky splňuje polynom:
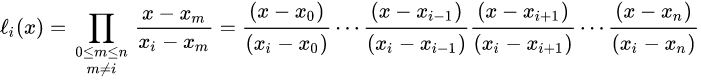
Ve skutečnosti nemusíme koeficienty Lagrangeova polynomu explicitně počítat vlastním algoritmem, protože knihovna Numpy již příslušné výpočty obsahuje (ovšem i vlastní výpočet si ukážeme, a to hned v navazující kapitole). Následující demonstrační příklad vykreslí základní polynomy, z nichž lze posléze složit výslednou funkci (a tím pádem i křivku):
"""Koeficienty Lagrangeova polynomu."""
# Založeno na příkladu z článku:
# https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html
import numpy as np
import numpy.polynomial.polynomial as poly
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = [0, 1, 2]
# vstupní koeficienty
P1_coeff = [1,-1.5,.5]
P2_coeff = [0, 2,-1]
P3_coeff = [0,-.5,.5]
# získání funkcí pro výpočet křivky na základě báze
P1 = poly.Polynomial(P1_coeff)
P2 = poly.Polynomial(P2_coeff)
P3 = poly.Polynomial(P3_coeff)
x_new = np.arange(-1.0, 3.1, 0.1)
# rozměry grafu při uložení: 640x480 pixelů
fig = plt.figure(figsize=(6.4, 4.8))
# vykreslení jednotlivých bází
plt.plot(x_new, P1(x_new), 'b', label = 'P1')
plt.plot(x_new, P2(x_new), 'r', label = 'P2')
plt.plot(x_new, P3(x_new), 'g', label = 'P3')
# zobrazení pomocných bodů v mřížce
plt.plot(x, np.ones(len(x)), 'ko', x, np.zeros(len(x)), 'ko')
# popisky grafu
plt.title('Lagrange Basis Polynomials')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
# uložení grafu do rastrového obrázku
plt.savefig("langrange_poly_1.png")
# zobrazení grafu
plt.show()
S tímto výsledkem:
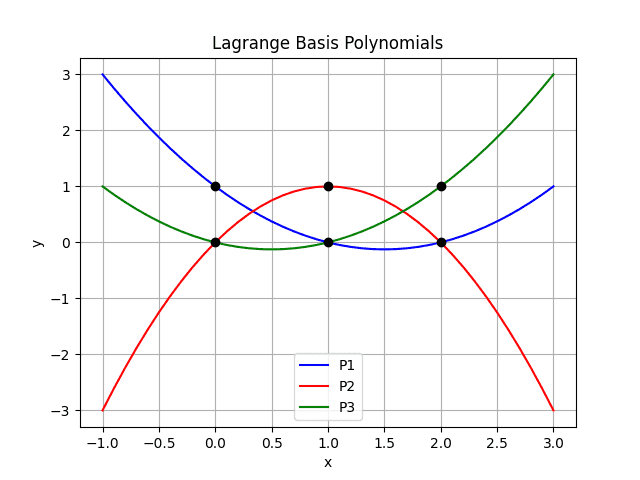
Obrázek 4: Polynomy, z nichž je možné složit výslednou interpolační křivku. Povšimněte si, že pro některé klíčové hodnoty jsou tyto polynomy buď nulové nebo se vyhodnotí na jedničku (vyznačené body).
4. Interpolační křivka získaná Lagrangeovou metodou
Nyní již můžeme demonstrační příklad z předchozí kapitoly rozšířit takovým způsobem, aby se vykreslila interpolační křivka procházející třemi zadanými body. Získání interpolační křivky pro trojici y-ových hodnot (1, 3, 2) bude vypadat takto:
# interpolační křivka L = P1 + 3*P2 + 2*P3
Vykreslením této křivky příkazem:
# vykreslení interpolační křivky i vstupních bodů plt.plot(x_new, L(x_new), 'b', x, y, 'ro')
získáme tento obrázek:

Obrázek 5: Interpolační křivka získaná Lagrangeovou metodou.
Celý skript vypadá následovně:
"""Koeficienty Lagrangeova polynomu + výpočet interpolační křivky."""
# Založeno na příkladu z článku:
# https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html
import numpy as np
import numpy.polynomial.polynomial as poly
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = [0, 1, 2]
# hodnoty na y-ové ose
y = [1, 3, 2]
P1_coeff = [1,-1.5,.5]
P2_coeff = [0, 2,-1]
P3_coeff = [0,-.5,.5]
# získání funkcí pro výpočet křivky na základě báze
P1 = poly.Polynomial(P1_coeff)
P2 = poly.Polynomial(P2_coeff)
P3 = poly.Polynomial(P3_coeff)
x_new = np.arange(-1.0, 3.1, 0.1)
# interpolační křivka
L = P1 + 3*P2 + 2*P3
# rozměry grafu při uložení: 640x480 pixelů
fig = plt.figure(figsize=(6.4, 4.8))
# vykreslení interpolační křivky i vstupních bodů
plt.plot(x_new, L(x_new), 'b', x, y, 'ro')
# popisky grafu
plt.title('Lagrange Polynomial')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
# uložení grafu do rastrového obrázku
plt.savefig("langrange_poly_2.png")
# zobrazení grafu
plt.show()
Samozřejmě nemusíme použít předpřipravené funkce z knihovny Numpy, ale můžeme si interpolační křivku založenou na Lagrangeově polynomu vypočítat vlastním algoritmem podle vzorečku z předchozí kapitoly. Ve skutečnosti to není nic těžkého. Výpočet na základě hodnot ve vstupních polích (nebo seznamech) x a y může vypadat takto:
# výpočet interpolační křivky
for i in range(n):
p = 1
for j in range(n):
if i != j:
p = p * (xp-x[j])/(x[i] - x[j])
yp += p * y[i]
Výsledkem je dvojice vektorů xp a yp s body ležícími na interpolační křivce, která bude procházet všemi zadanými body.
Celý skript může vypadat následovně:
"""Interpolace Lagrangeovým polynomem."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = [0, 1, 2]
# hodnoty na y-ové ose
y = [1, 3, 2]
# odvození stupně Lagrangeova polynomu
n = len(x)
# příprava polí pro výpočet hodnot Lagrangeovým polynomem
xp = np.arange(-1.0, 3.0, 0.1)
yp = np.zeros(40)
# výpočet interpolační křivky
for i in range(n):
p = 1
for j in range(n):
if i != j:
p = p * (xp-x[j])/(x[i] - x[j])
yp += p * y[i]
# rozměry grafu při uložení: 640x480 pixelů
fig = plt.figure(figsize=(6.4, 4.8))
# vstupní hodnoty
plt.plot(x, y, 'ko')
# vlastní interpolace polynomem
plt.plot(xp, yp, 'r-')
# popisky grafu
plt.title('Lagrange Interpolation')
plt.xlabel('x')
plt.ylabel('y')
# zobrazení mřížky
plt.grid()
# uložení grafu do rastrového obrázku
plt.savefig("langrange_interpolation_1.png")
# zobrazení grafu
plt.show()
S výsledkem:
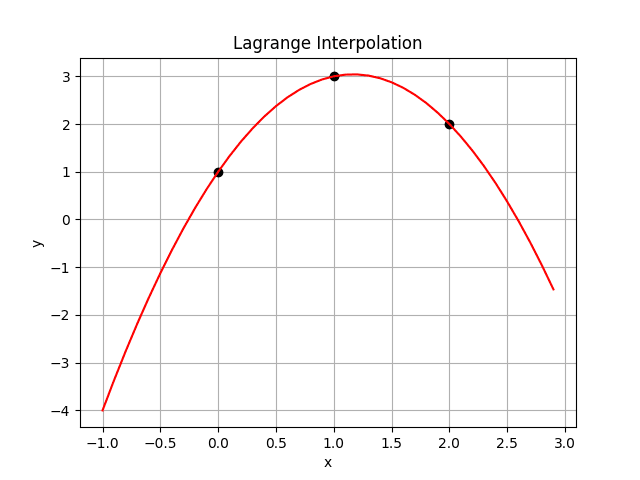
Obrázek 6: Interpolační křivka získaná Lagrangeovou metodou.
5. Zákmity interpolační křivky u polynomů vyšších stupňů
Nevýhodou interpolačních křivek založených na polynomech jsou zákmity, které nastávají při snaze o to, aby křivka skutečně procházela všemi zadanými body a současně je těchto bodů větší množství (tím se zvyšuje stupeň polynomu). Toto chování si můžeme ukázat na interpolační křivce procházející deseti řídicími body:
"""Interpolace Lagrangeovým polynomem."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(1, 11, 1)
# hodnoty na y-ové ose
y = [1, 3, 2, 3, -1, 3, 2, 2, -1, 0]
# odvození stupně Lagrangeova polynomu
n = len(x)
# příprava polí pro výpočet hodnot Lagrangeovým polynomem
xp = np.arange(1, 10.1, 0.1)
yp = np.zeros(91)
# výpočet interpolační křivky
for i in range(n):
p = 1
for j in range(n):
if i != j:
p = p * (xp-x[j])/(x[i] - x[j])
yp += p * y[i]
# rozměry grafu při uložení: 640x480 pixelů
fig = plt.figure(figsize=(6.4, 4.8))
# vstupní hodnoty
plt.plot(x, y, 'ko')
# vlastní interpolace polynomem
plt.plot(xp, yp, 'r-')
# popisky grafu
plt.title('Lagrange Interpolation')
plt.xlabel('x')
plt.ylabel('y')
# zobrazení mřížky
plt.grid()
# uložení grafu do rastrového obrázku
plt.savefig("langrange_interpolation_2.png")
# zobrazení grafu
plt.show()
S výsledkem:

Obrázek 7: Interpolační křivka získaná Lagrangeovou metodou. Povšimněte si zákmitů na obou koncích křivky.
6. Aproximační polynom
Dalším typem křivek, které se využívají v mnoha oborech (zdaleka tedy nejenom v počítačové grafice), jsou aproximační křivky. Tyto křivky obecně neprochází všemi zadanými body, ovšem tyto body nějakým způsobem ovlivňují tvar výsledných křivek. Typicky se jedná o křivky zadané polynomem, a to buď explicitně ve tvaru y=f(x) (proložení křivky naměřenými body, například s využitím dále zmíněné metody nejmenších čtverců) nebo parametricky ve tvaru bodové funkce x=f1(t), y=f2(t). Nejprve si ukážeme křivky zapsané explicitně a posléze se zaměříme na parametrické křivky, které jsou používány v počítačové grafice (a zhruba milion jich můžete vidět při pročítání tohoto článku).
7. Metoda nejmenších čtverců
V technické praxi (například při zpracování naměřených dat) velmi často stojíme před problémem nalezení vhodné křivky, která sice neprochází přesně zadanými body, ale vystihuje závislost dvou veličin, jejichž hodnoty získáme měřením (popř. jedné veličiny, která se mění v čase). Tyto křivky získáváme takzvanou metodou nejmenších čtverců a nejčastěji je hledáme právě ve tvaru polynomu (relativně nízkého stupně).
Podívejme se na ilustrační příklad, v němž simulujeme chyby při měření veličiny, jejíž průběh v čase je víceméně lineární. Průběh by tedy měl odpovídat lineární funkci neboli polynomu stupně jedna:
"""Vykreslení sady (pseudo)náhodných dat."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(-20, 20)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = x + 10*rng.random((40))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Pseudonáhodná data', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# uložení grafu do rastrového obrázku
plt.savefig("random_data_linear.png")
# zobrazení grafu
plt.show()
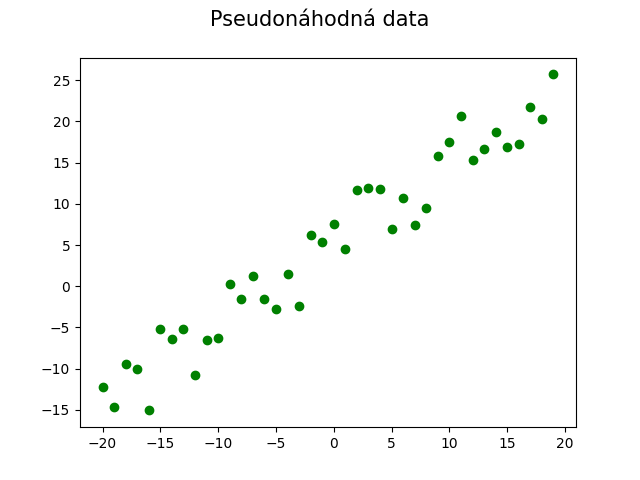
Obrázek 8: Pseudonáhodné body měřené veličiny, jejíž průběh v čase (nebo závislost na vstupu x) je víceméně lineární.
8. Lineární regrese
V knihovně Numpy nalezneme funkci nazvanou polyfit, která dokáže vypočítat polynom zadaného stupně ze zadaných vstupních dat. Pro výpočet se přitom používá metoda nejmenších čtverců. Tato metoda je založena na nalezení takového polynomu, v němž je součet druhých mocnin vzdáleností od naměřených bodů nejmenší a tudíž výsledný polynom v nejlepší možné míře reprezentuje předpokládaný průběh vstupní veličiny. Výsledkem volání této funkce jsou koeficienty polynomu zadaného stupně. Z těchto koeficientů vytvoříme funkci zavoláním poly1d.
Ukažme si nyní použití této funkce na proložení naměřených dat přímkou, tedy polynomem stupně jedna. Jedná se o klasickou lineární regresi používanou v mnoha technických oborech:
"""Vykreslení sady (pseudo)náhodných dat + lineární regrese."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 50)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = x + 10*rng.random((len(x))) - 5
# výpočet lineární regrese
coefficients = np.polyfit(x, y, 1)
# koeficienty úsečky
print(coefficients)
# konstrukce lineární funkce
poly1d_fn = np.poly1d(coefficients)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Lineární regrese', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# vykreslení interpolační křivky
plt.plot(poly1d_fn(np.arange(0, len(x))), 'r-')
# uložení grafu do rastrového obrázku
plt.savefig("linear_regression_1.png")
# zobrazení grafu
plt.show()
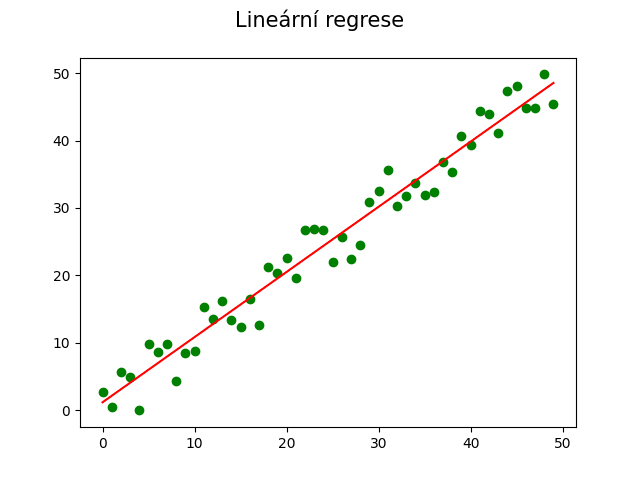
Obrázek 9: Lineární regrese naměřenými daty.
Pokud je chyba měření menší, bude výsledná přímka lépe odpovídat předpokládanému průběhu:
"""Vykreslení sady (pseudo)náhodných dat + lineární regrese."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 50)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = x + 2*rng.random((len(x))) - 1
# výpočet lineární regrese
coefficients = np.polyfit(x, y, 1)
# koeficienty úsečky
print(coefficients)
# konstrukce lineární funkce
poly1d_fn = np.poly1d(coefficients)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Lineární regrese', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# vykreslení interpolační křivky
plt.plot(poly1d_fn(np.arange(0, len(x))), 'r-')
# uložení grafu do rastrového obrázku
plt.savefig("linear_regression_2.png")
# zobrazení grafu
plt.show()
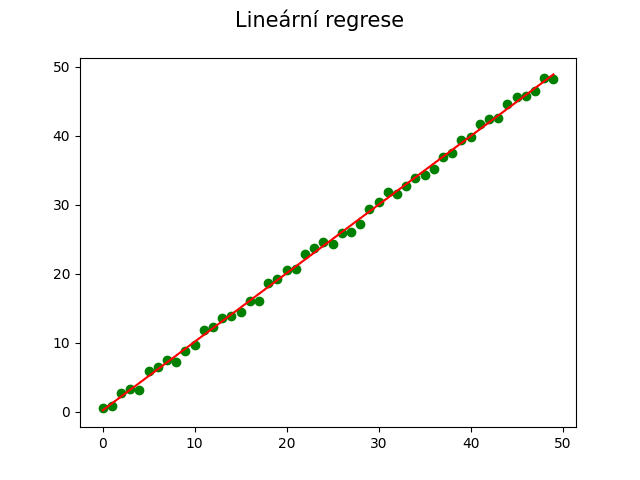
Obrázek 10: Lineární regrese naměřenými daty s menší chybou měření.
Pro příliš malý počet naměřených bodů nebo pro velkou chybu měření přestává lineární regrese poskytovat dostatečně kvalitní a použitelné výsledky:
"""Vykreslení sady (pseudo)náhodných dat + lineární regrese."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 10)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = x + 20*rng.random((len(x))) - 10
# výpočet lineární regrese
coefficients = np.polyfit(x, y, 1)
# koeficienty úsečky
print(coefficients)
# konstrukce lineární funkce
poly1d_fn = np.poly1d(coefficients)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Lineární regrese', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# vykreslení interpolační křivky
plt.plot(poly1d_fn(np.arange(0, len(x))), 'r-')
# uložení grafu do rastrového obrázku
plt.savefig("linear_regression_3.png")
# zobrazení grafu
plt.show()
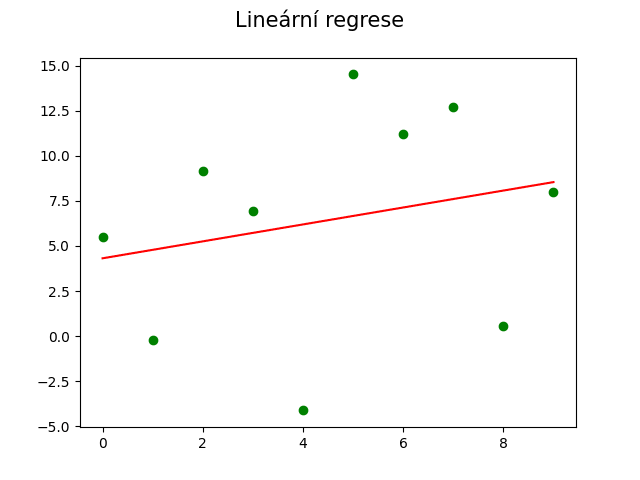
Obrázek 11: Lineární regrese naměřenými daty s větší chybou měření a menším počtem naměřených bodů.
9. Použití polynomů vyšších stupňů namísto přímky
Některá měřená data není vhodné prokládat přímkou, ale spíše polynomem vyššího stupně. Ukažme si tuto možnost na dalším demonstračním příkladu, v němž jsou data odpovídající kvadratické funkci zatížena chybou měření:
"""Vykreslení sady (pseudo)náhodných dat."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 50)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = np.power(x, 2) + 10*rng.random((len(x))) - 5
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Pseudonáhodná data', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# uložení grafu do rastrového obrázku
plt.savefig("random_data_poly.png")
# zobrazení grafu
plt.show()
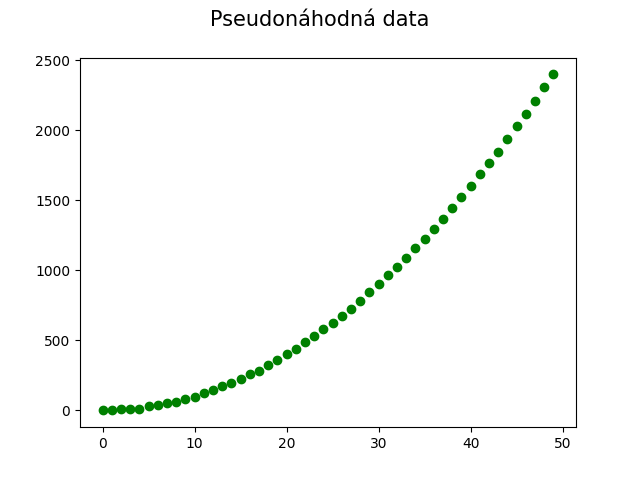
Obrázek 12: Pseudonáhodné body měřené veličiny, jejíž průběh v čase (nebo závislost na vstupu x) je víceméně kvadratický.
Proložení takových dat přímkou (tedy použití lineární regrese) nedává význam a může být dokonce velmi zavádějící:
"""Vykreslení sady (pseudo)náhodných dat + polynomiální regrese."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 50)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = np.power(x, 2) + 100*rng.random((len(x))) - 50
# výpočet lineární regrese
coefficients = np.polyfit(x, y, 1)
# koeficienty úsečky
print(coefficients)
# konstrukce polynomu
poly1d_fn = np.poly1d(coefficients)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Polynomiální regrese', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# vykreslení interpolační křivky
plt.plot(poly1d_fn(np.arange(0, len(x))), 'r-')
# uložení grafu do rastrového obrázku
plt.savefig("poly_regression_1.png")
# zobrazení grafu
plt.show()
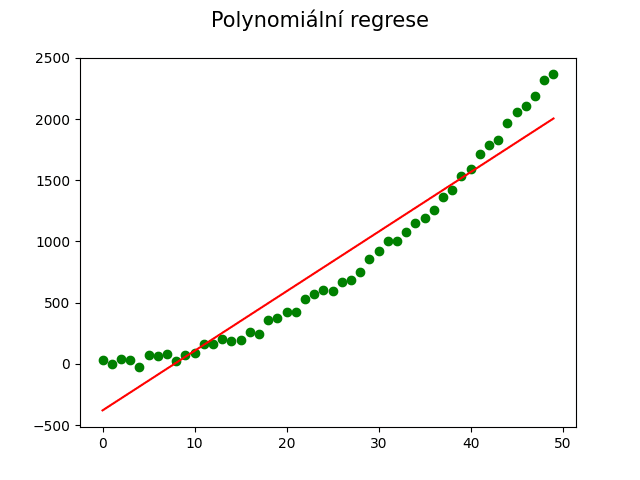
Obrázek 13: Pseudonáhodné body měřené veličiny, jejíž průběh v čase (nebo závislost na vstupu x) je víceméně kvadratický; proložení přímkou.
V tomto případě je mnohem lepší použít proložení polynomem druhého stupně tak, jak je to ukázáno v následujícím demonstračním příkladu:
"""Vykreslení sady (pseudo)náhodných dat + polynomiální regrese."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.arange(0, 50)
# generátor pseudonáhodných dat
rng = np.random.default_rng(seed=42)
# hodnoty na y-ové ose
y = np.power(x, 2) + 100*rng.random((len(x))) - 50
# výpočet lineární regrese
coefficients = np.polyfit(x, y, 2)
# koeficienty úsečky
print(coefficients)
# konstrukce polynomu
poly1d_fn = np.poly1d(coefficients)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Polynomiální regrese', fontsize=15)
# vrcholy na křivce
ax.plot(x, y, 'go')
# vykreslení interpolační křivky
plt.plot(poly1d_fn(np.arange(0, len(x))), 'r-')
# uložení grafu do rastrového obrázku
plt.savefig("poly_regression_2.png")
# zobrazení grafu
plt.show()
Nyní je již výsledek mnohem lepší:
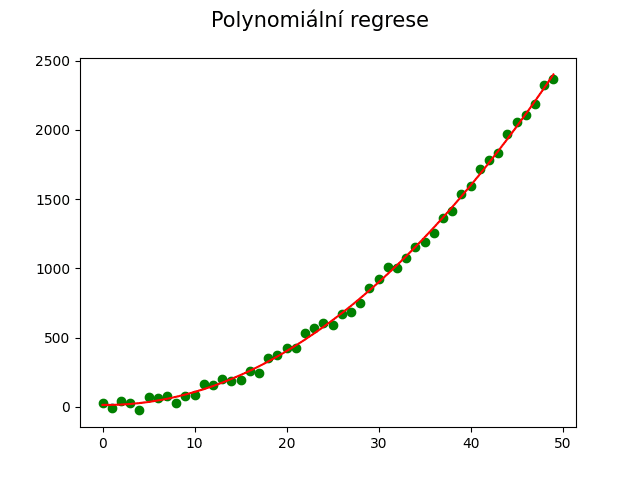
Obrázek 14: Pseudonáhodné body měřené veličiny, jejíž průběh v čase (nebo závislost na vstupu x) je víceméně kvadratický; proložení polynomem druhého stupně.
10. Aproximace funkce Taylorovou řadou
V další části dnešního článku si ukážeme, jak je možné vytvořit graf, v němž dochází ke stále přesnější aproximaci nějaké funkce ve vybraném bodě Taylorovým polynomem, tedy opět nějakou polynomiální aproximační křivkou. Opět se jedná o oblast, v níž může být animace přehlednější než jediný statický graf s větším množstvím funkcí, jejichž průběhy se navíc v některých intervalech překrývají.
V dalším příkladu je použit vzorec pro výpočet Taylorovy řady pro goniometrickou funkci sinus v daném bodě (pro jiné funkce budou členy řady odlišné):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
import numpy as np
import matplotlib.pyplot as plt
def taylor_series(x, order):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-20, 20, 500)
# funkce kterou aproximujeme Taylorovou řadou
y = np.sin(x)
# vykreslení původní funkce
plt.plot(x, y, label='sin(x)')
# příprava pro vlastní výpočet
ys = np.vectorize(taylor_series)
# aproximace Taylorovou řadou
N = 1
# výpočet s převodem na typ numpy.array
approx = ys(x, N)
# vykreslení aproximace funkce
plt.plot(x, approx, label='order {o}'.format(o=N))
# limity na ose y
plt.ylim([-3, 3])
# legenda grafu
plt.legend()
# uložení grafu do rastrového obrázku
plt.savefig("taylor_sin_1.png")
# zobrazení grafu
plt.show()
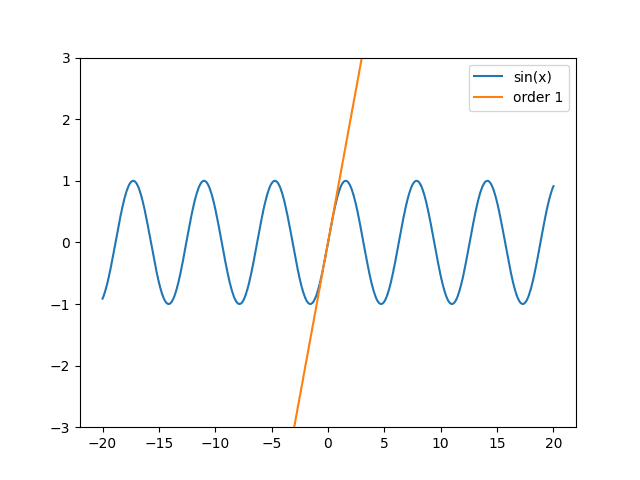
Obrázek 15: Aproximace funkce sinus Taylorovým polynomem prvního stupně – přímkou.
Čím větší je stupeň Taylorova polynomu, tím přesnější bude aproximace (a tím náročnější jsou i všechny výpočty):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
import numpy as np
import matplotlib.pyplot as plt
def taylor_series(x, order):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-20, 20, 500)
# funkce kterou aproximujeme Taylorovou řadou
y = np.sin(x)
# vykreslení původní funkce
plt.plot(x, y, label='sin(x)')
# příprava pro vlastní výpočet
ys = np.vectorize(taylor_series)
# aproximace Taylorovou řadou
N = 2
# výpočet s převodem na typ numpy.array
approx = ys(x, N)
# vykreslení aproximace funkce
plt.plot(x, approx, label='order {o}'.format(o=N))
# limity na ose y
plt.ylim([-3, 3])
# legenda grafu
plt.legend()
# uložení grafu do rastrového obrázku
plt.savefig("taylor_sin_2.png")
# zobrazení grafu
plt.show()
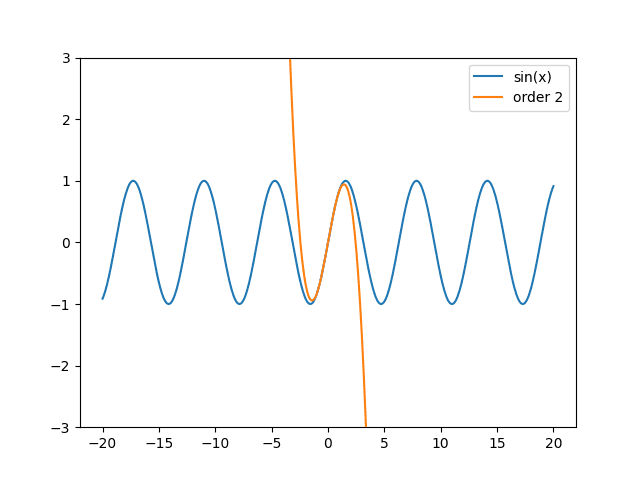
Obrázek 16: Aproximace funkce sinus Taylorovým polynomem druhého stupně.
V posledním příkladu ukazujícího Taylorův polynom opět budeme aproximovat sinusovku, nyní ovšem polynomem stupně 2 až 12. Z výsledků je opět patrné stále lepší a lepší aproximace v okolí zvoleného bodu:
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
import numpy as np
import matplotlib.pyplot as plt
def taylor_series(x, order):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-20, 20, 500)
# funkce kterou aproximujeme Taylorovou řadou
y = np.sin(x)
# vykreslení původní funkce
plt.plot(x, y, label='sin(x)')
# příprava pro vlastní výpočet
ys = np.vectorize(taylor_series)
# aproximace
N = 12
for order in range(1, N+1):
# výpočet s převodem na typ numpy.array
approx = ys(x, order)
plt.plot(x, approx, label='order {o}'.format(o=order))
# limity na ose y
plt.ylim([-3, 3])
# legenda grafu
plt.legend()
# uložení grafu do rastrového obrázku
plt.savefig("taylor_sin_1_12.png")
# zobrazení grafu
plt.show()
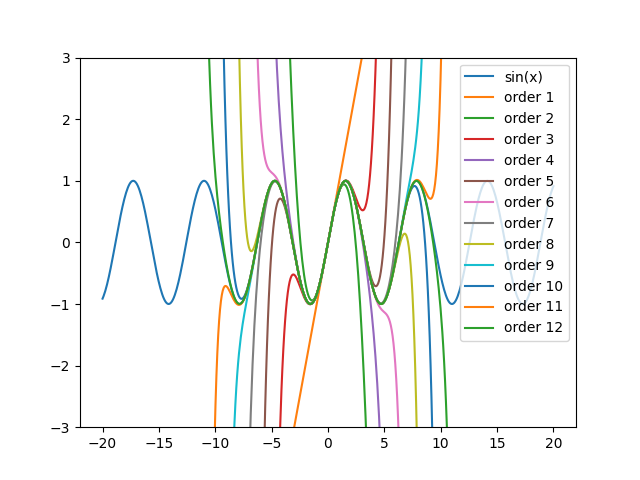
Obrázek 17: Aproximace funkce sinus Taylorovým polynomem druhého až dvanáctého stupně.
11. Aproximační parametrické křivky pro počítačovou grafiku
V počítačové grafice se nejčastěji setkáme s parametrickými křivkami, tedy křivkami, jejichž tvar je určen bodovou funkcí závislou pouze na parametru t. Tyto křivky jsou založeny na polynomech nízkých stupňů, u nichž se nevyskytují velké zákmity, lze zajistit jejich hladké napojení (jak parametrické, tak i geometrické) a navíc je jejich výpočet většinou uspokojivě rychlý. Typicky se tak setkáme s polynomy druhého a třetího stupně, neboli s kvadrikami a kubikami.
V interaktivní počítačové grafice (což je podmnožina grafiky jako celku) se nejčastěji používají polynomy třetího stupně, protože u polynomů nižších stupňů nelze vždy zaručit podmínky napojení (C2), což však nevadí například u fontů. Kubický polynom zaručuje spojitost C1 a C2 (a samozřejmě také G1 a G2) a poskytuje tak uspokojivé modelovací možnosti. Použití polynomů vyššího stupně vede ke zvýšení časové náročnosti výpočtů, možnému vzniku numerických chyb, případně i k nežádoucím oscilacím zmíněným výše.
Jen pro připomenutí si ukažme, jak se vlastně vykresluje parametricky zadaná křivka:
"""Parametrická křivka: kružnice."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
# poloměr kružnice
r = 2.0
# výpočet bodů ležících na kružnici
x = r*np.cos(t)
y = r*np.sin(t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Kružnice', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# vrcholy na křivce (každý čtvrtý)
ax.plot(x[::4], y[::4], 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("circle.png")
# zobrazení grafu
plt.show()
S výsledkem:
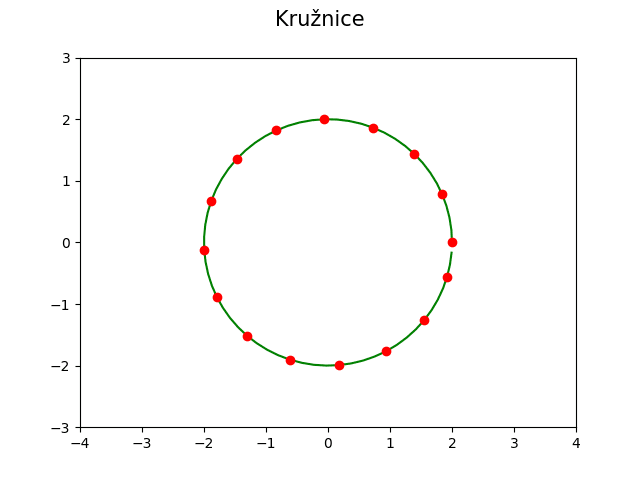
Obrázek 18: Parametricky zadaná kružnice.
12. Požadované vlastnosti parametrických křivek
Mezi často požadované vlastnosti parametrických křivek (a i pro jejich zobecnění do ploch) patří:
- Invariance k lineárním transformacím popř. i k perspektivní projekci. Tato vlastnost zaručuje, že lineární transformace popř. projekce aplikované na řídící body parametrické plochy má stejný výsledek, jako aplikace této transformace na každý bod vygenerované plochy. Je zřejmé, že při splnění podmínky invariance je z výkonnostního hlediska výhodnější aplikovat transformace pouze na řídící body parametrické plochy. Většina používaných aproximačních ploch podmínku invariance splňuje vzhledem k lineárním transformacím, u racionálních křivek a ploch (mezi něž patří i NURBS) je současně splněna i invariance vzhledem k perspektivní projekci. Dále probírané (neracionální) Bézierovy křivky resp. Coonsovy oblouky však nejsou invariantní vzhledem k perspektivní projekci, což ovšem v 2D grafice nevadí.
- Vlastnost konvexní obálky zaručuje, že všechny body vygenerované parametrické křivky či plochy leží v konvexní obálce všech svých řídících bodů. Může se použít i slabší podmínka, kde pouze část plochy leží v konvexní obálce některých řídících bodů. Pokud zaručíme tuto vlastnost, zjednoduší se velké množství algoritmů prováděných s modely těles, například test na průnik dvou těles, vytváření obalových těles nebo test průsečíku paprsku s tělesem. Bézierovy křivky i plochy leží uvnitř konvexní obálky, stejně jako Coonsovy oblouky. Totéž platí pro racionální Bézierovy plochy a křivky, ovšem za předpokladu, že jsou váhy všech řídících bodů kladné (což je téma navazujícího článku).
- Lokalita změn zaručuje, že se změnou polohy jednoho řídícího bodu se změní tvar jen části křivky/plochy přiléhající k tomuto řídícímu bodu, nikoli plocha celá. Tato vlastnost je důležitá především při interaktivním modelování těles pomocí parametrických ploch, protože lze dopředu odhadnout vliv editačních operací na tvar výsledné plochy. Neméně důležitá je i v interaktivní 2D grafice – proto jsou zde ostatně často nasazovány Bézierovy křivky
- Křivka nebo plocha může procházet krajními body svého řídícího polygonu. Tuto vlastnost, která je zaručena například u Bézierových křivek a ploch, lze využít pro snadné napojování jednotlivých plátů s dodržením požadované třídy spojitosti C0, C1, G1 nebo G2. Této vlastnosti lze dosáhnout i u B-spline ploch použitím takzvaných násobných řídících bodů, tj. bodů majících stejné souřadnice v prostoru. I s touto technikou se dnes setkáme.
13. Coonsova kubika
Velmi důležitou křivkou definovanou polynomem třetího stupně je Coonsova kubika, která je někdy známá i jako Coonsův oblouk (Coons arc). Tato křivka je definována čtyřmi řídicími body, kterými obecně neprochází – je to tedy skutečná aproximační křivka. Ve skutečnosti tato křivka začíná a končí v antitěžišti trojúhelníků tvořených prvními resp. posledními třemi řídicími body (antitěžiště leží, podobně jako těžiště, na těžnici, ovšem v opačné třetině než těžiště). Coonsovu kubiku lze vypočítat jako lineární kombinaci Coonsových bázových polynomů, z nichž každý určuje váhu jednoho z řídicích bodů – pro t=0 má nejvyšší váhu první řídicí bod, pro t=1 má nejvyšší váhu bod poslední atd. Další demonstrační příklad tyto bázové polynomy vykreslí:
"""Bázové polynomy Coonsovy kubiky."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.02)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Bázové polynomy', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 1)
ax.set_ylim(0, 4)
# bázové polynomy
ax.plot(t, C[0], 'r-')
ax.plot(t, C[1], 'g-')
ax.plot(t, C[2], 'b-')
ax.plot(t, C[3], 'k-')
# uložení grafu do rastrového obrázku
plt.savefig("coons_basis.png")
# zobrazení grafu
plt.show()
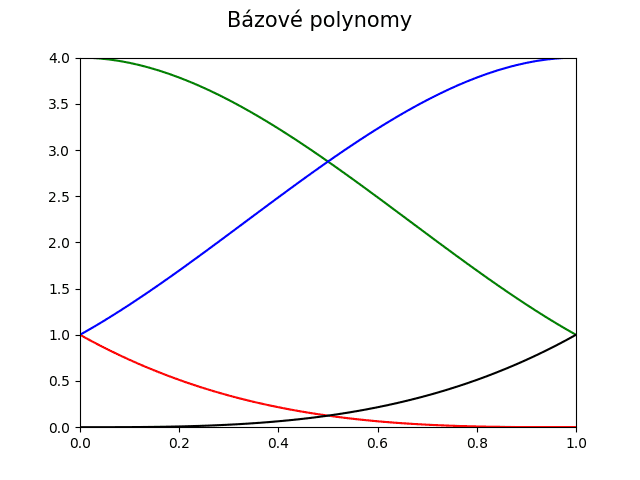
Obrázek 19: Bázové polynomy Coonsovy kubiky. Ve skutečnosti je ještě na konci nutné podělit hodnoty na y-ové ose šesti (viz další příklad).
Ze znalosti bázových polynomů již můžeme Coonsovu kubiku snadno vykreslit pro zadanou čtveřici řídicích bodů:
"""Parametrická křivka: Coonsova kubika."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.05)
# řídicí body Coonsovy kubiky
xc = (1, 1, 3, 3)
yc = (1, 2, 2, 0.5)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Coonsova kubika', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(0, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# řídicí body Coonsovy kubiky
ax.plot(xc, yc, 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("coons.png")
# zobrazení grafu
plt.show()
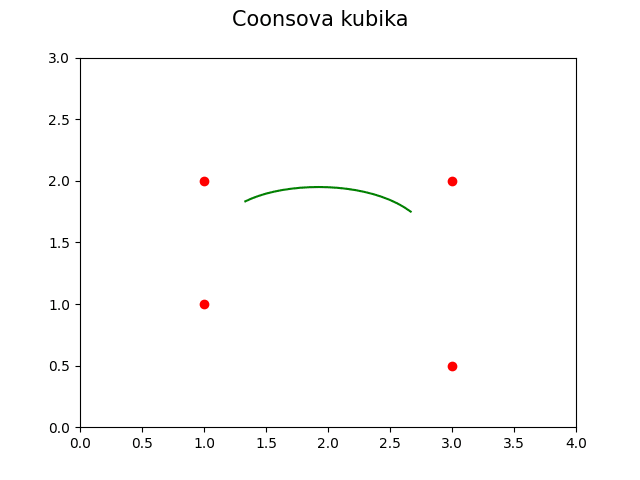
Obrázek 20: Coonsova kubika pro čtyři řídicí body.
14. Bézierova kvadrika – zdaleka nejčastěji používaná křivka
Bézierovy křivky patří v počítačové grafice mezi jedny z nejpoužívanějších typů parametrických (aproximačních) křivek. Jsou totiž velmi jednoduché jak na vytváření a editaci (tj. nepřináší žádné větší komplikace pro uživatele), tak i velmi rychlé při vykreslování, což je výhoda pro programátora nebo pro hardwarovou implementaci vykreslování (to se projeví například i v rychlejším RIPování PostScriptových souborů). Bézierovy křivky stupně dvě a tři, tj. kvadriky a kubiky, jsou použity v mnoha aplikacích a technologiích, včetně PostScriptu a PostScriptových fontů (kubické křivky), TrueType fontů (kvadratické křivky), formátech aplikace Inkscape, CorelDraw!, Adobe Illustrator a „vektorového“ XML formátu SVG – Scalable Vector Graphics.
V některých aplikacích, kde se pracuje s parametrickými křivkami (například tvorba fontů TrueType), jsou využity i jednodušší Bézierovy kvadratické křivky, které jsou určeny pouze jedním řídicím bodem a dvojicí bodů kotvicích. Křivka prochází prvním a třetím bodem (kotvicí body), druhý bod (řídicí) určuje současně oba tečné vektory. Jedná se o zdaleka nejpoužívanější křivky vůbec, protože například tento článek má přibližně 90kB, což odpovídá přibližně 60000 znakům. Pokud je každý znak reprezentován deseti oblouky Bézierovy kvadriky, vidíte jen na této stránce cca 600 000 těchto křivek!
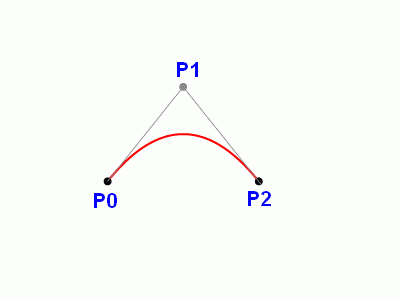
Obrázek 21: Bézierova kvadrika.
Několika způsoby konstrukce Bézierových křivek se budeme podrobněji věnovat příště, takže si nyní pouze ukažme, jak vypadají její bázové polynomy nazvané Bernsteinovy polynomy a jak se jejich lineární kombinací vykreslí křivka:
"""Parametrická křivka: Bézierova kvadrika."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.05)
# řídicí body Bézierovy kubiky
xc = (1, 2, 3)
yc = (1, 2.9, 1)
# Bernsteinovy polynomy
B = [(1-t)**2,
2*t*(1-t),
t**2]
# výpočet bodů ležících na Bézierově kvadrice
x = 0
y = 0
for i in range(0, 3):
x += xc[i]*B[i]
y += yc[i]*B[i]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Bézierova kvadrika', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(0, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# řídicí body Bézierovy kvadriky
ax.plot(xc, yc, 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("bezier_quadric.png")
# zobrazení grafu
plt.show()
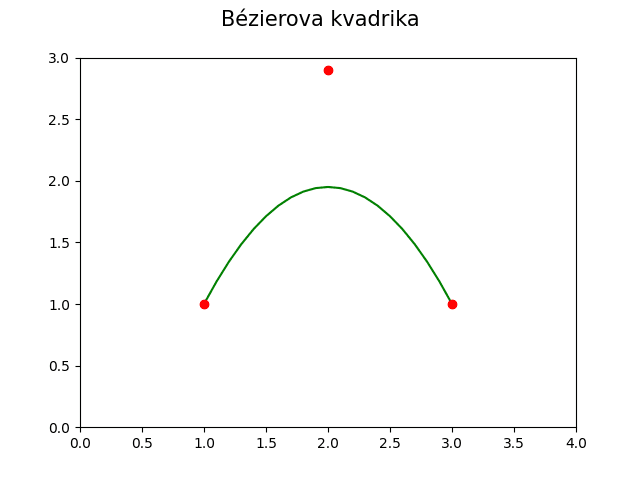
Obrázek 22: Bézierova kvadrika.
15. Bézierova kubika
Bézierovy kubické křivky jsou zadány pomocí čtyř bodů v ploše či v prostoru. Křivka přitom prochází prvním a posledním (kotvicím) bodem, druhý a třetí bod (řídicí) určují tečné vektory na začátku a na konci křivky. Křivka tedy druhým a třetím řídicím bodem obecně neprochází, což je patrné i z dalšího ilustračního obrázku:
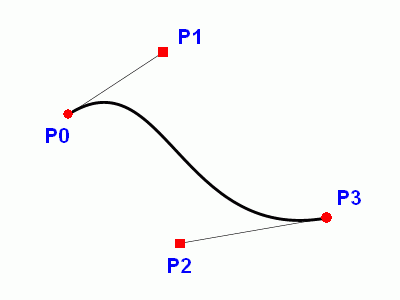
Obrázek 23: Bézierova kubika.
Další příklad obsahuje definice čtyř Bernsteinových polynomů Bézierovy kubiky:
"""Bázové polynomy Bézierovy kubiky."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.02)
# Bernsteinovy polynomy
B = [(1-t)**3,
3*t*(1-t)**2,
3*t**2*(1-t),
t**3]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Bázové polynomy', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
# bázové polynomy
ax.plot(t, B[0], 'r-')
ax.plot(t, B[1], 'g-')
ax.plot(t, B[2], 'b-')
ax.plot(t, B[3], 'k-')
# uložení grafu do rastrového obrázku
plt.savefig("bezier_basis.png")
# zobrazení grafu
plt.show()
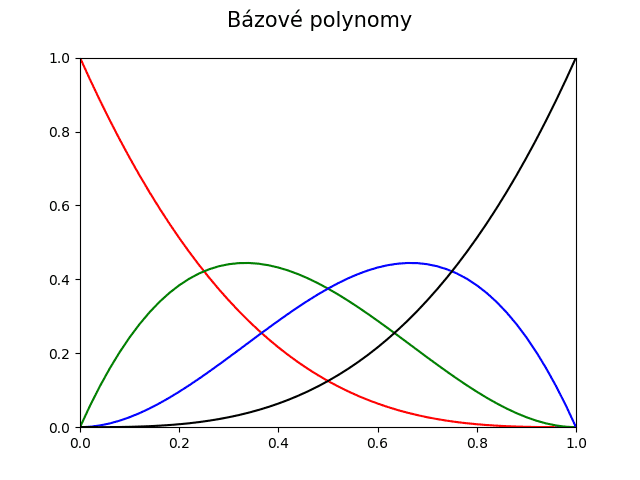
Obrázek 24: Bernsteinovy polynomy pro Bézierovu kubiku.
Způsob vykreslení Bézierovy kubiky definované čtyřmi řídicími body se nijak neliší například od vykreslení Coonsova oblouku – liší se jen bázové polynomu:
"""Parametrická křivka: Bézierova kubika."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.05)
# řídicí body Bézierovy kubiky
xc = (1, 1, 3, 3)
yc = (1, 2.9, 0.1, 2)
# Bernsteinovy polynomy
B = [(1-t)**3,
3*t*(1-t)**2,
3*t**2*(1-t),
t**3]
# výpočet bodů ležících na Bézierově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*B[i]
y += yc[i]*B[i]
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Bézierova kubika', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(0, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# řídicí body Bézierovy kubiky
ax.plot(xc, yc, 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("bezier.png")
# zobrazení grafu
plt.show()

Obrázek 25: Bézierova kubika.
16. B-spline zkonstruovaná z Coonsových oblouků
Z na sebe navazujících Coonsových oblouků je možné vytvořit uniformní neracionální B-spline křivku definovanou n řídicími body. Postup je snadný – vždy čtyři po sobě jdoucí body vytváří Coonsův oblouk; celkově je nutné vykreslit n-3 takových oblouků. Přitom je zaručeno, že tyto oblouky na sebe hladce navazují, což je ostatně ukázáno i v dalším (dnes již posledním) demonstračním příkladu:
"""Parametrická křivka: B-spline složená z Coonsových oblouků."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.05)
# řídicí body B-spline
xc = (1, 1, 2, 2.5, 3, 2)
yc = (1, 2, 2, 0.1, 2.9, 2.9)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(0, 3)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# první oblouk
draw_coons_arc(xc[0:4], yc[0:4], ax, "r-")
# druhý oblouk
draw_coons_arc(xc[1:5], yc[1:5], ax, "b-")
# třetí oblouk
draw_coons_arc(xc[2:6], yc[2:6], ax, "g-")
# uložení grafu do rastrového obrázku
plt.savefig("B-spline_1.png")
# zobrazení grafu
plt.show()
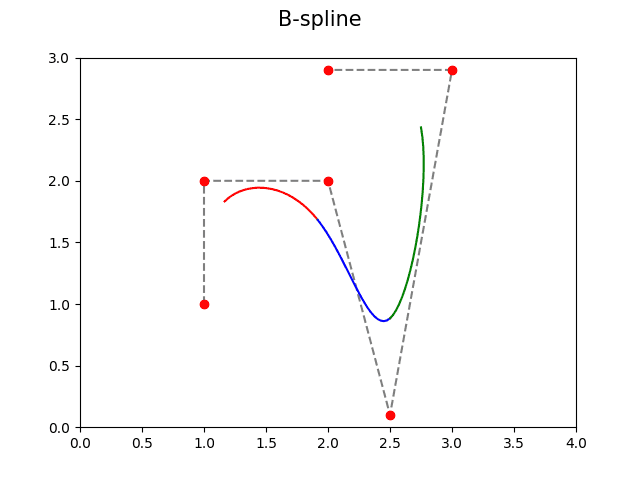
Obrázek 26: B-spline vytvořená z Coonsových oblouků.
17. Násobné body v B-spline
Při práci s B-spline křivkami se často používají takzvané násobné řídící body, což jsou sousední řídící body, které jsou umístěny na stejné souřadnici v ploše či v prostoru. S využitím násobných řídících bodů lze na křivce vytvářet zlomy či úseky, které se k řídícím bodům více přimykají (tím se částečně nahrazují váhy řídících bodů). Také lze zajistit, aby křivka procházela svými krajními body; u B-spline totiž tato vlastnost běžně splněna není, na rozdíl od Bézierových křivek, které vždy svými krajními body prochází.
V dalším demonstračním příkladu se pro první a poslední oblouk používají násobné body:
"""Parametrická křivka: B-spline složená z Coonsových oblouků, násobné body."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 1.05, 0.05)
# řídicí body B-spline
xc = (1, 1, 2, 2.5, 3, 2)
yc = (1, 2, 2, 0.1, 2.9, 2.9)
# Coonsovy polynomy
C = [(1-t)**3,
3*t**3 - 6*t**2 + 4,
-3*t**3 + 3*t**2 + 3*t + 1,
t**3]
def draw_coons_arc(xc, yc, ax, style):
# výpočet bodů ležících na Coonsově kubice
x = 0
y = 0
for i in range(0, 4):
x += xc[i]*C[i]
y += yc[i]*C[i]
# konečná úprava sumy
x /= 6
y /= 6
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, style)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('B-spline', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(0, 4)
ax.set_ylim(0, 3)
# řídicí body B-spline
ax.plot(xc, yc, 'k--', alpha=0.5)
ax.plot(xc, yc, 'ro')
# oblouk s násobnými body
draw_coons_arc((xc[0], xc[0], xc[1], xc[2]),
(yc[0], yc[0], yc[1], yc[2]), ax, "k-")
# první oblouk
draw_coons_arc(xc[0:4], yc[0:4], ax, "r-")
# druhý oblouk
draw_coons_arc(xc[1:5], yc[1:5], ax, "b-")
# třetí oblouk
draw_coons_arc(xc[2:6], yc[2:6], ax, "g-")
# oblouk s násobnými body
draw_coons_arc((xc[3], xc[4], xc[5], xc[5]),
(yc[3], yc[4], yc[5], yc[5]), ax, "k-")
# uložení grafu do rastrového obrázku
plt.savefig("B-spline_2.png")
# zobrazení grafu
plt.show()
Přidané oblouky vytvořené násobnými body jsou zobrazeny černou barvou:
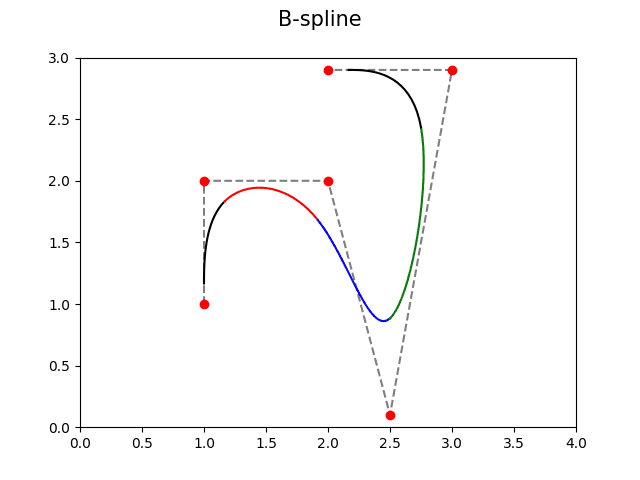
Obrázek 27: B-spline s násobnými body.
18. Křivky pro počítačovou animaci
Poměrně specifickou skupinou křivek jsou křivky používané v počítačem řízené animaci. Změny vlastností předmětů ve scéně mezi jednotlivými klíčovými snímky (keyframes) totiž většinou neprobíhají lineárně, podobně jako (předpřipravený) pohyb předmětů a objektů. Pohyb předmětů však většinou není vhodné popisovat například B-spline křivkou či sadou na sebe navazujících Bézierových křivek. Je tomu tak z toho důvodu, že při konstantní změně nezávislé proměnné t, kterou zde můžeme považovat za čas, by se pohyb odehrával různou rychlostí – typicky by byl závislý na vzájemné vzdálenosti řídicích bodů, lokální křivosti křivky atd. Bylo by tedy lepší použít spíše parametrické křivky, v nichž změna nezávislé proměnné t o nějakou konstantu dt povede i k pohybu, jehož rychlost se nebude měnit. A právě tuto podmínku (i některé další) splňují animační křivky, které si popíšeme příště.
19. Repositář s demonstračními příklady
Všechny předminule, minule i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
20. Odkazy na Internetu
- Famous Curves Index
https://mathshistory.st-andrews.ac.uk/Curves/ - Curve (Wikipedia)
https://en.wikipedia.org/wiki/Curve - Mathematical curves
https://www.2dcurves.com/index.html - Curves (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Curves.html - Smooth Curve (Wolfram MathWorld)
https://mathworld.wolfram.com/SmoothCurve.html - Spirals (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Spirals.html - An Interactive Introduction to Splines
https://ibiblio.org/e-notes/Splines/Intro.htm - Parabola
https://www.2dcurves.com/conicsection/conicsectionp.html - Hyperbola
https://www.2dcurves.com/conicsection/conicsectionh.html - Dioklova kisoida
https://cs.wikipedia.org/wiki/Dioklova_kisoida - Archimédova spirála
https://cs.wikipedia.org/wiki/Archim%C3%A9dova_spir%C3%A1la - Conchoid (mathematics)
https://en.wikipedia.org/wiki/Conchoid_(mathematics) - Algebraic curve
https://en.wikipedia.org/wiki/Algebraic_curve - Transcendental curve
https://en.wikipedia.org/wiki/Transcendental_curve - Spiral
https://en.wikipedia.org/wiki/Spiral - List of spirals
https://en.wikipedia.org/wiki/List_of_spirals - Hyperbolická spirála
https://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_spir%C3%A1la - Hyperbolic Spiral
https://mathworld.wolfram.com/HyperbolicSpiral.html - Lituus (mathematics)
https://en.wikipedia.org/wiki/Lituus_(mathematics) - Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/ - Cornu Spiral
http://hyperphysics.gsu.edu/hbase/phyopt/cornu.html - Spiral
https://www.2dcurves.com/spiral/spiral.html - Algebraic Curves
https://mathworld.wolfram.com/topics/AlgebraicCurves.html - Elliptic Curves
https://mathworld.wolfram.com/topics/EllipticCurves.html - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Curves we (mostly) don't learn in high school (and applications)
https://www.youtube.com/watch?v=3izFMB91K_Q - Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
https://www.maa.org/press/periodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions - Apollonius of Perga
https://en.wikipedia.org/wiki/Apollonius_of_Perga - Catenary arch
https://en.wikipedia.org/wiki/Catenary_arch - Parabolic arch
https://en.wikipedia.org/wiki/Parabolic_arch - Wattova křivka
https://www.geogebra.org/m/gNh4bW9r - Model stegosaura byl získán na stránce
http://www.turbosquid.com/HTMLClient/FullPreview/Index.cfm/ID/171071/Action/FullPreview - Obrázek nohy dinosaura byl získán na adrese
http://perso.wanadoo.fr/rimasson/3d/leg.htm - Spirograph
https://en.wikipedia.org/wiki/Spirograph - Epicykloida
https://cs.wikipedia.org/wiki/Epicykloida - Hypocykloida
https://cs.wikipedia.org/wiki/Hypocykloida - Hypotrochoida
https://cs.wikipedia.org/wiki/Hypotrochoida - Superelipsoidy a kvadriky v POV-Rayi
https://www.root.cz/clanky/superelipsoidy-a-kvadriky-v-pov-rayi/ - Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
https://elepa.files.wordpress.com/2013/11/fifty-famous-curves.pdf - Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981 - Bourke Paul: Quadrics,
July 1996 - Bourke Paul: Superellipse and Superellipsoid,
January 1990 - Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979 - Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968 - Glossary of Bridge Terminology
http://sdrc.lib.uiowa.edu/eng/bridges/WaddellGlossary/GlossC.htm - Brachistochrona
https://cs.wikipedia.org/wiki/Brachistochrona - Missions: Cassini
https://solarsystem.nasa.gov/missions/cassini/overview/ - Giovanni Domenico Cassini
https://en.wikipedia.org/wiki/Giovanni_Domenico_Cassini - Cassini Ovals
https://mathworld.wolfram.com/CassiniOvals.html - Geocentrismus
https://cs.wikipedia.org/wiki/Geocentrismus - Who was Giovanni Cassini?
https://www.universetoday.com/130823/who-was-giovanni-cassini/ - Special plane curves
http://xahlee.info/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html - Why Does Slicing a Cone Give an Ellipse?
https://infinityisreallybig.com/2019/02/08/why-does-slicing-a-cone-give-an-ellipse/ - Interpolace
https://mathonline.fme.vutbr.cz/pg/Algoritmy/05_APROX_KRIVKY.htm - Lagrange Polynomial Interpolation
https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html - Python Program for Lagrange Interpolation Method (with Output)
https://www.codesansar.com/numerical-methods/python-program-lagrange-interpolation-method.htm






































