Křivky v přírodě, architektuře, stavitelství i v počítačové grafice

Obsah

1. Křivky (nejenom) v počítačové grafice

2. Eukleidovské konstrukce

3. Příklad Euklidovské konstrukce

4. Slavné geometrické úlohy, které nelze vyřešit jen pravítkem (bez měřítka) a kružítkem

5. Další milník: kuželosečky

6. Řetězovka: křivka používaná nejenom v architektuře

7. Svět spirál

8. Spline

9. Křivky v industriální době

10. Praktická část článku

11. Základní kuželosečky vytvořené v nástroji GeoGebra

12. Kuželosečka procházející pěti vybranými body

13. Jednoduchá úsečka, parabola a hyperbola vykreslená Matplotlibem

14. Řetězovka

15. Rozdíl mezi řetězovkou a parabolou

16. Elipsa specifikovaná parametricky, obecná elipsa

17. Vykreslení křivek v polárním souřadném systému

18. Spirály

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

1. Křivky (nejenom) v počítačové grafice

V přírodě, architektuře, v dopravě (doslova v každé zatáčce či na železnici v každém oblouku) i ve světě počítačů se prakticky na každém kroku setkáme s nějakou formou křivky. Tyto útvary byly zkoumány již ve starověku, ovšem písemné důkazy a dokonce i jména některých učenců pochází až z antického Řecka. Původně byly křivky zkoumány a konstruovány ryze geometrickými cestami. Takto navržené křivky se uplatnily i v architektuře. Změnu v tomto pohledu na křivky přinesl až slavný René Descartes v sedmnáctém století, který začal křivky popisovat pomocí vzorců (funkcí). Křivky popsané analytickou geometrií zavedenou Descartesem, konkrétně především elipsa, navíc umožnily popis pohybu planet či jiných těles ve vesmíru s využitím tří Keplerových zákonů. Později se křivky začaly stále více uplatňovat s rozvojem strojů (viz například Wattovu křivku), v designu (spline křivky), CAD/CAM (NURBS) atd.

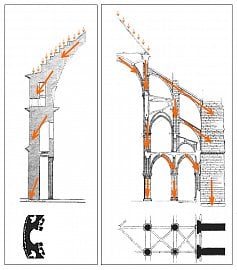
Obrázek 1: Křivky se používají pro návrh oblouků v architektuře.
Zdroj obrázku: Wikipedia, https://upload.wikimedia.or­g/wikipedia/commons/8/83/Ro­manesque_and_Gothic_loads­.jpg

Dnešní článek se snaží být jakýmsi úvodem do celé problematiky, takže se (alespoň prozatím) nebudeme zabývat teorií křivek. Spíše se seznámíme s některými zajímavými historickými fakty, které s křivkami souvisí a ve druhé polovině článku si ukážeme i to, jak lze vybrané křivky vytvořit, a to buď v interaktivním nástroji GeoGebra nebo v kombinaci Pythonu a knihovny Matplotlib (tyto příklady je možné si vyzkoušet i v Jupyter Notebooku, a to bez nutnosti jejich modifikace).

Obrázek 2: Pečlivě vypočtené křivky tvoří základ horské dráhy (nejedná se o kruhové oblouky).

2. Eukleidovské konstrukce

Nejprve se budeme zabývat klasickou (antickou) geometrií, protože se (alespoň podle mého názoru) jedná o nejnázornější oblast matematiky a samotná teorie křivek více či méně vychází právě z původní geometrie. Začneme takzvanými euklidovskými konstrukcemi. V původních eukleidovských konstrukcích se pro narýsování nějakého útvaru nebo křivky používají pouze dva nástroje – pravítko a kružítko. Ovšem na rozdíl od dnes běžných pravítek a kružítek jsou pro eukleidovské konstrukce používány zjednodušené (abstraktní) formy těchto nástrojů. Konkrétně pravítko má pouze jedinou hranu (tedy nejedná se o běžný trojúhelník atd.) a navíc na sobě nemá žádné značky pro odečet vzdálenosti či pro narýsování úsečky o zadané délce. Kružítko je ve zcela abstraktní podobě taktéž odlišné od běžného kružítka – po zvednutí kružítka z papíru se automaticky zavře (collapse), což v důsledku znamená, že ho nelze použít pro přenášení vzdálenosti, například tak, jak je to použito při konstrukci šestiúhelníků. Někdy se v tomto kontextu setkáme s názvem euklidovské kružítko.

V praxi se však i u eukleidovských konstrukcí většinou používá běžné kružítko, které si „pamatuje“ nastavenou vzdálenost (tedy poloměr kreslených oblouků a kružnic), protože existuje důkaz toho, že i s použitím pravítka a zavírajícího se kružítka lze přenést vzdálenost (viz například [zajímavý důkaz provedený zde]).

Obrázek 3: Fragment slavných Euklidových spisů.

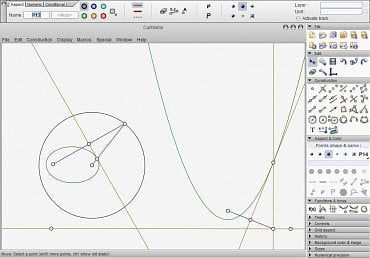
Obrázek 4: Takto vypadá aplikace CaRMetal zmíněná v předchozím odstavci.
Zdroj obrázku: Wikipedia.

3. Příklad Euklidovské konstrukce

Jen pro ukázku toho, jak se v antice konstruovaly rovinné útvary si řekneme, které operace jsou vlastně povoleny při kreslení geometrických útvarů. Eukleidovská konstrukce typicky začíná na prázdné ploše, do které je nakreslen bod či několik bodů. Následně jsou povoleny pouze následující operace:

• Nakreslení nové úsečky, která protíná dva zvolené body. Pro tuto konstrukci pochopitelně dostačuje pravítko s jednou hranou a bez značek pro vzdálenost.
• Nakreslení kružnice se středem ve zvoleném bodě takovým způsobem, aby protínala jiný zvolený bod. Zde postačuje použít kružítko, které se přímo na papíře (ploše) roztáhne do požadované vzdálenosti (Eukleidovské kružítko či klasické kružítko).
• Nakreslení nového bodu, který je vytvořen v průsečíku dvou protínajících se úseček. Žádné nástroje nejsou pro provedení této operace zapotřebí.
• Nakreslení jednoho nebo dvou nových bodů vytvořených v průsečíku kružnice a úsečky (za předpokladu, že se protínají, opět jednoduché a nevyžadující nástroje).
• Nakreslení jednoho nebo dvou nových bodů vytvořených v průsečíku dvou kružnic (opět pochopitelně za předpokladu, že se protínají).

Obrázek 5: Přeložené Euklidovy spisy o geometrii vydané v patnáctém století.

4. Slavné geometrické úlohy, které nelze vyřešit jen pravítkem (bez měřítka) a kružítkem

I s využitím pouhé dvojice pomůcek zmíněných v předchozích dvou kapitolách je možné vyřešit až překvapivé množství geometrických problémů a zkonstruovat mnoho tvarů (včetně pravidelných n-úhelníků splňujících Gauss–Wantzelův teorém – samotný teorém je pochopitelně pozdějšího data). Existují ovšem některé úlohy, kde si již s pravítkem bez značek s délkami a kružítkem nevystačíme. Takovými klasickými úlohami formulovanými již v pátém století před naším letopočtem je kvadratura kruhu a trisekce úhlu.

Kvadratura kruhu, což je sousloví, které se dostalo do běžné řeči (a mnozí ho používají často bez přesné znalosti původního významu) je geometrická úloha, v níž se má s využitím vhodně vymyšlené euklidovské konstrukce v konečném počtu kroků zkonstruovat čtverec o stejném obsahu, jako má daný (již nakreslený) kruh. Důkaz, že to není možné (tedy že pro takovou úlohu euklidovské konstrukce nedostačují), ovšem pochází až z roku 1882 – potvrdil se tím předpoklad, který ostatně vyslovili již staří Řekové, ovšem bez přesného důkazu. Podobně trisekce úhlu je geometrická úloha, jejímž cílem je rozdělit obecný úhel na třetiny (zatímco rozdělení na polovinu, čtvrtinu atd. je triviální, ostatně se jedná o běžnou úlohu vyučovanou na školách).

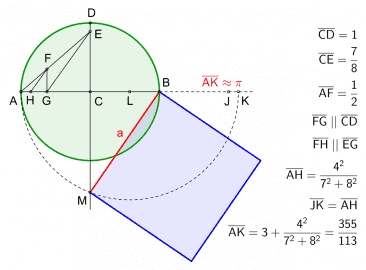
Obrázek 6: Jedna z možných aproximací, tedy přibližné řešení úlohy kvadratury kruhu.
Zdroj obrázku: Wikipedie.

5. Další milník: kuželosečky

Již Eukleidés, s nímž jsme se nepřímo setkali v předchozím textu, si ovšem uvědomoval, že geometrické konstrukce založené na použití pravítka a kružítka ve skutečnosti nedokážou popsat všechny tvary, s nimiž se lze setkat jak v přírodě (hod předmětu), tak i v architektuře. Proto se mj. začal věnovat studiu křivek, které dnes nazýváme kuželosečkami. Ovšem Eukleidés nebyl první, protože minimálně dvě z kuželoseček – konkrétně parabolu a hyperbolu – pro západní svět objevil Menaechmus (přítel Platóna) již okolo roku 350 př.n.l. Na Eukleida navázal jeho žák Apollónios z Pergy (cca 200 př.n.l.), který zavedl pojmenování „hyperbola“ a „parabola“, jenž jsme převzali a používáme dodnes. Apollónios taktéž objevil, že hyperbola má dvě větve, zatímco Eukleidés pracoval pouze s větví v prvním kvadrantu.

Paraboly našly své využití v reflektorech, anténách atd. Uvádí se i (v moderní době nakonec prakticky ověřené) zapalování lodí s využitím odražených slunečních paprsků, které prý použil Archimedes při obléhání jeho rodných Syrakus. Zrcadla, pokud tedy byla pro tento účel skutečně použita, vytvořila přibližný tvar paraboly (a Archimedes se skutečně parabolami podrobně zabýval, takže věděl, jaký je praktický význam jejich ohniska atd.). Stejný princip, tedy využití ohnisek paraboly (jedno z nich je v nekonečnu) je použito i při zapalování olympijského ohně:

Obrázek 7: Zapalování olympijského ohně.
Zdroj obrázku: Wikipedie, https://en.wikipedia.org/wi­ki/Olympic_flame#/media/Fi­le:Olympic_Torch_2010.jpg

6. Řetězovka: křivka používaná nejenom v architektuře

V úvodním textu jsme se zmínili o použití křivek v architektuře. V tomto oboru má výsadní místo křivka nazývaná řetězovka. Jedná se o přiléhavý název, protože tuto křivku můžeme vidět například na prověšeném řetězu. Ovšem stejnou křivku tvoří i prověšená lana, dráty (vysokého) napětí apod. Řetězovka, tentokrát ovšem v opačné podobě (obloukem nahoru), se používá při návrhu některých typů mostů, staví a stavěly se oblouky mající tvar této křivky. Hezký příklad takového oblouku můžete vidět na následující fotce:

Obrázek 8: Řetězovka tvoří základní křivku, na jejímž základě byla zkonstruována klenba.
Zdroj obrázku: Wikipedie, https://en.wikipedia.org/wi­ki/File:Celler_de_Sant_Cu­gat_lateral.JPG

Obrázek 9: Parabola vzniklá zavěšením závaží na lano.
Zdroj obrázku: 2dcurves.com, https://2dcurves.com/conic­section/conicsectionp.html

7. Svět spirál

Spirály se objevují na mnoha místech v přírodě. Jejich lidmi vytvořené podoby můžeme nalézt již v prehistorii, například vyryté na kamenech ve slavném Newgrange. Jejich systematické studium ovšem začalo – kde jinde – v antickém Řecku. V tomto kontextu je důležité především dílo „O závitnicích“ (Περι ελικων), které sepsal Archimédes. Po něm je ostatně pojmenována i Archimédova spirála.

Obrázek 10: Trojité spirály v Newgrange.

Velmi důležitý byl objev logaritmické spirály nazývané taktéž Spira Mirabilis. Tuto spirálu poprvé popsal Albrech Dürer, zabývali se jí i René Descartes a později i Jacob Bernoulli (tedy samá slavná jména). Tuto křivku nalezneme i na mnoha místech v přírodě (a to na široké škále). Například jí odpovídají ramena spirálních galaxií, tropických cyklón, schránky některých měkkýšů, dráha, po které se hmyz pohybuje k bodovému světlu atd. Tuto spirálu nalezneme (ve všech škálách) i v Mandelbrotově množině.

Obrázek 11: Logaritmická spirála v Mandelbrotově množině.

8. Spline

V praxi, například při návrhu trupů lodí a později letadel, se používaly spline. Jednalo se o dřevěné nebo kovové proužky, které se na vhodných místech natahovaly a stlačovaly. Při návrhu trupů lodí se tyto proužky na koncích zatěžovaly závažím. Pružný materiál proužků mezi těmito místy vytvořil hladkou křivku. Později se termín spline začal používat pro matematicky definované křivky, které však mají podobné vlastnosti – je možná lokální změna tvarů křivek, například posunem řídicích bodů, změnou parametrů (vah) atd. V současnosti existuje okolo spline křivek velmi dobrý teoretický základ, s nímž se seznámíme v některém z dalších pokračování tohoto seriálu.

9. Křivky v industriální době

Křivky se začaly ještě více uplatňovat v industriální době. Příkladem může být již výše zmíněná Wattova křivka popisující tvar dráhy některých důležitých částí Wattova parního stroje (ojnice atd.). Další typ křivky – klotoida – se začala využívat nejdříve na železnici pro nájezdy a výjezdy z oblouků a později i při stavbě silnic pro tentýž účel. Samostatnou kapitolou jsou pak křivky používané v designu. Příkladem mohou být Bézierovy křivky využívané například při popisu tvaru znaků. Tyto křivky ovšem nalezneme i v grafických editorech apod. I těmito typy křivek, které vidíme prakticky dennodenně, se budeme zabývat v samostatném článku.

10. Praktická část článku

Praktická část dnešního článku je rozdělena na dvě části. V první části si ukážeme základní použití nástroje GeoGebra, ve druhé pak kombinaci programovacího jazyka Python a knihoven Matplotlib s Numpy. Jedná se prozatím o úvod do celé problematiky, takže i demonstrační příklady jsou prozatím velmi jednoduché – „raketovou vědou“ související s problematikou křivek se budeme zabývat někdy příště.

11. Základní kuželosečky vytvořené v nástroji GeoGebra

V modulu Geometry interaktivní aplikace GeoGebra nalezneme i nástroje určené pro kreslení všech typů kuželoseček, ovšem způsoby specifikace umístění a tvaru jednotlivých kuželoseček se od sebe odlišují. Nejvíce možností máme u kružnice, což je ovšem pochopitelné, protože ta se v geometrických konstrukcích používá nejčastěji (a nejčastěji ji nalezneme i v reálném světě). Kružnici lze zadat středem a poloměrem, středem a bodem, kterým kružnice prochází, popř. třemi body, kterými kružnice prochází. Kromě kružnic lze v případě potřeby zkonstruovat i kruhové oblouky.

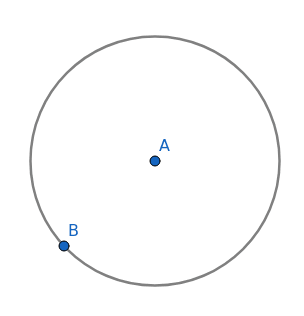
Obrázek 12: Kružnice je při geometrických konstrukcích nejpoužívanější kuželosečkou.

Dále je možné pracovat s elipsami, ovšem možnosti konstrukce elipsy jsou poněkud více omezené – musí se specifikovat souřadnice obou ohnisek elipsy a poté bod, kterým elipsa prochází. Způsob konstrukce této kuželosečky je patrný z následujícího obrázku:

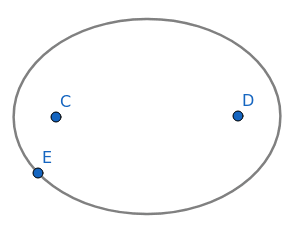
Obrázek 13: Elipsa specifikovaná dvěma ohnisky a bodem na ní ležícím.

Ještě zajímavější je způsob konstrukce paraboly. U ní je nutné specifikovat její ohnisko a taktéž takzvanou řídicí přímku (ta musí být již dopředu nakreslena):

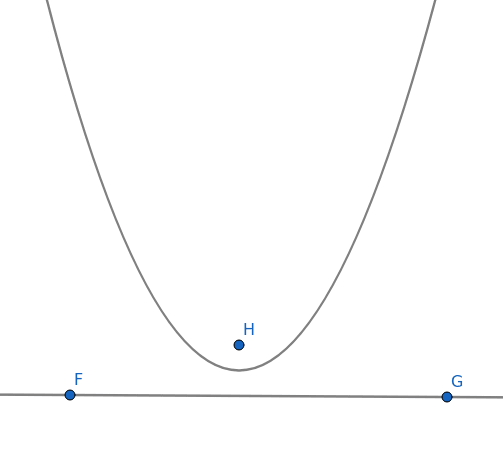
Obrázek 14: Parabola specifikovaná svým ohniskem a řídicí přímkou.

Poslední kuželosečkou je hyperbola. Podobně jako v případě elipsy je i hyperbola zadaná dvojicí ohnisek a bodem, kterým prochází jedna z polovin hyperboly – viz též následující screenshot, který vše osvětluje:

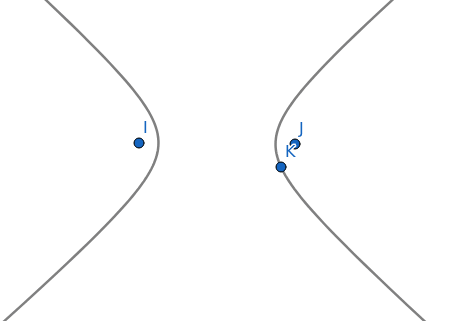
Obrázek 15: Hyperbola specifikovaná ohnisky a bodem na ní ležícím.

Příklad interaktivní (a alternativní) geometrické konstrukce paraboly naleznete na adrese https://www.geogebra.org/m/azpBrsr8.

12. Kuželosečka procházející pěti vybranými body

Logo celého programu GeoGebra je tvořeno kuželosečkou specifikovanou pěti body, kterými tato kuželosečka prochází. Může se jednat o kružnici, elipsu, parabolu i hyperbolu – vše v závislosti na vzájemné poloze oněch pěti bodů. Díky existenci tohoto nástroje lze i parabolu nebo hyperbolu zkonstruovat i bez nutnosti znalosti přesné polohy jejich ohnisek. Podívejme se na následující příklad:

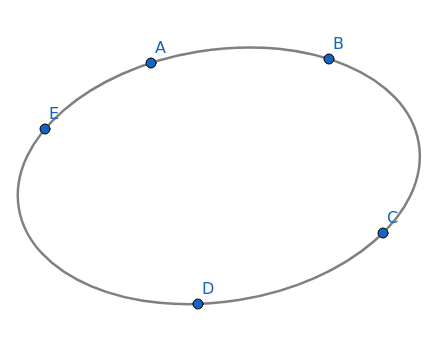
Obrázek 16: Logo programu GeoGebra – kuželosečka procházející pěticí zadaných bodů.

Pomocí pěti bodů se nastavuje deset parametrů.

13. Jednoduchá úsečka, parabola a hyperbola vykreslená Matplotlibem

Nyní si vyzkoušíme práci s Pythonem a knihovnou Matplotlib společně s knihovnou Numpy (těmito technologiemi jsme se již na stránkách Roota zabývali). V prvním příkladu vykreslíme úsečku, kterou je možné reprezentovat funkcí y=sx, kde s představuje směrnici úsečky. Vytvoříme tedy sérii x-ových hodnot a vypočteme z nich y-ové hodnoty. Ty se následně vykreslí:

"""Nejjednodušší křivka: úsečka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.arange(0, 100)
 
# hodnoty na y-ové ose (sklon úsečky řízen konstantou)
y = x * 0.3
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Úsečka', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý pátý)
ax.plot(x[::5], y[::5], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("line.png")
 
# zobrazení grafu
plt.show()

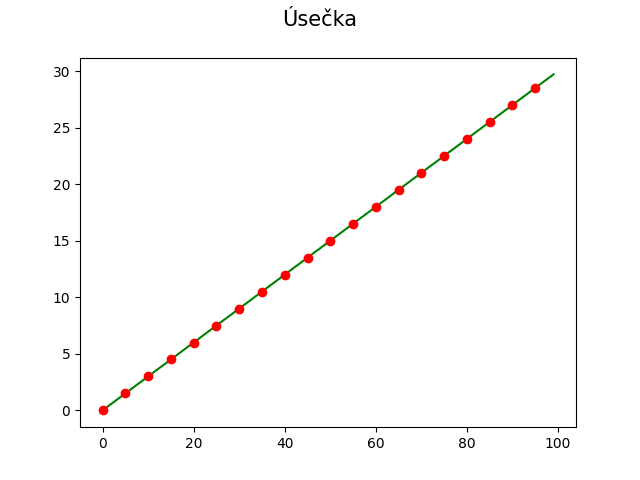
Obrázek 17: Úsečka je nejjednodušší křivkou.

Podobným způsobem lze vypočítat a vykreslit body na parabole:

"""Parabola."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.arange(-100, 101)
 
# hodnoty na y-ové ose
y = np.power(x, 2)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Parabola', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý pátý)
ax.plot(x[::5], y[::5], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola.png")
 
# zobrazení grafu
plt.show()

Obrázek 18: Parabola.

Při výpočtu hyperboly sice dojde k dělení nulou, ale to knihovna Numpy bez problémů „přežije“:

"""Hyperbola."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty na x-ové ose
x = np.arange(-100, 101, 1)
 
# hodnoty na y-ové ose
y = 1/x
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Hyperbola', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý pátý)
ax.plot(x[::5], y[::5], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbola.png")
 
# zobrazení grafu
plt.show()

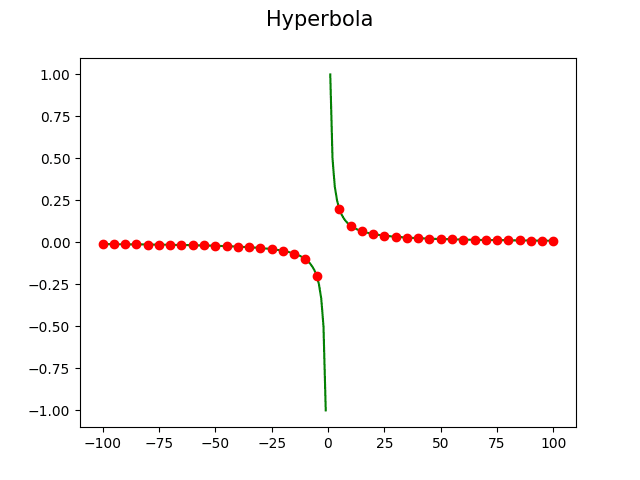
Obrázek 19: Hyperbola.

14. Řetězovka

Řetězovka, tedy křivka důležitá v architektuře, se vypočte pomocí funkce cosh a dalšího parametru a, který řídí, jak moc je lano/řetěz napnutý:

"""Rovinná křivka: řetězovka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru x
x = np.arange(-4, 4, 0.04)
 
# poloměr křivosti ve vrcholu
a = 1.0
 
# výpočet bodů ležících na řetězovce
y = a*np.cosh(x/a)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Řetězovka', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý pátý)
ax.plot(x[::5], y[::5], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("cateanry.png")
 
# zobrazení grafu
plt.show()

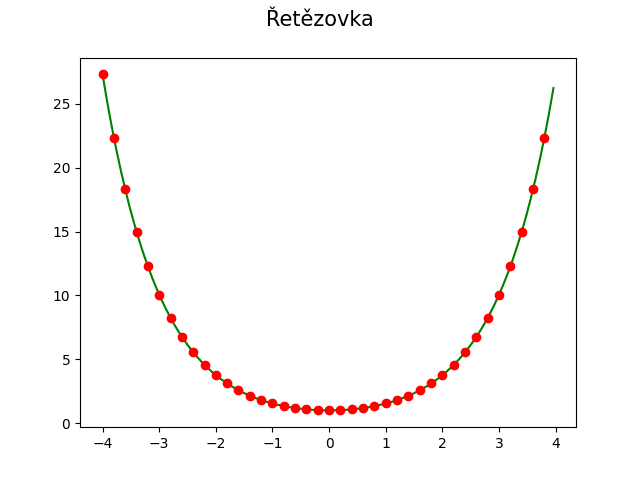
Obrázek 20: Řetězovka.

15. Rozdíl mezi řetězovkou a parabolou

Řetězovka byla sice používána v architektuře poměrně dlouhou dobu, ovšem původně byla konstruována pomocí provázků a závaží. Analýza této funkce byla dlouho problematická a dokonce se věřilo, že řetězovka je vlastně určitou podobou vhodně parametrizované paraboly. Ve skutečnosti to není pravda, což si ostatně můžeme ukázat na následujícím demonstračním příkladu, který obě křivky vizuálně porovnává bez další úpravy parametrů (pouze došlo k posunu řetězovky):

"""Parabola versus řetězovka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru x
x = np.arange(-3, 3, 0.04)
 
# parabola: hodnoty na y-ové ose (sklon úsečky řízen konstantou)
y1 = np.power(x, 2)
 
# poloměr křivosti ve vrcholu
a = 1.0
 
# řetězovka: výpočet bodů ležících na řetězovce
y2 = a*np.cosh(x/a)-1
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Parabola versus řetězovka #1', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y1, 'g-', label="Parabola")
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y2, 'r-', label="Řetězovka")
 
# zobrazení popisku křivek
plt.legend()
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola_catenary.png")
 
# zobrazení grafu
plt.show()

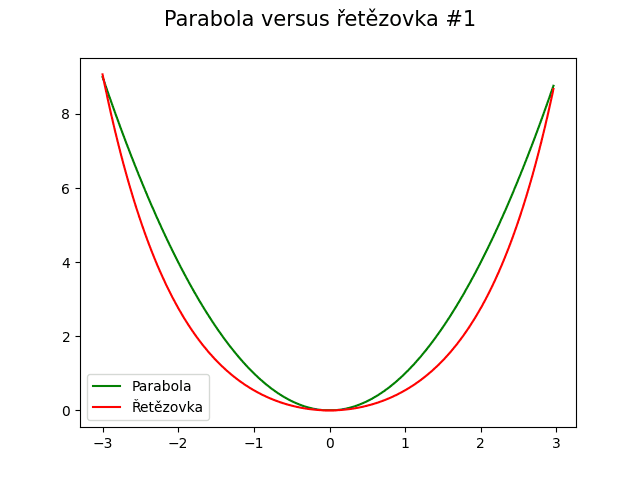
Obrázek 21: Porovnání řetězovky a paraboly (bez další úpravy parametrů).

Nejlepší shody mezi řetězovkou a parabolou dosáhneme vhodnou změnou jejich parametrů, viz též „magické“ konstanty zvýrazněné v dalším demonstračním příkladu:

"""Parabola versus řetězovka."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru x
x = np.arange(-2, 2, 0.04)
 
# parabola: hodnoty na y-ové ose (sklon úsečky řízen konstantou)
y1 = 3-0.65*np.power(x, 2)
 
# poloměr křivosti ve vrcholu
a = 1.0
 
# řetězovka: výpočet bodů ležících na řetězovce
y2 = 4-a*np.cosh(x/a)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Parabola versus řetězovka #2', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y1, 'g-', label="Parabola")
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y2, 'r-', label="Řetězovka")
 
# zobrazení popisku křivek
plt.legend()
 
# uložení grafu do rastrového obrázku
plt.savefig("parabola_catenary_2.png")
 
# zobrazení grafu
plt.show()

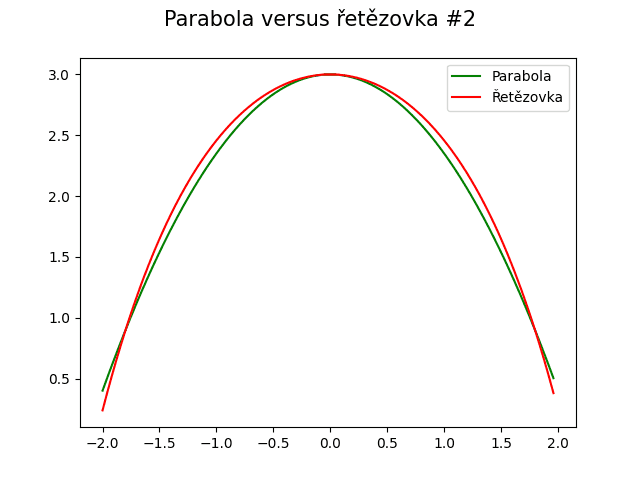
Obrázek 22: Porovnání řetězovky a paraboly (nejlepší možná shoda).

16. Elipsa specifikovaná parametricky, obecná elipsa

V dalším demonstračním příkladu je ukázáno vykreslení elipsy, tentokrát s využitím jejího parametrického vyjádření popř. parametrických rovnic. Jedná se o rovnice s funkcemi, které nezávisí na hodnotě souřadnice x, ale na dalším parametru t. Díky tomu lze vykreslit i uzavřené křivky, křivky, které se protínají atd.:

"""Parametrická křivka: elipsa."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
 
# poloměry elipsy v osách
a = 2.0
b = 1.5
 
# výpočet bodů ležících na elipse
x = a*np.cos(t)
y = b*np.sin(t)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Elipsa', fontsize=15)
 
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý čtvrtý)
ax.plot(x[::4], y[::4], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("ellipse_parametric.png")
 
# zobrazení grafu
plt.show()

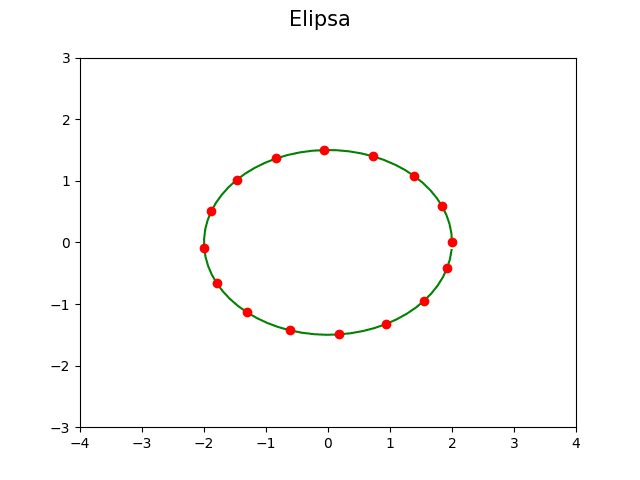
Obrázek 23: Parametrická křivka: elipsa.

Poněkud složitější je výpočet obecné elipsy, opět zadané v parametrickém tvaru. Tato elipsa může být posunuta (parametry xc a yc), natočena (parametr phi) a samozřejmě lze specifikovat i délky obou poloos s využitím parametrů a a b:

"""Parametrická křivka: obecná elipsa."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
 
# poloměry elipsy v osách
a = 3.0
b = 2.0
 
# natočení celé elipsy
phi = np.pi / 4
 
# střed elipsy
xc = 0
yc = 0
 
# výpočet bodů ležících na elipse
x = xc + a*np.cos(t)*np.cos(phi) - b*np.sin(t)*np.sin(phi)
y = yc + a*np.cos(t)*np.sin(phi) + b*np.sin(t)*np.cos(phi)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Obecná elipsa', fontsize=15)
 
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý čtvrtý)
ax.plot(x[::4], y[::4], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("ellipse_general.png")
 
# zobrazení grafu
plt.show()

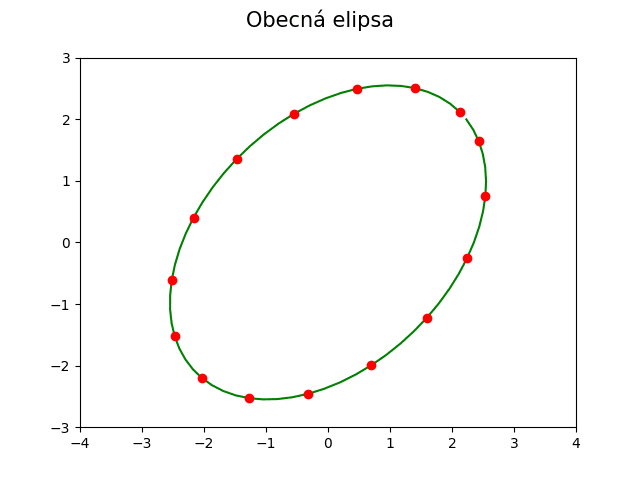
Obrázek 24: Obecná elipsa.

17. Vykreslení křivek v polárním souřadném systému

Podobným způsobem, tedy parametricky, si můžeme nechat vykreslit i „obyčejnou“ kružnici:

"""Parametrická křivka: kružnice."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
 
# poloměr kružnice
r = 2.0
 
# výpočet bodů ležících na kružnici
x = r*np.cos(t)
y = r*np.sin(t)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
 
# titulek grafu
fig.suptitle('Kružnice', fontsize=15)
 
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
 
# vrcholy na křivce (každý čtvrtý)
ax.plot(x[::4], y[::4], 'ro')
 
# uložení grafu do rastrového obrázku
plt.savefig("circle_parametric.png")
 
# zobrazení grafu
plt.show()

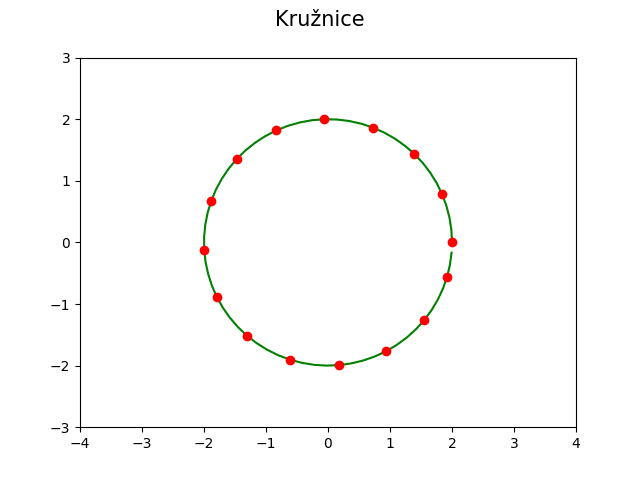
Obrázek 25: Parametrická křivka: kružnice.

Mnohem jednodušší je však v tomto případě použití polárního souřadného sytému, který za nás vyřeší natočení vektoru, jehož délka pro každý úhel udává tvar křivky. Nejjednodušší křivkou vykreslenou v polárním systému tak není úsečka ale právě kružnice:

"""Kružnice vykreslená v polárním grafu."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.arange(0.00, 2*np.pi, 0.05)
 
a = 1.0
 
# funkce: vzdálenost od středu
radius = np.repeat(a, len(theta))
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
 
# titulek grafu
fig.suptitle('Kružnice', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
 
# uložení grafu do rastrového obrázku
plt.savefig("circle_polar.png")
 
# zobrazení grafu
plt.show()

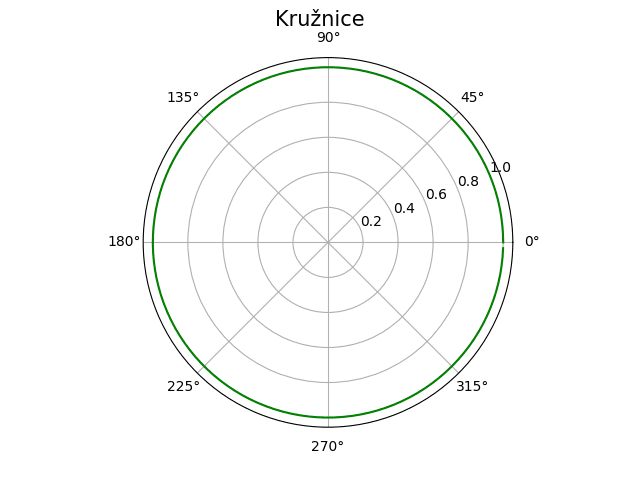
Obrázek 26: Opět kružnice, tentokrát ovšem vykreslená v polárním souřadném systému.

18. Spirály

Polární souřadný systém nám umožňuje zjednodušit výpočet spirál. Archimédova spirála, resp. její vzorec, se tak ztenčí na pouhé radius = theta:

"""Archimedova spirála."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.linspace(0.01, 8*np.pi, 150)
 
# funkce: vzdálenost od středu
radius = theta
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
 
# titulek grafu
fig.suptitle('Archimedova spirála', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
 
# uložení grafu do rastrového obrázku
plt.savefig("archimedes_spiral.png")
 
# zobrazení grafu
plt.show()

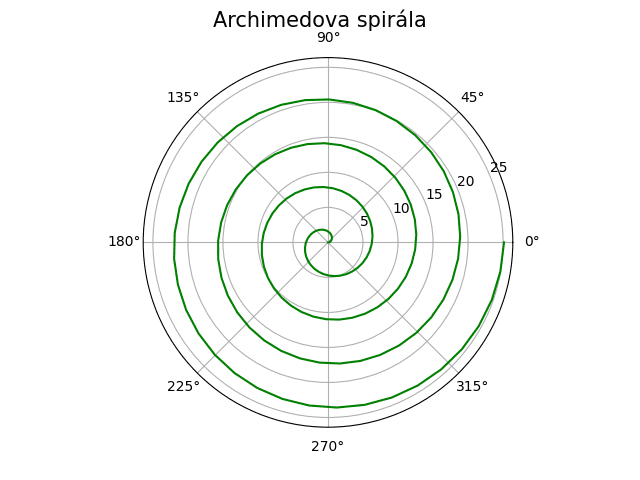
Obrázek 27: Archimédova spirála.

Logaritmická spirála s parametrem k:

"""Logaritmická spirála."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.linspace(0.01, 8*np.pi, 150)
 
k = 0.15
 
# funkce: vzdálenost od středu
radius = np.exp(k*theta)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
 
# titulek grafu
fig.suptitle('Logaritmická spirála', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
 
# uložení grafu do rastrového obrázku
plt.savefig("logarithmic_spiral.png")
 
# zobrazení grafu
plt.show()

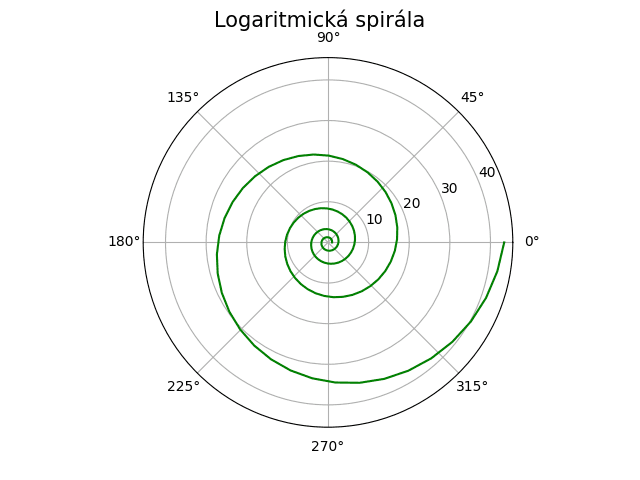
Obrázek 28: Logaritmická spirála.

Fermatova spirála s parametrem a:

"""Fermatova spirála."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.arange(0.00, 20.0, 0.05)
 
a = 1.0
 
# funkce: vzdálenost od středu
radius = a*np.sqrt(theta)
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
 
# titulek grafu
fig.suptitle('Fermatova spirála', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
 
# uložení grafu do rastrového obrázku
plt.savefig("fermat_spiral.png")
 
# zobrazení grafu
plt.show()

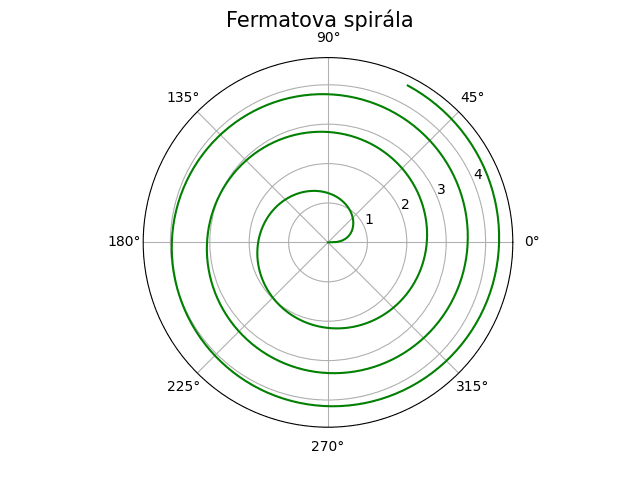
Obrázek 29: Fermatova spirála.

A konečně spirála hyperbolická, opět s parametrem a:

"""Hyperbolická spirála."""
 
import numpy as np
import matplotlib.pyplot as plt
 
# úhel v polárním grafu
theta = np.arange(1.00, 50.0, 0.05)
 
a = 1.0
 
# funkce: inverzní vzdálenost od středu
radius = a/theta
 
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
 
# titulek grafu
fig.suptitle('Hyperbolická spirála', fontsize=15)
 
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
 
# uložení grafu do rastrového obrázku
plt.savefig("hyperbolic_spiral.png")
 
# zobrazení grafu
plt.show()

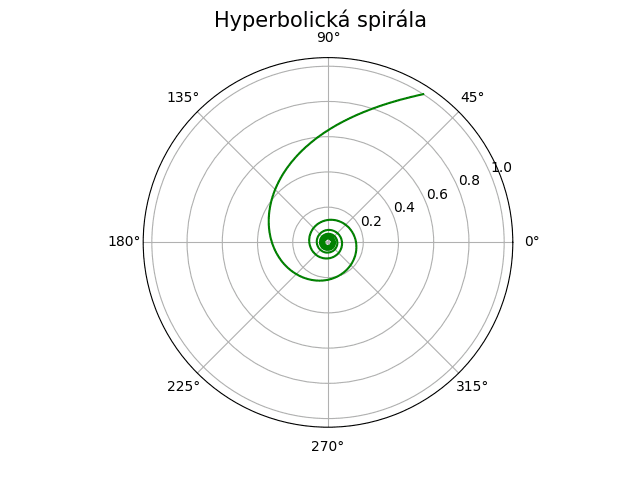
Obrázek 30: Hyperbolická spirála.

19. Repositář s demonstračními příklady

Všechny dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/pre­sentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:

20. Odkazy na Internetu

1. Curve (Wikipedia)
   https://en.wikipedia.org/wiki/Curve
2. Mathematical curves
   https://www.2dcurves.com/index.html
3. Curves (Wolfram MathWorld)
   https://mathworld.wolfram­.com/topics/Curves.html
4. Smooth Curve (Wolfram MathWorld)
   https://mathworld.wolfram­.com/SmoothCurve.html
5. Spirals (Wolfram MathWorld)
   https://mathworld.wolfram­.com/topics/Spirals.html
6. An Interactive Introduction to Splines
   https://ibiblio.org/e-notes/Splines/Intro.htm
7. Parabola
   https://www.2dcurves.com/co­nicsection/conicsectionp.html
8. Hyperbola
   https://www.2dcurves.com/co­nicsection/conicsectionh.html
9. Dioklova kisoida
   https://cs.wikipedia.org/wi­ki/Dioklova_kisoida
10. Archimédova spirála
    https://cs.wikipedia.org/wi­ki/Archim%C3%A9dova_spir%C3%A1la
11. Conchoid (mathematics)
    https://en.wikipedia.org/wi­ki/Conchoid_(mathematics)
12. Algebraic curve
    https://en.wikipedia.org/wi­ki/Algebraic_curve
13. Transcendental curve
    https://en.wikipedia.org/wi­ki/Transcendental_curve
14. Spiral
    https://en.wikipedia.org/wiki/Spiral
15. List of spirals
    https://en.wikipedia.org/wi­ki/List_of_spirals
16. Hyperbolická spirála
    https://cs.wikipedia.org/wi­ki/Hyperbolick%C3%A1_spir%C3%A1la
17. Hyperbolic Spiral
    https://mathworld.wolfram­.com/HyperbolicSpiral.html
18. Lituus (mathematics)
    https://en.wikipedia.org/wi­ki/Lituus_(mathematics)
19. Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
    https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/
20. Cornu Spiral
    http://hyperphysics.gsu.e­du/hbase/phyopt/cornu.html
21. Spiral
    https://www.2dcurves.com/spi­ral/spiral.html
22. Algebraic Curves
    https://mathworld.wolfram­.com/topics/AlgebraicCurves­.html
23. Elliptic Curves
    https://mathworld.wolfram­.com/topics/EllipticCurves­.html
24. Eukleidovská konstrukce
    https://cs.wikipedia.org/wi­ki/Eukleidovsk%C3%A1_konstruk­ce
25. Euclidean Constructions
    http://www.cs.cas.cz/portal/Al­goMath/Geometry/PlaneGeome­try/GeometricConstruction­s/EuclideanConstructions.htm
26. Kvadratura kruhu
    https://cs.wikipedia.org/wi­ki/Kvadratura_kruhu
27. Trisekce úhlu
    https://cs.wikipedia.org/wi­ki/Trisekce_%C3%BAhlu
28. Straightedge and compass construction
    https://en.wikipedia.org/wi­ki/Straightedge_and_compas­s_construction
29. C.a.R.
    http://car.rene-grothmann.de/doc_en/index.html
30. CaRMetal (Wikipedia)
    https://en.wikipedia.org/wiki/C.a.R.
31. CaRMetal (Španělsky a Francouzsky)
    http://carmetal.org/index.php/fr/
32. CaRMetal (Wikipedia)
    https://en.wikipedia.org/wi­ki/CaRMetal
33. Regular Polygon
    http://mathforum.org/dr.mat­h/faq/formulas/faq.regpoly­.html
34. Geometric Construction with the Compass Alone
    http://www.cut-the-knot.org/do_you_know/compass.shtml
35. Kvadratura kruhu (Wikipedie)
    https://cs.wikipedia.org/wi­ki/Kvadratura_kruhu
36. Compass equivalence theorem
    https://en.wikipedia.org/wi­ki/Compass_equivalence_the­orem
37. Curves we (mostly) don't learn in high school (and applications)
    https://www.youtube.com/wat­ch?v=3izFMB91K_Q
38. Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
    https://www.maa.org/press/pe­riodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions
39. Apollonius of Perga
    https://en.wikipedia.org/wi­ki/Apollonius_of_Perga
40. Catenary arch
    https://en.wikipedia.org/wi­ki/Catenary_arch
41. Parabolic arch
    https://en.wikipedia.org/wi­ki/Parabolic_arch
42. Wattova křivka
    https://www.geogebra.org/m/gNh4bW9r