Obsah
1. Křivky v přírodě, architektuře, stavitelství i v počítačové grafice: matematický popis křivek
2. Popis křivek explicitní funkcí typu y=f(x)
4. Zobecnění parametrických křivek: parametrické plochy
5. Popis křivky implicitní funkcí typu F(x,y)=0
7. Křivky vzniklé odvalováním kružnice – cykloidy, epicykloidy a hypocykloidy
8. Epitrochoidy a hypotrochoidy – křivky z grafické pomůcky Inspiro/Spirograph
17. Křivky zadané implicitní funkcí
18. Vykreslení implicitně zadaných křivek
19. Repositář s demonstračními příklady
1. Křivky v přírodě, architektuře, stavitelství i v počítačové grafice: matematický popis křivek
V úvodním článku o křivkách, které můžeme nalézt v přírodě, architektuře a v moderní době i v počítačové grafice, jsme se mj. ve stručnosti seznámili s tím, že některé křivky, zejména kuželosečky a posléze i křivky získané řezem anuloidu, byly prozkoumány a popsány již v antickém Řecku. Ovšem staří Řekové se soustředili především na geometrické konstrukce, nikoli na čistě matematický popis křivek. Tento další velmi významný další krok byl uskutečněn až o přibližně 1800 let později slavným René Descartem, a to konkrétně na přelomu šestnáctého a sedmnáctého století. Právě Descartes je společně s Fermatem považován za zakladatele takzvané analytické geometrie, tedy vlastně číselného a analytického zkoumání geometrických objektů. Tyto své teorie, společně s popisem neméně důležitého kartézského systému souřadnic (další významný pokrok) Descartes publikoval ve svém stěžejním díle Geometrii (ve skutečnosti ovšem napsal více stěžejních děl, od filozofických spisů přes fyziku právě až po matematiku). Většina údajů, s nimiž se v dnešním článku setkáme, přímo či nepřímo souvisí právě s objevy a teoriemi prezentovanými Descartem.
Descartovým současníkem byl mj. i další slavný učenec Johannes Kepler, který některé postupy související s matematickým popisem křivek využil při formulaci svých (Keplerových) zákonů odvozených z předpokladu, že planety obíhají okolo Slunce (tedy mnohem hmotnějšího tělesa) po elipsách, přičemž Slunce leží v jednom ohnisku elipsy. Tento model byl (v běžných podmínkách a v „rozumném“ časovém období) již dostatečně přesný na to, aby byl široce akceptován a právě zde se ukázala síla novodobé matematiky, která překonala původní modely planetární soustavy odvozené od soustavy kružnic (resp. jak uvidíme dále epicykloidů), která se společně s přesnějšími měřeními stávala značně složitou – musely se totiž postupně přidávat další a další odvalující se kružnice, aby odhady odpovídaly pozorování.
2. Popis křivek explicitní funkcí typu y=f(x)
Některé křivky – ovšem je to ve skutečnosti jen podmnožina všech křivek – můžeme popsat takzvanou explicitní rovnicí ve tvaru:
y = f(x)
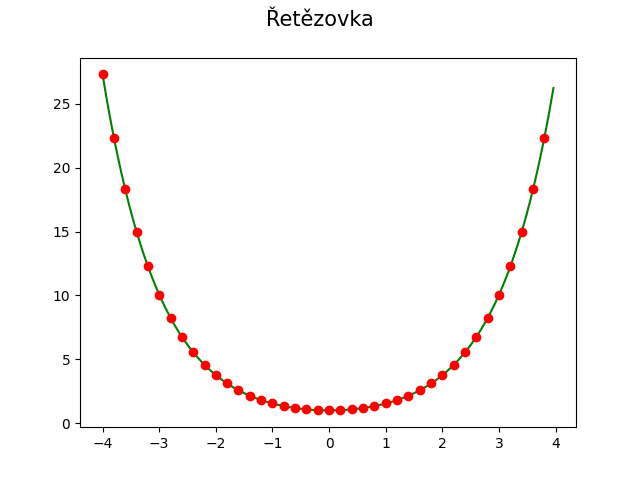
Obrázek 1: Explicitní rovnicí lze popsat například řetězovka zmíněná minule.
Tento popis je sice nejjednodušší a umožňuje popsat jak (některé) křivky algebraické, tak i křivky transcendentní, ovšem není možné ho použít například ve chvíli, kdy křivka obsahuje dva či více bodů ležících přímo nad sebou. Příkladem jsou jak obecně umístěné kuželosečky, tak i například spirály, z nichž některé jsme si (prozatím ovšem bez důkladnějšího popisu) uvedli minule. V případě kuželoseček se tento problém může řešit tak, že funkce f představuje jen polovinu kuželosečky – ovšem výsledná reprezentace již nedokáže popsat plynulý pohyb bodu po kuželosečce (či obecně po křivce).
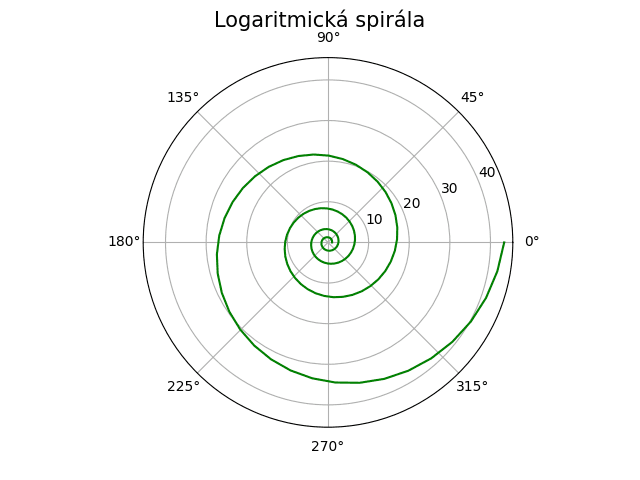
Obrázek 2: Logaritmická spirála, kterou nelze popsat explicitní funkcí.
3. Parametrické křivky
Velkým krokem vpřed při matematickém popisu křivek bylo zavedení bodové funkce. Bodovou funkci parametrické křivky P3D(t) s parametrem t lze zapsat ve tvaru:
P3D(t)=[x(t), y(t), z(t)]
V ploše se zápis zjednoduší, protože není nutné vyjadřovat z-ovou souřadnici:
P2D(t)=[x(t), y(t)]
kde x a y jsou na sobě nezávislé funkce.
Díky tomu, že parametr t již není vázaný na x-ovou souřadnici, je možné bodovou funkcí popsat například i spirály, křivky, jejichž body mají shodnou x-ovou souřadnici atd. Ovšem – a to je již téma pro samostatný článek – ani tento popis není vhodný pro všechny typy křivek; typicky neobstojí u fraktálních křivek (sněhová vločka Helge von Kocha atd.).
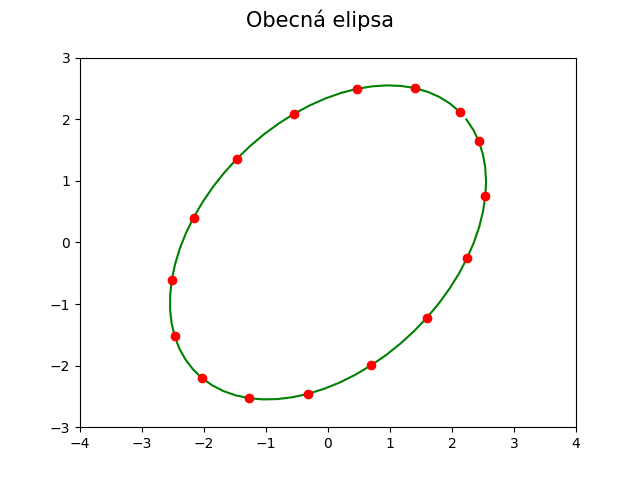
Obrázek 3: Obecná elipsa je plně popsatelná bodovou funkcí.
4. Zobecnění parametrických křivek: parametrické křivky
S parametrickými křivkami (tedy objekty s jednou dimenzí, které existují v 2D či 3D prostoru) souvisí jejich zobecnění – parametrické plochy. Jen krátce se o nich zmiňme, protože, i když se nejedná o křivky, mají velký až obrovský význam v 3D grafice, v CAD/CAM atd. Při popisu hranice tělesa s využitím takzvané parametrické hraniční reprezentace je povrch tělesa rozdělen na elementární části nazývané pláty či záplaty (anglicky patch). Výsledná plocha tělesa se získá navázáním těchto plátů na sebe. Každý z plátů je přitom vyjádřen takzvanou bodovou rovnicí zmíněnou výše. V současné počítačové grafice se nejčastěji používají bodové rovnice, které jako své bázové funkce obsahují polynomy nízkého stupně, protože tyto jsou snadno diferencovatelné a lze provádět rychlé výpočty hodnot těchto funkcí pomocí Hornerova schématu, ve kterém jsou použity pouze jednoduché a rychlé operace sčítání a násobení (ve skutečnosti se však používají i další algoritmy vhodné pro realizaci na GPU).

Obrázek 4: Plát popsaný bodovou funkcí.
Podobně jako v případě parametrických křivek je možné i u parametrických ploch zapsat bodovou funkci parametrické plochy Q(u, v) s parametry u a v:
Q3D(u, v)=[x(u,v), y(u,v), z(u,v)]
Kde x(u,v), y(u,v) a z(u,v) jsou (vybrané) funkce dvou parametrů u a v. Tyto parametry mohou nabývat hodnot z rozsahu 0 až 1. Jinými slovy znamená zápis bodové funkce fakt, že bodu o souřadnicích [u, v] v prostoru parametrickém (což je plocha) odpovídá bod o souřadnicích [x, y, z] v trojrozměrném prostoru.

Obrázek 5: Detail modelu vytvořeného z parametrických ploch (konkrétně NURBS).
Na parametrickou plochu se můžeme dívat jako na množinu bodů vzniklou tažením křivky po určité trajektorii. Tato křivka při svém pohybu může měnit tvar. Z bodové rovnice lze jednoduše vyjádřit rovnice tečných vektorů ve směrech parametrů u a v k ploše Q(u, v) a z těchto dvou vektorů vypočítat normálu k povrchu:
n=(qu x qv) / |qu x qv|
Kde x znamená operaci vektorového součinu.

Obrázek 6: Modely těles vytvořené z NURBS.
5. Popis křivky implicitní funkcí typu F(x,y)=0
Kromě popisu křivky explicitní funkcí nebo bodovou funkcí je možné křivky popsat takzvanou funkcí implicitní, která se zapisuje ve tvaru:
F(x,y)=0
V porovnání s předchozí dvojicí popisů křivek je popis implicitní funkcí obecnější, neboť s jeho využitím můžeme reprezentovat křivky obsahující několik samostatných cest apod. Následuje příklad implicitní funkce popisující mj. i všechny kuželosečky (záleží pouze na výběru koeficientů A až F):
Ax2+Bxy+Cy2+Dx+Ey+F=0
Poměrně velký význam má zobecnění křivek zadaných implicitní funkcí na plochy reprezentované funkcí:
F(x,y,z)=0
Tento způsob reprezentace totiž umožňuje relativně snadný výpočet průsečíku paprsku s plochou, takže se tento způsob používá v raytracerech.

Obrázek 7: Implicitní plochy jsou použité pro reprezentaci těles nazývaných „metaballs“.

Obrázek 8: Další možnosti popisu těles implicitními plochami.
6. Superelipsy
Superelipsa je křivka, která vznikla zobecněním běžné elipsy (ovšem zobecněním elipsy vznikly i další křivky). Parametricky lze klasickou elipsu se středem ležícím v počátku souřadné soustavy a s poloměry obou poloos rx a ry (někdy se označují a a b) popsat dvojicí rovnic s jedním nezávislým parametrem φ, který nabývá hodnot z rozsahu 0..2π. Konkrétní tvar těchto vzorů vypadá následovně:
x(φ) = rxcos(φ)
y(φ) = rysin(φ)
U parametrických rovnic superelipsy je navíc funkce sinus a kosinus umocněna zadanou konstantou n>1, pomocí níž lze dále tvar superelipsy vhodným způsobem modifikovat:
x(φ) = rxcosn(φ)
y(φ) = rysinn(φ)
Elipsu je kromě parametrického tvaru popsat také jedinou implicitní funkcí, která vyjadřuje podmínku platnou pro všechny body ležící na elipse:
f(x,y) = (x/rx)2+(y/ry)2-1 = 0
Totéž lze samozřejmě provést i u superelipsy, a to takto:
f(x,y) = (x/rx)2/n+(y/ry)2/n-1 = 0
Zajímavé je, jak se pomocí konstanty n dá měnit tvar výsledné superelipsy:
| Hodnota n | Výsledný tvar | Tvar pro rx=ry |
|---|---|---|
| 0 | obdélník | čtverec |
| <1 | zaoblený obdélník | zaoblený čtverec |
| 1 | elipsa | kružnice |
| 2 | diamant | diamant |
| >2 | hvězda | hvězda |
| >>2 | limitně tvar kříže | |
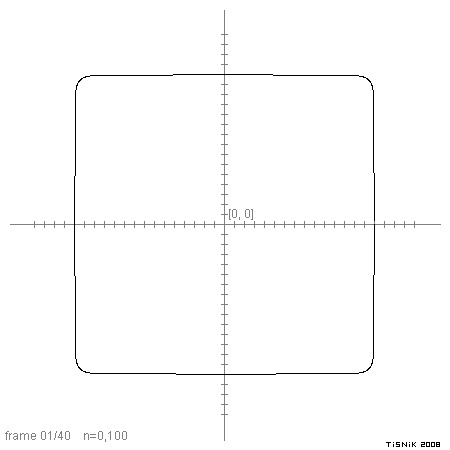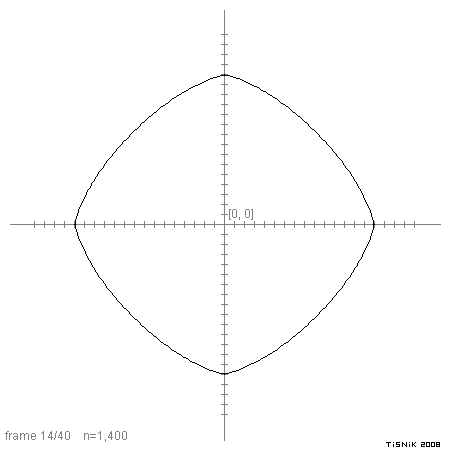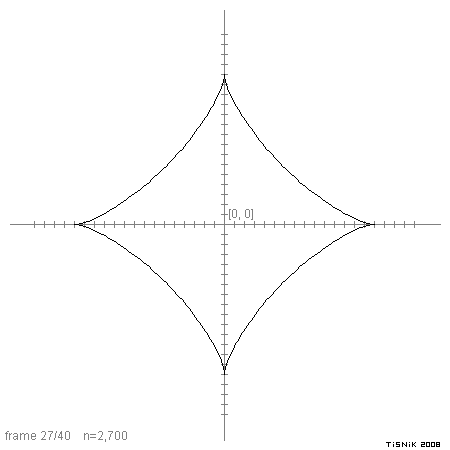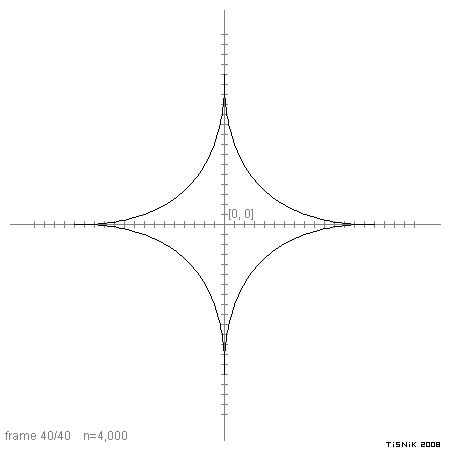
Obrázek 9: Postupná změna tvaru superelipsy s rostoucí hodnotou n.
Superelipsu, tedy rovinný útvar, je možné rozšířit do 3D prostoru, čímž vznikne superelipsoid. Na následujícím obrázku je vykresleno několik superelipsoidů, každý s odlišnými koeficienty, které určují jeho přesný tvar:

Obrázek 10: Superelipsoidy.
7. Křivky vzniklé odvalováním kružnice – cykloidy, epicykloidy a hypocykloidy
Velmi důležitou skupinou křivek jsou křivky, které vzniknou odvalováním kružnice na jiném tvaru, typicky na úsečce či na jiné kružnici. Při odvalování přitom křivku „kreslí“ bod, který se nachází buď přímo na této kružnici, nebo na polopřímce vycházející ze středu této kružnice (může se nacházet jak uvnitř, tak i vně). Tyto křivky obsahují ve svém názvu slovo „cycloid“.
Základní křivkou tohoto typu je cykloida. Ta vzniká odvalováním kružnice po úsečce tak, jak je to naznačeno na další animaci:

Obrázek 11: Animace vzniku cykloidy.
Cykloida byla taktéž nazývána „Helena geometrů“, což je narážka na Helenu Trojskou, protože se na začátku novověku o cykloidě vedly časté hádky. Cykloida byla pravděpodobně známá již ve starověku, ovšem o její pojmenování se zapříčinil až Galileo Galilei. Zajímavé je, že sice jak úsečka, tak i kružnice jsou křivkami algebraickými, samotná cykloida je ovšem transcendentní – nelze tedy vyjádřit polynomem, ale pomocí goniometrických funkcí:
x=r(t-sin t)
y=r(1-cos t)
Cykloidy se používají například při návrhu mostních oblouků, protože unesou největší zatížení. Ovšem tato křivka má i mnohem zajímavější vlastnosti. Například brachistochrona, tedy křivka nejkratšího spádu, je ve skutečnosti tvořena částí oblouku cykloidy (pokud pustíme kuličku po této dráze, dosáhne cíle rychleji, než po jakékoli jiné dráze):

Obrázek 12: Brachistochrona.
Stejně tak je cykloida základem pro další křivku nazvanou tautochrona. Pokud pustíme více kuliček z různých startovních bodů na křivce, dosáhnou cíle ve shodném čase.
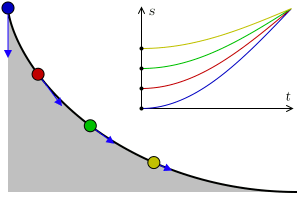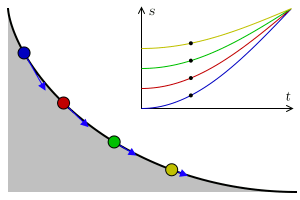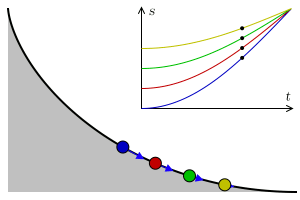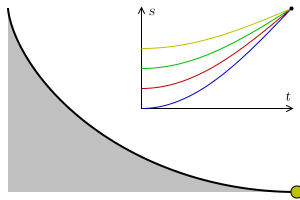
Obrázek 13: Tautochrona.
Další zajímavé křivky vzniknou odvalováním kružnice po jiné kružnici, přičemž křivku opět kreslí bod ležící na odvalované kružnici. Existují dva typy těchto křivek, které se liší tím, zda se kružnice odvaluje vně či uvnitř druhé (statické) kružnice. První typ se jmenuje epicykloida, druhý hypocykloida. S vlastnostmi těchto křivek se setkáme v praktické části dnešního článku.
8. Epitrochoidy a hypotrochoidy – křivky z grafické pomůcky Inspiro/Spirograph
Cykloidních křivek existuje velké množství, ovšem zmínit se musíme zejména o epitrochoidě a hypotrochoidě. Jedná se o zobecnění epicykloidy popř. hypotrochoidy – bod kreslicí křivku není v tomto případě umístěn přímo na odvalující se kružnici, ale buď uvnitř či naopak vně této kružnice. Tyto typy křivek je možné kreslit s využitím pomůcky, které se u nás prodávala pod názvem Inspiro, ve světě pak pod názvem Spirograph. Princip obou pomůcek je jednoduchý – používá se soustava dvou ozubených kol (nebo mezikruží), přičemž jedno z těchto kol je pevně umístěno na papír a druhé se může odvalovat okolo něj. Přitom je možné vybrat otvor uvnitř ozubeného kola, do kterého se vloží propiska či fixa, která obrazec s křivkou při troše snahy vykreslí.
Obrázky této pomůcky, která mě poprvé přivedla k fascinaci křivkami.
9. Lissajousovy obrazce
Další důležitá křivka, která nachází své využití například při analýze periodických signálů, je Lissajousova křivka, taktéž známá pod názvem Lissajousovy obrazce. Tato křivka je popsána bodovou rovnicí:
x=Asin(at+δ)
y=Bsin(bt)
kde koeficienty A, B, a, b a taktéž δ ovlivňují výsledný tvar křivky. Lissajousovu křivku dokáže vykreslit například osciloskop, když na jeho horizontální vychylovací destičky přivedeme jeden harmonický signál (například běžnou sinusovku) a na vertikální vychylovací destičky signál druhý (generátor časové základny je tedy vypnut). V případě, že oba signály mají shodnou frekvenci, je možné snadno změřit rozdíl ve fázi obou signálů – pokud je fáze nulová, vykreslí se kružnice, jinak elipsa. Taktéž lze velmi snadno vizuálně (bez nutnosti odečítat číselné hodnoty) porovnat frekvence signálů – kružnice či elipsa znamená shodnou frekvenci, každá změna se ihned vizuálně projeví. Podobně signály, jejichž poměr frekvencí se liší například 2×, o koeficient 3/2, 6/8 atd. jsou zobrazeny stylem, z něhož lze poměr mezi frekvencemi jednoduše vyčíst.
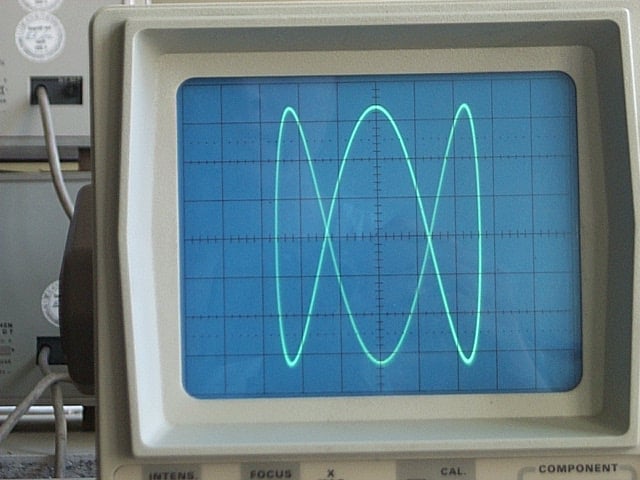
Obrázek 14: Lissajousův obrazec zobrazený na osciloskopu.
10. Praktická část článku
Praktická část dnešního článku je zaměřena na využití kombinace programovacího jazyka Python a knihoven Matplotlib společně s Numpy pro vykreslení křivek zadaných parametricky popř. implicitní funkcí. Jedná se prozatím o úvod do celé problematiky, takže i demonstrační příklady jsou prozatím velmi jednoduché (ostatně podobně jako minule) – „raketovou vědou“ související s problematikou křivek se budeme zabývat někdy příště.
Podrobnější informace o Matplotlibu a knihovně Numpy naleznete v těchto článcích:
- Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib (dokončení)
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib-dokonceni/ - Vykreslování grafů do framebufferu Raspberry Pi s použitím knihoven Pygame a Matplotlib
https://mojefedora.cz/vykreslovani-grafu-do-framebufferu-raspberry-pi-s-pouzitim-knihoven-pygame-a-matplotlib/ - Slajdy z prezentace o knihovně Numpy
https://raw.githubusercontent.com/tisnik/presentations/4d867531ac5373d906dc08f9a2750a44ecf693f0/linuxdays2019/numpy/numpy.txt
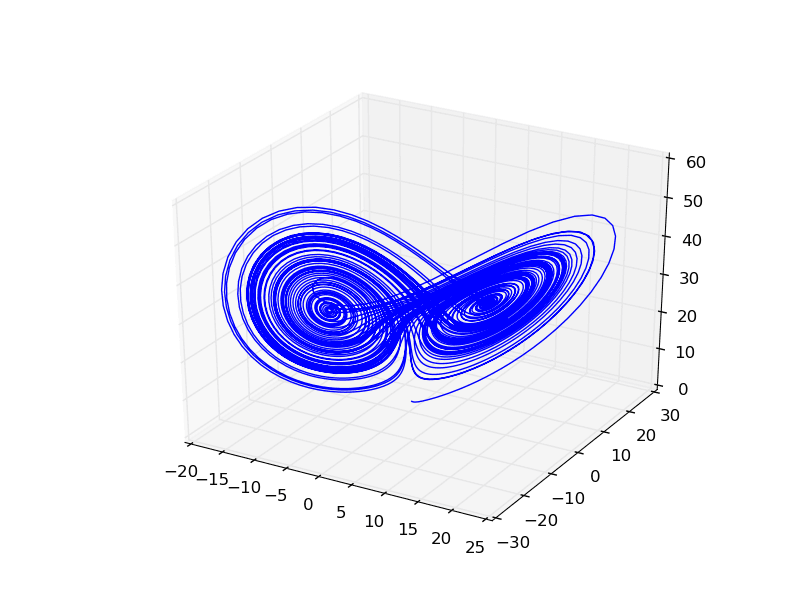
Obrázek 15: Jak uvidíme v navazujících článcích, je možné s využitím Matplotlibu vykreslit i křivku v 3D prostoru. Mimochodem – takto křivka je dosti zvláštní a nazývá se „podivný atraktor“. Podrobnosti o tomto fenoménu, který můžeme nalézt i v přírodě, si řekneme příště.
11. Superelipsy
Se superelipsami a částečně též se superelipsoidy jsme se setkali v šesté kapitole. Známe již tedy jak parametrický popis superelipsy, tak i její popis implicitní funkcí. Prozatím si ukazujeme vykreslení křivek zadaných parametricky, což dodržíme i v případě superelips. Následující skript vykreslí superelipsu, jejíž koeficient n ovlivňující její tvar je nastaven na jedničku. To vlastně znamená, že z původního parametrického popisu:
x(φ) = rxcosn(φ)
y(φ) = rysinn(φ)
Dostaneme po dosazení n=1 běžnou elipsu:
x(φ) = rxcos(φ)
y(φ) = rysin(φ)
Skript vypadá následovně:
"""Parametrická křivka: superelipsa."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
# poloměry superelipsy v osách
a = 3.0
b = 3.0
# určení tvaru křivky
n = 1
# výpočet bodů ležících na elipse
x = a*(np.cos(t) ** n)
y = b*(np.sin(t) ** n)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Superelipsa', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("superellipse1.png")
# zobrazení grafu
plt.show()

Obrázek 16: Superelipsa s koeficientem n=1.
Naopak po dosazení koeficientu n=3 bude výsledná superelipsa vypadat zcela odlišně:
"""Parametrická křivka: superelipsa."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.1)
# poloměry superelipsy v osách
a = 3.0
b = 3.0
# určení tvaru křivky
n = 3
# výpočet bodů ležících na elipse
x = a*(np.cos(t) ** n)
y = b*(np.sin(t) ** n)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Superelipsa', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("superellipse2.png")
# zobrazení grafu
plt.show()
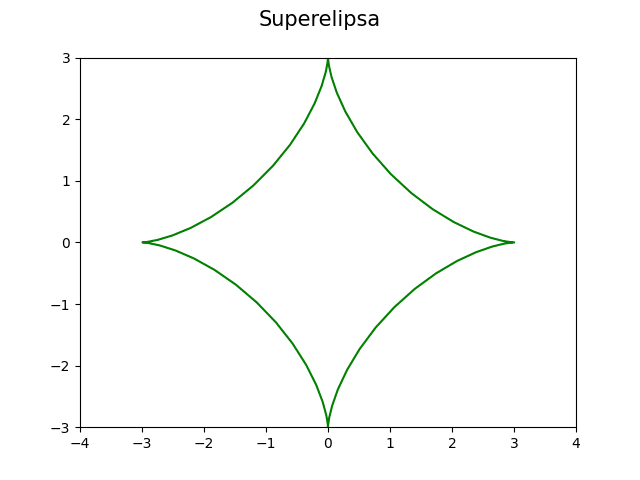
Obrázek 17: Superelipsa s koeficientem n=3.
12. Cykloida
Každý bod na plášti kola (pokud zanedbáme lokální deformaci pláště při styku s vozovkou) vykonává pohyb, který odpovídá cykloidě. Její tvar je závislý na jediném koeficientu – poloměru kružnice představující idealizované kolo. Po přepisu geometrického popisu křivky do parametrického tvaru získáme vzorce:
x = a*(t-sin(t))
y = a*(1-cos(t))
Ty je již možné snadno použít ve skriptu pro vykreslení cykloidy:
"""Parametrická křivka: cykloida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 3*np.pi, 0.1)
# poloměr kružnice
a = 1.0
# výpočet bodů ležících na cykloidě
x = a*(t-np.sin(t))
y = a*(1-np.cos(t))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Cykloida', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# vrcholy na křivce (každý pátý)
ax.plot(x[::5], y[::5], 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("cycloid.png")
# zobrazení grafu
plt.show()
Výsledný graf s křivkou:
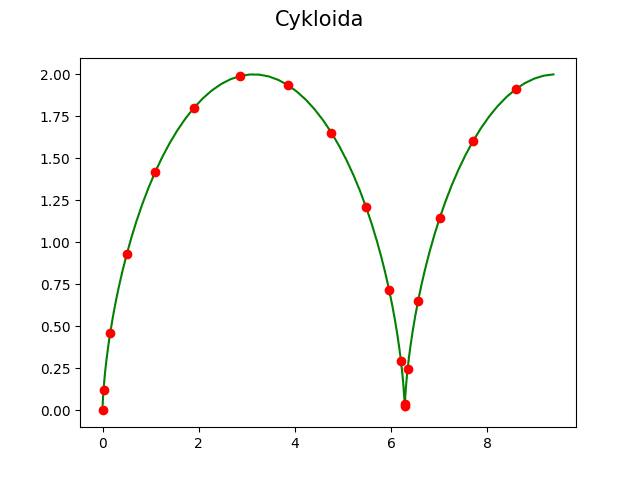
Obrázek 18: Základní tvar cykloidy.
13. Epicykloidy
Další křivky, o nichž jsme se zmínili v předchozích (teoretických) kapitolách, jsou epicykloidy. Tyto křivky lze vyjádřit parametricky, tedy bodovou funkcí:
x = (a+b)*cos(t)-b*cos((a/b+1)*t)
y = (a+b)*sin(t)-b*sin((a/b+1)*t)
kde koeficienty a a b určují tvar křivky (někdy se označují R a r), protože se jedná o poloměr „pevné“ kružnice a odvalující se kružnice. Důležitá je hodnota k vypočtená jako R/r. V případě, že je k celým číslem, odvalí se menší kružnice k-krát po větší kružnici. Pokud se jedná o číslo racionální (zlomek), bude se křivka protínat a vznikne „květ“. V případě, že poměr je číslo iracionální, bude se epicykloida dotýkat vnitřní kružnice pokaždé v jiném bodě.
Následuje ukázka epicykloidy s koeficienty 8 a 5, takže podílem vznikne racionální číslo. Hodnota parametru t leží v rozsahu 0 až 2πb:
"""Parametrická křivka: epicykloida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 10*np.pi, 0.01)
# koeficienty
a = 8
b = 5
# výpočet bodů ležících na křivce
x = (a+b)*np.cos(t)-b*np.cos((a/b+1)*t)
y = (a+b)*np.sin(t)-b*np.sin((a/b+1)*t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Epicykloida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-32, 32)
ax.set_ylim(-24, 24)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("epicyclodid1.png")
# zobrazení grafu
plt.show()
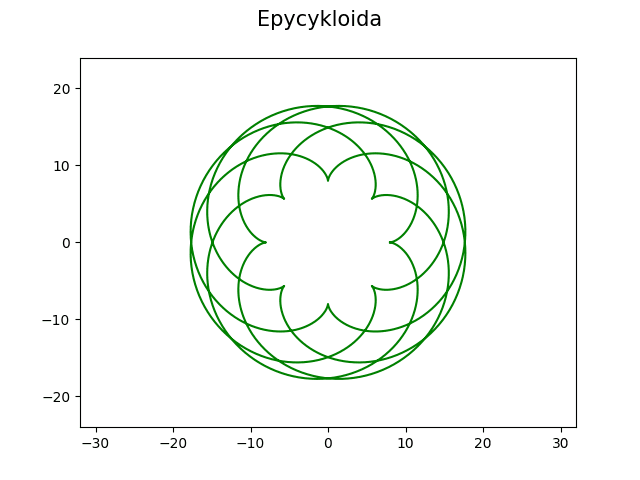
Obrázek 19: Epicykloida s koeficienty 8 a 5.
Hustší „květ“ vznikne v případě, kdy se zvyšuje hodnota koeficientu a. Hodnota parametru t opět leží v rozsahu 0 až 2πb::
"""Parametrická křivka: epicykloida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 26*np.pi, 0.01)
# koeficienty
a = 11
b = 13
# výpočet bodů ležících na křivce
x = (a+b)*np.cos(t)-b*np.cos((a/b+1)*t)
y = (a+b)*np.sin(t)-b*np.sin((a/b+1)*t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Epicyklodia', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-64, 64)
ax.set_ylim(-48, 48)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("epicyclodid2.png")
# zobrazení grafu
plt.show()
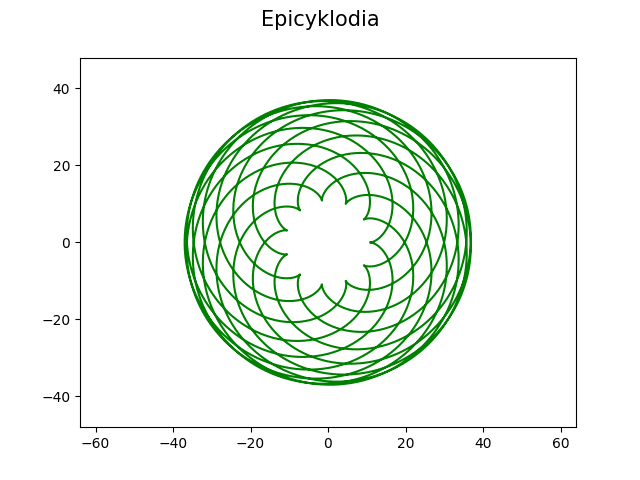
Obrázek 20: Epicykloida s koeficienty 11 a 13.
14. Hypocykloidy
Hypocykloida je křivka, která vznikne odvalováním kružnice okolo další (pevné) kružnice, přičemž odvalující se kružnice se nachází uvnitř pevné kružnice. Tuto křivku lze popsat bodovou funkcí:
x=(R-r)cos φ + r cos((R-r/r)φ
y=(R-r)sin φ – r sin((R-r/r)φ
V jiných materiálech se namísto koeficientů R a r používají koeficienty a a b, parametr φ bývá nahrazen za běžnější t:
"""Parametrická křivka: hypocykloida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 6*np.pi, 0.01)
# koeficienty
a = 5
b = 3
# výpočet bodů ležících na křivce
x = (a-b)*np.cos(t)+b*np.cos((a/b-1)*t)
y = (a-b)*np.sin(t)-b*np.sin((a/b-1)*t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hypocykloida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-8, 8)
ax.set_ylim(-6, 6)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hypocycloid1.png")
# zobrazení grafu
plt.show()

Obrázek 21: Hypocykloida s koeficienty a=5, b=3.
Ve skutečnosti nám ovšem nic nebrání v tom, aby „menší“ kružnice měla ve skutečnosti větší poloměr, i když to po geometrické stránce postrádá smysl:
"""Parametrická křivka: hypocykloida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 14*np.pi, 0.01)
# koeficienty
a = 2
b = 7
# výpočet bodů ležících na křivce
x = (a-b)*np.cos(t)+b*np.cos((a/b-1)*t)
y = (a-b)*np.sin(t)-b*np.sin((a/b-1)*t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hypocykloida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-18, 18)
ax.set_ylim(-12, 12)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hypocycloid2.png")
# zobrazení grafu
plt.show()
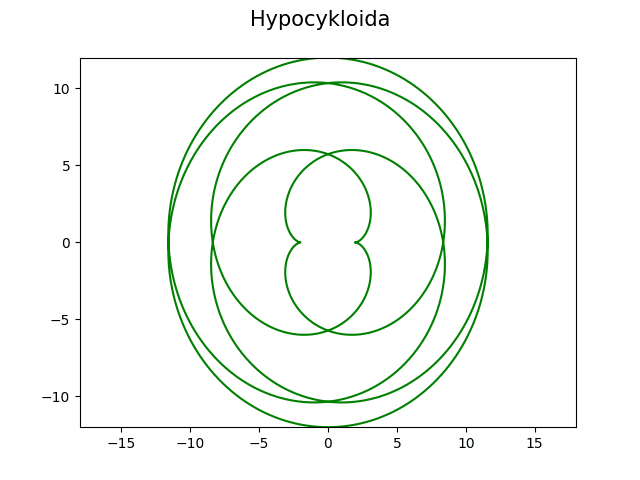
Obrázek 22: Hypocykloida s koeficienty a=2, b=7.
15. Hypotrochoidy
Poslední „cykloidní“ funkcí, s níž se dnes v praktické části seznámíme, je hypotrochoida. Bodová funkce této křivky je nepatrně složitější, než tomu bylo u předchozích funkcí, protože je ještě zaveden nový koeficient d (neboli vzdálenost bodu, který křivku určuje, od středu kružnice):
x = (R-r)*cos(t)+d*cos(t * (R-r/r))
y = (R-r)*sin(t)-d*sin(t * (R-r/r))
Podívejme se nyní na první příklad hypotrochoidy:
"""Parametrická křivka: hypotrochoida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.01)
# koeficienty
R = 5
r = 3
d = 5
# výpočet bodů ležících na křivce
x = (R-r)*np.cos(t)+d*np.cos(t * (R-r/r))
y = (R-r)*np.sin(t)-d*np.sin(t * (R-r/r))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hypotrochoida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-12, 12)
ax.set_ylim(-9, 9)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hypotrochoid.png")
# zobrazení grafu
plt.show()

Obrázek 23: Hypotrochoida s koeficienty R=5, r=3 a d=5.
Další příklad, tentokrát s odlišnými koeficienty:
"""Parametrická křivka: hypotrochoida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.01)
# koeficienty
R = 6
r = 1
d = 8
# výpočet bodů ležících na křivce
x = (R-r)*np.cos(t)+d*np.cos(t * (R-r/r))
y = (R-r)*np.sin(t)-d*np.sin(t * (R-r/r))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hypotrochoida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-24, 24)
ax.set_ylim(-18, 18)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hypotrochoid2.png")
# zobrazení grafu
plt.show()
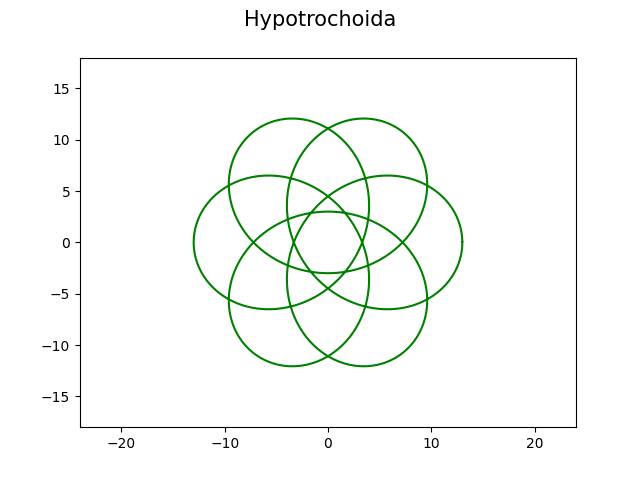
Obrázek 24: Hypotrochoida s koeficienty R=6, r=1 a d=8.
A konečně mezní případ, kdy d=2:
"""Parametrická křivka: hypotrochoida."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.01)
# koeficienty
R = 3
r = 1
d = 2
# výpočet bodů ležících na křivce
x = (R-r)*np.cos(t)+d*np.cos(t * (R-r/r))
y = (R-r)*np.sin(t)-d*np.sin(t * (R-r/r))
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Hypotrochoida', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-6, 6)
ax.set_ylim(-4, 4)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hypotrochoid3.png")
# zobrazení grafu
plt.show()
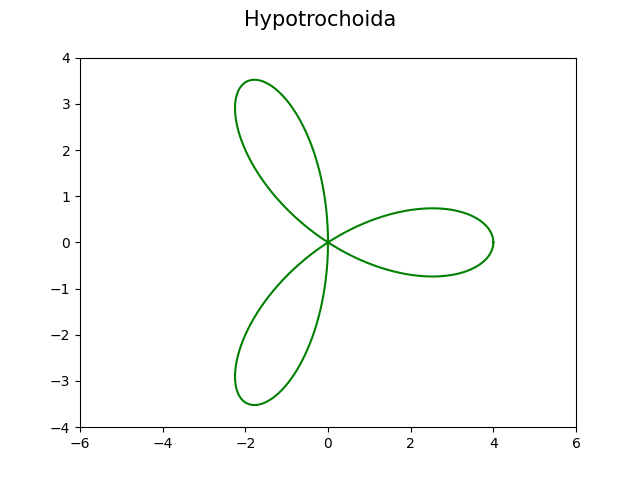
Obrázek 25: Hypotrochoida s koeficienty R=3, r=1 a d=2.
16. Lissajousovy obrazce
Lissajousova křivka popř. alternativně nazvaná Lissajousův obrazec se vykreslí snadno s využitím bodové rovnice odvozené od goniometrických funkcí sinus a kosinus tak, jak je to naznačeno v dalším demonstračním příkladu:
"""Parametrická křivka: Lissajousův obrazec."""
import numpy as np
import matplotlib.pyplot as plt
# hodnoty parametru t
t = np.arange(0, 2*np.pi, 0.02)
# poloměry v osách
a = 3.0
b = 3.0
# koeficienty
kx = 3
ky = 2
# výpočet bodů ležících na obrazci
x = a*np.cos(kx*t)
y = b*np.sin(ky*t)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Lissajousův obrazec', fontsize=15)
# určení rozsahů na obou souřadných osách
ax.set_xlim(-4, 4)
ax.set_ylim(-3, 3)
# vrcholy na křivce pospojované úsečkami
ax.plot(x, y, 'g-')
# vrcholy na křivce (každý čtvrtý)
ax.plot(x[::4], y[::4], 'ro')
# uložení grafu do rastrového obrázku
plt.savefig("lissajous.png")
# zobrazení grafu
plt.show()
S tímto výsledkem:
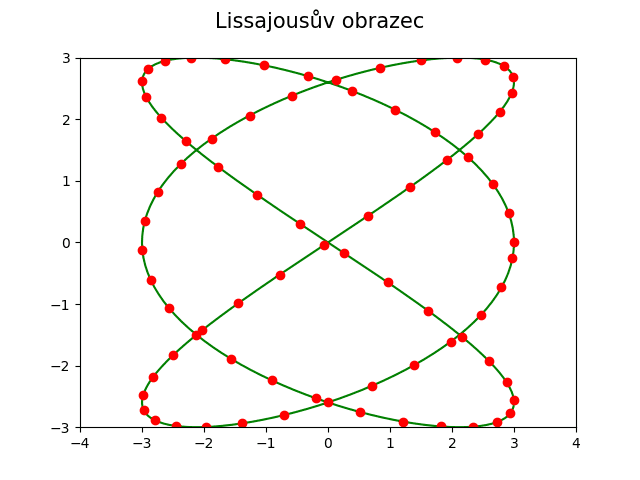
Obrázek 26: Lissajousův obrazec.
17. Křivky zadané implicitní funkcí
Křivky zadané implicitní funkcí je možné zobrazit i s využitím knihovny Matplotlib, i když pro tento typ zobrazení (zdánlivě) neexistuje přímá podpora. Pro vykreslení implicitně zadaných křivek je možné použít graf s konturami (contour), v němž zvolíme, že nás zajímá pouze kontura pro hodnotu 0, protože právě nula je na pravé straně rovnice s implicitní funkcí. Celý postup je ukázán v navazující kapitole, ovšem podrobnější popis si necháme až na příště.
18. Vykreslení implicitně zadaných křivek
Skript, který vykreslí křivku zadanou implicitní funkcí, může vypadat následovně. Podrobnosti si řekneme v dalším článku:
"""Implicitně zadaná křivka."""
import numpy as np
import matplotlib.pyplot as plt
# příprava vektorů pro konstrukci mřížky
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
# konstrukce mřížky
x, y = np.meshgrid(x, y)
# implicitní funkce
z = x**2-2*x*y+y**2-2*x
# hodnoty, které se mají zvýraznit na isoploše
levels = np.arange(1, 5, 0.5)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8))
# titulek grafu
fig.suptitle('Implicit curve', fontsize=15)
# vykreslení implicitní funkce
ax.contour(x, y, z, levels)
# zobrazit mřížku
ax.grid(True)
# zachovat poměr stran
ax.axis('scaled')
# popisek os
plt.xlabel('Osa x')
plt.ylabel('Osa y')
# uložení grafu do rastrového obrázku
plt.savefig("implicit.png")
# zobrazení grafu
plt.show()
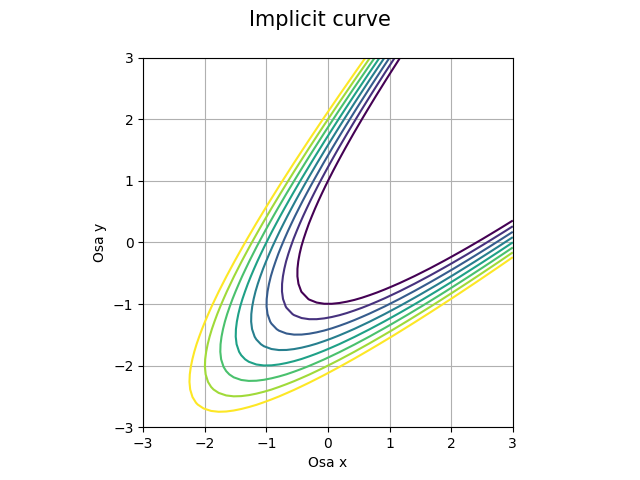
Obrázek 27: Křivky zadané implicitní funkcí.
19. Repositář s demonstračními příklady
Všechny minule i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
20. Odkazy na Internetu
- Famous Curves Index
https://mathshistory.st-andrews.ac.uk/Curves/ - Curve (Wikipedia)
https://en.wikipedia.org/wiki/Curve - Mathematical curves
https://www.2dcurves.com/index.html - Curves (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Curves.html - Smooth Curve (Wolfram MathWorld)
https://mathworld.wolfram.com/SmoothCurve.html - Spirals (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Spirals.html - An Interactive Introduction to Splines
https://ibiblio.org/e-notes/Splines/Intro.htm - Parabola
https://www.2dcurves.com/conicsection/conicsectionp.html - Hyperbola
https://www.2dcurves.com/conicsection/conicsectionh.html - Dioklova kisoida
https://cs.wikipedia.org/wiki/Dioklova_kisoida - Archimédova spirála
https://cs.wikipedia.org/wiki/Archim%C3%A9dova_spir%C3%A1la - Conchoid (mathematics)
https://en.wikipedia.org/wiki/Conchoid_(mathematics) - Algebraic curve
https://en.wikipedia.org/wiki/Algebraic_curve - Transcendental curve
https://en.wikipedia.org/wiki/Transcendental_curve - Spiral
https://en.wikipedia.org/wiki/Spiral - List of spirals
https://en.wikipedia.org/wiki/List_of_spirals - Hyperbolická spirála
https://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_spir%C3%A1la - Hyperbolic Spiral
https://mathworld.wolfram.com/HyperbolicSpiral.html - Lituus (mathematics)
https://en.wikipedia.org/wiki/Lituus_(mathematics) - Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/ - Cornu Spiral
http://hyperphysics.gsu.edu/hbase/phyopt/cornu.html - Spiral
https://www.2dcurves.com/spiral/spiral.html - Algebraic Curves
https://mathworld.wolfram.com/topics/AlgebraicCurves.html - Elliptic Curves
https://mathworld.wolfram.com/topics/EllipticCurves.html - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Curves we (mostly) don't learn in high school (and applications)
https://www.youtube.com/watch?v=3izFMB91K_Q - Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
https://www.maa.org/press/periodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions - Apollonius of Perga
https://en.wikipedia.org/wiki/Apollonius_of_Perga - Catenary arch
https://en.wikipedia.org/wiki/Catenary_arch - Parabolic arch
https://en.wikipedia.org/wiki/Parabolic_arch - Wattova křivka
https://www.geogebra.org/m/gNh4bW9r - Model stegosaura byl získán na stránce
http://www.turbosquid.com/HTMLClient/FullPreview/Index.cfm/ID/171071/Action/FullPreview - Obrázek nohy dinosaura byl získán na adrese
http://perso.wanadoo.fr/rimasson/3d/leg.htm - Spirograph
https://en.wikipedia.org/wiki/Spirograph - Epicykloida
https://cs.wikipedia.org/wiki/Epicykloida - Hypocykloida
https://cs.wikipedia.org/wiki/Hypocykloida - Hypotrochoida
https://cs.wikipedia.org/wiki/Hypotrochoida - Superelipsoidy a kvadriky v POV-Rayi
https://www.root.cz/clanky/superelipsoidy-a-kvadriky-v-pov-rayi/ - Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
https://elepa.files.wordpress.com/2013/11/fifty-famous-curves.pdf - Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981 - Bourke Paul: Quadrics,
July 1996 - Bourke Paul: Superellipse and Superellipsoid,
January 1990 - Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979 - Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968 - Glossary of Bridge Terminology
http://sdrc.lib.uiowa.edu/eng/bridges/WaddellGlossary/GlossC.htm - Brachistochrona
https://cs.wikipedia.org/wiki/Brachistochrona