Obsah
1. Křivky v přírodě i v počítačové grafice – svět spirál
2. Vykreslování spirál v Pythonu
8. Korektní vykreslení atomické spirály – zpracování záporných hodnot vzdáleností od středu
11. Spirály v systémech iterovaných funkcí (IFS)
12. Algoritmus náhodné procházky
13. Implementace algoritmu náhodné procházky v Pythonu
15. Spirály ve slavné Mandelbrotově množině
17. Seahorse valley a West seahorse valley
18. Triple spiral valley a Quad spiral valley
19. Repositář s demonstračními příklady
1. Křivky v přírodě i v počítačové grafice – svět spirál
Spirály, o nichž jsme se krátce zmínili i v úvodním článku tohoto seriálu, se v různé podobě objevují na mnoha místech v přírodě, a to jak v malých škálách (příkladem mohou být například ulity, popínavé rostliny), tak i na škálách odpovídajících planetám (víry v atmosféře) či dokonce celým galaxiím (spirální galaxie). Některé konkrétní spirály, typicky logaritmické spirály s koeficientem odpovídajícím zlatému řezu, vznikají jako důsledek snahy o (lokální) optimalizace nějakých procesů (ale ostatně i víry jsou tvary vzniklé tak, aby v co největší míře optimalizovaly proudění resp. tok hmoty v daném směru).

Obrázek 1: Stonek kapradiny zatočený do spirály.
Spirály namalované, vytesané či vymodelované lidmi můžeme nalézt již v prehistorii, například vyryté na kamenech ve slavném Newgrange (ale zdaleka nejenom tam). Jejich systematické studium ovšem začalo – ostatně kde jinde – v antickém Řecku. V tomto kontextu je důležité především dílo „O závitnicích“ (Περι ελικων), které sepsal Archimédes. Po něm je ostatně pojmenována i Archimédova spirála, s níž se setkáme ve třetí kapitole. A pochopitelně nesmíme zapomenout na použití spirál v architektuře; asi nejznámějším příkladem jsou hlavice Iónského řádu.

Obrázek 2: Vír v atmosféře ve tvaru takřka dokonalé spirály.
Velmi důležitý byl objev logaritmické spirály nazývané taktéž Spira Mirabilis. Tuto spirálu poprvé popsal Albrech Dürer, zabývali se jí i René Descartes a později i Jacob Bernoulli (tedy samá slavná jména). Tuto křivku nalezneme i na mnoha místech v přírodě (a to na široké škále). Například jí odpovídají již v úvodním odstavci zmíněná ramena spirálních galaxií, tropických cyklón, schránky některých měkkýšů, dráha, po které se hmyz pohybuje k bodovému světlu atd. Tuto spirálu nalezneme (opět ve všech škálách) i v Mandelbrotově množině, což je téma, kterému se dnes budeme taktéž věnovat.

Obrázek 3: Spirálovitý minaret v Samaře.
Z matematického pohledu je spirála křivka, která obíhá pevně daný ústřední bod (zvaný též pól spirály) a přitom se od tohoto bodu soustavně vzdaluje (důležité je zde přitom slovo „soustavně“, které dosti podstatným způsobem omezuje, co je a co už není spirála). Existují ovšem i spirály, které tomuto popisu zcela přesně neodpovídají, například proto, že mají dvě ramena nebo jsou založeny na přibližně eliptickém tvaru (vzdalující se Měsíc apod.). Mezním případem je potom triviální spirála neboli klasická kružnice.
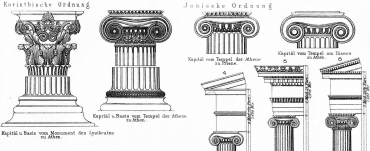
Obrázek 4: Spirály v klasických sloupových řádech.

Obrázek 5: Šnečí ulita.
2. Vykreslování spirál v Pythonu
Vykreslování prakticky všech běžných spirál můžeme provést s využitím knihovny Matplotlib, s níž jsme se již v tomto seriálu setkali. Navíc si vypomůžeme funkcemi z knihovny Numpy. Princip je jednoduchý – víme již, že spirála je křivka, která obíhá pevně daný ústřední bod. Trajektorii tohoto oběhu lze pochopitelně popsat mnoha různými způsoby, například v běžné kartézské souřadné soustavě apod. Ovšem mnohem jednodušší je využít polárních souřadnic, v nichž je souřadnice bodu popsána úhlem a vzdáleností od středu. To však pro některé typy spirál nebude dostačovat, a to z toho důvodu, že je nutné správně pracovat i s body, jejichž vzdálenost od středu je „záporná“ (což je z matematického pohledu nesmysl – vzdálenost neboli metrika, je vždy nezáporná). Záporné vzdálenosti – jakkoli zní nesmyslně – budeme proto z geometrického hlediska považovat za zápis souřadnice bodu, který je okolo počátku otočen o 180°. Tyto speciální případy je ovšem nutné ošetřit i programově, což ostatně uvidíme i v některých dalších demonstračních příkladech, například u atomické spirály.
Vraťme se však ke knihovnám Matplotlib a Numpy. Budeme vykreslovat křivku, jejíž koncový bod bude obíhat okolo počátku a přitom bude křivka popsána funkcí:
r = f(θ)
a to pochopitelně v polárních souřadnicích.
Nejprve si tedy vytvoříme vektor hodnot θ. Nemusíme se přitom omezovat na rozsah úhlů od 0 do 2π, neboť u některých spirál budeme chtít vykreslit větší množství závitů. Připravíme si tudíž vektor například pro čtyři závity:
# počet bodů na spirále points = 150 # úhel v polárním grafu theta = np.linspace(0.0, 8*np.pi, points)
Nějakým způsobem, který se bude lišit podle typu spirály, vypočítáme vzdálenosti od středu:
# funkce: vzdálenost od středu radius = f(theta)
Dále vytvoříme objekt reprezentující graf:
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
Vykreslíme do prozatím prázdného grafu spirálu:
# vrcholy na křivce pospojované úsečkami ax.plot(theta, radius, 'g-')
Graf následně uložíme do souboru a zobrazíme:
# uložení grafu do rastrového obrázku
plt.savefig("some_interesting_spiral.png")
# zobrazení grafu
plt.show()
3. Triviální spirála
O takzvané triviální spirále jsme se již ve stručnosti zmínili v úvodní kapitole. Jedná se o mezní případ spirály, kdy bod tvořící svým pohybem křivku sice obíhá okolo pólu spirály, ovšem ani se od něj nevzdaluje, ani nepřibližuje. Lze ji tedy vyjádřit rovnicí:
r = a
kde a je koeficient triviální spirály určující vzdálenost každého jejího bodu od pólu spirály.
Výsledkem je pochopitelně běžná kružnice, kterou lze výše uvedeným postupem pro vykreslení spirály zkonstruovat a zobrazit následujícím způsobem:
"""Triviální spirála - kružnice."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 150
# úhel v polárním grafu
theta = np.linspace(0.0, 8*np.pi, points)
# funkce: vzdálenost od středu
radius = np.full(shape=points, fill_value=1)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Triviální spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("trivial_spiral.png")
# zobrazení grafu
plt.show()
Výsledek po spuštění tohoto jednoduchého demonstračního příkladu bude vypadat následovně:
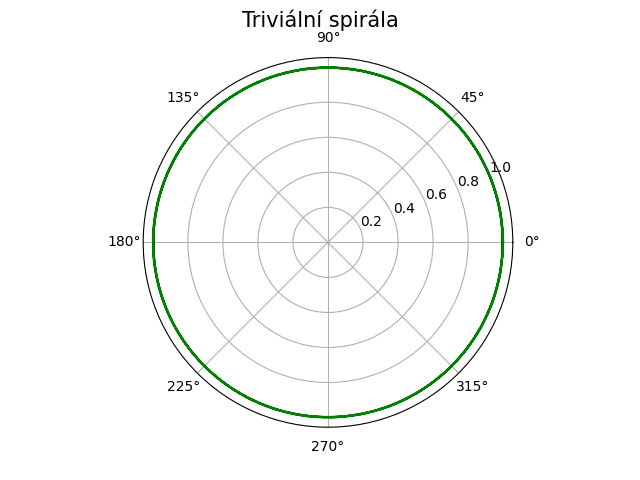
Obrázek 6: Triviální spirála neboli kružnice vykreslená demonstračním příkladem z této kapitoly.
4. Archimédova spirála
První „skutečnou“ spirálou, s níž se v dnešním článku seznámíme, je známá Archimédova spirála. Tvar této spirály byl sice používán již v prehistorické době, ovšem její první nám známý historický popis pochází od Archiméda, který se o této spirále zmiňuje v důležité knize „O spirálách“ („O závitnicích“) pocházející z roku 225 př.n.l. – „Otáčí-li se přímka v rovině stejnoměrnou rychlostí kolem svého počátku, který nehybným zůstává, a pohybuje-li se v ní zároveň, z počátku vycházeje, bod rychlostí též stejnoměrnou, opisuje bod tento závitnici.“ Mimochodem – výše zmíněné dílo „O spirálách“ je dosti zásadním počinem v matematické literatuře, protože kromě Archimédovy spirály se zde zmiňuje problematika kvadratury kruhu a nalezneme zde i stať o trisekci úhlu, tedy o klasických problémech starořecké geometrie. Vraťme se však k samotné Archimédově spirále. Její tvar je možné popsat v polárních souřadnicích snadno zapamatovatelnou rovnicí:
r = a θ
přičemž koeficient spirály a je ostře větší než nula.
Takto definovaná spirála prochází pólem spirály, kterým je počátek souřadné soustavy. Taktéž stojí za povšimnutí, že pokud vyšleme z pólu spirály paprsek libovolným směrem, bude protínat spirálu v bodech, jejichž vzdálenosti od pólu tvoří aritmetickou posloupnost, neboli že vzdálenosti mezi závity jsou konstantní. Někdy se můžeme setkat se zobecněním této spirály tak, že nebude procházet pólem spirály:
r = a θ + b
V tomto případě druhý z koeficientů b určuje vzdálenost počátku spirály od jejího pólu.
Archimédovu spirálu lze vykreslit tímto skriptem:
"""Archimedova spirála."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 150
# úhel v polárním grafu
theta = np.linspace(0.01, 8*np.pi, points)
# funkce: vzdálenost od středu
radius = theta
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Archimedova spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("archimedes_spiral.png")
# zobrazení grafu
plt.show()
S výsledkem:

Obrázek 7: Archimédova spirála.
5. Logaritmická spirála
Dalším velmi důležitým typem spirály je logaritmická spirála. Jedná se o křivku, jejíž poloměr roste exponenciálně s velikostí úhlu θ. Tvar této spirály je možné v polárních souřadnicích vyjádřit rovnicí:
r = a ebθ
kde a a b jsou koeficienty logaritmické spirály. Paprsek vycházející z pólu logaritmické spirály protíná spirálu v bodech, jejichž vzdálenosti od pólu tvoří geometrickou posloupnost (naproti tomu již víme, že u Archimédovy spirály se jedná o posloupnost aritmetickou).
Poměrně velké množství tvarů v přírodě lze popsat logaritmickou spirálou. O těchto tvarech jsme se již zmiňovali v úvodní kapitole, takže jen v krátkosti: tento tvar mají ulity některých měkkýšů, víry, ramena spirálních galaxií apod. Tuto spirálu poprvé popsal Albrech Dürer, zabývali se jí i René Descartes a později i Jacob Bernoulli (tedy samá slavná jména). A právě Jacob Bernoulli ji nazval Spira mirabilis. Dnes se tato spirála používá při návrhu spirálních antén, které při relativně malých rozměrech dokážou přijímat/vysílat v širokém frekvenčním spektru.
r = a ebθ, kde b=ln φ/(π/2)
Skript pro vykreslení logaritmické spirály:
"""Logaritmická spirála."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 150
# úhel v polárním grafu
theta = np.linspace(0.01, 8*np.pi, points)
# koeficient spirály
k = 0.15
# funkce: vzdálenost od středu
radius = np.exp(k*theta)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Logaritmická spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("logarithmic_spiral.png")
# zobrazení grafu
plt.show()
S tímto výsledkem:
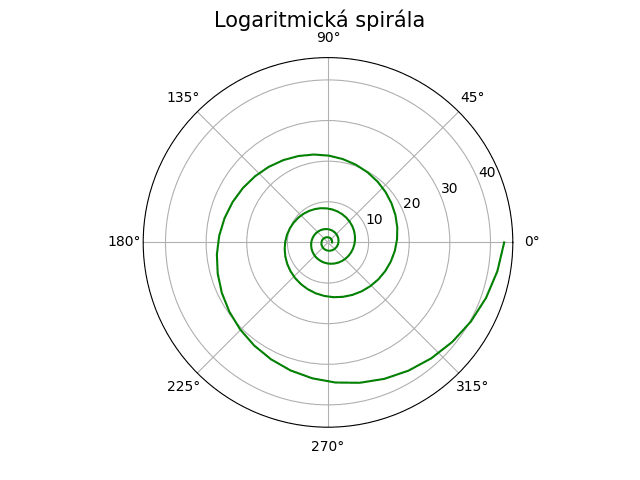
Obrázek 8: Logaritmická spirála.
6. Hyperbolická spirála
Další známou spirálou, s níž se v dnešním článku seznámíme, je hyperbolická spirála, která byla matematicky popsána v roce 1704 Pierrem Varignonem a posléze studována například i Johannem Bernoullim (ten se tedy zabýval studiem většího množství typů spirál). Tvar této spirály lze v polárních souřadnicích popsat touto rovnicí:
r = a / θ
Tato spirála se ve skutečnosti chová odlišně od běžných spirál, protože (pro nulový úhel θ) začíná v nekonečnu a postupně se přibližuje ke svému pólu, jenž neustále ovijí ve stále těsnějších smyčkách a pólu dosáhne pouze limitně.
Hyperbolická spirála může být vykreslena následujícím skriptem:
"""Hyperbolická spirála."""
import numpy as np
import matplotlib.pyplot as plt
# úhel v polárním grafu
theta = np.arange(1.00, 50.0, 0.05)
a = 1.0
# funkce: inverzní vzdálenost od středu
radius = a/theta
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Hyperbolická spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("hyperbolic_spiral.png")
# zobrazení grafu
plt.show()
S následujícím výsledkem:
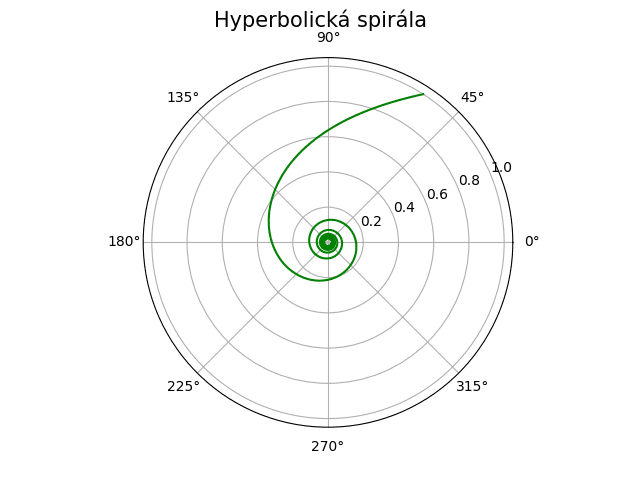
Obrázek 9: Hyperbolická spirála s jedním ramenem.
Vykreslit lze i hyperbolickou spirálu s oběma rameny, kde druhé rameno odpovídá záporným hodnotám úhlu θ:
"""Hyperbolická spirála."""
import numpy as np
import matplotlib.pyplot as plt
# úhel v polárním grafu
theta = np.arange(1.00, 50.0, 0.05)
a = 1.0
# funkce: inverzní vzdálenost od středu
radius = a/theta
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Hyperbolická spirála - obě ramena', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'r-')
# vrcholy na křivce pospojované úsečkami
ax.plot(np.pi - theta, radius, 'b-')
# uložení grafu do rastrového obrázku
plt.savefig("hyperbolic_spiral_2.png")
# zobrazení grafu
plt.show()
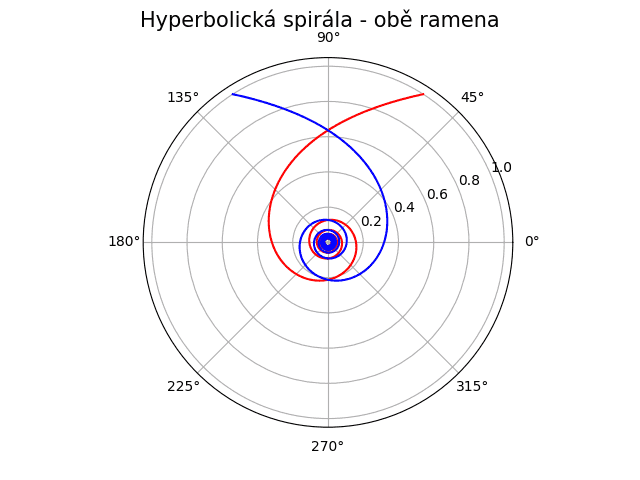
Obrázek 10: Hyperbolická spirála s oběma rameny.
7. Atomická spirála
V roce 2002 byla představena atomická spirála. Ta je zajímavá tím, že má dvě asymptoty – jednou z nich je jednotková kružnice a druhou pak přímka θ = a. Atomická spirála je v polárních souřadnicích určena rovnicí:
r = θ / (theta – a)
Jedná se tedy o jakýsi hybrid mezi Archimédovou spirálou (θ v čitateli) a hyperbolickou spirálou (θ ve jmenovateli).
Podívejme se nyní na první verzi skriptu pro vykreslení atomické spirály:
"""Atomická spirála."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 250
# úhel v polárním grafu
theta = np.linspace(-6*np.pi, 6*np.pi, points)
# koeficient spirály
a = 1
# funkce: vzdálenost od středu
radius = theta / (theta - a)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Atomická spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta, radius, 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("atomic_spiral.png")
# zobrazení grafu
plt.show()
S výsledkem:
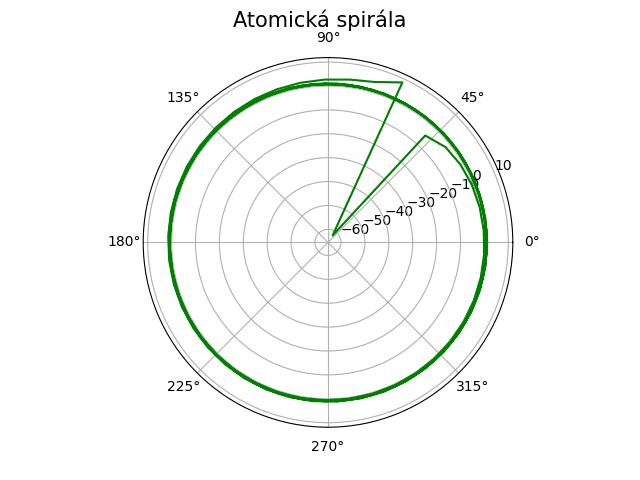
Obrázek 11: Atomická spirála vykreslená předchozím skriptem.
8. Korektní vykreslení atomické spirály – zpracování záporných hodnot vzdáleností od středu
Ve skutečnosti obrázek číslo 11 neobsahuje korektní atomickou spirálu. Je tomu tak z toho důvodu, že z její rovnice pro některé hodnoty vstupního úhlu θ dostaneme záporné vzdálenosti od středu (resp. možná přesněji řečeno od pólu spirály). Knihovna Matplotlib v tomto případě upraví polární graf takovým způsobem, že se v jeho středu nebude nacházet bod se souřadnicí nula (a libovolným úhlem), ale naopak bod, jehož souřadnice bude nejmenší hodnota z vykreslované sekvence bodů (opět viz obrázek číslo 11).
Ovšem oprava skriptu není příliš složitá. Budeme pouze muset nahradit následující volání, ve kterém předáváme úhly a vzdálenosti od počátku polární souřadné soustavy:
# vrcholy na křivce pospojované úsečkami ax.plot(theta, radius, 'g-')
Za nepatrně upravené volání, v němž jsou vzdálenosti vždy kladné (np.abs) a současně se pro původní záporné vzdálenosti upraví úhel θ posunem o hodnotu π:
# vrcholy na křivce pospojované úsečkami ax.plot(theta + (radius<0)*np.pi, np.abs(radius), 'g-')
Upravený skript vypadá takto:
"""Atomická spirála."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 150
# úhel v polárním grafu
theta = np.linspace(-6*np.pi, 6*np.pi, points)
# koeficient spirály
a = 1
# funkce: vzdálenost od středu
radius = theta / (theta - a)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Atomická spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta + (radius<0)*np.pi, np.abs(radius), 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("atomic_spiral.png")
# zobrazení grafu
plt.show()
S výsledkem:
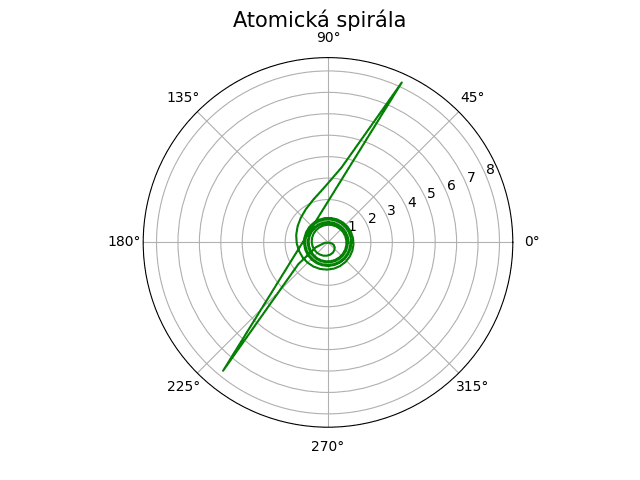
Obrázek 12: Korektní atomická spirála vykreslená předchozím skriptem.
9. Fermatova spirála
Další zajímavou spirálou je spirála objevená známým Pierre de Fermatem. Body ležící na této spirále splňují v polárních souřadnicích rovnici:
r2 = a2 θ
Odvozením získáme vztah pro hodnoty r:
r = ± a √θ
Tato spirála má tedy dvě ramena; jedno pro kladné hodnoty r, druhé pro záporné hodnoty (což je rameno se stejným tvarem, pouze otočené o 180°).
Skript pro vykreslení Fermatovy spirály vypadá následovně:
"""Fermatova spirála."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 150
# úhel v polárním grafu
theta = np.linspace(0, 4*np.pi, points)
# funkce: vzdálenost od středu
radius = np.sqrt(theta)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Fermatova spirála', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta + (radius<0)*np.pi, np.abs(radius), 'r-')
# druhá polovina křivky
ax.plot(np.pi + theta + (radius<0)*np.pi, np.abs(radius), 'b-')
# uložení grafu do rastrového obrázku
plt.savefig("fermat_spiral.png")
# zobrazení grafu
plt.show()
Výsledek získaný po spuštění tohoto příkladu:
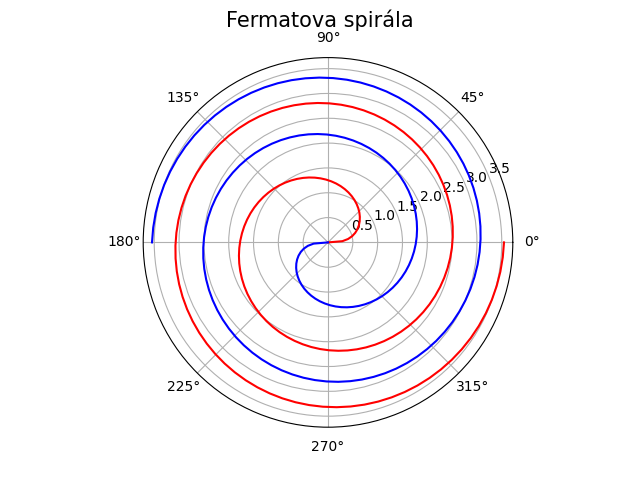
Obrázek 13: Fermatova spirála.
10. Lituus
Poslední spirála vykreslená v polárních souřadnicích, s níž se dnes setkáme, se nazývá lituus, což je název odvozený od starořímské polnice. Tato spirála je v polárních souřadnicích popsána rovnicí:
r2 θ = k
Z tohoto vztahu lze opět odvodit funkci pro výpočet r:
r = ± √ k / √θ
Tato spirála má tedy opět dvě ramena; jedno pro kladné hodnoty r, druhé pro záporné hodnoty (což je rameno se stejným tvarem, pouze otočené o 180°).
Vykreslení jednoho ramena této spirály zajišťuje následující skript:
"""Lituus."""
import numpy as np
import matplotlib.pyplot as plt
# počet bodů na spirále
points = 300
# úhel v polárním grafu
theta = np.linspace(0.1, 8*np.pi, points)
# koeficient spirály
k = 1
# funkce: vzdálenost od středu
radius = k / np.sqrt(theta)
# rozměry grafu při uložení: 640x480 pixelů
fig, ax = plt.subplots(1, figsize=(6.4, 4.8), subplot_kw={'projection': 'polar'})
# titulek grafu
fig.suptitle('Lituus', fontsize=15)
# vrcholy na křivce pospojované úsečkami
ax.plot(theta + (radius<0)*np.pi, np.abs(radius), 'g-')
# uložení grafu do rastrového obrázku
plt.savefig("lituus.png")
# zobrazení grafu
plt.show()
Výsledek:
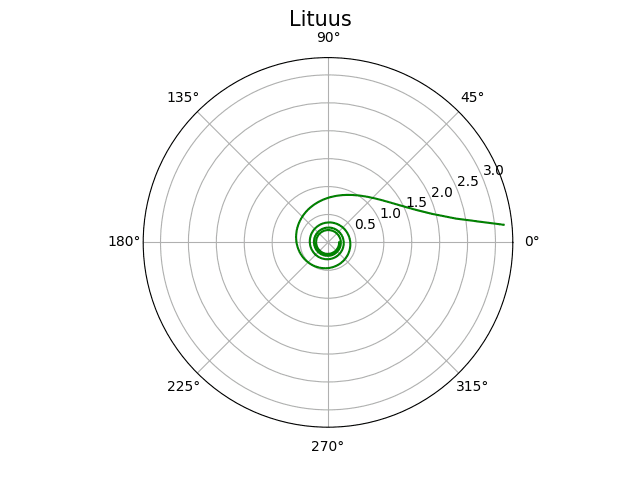
Obrázek 14: Lituus.
11. Spirály v systémech iterovaných funkcí (IFS)
Spirály můžeme snadno vytvořit i v systémech iterovaných funkcí, s nimiž jsme se seznámili v seriálu o fraktálech v počítačové grafice.
Název IFS systémů je odvozen z původního anglického označení Iterated Function System, česky lze tento název přeložit jako systém iterovaných funkcí. První publikace, které se týkaly IFS systémů, vydali už v roce 1985 Demko a následně pak v roce 1987 Michael Barnsley. Tvorba obrázků pomocí IFS systémů patří mezi generativní metody vytváření fraktálů, kterou řadíme mezi metody deterministické (viz popsané metody pro vytváření fraktálních objektů v komplexní rovině, které byly stručně uvedeny v předchozích dílech seriálu o fraktálech). Algoritmus pro generování IFS fraktálů však může být jak deterministický, tak nedeterministický (tj. stochastický – viz v dalších kapitolách uvedený algoritmus RWA).
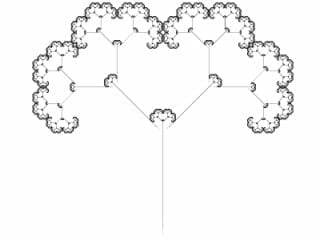
Obrázek 15: Dvojrozměrný IFS systém vykazující základní znak fraktálů – soběpodobnost.
Jednou z možností, kde lze v počítačové grafice využít systémy IFS, je mj. i procedurální konstrukce třídimenzionálních objektů, například stromů či rostlin, s následnou možností jejich vizualizace či animace. V této oblasti se využívají jak systémy IFS, tak i L-systémy. Každá z těchto metod pro vytváření fraktálních obrazců se hodí pro jiný účel. Pomocí L-systémů lze vytvářet polygonové objekty nabízející možnost dalšího zpracování v CAD systémech či jejich vykreslování pomocí současných grafických akcelerátorů, například přes knihovnu OpenGL (Vulkan). Pomocí IFS systémů se naopak vytvoří jednotlivé pixely v rovině či body v prostoru. Body rozmístěné v prostoru lze pro účely dalšího zpracování a následného zobrazení na obrazovce považovat buď za neorientované částice (particles) nebo za prostorově orientované elementární plošky – surfely (surface element).

Obrázek 16: (Poměrně naivn) 3D scéna vytvořená pomocí IFS systémů.
Hlavním znakem většiny fraktálních útvarů je soběpodobnost. Pokud je fraktál soběpodobný, můžeme najít zobrazení, které transformuje (mapuje) celek na jednotlivé části. Iterace tohoto zobrazení má za výsledek konvergenci k atraktoru fraktálu. Systémy iterovaných funkcí jsou z matematického hlediska vlastně množiny několika zobrazení (resp. v rovině R2 či prostoru R3 transformacemi x->F(x); tyto transformace jsou většinou afinní). Celý IFS fraktál je poté popsán množinou několika zobrazení (transformací), které budeme označovat symboly φ1 až φn. Většinou se jedná o lineární transformace, tj. změnu měřítka, posun, rotaci a zkosení, v některých případech se však používají i transformace nelineární, jakými jsou ohyb, zkrut, zborcení apod.

Obrázek 17: Další známý dvojrozměrný soběpodobný IFS systém – Sierpinského trojúhelník.
12. Algoritmus náhodné procházky
Princip generování IFS fraktálu je v nejjednodušším případě založený na takzvaném algoritmu náhodné procházky, který iterativně provádí následující výpočet: na bod Piter, který se nachází v rovině R2 nebo v prostoru R3, jsou buď deterministicky nebo náhodně (oním algoritmem náhodné procházky) aplikovány jednotlivé transformace φn. Výsledkem je nová pozice bodu Piter+1. IFS fraktál je poté zobrazen jako koláž složená ze všech vygenerovaných bodů Pi, i=(1..maxiter).
Před vlastním generováním je zapotřebí určit počáteční pozici startovního bodu P0. V předchozí sekci bylo řečeno, že všechny transformace jsou zároveň i transformacemi změny měřítka s koeficientem menším než 1 – jde tedy o kontrahující transformace zajišťující směřování systému ke svému atraktoru. Proto je možné pozici startovního bodu P0 zvolit libovolně, protože po několika počátečních iteracích se díky kontrahujícím transformacím posloupnost generovaných bodů Pi samovolně dostane do atraktoru IFS. Většinou se volí P0=[0, 0] v rovině R2 resp. P0=[0, 0, 0] v prostoru R3.
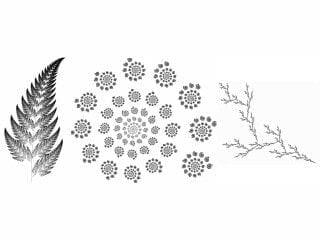
Obrázek 18: Ukázka dvojrozměrných IFS systémů (uprostřed soběpodobné spirály!).
Transformace, které se budou v daném iteračním kroku aplikovat na bod Pi lze vybírat buď deterministicky nebo náhodně. Rozbory obou těchto metod a jejich různých variant budou uvedeny v dalším textu. Na osmnáctém obrázku jsou zobrazeny ukázky IFS fraktálů generovaných algoritmem náhodné procházky (random walk). Na obrázku devatenáctém je zobrazena třídimenzionální scéna, která je sestrojena pouze z IFS fraktálů.

Obrázek 19: Další 3D scéna vygenerovaná pomocí IFS.
Při matematickém popisu systémů iterovaných funkcí IFS se vychází z matematické teorie pevných bodů (fixed points). Celá tato teorie, která se ostatně objevuje v jiném kontextu i v teoretické informatice, je ve své podstatě aplikací věty o Banachově pevném bodu:
Nechť U je metrický prostor s metrikou d. Dále, nechť f je funkce mapující množinu A na množinu U:
f: A → U
přičemž A je podmnožinou množiny U.
Jestliže dále pro funkci f existuje bod x0 takový, že platí:
f(x0)=x0
tj. bod x0 je funkcí f mapován na sám sebe, pak se bod (jsme v metrickém prostoru) x0 nazývá pevný bod. Pro funkci f s existujícím pevným bodem x0 platí mimo jiné i následující věta:
Jestliže je množina A podmnožinou množiny U a f je taková funkce, která mapuje množinu A do sebe sama (tj. f: A → A), přičemž existuje určitá konstanta δ (nazývaná kvůli své geometrické interpretaci kontrakční faktor), pro kterou platí 0<δ<1, potom:
d[f(x), f(y)]<=δd[x,y]
a funkce f se nazývá kontrakce.
d=(xn2+yn2)-2
Pomocí vektoru kontrakcí a vektoru pravděpodobností (ten si popíšeme příště) je možné popsat celý IFS systém, a to v jakémkoli metrickém prostoru, včetně roviny R2 či trojrozměrného prostoru R3. Podrobnější výklad takto pojatého IFS systému bude uveden v dalším pokračování tohoto seriálu.

Obrázek 20: Systém iterovaných funkcí tvořený rovnicí P-1(z)=(z-c)-2.
Velkou předností systémů iterovaných funkcí je možnost jejich interaktivního návrhu, při kterém uživatel nemusí pracovat pouze s numerickými hodnotami, ale s geometrickými tvary. Plošné či prostorové objekty, které budou tvořit základ pro generování fraktálních objektů pomocí systémů iterovaných funkcí, je vhodné reprezentovat obrysově. Existují i jiné možnosti reprezentace základního objektu, například reprezentace plošná, u níž je transformační matice rozšířena o změnu barvy a kontrastu, avšak obrysová reprezentace má tu výhodu, že je jednoduchá jak pro interaktivní zadávání dat uživatelem, tak i pro uložení dat v operační paměti počítače.
Práce uživatele při návrhu fraktálního obrazce pomocí systému iterovaných funkcí spočívá v tom, že uživatel navrhne bázový (základní) objekt, což není nic jiného než uspořádaný seznam vrcholů navzájem pospojovaných úsečkami. Zde se na uživatele nekladou žádné meze, je možné například vytvořit objekt, který má některé své hrany protnuté. Na výsledný fraktální objekt nemá tvar základního objektu žádný vliv, jedná se pouze o vizuální pomůcku pro uživatele.
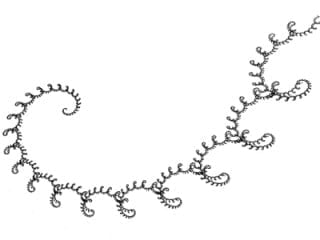
Obrázek 21: Další spirály nalezené ve vhodně zkonstruovaném IFS.
13. Implementace algoritmu náhodné procházky v Pythonu
Algoritmus náhodné procházky (RWA – Random Walk Algorithm) patří mezi nejjednodušší algoritmy pro generování fraktálních objektů pomocí systémů iterovaných funkcí. Jeho předností je jednoduchost a malá paměťová náročnost. Mezi jeho nevýhody patří nutnost generování velkého množství bodů pro reprezentaci fraktálu. Některé části fraktálu se generují vícekrát, zatímco některé pouze jednou a při malém počtu iterací může dokonce docházet k tomu, že se některé části fraktálu nevykreslí.

Obrázek 22: Trojrozměrné systémy iterovaných funkcí.
Generování IFS fraktálu se nastartuje tak, že se zvolí náhodný bod P0 v rovině E2 či prostoru E3. Poloha počátečního bodu nemá na výslednou koláž žádný větší vliv, nemusí tedy nutně ležet uvnitř atraktoru systému iterovaných funkcí:
# libovolné počáteční souřadnice v rovině x1 = y1 = 0
Poté je náhodně vybrána nějaká transformace φi z množiny Φ. Při výběru transformace je nutné přihlédnout k tomu, aby počet použití dané transformace odpovídal její pravděpodobnosti πi, jinak se bude výsledná koláž generovat neúměrně dlouho:
# pp leží v rozsahu 0.0 - 1.0
pp = random()
# na základě náhodného čísla najít transformaci
suma = 0
j = 0
while suma <= pp:
suma += ifs[j][6]
j += 1
j -= 1
Poté co byla některá transformace vybrána, je možné ji aplikovat na daný bod. Souřadnice tohoto bodu se změní (bod se podrobní transformaci). Na tento nový bod je posléze iterativně aplikována další náhodně vybraná transformace. Iterace probíhají tak dlouho, dokud není dosaženo zadaného maximálního počtu iterací:
# pokud byl překročen počet startovních iterací
# vypočítat a zobrazit bod
x2 = (x1-xmin) * width/delitel
y2 = (y1-ymin) * height/delitel
x = int(x2)
y = int(y2)
if x >= 0 and y >= 0 and x < IMAGE_WIDTH and y < IMAGE_HEIGHT:
image.putpixel((x, y), 0xffffff)
Jelikož první bod P0 nemusí nutně ležet v atraktoru IFS, je nutné několik prvních iterací počátečního bodu nezobrazovat:
# pokud byl překročen počet startovních iterací
if i > startiter:
# vypočítat a zobrazit bod
x2 = (x1-xmin) * width/delitel
y2 = (y1-ymin) * height/delitel
x = int(x2)
y = int(y2)
if x >= 0 and y >= 0 and x < IMAGE_WIDTH and y < IMAGE_HEIGHT:
image.putpixel((x, y), 0xffffff)
Z teorie IFS systémů, kterou jsem uvedl v předchozích kapitolách, vyplývá, že se systém automaticky dostane po několika iteracích do svého atraktoru, v němž již setrvá. Kvalitu výsledného fraktálního objektu lze ovlivnit zadáním maximálního počtu iterací, které se mají provést. Malý počet iterací způsobuje, že je obrázek složený z malého počtu bodů a tím pádem je hůře viditelný. Příliš velký počet iterací naopak způsobuje dlouhou dobu generování výsledné IFS koláže. V programovacím jazyce Python je možné algoritmus náhodné procházky pro generování IFS koláže napsat následovně:
#!/usr/bin/env python
"""IFS systémy."""
from PIL import Image
from random import random
# rozměry obrázku s fraktálem
IMAGE_WIDTH = 512
IMAGE_HEIGHT = 512
# transformace a jejich pravděpodobnosti
IFS_SYSTEMS = {
"binary": (
( 0.500000, 0.000000, 0.000000, 0.500000,-2.563477,-0.000003, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 2.436544,-0.000003, 0.333333),
( 0.000000,-0.500000, 0.500000, 0.000000, 4.873085, 7.563492, 0.333333)),
"coral": (
( 0.307692,-0.531469,-0.461538,-0.293706, 5.401953, 8.655175, 0.400000),
( 0.307692,-0.076923, 0.153846,-0.447552,-1.295248, 4.152990, 0.150000),
( 0.000000, 0.545455, 0.692308,-0.195804,-4.893637, 7.269794, 0.450000)),
"crystal": (
( 0.696970,-0.481061,-0.393939,-0.662879, 2.147003,10.310288, 0.747826),
( 0.090909,-0.443182, 0.515152,-0.094697, 4.286558, 2.925762, 0.252174)),
"dragon": (
( 0.824074, 0.281482,-0.212346, 0.864198,-1.882290,-0.110607, 0.787473),
( 0.088272, 0.520988,-0.463889,-0.377778, 0.785360, 8.095795, 0.212527)),
"dragon2": (
( 0.824074, 0.281481,-0.212346, 0.864197,-1.772710, 0.137795, 0.771268),
(-0.138580, 0.283951,-0.670062,-0.279012, 2.930991, 7.338924, 0.228732)),
"feather": (
( 0.870370, 0.074074,-0.115741, 0.851852,-1.278016, 0.070331, 0.798030),
(-0.162037,-0.407407, 0.495370, 0.074074, 6.835726, 5.799174, 0.201970)),
"fern": (
( 0.850000, 0.040000,-0.040000, 0.850000, 0.000000, 1.600000, 0.850000),
( 0.200000,-0.260000, 0.230000, 0.220000, 0.000000, 1.600000, 0.070000),
(-0.150000, 0.280000, 0.260000, 0.240000, 0.000000, 0.440000, 0.070000),
( 0.000000, 0.000000, 0.000000, 0.160000, 0.000000, 0.000000, 0.010000)),
"koch": (
( 0.307692, 0.000000, 0.000000, 0.294118, 4.119164, 1.604278, 0.151515),
( 0.192308,-0.205882, 0.653846, 0.088235,-0.688840, 5.978916, 0.253788),
( 0.192308, 0.205882,-0.653846, 0.088235, 0.668580, 5.962514, 0.253788),
( 0.307692, 0.000000, 0.000000, 0.294118,-4.136530, 1.604278, 0.151515),
( 0.384615, 0.000000, 0.000000,-0.294118,-0.007718, 2.941176, 1.000000)),
"spiral": (
( 0.787879,-0.424242, 0.242424, 0.859848, 1.758647, 1.408065, 0.895652),
(-0.121212, 0.257576, 0.151515, 0.053030,-6.721654, 1.377236, 0.052174),
( 0.181818,-0.136364, 0.090909, 0.181818, 6.086107, 1.568035, 0.052174)),
"tree": (
( 0.000000, 0.000000, 0.000000, 0.500000, 0.000000, 0.000000, 0.050000),
( 0.420000,-0.420000, 0.420000, 0.420000, 0.000000, 0.200000, 0.400000),
( 0.420000, 0.420000,-0.420000, 0.420000, 0.000000, 0.200000, 0.400000),
( 0.100000, 0.000000, 0.000000, 0.100000, 0.000000, 0.200000, 0.150000)),
"triangle": (
( 0.500000, 0.000000, 0.000000, 0.500000,-0.500000, 0.000000, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 0.500000, 0.000000, 0.333333),
( 0.500000, 0.000000, 0.000000, 0.500000, 0.000000, 0.860000, 0.333334)),
}
def generate_ifs(image, width, height, maxiter, startiter, ifs):
delitel = 12.0
# obdélník opsaný IFS
xmin = -7.0
xmax = 10.0
ymin = -1.0
ymax = 0.0
# libovolné počáteční souřadnice v rovině
x1 = y1 = 0
for i in range(maxiter):
# pp leží v rozsahu 0.0 - 1.0
pp = random()
# na základě náhodného čísla najít transformaci
suma = 0
j = 0
while suma <= pp:
suma += ifs[j][6]
j += 1
j -= 1
# aplikovat vybranou transformaci
x2 = x1*ifs[j][0] + y1*ifs[j][1] + ifs[j][4]
y2 = x1*ifs[j][2] + y1*ifs[j][3] + ifs[j][5]
x1 = x2
y1 = y2
# pokud byl překročen počet startovních iterací
if i > startiter:
# vypočítat a zobrazit bod
x2 = (x1-xmin) * width/delitel
y2 = (y1-ymin) * height/delitel
x = int(x2)
y = int(y2)
if x >= 0 and y >= 0 and x < IMAGE_WIDTH and y < IMAGE_HEIGHT:
image.putpixel((x, y), 0xffffff)
# vykreslit všechny IFS
for name, transformations in IFS_SYSTEMS.items():
print(name)
# inicializace prázdného obrázku
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
# vykreslení IFS
generate_ifs(image, IMAGE_WIDTH, IMAGE_HEIGHT, 100000, 1000, transformations)
# uložení obrázku do souboru
image.save(name + ".png")
14. Spirály v IFS
Skriptem popsaným v předchozí kapitole byly mj. vygenerovány i tyto obrazce se spirálami:

Obrázek 23: „Dragon“.

Obrázek 24: „Dragon 2“.

Obrázek 25: „Feather“.

Obrázek 26: „Fern“.
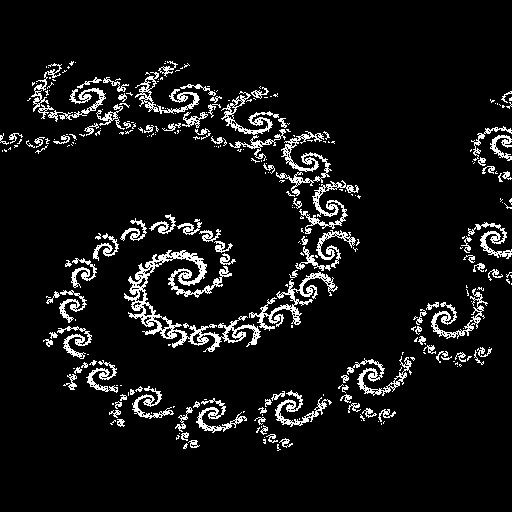
Obrázek 27: „Spiral“.
15. Spirály ve slavné Mandelbrotově množině
V Mandelbrotově množině se nachází velké množství zajímavých oblastí, přičemž zobrazované tvary jsou soběpodobné, tj. při různém zvětšení se opakují. Některé typické tvary byly podle svého vzhledu dokonce pojmenovány. Popis zajímavých oblastí začneme částí Mandelbrotovy množiny, která se nachází v okolí takzvaného Feigenbaumova bodu. S prací Feigenbauma jsme se setkali již při popisování dynamických systémů a bifurkačních diagramů. Feigenbaumův bod je místo v Mandelbrotově množině, v jehož okolí nastává stejný jev jako v bifurkačním diagramu – prudké zdvojování period vedoucích až k chaosu. Tento bod má v komplexní rovině souřadnice -1,401155+0,0i, leží tedy v záporné části reálné osy. Na dalším obrázku je zobrazena Mandelbrotova množina zvětšená do oblasti se středem ve Feigenbaumově bodu:.

Obrázek 28: Mandelbrotova množina v oblasti Feigenbaumova bodu.
16. Elephant valley
Další zajímavá oblast Mandelbrotovy množiny byla nazvána Elephant valley proto, že některé tvary zde obsažené připomínaly autorům názvu hlavu slona i se zatočeným chobotem. Oblast se nachází v okolí bodu 0,25+0,0i, tj. na kladné části reálné osy, která při celkovém pohledu na Mandelbrotovu množinu obsahuje vrchol největší (srdcovité) části množiny. Při velkém zvětšení můžeme v Elephant valley nalézt například množství zborcených „kopií“ základního tvaru Mandelbrotovy množiny:

Obrázek 29: Mandelbrotova množina v okolí oblasti nazvané ‚Elephant valley‘.

Obrázek 30: Mandelbrotova množina v okolí oblasti nazvané ‚Elephant valley‘.
Další zajímavá oblast Mandelbrotovy množiny je nazvaná Seahorse valley. Pojmenování vzniklo tak, že při větším přiblížení (zoomu) mohou tvary viditelné v této oblasti připomínat tělo mořského koníka. Oblast se nachází v okolí bodu -0,75+0,0i, tj. v místě, ve kterém se spojuje největší (srdcovitá) oblast Mandelbrotovy množiny s kruhovou oblastí umístěnou vlevo. Při velkém přiblížení zde můžeme nalézt zejména na sebe navazující dvouramenné spirály:

Obrázek 31: Mandelbrotova množina v okolí oblasti nazvané ‚Seahorse valley‘.

Obrázek 32: Mandelbrotova množina v okolí oblasti nazvané ‚Seahorse valley‘.
17. Seahorse valley a West seahorse valley
Na „západ“ od Seahorse valley, tj. ve směru záporné části reálné osy, se nachází takzvaná West seahorse valley. Jedná se o oblast nacházející se v okolí bodu -1,26+0,0i. Při celkovém pohledu na Mandelbrotovu množinu zjistíme, že se zde spojují dvě kruhové části Mandelbrotovy množiny. Tvary, které se při větším přiblížení nachází ve West seahorse valley jsou podobné tvarům z předchozí oblasti, ovšem s tím rozdílem, že zde také můžeme nalézt části Mandelbrotovy množiny, které jsou zdánlivě odtržené. Ve skutečnosti to však není pravda, protože je matematicky dokázáno, že Mandelbrotova množina je spojitá. A skutečně, při větším zvětšení zjistíme, že zdánlivě odtržené části jsou se zbytkem množiny propojeny tenkými vlákny:

Obrázek 33: Mandelbrotova množina v okolí oblasti nazvané ‚West seahorse valley‘.

Obrázek 34: Mandelbrotova množina v okolí oblasti nazvané ‚West seahorse valley‘.
18. Triple spiral valley a Quad spiral valley
Oblast nazvaná výstižně Triple spiral valley se nachází v okolí bodu -0,088+0,655i, tj. v „severní“ části Mandelbrotovy množiny. Zrcadlově symetrická oblast se samozřejmě nachází i v okolí bodu -0,088–0,654i. Jak je již z názvu této oblati patrné, je zde možné nalézt množství trojramenných spirál:

Obrázek 35: Mandelbrotova množina v okolí oblasti nazvané ‚Triple spiral valley‘.

Obrázek 36: Mandelbrotova množina v okolí oblasti nazvané ‚Triple spiral valley‘.
Oblast Quad spiral valley, jež se nachází v blízkém okolí bodu 0,274+0,482i (resp. u zrcadlového bodu 0,274–0,482i), se při větším přiblížení vyznačuje (nekonečným) množstvím tvarů podobných spirále se čtyřmi rameny:

Obrázek 37: Mandelbrotova množina v okolí oblasti nazvané ‚Quad spiral valley‘.

Obrázek 38: Mandelbrotova množina v okolí oblasti nazvané ‚Quad spiral valley‘.

Obrázek 39: Další spirály v Mandelbrotově množině.

Obrázek 40: Další spirály v Mandelbrotově množině.
19. Repositář s demonstračními příklady
Všechny dříve i dnes popisované demonstrační příklady určené pro Python 3 a knihovnu Matplotlib byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již poměrně rozsáhlý) repositář:
20. Odkazy na Internetu
- The spiral: the eternal sign of the creative and organising principle at work in the universe
https://geoffjward.medium.com/the-spiral-the-eternal-sign-of-the-creative-and-organising-principle-at-work-in-the-universe-8889ba092300 - Speira(Spiral): one of the oldest and most powerful symbols in the world
https://www.greecehighdefinition.com/blog/speira-spiral-oldest-greek-symbols-in-the-world-ancient-greece - Spirals
https://web.stanford.edu/~siegelr/photography/spirals.html - Why Do Spirals Exist Everywhere in Nature?
https://www.samwoolfe.com/2014/05/spirals-everywhere.html - Patterns In Nature: Where to Spot Spirals
https://www.scienceworld.ca/stories/patterns-nature-where-spot-spirals/ - Spirals in Nature
https://extension.illinois.edu/blogs/naturalist-news/2021–06–23-spirals-nature - The Curves of Life (Dover Books Explaining Science)
https://www.amazon.com/Curves-Dover-Books-Explaining-Science/dp/048623701X - Famous Curves Index
https://mathshistory.st-andrews.ac.uk/Curves/ - Curve (Wikipedia)
https://en.wikipedia.org/wiki/Curve - Mathematical curves
https://www.2dcurves.com/index.html - Curves (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Curves.html - Smooth Curve (Wolfram MathWorld)
https://mathworld.wolfram.com/SmoothCurve.html - Spirals (Wolfram MathWorld)
https://mathworld.wolfram.com/topics/Spirals.html - An Interactive Introduction to Splines
https://ibiblio.org/e-notes/Splines/Intro.htm - Parabola
https://www.2dcurves.com/conicsection/conicsectionp.html - Hyperbola
https://www.2dcurves.com/conicsection/conicsectionh.html - Dioklova kisoida
https://cs.wikipedia.org/wiki/Dioklova_kisoida - Archimédova spirála
https://cs.wikipedia.org/wiki/Archim%C3%A9dova_spir%C3%A1la - Conchoid (mathematics)
https://en.wikipedia.org/wiki/Conchoid_(mathematics) - Algebraic curve
https://en.wikipedia.org/wiki/Algebraic_curve - Transcendental curve
https://en.wikipedia.org/wiki/Transcendental_curve - Spiral
https://en.wikipedia.org/wiki/Spiral - List of spirals
https://en.wikipedia.org/wiki/List_of_spirals - Hyperbolická spirála
https://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_spir%C3%A1la - Hyperbolic Spiral
https://mathworld.wolfram.com/HyperbolicSpiral.html - Lituus (mathematics)
https://en.wikipedia.org/wiki/Lituus_(mathematics) - Spiral of Spirals Fractals 2 with Python Turtle (Source Code)
https://pythonturtle.academy/spiral-of-spirals-fractals-2-with-python-turtle-source-code/ - Cornu Spiral
http://hyperphysics.gsu.edu/hbase/phyopt/cornu.html - Spiral
https://www.2dcurves.com/spiral/spiral.html - Algebraic Curves
https://mathworld.wolfram.com/topics/AlgebraicCurves.html - Elliptic Curves
https://mathworld.wolfram.com/topics/EllipticCurves.html - Eukleidovská konstrukce
https://cs.wikipedia.org/wiki/Eukleidovsk%C3%A1_konstrukce - Euclidean Constructions
http://www.cs.cas.cz/portal/AlgoMath/Geometry/PlaneGeometry/GeometricConstructions/EuclideanConstructions.htm - Kvadratura kruhu
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Trisekce úhlu
https://cs.wikipedia.org/wiki/Trisekce_%C3%BAhlu - Straightedge and compass construction
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction - C.a.R.
http://car.rene-grothmann.de/doc_en/index.html - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/C.a.R. - CaRMetal (Španělsky a Francouzsky)
http://carmetal.org/index.php/fr/ - CaRMetal (Wikipedia)
https://en.wikipedia.org/wiki/CaRMetal - Regular Polygon
http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html - Geometric Construction with the Compass Alone
http://www.cut-the-knot.org/do_you_know/compass.shtml - Kvadratura kruhu (Wikipedie)
https://cs.wikipedia.org/wiki/Kvadratura_kruhu - Compass equivalence theorem
https://en.wikipedia.org/wiki/Compass_equivalence_theorem - Curves we (mostly) don't learn in high school (and applications)
https://www.youtube.com/watch?v=3izFMB91K_Q - Can You Really Derive Conic Formulae from a Cone? – Menaechmus' Constructions
https://www.maa.org/press/periodicals/convergence/can-you-really-derive-conic-formulae-from-a-cone-menaechmus-constructions - Apollonius of Perga
https://en.wikipedia.org/wiki/Apollonius_of_Perga - Catenary arch
https://en.wikipedia.org/wiki/Catenary_arch - Parabolic arch
https://en.wikipedia.org/wiki/Parabolic_arch - Wattova křivka
https://www.geogebra.org/m/gNh4bW9r - Model stegosaura byl získán na stránce
http://www.turbosquid.com/HTMLClient/FullPreview/Index.cfm/ID/171071/Action/FullPreview - Obrázek nohy dinosaura byl získán na adrese
http://perso.wanadoo.fr/rimasson/3d/leg.htm - Spirograph
https://en.wikipedia.org/wiki/Spirograph - Epicykloida
https://cs.wikipedia.org/wiki/Epicykloida - Hypocykloida
https://cs.wikipedia.org/wiki/Hypocykloida - Hypotrochoida
https://cs.wikipedia.org/wiki/Hypotrochoida - Superelipsoidy a kvadriky v POV-Rayi
https://www.root.cz/clanky/superelipsoidy-a-kvadriky-v-pov-rayi/ - Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers
https://elepa.files.wordpress.com/2013/11/fifty-famous-curves.pdf - Barr, A.H.: Superquadrics and Angle Preserving Transformations,
IEEE Computer Graphics and Applications, January 1981 - Bourke Paul: Quadrics,
July 1996 - Bourke Paul: Superellipse and Superellipsoid,
January 1990 - Faux, I.D. a Pratt, M.J.: Computational Geometry for Design and Manufacture,
Ellis Horwood Ltd., Wiley & Sons, 1979 - Wallace A.: Differential Topology,
Benjamin/Cummings Co., Reading, Massachussetts, USA, 1968 - Glossary of Bridge Terminology
http://sdrc.lib.uiowa.edu/eng/bridges/WaddellGlossary/GlossC.htm - Brachistochrona
https://cs.wikipedia.org/wiki/Brachistochrona - Missions: Cassini
https://solarsystem.nasa.gov/missions/cassini/overview/ - Giovanni Domenico Cassini
https://en.wikipedia.org/wiki/Giovanni_Domenico_Cassini - Cassini Ovals
https://mathworld.wolfram.com/CassiniOvals.html - Geocentrismus
https://cs.wikipedia.org/wiki/Geocentrismus - Who was Giovanni Cassini?
https://www.universetoday.com/130823/who-was-giovanni-cassini/ - Special plane curves
http://xahlee.info/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html - Why Does Slicing a Cone Give an Ellipse?
https://infinityisreallybig.com/2019/02/08/why-does-slicing-a-cone-give-an-ellipse/ - Interpolace
https://mathonline.fme.vutbr.cz/pg/Algoritmy/05_APROX_KRIVKY.htm - Lagrange Polynomial Interpolation
https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.04-Lagrange-Polynomial-Interpolation.html - Python Program for Lagrange Interpolation Method (with Output)
https://www.codesansar.com/numerical-methods/python-program-lagrange-interpolation-method.htm - Smooth Paths Using Catmull-Rom Splines
https://qroph.github.io/2018/07/30/smooth-paths-using-catmull-rom-splines.html - Lecture 11: Linear Interpolation Again – Bézier Curves
http://www.math.kent.edu/~reichel/courses/intr.num.comp.1/fall09/lecture12/bez.pdf - Geometrie/Úvod do křivek
https://cs.wikibooks.org/wiki/Geometrie/%C3%9Avod_do_k%C5%99ivek - B-Spline Curves and Surfaces (1)
http://www.cad.zju.edu.cn/home/zhx/GM/006/00-bscs1.pdf - Praktické ukázky možností aplikace Mandelbulber při tvorbě animací
https://www.root.cz/clanky/prakticke-ukazky-moznosti-aplikace-mandelbulber-pri-tvorbe-animaci/ - Kochanek–Bartels spline
https://en.wikipedia.org/wiki/Kochanek%E2%80%93Bartels_spline - class KochanekBartels
https://splines.readthedocs.io/en/latest/_modules/splines.html#KochanekBartels - Fraktály v počítačové grafice XVIII
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-xviii/ - Fraktály v počítačové grafice XVI
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-xvi/ - Fraktály v počítačové grafice IV
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iv/ - Systémy iterovaných funkcí a algoritmus náhodné procházky
https://www.root.cz/clanky/systemy-iterovanych-funkci-a-algoritmus-nahodne-prochazky/ - Pravděpodobnosti transformací v systémech iterovaných funkcí
https://www.root.cz/clanky/pravdepodobnosti-transformaci-v-systemech-iterovanych-funkci/





































