Obsah
1. Křížová validace modelů v knihovně scikit-learn
3. Ukázka činnosti rozdělení datové sady na oddíly (foldy)
4. Výběr prvků do trénovací a testovací datové sady na základě algoritmu K-fold
5. Křížová validace KNN modelu pro datovou sadu Iris
6. Nalezení ideální hodnoty hyperparametru pro KNN model
7. Grafická vizualizace vlivu hodnoty hyperparametru na úspěšnost modelu
8. Zjištění, zda je lepší použít model KNN či LogisticRegression
9. Zjištění, které atributy je nejlepší použít pro trénink modelu
10. Výpočet všech možných variací atributů pro datovou sadu Iris
11. Výpis všech možných variací atributů v datové sadě Iris
12. Skript pro otestování modelu pro všechny možné variace atributů datové sady Iris
13. Porovnání kvality natrénování modelu na grafu
14. Výsledky činnosti skriptů v tabulkové i grafické podobě
15. Skript pro otestování modelu pro všechny možné variace atributů datové sady California Housings
18. Výsledky: nalezení nejlepší sady atributů pro natrénování modelu
19. Repositář s demonstračními příklady
1. Křížová validace modelů v knihovně scikit-learn
V dnešním článku o nástroji scikit-learn úzce navážeme na všechny tři předchozí části. Zabývat se totiž budeme poměrně důležitou problematikou – jakým způsobem vybrat co nejvhodnější model, jak nastavit hyperparametry modelů a jak vlastně zjistit, které atributy se mají použít při tréninku modelu. Tato problematika je obecně dosti komplikovaná, ovšem k dispozici máme jeden velmi užitečný nástroj, který se nazývá křížová validace neboli cross-validation. V dnešním článku si ukážeme základní způsoby použití tohoto nástroje.
Při použití scikit-learn máme k dispozici poměrně velké množství modelů, z nichž je možné (a vlastně i nutné) si vybrat ten nejvhodnější model. Ovšem i když vybereme jeden model, musíme zjistit, jak nastavit jeho hyperparametry a jak rozdělit vstupní datovou sadu na trénovací a testovací část. Většinou se navíc chceme vyvarovat přetrénování modelu, použití příliš složitého modelu (u něj totiž není zřejmé, co se vlastně naučil – chová se jako černá skříňka) a taktéž může nastat situace, kterou jsme viděli minule – model může být pro náhodně vybrané vzorky natrénován korektně a pro jiné vzorky nikoli. Většinou tedy budeme potřebovat model natrénovat hned několikrát (pro různé hyperparametry atd.) a následně zjistit úspěšnost tréninku, například výpočtem průměru dosažených skóre.
2. K-fold validace
V knihovně scikit-learn nalezneme mj. i podporu pro takzvanou K-fold validaci. Při použití této formy validace dojde k rozdělení původní datové sady na K oddílů se stejnou velikostí (pokud to je možné, jinak se mohou velikosti lišit). Tyto oddíly se nazývají folds. Poté je model trénován a testován, přičemž vždy jeden z oddílů (foldů) bude použit pro testování, ostatní oddíly pro trénink – viz též grafická vizualizace. Následně se vypočítá přesnost odpovědí modelů. Celý cyklus výběru oddílu pro testování, trénink modelu, otestování modelu, výpočet skóre se opakuje (typicky 3K krát) a následně se vypočítá průměrná hodnota přesnosti odpovědí modelu. Celý postup je z pohledu programátora realizován funkcí cross_val_score.
Samotný algoritmus K-foldingu je realizován třídou KFold:
from sklearn.model_selection import KFold help(KFold)
Tato třída je, ostatně jako většina tříd a funkcí ze scikit-learn, poměrně dobře zdokumentována:
Help on class KFold in module sklearn.model_selection._split: class KFold(_BaseKFold) | KFold(n_splits=5, *, shuffle=False, random_state=None) | | K-Fold cross-validator. | | Provides train/test indices to split data in train/test sets. Split | dataset into k consecutive folds (without shuffling by default). | | Each fold is then used once as a validation while the k - 1 remaining | folds form the training set. | | Read more in the :ref:`User Guide <k_fold>`. | | For visualisation of cross-validation behaviour and | comparison between common scikit-learn split methods | refer to :ref:`sphx_glr_auto_examples_model_selection_plot_cv_indices.py` | | Parameters | ---------- | n_splits : int, default=5 | Number of folds. Must be at least 2. | | .. versionchanged:: 0.22 | ``n_splits`` default value changed from 3 to 5. | | shuffle : bool, default=False | Whether to shuffle the data before splitting into batches. | Note that the samples within each split will not be shuffled. | | random_state : int, RandomState instance or None, default=None | When `shuffle` is True, `random_state` affects the ordering of the | indices, which controls the randomness of each fold. Otherwise, this | parameter has no effect. | Pass an int for reproducible output across multiple function calls. | See :term:`Glossary <random_state>`.
3. Ukázka činnosti rozdělení datové sady na oddíly (foldy)
V některé dokumentaci a knihách se setkáte s dnes již nepodporovaným způsobem použití algoritmu K-fold. Uvádím ho zde jen kvůli úplnosti, ale nejedná se o kód, který je nekompatibilní s novějšími verzemi scikit-learnu:
# puvodni zpusob pouziti tridy KFold
from sklearn.cross_validation import KFold
kf = KFold(20, n_fonds=5, shuffle=False)
# iteration training set testing set
for iteration, data in enumerate(kf, start=1)
print(iteration, data[0], data[1])
Podívejme se na způsob, který je podporován. Budeme chtít rozdělit datovou sadu s deseti hodnotami (záznamy) do celkem pěti oddílů (foldů) a následně projdeme všemi kombinacemi [trénovací oddíl + testovací oddíly], které budou algoritmem K-foldu vygenerovány:
import numpy as np
from sklearn.model_selection import KFold
k_fold = KFold(n_splits=5, shuffle=False)
print(k_fold)
X = 1000 * np.linspace(1, 10, 10)
print(f"Original X: {X}")
for i, (train_index, test_index) in enumerate(k_fold.split(X)):
print(f"Fold {i}:")
print(f" Train: index={train_index}")
print(f" Test: index={test_index}")
Výsledek získaný po spuštění tohoto skriptu bude vypadat následovně:
KFold(n_splits=5, random_state=None, shuffle=False) Original X: [ 1000. 2000. 3000. 4000. 5000. 6000. 7000. 8000. 9000. 10000.] Fold 0: Train: index=[2 3 4 5 6 7 8 9] Test: index=[0 1] Fold 1: Train: index=[0 1 4 5 6 7 8 9] Test: index=[2 3] Fold 2: Train: index=[0 1 2 3 6 7 8 9] Test: index=[4 5] Fold 3: Train: index=[0 1 2 3 4 5 8 9] Test: index=[6 7] Fold 4: Train: index=[0 1 2 3 4 5 6 7] Test: index=[8 9]
Povšimněte si, že vůbec nezáleží na obsahu vstupní datové sady, pouze na počtu záznamů. Dále je vytvořeno celkem pět oddílů obsahujících nikoli přímo hodnoty z datové sady, ale „pouze“ jejich indexy. Jedná se o oddíly, z nichž každý obsahuje 10/5=2 indexy: [0, 1], [2 3], [4, 5], [6, 7] a [8, 9]. A v posledním kroku se zobrazí indexy záznamů použitých pro trénink (vždy osm) a indexy záznamů použitých pro testování (vždy jen dva).
V některých případech není možné, aby měly všechny oddíly stejný počet prvků (resp. indexů), což si můžeme ukázat při pokusu o rozdělení deseti prvků na tři oddíly:
import numpy as np
from sklearn.model_selection import KFold
k_fold = KFold(n_splits=3, shuffle=False)
print(k_fold)
X = 1000 * np.linspace(1, 10, 10)
print(f"Original X: {X}")
for i, (train_index, test_index) in enumerate(k_fold.split(X)):
print(f"Fold {i}:")
print(f" Train: index={train_index}")
print(f" Test: index={test_index}")
V tomto případě má první oddíl více prvků, než ostatní dva oddíly:
KFold(n_splits=3, random_state=None, shuffle=False) Original X: [ 1000. 2000. 3000. 4000. 5000. 6000. 7000. 8000. 9000. 10000.] Fold 0: Train: index=[4 5 6 7 8 9] Test: index=[0 1 2 3] Fold 1: Train: index=[0 1 2 3 7 8 9] Test: index=[4 5 6] Fold 2: Train: index=[0 1 2 3 4 5 6] Test: index=[7 8 9]
4. Výběr prvků do trénovací a testovací datové sady na základě algoritmu K-fold
Vzhledem k tomu, že algoritmus K-foldu generuje vektory indexů a nikoli přímo záznamů z původní datové sady, můžeme v případě potřeby tento další krok realizovat vlastními silami. Je to vlastně velmi jednoduché, a to z toho důvodu, že ze záznamů z datové sady můžeme provést vícenásobný výběr tak, že namísto jediného indexu (ten by vybral n-tý záznam) použijeme vektor indexů, což je funkcionalita nabízená n-rozměrnými poli knihovny Numpy. Pokud tento vektor bude obsahovat například indexes=[2, 3, 4] provedeme výběr prvků s indexy 2, 3 a 4 takto:
X[indexes]
Jak tedy bude celý postup probíhat v případě vstupní datové sady obsahující hodnoty 1000, 2000, … 10000?:
import numpy as np
from sklearn.model_selection import KFold
k_fold = KFold(n_splits=3, shuffle=False)
print(k_fold)
X = 1000 * np.linspace(1, 10, 10)
print(f"Original X: {X}")
for i, (train_index, test_index) in enumerate(k_fold.split(X)):
print(f"Fold {i}:")
print(f" Train data: index={X[train_index]}")
print(f" Test data: index={X[test_index]}")
Výsledky mohou vypadat následovně (požadovali jsme rozdělení do tří oddílů):
KFold(n_splits=3, random_state=None, shuffle=False) Original X: [ 1000. 2000. 3000. 4000. 5000. 6000. 7000. 8000. 9000. 10000.] Fold 0: Train data: index=[ 5000. 6000. 7000. 8000. 9000. 10000.] Test data: index=[1000. 2000. 3000. 4000.] Fold 1: Train data: index=[ 1000. 2000. 3000. 4000. 8000. 9000. 10000.] Test data: index=[5000. 6000. 7000.] Fold 2: Train data: index=[1000. 2000. 3000. 4000. 5000. 6000. 7000.] Test data: index=[ 8000. 9000. 10000.]
5. Křížová validace KNN modelu pro datovou sadu Iris
Nyní již do jisté míry známe teorii, která se za křížovou validací skrývá, takže se podívejme na první ze způsobů jejího praktického použití. Zjistíme úspěšnost modelu KNN (KNeighborsClassifier) pro K=5 (pozor, toto K nemá nic společného s K-foldy, je to jen čistě náhodou stejný symbol, který dokonale mate). Jak budeme postupovat? Nejdříve vytvoříme instanci modelu s nastavením jeho hyperparametrů (tedy K=5) a následně využijeme funkci cross_val_score pro automatické rozdělení datové sady do K-foldů, opakovaný trénink modelu, opakované vyhodnocení modelu atd. atd. – vše je provedeno za nás, takže tyto části nemusíme programovat. Následně jen vypíšeme zjištěná skóre (čím vyšší, tím lepší) a vypočteme jejich průměr:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# konstrukce klasifikatoru
knn = KNeighborsClassifier(n_neighbors=5)
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
print("Scores:")
for i, score in enumerate(scores):
print(i, score)
# prumer skore
print()
print("Average score:", scores.mean())
# search for an optimal value of K for KNN
k_range = list(range(1, 31))
k_scores = []
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
k_scores.append(scores.mean())
print(k_scores)
Výsledky mohou vypadat následovně (je z nich patrné, že někdy byl model více úspěšný a někdy méně, to ovšem u tak malé datové sady není překvapující):
Scores: 0 1.0 1 0.9333333333333333 2 1.0 3 1.0 4 0.8666666666666667 5 0.9333333333333333 6 0.9333333333333333 7 1.0 8 1.0 9 1.0
Průměrné skóre modelu pro K=5 (tedy pět sousedů):
Average score: 0.9666666666666668
Následně zjistíme průměrná skóre pro K=1 až K=31, tedy v případě, kdy měníme hyperparametry modelu:
[0.96, 0.9533333333333334, 0.9666666666666666, 0.9666666666666666, 0.9666666666666668, 0.9666666666666668, 0.9666666666666668, 0.9666666666666668, 0.9733333333333334, 0.9666666666666668, 0.9666666666666668, 0.9733333333333334, 0.9800000000000001, 0.9733333333333334, 0.9733333333333334, 0.9733333333333334, 0.9733333333333334, 0.9800000000000001, 0.9733333333333334, 0.9800000000000001, 0.9666666666666666, 0.9666666666666666, 0.9733333333333334, 0.96, 0.9666666666666666, 0.96, 0.9666666666666666, 0.9533333333333334, 0.9533333333333334, 0.9533333333333334]
6. Nalezení ideální hodnoty hyperparametru pro KNN model
Velmi jednoduše lze nalézt ideální hodnotu hyperparametru K (tedy počtu sousedů) pro KNN model, a to jen nepatrnou úpravou předchozího skriptu. S využitím křížové validace budeme trénovat a testovat model pro K=1 až K=50 a zapamatujeme si to K, pro které bylo výsledné skóre nejlepší. A jak bude z výsledků patrné, zdaleka neplatí, že čím vyšší K (tedy čím „složitější“ model) použijeme, tím lépe bude odpovídat. Naopak – větší K znamená i vyšší riziko přeučení modelu:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
best_score = 0
best_index = -1
# hledani optimalniho poctu regionu pro KNN
for k in range(1, 50):
# konstrukce klasifikatoru
knn = KNeighborsClassifier(n_neighbors=k)
# vypocet skore
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
avg_score = scores.mean()
# dosahli jsme lepsiho ohodnoceni?
if avg_score > best_score:
best_index = k
best_score = avg_score
# vypsani prumerneho skore do tabulky
print(k, avg_score)
print()
print(f"Best score {best_score} for K={best_index}")
Vypočtené a vypsané výsledky:
1 0.96 2 0.9533333333333334 3 0.9666666666666666 4 0.9666666666666666 5 0.9666666666666668 6 0.9666666666666668 7 0.9666666666666668 8 0.9666666666666668 9 0.9733333333333334 10 0.9666666666666668 11 0.9666666666666668 12 0.9733333333333334 13 0.9800000000000001 14 0.9733333333333334 15 0.9733333333333334 16 0.9733333333333334 17 0.9733333333333334 18 0.9800000000000001 19 0.9733333333333334 20 0.9800000000000001 21 0.9666666666666666 22 0.9666666666666666 23 0.9733333333333334 24 0.96 25 0.9666666666666666 26 0.96 27 0.9666666666666666 28 0.9533333333333334 29 0.9533333333333334 30 0.9533333333333334 31 0.9466666666666667 32 0.9466666666666667 33 0.9466666666666667 34 0.9466666666666667 35 0.9466666666666667 36 0.9466666666666667 37 0.9466666666666667 38 0.9466666666666667 39 0.9533333333333334 40 0.9533333333333334 41 0.9533333333333334 42 0.9533333333333334 43 0.9466666666666667 44 0.9400000000000001 45 0.9333333333333333 46 0.9333333333333333 47 0.9333333333333333 48 0.9333333333333333 49 0.9400000000000001
Následně se vypíše nejlepší hodnota hyperparametru modelu, což je konkrétně hodnota K=13. Model zde dosahuje úspěšnosti téměř 99%:
Best score 0.9800000000000001 for K=13
7. Grafická vizualizace vlivu hodnoty hyperparametru na úspěšnost modelu
Při postupné změně nějakého hyperparametru má většinou grafický průběh s přesností/úspěšností modelu tvar obráceného písmena U, tj. typicky zde nalezneme nějakou hodnotu, pro niž má model nejlepší předpovědi. Pokusme se tedy předchozí skript nepatrně vylepšit: dosažené skóre modelu si necháme vizualizovat, opět (prozatím) s využitím základní knihovny Matplotlib. A předpokládáme přitom, že pro K=13 bude v grafu maximum (nikoli lokální, ale globální):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
avg_scores = []
r = range(1, 70)
# hledani optimalniho poctu regionu pro KNN
for k in r:
# konstrukce klasifikatoru
knn = KNeighborsClassifier(n_neighbors=k)
# vypocet skore
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
avg_score = scores.mean()
# vypsani prumerneho skore do tabulky
print(k, avg_score)
avg_scores.append(avg_score)
plt.plot(r, avg_scores)
plt.xlabel("Změna K pro KNN")
plt.ylabel("Přesnost modelu")
# ulozeni grafu do souboru
plt.savefig("105.png")
# vykresleni grafu na obrazovku
plt.show()
Vypočtený a zobrazený výsledek by měl vypadat následovně:
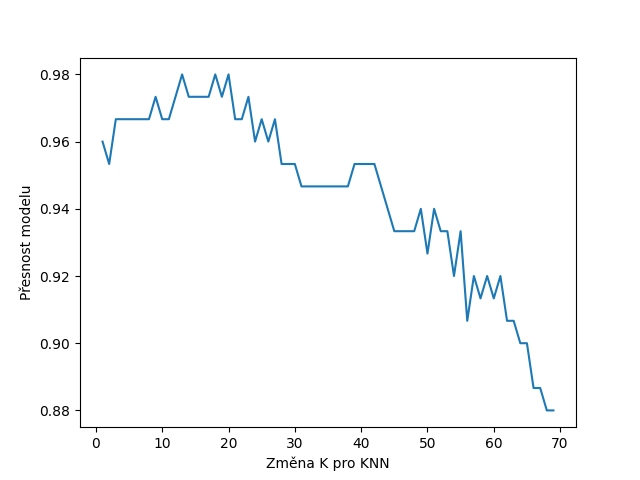
Obrázek 1: Graf s přibližným tvarem obráceného U s maximem pro K=13 (což není v tak malém rozlišení příliš patrné).
8. Zjištění, zda je lepší použít model KNN či LogisticRegression
Křížovou validaci můžeme použít i pro zjištění, který z dostupných modelů použít. Již v předchozích článcích jsme podobnou úlohu řešili, a to „ručními“ výpočty:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# trening modelu (se vsemi dostupnymi daty)
knn_1_classifier.fit(X, y)
knn_2_classifier.fit(X, y)
lr_classifier_1.fit(X, y)
lr_classifier_2.fit(X, y)
def score(model):
# očekávané výsledky
expexted_labels = iris.target
# výsledky modelu (predikované výsledky)
predicted_labels = model.predict(iris.data)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
Mnohem kratší (a přesnější!) je využití křížové validace a funkce cross_val_score:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
knn_1_classifier = KNeighborsClassifier(n_neighbors=1)
knn_2_classifier = KNeighborsClassifier(n_neighbors=5)
lr_classifier_1 = LogisticRegression(max_iter=1)
lr_classifier_2 = LogisticRegression(max_iter=1000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
def score(model):
scores = cross_val_score(model, X, y, cv=10, scoring='accuracy')
return scores.mean()
print(f"KNN classifier with K=1: {score(knn_1_classifier):5.2f}%")
print(f"KNN classifier with K=5: {score(knn_2_classifier):5.2f}%")
print(f"LogisticRegression with max_iter=1: {score(lr_classifier_1):5.2f}%")
print(f"LogisticRegression with max_iter=1000: {score(lr_classifier_2):5.2f}%")
Výsledky by měly vypadat následovně:
KNN classifier with K=1: 0.96% KNN classifier with K=5: 0.97% LogisticRegression with max_iter=1: 0.33% LogisticRegression with max_iter=1000: 0.97%
9. Zjištění, které atributy je nejlepší použít pro trénink modelu
Křížovou validaci je možné využít mnoha různými způsoby. Například můžeme zjistit, jakou kombinaci atributů je nejlepší použít pro natrénování modelu – může se totiž stát, že některé atributy způsobí, že model bude natrénován hůře, než v případě, že tento atribut či atributy vůbec nepoužijeme. Nejprve tedy musíme získat všechny možné variace atributů. Pro n atributů je těchto variací 2n-1, což například pro datovou sadu Iris znamená patnáct variací.
10. Výpočet všech možných variací atributů pro datovou sadu Iris
Jedno z možných řešení výpočtů všech variací je ukázáno v následujícím skriptu, který nejprve vypočte hodnotu 1..2n a tu následně použije jako bitovou masku určující, které atributy se mají v dané iteraci použít a které nikoli (ovšem možných řešení existuje celá řada):
import numpy as np
from sklearn.datasets import load_iris
# nacteni datove sady
iris = load_iris()
feature_names = np.array(iris.feature_names)
print("n", "selectors", "features")
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
print(i, selectors, feature_names[selectors])
11. Výpis všech možných variací atributů v datové sadě Iris
Podívejme se nyní na to, jak může vypadat výsledek činnosti skriptu, jehož úplný zdrojový kód byl uveden v předchozí kapitole. Celkem se vypíše všech patnáct možných variací, protože jsme vynechali variantu, v níž není použit žádný atribut. Taková varianta nemá v praxi žádný význam:
n selectors features 1 [0] ['sepal length (cm)'] 2 [1] ['sepal width (cm)'] 3 [0 1] ['sepal length (cm)' 'sepal width (cm)'] 4 [2] ['petal length (cm)'] 5 [0 2] ['sepal length (cm)' 'petal length (cm)'] 6 [1 2] ['sepal width (cm)' 'petal length (cm)'] 7 [0 1 2] ['sepal length (cm)' 'sepal width (cm)' 'petal length (cm)'] 8 [3] ['petal width (cm)'] 9 [0 3] ['sepal length (cm)' 'petal width (cm)'] 10 [1 3] ['sepal width (cm)' 'petal width (cm)'] 11 [0 1 3] ['sepal length (cm)' 'sepal width (cm)' 'petal width (cm)'] 12 [2 3] ['petal length (cm)' 'petal width (cm)'] 13 [0 2 3] ['sepal length (cm)' 'petal length (cm)' 'petal width (cm)'] 14 [1 2 3] ['sepal width (cm)' 'petal length (cm)' 'petal width (cm)'] 15 [0 1 2 3] ['sepal length (cm)' 'sepal width (cm)' 'petal length (cm)' 'petal width (cm)']
12. Skript pro otestování modelu pro všechny možné variace atributů datové sady Iris
Nyní již máme k dispozici všechny informace potřebné pro otestování modelu pro všechny možné variace atributů vstupní datové sady (použité částečně pro trénink a částečně pro otestování). Nejprve využijeme datovou sadu Iris se čtyřmi atributy. Model je tedy možné natrénovat s využitím patnácti variací těchto atributů (viz předchozí kapitolu). Necháme si tedy postupně vygenerovat všechny variace těchto atributů a pro každou variaci spustíme křížovou validaci modelu. Výsledkem bude tabulka s patnácti řádky obsahující vždy názvy všech použitých atributů a dosažený průměr přesnosti modelu:
import numpy as np
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
feature_names = np.array(iris.feature_names)
print("n", "selectors", "features")
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
knn_classifier = KNeighborsClassifier(n_neighbors=5)
selected_features = X[:, selectors]
scores = cross_val_score(knn_classifier, selected_features, y, cv=10, scoring='accuracy')
print(i, selectors, feature_names[selectors], scores.mean())
13. Porovnání kvality natrénování modelu na grafu
V případě, že je variací větší množství, je výhodnější porovnání výsledků modelu na grafu. V tomto případě použijeme sloupcový graf, který lze vygenerovat skriptem, jenž se do značné míry podobá skriptu z předchozí kapitoly, pouze je dopsáno vykreslení grafu a nastavení jeho atributů:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
feature_names = np.array(iris.feature_names)
print("n", "selectors", "features")
attributes = []
final_scores = []
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
knn_classifier = KNeighborsClassifier(n_neighbors=5)
selected_features = X[:, selectors]
scores = cross_val_score(knn_classifier, selected_features, y, cv=10, scoring='accuracy')
attributes.append("\n".join(feature_names[selectors]))
avg_score = scores.mean()
final_scores.append(avg_score)
print(i, selectors, feature_names[selectors], avg_score)
fig = plt.figure()
fig.set_figwidth(14)
fig.set_figheight(6)
fig.subplots_adjust(bottom=0.3)
plt.bar(attributes, final_scores)
plt.xticks(rotation=90)
plt.xlabel("Atributy")
plt.ylabel("Přesnost modelu")
# ulozeni grafu do souboru
plt.savefig("111.png")
# vykresleni grafu na obrazovku
plt.show()
14. Výsledky činnosti skriptů v tabulkové i grafické podobě
Nejprve se podívejme na tabulku vypsanou předchozími skripty a jen nepatrně upravenou pro vyšší čitelnost:
n selectors features average score 1 [0] ['sepal length (cm)'] 0.6533333333333333 2 [1] ['sepal width (cm)'] 0.5199999999999999 3 [0 1] ['sepal length (cm)' 'sepal width (cm)'] 0.76 4 [2] ['petal length (cm)'] 0.9533333333333334 5 [0 2] ['sepal length (cm)' 'petal length (cm)'] 0.9400000000000001 6 [1 2] ['sepal width (cm)' 'petal length (cm)'] 0.9533333333333334 7 [0 1 2] ['sepal length (cm)' 'sepal width (cm)' 'petal length (cm)'] 0.9466666666666667 8 [3] ['petal width (cm)'] 0.96 9 [0 3] ['sepal length (cm)' 'petal width (cm)'] 0.96 10 [1 3] ['sepal width (cm)' 'petal width (cm)'] 0.9533333333333334 11 [0 1 3] ['sepal length (cm)' 'sepal width (cm)' 'petal width (cm)'] 0.9533333333333334 12 [2 3] ['petal length (cm)' 'petal width (cm)'] 0.9666666666666666 13 [0 2 3] ['sepal length (cm)' 'petal length (cm)' 'petal width (cm)'] 0.96 14 [1 2 3] ['sepal width (cm)' 'petal length (cm)' 'petal width (cm)'] 0.9666666666666668 15 [0 1 2 3] ['sepal length (cm)' 'sepal width (cm)' 'petal length (cm)' 'petal width (cm)'] 0.9666666666666668
Grafická podoba výsledků vypadá takto:
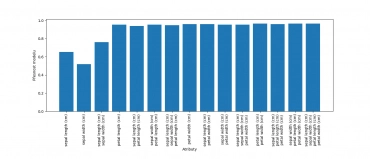
Obrázek 2: Vliv výběru atributů pro trénink modelu na jeho přesnost.
15. Skript pro otestování modelu pro všechny možné variace atributů datové sady California Housings
Prakticky stejným způsobem, jakým jsme zjistili, které variace atributů je vhodné použít pro natrénování modelu daty z datové sady Iris, můžeme postupovat u datové sady California Housings. Ta má více atributů (osm namísto čtyř) a navíc odhadujeme cenu, takže použijeme model pro provedení regrese a nikoli klasifikace. Ovšem důležitější změnou je odlišné otestování modelu, protože nyní použijeme metodu pro výpočet MSE (tedy střední kvadratické chyby). Při výpočtu se vrací záporná hodnota, protože čím větší je MSE, tím je model hůře natrénován a většina postupů se snaží o vyhledání maximální hodnoty (tedy vlastně v tomto případě nejmenší chyby):
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn import linear_model
from sklearn.model_selection import cross_val_score
# nacteni datove sady
housings = fetch_california_housing()
# X je matice (feature matrix)
X = housings.data
# y je vektor (response vector)
y = housings.target
feature_names = np.array(housings.feature_names)
print("n", "selectors", "features")
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
# konstrukce modelu
lr = linear_model.LinearRegression()
selected_features = X[:, selectors]
scores = -cross_val_score(lr, selected_features, y, cv=10, scoring='neg_mean_squared_error')
print(i, selectors, feature_names[selectors], scores.mean())
Alternativně můžeme počítat r2_score namísto MSE:
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn import linear_model
from sklearn.model_selection import cross_val_score
# nacteni datove sady
housings = fetch_california_housing()
# X je matice (feature matrix)
X = housings.data
# y je vektor (response vector)
y = housings.target
feature_names = np.array(housings.feature_names)
print("n", "selectors", "features")
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
# konstrukce modelu
lr = linear_model.LinearRegression()
selected_features = X[:, selectors]
scores = -cross_val_score(lr, selected_features, y, cv=10, scoring='r2')
print(i, selectors, feature_names[selectors], scores.mean())
16. Výsledky činnosti skriptu
Pokud skript z předchozí kapitoly spustíme, měl by se model postupně natrénovat se všemi možnými variacemi atributů (tedy „sloupců“). Pro trénink a otestování modelu se používá nám již známá technika křížové validace s využitím K-fold a s ohodnocením toho, jak dobře či naopak špatně byl model natrénován. Vzhledem k tomu, že datová sada California Housings má osm atributů, bude model natrénován 255× a výsledky by měly vypadat zhruba následovně:
n selectors features 1 [0] ['MedInc'] 0.7264558762632901 2 [1] ['HouseAge'] 1.3722534258632304 3 [0 1] ['MedInc' 'HouseAge'] 0.67769950759471 4 [2] ['AveRooms'] 1.3648838707766504 5 [0 2] ['MedInc' 'AveRooms'] 0.7278034142338758 6 [1 2] ['HouseAge' 'AveRooms'] 1.35356204264345 ... ... ... 'Longitude'] 0.5634932212002323 248 [3 4 5 6 7] ['AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 1.0375854748138316 249 [0 3 4 5 6 7] ['MedInc' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5697840889091118 250 [1 3 4 5 6 7] ['HouseAge' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 1.0446449942331266 251 [0 1 3 4 5 6 7] ['MedInc' 'HouseAge' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.559583975584127 252 [2 3 4 5 6 7] ['AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.8464478540402298 253 [0 2 3 4 5 6 7] ['MedInc' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5609103612635253 254 [1 2 3 4 5 6 7] ['HouseAge' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.851004133606707 255 [0 1 2 3 4 5 6 7] ['MedInc' 'HouseAge' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5509524296956632
17. Skript, který nalezne nejlepší variace atributů pro trénink modelu pro datovou sadu California Housings
Nyní si ukažme skript, jenž otestuje, která z 255 možných variací atributů datové sady California Housings je nejvýhodnější pro trénink modelu provádějícího lineární regresi (tedy vlastně toho nejjednoduššího modelu vůbec). Skript je založen na předchozím příkladu, ovšem nyní dokáže nalézt nejlepší skóre s odpovídající zvolenou variací atributů:
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn import linear_model
from sklearn.model_selection import cross_val_score
# nacteni datove sady
housings = fetch_california_housing()
# X je matice (feature matrix)
X = housings.data
# y je vektor (response vector)
y = housings.target
feature_names = np.array(housings.feature_names)
print("n", "selectors", "features")
best_score = -1e10
best_selectors = []
for i in range(1, 2**len(feature_names)):
indexes = []
n = i
for j in range(len(feature_names)):
if n % 2 == 1:
indexes.append(j)
n //= 2
selectors = np.array(indexes, dtype=int)
# konstrukce modelu
lr = linear_model.LinearRegression()
selected_features = X[:, selectors]
scores = cross_val_score(lr, selected_features, y, cv=10, scoring='r2')
avg_scores = scores.mean()
if avg_scores > best_score:
best_score = avg_scores
best_selectors = selectors
print(i, selectors, feature_names[selectors], avg_scores)
print()
print("Best score:", best_score)
print("With features", feature_names[best_selectors])
18. Výsledky: nalezení nejlepší sady atributů pro natrénování modelu
Po spuštění skriptu popsaného v předchozí kapitole by se měl trénink a ověření modelu spustit s 255 možnými variacemi atributů, které budou použity. Průběžně se sleduje i chyba odhadu modelu a následně se vybere taková variace atributů, která model natrénuje nejlépe:
n selectors features 1 [0] ['MedInc'] 0.3483800124754965 2 [1] ['HouseAge'] -0.2676224311757101 3 [0 1] ['MedInc' 'HouseAge'] 0.3895907438613606 4 [2] ['AveRooms'] -0.2614288891724069 5 [0 2] ['MedInc' 'AveRooms'] 0.34491558678359774 6 [1 2] ['HouseAge' 'AveRooms'] -0.2553626424315237 7 [0 1 2] ['MedInc' 'HouseAge' 'AveRooms'] 0.3866358153843511 8 [3] ['AveBedrms'] -0.2734471504229889 9 [0 3] ['MedInc' 'AveBedrms'] 0.3480449795351417 10 [1 3] ['HouseAge' 'AveBedrms'] -0.2682477414184001 ... ... ... 247 [0 1 2 4 5 6 7] ['MedInc' 'HouseAge' 'AveRooms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.503734153650471 248 [3 4 5 6 7] ['AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.06304487614251124 249 [0 3 4 5 6 7] ['MedInc' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5005616909146572 250 [1 3 4 5 6 7] ['HouseAge' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.05875309913453884 251 [0 1 3 4 5 6 7] ['MedInc' 'HouseAge' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5059557816071801 252 [2 3 4 5 6 7] ['AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.253637001880857 253 [0 2 3 4 5 6 7] ['MedInc' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5052686713242268 254 [1 2 3 4 5 6 7] ['HouseAge' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.24749723159992967 255 [0 1 2 3 4 5 6 7] ['MedInc' 'HouseAge' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup' 'Latitude' 'Longitude'] 0.5110068610523775
Nejlepší je kombinace sedmi atributů (s vynecháním atributu Population), což je ostatně patrné i z následujícího výpisu:
Best score: 0.5115316995802758 With features ['MedInc' 'HouseAge' 'AveRooms' 'AveBedrms' 'AveOccup' 'Latitude' 'Longitude']
Ignored attribute MSE r2 score MedInc 0.805 0.392 HouseAge 0.535 0.601 AveRooms 0.536 0.596 AveBedrms 0.541 0.598 Population 0.525 0.605 AveOccup 0.539 0.596 Latitude 0.617 0.535 Longitude 0.619 0.538
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/





































