Lorenzův systém: ideální pomůcka pro studium chaosu

Obsah

1. Lorenzův systém: ideální pomůcka pro studium chaosu

2. Chování Lorenzova systému

3. Výchozí parametry, pevné body odvozené z rovnic

4. Vizualizace dynamického chování Lorenzova systému: klíč k jeho pochopení

5. Vývoj Lorenzova systému pro některé typické vstupní parametry

6. Zobrazení fázového prostoru ve formě 3D grafu, popř. průmětů do vybraných rovin

7. Vliv parametru r na chování Lorenzova systému: mez stability

8. Chování Lorenzova systému na mezí stability: výběr mezi dvěma budoucnostmi vesmíru

9. Chování Lorenzova systému za mezí stability: animace podivného Lorenzova atraktoru

10. Výsledná animace a vybrané snímky

11. Studie tvarů Lorenzova systému při změně parametrů σ i r

12. Úplný zdrojový kód skriptu pro vykreslení několika Lorenzových systémů pro různé parametry

13. Vizualizace Lorenzových systémů pro různé parametry ve formě mřížky grafů

14. Úplný zdrojový kód skriptu pro vykreslení několika Lorenzových systémů do mřížky

15. Vliv počátečních podmínek na tvar Lorenzova systému

16. Jednotlivé Lorenzovy systémy vykreslené pro různé počáteční podmínky do mřížky

17. Animace postupného vývoje Lorenzových systémů

18. Výsledné animace se stručným popisem

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

1. Lorenzův systém: ideální pomůcka pro studium chaosu

Jak již bylo napsáno v perexu dnešního článku, navážeme v něm na článek Emergence: struktury vzniklé ze zdánlivého chaosu. Připomeňme si, že jsme si v něm ukázali, že i aplikací velmi jednoduchých pravidel (což konkrétně byly vzorečky pro výpočet síly, kterou se odpuzují částice doplněné o rovnice pohybu) je možné získat komplexní systém, ve kterém se začínají objevovat emergentní struktury. Toto téma do značné míry souvisí s teorií chaosu. A v této oblasti má již od roku 1963 poměrně výsadní postavení Lorenzův systém, už jen z toho důvodu, že byl zkoumán jako první a i z jeho vizualizace lze odvodit některé důležité vlastnosti takzvaných podivných atraktorů.

Tento systém sestávající ze tří dynamických rovnic použil Edward Lorenz již v roce 1963 při snaze o zjednodušení výpočtů používaných pro simulaci vývoje počasí. Použil přitom tři velká zjednodušení:

1. Zjednodušil modelovaný systém na (zjednodušeně řečeno) dvourozměrný „hrnec“ (ale může se jednat i o toroid, kde je omezena role tvaru „hrnce“) s kapalinou, který je v dolní části zahříván a v horní části naopak ochlazován (vzduch je taktéž zahříván na povrchu Země, takže to má i svůj fyzikální význam)
2. Snažil se o simulaci proudění kapaliny (konvence) na základě rozdílných teplot (a nikoli proudění stlačitelného plynu)
3. Nahradil Navierovy-Stokesovy rovnice mnohem jednodušším systémem tří diferenciálních rovnic

Snahy o zjednodušení modelovaného systému i zjednodušení modelu má svůj důvod – musíme si totiž uvědomit, jak drahý byl v roce 1963, kdy Lorenz tento systém vytvořil, výpočetní čas a jak byly výpočty s tehdejším HW pomalé.

Taktéž došlo ke snížení počtu parametrů tohoto systému na pouhé tři parametry:

1. Prandtlovo číslo
2. Rayleightovo číslo
3. Číslo odpovídající rozměrům vrstvy tekutiny

Diferenciální rovnice Lorenzova atraktoru mají po převodu na diferenční tvar následující formát:

dx/dt = σ (y-x)
dy/dt = x(ρ - z) - y
dz/dt = xy - Βz

Takže pro iterativní (samozřejmě že nepřesný) výpočet můžeme pracovat s následujícími vztahy, které pro dostatečně malé dt vedou k výpočtu bodů ležících na Lorenzově atraktoru:

xn+1=xn+(σ (y-x)) dt
yn+1=yn+(x(ρ - z) - y) dt
zn+1=zn+(xy - Βz) dt

2. Chování Lorenzova systému

Jak již bylo řečeno v úvodní kapitole, je kapalina ve dvourozměrném „hrnci“ dole zahřívána a nahoře ochlazována. To vede k termické konvenci, jejíž chování je ovlivněno všemi třemi výše zmíněnými parametry (z nichž jeden odpovídá rozdílu teploty). Při relativně malých rozdílech nastává cirkulace tekutiny (to už značí bifurkaci – tekutina si náhodně vybere směr cirkulace) a při velkých rozdílech se chování stává chaotické.

Chování systému v určitém čase vyjadřují hodnoty x, y a z počítané výše uvedenými rovnicemi:

• rychlost cirkulace a její směr
• gradient teplot v horizontálním směru
• gradient teplot ve vertikálním směru

Tyto hodnoty tvoří body ve fázovém prostoru, ke kterému se vrátíme v navazujících kapitolách.

3. Výchozí parametry, pevné body odvozené z rovnic

Edward Lorenz ve svém prvním článku o svém dynamickém systému popsal, že se tento systém chová chaoticky pro vstupní parametry σ=10, b=8/3 a r=28. Ovšem my si v dalším textu ukážeme, jaký je vliv těchto parametrů na tvar dynamického systému při jejich modifikaci.

Dále lze z rovnic zjistit pevné body Lorenzova systému:

• x=0, y=0, z=0
• x=+√b(r−1), y=+√b(r−1), z=r-1
• x=-√b(r−1), y=-√b(r−1), z=r-1

4. Vizualizace dynamického chování Lorenzova systému: klíč k jeho pochopení

Lorenzův systém je možné zkoumat několika způsoby. Samozřejmě je možná jeho matematická analýza, tedy například zjištění pevných bodů (fixed points), to, zda systém obsahuje nějaké stabilní atraktory či naopak „odpuzovače“, to, zda se postupným vývojem systému (jde o dynamický systém vyvíjející se v čase) dosáhne nějakého stabilního stavu, periodického chování či chování chaotického atd. Taktéž je možné se pokusit o nějakou formu numerické analýzy, kterou je však v tomto případě velmi vhodné doplnit i vhodnou formou vizualizace, protože (jak si ukážeme dále) nám právě vizualizace poskytnou ucelenější pohled na chování celého Lorenzova systému.

Nejjednodušší formou vizualizace je výpočet a zobrazení postupného vývoje (resp. možná přesněji řečeno postupných změn) hodnot x, y a z v čase. Necháme se tedy zobrazit trojici grafů s funkcemi x(t), y(t) a z(t), protože na postupnou změnu hodnot se skutečně můžeme dívat jako na nějakou funkci, kterou s určitými nepřesnostmi numericky počítáme. Realizace zobrazení takových průběhů je s využitím knihovny Matplotlib poměrně přímočará:

# import všech potřebných knihoven - Numpy a Matplotlibu
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 2000
 
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
 
# počáteční hodnoty
x[0], y[0], z[0] = (0.0, 1.0, 1.05)
 
# vlastní výpočet bodů x, y, z, z nichž se postupně
# vytváří Lorenzův systém
for i in range(n - 1):
    x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
    x[i + 1] = x[i] + x_dot * dt
    y[i + 1] = y[i] + y_dot * dt
    z[i + 1] = z[i] + z_dot * dt
 
# konstrukce 2D grafu s nastavením rozlišení výsledného obrázku
fig = plt.figure(figsize=(8, 6))
 
# vykreslení grafu
 
ax = fig.add_subplot(3, 1, 1)
ax.plot(x)
 
ax = fig.add_subplot(3, 1, 2)
ax.plot(y)
 
ax = fig.add_subplot(3, 1, 3)
ax.plot(z)
 
# změna velikosti komponent v grafu.
plt.tight_layout()
 
# uložení grafu
plt.savefig("lorenz_x_y_z.png")
 
# zobrazení grafu
plt.show()

Po spuštění tohoto skriptu by se měl zobrazit následují obrázek s vývojem trojice hodnot x, y a z.

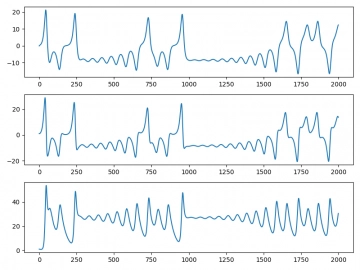
Obrázek 1: Trojice průběhů s postupným vývojem hodnot x, y a z.

5. Vývoj Lorenzova systému pro některé typické vstupní parametry

I poměrně triviální až primitivní způsob vizualizace Lorenzova systému, který jsme si popsali v předchozí kapitole, nám ovšem může poskytnout dosti důležité informace o některých vlastnostech tohoto dynamického systému. Například můžeme zjistit, jak se systém chová pro různě nastavené parametry σ, r a b (už složitěji si však ověříme kombinace parametrů, o tom se však ještě budeme bavit v dalším textu). Podívejme se alespoň na pět průběhů získaných pro takové parametry, pro které se systém chová typickými způsoby (ovšem nejzajímavější je stále první obrázek s chaotickým chováním):

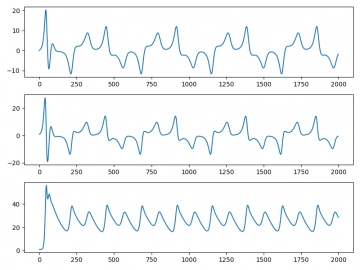
Obrázek 2: Pro b=0 lze dosáhnout zdánlivě periodického chování.

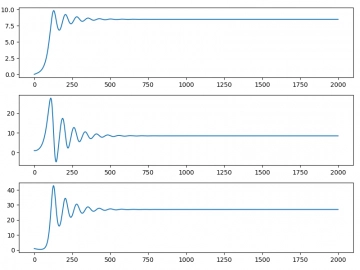
Obrázek 3: Systém směřující do pevného bodu (x a y tedy konvergují ke stejné hodnotě a můžeme odhadnout hodnotu parametru r).

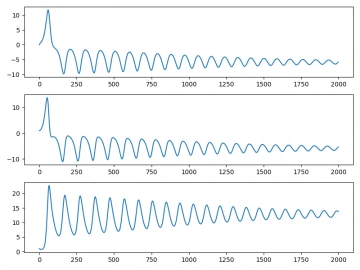
Obrázek 4: Systém blízko meze jeho chaotického chování pro r=13,92.

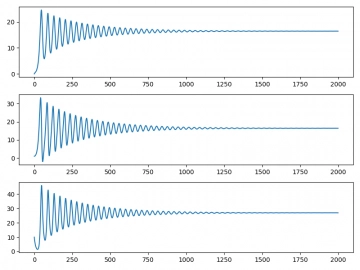
Obrázek 5: Opět stav, ve kterém systém směřuje k jednomu ze tří pevných bodů (a opět lze odhadnout, že hodnota r=28).

Obrázek 6: Pro r=1 se systém musí ustálit na pevném bodu [0, 0, 0] (viz úvodní kapitoly).

6. Zobrazení fázového prostoru ve formě 3D grafu, popř. průmětů do vybraných rovin

Některé vlastnosti Lorenzova systému je skutečně možné vysledovat ze samostatných průběhů hodnot x, y a z, ovšem mnohé důležité vlastnosti a stavy tímto způsobem neodhalíme. Proto se – právě v oblasti studia podivných atraktorů – používá odlišný způsob vizualizace založený na zobrazení postupně se měnících hodnot x, y a z ve formě bodů v takzvaném fázovém prostoru (phase space), v němž neexistuje osa (dimenze) s explicitně vymezeným časem. Tento způsob vizualizace nám umožní rozlišit mezi periodickým, kvaziperiodickým a chaotickým chováním atd.

Knihovna Matplotlib nám umožňuje jak zobrazení 3D grafu, tak i například „sploštění“ 3D grafu o 2D plochy tak, že vždy odstraníme jednu sadu souřadnic (x, y nebo z):

# Lorenz attractor
 
# import všech potřebných knihoven - Numpy a Matplotlibu
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
 
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
 
# počáteční hodnoty
x[0], y[0], z[0] = (0.0, 1.0, 1.05)
 
# vlastní výpočet atraktoru
for i in range(n - 1):
    x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
    x[i + 1] = x[i] + x_dot * dt
    y[i + 1] = y[i] + y_dot * dt
    z[i + 1] = z[i] + z_dot * dt
 
# konstrukce 3D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(projection="3d")
 
# změna velikosti komponent v grafu.
plt.tight_layout()
 
# vykreslení grafu
ax.plot(x, y, z)
 
# uložení grafu
plt.savefig("lorenz_1.png")
 
# zobrazení grafu
plt.show()
 
# grafy s více pohledy na atraktor
ch_3d = np.stack((x, y, z))
lim_xyz = [(np.min(ch_3d[ii]), np.max(ch_3d[ii])) for ii in range(3)]
 
fig2 = plt.figure("3D Coordinates", figsize=(8, 6))
plt.subplot(2, 2, 1)
plt.plot(y, x, linewidth=0.75)
plt.grid()
plt.xlabel("X")
plt.ylabel("Y")
plt.xlim(lim_xyz[1])
plt.ylim(lim_xyz[0])
 
plt.subplot(2, 2, 2)
plt.plot(y, z, linewidth=0.75)
plt.grid()
plt.xlabel("Z")
plt.ylabel("Y")
plt.xlim(lim_xyz[1])
plt.ylim(lim_xyz[2])
 
plt.subplot(2, 2, 3)
plt.plot(z, x, linewidth=0.75)
plt.grid()
plt.xlabel("X")
plt.ylabel("Z")
plt.xlim(lim_xyz[2])
plt.ylim(lim_xyz[0])
 
ax = fig2.add_subplot(2, 2, 4, projection="3d")
ax.plot(x, y, z, linewidth=0.7)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
 
plt.tight_layout()
 
# uložení grafu

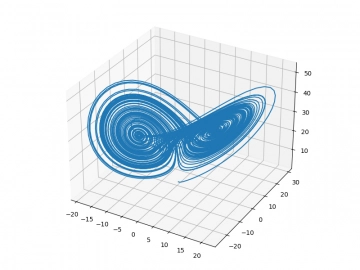
Obrázek 7: 3D graf se zobrazením fázového prostoru Lorenzova systému.

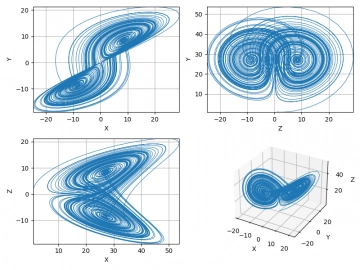
Obrázek 8: Průměty do jednotlivých os.

7. Vliv parametru r na chování Lorenzova systému: mez stability

Největší vliv na chování Lorenzova dynamického systému má parametr r. Nejmenší možná (praktická) hodnota tohoto parametru je rovna jedné. V takovém případě se systém dříve či později ustálí, protože dojde do stabilního bodu [0, 0, 0], resp. ve skutečnosti v tomto případě do „trojitého“ stabilního bodu splňujícího tyto vlastnosti:

• x=0, y=0, z=0
• x=+√b(r−1), y=+√b(r−1), z=r-1 (což je stejné jako u 1, tento bod označme C1)
• x=-√b(r−1), y=-√b(r−1), z=r-1 (což je stejné jako u 1, tento bod označme C2)

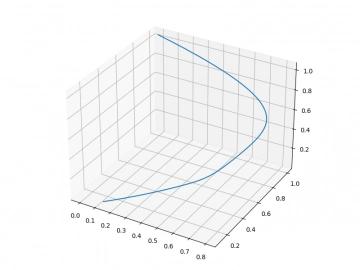
Obrázek 9: Pro r=1 se Lorenzův systém ustálí v atraktoru 0, 0, 0.

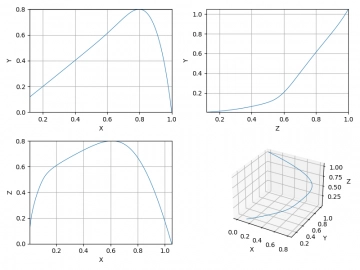
Obrázek 10: Dtto, ale v 2D provedení (průběhy směřují do levého dolního rohu).

8. Chování Lorenzova systému na mezí stability: výběr mezi dvěma budoucnostmi vesmíru

Pro r=2 již neexistuje jediný fixní bod, ale tři body (v počátku a dva symetricky umístěné body závisející na parametrech b a r). Na základě počátečních hodnot [x, y, z] pak systém směřuje k jednomu z těchto bodů a systém se dříve či později (mnohdy mnohem později) stane stabilním. Mnohem důležitější je však chování Lorenzova systému na mezi stability, která se nachází v oblasti r=13.92. Zde již systém nebude stabilní, ale jeho chování se stává chaotické. Podívejme se však nejprve na chování pro hodnotu r ležící těsně pod touto hranicí. Na základě počáteční podmínky se systém ustálí v bodě C1 nebo C2, což si nejlépe zobrazíme právě ve fázovém prostoru:

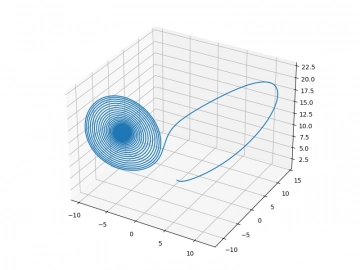
Obrázek 11: Postupný vývoj k bodu C1 (3D graf).

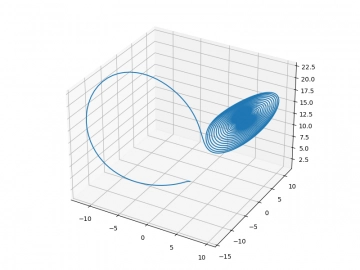
Obrázek 12: Postupný vývoj k bodu C2 (3D graf).

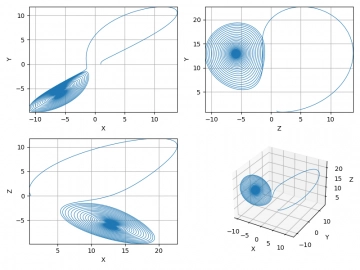
Obrázek 13: Postupný vývoj k bodu C1 (2D průměty).

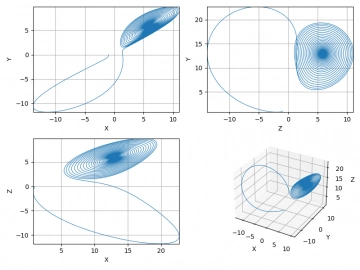
Obrázek 14: Postupný vývoj k bodu C2 (2D průměty).

9. Chování Lorenzova systému za mezí stability: animace podivného Lorenzova atraktoru

Pro zjištění, jak se Lorenzův dynamický systém chová za mezí stability, bude nejlepší si vše ukázat na jednoduché animaci, v níž se postupně vyvíjí tři Lorenzovy systémy, které se od sebe liší pouze odlišnými počátečními hodnotami [x, y, z]. Takovou animaci vytvoříme následujícím skriptem, který se vlastně příliš neodlišuje od původního kódu, ovšem do 3D grafu vykresluje tři průběhy a nikoli průběh jediný:

import matplotlib.pyplot as plt
import numpy as np
 
 
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 1000
 
 
def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0):
    """Vykreslení Lorenzova atraktoru."""
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
 
    # počáteční hodnoty
    x[0], y[0], z[0] = (x0, y0, z0)
 
    # vlastní výpočet atraktoru
    for i in range(n - 1):
        x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
        x[i + 1] = x[i] + x_dot * dt
        y[i + 1] = y[i] + y_dot * dt
        z[i + 1] = z[i] + z_dot * dt
 
    # vykreslení grafu
    ax.plot(x.copy(), y.copy(), z.copy())
 
 
def draw_butterfly_effect(n):
    # konstrukce 3D grafu
    fig = plt.figure(figsize=(8, 6))
    ax = fig.add_subplot(projection="3d")
    ax.set_xlim(-20, 20)
    ax.set_ylim(-20, 20)
 
    # změna velikosti komponent v grafu.
    plt.tight_layout()
 
    draw_lorenz_for_input_values(ax, dt, n, 0.0, 0.9, 1.05)
    draw_lorenz_for_input_values(ax, dt, n, 0.0, 0.8, 1.05)
    draw_lorenz_for_input_values(ax, dt, n, 0.0, 0.7, 1.05)
 
    # uložení grafu
    plt.savefig(f"butterfly_{n:04d}.png")
 
    # zobrazení grafu
    # plt.show()
    plt.close()
 
 
for n in np.linspace(50, 1500, 100):
    draw_butterfly_effect(int(n))

10. Výsledná animace a vybrané snímky

Výsledná animace převedená do GIFu vypadá následovně:

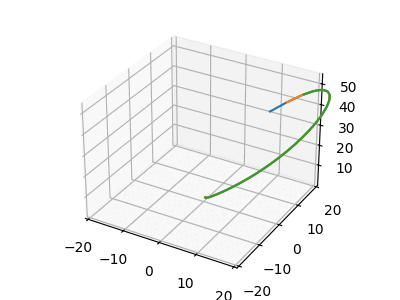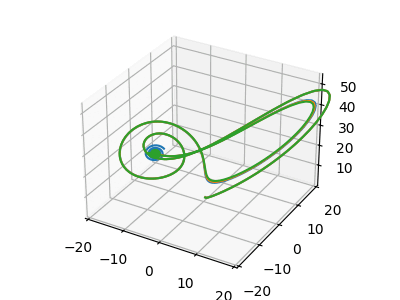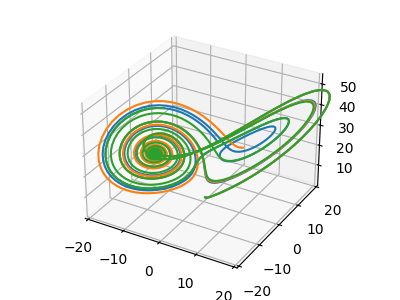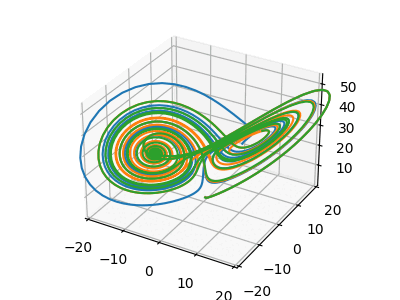
Obrázek 15: Animace chování Lorenzova systému pro tři různé vstupní podmínky.

Podívejme se navíc na jednotlivé snímky, které ukazují charakter Lorenzova systému:

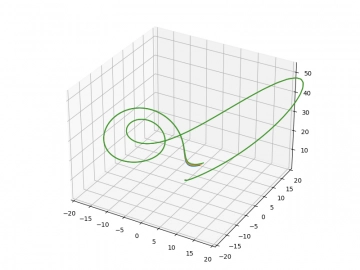
Obrázek 16: Systémy byly zpočátku prakticky totožné, zde se ovšem již jejich cesty rozdělují.

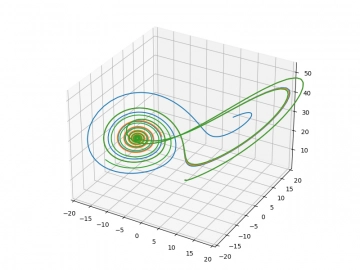
Obrázek 17: Tři různé trajektorie, nyní již zcela odlišné.

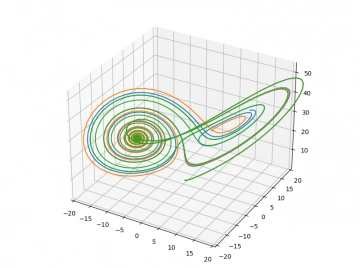
Obrázek 18: Ani jeden z průběhů se nestabilizuje v jednom z bodů C1 či C2, neustále se nemohou „rozhodnout“.

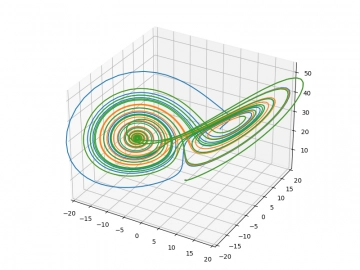
Obrázek 19: Navíc se křivky nikdy neprotnou; to by totiž znamenalo, že se jejich křivky opět spojí (fázový prostor je zde totožný s vektorovým prostorem).

11. Studie tvarů Lorenzova systému při změně parametrů σ i r

Do jisté míry již víme, jakým způsobem je tvar Lorenzova systému (resp. přesněji řečeno umístění atraktorů; pevných bodů) ovlivněno parametrem r. Ovšem tento dynamický systém má ve skutečnosti tři parametry; kromě již zmíněného r ještě parametr σ (sigma) a taktéž parametr b (někdy je zapisován jako β). Zkusme si tedy vynést do jednoho grafu několik tvarů Lorenzova systému pro různé parametry σ a r (totéž si později můžete sami vyzkoušet pro další dvě možné dvojice parametrů).

Nejprve si připravíme funkci, která do grafu (resp. v terminologii Matplotlibu do jedné jeho „osy“ ax) vykreslí Lorenzův systém pro zadané parametry i pro vstupní podmínky (pozici prvního bodu):

def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0, s, r, b):
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
    ...
    ...
    ...
    # vykreslení grafu
    ax.plot(y.copy(), z.copy())

Dále nám již stačí si připravit prázdný graf a provést vykreslení Lorenzova systému pro různé hodnoty s (sigma) a r, zatímco parametr b bude konstantní:

# konstrukce 2D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.gca()
 
b = 2.667
# vykreslení Lorenzova atraktoru s různými parametry s a r
for s in np.arange(0, 10, 1.0):
    for r in np.arange(0, 28, 4):
        draw_lorenz_for_input_values(ax, dt, n, 0.0, 1.0, 1.05, s, r, b)

A takto vypadají výsledky:

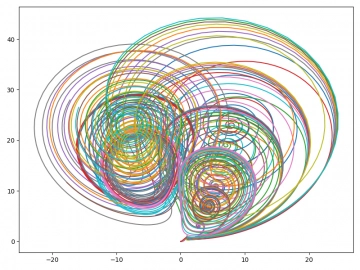
Obrázek 20: Několik Lorenzových systémů vykreslených pro různé parametry s a r, zatímco parametr b zůstává konstantní.

12. Úplný zdrojový kód skriptu pro vykreslení několika Lorenzových systémů pro různé parametry

# Vykreslení Lorenzova atraktoru s různými parametry s a r
 
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 500
 
 
def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0, s, r, b):
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
 
    # počáteční hodnoty
    x[0], y[0], z[0] = (x0, y0, z0)
 
    # vlastní výpočet atraktoru
    for i in range(n - 1):
        x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i], s, r, b)
        x[i + 1] = x[i] + x_dot * dt
        y[i + 1] = y[i] + y_dot * dt
        z[i + 1] = z[i] + z_dot * dt
 
    # vykreslení grafu
    ax.plot(y.copy(), z.copy())
 
 
# konstrukce 2D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.gca()
 
b = 2.667
 
# vykreslení Lorenzova atraktoru s různými parametry s a r
for s in np.arange(0, 10, 1.0):
    for r in np.arange(0, 28, 4):
        draw_lorenz_for_input_values(ax, dt, n, 0.0, 1.0, 1.05, s, r, b)
 
# změna velikosti komponent v grafu.
plt.tight_layout()
 
# uložení grafu
plt.savefig("variable_s_r_params.png")
 
# zobrazení grafu
plt.show()

13. Vizualizace Lorenzových systémů pro různé parametry ve formě mřížky grafů

Skript z předchozí kapitoly lze snadno upravit do takové podoby, že se jednotlivé Lorenzovy systémy nebudou vykreslovat do jediného grafu, ale využijeme další vlastnost Matplotlibu – takzvanou mřížku grafů, kdy je v jedné ploše (pro nás v rastrovém obrázku) umístěno větší množství grafů, přičemž v jednom směru se mění jeden parametr s a ve druhém směru se mění parametr r. Úprava zdrojového kódu je ve skutečnosti triviální a vypadá následovně:

for si in range(5):
    for ri in range(5):
        ax = fig.add_subplot(5, 5, si + 1 + ri * 5)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        draw_lorenz_for_input_values(
            ax, dt, n, 0.0, 1.0, 1.05, si * 2.0 + 1.0, 4.0 + ri * 4, b
        )

Tato úprava nám umožní následující vizualizace:

Obrázek 21: Lorenzovy systémy s nastaveným b=0 a proměnnými parametry s a r.

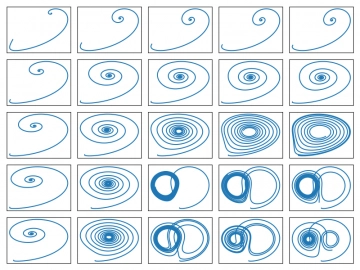
Obrázek 22: Lorenzovy systémy s nastaveným b=2,667 (standardní hodnota) a proměnnými parametry s a r.

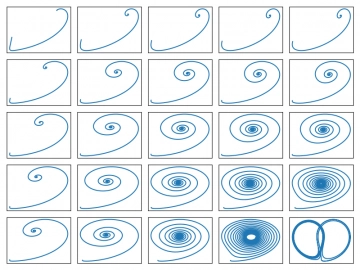
Obrázek 23: Lorenzovy systémy s nastaveným b=5proměnnými parametry s a r.

14. Úplný zdrojový kód skriptu pro vykreslení několika Lorenzových systémů do mřížky

Opět se pro úplnost podívejme na celý zdrojový kód takto upraveného skriptu:

# Vykreslení Lorenzova atraktoru s různými parametry s a r
 
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 1000
 
 
def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0, s, r, b):
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
 
    # počáteční hodnoty
    x[0], y[0], z[0] = (x0, y0, z0)
 
    # vlastní výpočet atraktoru
    for i in range(n - 1):
        x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i], s, r, b)
        x[i + 1] = x[i] + x_dot * dt
        y[i + 1] = y[i] + y_dot * dt
        z[i + 1] = z[i] + z_dot * dt
 
    # vykreslení grafu
    ax.plot(y.copy(), z.copy())
 
 
# konstrukce 2D grafu
fig = plt.figure(figsize=(8, 6))
 
b = 2.667
 
# vykreslení Lorenzova atraktoru s různými parametry s a r
for si in range(5):
    for ri in range(5):
        ax = fig.add_subplot(5, 5, si + 1 + ri * 5)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        draw_lorenz_for_input_values(
            ax, dt, n, 0.0, 1.0, 1.05, si * 2.0 + 1.0, 4.0 + ri * 4, b
        )
 
# změna velikosti komponent v grafu.
plt.tight_layout()
 
# uložení grafu
plt.savefig("variable_s_r_params_multiplot.png")
 
# zobrazení grafu
plt.show()

15. Vliv počátečních podmínek na tvar Lorenzova systému

Na tvar Lorenzova systému mají kromě jeho parametrů vliv i počáteční podmínky, což konkrétně znamená hodnoty x0, y0 a z0. Opět se můžeme pokusit o vykreslení všech Lorenzových systémů pro různé kombinace hodnot x0+y0, x0+z0 či y0+z0 do jediného grafu. Mírně přitom budeme modifikovat již existující kód a to pouhou změnou programových smyček, v nichž se vykreslování provádí. Zde konkrétně budeme měnit hodnoty x0+y0, ovšem sami si můžete vyzkoušet i další možnosti:

# vykreslení Lorenzova atraktoru s různými počátečními souřadnicemi x0 a y0
for y0 in np.arange(-1.5, 1.5, 0.5):
    for x0 in np.arange(-1.5, 1.5, 0.5):
        draw_lorenz_for_input_values(ax, dt, n, x0, y0, 1.05)

Podívejme se na několik zobrazení získaných pro různé hodnoty vstupního parametru r, který ovlivňuje „chaotičnost“ celého Lorenzova systému:

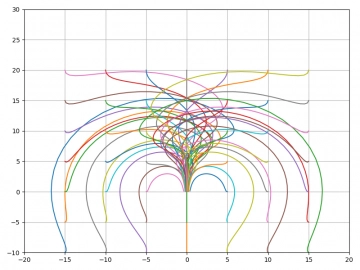
Obrázek 24: Pro r=1 všechny systémy směřují k pevnému bodu [0, 0, 0] (uprostřed grafu mírně pod jeho středem).

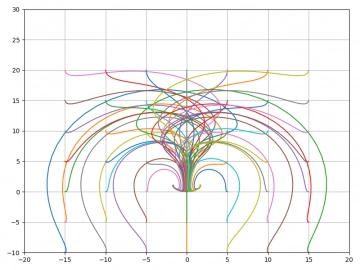
Obrázek 25: Pro r=2 nastává bifurkace a systém směruje buď k pevnému bodu [+√b, +√b, 0] nebo [=√b, =√b, 0]

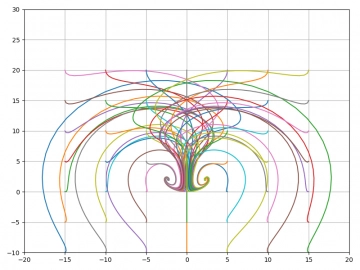
Obrázek 26: Pro r=3 je směřování k jednomu ze dvou pevných bodů ještě více viditelné.

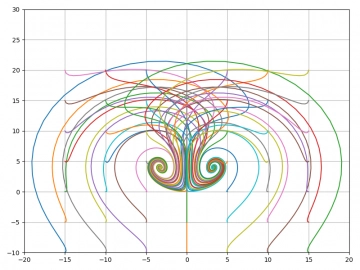
Obrázek 27: Pro r=5 již jasně oba pevné body vidíme na konci spirál.

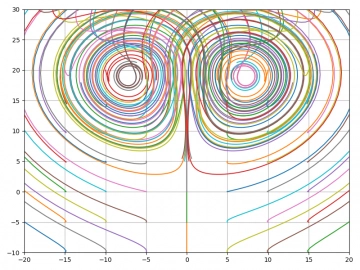
Obrázek 28: Pro r=20 trvá mnohem delší čas, než se systém dostane do jednoho pevného bodu.

16. Jednotlivé Lorenzovy systémy vykreslené pro různé počáteční podmínky do mřížky

To, zda se konkrétní Lorenzův systém ustálí v některém pevném bodě, nebo bude chaotický, záleží, jak již víme, i na počátečních podmínkách, tedy na hodnotách x0, y0 a z0. Vliv hodnot x0 a y0 pro pevně nastavené z0 si můžeme vizualizovat i tímto způsobem:

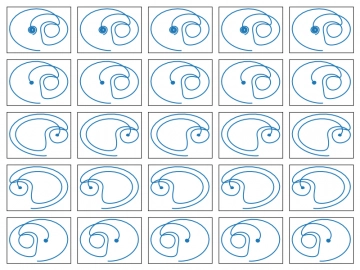
Obrázek 29: Mřížka s Lorenzovými systémy pro různé hodnoty x0 a y0.

Tato mřížka byla vykreslena následujícím skriptem:

# Vykreslení Lorenzova atraktoru s různými parametry počátečními podmínkami
 
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=28, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 500
 
 
def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0):
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
 
    # počáteční hodnoty
    x[0], y[0], z[0] = (x0, y0, z0)
 
    # vlastní výpočet atraktoru
    for i in range(n - 1):
        x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
        x[i + 1] = x[i] + x_dot * dt
        y[i + 1] = y[i] + y_dot * dt
        z[i + 1] = z[i] + z_dot * dt
 
    # vykreslení grafu
    ax.plot(y.copy(), z.copy())
 
 
# konstrukce 2D grafu
fig = plt.figure(figsize=(8, 6))
 
# Vykreslení Lorenzova atraktoru s různými parametry s a r
for yi in range(5):
    for xi in range(5):
        ax = fig.add_subplot(5, 5, xi + 1 + yi * 5)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        x0 = -1.5 + yi * 3.0 / 5.0
        y0 = -1.5 + yi * 3.0 / 5.0
        draw_lorenz_for_input_values(ax, dt, n, x0, y0, 1.05)
 
# změna velikosti komponent v grafu.
plt.tight_layout()
 
# uložení grafu
plt.savefig("variable_x0_y0_params_multiplot.png")
 
# zobrazení grafu
plt.show()

17. Animace postupného vývoje Lorenzových systémů

Postupný vývoj Lorenzových systémů pro různé počáteční souřadnice si samozřejmě můžeme vizualizovat s využitím animace, čímž vlastně do grafu přidáme i „časovou osu“, která se jinak při zobrazení fázového prostoru explicitně nevyužívá. Podívejme se nejdříve na zdrojový kód se skriptem, který animace vytvoří, jejich stručný popis bude uveden v navazující kapitole:

# Vykreslení Lorenzova atraktoru s různými počátečními souřadnicemi x0 a y0
 
import matplotlib.pyplot as plt
import numpy as np
 
 
def lorenz(x, y, z, s=10, r=2.0, b=2.667):
    """Výpočet dalšího bodu Lorenzova atraktoru."""
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return x_dot, y_dot, z_dot
 
 
# krok (změna času)
dt = 0.01
 
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 20000
 
 
def draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0, r):
    # prozatím prázdné pole připravené pro výpočet
    x = np.zeros((n,))
    y = np.zeros((n,))
    z = np.zeros((n,))
 
    # počáteční hodnoty
    x[0], y[0], z[0] = (x0, y0, z0)
 
    # vlastní výpočet atraktoru
    for i in range(n - 1):
        x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i], r=r)
        x[i + 1] = x[i] + x_dot * dt
        y[i + 1] = y[i] + y_dot * dt
        z[i + 1] = z[i] + z_dot * dt
 
    # vykreslení grafu
    ax.plot(y.copy(), z.copy())
 
 
def attractor_for_r(r):
    # konstrukce 2D grafu
    fig = plt.figure(figsize=(8, 6))
    ax = fig.gca()
    ax.set_xlim(-20, 20)
    ax.set_ylim(-10, 30)
 
 
    # vykreslení Lorenzova atraktoru s různými počátečními souřadnicemi x0 a y0
    x0 = 0.0
    for y0 in np.linspace(-15.0, 15.0, 7):
        for z0 in np.linspace(-10.0, 20.0, 7):
            draw_lorenz_for_input_values(ax, dt, n, x0, y0, z0, r)
 
    plt.grid()
    # změna velikosti komponent v grafu.
    plt.tight_layout()
 
    # uložení grafu
    plt.savefig(f"variable_x0_y0_params_r_{r:04.1f}.png")
 
    # zobrazení grafu
    #plt.show()
    plt.close()
 
 
for r in np.linspace(1.0, 10.0, 5):
    attractor_for_r(r)

18. Výsledné animace se stručným popisem

S využitím skriptu z předchozí kapitoly bylo vytvořeno celkem pět animací, které poměrně dobře ukazují způsoby vývoje Lorenzových systémů pro různé počáteční souřadnice x0 a y0 a navíc v závislosti na parametru r, který ovlivňuje, jak již víme, celkové chování systému – jeho stabilitu či naopak chaotičnost. Vzhledem k velikostem animací budou uvedeny pouze odkazy na ně (jedná se o běžné animované GIFy):

1. Pro r=1 všechny systémy směřují k pevnému bodu [0, 0, 0]
2. Pro r=2 nastává bifurkace a systémy směřují buď k bodu [0, 0, 0] nebo k C1 či C2
3. Pro r=5 je bifurkace ještě více patrná
4. Pro r=14 jsme překročili mezi stability a některé systémy se již neustálí
5. Pro r=28 je nestabilita ještě více patrná – mnohé systémy se neustálí (až na některé, které začínají s x0=0)

19. Repositář s demonstračními příklady

Všechny skripty, které byly v předchozích kapitolách použity pro tvorbu obrázků a animací, jsou uloženy v Git repositáři dostupném na adrese https://github.com/tisnik/fractals/. Následují odkazy na jednotlivé příklady:

20. Odkazy na Internetu

1. The Lorenz Attractor by Dr. Bruce Stewart
   https://www.youtube.com/wat­ch?v=YS_xtBMUrJg
2. Welcome – Dynamical Systems | Intro Lecture
   https://www.youtube.com/wat­ch?v=41P4vFP7RWo
3. The Lorenz Equations – Dynamical Systems | Lecture 27
   https://www.youtube.com/watch?v=0Rpy-xSsAo8
4. Phase space
   https://en.wikipedia.org/wi­ki/Phase_space
5. Fázový prostor
   https://cs.wikipedia.org/wi­ki/F%C3%A1zov%C3%BD_prostor
6. Lorenzův atraktor
   https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02
7. Lorenzův atraktor
   https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03
8. Lorenz system
   https://en.wikipedia.org/wi­ki/Lorenz_system
9. The Lorenz system – An introduction to chaos
   https://www.math.toronto.e­du/kzhang/teaching/courses/mat332–2022/_8-lorenz-system/
10. Dynamical system
    https://en.wikipedia.org/wi­ki/Dynamical_system
11. What are Dynamical Systems?
    https://math.libretexts.or­g/Bookshelves/Scientific_Com­puting_Simulations_and_Mo­deling/Introduction_to_the_Mo­deling_and_Analysis_of_Com­plex_Systems_(Sayama)/03%3A_Ba­sics_of_Dynamical_Systems/3­.01%3A_What_are_Dynamical_Sys­tems%3F
12. TEACHING MATHEMATICS WITH A HISTORICAL PERSPECTIVE: Lecture 11: Dynamical systems
    https://abel.math.harvard­.edu/~knill/teaching/mathe320_2022/han­douts/10-dynamics.pdf
13. Emergence (Wikipedia CS)
    https://cs.wikipedia.org/wi­ki/Emergence
14. Emergence (Wikipedia EN)
    https://en.wikipedia.org/wi­ki/Emergence
15. Particle Life: Vivid structures from rudimentary rules
    https://particle-life.com/
16. Self-organization
    https://en.wikipedia.org/wiki/Self-organization
17. Samoorganizace
    https://cs.wikipedia.org/wi­ki/Samoorganizace
18. Spontaneous order
    https://en.wikipedia.org/wi­ki/Spontaneous_order
19. NumPy Home Page
    http://www.numpy.org/
20. NumPy v1.10 Manual
    http://docs.scipy.org/doc/num­py/index.html
21. NumPy (Wikipedia)
    https://en.wikipedia.org/wiki/NumPy
22. Matplotlib Home Page
    http://matplotlib.org/
23. matplotlib (Wikipedia)
    https://en.wikipedia.org/wi­ki/Matplotlib
24. Rössler attractor
    https://en.wikipedia.org/wi­ki/R%C3%B6ssler_attractor
25. Rossler attractor
    http://scholarpedia.org/ar­ticle/Rossler_attractor
26. List of chaotic maps
    https://en.wikipedia.org/wi­ki/List_of_chaotic_maps