V následujícím článku se pokusme představit některé zajímavé funkce programu wxMaxima, který jsme představili v minulém díle našeho seriálu o matematickém softwaru. Pokusíme se představit některé základní funkce, syntaxi, přiblížit ovládání systému a přinést některé základní typy a triky. A zaměříme se především na začínající uživatele.
Základní syntaxe
Ač je wxMaxima program, který je možné v zásadě ovládat téměř výhradně klikáním, velmi brzy zjistíme, že se nejedná o právě nejpohodlnější způsob zacházení s tímto nástrojem. Na klikání jsou vhodné především méně často užívané funkce, to, co používáme častěji je daleko efektivnější ručně vypisovat. Navíc se hodí základní syntaktická znalost v případě, že potřebujeme zpracovat nějaký složený dotaz, upravit složitější funkci atp.
Uživatelé, kteří mají zkušenosti s programováním ve funkcionálním jazyce libovolného druhu, se s ovládáním sžijí poměrně snadno. Jednotlivé části výrazu (příkazu) jsou do sebe zanořeny a je možné je částečně izolovat pomocí závorek. Funkce, které vyžadují více parametrů (například integrál), oddělují jednotlivé parametry čárkami. Například:
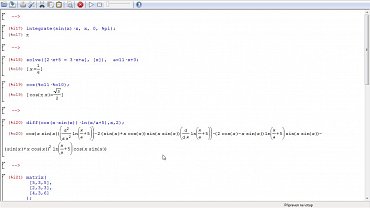
integrate(sin(x)*x, x, 0, %pi);
Znamená: proveď určitý integrál z výrazu sin(x)*x dx, od 0 do pí. Na tomto příkladu jsou vidět ještě další syntaktické nutnosti – příkaz, který má být vyhodnocen končí středníkem, hodnotu čísla pí zapíšeme jako %pi a v neposlední řadě příkaz s více parametry je tvořen názvem, kulatou závorkou s parametry v patřičném pořadí, které jsou odděleny závorkou. V místech pro meze může být libovolná jiná funkce. Náš výraz vrátí stejnou hodnotu i pro příkaz:
integrate(sin(x)*x, x, 0, integrate(sin(x)*x, x, 0, %pi));
program umí samozřejmě pracovat i s konstantami, takže je možné napsat:
diff(cos(ln(x*a))+b*x,x,1);
Kde a a b jsou chápány jako konstanty. Ty je možné samozřejmě vyjádřit, a to pomocí čárky umístěné za výraz:
diff(cos(ln(x*a))+b*x,x,1), a=cos(x), b=integrate(sin(x)*x, x, 0,%pi);
To umožňuje poměrně snadnou dekompozici výrazu na podstatně snazší části. Zajímavou vlastností wxMaxima je to, že ač neumí něco dopočítat, je schopná nabídnout alespoň takovou část výsledku, ke které dospěla.
Další zajímavou funkcí je odkazování se na předchozí výsledky. wxMaxima čísluje výsledky na začátku řádku značkou %oX, kde X je nějaké číslo. Do svého výrazu se tak snadno můžete odvolat například na krok výpočtu č. 25:
cos(3*%o56)+sin(%o56/2);
Při každém přepočtu se řádky přečíslovávají. Odkazovat lze i na již neviditelné výsledky, ale pokud provedete nějakou změnu, kterou chce zanést níže, je potřeba si vše pečlivě pohlídat. wxMaxima toho syntakticky zvládá mnohem více – je možné si nastavovat výstupní formát, pracovat s maticemi a vektory, které se zadávají pomocí []… To jsou již ale věci, které je možné najít v literatuře nebo v nápovědě a nejsou nutné k zvládnutí základního ovládání.
Základní operace
Jelikož většina začínajících uživatelů bude z počátku potřebovat především algebraické operace, zaměříme se alespoň letmo právě na ně. Po jejich zvládnutí je již rozšiřování funkčnosti hlavně otázkou cviku a šikovnosti.
Již ve výše uvedených příkladech jsem ukázali, jakým způsobem se integruje a derivuje. U integrálu není potřeba vyplňovat poslední dva parametry a získáte neurčitý integrál. U derivací je možné stupeň derivace přímo nastavit pomocí čísla (v příkladu je nastavená 1). Násobné integrály je nutné ručně skládat do sebe:
integrate(integrate(sin(x), x), y);
Asi jedním z nejčastěji užívaných nástrojů je funkce solve, která umožňuje řešit rovnice. Jako první parametr zadáte rovnici a jako druhý neznámé, vzhledem ke kterým má být rovnice řešena.
solve([sin(x)=cos(%pi/2+a)], [x]), a =x;
Zákeřností, na kterou je třeba si dát pozor je práce s goniometrickými funkcemi. Ty zpracovává vlastní sada příkazů, které najdete v menu zjednodušit a trigonometrické výrazy. S těmi je práce celkově poměrně obtížná a řešit rovnice s goniometrickými funkcemi je poměrně dosti pracné. Na ilustraci alespoň příklad se zjednodušením goniometrického výrazu:
trigreduce(sin(2*x)^2*cos(2*x)^2/tang(2*x));
Téměř vše se dá poměrně snadno naklikat a pokud máte základní znalost syntaxe, tak i poměrně snadno kombinovat, takže obvykle dosažení dobrého výsledku není nijak obtížné. Ze zajímavých funkcí uveďme například hledání kořenů rovnice, řešení soustavy rovnic, určení vlastních hodnot a vlastních vektorů matice, operace s maticemi, výpočet limit či práce s řadami.
Kudy dál
wxMaxima je poměrně rozšířený a hojně užívaný program, takže k dispozici je poměrně velké množství příkladů, návodů a učebnic, které mohou poukázat na nejen základní možnosti aplikace, ale také na využití v tom kterém oboru, v němž pracujete. Základní a poměrně bohatá knihovnička je k dispozici přímo na stránkách projektu.
Pokud používáte Maximu bez grafické nástavby, pak je výborným zdrojem přiložený podrobný integrovaný manuál, který je plný konkrétních jednoduchých i složitějších příkladů. Užitečným zdrojem nápadů je i dialog typů a triků. Zajímavě vypadá také nově se rozvíjející blog s několika pokročilejšími demonstracemi, nebo jiný systematičtěji pojatý web. Pro začátečníky je pak určený poněkud upovídaný seriál o základním ovládání a funkcionalitě.
Jak je vidět k dispozici je zdrojů více než dost, stačí si jen nějaký zdroj vybrat a pustit se do studia. wxMaxima je velmi silný nástroj, který rozhodně má smysl používat.