Metapost: vlastnosti a konstrukce datového typu path

Průsečíky cest

Průsečíky cest vytváří metapost jako řešení soustavy rovnic, kdy jedna rovnice definuje jednu a druhá druhou křivku. Základní syntaxe je:

z = a intersectionpoint b;, kdy z je proměnná typu pair (= souřadnice bodu); a a b jsou cesty. Pokud se cesty neprotínají, hlásí metapost chybu. Tomuto chybovému hlášení lze předejít použitím funkce intersectionti­mes, která vrací hodnotu (-1,–1) v případě, že se cesty neprotínají a testováním této hodnoty (bude probráno, až budeme hovořit o řízení chodu programů v metapostu).

V proměnné z jsou uloženy časy průsečíku na cestěa a b lze je separovat jako xpart z a ypart z.

Problémy s průsečíky nastávají u složitěji tvarovaných cest, které se protínají vícenásobně. Zpravidla to musíme řešit rozdělením cesty na více subpath (viz níže), protože vyhodnocení průsečíků nemusí odpovídat naší představě. Uvedenou problematiku kopíruje metapost z metafontu a jsou popsány v Metafontbooku D. Knutha.

Zádrhelem výše uvedeného rozdělení cesty na subpath před a po prvním protětím cest je skutečnost, že samotný průsečík je někdy součástí první, někdy součástí druhé části rozdělené cesty (patrně souvisí se zaokrouhlováním).

Nejjednodušším řešením je vyznačení příslušné subpath a protínajícího bodu (jiným typem pera, případně barvou – viz dále), abychom viděli, zda metapost průsečík vyznačí na samém začátku vyznačeného úseku cesty, nebo až na dalším průsečíku.

Vytvoření vyplnitelné plochy z více cest

Pokud se více cest protíná, mohou jejich části po spojení vytvořit ohraničení plošného útvaru. V takovém případě je možné definovat cestu okolo tohoto útvaru (jako části cest od průsečíku k průsečíku a spojit).

cestaokolo=bu­ildcycle(cesta­jedna,cestadve,ces­tatri,cestacty­ri);

A následně ji můžeme vyplnit:

fill cestaokolo

Nepodaří se to vždy, alespoň dle mých zkušeností, v případě, kdy všechny zúčastněné cesty jsou křivky (vytvořené z1..z2.. atd.). Prakticky vždy jsme úspěšní tehdy, když alespoň jedna z nich je úsečka nebo lomená čára. Metapost sice v případě nezdaru neohlásí žádnou chybu, ale nevytvoří vyplnění. I v základním manuálu od autora metapostu je příklad s kombinací křivek a úseček. Patrně se opět jedná o výše zmíněné zaokrouhlovací chyby v metapostu, díky nimž se dílčí křivky nedotýkají. Problém je někdy nutno obcházet konstrukcí úseček, spojujících konce křivek (které jsou velmi krátké a v reálu se nevykreslí).

Jinými slovy, pokud se bez nějakého chybového hlášení cestaokolo nevykreslí, případně nevyplní, potom pomůže spojit koncové body jednotlivých částí úsečkami. Nebo spíše samotné cesty propojit pomocí -- . Jen musíme dávat pozor na orientaci dílčích cest, jinak se objeví spojnice nikoli s nejbližším koncem navazující cesty (okem nepostřehnutelná ani při velkém zvětšení, ale s protilehlým koncem cesty). Změnu orientace (resp. vytvoření cesty stejného průběhu ale s opačnou orientací) uvádím níže.

Čas na cestě

Cesta je zadána jednotlivými body, např.:

mojecesta=z1.­.z2..z3..z4..z5;

Čas cesty je v počátečním bodě 0, v následujícím bodě 1, v dalším 2 atd. (takže v bodě z5 bude 4). Pokud nevíme, kolika body je křivka zadána (případně tvoříme nějaké makro, které může zpracovávat cesty o různé délce, můžeme časovou délku křivky získat příkazem:

delka = length mojecesta;, kdy delka je proměnná typu numeric a mojecesta je proměnná typu path. Pokud je vzdálenost mezi jednotlivými body vymezujícími cestu různá, mají i zlomkové úseky cesty na jejích různých místech různou délku (v délkových mírách), byť jsou třeba numericky (v hodnotě časové délky) shodné.

Pokud definujeme nějaký čas na křivce (i necelé číslo), příslušný bod dostaneme příkazem:

z = point t of mojecesta;, kdy z je proměnná typu pair, do níž jsou uloženy souřadnice bodu, ležícího na cestě mojecesta v čase t.

Čas na cestě je v případě křivek a cest s různou tenzí rozložen nerovnoměrně. Můžeme si to demonstrovat na následujícím obrázku:

prologues:=0;
u=10mm;
beginfig(1);
path cesta[];
z0=origin;z10=(7u,7u);z20=(0,-7u);z30=(7u,0);
cesta0:=z0..z10;cesta1:=z20..tension 1 and 100..z30;
% Následující konstrukce je cyklus. Zde se jedná o cyklus s pevně
% nastavenou velikostí kroků na 1 a počtem kroků, tedy obdoba for
% cyklu v BASICu nebo Perlu
for i = 1 upto 9:
b:=i+20;
z[i]=point (i/10) of cesta0;
z[b]=point (i/10) of cesta1;
endfor;
draw cesta0; draw cesta1;

pickup pencircle scaled .2u;
% Následující cyklus nadělá puntíky v místě definovaných bodů
for i=0 upto 10: drawdot z[i]; drawdot z[i+20]; endfor;
endfig;
end;

Toto je výsledný obrázek, díky řazení pod sebou vidíme posun bodů, odpovídajících stejnému časovému úseku na cesta1.

Část cesty vymezená pomocí časů

Část cesty, vymezenou dvěma časy na ní, získáme příkazem:

castmojicesty = subpath (t1,t2) of mojecesta;, kdy mojecesta je původní cesta a castmojicestyje její část mezi body v časech t1 a t2. Připomínka: Do metapostu obecně nelze zadat jména proměnných obsahující čísla. Takže časy (jedná se o proměnné typu numeric, které není nutno deklarovat) bychom museli označit nějakým platným názvem (jen velká a malá písmena bez diakritiky) nebo mít deklarované pole numeric t[];, potom by t1 a t2 byly druhý a třetí prvek tohoto pole (první je t0).

Ukázka spojení částí cest podle času do cyklu a jeho vyplnění

prologues:=1;
u=3mm;
beginfig(1);
z0=(0,0);z1=(0,10u);z2=(10u,10u);z3=(10u,0);% definice bodů
z4=(1u,-5u);z5=(2u,15u);
z6=(11u,-6u);z7=(9u,16u);
z8=(-5u,0);z9=(14u,0);
z10=(-4u,10u);z11=(15u,10u);
path cesta[],cestajedna,cestadve,cestatri,cestactyri,cestaokolo;
cesta1:=z8--z0--z3--z9;        % definování základních cest
cesta2:=z10--z1--z2--z11;
cesta3:=z4..z0..z1..z5;
cesta4:=z6..z3..z2..z7;
cestajedna:= subpath(1,2) of cesta1; % definování úseků na nich
cestadve:= subpath(1,2) of cesta2;
cestatri:= subpath(1,2) of cesta3;
cestactyri:= subpath(1,2) of cesta4;
                                     % spojení do cyklu
cestaokolo:=buildcycle(cestajedna,cestatri,cestadve,cestactyri);
                                     % vykreslení cest
draw cesta1; draw cesta2; draw cesta3; draw cesta4;
                                     % vyplnění cyklu
fill cestaokolo;
dotlabels(0,1,2,3,4,5,6,7,8,9,10,11);% vyznačení bodů
endfig;                              % pro lepší orientaci
end;

Výsledek činnosti předchozího programu

Vymezení části cesty průsečíkem

Jestliže se dvě cesty a a b protínají, tak:

mojecesta=a cutbefore b; přiřadí proměnné mojecesta část cesty a od průsečíku s cestou b do konce.

Mojecesta=b cutafter a; přiřadí proměnnéMojecesta část cesty b od začátku do jejího průsečíku s cestou a.

Pokud se cesty protínají vícenásobně, je brán bod s nižšími hodnotami souřadnic. Není to ovlivněno pořadím, v jakém byly definovány body cest. I zde platí výše uvedené, že samotný bod průsečíku někdy je někdy není součástí výsledné cesty. Tudíž se nelze spolehnout, že při křížení úsečky a jednoduché uzavřené cesty (jako je kruh, čtverec, obdélník apod.) se bude intersectionpoint nové (zkrácené) úsečky druhým zkřížením původní úsečky s uzavřenou cestou.

Průsečík přímek

Toto již bylo uvedeno při definici bodů (datový typ pair), ale pro úplnost uvádím i zde:

Průsečík přímek řešíme pomocí neznámé proměnné whatever. Pro průsečík přímek z1–z2 a z3–z4 použijeme konstrukci:

z5=whatever[z1,z2]=w­hatever[z3,z4];

z5 nemusí ležet mezi zadanými body, může se nacházet i za hranicemi úseček které vymezují.

Čas průsečíku na cestách

Máme-li cestu a a cestu b, potom:

z=a intersectiontimes b;, kdy z je proměnná typu pair a časy průsečíku z ní dostaneme následně:

• casa=xpart z;
• casb=ypart z;

casa a casb jsou proměnné typu numeric, z nichž první je čas bodu zkřížení na cestě a a druhý čas zkřížení na cestě b.

Pokud se cesty neprotínají, je vrácena hodnota (-1,–1). Tím lze opět testovat existenci alespoň jednoho průsečíku zadaných cest.

Směry na křivce

Na cestě, která je křivkou (u úsečky to nemá význam) můžeme pro jednotlivé body zjistit vektor této křivky, dále pro jednotlivé vektory určit čas, ve kterém cesta má jejich směr a určit i bod na křivce v místě tohoto směru.

• vektor = direction t of mojecesta; vrací vektor cesty mojecesta v bodě o času t (proměnná typu pair).
• cas = directiontime vektor of mojecesta; vrací proměnnou typu numeric při zadaném vektoru a cestě.
• z = directionpoint vektor of mojecesta; vrací proměnnou typu pair jako souřadnice bodu, v němž má cesta mojecesta směr zadaného vektoru.

Vytvoření cesty opačné orientace

Můžeme použít dvě konstrukce, výsledek je stejně použitelný

1. cesta2:=cesta1 reverse;
2. cesta2:=subpath (tk,tz) of cesta1;, kdy tz je čas na počátečním bodě cesta1 (až na výjimky 0) a tk je čas na koncovém bodě cesta1 (závisí na počtu bodů, kterými je path definována).

Význam směru při spojování cest můžeme demonstrovat následujícícm příkladem:

prologues:=1;
u=10mm;
path cesta[];
beginfig(1);
z0=origin;z1=(1/3)[z0,z3];z2=(2/3)[z0,z3];z3=(10u,0);
cesta0:=z0{dir90}..{dir270}z1;
cesta1:=z1{dir90}..{dir270}z2;
cesta2:=z2{dir90}..{dir270}z3;
% shifted patří mezi transformace (viz příště) a jedná se o
% posun objektu o zadaný vektor
cesta3:=subpath(1,0)of cesta1 shifted (0,u);
cesta4:=reverse cesta1 shifted (0,-u);
cesta12:=cesta0--cesta1--cesta2;
cesta13:=cesta0--cesta3--cesta2;
cesta14:=cesta0--cesta4--cesta2;
pickup pencircle scaled .1u;
draw cesta12;
draw cesta13 shifted (0,3u);
draw cesta14 shifted (0,-3u);
endfig;
end;

Prostřední řada oblouků na sebe navazuje. U horní a dolní řady byl prostřední oblouk vložen opačně nasměrovaný. Jeho posun nahoru, resp. dolů byl proveden jen proto, aby spojnice jeho konců s krajními oblouky nesplynuly do jedné.

Úhlové míry na křivce

uhel = arclenght mojecesta; vrací obloukovou míru cesty mojecesta.

cas = arctime uhel of mojecesta; vrací čas odpovídající obloukové míře uhel na cestě mojecesta.

Čas na kružnici

casnakruznici Kružnice má implicitně čas 8 (body t = 0 a t = 8 jsou totožné). Jednotková délka tedy připadá 45 stupňů oblouku. Části kružnice tedy můžeme nadefinovat (např. při konstrukci koláčového grafu) příkazem:

mujoblouk = subpath (t1, t2) of mojekruznice;, kdy mojekruznice je kružnice definovaná poloměrem a t1, t2 jsou hodnoty z intervalu 0 – 8.

Standardní funkce a makra pro typ path

• & spojuje dvě cesty, podmínkou je jejich kontakt (konec jedné a začátek druhé musejí být v identickém bodě). S výhodou lze použít tam, kde potřebujeme cestu lomit, aby nebyl zohledněn ani předchozí ani následujícíc průběh. Stejný operátor se používá i pro spojování řetězců.
• arclength úhlová délka zadané cesty
• arctime of čas na cestě (od počátku), na němž je dosaženo zadaného úhlu
• bbox rovnoběžník se stranami rovnoběžnými s osami, který je opsaný zadané cestě (větší využití má toto standardní makro pro datový typ picture, na který se dají převést i písmena)
• center střed o bod výše uvedeného boxu
• podobně llcorner lrcorner ulcorner urcorner definují rohy bboxu
• cutafter a cutbefore jsou části cesty za a před průsečíkem s jinou křivkou.
  cesta0:=cesta1 cutbefore cesta2 vloží do cesta0 část cesta1 před jejím průsečíkem s cesta2
• cycle
  b:=cycle(cesta ) vloží do booleovské proměnné hodnotu true, je-li cesta uzavřená a false, je-li neuzavřená
• direction of directionpoint of directiontime of 
  

  d:=direction t of cesta vloží do proměnné d (pair) směrový vektor cesty cesta v čase t
  

  cas:=direction­point vektor of cesta vloží do numerické proměnné cas čas na cestě cesta, kde zaujímá směr definovaný proměnnou typu pair vektor (toto je standardní makro)

  cas:=direction­times vektor of cesta velmi podobné jako předchozí, ale jedná se přímo o vestavěnou funkci
• intersectionpoint bod průsečíku dvou cest
  bod:= cesta1 intersectionpoint cesta2 vloží do proměnné typu pair bod, v němž se obě protnou. Neprotínají-li se dojde k chybovému
• intersectiontimes
  dvojice:= cesta1 intersectiontimes cesta2 vloží do proměnné dvojice typu pair časy na cesta1 a cesta2, v nichž se protnou
• makepath makepen první vytvoří z proměnné typu pero uzavřenou cestu, druhá z uzavřené cesty proměnnou typu pen (kterou je možné následně kreslit)
  Syntaxe vytvoření pera je: pero makepen cesta, druhá funkce má syntaxi analogickou.
• point of nalezne bod na cestě o zadaném čase
  bod:=point t of cesta vloží do proměnné typu pair souřadnice bodu na cestě cesta, který je na ni umístěm v čase t
• postcontrol of precontrol of definují pozice Bezierových kontrolních bodů
  bod:= precontrol t of cesta;vloží do proměnné bod souřadnice posledního Beziérova kontrolního bodu na úseku cesty končícím zadaným časem t, postcontrol obdobně vkládá souřadnice prvního Beziérova kontrolního bodu za bodem v čase t
• reverse na základě cesty1 vytvoří cestu2 opačně orientovanou (při vykreslení šipkou, při definování bodů časem)
  cesta1:= cesta2 reverse na základě cesty1 vytvoří cestu2 opačně orientovanou (při vykreslení šipkou, při definování bodů časem)
• rotated, scaled, shifted, slanted, transformed, xscaled, yscaled, zscaled jsou transformace, budou probrány u datového typu transform
• subpath of definování částí cesty časy vloženými do proměnné typu pair
  cesta1:=subpath dvojice of cesta;
• fullcircle, halfcircle, quartercircle, unitsquare jsou systémem definované cesty (kruh, půlkruh, čtvrtkruh, jednotkový čtverec)

Malý tutoriál

V tomto tutoriálu si nakreslíme stylizovaný obrázek listu. Při jeho zpracování se postupně seznámíme s jevy, které jsme probrali v minulém a tomto díle.

Základ

Nejprve vytvoříme základ obrázku, cesty s nimiž budeme dále pracovat. K tomu využijeme příkaz dir, popsaný v minulém díle.

prologues:=1;
u=10mm;
pair bod[];
path linka[];
bod0:=origin;bod1:=(5u,5u);bod2:=(4u,4u);bod3:=(-2u,-u);bod4:=bod3+(.5u,-.5u);
linka0:=bod0{dir180}..{dir45}bod1;linka1:=bod1{dir225}..{dir90}bod0;
linka2:=bod2..{dir210}bod3;linka3:=bod2..{dir220}bod4;linka4:=bod3..bod4;

První obrázek

Na tomto obrázku si ukážeme jen průběh cest; je vcelku jasné, že na počátku práce jsem tento obrázek vícekrát překresloval, dokud jsem nebyl s průbehem jednotlivých cest spokojen.

beginfig(1);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
endfig;

(Pro znalé metapostu:) Je mi jasné, že vykreslení očíslovaných cest by se jednodušeji udělalo cyklem (ale to jsme ještě nebrali); navíc, protože ty cestu budeme vykreslovat ještě v dalších obrázcích, bych normálně k jejich vykreslení nadefinoval makro (to jsme taky ještě nebrali) a volal je z dalších obrázků.

Druhý obrázek, aneb malý úkrok stranou

Zde jsem si jen dovolil na jednu z cest v „pravidelných“ (z hlediska času na cestě) intervalech umístit body. Mělo by to názorně ukázat, že fyzická vzdálenost bodů vzdálených od sebe stejný čas na křivce je různá podle míry jejího zakřivení, což vede k tomu, že se pomocí bodů se stejnou vzdáleností v čase přímky nedají na nepravidelně probíhající křivce rozmístit pravidelně nějaké útvary. (Zato je tento způsob plně použitelný při podobné práci s kružnicí nebo jejími částmi.)

beginfig(2);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
bod10:=point .2 of linka0;bod11:=point .4 of linka0;

bod12:=point .6 of linka0;bod13:=point .8 of linka0;
pickup pencircle scaled .15u;
drawdot bod10; drawdot bod11;drawdot bod12;drawdot bod13;
endfig;

Zde je nadefinována subpath linka0 pomocí jejího průsečíku s linka2.

beginfig(3);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
bod20:= linka0 intersectionpoint linka2;
pickup pencircle scaled .15u; drawdot bod20;
bod21:= linka0 intersectiontimes linka2;
pomt:=xpart(bod21); linka5:=subpath(pomt,1) of linka0;
pickup pencircle scaled .075u; draw linka5;
endfig;

Na následujícím obrázku jsou šipkami vyznačeny směry cest, což bude zapotřebí při jejich spojování do jedné uzavřené cesty (toto je poměrně jednoduchý obrázek, kde by si to měl člověk uhlídat; u složitějších obrázků, případně když jsme nuceni práci přerušovat, je vyznačení směrů přinejmenším doporučeníhodné).

beginfig(4);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
bod21:= linka0 intersectiontimes linka2;
pomta:=xpart(bod21); linka5:=subpath(pomta,1) of linka0;
bod22:= linka1 intersectiontimes linka3;
pomtb:=xpart(bod22); linka6:=subpath(0,pomtb) of linka1;
pomtc:=ypart(bod21); linka7:=subpath(0,pomtc) of linka2;
pomtd:=ypart(bod22); linka8:=subpath(pomtd,0) of linka3;
pickup pencircle scaled .07u;
drawarrow linka5;%1
drawarrow linka6;%2
drawarrow linka7;%4
drawarrow linka8;%3
endfig;

Na následujícím obrázku jsem se jen přesvědčil, že cesty, ohraničující čepel listu, se skutečně spojily do jediné uzavřené a vyplnitelné. Vidíme (5. řádek zdola), že se nepodařilo vytvořit uzavřenou cestu pomocí buildcycle a byla použita podobná konstrukce, jaká se užívá na vytváření uzavřené cesty spojením bodů.

beginfig(5);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
bod21:= linka0 intersectiontimes linka2;
pomta:=xpart(bod21); linka5:=subpath(pomta,1) of linka0;
bod22:= linka1 intersectiontimes linka3;
pomtb:=xpart(bod22); linka6:=subpath(0,pomtb) of linka1;
pomtc:=ypart(bod21); linka7:=subpath(0,pomtc) of linka2;
pomtd:=ypart(bod22); linka8:=subpath(pomtd,0) of linka3;
%linka9:=buildcycle(linka5,linka6,linka8,linka7);
pickup pencircle scaled .07u;

linka9:= linka5--linka6--linka8--linka7--cycle;
fill linka9;
endfig;

Stejným způsobem byla vytvořena uzavřená cesta z cest, ohraničujících „řapík“.

beginfig(6);
draw linka0;draw linka1;draw linka2;draw linka3;draw linka4;
bod21:= linka0 intersectiontimes linka2;
pomta:=xpart(bod21); linka5:=subpath(pomta,1) of linka0;
bod22:= linka1 intersectiontimes linka3;

pomtb:=xpart(bod22); linka6:=subpath(0,pomtb) of linka1;
pomtc:=ypart(bod21); linka7:=subpath(0,pomtc) of linka2;
pomtd:=ypart(bod22); linka8:=subpath(pomtd,0) of linka3;
pickup pencircle scaled .07u;
linka9:= linka5--linka6--linka8--linka7--cycle;
linka10:=subpath(1,0) of linka3;
linka11:=linka2--linka4--linka10--cycle;
draw linka11;
endfig;

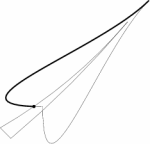
A toto už je výsledný obrázek:

beginfig(7);
bod21:= linka0 intersectiontimes linka2;
pomta:=xpart(bod21); linka5:=subpath(pomta,1) of linka0;
bod22:= linka1 intersectiontimes linka3;
pomtb:=xpart(bod22); linka6:=subpath(0,pomtb) of linka1;
pomtc:=ypart(bod21); linka7:=subpath(0,pomtc) of linka2;
pomtd:=ypart(bod22); linka8:=subpath(pomtd,0) of linka3;
pickup pencircle scaled .07u;
linka9:= linka5--linka6--linka8--linka7--cycle;
linka10:=subpath(1,0) of linka3;
linka11:=linka2--linka4--linka10--cycle;
fill linka9; unfill linka11; draw linka11;
endfig;
end;

Pochopitelně, je to jednoduchý obrázek, takže příliš nevadilo, že řadu důležitých konstrukcí metapostu dosud neznáme.

Co bude v příštím dílu

Datový typ path je skutečně velice rozsáhlý. V příštím dílu budou probrány datový typ transform a datový typ color. Jsou zcela jistě velice důležité, ale neoplývají tolika různorodými vlastnostmi jako datový typ path.