Obsah
1. Metoda přesouvání prostředního bodu
2. Postupné půlení úsečky
3. První demonstrační příklad
4. Změna koeficientu Δ podle nastaveného Hurstova exponentu
5. Druhý demonstrační příklad
6. Rekurzivní dělení čtverce
7. Třetí demonstrační příklad – plasma
8. Obsah dalšího pokračování tohoto seriálu
1. Metoda přesouvání prostředního bodu
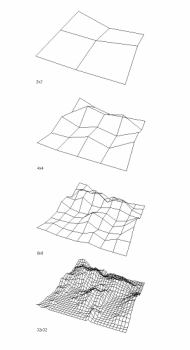
Pravděpodobně nejznámější a nejpoužívanější metodou určenou pro generování stochastických (náhodných) fraktálů je metoda nazvaná „přesouvání prostředního bodu“ (Midpoint Displacement Method – MDM), aplikovatelná jak na ploše, tak i v trojrozměrném prostoru. Tato metoda se velmi často v počítačové grafice používá k vygenerování a následné vizualizaci přírodní krajiny, povrchů vesmírných těles apod. Je velmi pravděpodobné, že jste se s touto metodou již několikrát setkali, například v počítačových hrách či v renderovaných filmech.
Volbou maximální odchylky Δ při posunu prostředního bodu je možné měnit celkový ráz krajiny od rovinné stepi přes poušť či pahorkatinu až po vysokohorskou krajinu se strmými štíty a údolími. Maximální odchylka a průběh jejího klesání také určuje Hausdorffovu dimenzi (fraktální dimenzi) vytvořeného modelu. Tutéž metodu je však možné rozšířit o jednu dimenzi a generovat pomocí ní realisticky vypadající modely mraků – podrobnosti se dozvíme v dalším pokračování tohoto seriálu.
Obrázek 1: Postupné vytváření a zjemňování modelu krajiny pomocí metody přesouvání prostředního bodu
Ve druhé kapitole si popíšeme základ metody přesouvání prostředního bodu aplikované na úsečku. Metodu si rozšíříme v kapitole čtvrté o možnost změny koeficientu Δ a Hurstova exponentu, které mají vliv na fraktální dimenzi vytvořeného objektu. Další rozšíření, které je popsané v šesté kapitole již vede k rekurzivnímu dělení čtverce, což nám umožňuje tvořit prostorové modely krajin a také obrázky známé pod označením plasma.
2. Postupné půlení úsečky
V nejjednodušším případě se metoda přesouvání prostředního bodu rekurzivně aplikuje na obyčejnou úsečku. Popišme si nyní obecný postup rekurzivního dělení horizontální úsečky tak, aby vznikl fraktální útvar:
- Vytváření obrazce začíná s jednoduchou horizontální úsečkou u0 o specifikované délce L0. Přímka je zadaná dvojicí bodů P10 a P20, kde horní index značí počet rekurzivního volání metody.
- Pro zadaný počet iterací imax (který odpovídá počtu dělení úsečky) se opakovaně provádí následující postup:
- Ke každé úsečce, jež se v obrazci nachází, je nalezen její prostřední bod Psi=1/2(P1i+P2i).
- Prostřední bod je vertikálně posunut o náhodnou hodnotu zadanou koeficientem Δi a vznikne tak nový bod Psi'.
- Daná úsečka je rozdělena na dvě poloviny: u1i=P1iPsi‚, u2i=Psi‘P2i
- Hodnota koeficientu Δi se s každou další iterací sníží tak, aby se limitně blížil k nule.
- Pokud se nedosáhlo kýženého množství iterací, resp. počtu dělení původní úsečky, opakuje se celý postup od třetího bodu.
Obrázek 2: Průběh postupného dělení úsečky pro 0–9 iterací
3. První demonstrační příklad
V dnešním prvním demonstračním příkladu je ukázáno, jakým způsobem je možné rekurzivně dělit úsečku tak, aby vznikl fraktální obrazec. Vstupem pro algoritmus je horizontálně orientovaná úsečka. Tato úsečka je v každém kroku rekurze rozdělena na polovinu a poté je její středový bod posunut o náhodnou hodnotu, jejíž maximální výchylka je zadaná parametrem Delta. Dělení rekurzivně pokračuje dále, přičemž se (spolu se zmenšující se délkou dělené úsečky) zmenšuje i hodnota parametru Delta, tak, aby v navazujícím kroku byla hodnota poloviční. Tímto způsobem dostaneme obrazec, jehož fraktální dimenze bude přibližně rovna 1,5.
Celý výpočet fraktálně rozdělené úsečky je založen na dvou funkcích. První funkce slouží k inicializaci celého výpočtu, druhá funkce je rekurzivně volána do té doby, než je rozhodnuto, že dělení úsečky dosáhlo své dolní meze. První funkce se jménem recalcFractal() po svém vyvolání pod sebe vykreslí deset fraktálních obrazců, které se od sebe liší maximálním počtem rekurzivního zanoření. V nultém kroku získáme původní úsečku, v prvním kroku dvě na sebe navazující úsečky, ve druhém kroku čtyři úsečky atd. Nalevo od vykreslovaných fraktálních obrazců je zobrazen i jejich popis. Funkce recalcFractal() má tvar:
//-----------------------------------------------------------------------------
// Překreslení fraktálního útvaru pro několik hodnot maximálních počtů iterací
//-----------------------------------------------------------------------------
void recalcFractal(float Delta)
{
char str[100];
int i;
for (i=0; i<10; i++) { // pro zadaný maximální počet iterací
srand(123456); // nastavit vždy stejné semínko RNG
drawString(10, 30+i*40, 0.0, 1.0, 1.0, itoa(i, str, 10));
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINES); // vykreslení rozdělené úsečky pro daný počet iterací
mdaRecursive1D(20, 30+i*40, WINDOW_WIDTH-10, 30+i*40, Delta, i);
glEnd();
}
} Obrázek 3: Screenshot prvního demonstračního příkladu při vypnutém antialiasingu
Mnohem zajímavější je však funkce, která je rekurzivně volána pro rozdělení úsečky. Tato funkce se jménem mdaRecursive1D() provádí při návratu z rekurze vykreslování rozdělených úseček pomocí příkazů z grafické knihovny OpenGL. Funkce má tvar:
//-----------------------------------------------------------------------------
// Rekurzivně volaná metoda, která provede rozdělení úsečky a posun
// prostředního bodu
//-----------------------------------------------------------------------------
void mdaRecursive1D(float x1, float y1, float x2, float y2, float Delta, int iter)
{
float x,y;
if (!iter) { // pokud jsme dosáhli maximálního množství iterací
glVertex2f(x1, y1); // vykreslení rozdělené úsečky na nejnižší úrovni
glVertex2f(x2, y2);
return; // a ukončení rekurze
}
x=(x1+x2)/2.0; // výpočet polohy prostředního bodu
y=(y1+y2)/2.0;
y+=my_random()*Delta-Delta/2.0; // posun prostředního bodu
mdaRecursive1D(x1, y1, x, y, Delta/2.0, iter-1); // rekurzivní volání na první polovinu úsečky
mdaRecursive1D(x, y, x2, y2, Delta/2.0, iter-1); // rekurzivní volání na druhou polovinu úsečky
} Obrázek 4: Screenshot prvního demonstračního příkladu při zapnutém antialiasingu
Zdrojový kód prvního demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka s obarvenou syntaxí. Ovládání tohoto demonstračního příkladu je velmi jednoduché: pomocí kurzorových kláves [Šipka nahoru] a [Šipka dolů] se mění vertikální měřítko obrazu, klávesou [A] se zapíná a vypíná antialiasing a konečně klávesou [Esc] se běh programu ukončí.
4. Změna koeficientu Δ podle nastaveného Hurstova exponentu
V prvním demonstračním příkladu jsme si uvedli způsob dělení úsečky tak, jak je většinou implementován v aplikacích, které tuto metodu používají například pro tvorbu horizontů s horami apod. Vzhledem k tomu, že se v každém kroku rekurze snižuje hodnota koeficientu Δ („amplituda“ náhodné hodnoty) na polovinu, je vykreslen obrazec s fraktální dimenzí rovnou 1,5. Jakým způsobem je však možné metodu dělení úsečky modifikovat tak, aby se fraktální dimenze dala uživatelsky či programově nastavit? Ukazuje se, že minimálně jeden použitelný způsob existuje, je však nutné provést celkem dvě změny do výše uvedeného postupu:
- První změna spočívá v tom, že se knihovní generátor náhodných čísel (RNG) změní na generátor s Gaussovským rozložením. Existuje více způsobů, jak toho dosáhnout, nejjednodušší je však výpočet průměru několika náhodných čísel generovaných běžným kongruentním generátorem, jaký je použit například ve standardní céčkové knihovně.
- Druhá změna je již závažnější, protože při požadavku na tvorbu obrazců s různou fraktální dimenzí se musí změnit rozptyl v Gaussově rozložení. Vztah pro výpočet rozptylu v i-té iteraci je následující:
σi2=σ2/(22H(i+1))
kde H je takzvaný Hurstův exponent, který určuje fraktální dimenzi D:
D=2-H
Z výše uvedené dvojice bodů vidíme, že změny není složité naprogramovat, o čemž se ostatně můžeme přesvědčit ve druhém demonstračním příkladu, který je popsán v následující kapitole.
5. Druhý demonstrační příklad
V dnešním druhém demonstračním příkladu jsou implementovány obě modifikace rekurzivního dělení úsečky uvedené v předchozí kapitole. Gaussovský generátor náhodných čísel je nahrazen funkcí randomGauss(), která provádí výpočet průměru deseti náhodných čísel získaných ze standardního kongruentního generátoru, tj. z funkce rand(). Implementovaná funkce randomGauss() má tvar:
//-----------------------------------------------------------------------------
// Vygenerování náhodného čísla v rozsahu 0..1 s přibližným Gaussovým rozložením
//-----------------------------------------------------------------------------
float randomGauss(void)
{
#define N 10
float sum=0.0;
int i;
for (i=0; i<N; i++)
sum+=(float)rand()/(float)RAND_MAX;
return sum/N;
} Funkce provádějící překreslení fraktálu má – stejně jako v prvním demonstračním příkladu – název recalcFractal(). Její tvar se příliš nezměnil, pouze se zvýšil počet parametrů (o Hurstův exponent) a také počet argumentů, se kterými se volá funkce mdaRecursive1D(). Tvar funkce recalcFractal() je následující:
//-----------------------------------------------------------------------------
// Překreslení fraktálu
//-----------------------------------------------------------------------------
void recalcFractal(float Delta, float Hexp)
{
char str[100];
int i;
for (i=0; i<10; i++) { // pro zadaný maximální počet iterací
srand(123456); // nastavit vždy stejné semínko RNG
drawString(10, 60+i*40, 0.0, 1.0, 1.0, itoa(i, str, 10));
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINES); // vykreslení rozdělené úsečky pro daný počet iterací
mdaRecursive1D(20, 60+i*40, WINDOW_WIDTH-10, 60+i*40, Delta, Hexp, i, 0);
glEnd();
}
} Největší změny nastaly ve funkci mdaRecursive1D(), která slouží k rekurzivnímu rozdělování úsečky. Přidané parametry Hexp a i slouží k postupné změně hodnoty Δ tak, aby byl vytvořen fraktální obrazec se zadaným Hurstovým exponentem H. Funkce mdaRecursive1D() nabyla podoby:
//-----------------------------------------------------------------------------
// Rekurzivně volaná metoda, která provede rozdělení úsečky a posun
// prostředního bodu
//-----------------------------------------------------------------------------
void mdaRecursive1D(float x1, float y1,
float x2, float y2,
float Delta, float Hexp,
int iter, int i)
{
float x,y;
float d;
if (!iter) { // pokud jsme dosáhli maximálního množství iterací
glVertex2f(x1, y1); // vykreslení rozdělené úsečky na nejnižší úrovni
glVertex2f(x2, y2);
return; // a ukončení rekurze
}
x=(x1+x2)/2.0; // výpočet polohy prostředního bodu
y=(y1+y2)/2.0;
d=Delta/(pow(2.0, 2.0*Hexp*(i+0)));
y+=randomGauss()*d-d/2.0; // posun prostředního bodu
mdaRecursive1D(x1, y1, x, y, Delta, Hexp, iter-1, i+1); // rekurzivní volání na první polovinu úsečky
mdaRecursive1D(x, y, x2, y2, Delta, Hexp, iter-1, i+1); // rekurzivní volání na druhou polovinu úsečky
} Obrázek 5: Screenshot druhého demonstračního příkladu při vypnutém antialiasingu
Zdrojový kód druhého demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka s obarvenou syntaxí. Ovládání tohoto demonstračního příkladu je stejné jako v příkladu prvním, pouze přibyla možnost změny Hurstova exponentu pomocí kurzorových kláves [Šipka doleva] a [Šipka doprava]. V dolní části okna se kromě Hurstova exponentu vypisuje i vypočtená fraktální dimenze.
Na šestém obrázku je zobrazena animace změny tvaru lomené úsečky v případě, že se mění Hurstův exponent z hodnoty 2,0 na hodnotu 0,0. To odpovídá rozsahům fraktální dimenze od 0,0 do 2,0. Vidíme, že pro rozsah fraktální dimenze 0,0..1,0 se stále jedná o dvojici spojených úseček a teprve pro rozsah 1,0..2,0 se charakteristika obrázku prudce mění. Ve skutečnosti je minimální fraktální dimenze lomené úsečky stále rovna jedné, vztah D=2-H je totiž platný pouze pro H>1.
Obrázek 6: Animace změny Hurstova exponentu a jí odpovídající změny fraktální dimenze
6. Rekurzivní dělení čtverce
Výše popsané rekurzivní dělení úsečky je možné rozšířit i na plošný útvar – čtverec. V tom nejjednodušším případě leží všechny krajní body čtverce v rovině x-y a při rekurzivním dělení jsou posouvány v kladném či záporném směru osy z. Možností, jak čtverec postupně rozdělovat je více, my si zde ukážeme v praxi tu nejčastěji používanou variantu, při které jsou v každém kroku rekurze vypočteny výšky bodů ležících v polovině hran čtverce (tj. výšky středů hran) a na jejich základě pak výška středu čtverce. Ta je posléze posunuta o náhodnou hodnotu, čímž je čtverec rozdělen na čtyři části, které jsou dále rekurzivně děleny.
Ve skutečnosti není zcela korektní mluvit o čtvercích, protože všechny čtyři vrcholy neleží v jedné rovině – spíše se jedná o obecnou přímkovou plochu, jejíž průmět do roviny x-y je čtvercový.
Popsané rekurzivní dělení čtverce je možné využít jak pro vytváření prostorových modelů terénu (příklad si uvedeme příště), tak i pro tvorbu obrázku, kterému se v počítačové grafice říká jednoduše plasma. Obrázek plasmy se tvoří tím způsobem, že je čtverec nahrazen rastrovým obrázkem (pro jednoduchost ve stupních šedi), kde pozice každého pixelu odpovídá souřadnicím bodu v rovině x-y a barva pixelu, tj. úroveň šedé, zbývající z-ové souřadnici bodu. Generování plasmy začíná v rozích rastrového obrázku a v jednotlivých krocích rekurze je obrázek dělen na čtvrtiny až do chvíle, kdy se dojde k velikosti jednoho pixelu, který se již dále samozřejmě nedělí.

Obrázek 7: Obrázek plasmy ve stupních šedi o rozlišení 256×256 pixelů
Kromě obrázků ve stupních šedi je možné generovat i barevné obrázky. Ty se tvoří dvojím způsobem – buď aplikací barvové palety (tak je plasma implementována například v programu FractInt), nebo vytvořením tří obrázků, z nichž každý odpovídá jednomu barvovému kanálu R, G, B. Druhá možnost je ukázána na osmém obrázku.

Obrázek 8: Plnobarevný obrázek plasmy o rozlišení 256×256 pixelů
7. Třetí demonstrační příklad – plasma
Dnešní třetí a současně i poslední demonstrační příklad slouží k tvorbě obrázku plasmy ve stupních šedi. Po spuštění příkladu je vytvořen obrázek o rozlišení 256×256 pixelů. Všechny čtyři krajní pixely mají nastavenu světlost na 50% (tj. 128), v programu je však možné tuto hodnotu změnit a tvořit tak i barevně odlišené obrázky. Veškerý výpočet plasmy obstarávají funkce recalcFractal() a plasma().
Funkce recalcFractal() zajišťuje inicializaci semínka pro generátor náhodných čísel (RNG) a také spouští rekurzivní výpočet s krajními body obrázku. Funkce má tvar:
//-----------------------------------------------------------------------------
// Přepočet fraktálu
//-----------------------------------------------------------------------------
void recalcFractal(void)
{
srand(123456); // semínko pro generátor náhodných čísel
if (amp<0) return;
plasma(0, 0, 256, 256, 128, 128, 128, 128, amp); // výpočet plasmy pro celou pixmapu
} Další významnou funkcí v třetím demonstračním příkladu je funkce plasma(), která provádí vlastní rekurzivní dělení čtverce. Vstupními parametry této funkce jsou souřadnice čtyř bodů tvořících dělený čtverec v pixmapě (x1, y1, x2, y2), hodnoty barev v těchto bodech (c1, c2, c3, c4) a maximální odchylka náhodné hodnoty při posunu prostředního bodu (delta). Ve funkci plasma() je nejprve zjištěno, zda je možné další dělení, tj. zda se nedosáhlo krajní velikosti 1×1 pixel. Pokud tomu tak je, je pixel vykreslen. V opačném případě, jsou vypočteny barvy ve středech hran čtverce i barva pixelu uprostřed čtverce. Tato barva je posléze změněna o náhodnou hodnotu a funkce plasma() je rekurzivně zavolána na všechny čtyři podčtverce:
//-----------------------------------------------------------------------------
// Rekurzivní dělení čtverce s generováním fraktální plasmy
//-----------------------------------------------------------------------------
void plasma(int x1, int y1, int x2, int y2,
int c1, int c2, int c3, int c4,
int delta)
{
#define avg(x, y) (((x)+(y))>>1)
#define step(x, y) (((x)-(y))>>1)
#define bound(x) if (x>255) x=255; if (x<0) x=0;
#define displac(x, delta) (x+(rand()%(delta*2)-delta))
if (x2-x1>1) { // pokud jsme nedosáhli jednopixelového kroku
int dc12=avg(c1, c2); // výpočet průměru barev na hranách čtverce
int dc13=avg(c1, c3);
int dc24=avg(c2, c4);
int dc34=avg(c3, c4);
int dc =avg(dc13, dc24); // výpočet průměrné barvy ve středu čtverce
int dx=step(x2, x1); // krok - polovina velikosti čtverce
int dy=step(y2, y1);
if ((x2-x1>2) && (delta>0))
dc=displac(dc, delta); // posun středního bodu o náhodnou hodnotu
bound(dc); // zajištění mezí barev v povoleném rozsahu
bound(c1);
bound(c2);
bound(c3);
bound(c4);
delta>>=1; // maximální náhodná hodnota se zmenšuje na polovinu
plasma(x1, y1, x1+dx, y1+dy, c1, dc12, dc13, dc, delta); // rekurzivní rozdělení všech
plasma(x1+dx, y1, x2, y1+dy, dc12, c2, dc, dc24, delta); // čtyř podčtverců
plasma(x1, y1+dy, x1+dx, y2, dc13, dc, c3, dc34, delta);
plasma(x1+dx, y1+dy, x2, y2, dc, dc24, dc34, c4, delta);
}
else { // bylo dosaženo hranice rozlišení pixmapy
putpixel(pix, x1, y1, (c1+c2+c3+c4)/4, (c1+c2+c3+c4)/4, (c1+c2+c3+c4)/4);
}
#undef avg
#undef step
#undef bound
} Zdrojový kód třetího demonstračního příkladu je opět dostupný ve formě zdrojového textu i jako HTML stránka s obarvenou syntaxí. Ovládání je v tomto příkladu velmi jednoduché – kurzorové šipky slouží ke změně maximální hodnoty Δ, klávesou [S] je možné obrázek plasmy uložit do externího souboru typu TGA (Targa) a aplikace se ukončuje buď klávesou [Q] nebo obligátním [Esc].

Obrázek 9: Screenshot třetího demonstračního příkladu
8. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu si ukážeme další možnosti tvorby krajiny (terénu). Budeme se zabývat metodou frekvenční syntézy, která je sice založena na zcela jiném principu, než dnes uvedená metoda, výsledky obou metod jsou však opticky velmi podobné. Kromě toho dokončíme část věnovanou tvorbě plasmy – prakticky si ukážeme, jakým způsobem je možné tvořit plnobarevnou plasmu a animovanou plasmu.