Obsah
1. Neuronové sítě v knihovně scikit-learn
2. Idealizovaný model neuronu používaný v umělých neuronových sítích
5. Vytvoření feed-forward sítě z jednotlivých neuronů
6. Vstupní vrstva, výstupní vrstva a skryté vrstvy neuronů
7. Trénink (učení) sítě s využitím trénovacích dat
8. Neuronová síť jako další typ modelu ve scikit-learn
9. Konstrukce neuronové sítě, její trénink a následné použití
10. Zobrazení vah neuronů v jednotlivých vrstvách
11. Zjištění přesnosti modelu vytvořeného neuronovou sítí, pomocí funkce accuracy_score
12. Konfigurace topologie neuronové sítě – počty neuronů ve skrytých vrstvách
13. Vliv počtu neuronů ve skrytých vrstvách na predikce neuronové sítě
14. Výsledky pro neuronovou síť s pěti skrytými vrstvami
15. Má další zvyšování počtu skrytých vrstev význam?
16. Lineární model provádějící regresi
17. Neuronová síť provádějící regresi
18. Změna počtu skrytých vrstev a neuronů v těchto vrstvách
19. Repositář s demonstračními příklady
1. Neuronové sítě v knihovně scikit-learn
V dnešním článku o knihovně scikit-learn se budeme zabývat problematikou vytvoření jednoduchých umělých neuronových sítí (zkráceně jen neuronových sítí neboli neural network, popř. nn) a taktéž způsobem tréninku (učení) těchto sítí s jejich následnou křížovou validací. Již na začátku je nutné říct, že se sice jedná o dosti rozsáhlou problematiku, pro jejíž pochopení se navíc očekává alespoň základní znalost teorie neuronových sítí, na druhou stranu je však použití těchto sítí (ve funkci blackboxu) ve scikit-learn až triviálně jednoduché, vlastně stejně jednoduché, jako použití jiných modelů.
Zpočátku se zaměříme na neuronové sítě typu feed-forward s volitelným počtem vrstev neuronů, přičemž neurony na sousedních vrstvách budou propojeny (synapsemi) systémem „každý s každým“ a informace mezi neurony potečou pouze jedním směrem (forward). V dalších částech tohoto seriálu si popíšeme i další typy sítí, v nichž bude použito více vrstev neuronů, neurony budou propojeny odlišným způsobem, budou použity jiné aktivační funkce atd. (což již ovšem částečně přesahuje možnosti scikit-learn a sáhneme tedy například po pytorchi atd.
Neuronové sítě se používají zejména v těch projektech, v nichž je zapotřebí vytvořit funkční systém už ve chvíli, kdy ještě neznáme všechny možné kombinace vstupů a výstupů, popř. když je chování systému, který se implementuje, tak složité, že klasický návrh a implementace algoritmů by byl příliš zdlouhavý nebo s danými prostředky (čas, počet vývojářů a testerů) neefektivní. Jednou z nevýhod neuronových sítí může být to, že je někdy velmi obtížné zjistit, jaký problém jsme vlastně neuronovou síť naučili řešit. Výsledná síť se totiž (pokud se nebudeme hodně snažit zjisti více) chová jako blackbox, o němž není snadné říct, jaké konkrétní rozhodování ten který neuron provádí (v některých případech to ovšem možné je). Kritickou úlohu zde sehrává výběr vhodné množiny trénovacích dat. K tomu se však dostaneme až v dalších částech seriálu, v nichž se zmíníme o již existujících trénovacích datech.
2. Idealizovaný model neuronu používaný v umělých neuronových sítích
Při práci s umělými neuronovými sítěmi je vhodné vědět, jak je vlastně taková síť zkonstruována a z jakých prvků se skládá. Základním stavebním prvkem je umělý neuron, resp. velmi zjednodušený a idealizovaný model skutečného neuronu. Původní model neuronu byl navržen Warrenem McCullochem a Walterem Pittsem (MCP) již ve čtyřicátých letech minulého století, z čehož plyne, že neuronové sítě nejsou jen módním výstřelkem poslední doby (naopak, moderní GPU umožňují jejich nasazení i tam, kde to dříve nebylo možné, to je však téma na samostatný článek.). Na dalším obrázku jsou naznačeny prvky modelu neuronu:

Obrázek 1: Idealizovaný model neuronu.
Vidíme, že neuron může mít libovolný počet vstupů (na obrázku jsou tři vstupy x1, x2 a x3, ovšem může to být jen jeden vstup nebo i sto vstupů) a má pouze jeden výstup y. Vstupem a výstupem jsou reálná čísla; typicky bývá výstup upraven aktivační funkcí tak, že leží v rozsahu ← 1..1> nebo <0..1>.
Dále na schématu vidíme váhy w1, w2 a w3. Těmito váhami jsou vynásobeny vstupní hodnoty. Váhy vlastně představují stav neuronu, tj. o funkci, na kterou byl neuron natrénován (naučen). Vstupní hodnoty x1 až xn jsou tedy postupně vynásobeny váhami w1 až wn a výsledky součinu jsou v neuronu sečteny, takže získáme jediné reálné číslo. Toto číslo je zpracováno aktivační funkcí (ta již většinou žádný stav nemá, ostatně stejně jako funkce pro výpočet sumy) výsledek této funkce je poslán na výstup neuronu.
Neuron tedy provádí tento výpočet:
y = f(w1x1 + w2x2 + … + wnxn)
3. Role biasu
Ve skutečnosti není stav neuronu pro n vstupů x1 až xn určen pouze n vahami w1 až wn. Musíme přidat ještě váhu w0, na kterou je připojena konstanta 1 (někdy se proto můžeme setkat s nákresem neuronové sítě, v níž se nachází speciální neurony bez vstupů a s jedničkou na výstupu). Model neuronu se přidáním nového vstupu nepatrně zkomplikuje:

Obrázek 2: Idealizovaný model neuronu s biasem.
I výpočet bude vypadat (nepatrně) odlišně, neboť do něho přidáme nový člen:
y = f(w0 + w1x1 + w2x2 + … + wnxn)
Tato přidaná váha se někdy nazývá bias, protože vlastně umožňuje posouvat průběh aktivační funkce nalevo a napravo, v závislosti na jeho hodnotě.
4. Aktivační funkce
Bez aktivační funkce by se neuron choval jednoduše – spočítal by vážený součet vstupů a výsledek by poslal na výstup. Aktivační funkce, kterou jsme v předchozích dvou kapitolách označovali symbolem f, do celého výpočtu vnáší nelinearitu (ta je velmi důležitá). Nejjednodušší aktivační funkce může pro vstupní hodnoty <0 vracet –1 a pro hodnoty ≥0 vracet 1, což vlastně říká, že je nutné dosáhnout určité hraniční hodnoty váženého součtu vstupů, aby byl neuron aktivován (tj. na výstup vyslal jedničku a nikoli –1). Ostatně právě zde znovu vidíme význam biasu, který onu hraniční hodnotu posunuje.

Obrázek 3: Aktivační funkce ReLU.
V praxi je však aktivační funkce složitější, než zmíněný jednotkový skok. Často se používá ReLU, sigmoid nebo hyperbolický tangent. Pro specializovanější účely se však používají i další funkce, které dokonce nemusí mít monotonní průběh. S dalšími podporovanými funkcemi se seznámíme příště.

Obrázek 4: Aktivační funkce Tanh.
5. Vytvoření feed-forward sítě z jednotlivých neuronů
Samostatné neurony i s aktivační funkcí stále provádí velmi jednoduchou činnost, ovšem aby se mohly stát součástí složitějšího systému (řekněme automatického řízení auta), musíme z nich vytvořit síť. Jedna z nejjednodušších forem umělé neuronové sítě se nazývá feed-forward, a to z toho důvodu, že informace (tedy vstupní hodnoty, mezihodnoty i hodnoty výstupní) touto sítí tečou jen jedním směrem (při učení je tomu jinak). Neurony jsou uspořádány pravidelně do vrstev:

Obrázek 5: Uspořádání neuronů do vrstev ve feed-forward síti.
Kolečka na obrázku představují jednotlivé neurony, přičemž žlutě jsou označeny neurony na vstupu, zeleně „interní“ (skryté) neurony a červeně neurony, které produkují kýžený výstup neuronové sítě.
Zcela nalevo jsou šipkami naznačeny vstupy. Jejich počet je prakticky zcela závislý na řešeném problému. Může se jednat jen o několik vstupů (viz naše testovací síť popsaná níže), ovšem pokud například budeme tvořit síť určenou pro rozpoznání objektů v rastrovém obrázku, může být počet vstupů roven počtu pixelů (což ovšem v praxi realizujeme odlišně – konvolučními sítěmi).
6. Vstupní vrstva, výstupní vrstva a skryté vrstvy neuronů
Vraťme se ještě jednou k obrázku číslo 5.
Povšimněte si, že vstupní neurony mají vlastně zjednodušenou funkci, protože mají jen jeden vstup. V mnoha typech sítí tyto neurony jen rozesílají vstup na další neurony a neprovádí žádný složitější výpočet, například u nich není použita aktivační funkce, ovšem to již záleží na konkrétní konfiguraci sítě. Dále stojí za povšimnutí, že neurony posílají svůj výstup neuronům na nejbližší další vrstvě; nejsou zde tedy žádné zkratky, žádné zpětné vazby atd.
Existují samozřejmě složitější typy sítí, těmi se teď ale nebudeme zabývat. Dále tato síť propojuje neurony na sousedních vrstvách systémem „každý s každým“. V našem konkrétním příkladu mají neurony na prostřední vrstvě dva vstupy, protože předchozí vrstva má jen dva neurony. Ovšem neurony na poslední vrstvě již musí mít tři vstupy.
První vrstva s jednoduchými („hloupými“) neurony se nazývá vstupní vrstva, poslední vrstva je vrstva výstupní. Vrstvy mezi vrstvou vstupní a výstupní, kterých může být teoreticky libovolné množství, se nazývají skryté vrstvy.
„Paměť“ neuronové sítě je tvořena vahami na vstupech neuronů (včetně biasu):
| Vrstva | Neuronů | Počet vstupů/neuron | Počet vah/neuron | Celkem |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 4 |
| 2 | 3 | 2 | 3 | 9 |
| 3 | 2 | 3 | 4 | 8 |
| ∑ | 7 | 21 |
V praxi se používají sítě s více vrstvami a především s větším počtem neuronů v každé vrstvě. Stavový prostor a tím i schopnosti sítě se tak prudce rozšiřují (viz již zmíněná problematika rozpoznávání objektů v rastrových obrázcích).
7. Trénink (učení) sítě s využitím trénovacích dat
Nejzajímavější je proces tréninku (učení) sítě. Ten může probíhat několika způsoby, ovšem nejčastější je učení založené na tom, že na vstup sítě přivedeme data, u nichž dopředu známe očekávaný výsledek. Síť pro tato vstupní data provede svůj odhad a na základě rozdílů mezi odhadem sítě a očekávaným výsledkem se více či méně sofistikovanými algoritmy nepatrně pozmění váhy wi na vstupech do neuronů (včetně biasu, tedy w0).
Konkrétní míra změn váhy na vstupech neuronů je globálně řízena dalším parametrem či parametry, z nichž ten nejdůležitější ovlivňuje rychlost učení. Ta by neměla být příliš nízká (to vyžaduje objemná trénovací data nebo jejich opakování), ale ani příliš vysoká. Základní algoritmus učení sítě se jmenuje backpropagation, protože se váhy skutečně mění v opačném směru – od výstupů (na něž se přivede vypočtená chyba) ke vstupům. Asi nejlépe je tento koncept popsán v článku dostupném na adrese https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/, tuto část za nás však vykoná knihovna scikit-learn zcela automaticky.
8. Neuronová síť jako další typ modelu ve scikit-learn
V knihovně scikit-learn se s neuronovými sítěmi pracuje prakticky stejným způsobem, jako s dalšími typy modelů. Implementace neuronových sítí tedy dělíme na klasifikátory a na sítě/modely provádějící regresi. Připomeňme si tedy, jakým způsobem se vytvoří model (NEzaložený na neuronové síti), který bude provádět klasifikaci, tj. na základě vstupu oznámí, že výstupní hodnota spadá do určité kategorie. V našem konkrétním případě se bude jednat o datovou sadu Iris a budeme rozlišovat čtyři možné druhy květin. Použijeme model KNeighborsClassifier:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
import numpy as np
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=1)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# trening modelu
classifier.fit(X_train, y_train)
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print(f"total: {total}")
print(f"same: {same}")
print(f"accuracy: {100.0*same/total:4.1f}%")
Po spuštění tohoto skriptu se zobrazí, že z třiceti vstupů (20% ze vstupní datové sady se 150 záznamy) se dobře klasifikovalo 29 vstupů a přesnost modelu je tedy 96,7%:
total: 30 same: 29 accuracy: 96.7%
9. Konstrukce neuronové sítě, její trénink a následné použití
Nyní provedeme jednoduchou záměnu – namísto modelu KNeighborsClassifier použijeme model MLPClassifier, což je model založený na neuronové síti (MLP znamená MultiLayer Perceptron). Model natrénujeme naprosto stejným způsobem, jako model z předchozí kapitoly, a následně jej i naprosto stejným způsobem otestujeme:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# trening modelu
classifier.fit(X_train, y_train)
# očekávané výsledky
expexted_labels = y_test
# výsledky modelu (predikované výsledky)
predicted_labels = classifier.predict(X_test)
# jak je náš model úspěšný?
total = 0
same = 0
# porovnání predikce s očekáváním
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
print(f"total: {total}")
print(f"same: {same}")
print(f"accuracy: {100.0*same/total:4.1f}%")
print(f"Features: {classifier.n_features_in_}")
print(f"Layers: {classifier.n_layers_}")
print(f"Outputs: {classifier.n_outputs_}")
print("Weights:")
for layer, weights in enumerate(classifier.coefs_):
print("\t", layer, weights.shape)
print("Biases:")
for layer, biases in enumerate(classifier.intercepts_):
print("\t", layer, biases.shape)
Výsledky pro několik běhů naznačují, že se při tréninku sítě používají náhodné hodnoty a tudíž výsledky nebudou vždy totožné:
total: 30 same: 30 accuracy: 100.0%
Další běh:
total: 30 same: 28 accuracy: 93.3%
10. Zobrazení vah neuronů v jednotlivých vrstvách
Povšimněte si, že na konci předchozího skriptu (po zjištění přesnosti modelu) si ještě necháme vypsat základní informace o neuronové síti. Zejména se vypíšou informace o počtu vstupů (features), počtu hladin (layers) i o počtu výstupů (outputs):
print(f"Features: {classifier.n_features_in_}")
print(f"Layers: {classifier.n_layers_}")
print(f"Outputs: {classifier.n_outputs_}")
print("Weights:")
Pro datovou sadu Iris se vypíše:
Features: 4 Layers: 3 Outputs: 3
Tj. bude se jednat o neuronovou síť, kde vstupní vrstva má čtyři neurony, výstupní vrstva má tři neurony (rozlišujeme tři druhy květin) a celkový počet vrstev bude roven třem (tedy k dispozici je jen jedna skrytá vrstva).
Dále si můžeme vypsat váhy vstupů jednotlivých neuronů i hodnoty bias:
for layer, weights in enumerate(classifier.coefs_):
print("\t", layer, weights.shape)
print("Biases:")
for layer, biases in enumerate(classifier.intercepts_):
print("\t", layer, biases.shape)
Výsledky:
Weights:
0 (4, 100)
1 (100, 3)
Biases:
0 (100,)
1 (3,)
Jak tyto údaje číst? Skrytá vrstva má sto neuronů, takže se propojuje stylem 4:100:3. Váhy jsou uloženy ve formě dvourozměrných matic s hodnotami typu float. A hodnoty bias jsou uloženy pro každou vrstvu formou vektorů (není zde realizováno propojení „každý s každým“, jde jen o vstup konstant do neuronů.
Pro neuronovou síť se třemi skrytými vrstvami, z nich každá má 10 neuronů, bude výstup vypadat následovně:
Features: 4
Layers: 5
Outputs: 3
Weights:
0 (4, 10)
1 (10, 10)
2 (10, 10)
3 (10, 3)
Biases:
0 (10,)
1 (10,)
2 (10,)
3 (3,)
11. Zjištění přesnosti modelu vytvořeného neuronovou sítí, pomocí funkce accuracy_score
Podobně jako u dalších typů modelů pochopitelně můžeme i u neuronových sítí zjistit přesnost modelu kombinací funkcí train_test_split a accuracy_score. Výsledkem by měly být podobné hodnoty, jaké jsme dostali v předchozím skriptu:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000)
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# trening modelu
classifier.fit(X_train, y_train)
# výsledky modelu (predikované výsledky)
y_pred = classifier.predict(X_test)
# vypoctena presnost modelu
print(accuracy_score(y_test, y_pred))
print(f"Features: {classifier.n_features_in_}")
print(f"Layers: {classifier.n_layers_}")
print(f"Outputs: {classifier.n_outputs_}")
print("Weights:")
for layer, weights in enumerate(classifier.coefs_):
print("\t", layer, weights.shape)
print("Biases:")
for layer, biases in enumerate(classifier.intercepts_):
print("\t", layer, biases.shape)
Skóre při prvním spuštění:
0.9666666666666667
Při dalším spuštění může být skóre vyšší (nebo nižší). Já měl štěstí – vyšel mi 100% korektní model:
1.0
A nakonec se opět vypíše konfigurace naučené neuronové sítě:
Features: 4
Layers: 3
Outputs: 3
Weights:
0 (4, 100)
1 (100, 3)
12. Konfigurace topologie neuronové sítě – počty neuronů ve skrytých vrstvách
Knihovna scikit-learn umožňuje částečnou konfiguraci topologie neuronové sítě. Volit totiž můžeme počty neuronů v jednotlivých skrytých vrstvách (nikoli ve vrstvě vstupní ani ve vrstvě výstupní – což je logické). Dosáhneme toho následujícím konstruktorem:
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = (počet_neuronů_ve_vrstvě1, počet_neuronů_ve_vrstvě2, ...))
To tedy znamená, že se počet neuronů předává ve formě n-tice, kde počet členů určí počet skrytých vrstev.
Ukažme si celý postup na jednoduchém demonstračním příkladu, v němž vytvoříme neuronovou síť se třemi skrytými vrstvami, přičemž každá vrstva bude obsahovat deset neuronů:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = (10, 10, 10))
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
# rozdělení na trénovací a testovací data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# trening modelu
classifier.fit(X_train, y_train)
# výsledky modelu (predikované výsledky)
y_pred = classifier.predict(X_test)
# vypoctena presnost modelu
print(accuracy_score(y_test, y_pred))
print(f"Features: {classifier.n_features_in_}")
print(f"Layers: {classifier.n_layers_}")
print(f"Outputs: {classifier.n_outputs_}")
print("Weights:")
for layer, weights in enumerate(classifier.coefs_):
print("\t", layer, weights.shape)
print("Biases:")
for layer, biases in enumerate(nn.intercepts_):
print("\t", layer, biases.shape)
Postupně získávané výsledky (přesnosti predikce modelu):
0.9666666666666667 0.9333333333333333 1.0
Zajímavá bude informace o samotné neuronové síti. Povšimněte si, že nyní je počet vrstev roven 1+3+1=5 a že váhy odpovídají tomu, že skryté vrstvy budou mít každá deset neuronů:
Features: 4
Layers: 5
Outputs: 3
Weights:
0 (4, 10)
1 (10, 10)
2 (10, 10)
3 (10, 3)
Biases:
0 (10,)
1 (10,)
2 (10,)
3 (3,)
13. Vliv počtu neuronů ve skrytých vrstvách na predikce neuronové sítě
Mohlo by se zdát, že větší neuronová síť (tedy více neuronů) může znamenat, že dostaneme i kvalitnější model a lepší výsledky. Ovšem v praxi můžeme narazit na úplný opak, a to ve chvíli, kdy se neuronová síť nedokáže správně zaučit – datová sada je buď příliš malá, nebo je neuronů tolik, že gradient při změně jejich vah je příliš malý nebo dokonce nulový. Ovšem zaměřme se nejdříve na případ, kdy vyšší počet neuronů má dobrý vliv na kvalitu modelu. Ostatně si to můžeme snadno ukázat – pro naši síť se třemi skrytými vrstvami budeme postupně zvyšovat počet neuronů v těchto vrstvách od 1 do 19 a budeme počítat úspěšnost takového modelu:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
avg_scores = []
r = range(1, 20)
# hledani optimalniho poctu neuronu ve vrstvach
for neurons in r:
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = (neurons, neurons, neurons))
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring='accuracy')
avg_score = scores.mean()
# vypsani prumerneho skore do tabulky
print(neurons, avg_score)
avg_scores.append(avg_score)
plt.plot(r, avg_scores)
plt.xlabel("Změna počtu neuronů ve třech vrstvách")
plt.ylabel("Přesnost modelu")
# ulozeni grafu do souboru
plt.savefig("139.png")
# vykresleni grafu na obrazovku
plt.show()
Numerické výsledky ukazují, že pro cca 8 neuronů ve vrstvě jsme dosáhli optimálního bodu:
1 0.33333333333333337 2 0.6533333333333333 3 0.7533333333333332 4 0.76 5 0.9666666666666668 6 0.9066666666666666 7 0.9466666666666667 8 0.9866666666666667 9 0.9866666666666667 10 0.9866666666666667 11 0.9666666666666668 12 0.9733333333333334 13 0.9666666666666668 14 0.9733333333333334 15 0.9733333333333334 16 0.9733333333333334 17 0.9733333333333334 18 0.9733333333333334 19 0.9733333333333334
Ještě lépe je to vidět na vykresleném grafu:
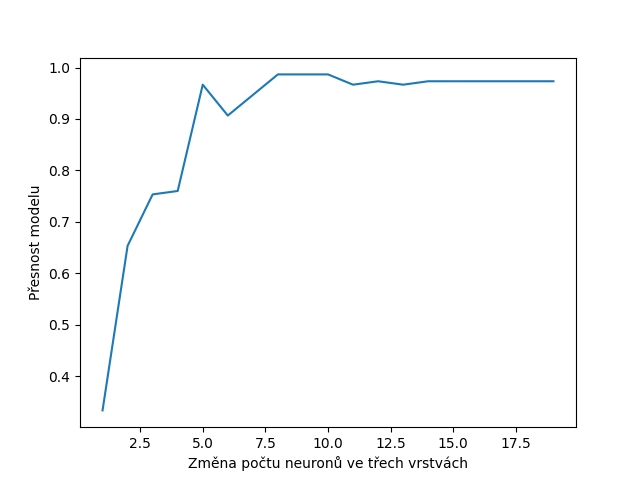
Obrázek 6: Vliv počtu neuronů na kvalitu modelu.
14. Výsledky pro neuronovou síť s pěti skrytými vrstvami
Pokusme se nyní zvýšit počet skrytých vrstev ze tří na pět. Skript bude prakticky stejný, jako tomu bylo v předchozí kapitole, pouze se změní n-tice předávaná do konstruktoru MLPClassifier. Nyní budeme specifikovat pět vrstev (hodnot v n-tici) a nikoli vrstvy tři:
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
avg_scores = []
r = range(1, 20)
# hledani optimalniho poctu neuronu ve vrstvach
for neurons in r:
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = (neurons, neurons, neurons, neurons, neurons))
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring='accuracy')
avg_score = scores.mean()
# vypsani prumerneho skore do tabulky
print(neurons, avg_score)
avg_scores.append(avg_score)
plt.plot(r, avg_scores)
plt.xlabel("Změna počtu neuronů v pěti vrstvách")
plt.ylabel("Přesnost modelu")
# ulozeni grafu do souboru
plt.savefig("140.png")
# vykresleni grafu na obrazovku
plt.show()
Výsledky nyní budou (na první pohled možná poněkud paradoxně) nepatrně horší, než tomu bylo v předchozím příkladu:
1 0.33333333333333337 2 0.4666666666666666 3 0.7133333333333333 4 0.7 5 0.9066666666666666 6 0.9733333333333334 7 0.9866666666666667 8 0.9133333333333333 9 0.9133333333333333 10 0.9733333333333334 11 0.9866666666666667 12 0.9866666666666667 13 0.9733333333333334 14 0.9733333333333334 15 0.9800000000000001 16 0.9733333333333334 17 0.9800000000000001 18 0.9800000000000001 19 0.9733333333333334
Grafické znázornění výsledků:
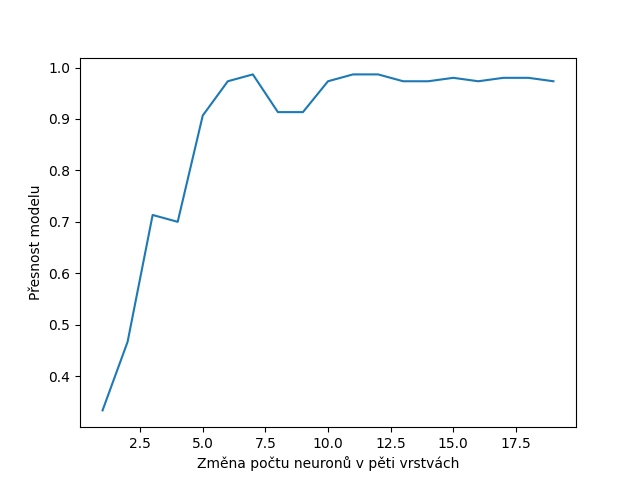
Obrázek 7: Vliv počtu neuronů na kvalitu modelu.
15. Má další zvyšování počtu skrytých vrstev význam?
Zajímavé bude taktéž zjistit, jestli má vůbec smysl zvyšovat počet skrytých vrstev nad určitou ideální hodnotu. Opět si to můžeme vyzkoušet, a to tak, že budeme měnit počet prvků v n-tici hidden_layer_sizes:
NEURONS = 5
r = range(1, 40)
# hledani optimalniho poctu neuronu ve vrstvach
for layers in r:
# konstrukce klasifikatoru
# (s hyperparametrem)
layer_sizes = (NEURONS, ) * layers
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = layer_sizes)
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
# nacteni datove sady
iris = load_iris()
# X je matice (feature matrix)
X = iris.data
# y je vektor (response vector)
y = iris.target
avg_scores = []
NEURONS = 5
r = range(1, 40)
# hledani optimalniho poctu neuronu ve vrstvach
for layers in r:
# konstrukce klasifikatoru
# (s hyperparametrem)
layer_sizes = (NEURONS, ) * layers
classifier = MLPClassifier(max_iter=5000, hidden_layer_sizes = layer_sizes)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring='accuracy')
avg_score = scores.mean()
# vypsani prumerneho skore do tabulky
print(layers, avg_score)
avg_scores.append(avg_score)
plt.plot(r, avg_scores)
plt.xlabel("Změna počtu vrstev")
plt.ylabel("Přesnost modelu")
# ulozeni grafu do souboru
plt.savefig("141.png")
# vykresleni grafu na obrazovku
plt.show()
Nyní jsou výsledky dosti odlišné od předchozích dvou výsledků, protože se model nejenom přestane zlepšovat, ale od cca 4–5 skrytých vrstev se naopak začíná zhoršovat, a to dosti podstatným způsobem (až k tomu, že začne hádat – což přesně odpovídá hodnotě 1/3, protože klasifikujeme jen tři druhy rostlin, a na hádání nám stačí funkce RND a nikoli neuronová síť):
1 0.9666666666666668 2 0.9800000000000001 3 0.8466666666666667 4 0.9733333333333334 5 0.9733333333333334 6 0.7133333333333333 7 0.8733333333333334 8 0.8866666666666667 9 0.5999999999999999 10 0.7466666666666667 11 0.7333333333333333 12 0.6799999999999999 13 0.5866666666666667 14 0.8066666666666666 15 0.4666666666666666 16 0.4666666666666666 17 0.4533333333333333 18 0.4333333333333333 19 0.39333333333333337 20 0.4 21 0.33333333333333337 22 0.33333333333333337 23 0.44666666666666666 24 0.33333333333333337 25 0.42000000000000004 26 0.4 27 0.33333333333333337 28 0.33333333333333337 29 0.33333333333333337 30 0.33333333333333337 31 0.33333333333333337 32 0.33333333333333337 33 0.33333333333333337 34 0.33333333333333337 35 0.33333333333333337 36 0.33333333333333337 37 0.33333333333333337 38 0.33333333333333337 39 0.33333333333333337
Grafické znázornění výsledků:
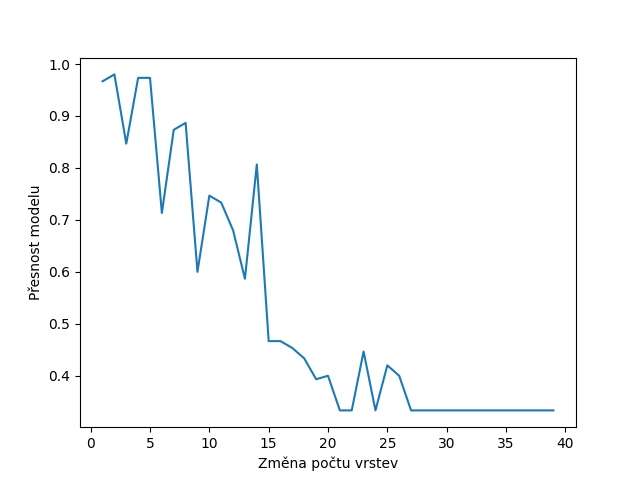
Obrázek 8: Vliv počtu skrytých vrstev na kvalitu modelu.
16. Lineární model provádějící regresi
V první části článku jsme si ukázali, jak podobné je použití libovolného modelu pro klasifikaci s neuronovou sítí, která taktéž provádí klasifikaci. Ovšem prakticky totéž platí i pro vztah mezi modely pro regresi a neuronovou sítí provádějící taktéž regresi (tedy zjednodušeně řečeno odhad numerické hodnoty z nějakého intervalu). Zopakujme si tedy, jak lze použít jednoduchý model pro lineární regresi a následně zjistit jeho (ne)přesnost. Použijeme přitom naši známou datovou sadu California Housings:
from sklearn import linear_model
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# X je matice, y je vektor
X = data
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.6)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X_train, y_train)
# predikce modelu
y_pred = lr.predict(X_test)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
Po spuštění tohoto skriptu se zobrazí koeficienty lineárního modelu a následně i přesnost (zde spíše nepatrná nepřesnost) odhadu výsledků:
Coefficients: [ 4.45786809e-01 9.72953693e-03 -1.35720128e-01 8.20514635e-01 -1.33231372e-06 -2.84786314e-03 -4.16735165e-01 -4.31811104e-01] Intercept: -36.869534449989914 Mean squared error: 0.53 Coefficient of determination: 0.61
17. Neuronová síť provádějící regresi
Nyní namísto modelu LinearRegression použijeme model nazvaný MLPRegressor. Jedná se o model založený na neuronové síti, který dokáže provádět regresi. A navíc do skriptu přidáme i (nyní známou) část, která vypíše základní parametry zkonstruované a natrénované neuronové sítě:
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# X je matice, y je vektor
X = data
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
# konstrukce modelu
nn = MLPRegressor(max_iter=5000)
# trénink modelu
nn.fit(X_train, y_train)
# predikce modelu
y_pred = nn.predict(X_test)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
print(f"Features: {nn.n_features_in_}")
print(f"Layers: {nn.n_layers_}")
print(f"Outputs: {nn.n_outputs_}")
print("Weights:")
for layer, weights in enumerate(nn.coefs_):
print("\t", layer, weights.shape)
print("Biases:")
for layer, biases in enumerate(nn.intercepts_):
print("\t", layer, biases.shape)
Po spuštění tohoto skriptu se opět nejdříve zobrazí výsledek validace modelu (s nepříliš lichotivými výsledky):
Mean squared error: 1.34 Coefficient of determination: -0.01
Posléze se zobrazí informace o neuronové síti. Ve vstupní vrstvě je osm neuronů, což odpovídá počtu atributů, na které byla síť natrénována. Výstupní vrstva má jeden neuron, což je opět pochopitelné, protože výstupem má být jediné reálné číslo. A celkový počet vrstev je roven třem – tedy kromě vstupní vrstvy a vrstvy výstupní máme jedinou skrytou vrstvu:
Features: 8 Layers: 3 Outputs: 1
Posledními údaji, které skript uvedený v této kapitole zobrazí, jsou tvary (shape) polí s váhami neuronů a taktéž pole s hodnotami bias. Tvary těchto polí plně odpovídají očekávané topologii neuronové sítě (tedy vazby 8:100:1 atd.):
Weights:
0 (8, 100)
1 (100, 1)
Biases:
0 (100,)
1 (1,)
18. Změna počtu skrytých vrstev a neuronů v těchto vrstvách
Podobně jako u neuronové sítě tvořící základ modelu MLPClassifier můžeme i u neuronové sítě v modelu MLPRegressor měnit jak počet skrytých vrstev, tak i počty neuronů v těchto vrstvách. K tomuto účelu se používá stejný nepovinný parametr hidden_layer_sizes, kterému se předává n-tice obsahující počty neuronů v jednotlivých vrstvách:
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# nacteni datove sady
housings = fetch_california_housing()
# precteni dat z datove sady
# urcenych pro trenink, validaci atd.
data = housings["data"]
# ceny bloku
targets = housings["target"]
# X je matice, y je vektor
X = data
y = targets
# rozdeleni dat na treninkovou a testovaci mnozinu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
neurons = 1000
# konstrukce modelu
nn = MLPRegressor(max_iter=5000, hidden_layer_sizes = (neurons, neurons, ))
# trénink modelu
nn.fit(X_train, y_train)
# predikce modelu
y_pred = nn.predict(X_test)
# chyba predikce
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 1 = nejlepší predikce modelu
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))
print(f"Features: {nn.n_features_in_}")
print(f"Layers: {nn.n_layers_}")
print(f"Outputs: {nn.n_outputs_}")
print("Weights:")
for layer, weights in enumerate(nn.coefs_):
print("\t", layer, weights.shape)
Na výsledky nyní budeme čekat delší dobu, a to kvůli pomalejšímu tréninku neuronové sítě:
Mean squared error: 0.65
Coefficient of determination: 0.51
Features: 8
Layers: 4
Outputs: 1
Weights:
0 (8, 1000)
1 (1000, 1000)
2 (1000, 1)
Biases:
0 (1000,)
1 (1000,)
2 (1,)
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/ - Linear regression (Wikipedia)
https://en.wikipedia.org/wiki/Linear_regression - Lineární regrese (Wikipedia)
https://cs.wikipedia.org/wiki/Line%C3%A1rn%C3%AD_regrese - Iris Flower Classification with MLP Classifier
https://www.metriccoders.com/post/iris-flower-classification-with-mlp-classifier