Obsah
1. Kombinační a sekvenční logické obvody v počítači
2. Tvorba složitějších logických funkcí pomocí kombinačních logických obvodů
3. Převody mezi různými kódy, multiplexory a demultiplexory
4. Realizace aritmetických operací – základ ALU
5. Klopné obvody – základ registrů a řadiče
6. Čítače a posuvné registry
7. Role hodinových signálů (časování)
8. Technologie logických členů
9. Obsah dalšího pokračování seriálu
1. Kombinační a sekvenční logické obvody v počítači
V předchozí části tohoto seriálu jsme si řekli, že činnost moderních počítačů je založená na Boolově algebře, logických funkcích a binární čili dvojkové číselné soustavě pracující s pouhými dvěma stavy, kterých mohou být reprezentovány pomocí binárních číslic (bitů). Základem Boolovy algebry jsou logické proměnné, které mohou nabývat pouze dvou hodnot 0 či I, a logické funkce, které taktéž mohou nabývat pouze hodnot 0 nebo I.
Logické proměnné jsou v počítači představovány většinou napěťovou úrovní, elektrickým proudem, úrovní magnetizace, polarizací paprsku atd. (samozřejmě v závislosti na použité technologii), zatímco logické funkce se implementují pomocí logických členů neboli hradel. Z logických členů se při návrhu počítače nebo jiného digitálního zařízení skládají větší celky, které jsou souhrnně nazývány logické obvody (ostatně jedna velmi dobrá kniha o této problematice má název „Od logických obvodů k mikroprocesorům“).
V praxi rozeznáváme dva typy logických obvodů. Jedná se o kombinační logické obvody a sekvenční logické obvody. Tyto obvody jsou sice na nižší úrovni sestaveny z těch samých členů, tj. hradel (a ještě níže pak většinou z tranzistorů), ale v jedné věci se od sebe zásadně odlišují. Výstupy kombinačních logických obvodů závisí pouze na vstupních kombinacích v daném časovém okamžiku (po ustálení případného přechodného děje). To znamená, že jedné vstupní kombinaci (vektoru bitů) odpovídá jediná a vždy stejná výstupní kombinace, tj. kombinační logický obvod nemá žádnou paměť, ve které by si mohl zapamatovat svůj předchozí stav.
Naproti tomu u obvodu sekvenčního závisí jeho výstupy nejen na kombinaci vstupů, ale i na jeho předchozím stavu. Z toho vyplývá, že sekvenční obvod musí obsahovat nějakou formu paměti, ve které má uložen svůj předchozí stav. Zajímavé je, že i tyto paměti jsou realizovány pomocí hradel, tj. obvodů, které samy o sobě paměťovou funkci nemají.

I moderní mikroprocesory jsou uvnitř sestaveny z kombinačních a logických obvodů
2. Tvorba složitějších logických funkcí pomocí kombinačních logických obvodů
Nejprve se budeme zabývat kombinačními logickými obvody, protože jsou jednodušší jak na návrh, tak i z hlediska jejich analýzy. Jak již bylo řečeno v úvodní kapitole, jsou kombinační logické obvody (ať již jsou jakkoli složité) složeny z hradel, které samy realizují jednoduché logické funkce s omezeným počtem vstupů. Typicky se jedná o funkce negace (NOT), logického součtu (OR), logického součinu (AND), negace logického součtu (NOR), negace logického součinu (NAND) a nonekvivalence (XOR), přičemž počet vstupů u typických hradel bývá od jednoho do čtyř, výjimečně i osm. Zkusme si nyní vypsat několik úkolů, které je možné s touto základní sadou hradel řešit, abychom viděli, že některé operace či instrukce probírané v dalších částech tohoto seriálu nejsou implementovány nějakými tajemnými postupy, ale „pouze“ sadou vhodně propojených hradel:
- V mnoha případech stojíme před problémem vytvoření kombinačního obvodu, který by implementoval nějakou základní logickou funkci o n-vstupních proměnných, kde n>4. Se znalostí vlastností Boolovy algebry (asociativity, komutativity, distributivity součtu vzhledem k součinu i naopak, de Morganových zákonů atd.) je tento úkol lehce splnitelný. Většinou jsou hradla uspořádána do stromové struktury – na začátku (tj. v kořenech stromu) jsou vždy zpracovány dvě navzájem si odpovídající hodnoty, výsledek je předán do nadřazených uzlů stromu atd. až se dojde ke kořenu tvořeného jediným hradlem, na jehož výstupu je požadovaný výsledek.
- Pomocí hradel typu logického součtu (OR) a logického součinu (AND) lze realizovat poměrně důležitou funkci přepínání informace. Princip je takový, že do vzniklého obvodu jsou přivedeny dva n-bitové vektory a na základě výběrového bitu (či signálu) se vybere vektor první či druhý. Podobný obvod je použit jak v operačních pamětech, tak i v samotných mikroprocesorech, například pro výběr registrů, jejichž obsah bude použit pro výpočet nějaké funkce v ALU.
- Dalším snadno řešitelným úkolem může být porovnání dvou n-bitových hodnot. Zde je možné použít například sadu hradel nonekvivalence (XOR). Jak uvidíme v dalších částech seriálu, jedná se o operaci, pro kterou bývá v mikroprocesorech vyhrazen zvláštní operační kód, protože porovnání dvou hodnot představuje základ pro tvorbu rozeskoků a tím i řízení běhu programu.
- Podobně lze, tentokrát ovšem pomocí hradel logického součtu (OR) realizovat test, zda je n-bitová hodnota nenulová, tj. zda je alespoň jeden bit nenulový či zda jsou všechny bity rovny nule. I tato operace je obsažena v instrukční sadě prakticky všech mikroprocesorů, z toho vyplývá, že funkce pro test nulovosti bývá součástí ALU (aritmeticko-logické jednotky).
- I s další funkcí se můžeme v některých mikroprocesorech setkat. Jedná se o funkce pro výpočet sudé či liché parity, resp. paritního bitu. Paritní bit se přidává k užitečné informaci například pro kontrolu správnosti přenosu. Pro sudou paritu platí, že paritní bit je roven 0 v případě, že je počet jedniček ve zpracovávané informaci (bitovém vektoru) sudý nebo nulový. Lichá parita má přesně opačnou podmínku. Funkci pro výpočet parity lze realizovat sérioparalelním zapojením hradel realizujících nonekvivalenci (XOR).
Počítač Mark I – jeden z prvních počítačů používající současnou architekturu (i když se to na první pohled nezdá)
3. Převody mezi různými kódy, multiplexory a demultiplexory
Poměrně často se v počítačích a dalších digitálních zařízeních používala taková zapojení hradel, která realizují převody binárních hodnot mezi různými kódy. Učebnicovým příkladem je převod jedné desítkové číslice reprezentované BCD kódem, tj. čtyřmi bity, na kód, který odpovídá zapojení sedmisegmentové zobrazovací jednotky, kterou všichni jistě znají z bezpočetného množství přístrojů – hodin, rádií, mikrovlnek, „takypočítače“ PMI-80 atd. Pro měření vzdálenosti či úhlu otočení se pro své výhodné vlastnosti používá takzvaný Grayův kód, který je před vlastním zpracováním měřené veličiny zapotřebí převést na poziční binární kód, který je již zpracovatelný v mikroprocesoru.
Příklad použití převodníků z nedávné minulosti: převod zvukových signálů z n-bitového pozičního binárního kódu na kód nelineární (µ-Law atd.), gamma korekce video signálu, pevná barevná paleta na některých osmibitových počítačích. Všechny tyto převodníky lze realizovat buď pomocí obvodů složených z hradel (tyto obvody se různými způsoby optimalizují, například na počet logických členů, maximální zpoždění atd.) nebo zapojením polovodičové paměti (typu ROM, PROM, EPROM, FLASH atd.): vstupní signály se zapojí na adresovou sběrnici a na sběrnici datové se po jisté době objeví přečtená informace.
Dalšími typy kombinačních obvodů jsou multiplexory a demultiplexory. Multiplexor (MUX) má na svém vstupu 2n datových vodičů (binárních signálů či hodnot) a n adresových vstupů. Na základě zapsané adresy se na výstup, tj. pouhý jeden bit, pošle jeden ze vstupních datových binárních hodnot. Použití multiplexorů je poměrně široké. Již na první pohled nás napadne serializace původně paralelního tvaru informace do tvaru sériového (místo 2n vodičů se použije pouze n+1 vodičů, protože se přenáší jak adresa, tak i vybraný bit).
To však není vše – multiplexor funguje jako jedna z forem funkce pro přepínání informace a ve své analogové podobě se například používá pro převod několika analogových signálů pomocí jednoho A/D převodníku. Digitální multiplexor se však dá také použít pro jednoduchou realizaci nějaké logické funkce, která by se jinak musela implementovat pomocí jednotlivých hradel, protože na adresové vodiče lze připojit vstupní signály dané funkce a datové vodiče jsou trvale připojeny buď na logickou jedničku nebo nulu (samozřejmě v závislosti na implementované funkci).
Demultiplexor (DMUX, DC) pracuje přesně opačným způsobem než multiplexor, tj. původní jednobitový stav převádí podle hodnoty n-bitové adresy na jeden z 2n výstupních vodičů. Kromě deserializace lze i demultiplexory použít pro realizaci složitějších logických funkcí. Vstupem jsou v tomto případě jak adresové vstupy, tak i jediný datový vstup a na výstup demoltiplexoru se typicky zapojují hradla typu OR.

Značky hradel se do schémat kreslí různými způsoby
4. Realizace aritmetických operací – základ ALU
V předchozích dvou kapitolách jsme si uvedli některé typické použití kombinačních logických obvodů. Tyto typy sice můžeme v počítačích i přímo mikroprocesorech najít na různých místech, ovšem jeden poměrně složitý kombinační logický obvod se svojí důležitostí poněkud vymyká. Jedná se o aritmeticko-logickou jednotku (zkráceně ALU), která provádí, jak její název ostatně napovídá, výpočet základních aritmetických a logických funkcí.
Princip ALU je poměrně jednoduchý: na její vstup jsou v typické konfiguraci přivedena dvě n-bitová čísla a dále i vodičů, pomocí kterých se zvolí příslušná operace. Na výstup ALU je po určitém zpoždění posláno m-bitové číslo, které odpovídá výsledku zvolené operace. Kromě toho může být na výstupu ALU ještě několik dalších signálů, které se nazývají příznaky (flags) nastavované v závislosti na výsledku či průběhu výpočtu. Jedním z příznaků může být příznak nulovosti (ten jsme si už uvedli) nebo příznak přetečení.
Jednodušší ALU, které byly použity ve většině osmibitových mikroprocesorů (s výjimkou slavné Motoroly 6809), typicky pracovaly s osmibitovými operandy, tj. dvojicí osmibitových čísel. Z operací, které ALU prováděly, se jednalo o součet dvou čísel (s přenosem i bez přenosu), rozdíl dvou čísel (opět s přenosem i bez přenosu), výpočet dvojkového doplňku čísla, porovnání obou operandů, negace všech bitů prvního operandu, bitový logický součin, bitový logický součet, nonekvivalence a v některých případech i posuny doleva či doprava – mnohdy však poslední dvě funkce vykonával samostatný obvod někdy nazývaný barrel shifter.
ALU použité v současných počítačích jsou mnohem složitější, neboť umí například provést vynásobení či vydělení dvou celých čísel. Počet logických hradel a tím i počet tranzistorů nutných pro implementaci těchto funkcí je samozřejmě obrovský. Poznamenejme ještě, že většinou se za ALU nepovažuje jednotka pro provádění operací v pohyblivé řádové čárce, neboli FPU. I když se dnes zpravidla jedná o jednotky umístěné na jednom čipu, stále se považují za dva oddělené funkční bloky, i když rozdíl mezi nimi se pomalu zmenšuje.

Příklad zapojení ALU v mikroprocesoru
5. Klopné obvody – základ registrů a řadiče
Aritmeticko-logická jednotka sice patří mezi základní stavební bloky mikroprocesorů, kromě ní se však v tomto klíčovém integrovaném obvodu musí nacházet i řadič a sada registrů. Tyto bloky mikroprocesoru se z velké části skládají ze sekvenčních logických obvodů, tj. obvodů, jejichž výstup závisí nejenom na stavu vstupů, ale také na jednom či více předchozích stavech obvodu – sekvenční logický obvod tedy obsahuje nějakou formu paměti. Mezi nejjednodušší sekvenční obvody patří klopné obvody, někdy také nazývané paměťové členy, protože jeden klopný obvod je možné považovat za jednobitovou paměťovou buňku.
Základním klopným obvodem, ze kterého se odvozují další typy klopných obvodů, je klopný obvod typu RS, jenž má dva vstupy označené symboly R (reset) a S (set) a jeden výstup označený symbolem Q (někdy je přítomný i negovaný výstup, to však není podstatné). Označení vstupů odpovídá jejich významu – přivedení logické jedničky na vstup R vede k přechodu do stavu 0, přivedení logické jedničky na vstup S naopak vede k přechodu obvodu do stavu I. Nastavený stav obvodu zůstane zachován i v případě, že jsou oba vstupy ve stavu logické nuly, tj. právě zde se projeví paměťová funkce obvodu. V případě, že jsou oba vstupy uvedeny do stavu logické jedničky, závisí chování obvodu na jeho vnitřním zapojení a obecně se jedná o zakázaný stav, kterému by se měl tvůrce zapojení vyhnout, což je naznačeno v pravdivostní tabulce klopného obvodu RS:
| Vstup S | Vstup R | Výstup Qi |
|---|---|---|
| 0 | 0 | Qi-1 |
| I | 0 | I |
| 0 | I | 0 |
| I | I | nedefinováno |

Schématická značka klopného obvodu typu D bez hodinového vstupu
Z klopného obvodu RS lze jednoduchou modifikací, konkrétně přidáním jednoho logického členu negace a dvou členů NAND či NOR, vytvořit paměťový člen D neboli klopný obvod D. Název je odvozen od slova data. Místo signálů R a S jsou použity dva vstupní signály D (data) a C (clock). Činnost tohoto obvodu je taková, že při C=I dochází k zapamatování aktuální hodnoty vstupu D, přičemž tato hodnota je zaznamenána na výstup až do dalšího příchodu impulsu (logické jedničky) na vstup C. Jedná se tedy o skutečný paměťový člen, jehož chování lze popsat jak pravdivostní tabulkou, tak i jednoduchým časovým diagramem. Všimněte si, že zde již nedochází k žádnému přechodu obvodu do nedefinovaného stavu:
| Vstup D | Vstup C | Výstup Qi |
|---|---|---|
| 0 | 0 | Qi-1 |
| I | 0 | Qi-1 |
| 0 | I | 0 |
| I | I | I |
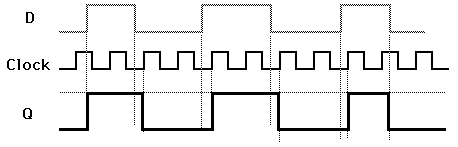
Časový diagram klopného obvodu D
Paralelním spojením několika klopných obvodů typu D (nebo i RS) vznikne registr. V něm je možné uschovat n-bitovou hodnotu. V mikroprocesorech je obecně umístěno větší množství registrů, typicky bývají minimálně dva registry na vstupech ALU a jeden registr pracuje ve funkci ukazatele na zpracovávanou instrukci. Starší mikroprocesory měly velmi omezenou sadu registrů, protože pro každý registr bylo zapotřebí použít poměrně velké množství hradel a tím i tranzistorů. U novějších procesorů, ve kterých počet tranzistorů jde do desítek milionů, toto omezení již neplatí, spíše jsme omezeni délkou instrukčního slova. Z těchto důvodů se současně používá cca 32 registrů, větší počet bývá rozdělen do takzvaného registrového okna (o této technologii si povíme příště).

Zapojení klopného obvodu typu D pomocí pěti dvouvstupových hradel NAND
Existují i další typy klopných obvodů, například klopný obvod T (trigger, toggle), nebo klopný obvod JK, které se od klopných obvodů RS a D liší především pravdivostní tabulkou a samozřejmě i interním zapojením. Klopný obvod T při hodinovém signálu změní, tj. neguje svůj stav. Klopný obvod JK vznikl vlastně spojením klopného obvodu RS a T – pro všechny stavy, kde platí R^S=0 se obvod chová jako typ RS, pro stav R^S=I dochází k negaci výstupu.

Schématická značka klopného obvodu typu JK bez hodinového vstupu
6. Čítače a posuvné registry
Dalším důležitým prvkem většiny mikroprocesorů je čítač. Ten je většinou použit na více místech, typicky pro postupné načítání mikroinstrukcí (v případě, že se jedná o mikroprocesor s mikroinstrukční sadou), přepínání jednotlivých stavů v mikroprocesoru, ale také ve funkci běžného čítače, což je doména jak mikrořadičů, které mají mnohdy více čítačů (counter) a časovačů (timer), ale také mnohých moderních mikroprocesorů. Čítače se také používají pro dělení kmitočtu, což je také důvod k tomu, že mnohé počítače mají své různé části taktované odlišným hodinovým signálem (sběrnice, paměť, procesor) a přitom používají jediný krystal. Čítače lze vytvořit vhodným zapojením několika klopných obvodů za sebe; většinou se jedná o klopné obvody typu T nebo JK. Vlastní přičtení jednotky je provedeno přivedením impulsu na hodinový vstup.
Posuvný registr pracující na podobném principu, který slouží k posunu n-bitové informace doprava či doleva, se taktéž v počítačích využívá na více místech. Může se jednat o převod paralelní informace (n bitů) na sériovou informaci či naopak, nebo se může jednat o běžný posun celého slova o jeden bit doprava či doleva, což vlastně realizuje operace dělení dvěma a násobení dvěma. S vhodně zvolenou zpětnou vazbou lze pomocí posuvného registru realizovat i jednoduché generátory pseudonáhodných čísel (takto se generoval například zvuk na osmibitových domácích počítačích Atari). Pro jeho realizaci se používají klopné obvody typu D, JK či RS.
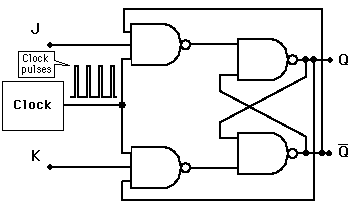
Zapojení klopného obvodu typu JK pomocí čtyř hradel NAND
7. Role hodinových signálů (časování)
Se zavedením složitějších kombinačních a zejména pak sekvenčních logických obvodů se ukázala potřeba synchronizace jednotlivých částí celého systému. Důvod je ten, že každý obvod pracuje poněkud odlišnou rychlostí (přesněji řečeno má jiné zpoždění) a proto je synchronizace nutná pro ustálení všech signálů před jejich dalším zpracováním, čímž se do velké míry zamezí vznikům tzv. hazardů a metastabilních stavů. Role čítačů a posuvných registrů je na časování dokonce přímo založená. Z tohoto důvodu je většina mikroprocesorů vybavena vstupem pro hodinový signál nebo přímo obsahuje obvody pro generování hodinového signálu (potom postačuje připojit vhodný oscilátor, většinou na bázi krystalu). Tento signál je buď použit ve své nezměněné podobě, nebo je násoben popř. dělen tak, aby se pomocí něj daly řídit interní moduly mikroprocesoru. Podrobnosti si ukážeme v další části tohoto seriálu.
8. Technologie logických členů
V současných učebnicích se automaticky předpokládá, že hradla a další logické obvody, tj. klopné obvody, čítače, aritmeticko-logické jednotky a další, jsou implementovány v integrovaných obvodech vyrobených nějakou starší či modernější technologií (PMOS, NMOS, CMOS, HMOS atd.). Ve skutečnosti je však možné tyto obvody pracující s binárními hodnotami implementovat například i pomocí relé, diskrétních tranzistorů či dokonce za pomoci optických tranzistorů (ty už byly vytvořeny i když prozatím nenašly při současném stavu technologie větší praktické uplatnění). Bez snahy o úplnost si některé technologie ukažme alespoň na obrázcích s krátkým vysvětlením.
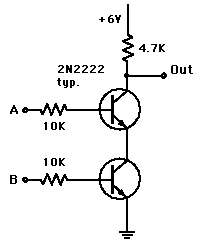
Hradla lze pro účely výuky vytvořit i z diskrétních součástek, i když v tomto případě nebudou mít takové statické a dynamické vlastnosti, jako integrované obvody. Na obrázku je zobrazeno hradlo typu NAND
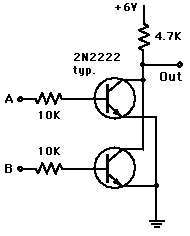
Příklad implementace hradla typu NOR pomocí diskrétních součástek. Z obou zapojení lze jednoduše odvodit, jak by vypadal invertor.
Skutečná hradla mívají interně složitější podobu, aby se zlepšily jejich statické a dynamické vlastnosti, tj. například se zrychlilo přepínání, dosáhlo se strmější charakteristiky atd. Příklad hradla typu NAND v TTL logice, ve které jsou na vstupu použity tranzistory s více emitory a na výstupu je pro tuto technologii typický totem.

Pohled do minulosti – elektronka zvaná trioda je vlastně předchůdcem dnešních tranzistorů, ale i CRT obrazovek či aktivních diplejů použitých například ve starších kalkulačkách, videích nebo dalších domácích spotřebičích.
I z elektronek lze vytvořit klopné obvody, i když použité napěťové úrovně, spotřeba, velikost a zpoždění je mnohem vyšší, než v případě použití integrovaných obvodů. Zde je zobrazena paměťová matice, kde každý bit je představován jednou elektronkou obsahující dvojici triod (každá baňka je tedy obdobou dvou tranzistorů, ze kterých lze sestavit bistabilní klopný obvod). Jako topení použitelné i dnes, doporučeno všemi akcionáři ČEZu.
9. Obsah dalšího pokračování seriálu
Dnes jsme se seznámili se základními prvky, ze kterých se skládají všechny moduly mikroprocesorů. V příští části tohoto seriálu si již konečně řekneme, jak vypadá vnitřní uspořádání mikroprocesorů a přiblížíme se tak pohledu na mikroprocesor, který je již známý všem programátorům pracujících ve strojovém kódu nebo assembleru.








































