Obsah
1. Od Lorenzova atraktoru k dalším typům atraktorů v ploše i prostoru
2. Upravený vzorec pro výpočet Lorenzova systému
4. Skript pro vykreslení Rösslerova dynamického systému
5. Wang Sunův dynamický systém
6. Podivné atraktory v 2D ploše
7. Kostra programu pro vykreslení dynamického systému v ploše s využitím Matplotlibu
8. Dynamické systémy, v nichž nelinearitu zajišťují goniometrické funkce
9. Dynamické systémy v nichž nelinearitu zajišťuje funkce sgn
10. Nelinearita zajištěná operací podílu
11. Dynamický systém nazvaný jednoduše Dynamic
12. Dynamický systém nazvaný Icon – výpočet v komplexní rovině
13. Dynamický systém nazvaný Kamtorus
15. Pomocné moduly pro vykreslení dynamických systémů s využitím knihovny Pygame
16. Ukázka skriptu pro vykreslení dynamického systému s využitím pomocných modulů
17. Ukázky dynamických systémů
18. Repositář s demonstračními příklady
1. Od Lorenzova atraktoru k dalším typům atraktorů v ploše i prostoru
Na článek Lorenzův systém: ideální pomůcka pro studium chaosu dnes navážeme. Pokusíme se totiž popsat si některé další dynamické systémy s podivným atraktorem (strange attractor), které je možné vykreslit v 3D prostoru nebo ve 2D rovině. Ovšem zatímco původní Lorenzův dynamický systém je skutečným (i když značně zjednodušeným) modelem navrženým pro analýzu reálných fyzikálních dějů, je tomu u většiny dynamických systémů popsaných dnes jinak – tyto systémy totiž byly navrženy takovým způsobem, aby jejich vizualizací primárně vznikly zajímavé obrázky; nejedná se tedy (v mnoha případech – je několik výjimek) o systémy získané jako model či řešení nějakých fyzikálních problémů.
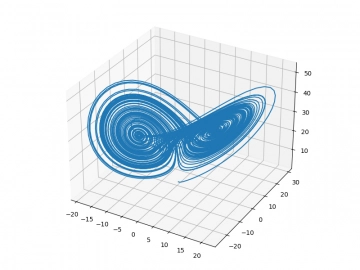
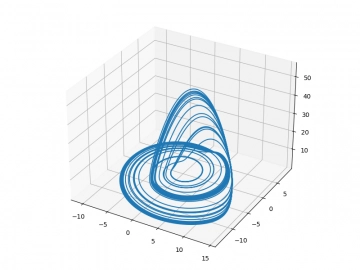
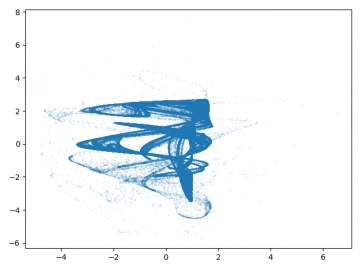
Obrázek 1: 3D graf se zobrazením fázového prostoru Lorenzova dynamického systému.
A podobně jako v předchozím článku, i dnes pro vizualizaci použijeme zejména knihovnu Matplotlib. Ovšem u dynamických systémů vykreslovaných v rovině navíc alternativně použijeme i knihovnu Pygame, protože pro vykreslení takových systémů nám postačuje vlastně pouze jediná grafická funkce – obarvení pixelu na zvolených souřadnicích. Řešení využívající knihovnu Pygame bude rychlejší, než vykreslování s využitím Matplotlibu; navíc je možný překlad těchto demonstračních příkladů do nativního kódu (Cython, Nuitka atd.) a otevírá se zde možnost použít nějakou hodnotu pro výpočet barvy.
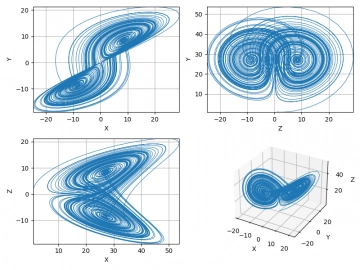
Obrázek 2: Průměty do jednotlivých os fázového prostoru Lorenzova dynamického systému.
2. Upravený vzorec pro výpočet Lorenzova systému
Dnešní článek začneme poměrně jednoduchým skriptem, v němž původní rovnice pro výpočet dalšího stavu Lorenzova systému poněkud pozměníme. Připomeňme si, že původně jsme Lorenzovy diferenciální rovince převedli do následující jednoduché podoby (samotná „integrace“ je provedena až v navazujícím programovém kódu):
def lorenz(x, y, z, s=10, r=28, b=2.667):
"""Výpočet dalšího bodu Lorenzova atraktoru."""
x_dot = s * (y - x)
y_dot = r * x - y - x * z
z_dot = x * y - b * z
return x_dot, y_dot, z_dot
Nyní tuto sadu tří výrazů upravíme do odlišné podoby, v níž se vyskytují celkem čtyři parametry nazvané alfa, beta, gamma a delta. Tyto parametry již nemají fyzikální význam. Proč k této změně došlo? Při použití původních rovnic pro Lorenzův atraktor je vykreslen obrazec, ve kterém jsou patrné dvě charakteristické smyčky, přičemž dráha počítaných bodů chaoticky mezi oběma smyčkami přeskakuje. Autoři Rick Miranda a Emily Stone vytvořili několik modifikací původních rovnic Lorenzova atraktoru tak, aby se při jejich aplikaci vytvořily obrazce s obecně různým počtem smyček. My si dnes jeden z jejich dynamických systémů implementujeme:
def lorenz_mod2(x, y, z, alfa, beta, gamma, delta):
"""Výpočet dalšího bodu Lorenzove mod2 atraktoru."""
x_dot = -alfa * x + y * y - z * z + alfa * gamma
y_dot = x * (y - beta * z) + delta
z_dot = -z + x * (beta * y + z)
return x_dot, y_dot, z_dot
Tuto novou funkci zaintegrujeme do původního skriptu určeného pro výpočet a vykreslení Lorenzova systému. Skript vykreslí 3D graf a posléze grafy s průměty do tří rovin definovaných souřadnými osami:
"""Výpočet a vykreslení upraveného Lorenzova podivného atraktoru."""
# Lorenz attractor
# import všech potřebných knihoven - Numpy a Matplotlibu
import matplotlib.pyplot as plt
import numpy as np
def lorenz_mod2(x, y, z, alfa, beta, gamma, delta):
"""Výpočet dalšího bodu Lorenzove mod2 atraktoru."""
x_dot = -alfa * x + y * y - z * z + alfa * gamma
y_dot = x * (y - beta * z) + delta
z_dot = -z + x * (beta * y + z)
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.001
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 100000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0.1, 0.1, 0)
# vlastní výpočet atraktoru
for i in range(n - 1):
x_dot, y_dot, z_dot = lorenz_mod2(x[i], y[i], z[i], 0.9, 5.0, 9.9, 1.0)
x[i + 1] = x[i] + x_dot * dt
y[i + 1] = y[i] + y_dot * dt
z[i + 1] = z[i] + z_dot * dt
# konstrukce 3D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(projection="3d")
# změna velikosti komponent v grafu.
plt.tight_layout()
# vykreslení grafu
ax.plot(x[50000:], y[50000:], z[50000:])
# uložení grafu
plt.savefig("lorenz_mod_1.png")
# zobrazení grafu
plt.show()
# grafy s více pohledy na atraktor
ch_3d = np.stack((x, y, z))
lim_xyz = [(np.min(ch_3d[ii]), np.max(ch_3d[ii])) for ii in range(3)]
fig2 = plt.figure("3D Coordinates", figsize=(8, 6))
plt.subplot(2, 2, 1)
plt.plot(y, x, linewidth=0.75)
plt.grid()
plt.xlabel("X")
plt.ylabel("Y")
plt.xlim(lim_xyz[1])
plt.ylim(lim_xyz[0])
plt.subplot(2, 2, 2)
Výsledkem běhu tohoto skriptu by měl být 3D graf s vykresleným systémem a taktéž graf s průměty do všech tří rovin:
Obrázek 3: 3D graf se zobrazením fázového prostoru upraveného Lorenzova dynamického systému.
Obrázek 4: Průměty do jednotlivých os fázového prostoru upraveného Lorenzova dynamického systému.
3. Rösslerův dynamický systém
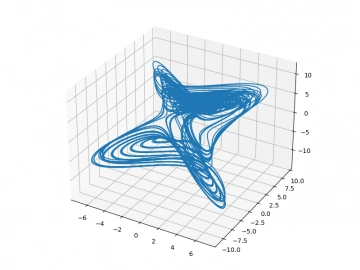
Další dynamický systém s velmi zajímavým atraktorem publikoval v sedmdesátých letech minulého století lékař Otto Rössler, který zkoumal problematiku bifurkací (stručně a nepřesně řečeno: rozdvojení bodů, které původně sledovaly prakticky totožnou trajektorii do zcela odlišných trajektorií). Jeho dynamický systém je, podobně jako je tomu u klasického Lorenzova atraktoru, tvořen trojicí diferenčních rovnic:
xn+1 = xn – yn × dt – zn × dt
yn+1 = yn + xn × dt + a yn × dt
zn+1 = zn + b × dt + xn × zn × dt – c × zn × dt
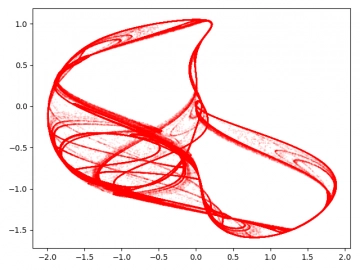
s počáteční podmínkou x0=y0=z0=1. Atraktor tohoto dynamického systému vytváří v prostoru (pochopitelně při použití vhodných parametrů) zajímavý obrazec, který připomíná několik do sebe vložených a ohnutých smyček (ohnutí do 3D je zde ještě více patrné, než u Lorenzova atraktoru, který vypadá plošší). A opět pochopitelně platí, že se tyto smyčky nikdy neprotínají, protože fázový prostor vlastně tvoří vektorové pole a při protnutí by systém musel pokračovat v původní cestě (byl by tedy periodický a nikoli chaotický).

Obrázek 5: Rösslerův atraktor (autor: Wofl, CC).
4. Skript pro vykreslení Rösslerova dynamického systému
Výpočet nového bodu ve fázovém prostoru Rösslerova dynamického systému je možné realizovat snadno, pouze úpravou tří výrazů v této funkci:
def rossler(x, y, z, a=0.2, b=0.2, c=5.7):
"""Výpočet dalšího bodu Rosslerova atraktoru."""
x_dot = -y - z
y_dot = x + a * y
z_dot = b + z * (x - c)
return x_dot, y_dot, z_dot
Pro úplnost se podívejme, jak bude vypadat skript, který po svém spuštění opět zobrazí trojrozměrný graf s fázovým prostorem Rösslerova dynamického systému a následně průměty do tří rovin (což už pro nás není nic nového):
"""Výpočet a vykreslení Rosslerova podivného atraktoru v 3D."""
# Rossler attractor
# import všech potřebných knihoven - Numpy a Matplotlibu
import matplotlib.pyplot as plt
import numpy as np
def rossler(x, y, z, a=0.2, b=0.2, c=5.7):
"""Výpočet dalšího bodu Rosslerova atraktoru."""
x_dot = -y - z
y_dot = x + a * y
z_dot = b + z * (x - c)
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.001
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 100000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0.1, 0.1, 6)
# vlastní výpočet atraktoru
for i in range(n - 1):
x_dot, y_dot, z_dot = rossler(x[i], y[i], z[i], 0.3, 0.2, 5.7)
x[i + 1] = x[i] + x_dot * dt
y[i + 1] = y[i] + y_dot * dt
z[i + 1] = z[i] + z_dot * dt
# konstrukce 3D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(projection="3d")
# změna velikosti komponent v grafu.
plt.tight_layout()
# vykreslení grafu
ax.plot(x[50000:], y[50000:], z[50000:])
# uložení grafu
plt.savefig("rossler_1.png")
# zobrazení grafu
plt.show()
# grafy s více pohledy na atraktor
ch_3d = np.stack((x, y, z))
lim_xyz = [(np.min(ch_3d[ii]), np.max(ch_3d[ii])) for ii in range(3)]
fig2 = plt.figure("3D Coordinates", figsize=(8, 6))
plt.subplot(2, 2, 1)
plt.plot(y, x, linewidth=0.75)
plt.grid()
plt.xlabel("X")
plt.ylabel("Y")
plt.xlim(lim_xyz[1])
plt.ylim(lim_xyz[0])
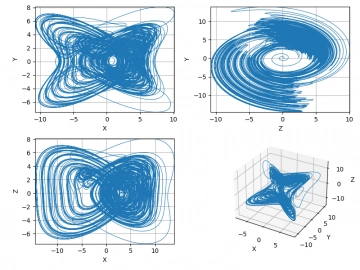
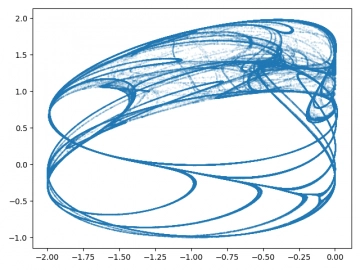
Obrázek 6: 3D graf se zobrazením fázového prostoru Rösslerova dynamického systému.
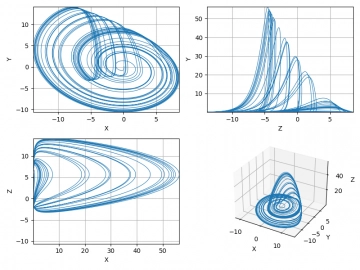
Obrázek 7: Průměty do jednotlivých os fázového prostoru Rösslerova dynamického systému.
5. Wang Sunův dynamický systém
Již bez podrobnějšího popisu se podívejme na Wang Sunův dynamický systém, který opět vychází z fyzikálního modelu, podobně jako původní Lorenzův atraktor:
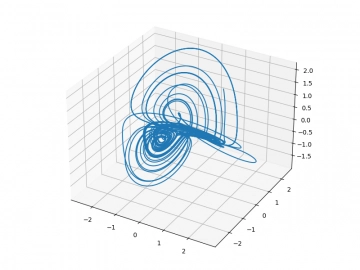
Obrázek 8: 3D graf se zobrazením fázového prostoru Wang Sunova dynamického systému.
Obrázek 9: Průměty do jednotlivých os fázového prostoru Wang Sunova dynamického systému.
Grafy vyobrazené na obrázcích 8 a 9 byly vytvořeny následujícím skriptem:
"""Výpočet a vykreslení Wang-Sunova podivného atraktoru."""
# # The Wang - Sun attractor
# Please also see https://hipwallpaper.com/view/9W3CM8
# import všech potřebných knihoven - Numpy a Matplotlibu
import matplotlib.pyplot as plt
import numpy as np
def wang_sun(x, y, z, alfa, beta, gamma, delta, epsilon, zeta):
"""Výpočet dalšího bodu Wang-Sunova atraktoru."""
x_dot = x * alfa + gamma * y * z
y_dot = x * beta + y * delta - x * z
z_dot = z * epsilon + zeta * x * y
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.001
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 1000000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (1.05, 1.1, 1.5)
# vlastní výpočet atraktoru
for i in range(n - 1):
x_dot, y_dot, z_dot = wang_sun(x[i], y[i], z[i], 0.2, -0.01, 1.0, -0.4, -1.0, -1.0)
x[i + 1] = x[i] + x_dot * dt
y[i + 1] = y[i] + y_dot * dt
z[i + 1] = z[i] + z_dot * dt
# konstrukce 3D grafu
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(projection="3d")
# změna velikosti komponent v grafu.
plt.tight_layout()
# vykreslení grafu
ax.plot(x, y, z)
# uložení grafu
plt.savefig("wang_sun_1.png")
# zobrazení grafu
plt.show()
# grafy s více pohledy na atraktor
ch_3d = np.stack((x, y, z))
lim_xyz = [(np.min(ch_3d[ii]), np.max(ch_3d[ii])) for ii in range(3)]
fig2 = plt.figure("3D Coordinates", figsize=(8, 6))
plt.subplot(2, 2, 1)
plt.plot(y, x, linewidth=0.75)
plt.grid()
plt.xlabel("X")
plt.ylabel("Y")
plt.xlim(lim_xyz[1])
plt.ylim(lim_xyz[0])
6. Podivné atraktory v 2D ploše
Dynamické systémy s podivnými atraktory mohou vznikat i v 2D ploše, nikoli nutně v 3D prostoru. Opět ovšem platí, že takový dynamický systém musí být popsán modelem s nelineárními závislostmi mezi (nyní jen dvojicí) hodnot x a y. Povšimněte si, že v dynamických systémech ve 3D byly tyto nelinearity realizovány vynásobením dvojice souřadnic (ostatní části výpočtu jsou lineární). V dále popsaných 2D systémech je tomu většinou jinak, protože zde namísto prostého součinu přímo nalezneme využití nelineárních funkcí, například goniometrických funkcí atd.

Obrázek 10: Dynamický systém nazvaný jednoduše Dynamic tak, jak ho vykreslil stařičký program FractInt.
7. Kostra programu pro vykreslení dynamického systému v ploše s využitím Matplotlibu
Pro vykreslení většiny dynamických systémů v ploše budeme používat stále stejnou „šablonu“ založenou na knihovně Matplotlib. Tato šablona vypadá následovně:
import matplotlib.pyplot as plt
import numpy as np
def dyn_system(x, y, a, b, c, d):
"""Funkce pro výpočet dalšího bodu podivného atraktoru."""
x_dot = ...
y_dot = ...
return x_dot, y_dot
# Celkový počet vypočtených bodů na atraktoru.
# (může se měnit)
n = 500000
# Počet bodů ze začátku výpočtu, které se nevykreslí.
# (může se měnit)
settle_down_points = 1000
# Prozatím prázdné pole připravené pro uložení výsledků výpočtu.
x = np.zeros((n,))
y = np.zeros((n,))
# Počáteční hodnoty pro výpočet podivného atraktoru.
# (mohou se měnit)
x[0], y[0] = (1.0, 1.0)
# Parametry ovlivňující výpočet prvního podivného atraktoru.
# (mohou se měnit)
A = ...
B = ...
C = ...
D = ...
# Vlastní výpočet podivného atraktoru.
for i in range(n - 1):
x_dot, y_dot = dyn_system(x[i], y[i], A, B, C, D)
x[i + 1] = x_dot
y[i + 1] = y_dot
# Vykreslení grafu s atraktorem.
plt.plot(x[settle_down_points:], y[settle_down_points:], "o", markersize=0.1)
# Změna velikosti komponent v grafu.
plt.tight_layout()
# Uložení grafu pro jeho další zpracování.
plt.savefig("dyn_system.png")
8. Dynamické systémy, v nichž nelinearitu zajišťují goniometrické funkce
Ukažme si nyní několik dynamických systémů, ve kterých potřebnou nelinearitu zajišťuje použití goniometrických funkcí. Vždy si pouze uvedeme funkci pro výpočet jednoho bodu takového systému a výsledné obrázky.
def bedhead(x, y, a, b):
x_dot = sin(x * y / b) * y + cos(a * x - y)
y_dot = x + sin(y) / b
return x_dot, y_dot
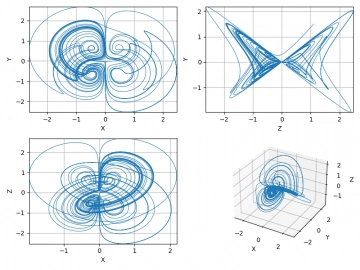
Obrázek 11: Dynamický systém nazvaný Bedhead.
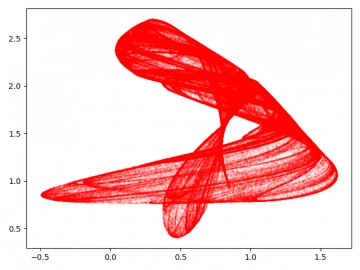
Obrázek 12: Dynamický systém nazvaný Bedhead.
def de_jong(x, y, a, b, c, d):
"""Funkce pro výpočet dalšího bodu De Jongova atraktoru."""
x_dot = sin(a * y) - cos(b * x)
y_dot = sin(c * x) - cos(d * y)
return x_dot, y_dot
Obrázek 13: De Jongův dynamický systém.
Obrázek 14: De Jongův dynamický systém.
def fractal_dream(x, y, a, b, c, d):
x_dot = sin(b * y) - c * sin(b * x)
y_dot = sin(a * x) - d * sin(a * y)
return x_dot, y_dot
Obrázek 15: Dynamický systém nazvaný Fractal Dream.
def rason_rampe_1(x, y, a, b, c, d):
x_dot = cos(b * y) + c * sin(b * x)
y_dot = cos(a * x) + d * sin(a * y)
return x_dot, y_dot
Obrázek 16: Dynamický systém navržený Jasonem Rampe (první varianta).
def rason_rampe_2(x, y, a, b, c, d):
x_dot = cos(b * y) + c * cos(b * x)
y_dot = cos(a * x) + d * cos(a * y)
return x_dot, y_dot
Obrázek 17: Dynamický systém navržený Jasonem Rampe (druhá varianta).
def rason_rampe_3(x, y, a, b, c, d):
x_dot = sin(b * y) + c * cos(b * x)
y_dot = cos(a * x) + d * sin(a * y)
return x_dot, y_dot
Obrázek 18: Dynamický systém navržený Jasonem Rampe (třetí varianta).
def pickover(x, y, a, b, c, d):
x_dot = sin(a * y) + c * cos(a * x)
y_dot = sin(b * x) + d * cos(b * y)
return x_dot, y_dot
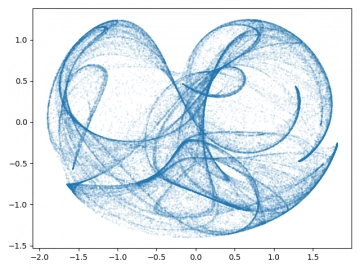
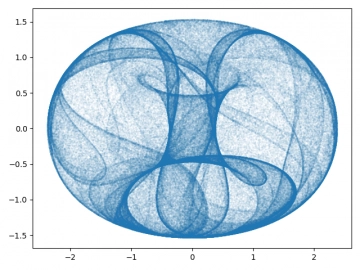
Obrázek 19: Pickoverův dynamický systém.
Obrázek 20: Pickoverův dynamický systém.
def svensson(x, y, a, b, c, d):
x_dot = d * sin(x * a) - sin(y * b)
y_dot = c * cos(x * a) + cos(y * b)
return x_dot, y_dot
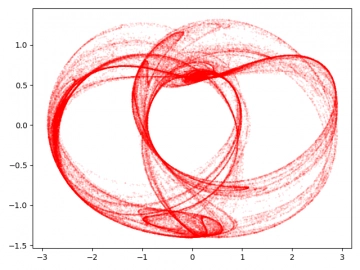
Obrázek 21: Svenssonův dynamický systém.
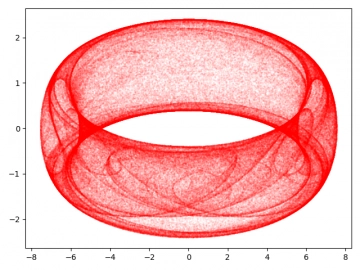
Obrázek 22: Svenssonův dynamický systém.
9. Dynamické systémy v nichž nelinearitu zajišťuje funkce sgn
Nelinearitu (a to skokovou změnu) zajišťuje pochopitelně i funkce pro detekci znaménka sgn. I takové dynamické systémy existují, takže si některé z nich ukažme.
def hopalong(x, y, a, b, c):
x_dot = y - sign(x) * sqrt(abs(b * x - c))
y_dot = a - x
return x_dot, y_dot
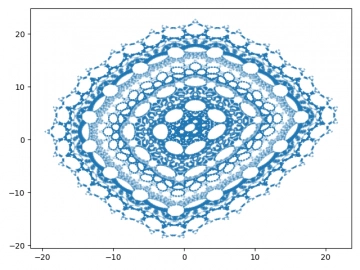
Obrázek 23: Dynamický systém Hopalong.
Obrázek 24: Dynamický systém Hopalong.
def quadruptwo(x, y, a, b, c):
x_dot = y - sign(x) * sin(ln(abs(b * x - c))) * atan(sqr(ln(abs(c * x - b))))
y_dot = a - x
return x_dot, y_dot
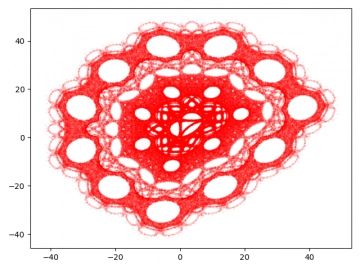
Obrázek 25: Dynamický systém Quadruptwo.
def threeply(x, y, a, b, c):
x_dot = y - sign(x) * abs(sin(x) * cos(b) + c - x * sin(a + b + c))
y_dot = a - x
return x_dot, y_dot
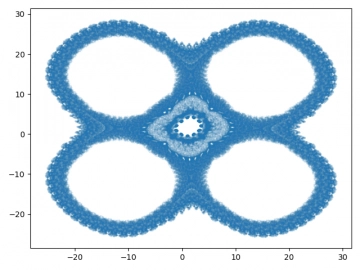
Obrázek 26: Dynamický systém Threeply.
10. Nelinearita zajištěná operací podílu
Nelinearitu mezi hodnotami x a y dokáže zajistit i operace podílu. Tato operace je využita například v dynamickém systému založeném na Gumowského funkci. Celý výpočet vypadá následovně:
def Gumowski(x, mu):
"""Gumovského funkce."""
g = x * mu + 2 * x * x * (1 - mu) / (1 + x * x)
return g
def gumowski_mira(x, y, a, b, mu):
"""Funkce pro výpočet dalšího bodu podivného atraktoru Gumowski-Mira."""
x_dot = a * y * (1 - b * y * y) + y + Gumowski(x, mu)
y_dot = -x + Gumowski(x_dot, mu)
return x_dot, y_dot
A takto vypadají vypočtené a vizualizované výsledky:
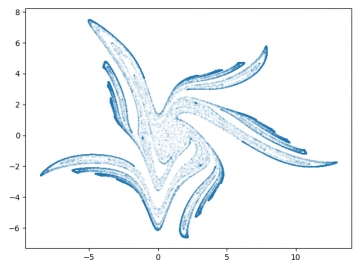
Obrázek 27: Dynamický systém Gumowski-Mira.
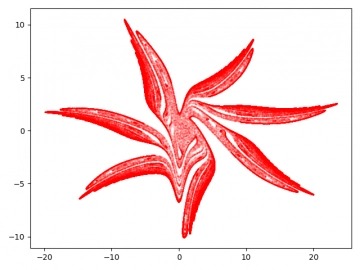
Obrázek 28: Dynamický systém Gumowski-Mira.
11. Dynamický systém nazvaný jednoduše Dynamic
Další dynamický systém, který si dnes ve stručnosti popíšeme, se jmenuje jednoduše Dynamic. Pro výpočet dalšího bodu ve fázovém prostoru se v tomto systému používá jednoduchý vztah založený na goniometrických funkcích, což je ostatně patrné i z následujícího výpisu kódu této funkce:
def dynamic(x, y, a, b):
"""Funkce pro výpočet dalšího bodu podivného atraktoru."""
x_dot = -sin(y + a * sin(b * y))
y_dot = sin(x + a * sin(b * x))
return x_dot, y_dot
Liší se ovšem způsob vykreslení, protože namísto jediného systému jich vykreslíme celou řadu, a to pro různé počáteční hodnoty x0 a y0 (ty budou začínat v pravidelné mřížce):
for x0 in range(0, max_x, step_x):
for y0 in range(0, max_y, step_y):
# Počáteční hodnoty pro výpočet.
x[i], y[i] = (x0, y0)
# Jedno "vlákno" atraktoru.
for r in range(1, maxiter):
x_dot, y_dot = dynamic(x[i], y[i], A, B)
x[i + 1] = x[i] + dt * x_dot
y[i + 1] = y[i] + dt * y_dot
i += 1
Výsledkem bude následující částečně uspořádaná struktura bodů (kterou lze navíc obarvit, což jsme si již ostatně ukázali):
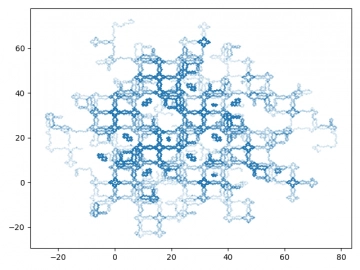
Obrázek 29: Sada dynamických systémů zvaná jako celek Dynamic.
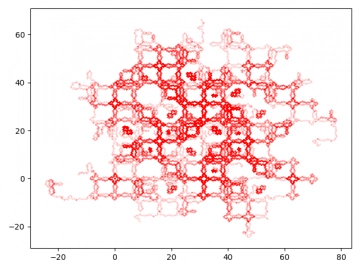
Obrázek 30: Sada dynamických systémů zvaná jako celek Dynamic.
Vzhledem k tomu, že se způsob vizualizace odlišuje od dříve popsaných dynamických systémů, si pro jistotu uvedeme celý zdrojový kód, který vykreslení provádí:
# Dynamic system renderer
# Import všech potřebných knihoven - Numpy, Matplotlibu a standardní
# matematické knihovny, ze které se využijí jen některé vybrané funkce.
from math import sin
import matplotlib.pyplot as plt
import numpy as np
def dynamic(x, y, a, b):
"""Funkce pro výpočet dalšího bodu podivného atraktoru."""
x_dot = -sin(y + a * sin(b * y))
y_dot = sin(x + a * sin(b * x))
return x_dot, y_dot
# Konstanta pro numerickou integraci. Menší hodnoty znamenají přesnější
# výpočty, ovšem na úkor výpočetního času.
dt = 0.3
# Parametry mřížky s počátečními hodnotami dynamického systému.
max_x = 50
step_x = 5
max_y = 50
step_y = 5
# Počet iterací pro zadané počáteční podmínky.
maxiter = 1000
# Počet vypočtených bodů na podivném atraktoru.
n = maxiter * max_x // step_x * max_y // step_y
# Prozatím prázdné pole připravené pro výpočet.
x = np.zeros((n,))
y = np.zeros((n,))
# Počáteční hodnoty pro výpočet.
# x[0], y[0] = (10, 10)
# Parametry ovlivňující výpočet podivného atraktoru.
A = -2.7
B = 2.8
i = 0
# Vlastní výpočet podivného atraktoru pro různé počáteční podmínky.
for x0 in range(0, max_x, step_x):
for y0 in range(0, max_y, step_y):
# Počáteční hodnoty pro výpočet.
x[i], y[i] = (x0, y0)
# Jedno "vlákno" atraktoru.
for r in range(1, maxiter):
x_dot, y_dot = dynamic(x[i], y[i], A, B)
x[i + 1] = x[i] + dt * x_dot
y[i + 1] = y[i] + dt * y_dot
i += 1
# Vykreslení grafu s podivným atraktorem.
plt.plot(x, y, "o", markersize=0.1)
# Změna velikosti komponent v grafu.
plt.tight_layout()
# Uložení grafu pro jeho další zpracování.
plt.savefig("dynamic_1.png")
# Zobrazení grafu.
plt.show()
# Druhý atraktor
# Parametry ovlivňující výpočet podivného atraktoru.
A = 2.7
B = -2.8
step_x = step_x // 2
step_y = step_y * 2
maxiter = maxiter // 2
i = 0
# Vlastní výpočet podivného atraktoru pro různé počáteční podmínky.
for x0 in range(0, max_x, step_x):
for y0 in range(0, max_y, step_y):
# Počáteční hodnoty pro výpočet.
x[i], y[i] = (x0, y0)
# Jedno "vlákno" atraktoru.
for r in range(1, maxiter):
12. Dynamický systém nazvaný Icon – výpočet v komplexní rovině
Další dynamický systém se jmenuje Icon. Tento systém je zvláštní tím, že se výpočty provádí v komplexní rovině (takže x a y tvoří komplexní hodnotu) a navíc je výsledný obrázek s vizualizovaným dynamickým systémem středově symetrický (je ovlivněno zejména parametrem degree). Vlastní výpočet dalšího bodu v komplexní rovině je realizován následující funkcí:
def icon(x, y, lambda_, alpha, beta, gamma, omega, degree):
"""Funkce pro výpočet dalšího bodu podivného atraktoru."""
zzbar = x * x + y * y
p = alpha * zzbar + lambda_
zreal = x
zimag = y
for i in range(degree - 2):
za = zreal * x - zimag * y
zb = zimag * x + zreal * y
zreal = za
zimag = zb
zn = x * zreal - y * zimag
p = p + beta * zn
x_dot = p * x + gamma * zreal - omega * y
y_dot = p * y - gamma * zimag + omega * x
return x_dot, y_dot
Výsledné obrazce:
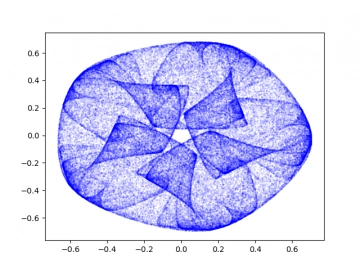
Obrázek 31: Středově symetrická vizualizace dynamického systému Icon.
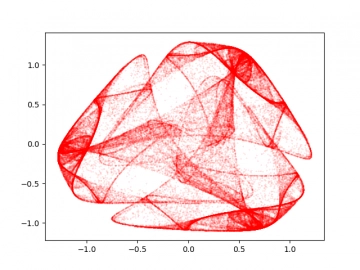
Obrázek 32: Středově symetrická vizualizace dynamického systému Icon.
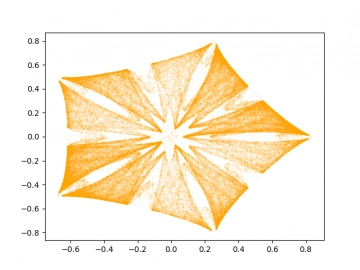
Obrázek 33: Středově symetrická vizualizace dynamického systému Icon.
13. Dynamický systém nazvaný Kamtorus
Poslední dynamický systém vizualizovaný v rovině, který si dnes popíšeme, se jmenuje Kamtorus, kde druhá část jména torus naznačuje, že pokud hodnotu orbit budeme chápat jako třetí souřadnici, získáme trojrozměrný graf, který skutečně do určité míry připomíná toroid. Nás však bude zajímat způsob vykreslení ve 2D. Tento dynamický systém je realizován následujícím kódem s dvojicí vnořených programových smyček (připomíná tak dynamický systém Dynamic):
def kam_torus(orbit_start, orbit_end, orbit_step, points_per_orbit, a):
"""Výpočet atraktoru."""
# Celkový počet vypočtených bodů na podivném atraktoru.
n = 100000
# Prozatím prázdné pole připravené pro výpočet.
x = np.zeros((n,))
y = np.zeros((n,))
# Vlastní výpočet podivného atraktoru.
i = 0
for orbit in frange(orbit_start, orbit_end, orbit_step):
x[i] = orbit / 3.0
y[i] = orbit / 3.0
i += 1
if i >= n:
return x, y
for p in range(1, points_per_orbit):
x[i] = x[i - 1] * cos(a) + (x[i - 1] * x[i - 1] - y[i - 1]) * sin(a)
y[i] = x[i - 1] * sin(a) - (x[i - 1] * x[i - 1] - y[i - 1]) * cos(a)
i += 1
if i >= n:
return x, y
return x, y
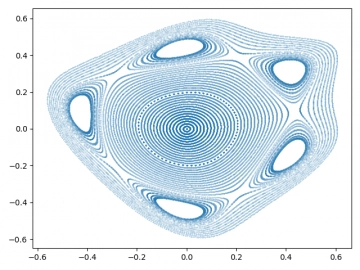
Obrázek 34: Dynamický systém nazvaný Kamtorus nebo Kam Torus.
14. Vylepšení vizualizace dynamických systémů v ploše: obarvení pixelů na základě počtu bodů, které reprezentují
Při vizualizaci dynamických systémů v rovině je možné vylepšit výsledné obrázky tak, že nezobrazíme pouze informaci o tom, zda nějaký pixel obsahuje bod (body) z počítaného dynamického systému, ale zdůrazníme i počet překreslení pixelu (tj. počet překrývajících se bodů). Výsledný rastrový obrázek tedy bude obsahovat i vizualizaci hustoty bodů. Pro tento účel naše vykreslovací algoritmy přepíšeme tak, že se namísto knihovny Matplotlib bude používat knihovna Pygame a vykreslování budeme provádět nepřímo – nejdříve do pomocné bitmapy a poté tuto bitmapu znormalizujeme a překreslíme na obrazovku. Pro snazší výpočty a normalizaci bude naše pomocná bitmapa obsahovat hodnoty typu float, což je sice na první pohled zvláštní, ale normalizace (do výsledného rozsahu 0..255) bude probíhat rychle a bez nutnosti triků s numerickými hodnotami.
15. Pomocné moduly pro vykreslení dynamických systémů s využitím knihovny Pygame
Demonstrační příklady, které jsou postaveny nad knihovnou Pygame (a nikoli nad Matplotlibem) používají čtyři pomocné moduly zajišťující vytvoření okna pro vykreslování, manipulaci s bitmapami i vlastní vizualizaci dynamického systému. Do těchto modulů postačuje pouze předat funkci pro výpočet jednoho bodu ve fázovém prostoru, parametry dynamického systému, měřítko a požadovaný kontrast výsledného obrázku.
colors.py
Obsahuje pouze výčet se jmény barev, použito při konstrukci okna pro vykreslování:
from enum import Enum
class Colors(Enum):
"""Named colors used everywhere on demo screens."""
BLACK = (0, 0, 0)
BLUE = (0, 0, 255)
CYAN = (0, 255, 255)
GREEN = (0, 255, 0)
YELLOW = (255, 255, 0)
RED = (255, 0, 0)
MAGENTA = (255, 0, 255)
WHITE = (255, 255, 255)
ui.py
Realizuje otevření okna pro vykreslování a obsahuje implementaci smyčky pro obsluhu událostí (event loop):
import sys
from typing import Tuple
import pygame
import pygame.locals
from colors import Colors
def initialize(
title: str, width: int, height: int
) -> Tuple[pygame.Surface, pygame.Surface, pygame.time.Clock]:
"""Initialize Pygame display, drawing surface, and clocks."""
# set window title
pygame.display.set_caption(title)
# initialize window
display = pygame.display.set_mode([width, height])
display.fill(Colors.BLACK.value)
# create all required Pygame objects
surface = pygame.Surface([width, height])
surface.fill(Colors.BLACK.value)
clock = pygame.time.Clock()
return display, surface, clock
def event_loop(
display: pygame.Surface, surface: pygame.Surface, clock: pygame.time.Clock
) -> None:
"""Event loop that just waits for keypress or window close operation."""
while True:
for event in pygame.event.get():
if event.type == pygame.locals.QUIT:
pygame.quit()
sys.exit()
if event.type == pygame.locals.KEYDOWN:
if event.key == pygame.locals.K_ESCAPE:
pygame.quit()
sys.exit()
if event.key == pygame.locals.K_RETURN:
pygame.quit()
sys.exit()
# all events has been processed - update scene and redraw the screen
display.blit(surface, (0, 0))
pygame.display.update()
clock.tick(25)
bitmap.py
Manipulace s bitmapou, do které je vykreslen dynamický systém. Realizuje i normalizaci hodnot pro vykreslení bitmapy do okna:
from typing import List, Tuple
from pygame import Surface
def compute_min_max(
bitmap: List[List[float]], width: int, height: int
) -> Tuple[float, float]:
# initial limits for pixel values normalization
min = float("inf")
max = float("-inf")
# retrieve minimal and maximal pixel values
for j in range(height):
for i in range(width):
z = bitmap[j][i]
if max < z:
max = z
if min > z:
min = z
return min, max
def create_bitmap(width: int, height: int) -> List[List[float]]:
return [[0 for x in range(width)] for y in range(height)]
def draw_bitmap(bitmap: List[List[float]], surface: Surface, max_factor: float) -> None:
print("contrast adjustment")
width, height = surface.get_size()
# retrieve minimal and maximal pixel values
min, max = compute_min_max(bitmap, width, height)
max *= max_factor
k = 255.0 / (max - min)
# contrast change
for y in range(height):
for x in range(width):
f = float(bitmap[y][x])
f -= min
f *= k
if f > 255.0:
f = 255
i = int(f) & 255
surface.set_at((x, y), i + (i << 8) + (i << 16))
renderer.py
Funkce realizující vykreslení dynamického systému; ústřední prvek celého „frameworku“:
from typing import Callable
from bitmap import create_bitmap, draw_bitmap
from pygame import Surface, image
def render_attractor(
surface: Surface,
x: float,
y: float,
scale: float,
x_offset: int,
y_offset: int,
max_points: int,
settle_down_points: int,
contrast: float,
attractor_formula: Callable,
filename: str,
**attractor_params: float
) -> None:
width, height = surface.get_size()
bitmap = create_bitmap(width, height)
for i in range(max_points):
x_dot, y_dot = attractor_formula(x, y, **attractor_params)
xi = width // 2 + int(scale * x_dot) + x_offset
yi = height // 2 + int(scale * y_dot) + y_offset
# try to draw pixel
if i > settle_down_points:
if xi >= 0 and yi >= 0 and xi < width and yi < height:
bitmap[yi][xi] += 1
# next point calculation
x, y = x_dot, y_dot
draw_bitmap(bitmap, surface, contrast)
image.save(surface, filename)
16. Ukázka skriptu pro vykreslení dynamického systému s využitím pomocných modulů
Takto jednoduše vypadá skript, který s využitím pomocných modulů z předchozí kapitoly vykreslí dynamický systém Svennson. Další dynamické systémy se vykreslují naprosto totožným způsobem:
from math import cos, sin
from typing import Tuple
from renderer import render_attractor
from ui import event_loop, initialize
# window settings
WINDOW_WIDTH = 800
WINDOW_HEIGHT = 600
WINDOW_TITLE = "Svensson dynamical system"
def svensson(
x: float, y: float, A: float, B: float, C: float, D: float
) -> Tuple[float, float]:
"""Calculate next point in the strange attractor."""
x_dot = D * sin(x * A) - sin(y * B)
y_dot = C * cos(x * A) + cos(y * B)
return x_dot, y_dot
def main() -> None:
# initialize user interface based on Pygame
display, surface, clock = initialize(WINDOW_TITLE, WINDOW_WIDTH, WINDOW_HEIGHT)
# redraw the whole dynamical system
render_attractor(
surface=surface,
x=0,
y=0,
scale=120.0,
x_offset=0,
y_offset=0,
max_points=1000000,
settle_down_points=10,
attractor_formula=svensson,
contrast=1 / 15.0,
filename="svensson.png",
A=-2.337,
B=-2.337,
C=0.533,
D=1.378,
)
# and enter the event loop
event_loop(display, surface, clock)
if __name__ == "__main__":
main()
17. Ukázky dynamických systémů

Obrázek 35: De Jongův systém.

Obrázek 36: Dynamický systém Fractal Dream.

Obrázek 37: Dynamický systém Gumowski Mira.

Obrázek 38: Dynamický systém Hopalong.

Obrázek 39: První dynamický systém Jasona Rampeho.
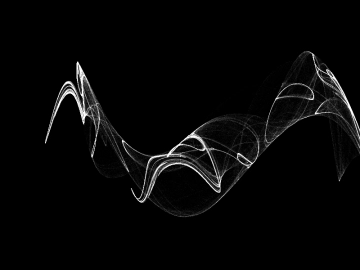
Obrázek 40: Druhý dynamický systém Jasona Rampeho.

Obrázek 41: Pickoverův dynamický systém.

Obrázek 42: Dynamický systém Quadruptwo.
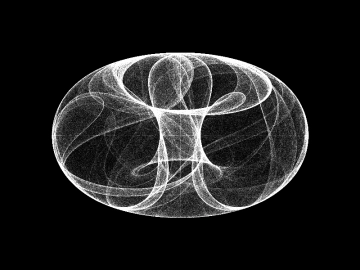
Obrázek 43: Dynamický systém Svensson.
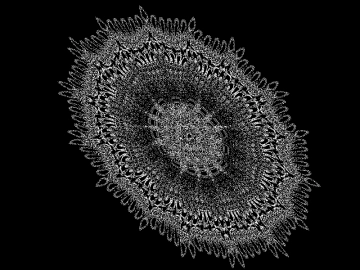
Obrázek 44: Dynamický systém Threeply.
18. Repositář s demonstračními příklady
Všechny skripty, které byly v předchozích kapitolách použity pro tvorbu obrázků a animací, jsou uloženy v Git repositáři dostupném na adrese https://github.com/tisnik/fractals/. Následují odkazy na jednotlivé příklady:
| # | Příklad | Stručný popis příkladu | Cesta ke zdrojovému kódu příkladu |
|---|---|---|---|
| 1 | Lorenz_x_y_z.py | zobrazení vývoje hodnot x, y a z v trojici samostatných grafů | https://github.com/tisnik/fractals/blob/master/attractors/3D/Lorenz_x_y_z.py |
| 2 | Lorenz.py | zobrazení fázového prostoru ve formě 3D grafu, popř. průmětů do vybraných rovin | https://github.com/tisnik/fractals/blob/master/attractors/3D/Lorenz.py |
| 3 | Lorenz_butterfly_effect.py | animace efektu motýlích křídel | https://github.com/tisnik/fractals/blob/master/attractors/3D/Lorenz_butterfly_effect.py |
| 4 | lorenz_change_params.py | vykreslení Lorenzova atraktoru s různými parametry s a r | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_change_params.py |
| 5 | lorenz_change_params_multiplot.py | vykreslení Lorenzova atraktoru s různými parametry s a r | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_change_params_multiplot.py |
| 6 | lorenz_change_params_anim.py | animace změny parametrů Lorenzova atraktoru | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_change_params_anim.py |
| 7 | lorenz_change_params_anim2.py | vylepšení animace změny atraktorů Lorenzova atraktoru | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_change_params_anim2.py |
| 8 | lorenz_2d_dynamic.py | Vliv počátečních podmínek na tvar Lorenzova systému, vykreslení do jediného grafu | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_2d_dynamic.py |
| 9 | lorenz_2d_dynamic_multiplot.py | Vliv počátečních podmínek na tvar Lorenzova systému, vykreslení do mřížky grafů | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_2d_dynamic_multiplot.py |
| 10 | Lorenz-mod-2.py | modifikovaný Lorenzův atraktor | https://github.com/tisnik/fractals/blob/master/attractors/3D/Lorenz-mod-2.py |
| 11 | Pickover.py | Pickoverův atraktor | https://github.com/tisnik/fractals/blob/master/attractors/3D/Pickover.py |
| 12 | Rossler.py | Rösslerův atraktor | https://github.com/tisnik/fractals/blob/master/attractors/3D/Rossler.py |
| 13 | Wang-Sun.py | Wang-Sunův atraktor | https://github.com/tisnik/fractals/blob/master/attractors/3D/Wang-Sun.py |
| 14 | lorenz_map.py | výpočet a zobrazení mapy Lorenzova atraktoru | https://github.com/tisnik/fractals/blob/master/attractors/3D/lorenz_map.py |
| 15 | rossler_map.py | výpočet a zobrazení mapy Rösslerova atraktoru | https://github.com/tisnik/fractals/blob/master/attractors/3D/rossler_map.py |
| 16 | Bedhead.py | atraktor nazvaný Bedhead s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Bedhead.py |
| 17 | De_jong.py | De Jongům atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/De_jong.py |
| 18 | Dynamic.py | atraktor nazvaný Dynamic s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Dynamic.py |
| 19 | Fractal_dream.py | atraktor nazvaný Fractal Dream s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Fractal_dream.py |
| 20 | Gumowski-Mira.py | atraktor autorů Gumowski a Mira s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Gumowski-Mira.py |
| 21 | Hopalong.py | atraktor nazvaný Hopalong s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Hopalong.py |
| 22 | Icon.py | atraktor nazvaný Icon s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Icon.py |
| 23 | JasonRampe1.py | první dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/JasonRampe1.py |
| 24 | JasonRampe2.py | druhý dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/JasonRampe2.py |
| 25 | JasonRampe3.py | třetí dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/JasonRampe3.py |
| 26 | Kam_Torus.py | atraktor nazvaný Kam Torus s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Kam_Torus.py |
| 27 | Pickover.py | Pickoverův atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pickover.py |
| 28 | Quadruptwo.py | atraktor nazvaný Quadruptwo s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Quadruptwo.py |
| 29 | Svensson.py | Svenssoneův atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Svensson.py |
| 30 | Threeply.py | atraktor nazvaný Threeply s 2D fázovým prostorem, vykresleno přes knihovnu Matplotlib | https://github.com/tisnik/fractals/blob/master/attractors/2D/Threeply.py |
| 31 | Bedhead.py | atraktor nazvaný Bedhead s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Bedhead.py |
| 32 | De_jong.py | De Jongům atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/De_jong.py |
| 33 | Fractal_dream.py | atraktor nazvaný Fractal Dream s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Fractal_dream.py |
| 34 | Gumowski-Mira.py | atraktor autorů Gumowski a Mira s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Gumowski-Mira.py |
| 35 | Hopalong.py | atraktor nazvaný Hopalong s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Hopalong.py |
| 36 | JasonRampe1.py | první dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/JasonRampe1.py |
| 37 | JasonRampe2.py | druhý dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/JasonRampe2.py |
| 38 | JasonRampe3.py | třetí dynamický systém Jasona Rampeho s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/JasonRampe3.py |
| 39 | Pickover.py | Pickoverův atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Pickover.py |
| 40 | Quadruptwo.py | atraktor nazvaný Quadruptwo s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Quadruptwo.py |
| 41 | Svensson.py | Svenssoneův atraktor s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Svensson.py |
| 42 | Threeply.py | atraktor nazvaný Threeply s 2D fázovým prostorem, vykresleno přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/Threeply.py |
| 43 | bitmap.py | pomocný modul pro manipulaci s bitmapami, jejich normalizaci atd. | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/bitmap.py |
| 44 | colors.py | pomocný modul se jmény barev | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/colors.py |
| 45 | ui.py | pomocný modul s funkcemi pro vytvoření jednoduchého uživatelského rozhraní přes knihovnu Pygame | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/ui.py |
| 46 | renderer.py | pomocný modul s funkcí pro vykreslení dynamického systému v 2D ploše | https://github.com/tisnik/fractals/blob/master/attractors/2D/Pygame/renderer.py |
20. Odkazy na Internetu
- The Lorenz Attractor by Dr. Bruce Stewart
https://www.youtube.com/watch?v=YS_xtBMUrJg - Welcome – Dynamical Systems | Intro Lecture
https://www.youtube.com/watch?v=41P4vFP7RWo - The Lorenz Equations – Dynamical Systems | Lecture 27
https://www.youtube.com/watch?v=0Rpy-xSsAo8 - Phase space
https://en.wikipedia.org/wiki/Phase_space - Fázový prostor
https://cs.wikipedia.org/wiki/F%C3%A1zov%C3%BD_prostor - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-vi/#k02 - Lorenzův atraktor
https://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Lorenz system
https://en.wikipedia.org/wiki/Lorenz_system - The Lorenz system – An introduction to chaos
https://www.math.toronto.edu/kzhang/teaching/courses/mat332–2022/_8-lorenz-system/ - Dynamical system
https://en.wikipedia.org/wiki/Dynamical_system - What are Dynamical Systems?
https://math.libretexts.org/Bookshelves/Scientific_Computing_Simulations_and_Modeling/Introduction_to_the_Modeling_and_Analysis_of_Complex_Systems_(Sayama)/03%3A_Basics_of_Dynamical_Systems/3.01%3A_What_are_Dynamical_Systems%3F - TEACHING MATHEMATICS WITH A HISTORICAL PERSPECTIVE: Lecture 11: Dynamical systems
https://abel.math.harvard.edu/~knill/teaching/mathe320_2022/handouts/10-dynamics.pdf - Emergence (Wikipedia CS)
https://cs.wikipedia.org/wiki/Emergence - Emergence (Wikipedia EN)
https://en.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Self-organization
https://en.wikipedia.org/wiki/Self-organization - Samoorganizace
https://cs.wikipedia.org/wiki/Samoorganizace - Spontaneous order
https://en.wikipedia.org/wiki/Spontaneous_order - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Rössler attractor
https://en.wikipedia.org/wiki/R%C3%B6ssler_attractor - Rossler attractor
http://scholarpedia.org/article/Rossler_attractor - List of chaotic maps
https://en.wikipedia.org/wiki/List_of_chaotic_maps - Wolfram MathWorld: Rössler attractor
https://mathworld.wolfram.com/RoesslerAttractor.html - Wolfram MathWorld: Lorenz attractor
https://www.wolframalpha.com/input?i=Lorenz+attractor&assumption=%22ClashPrefs%22±%3E+%7B%22MathWorld%22%2C+%22LorenzAttractor%22%7D - Attracteur de Rössler (interaktivní, lze používat i bez znalosti jazyka)
https://experiences.mathemarium.fr//Attracteur-de-Rossler.html - A 3-D four-wing attractor | Wang Sun attractor| Chaos Theory
https://www.youtube.com/watch?v=Agx8LsMmokA - This is not a Lorenz attractor | Sprott C attractor| Chaos Theory
https://www.youtube.com/watch?v=NoFkOwsT0XQ





































