OpenGL a nadstavbová knihovna GLU (10)

Obsah

1. Homogenní souřadnice
2. Parametrická reprezentace křivek a ploch
3. Lineární interpolace bodů
4. Lineární interpolace/kom­binace funkcí
5. Praktická ukázka lineární interpolace funkcí
6. Demonstrační příklady
7. Obsah dalšího pokračování
8. Seznam funkcí OpenGL a GLUT zmíněných v této části
9. Zkomprimovaná verze článku i s přílohami
 

1. Homogenní souřadnice

V dalším textu (zejména v následující části tohoto seriálu) budu často používat pojem homogenní souřadnice. I když se jedná o pojem v 3D počítačové grafice velmi často zmiňovaný, nebude myslím na škodu si jeho význam zopakovat, aby byl další text pochopitelný.

Pro snažší provádění všech lineárních transformací bodů a vektorů v prostoru je vhodné všechny body (včetně koncových bodů úseček a vektorů) specifikovat ve čtyřrozměrném prostoru, přičemž poslední souřadnice (označovaná písmenem w) je nastavena na hodnotu 1.0 pro body a 0.0 pro vektory. Poslední, tj. čtvrtá souřadnice se podle své úlohy při výpočtech nazývá váha (weight – z toho vyplývá i její jednopísmenné označení). Po tomto rozšíření původních 3D souřadnic do 4D prostoru je možné pro specifikaci lineárních transformací a současně i perspektivní projekce používat transformační matice o velikosti 4×4 prvky.

Při provádění perspektivní projekce, která se v 4D chová jako běžná lineární transformace, po provedení transformace je pouze nutné zachovat poslední souřadnice bodů na jedničce, což se provádí pomocí následujícího algoritmu:

1. Nejprve se musí načíst souřadnice bodu, jež jsou specifikované v běžném trojrozměrném prostoru, tj. X_3D=(x,y,z).
2. Poté se načte transformační matice M, která má velikost 4×4 prvky. Pomocí této matice může být specifikována libovolná lineární transformace (otáčení, změna měřítka, zkosení a jejich kombinace) i perspektivní projekce.
3. Následně je nutné zvolit váhu bodu či vektoru. Jak již bylo napsáno výše, pro body je (z více rozumných důvodů) zvolena váha 1, tj. w=1.0, pro vektory je váha nulová, tj. w=0.0. V dalším textu nás však budou zajímat transformace bodů se zadanou vahou, takže w nemusí být vždy nutně jednotkové.
4. Souřadnice bodu X_3D=(x, y, z) se převedou do homogenních souřadnic velmi snadno: X_4D=(wx, wy, wz, w), tj. každá souřadnice je vynásobena zvolenou vahou a za čtvrtou souřadnici je zvolena samotná váha.
5. Nyní je možné přistoupit k samotné transformaci v homogenním 4D prostoru. Tato transformace se provádí stejně jako v ploše či 3D prostoru, pouze je rozšířena transformační matice M na velikost 4×4 prvky:
   X'_4D=(x', y', z', w')=(wx, wy, wz, w)M^T.
   Poznámka: v literatuře se tato transformace uvádí nad sloupcovými vektory, vzhledem k omezení HTML jsem ji však popsal nad řádkovými vektory. Z toho důvodu je i transformační matice transponovaná a uvedená „za“ multiplikativní operací.
6. Před zobrazením se provede zpětná konverze bodu z homogenních souřadnic do 3D prostoru následovně:
   X'_3D=(x'/w', y'/w', z'/w'), tj. každá souřadnice se vydělí vahou, která může vzhledem k provedené transformaci nabývat libovolné (ale nenulové) hodnoty.

2. Parametrická reprezentace křivek a ploch

Již v minulé části tohoto seriálu jsme si uvedli, že v počítačové grafice je zcela běžné reprezentovat netriviální tvary (křivky a plochy) parametricky, tj. jednou bodovou rovnicí nebo sekvencí bodových rovnic. Pro jednoduchost dnes začneme popisovat NURB křivky, které jsou na vysvětlení poněkud jednodušší než NURB plochy/pláty, protože se v rovnicích pro křivky vyskytuje menší počet parametrů a křivky jsou také snáze zobrazitelné.

Parametrická křivka je vytvořena z nekonečné množiny bodů {r(t)}, jejichž poloha v ploše či prostoru se mění v závislosti na změně parametru t, který nabývá hodnot z předem známého rozsahu odt_min do t_max, tj.:

r(t)=∑_i=1ⁿP_if_i(t)

kde n značí celkový počet řídících bodů, P_i je poloha i-tého řídícího bodu a f_i(t) je takzvanábázová funkce. V případě použití Bézierových křivek je za bázovou funkci zvolen Bernsteinův polynom, u NURB křivek se však jedná o podstatně složitější výrazy založené na opakované lineární kombinaci/inter­polaci funkcí. Tyto výrazy se u NURBS nazývají normalizované bázové funkce (normalizované vzhledem k jejich maximální hodnotě), nebo též de Boorovy funkce.

3. Lineární interpolace bodů

Základ bázové funkce, která se používá u NURB křivek a ploch, spočívá v opakovaném použití lineární interpolace. Lineární interpolací lze jednoduše vyjádřit postupný pohyb bodu X z místa A do místa B, který je závislý na hodnotě parametru t:

X=(1-t)A+tB

kde jediný parametr t může nabývat reálných hodnot v rozsahu 0.0–1.0. Pohyb bodu X při lineární interpolaci je patrný z nákresu zobrazeného na prvním ilustračním obrázku.

Obrázek 1: Pohyb bodu X v závislosti na hodnotě parametru t

Z předchozího vztahu je také patrná i jeho další interpretace: poloha bodu X je vypočtena na základě barycentrické kombinace dvou bodů A a B (také lze tento vztah interpretovat jako lineární kombinaci dvou bázových vektorů a=A-0 ab=B-0, což je v podstatě to samé). Barycentrická kombinace však není omezena pouze pro dva body, je ji možné provádět pro libovolný počet bodů. Z tohoto důvodu lze polohu bodu X vyjádřit jako barycentrickou kombinaci n bodů {X₁…X_n}:

X=∑_i=1ⁿX_it_i

přičemž musí platit vztah:

∑_i=1ⁿt_i=1

který mimo jiné zajistí, že nově vypočtený bod X leží v konvexní obálce bodů X_i, podobně jako tomu bylo u Bézierových křivek a jejich řídících bodů.

4. Lineární interpolace/kom­binace funkcí

V předchozím odstavci jsme si ukázali, jakým způsobem lze provádět interpolaci dvou bodů A a B. Ve skutečnosti však lze interpolaci zobecnit i na funkce, tj. interpolace nemusí být prováděna pouze mezi dvěma či více body, ale přímo mezi funkcemi. Výsledkem interpolace je nová funkce, přičemž pro dále uváděné funkce platí tvrzení: Každá funkce může být vyjádřena pomocí kombinace bázových funkcí. Ukažme si tu nejjednodušší lineární interpolaci dvou libovolných funkcí f₁ a f₂ v závislosti na parametru t:

f(t)=(1-t)f₁(t)+tf₂(t)

Základem pro práci s NURB křivkami a plochami jsou jednoduché delta funkce:

b_i⁰(t)=1 pro t_i<=t<t_i+1, jinak 0

přičemž hodnoty t_i a t_i+1 musí být zvoleny tak, že t₁<t_i+1. Jak si ukážeme dále, tyto hodnoty jsou ve vzestupném pořadí uloženy do uzlového vektoru (knot vektoru). Všimněte si, že u takto definovaných funkcí žádné jiné omezení pro hodnoty parametrů t neexistuje, na rozdíl od Bernsteinových polynomů, kde mělo smysl používat pouze hodnoty z rozsahu 0–1.

Poznámka: výše zmíněná delta funkce je často v literatuře označována: N_i⁰.

5. Praktická ukázka lineární interpolace funkcí

Ukažme si nyní v praxi, jak bude lineární interpolace funkcí pracovat. Nejprve definujme hodnoty uzlového vektoru (knot vector), které musí tvořit neklesající posloupnost:

// uzlový vektor
float knot[]={0,1,2,3};

Dále definujme funkci b0(), která pro libovolnou hodnotu parametru t a dvě zadané složky uzlového vektoru (specifikované jedním parametrem, protože se nachází v sousedství) vrátí hodnotu 1, pokud je parametr t v rozsahu specifikovaném hodnotami v uzlovém vektoru. Pokud leží hodnota parametru t mimo daný rozsah, vrátí funkce b0()nulovou hodnotu:

float b0(const float t, const int i)
{
    if ((knot[i]<=t)&&(t<knot[i+1]))
        return 1.0f;
    else
        return 0.0f;
}

C-čkovská funkce pro názorné vykreslení průběhů funkce b0() může vypadat následovně:

void onDisplay(void)
{
    float d,f,x,y;
    int i;

    // smazání obrazovky
    glClear(GL_COLOR_BUFFER_BIT);

    // vykreslit čtyři průběhy
    for (i=0; i<4; i++) {
        // začátek kresby lomené čáry
        glBegin(GL_LINE_STRIP);
        for (d=0; d<4; d+=0.05) {
            // výpočet x-ové souřadnice
            x=50+80.0*d;
            f=b0(d, i);
            y=100*i+80-60.0*f;
            // výpočet y-ové souřadnice
            glVertex2f(x,y);
        }
        glEnd();
    }
    glFlush();
}

Jak je z výše uvedeného kódu patrné, jsou vykresleny celkově čtyři průběhy, z nichž každý odpovídá dvojici sousedních složek uzlového vektoru. Ukázka grafického výstupu této funkce je zobrazena na druhém obrázku:

Obrázek 2: Průběh funkce b0()

Nyní můžeme přistoupit k vlastní interpolaci. Definujme funkci b1()tak, aby v závislosti na indexu do uzlového vektoru a parametru t prováděla interpolaci funkce b0:

float b1(const float t, const int i)
{
    float   p,a,b;

    a=(t-knot[i]);
    b=(knot[i+1]-knot[i]);
    if (b==0)   p=0.0;
    else        p=b0(t,i)*a/b;

    a=(knot[i+2]-t);
    b=(knot[i+2]-knot[i+1]);
    if (b==0)   p+=0.0;
    else        p+=b0(t,i+1)*a/b;

    return  p;
}

Pokud pomineme mezní stavy, kdy je b rovno nule (tj. kdy jsou dvě sousední položky knot vektoru stejné), jedná se o klasickou lineární interpolaci funkce b0() v závislosti na dvou hodnotách uzlového vektoru a parametru t. Průběh interpolované funkce je zobrazen na třetím obrázku:

Obrázek 3: Průběh funkce b1()

To však není zdaleka vše, protože v interpolaci lze pokračovat tak, že se tentokrát bude provádět s nově vzniklou funkcí b1(). Průběh této nové funkce je již zajímavější, protože se původní „rampy“ (části průběhu funkce s konstantní směrnicí) interpolují spolu s konstantními částmi, a vzniká tak průběh podobný průběhu Bernsteinových polynomů použitých u Bézierových křivek. Vzniklá funkce/křivka má spojité i své první derivace, což u funkcí b0() a b1() neplatilo:

float b2(const float t, const int i)
{
    float   p,a,b;

    a=(t-knot[i]);
    b=(knot[i+2]-knot[i]);
    if (b==0)   p=0.0;
    else        p=b1(t,i)*a/b;

    a=(knot[i+3]-t);
    b=(knot[i+3]-knot[i+1]);
    if (b==0)   p+=0.0;
    else        p+=b1(t,i+1)*a/b;

    return  p;
}

Obrázek 4: Průběh funkce b2()

Při práci s NURB křivkami a plochami se většinou požaduje geometrická spojitost druhého stupně. Té se dosáhne použitím bázové funkce b3(), jež vzniká lineární interpolací funkce b2(). Způsob vytvoření této funkce je stejný jako způsob vytvoření funkce b2() s tím, že se opět musí ošetřit stav, kdy jsou hodnoty uzlového vektoru v určitém intervalu konstantní:

float b3(const float t, const int i)
{
    float   p,a,b;

    a=(t-knot[i]);
    b=(knot[i+3]-knot[i]);
    if (b==0)   p=0.0;
    else        p=b2(t,i)*a/b;

    a=(knot[i+4]-t);
    b=(knot[i+4]-knot[i+1]);
    if (b==0)   p+=0.0;
    else        p+=b2(t,i+1)*a/b;

    return  p;
}

Obrázek 4: Průběh funkce b3()

6. Demonstrační příklady

První demonstrační příklad ukazuje programový výpočet a vykreslení výše zmíněné funkce b0(), která tvoří základ pro výpočet dalších funkcí. Funkce b0() je přitom představována jednoduchou delta funkcí. Klávesou ESC je možné program ukončit.

Zdrojový kód prvního demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

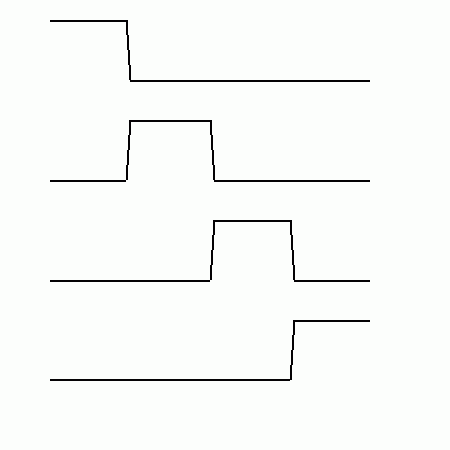
Obrázek 6: Screenshot prvního demonstračního příkladu

Druhý demonstrační příklad navazuje na příklad první s tím rozdílem, že zobrazuje průběh funkce b1(), která je lineární interpolací vypočtena ze základní funkce b0(), a má tak trojúhelníkový průběh.

Zdrojový kód druhého demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 7: Screenshot druhého demonstračního příkladu

Po spuštění třetího příkladu se zobrazí průběh funkce b2(), který je získán lineární interpolací funkce b1(). Interpolací trojúhelníkového tvaru funkce b1() je již získána hladká funkce bez skokové změny derivace.

Zdrojový kód třetího demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 8: Screenshot třetího demonstračního příkladu

Čtvrtý a poslední příklad po svém spuštění zobrazí průběh funkce b3(). Všimněte si nutnosti specifikace delšího uzlového vektoru.

Zdrojový kód čtvrtého demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 9: Screenshot čtvrtého demonstračního příkladu

7. Obsah dalšího pokračování

V dalším pokračování tohoto seriálu si popíšeme funkce, které nám nadstavbová knihovna GLU nabízí pro zjednodušení práce s NURB křivkami.

8. Seznam funkcí OpenGL a GLUT zmíněných v této části

glBegin()
glEnd()
glVertex2f()
glFlush()
 

9. Zkomprimovaná verze článku i s přílohami

Zkomprimovaná verze tohoto článku i s přílohami a demonstračními příklady je uložena zde.