OpenGL a nadstavbová knihovna GLU (19)

Obsah

1. Význam teselátorů a teselace

Grafická knihovna OpenGL obsahuje pouze ty funkce, které jsou jednoduše implementovatelné na současných grafických akcelerátorech založených na lineárních interpolátorech a rastrovém framebufferu – bližší informace jsou uvedeny v seriálu o OpenGL [OpenGL III] [OpenGL IV] [OpenGL XII]. Z tohoto důvodu je také možné pomocí funkcí nabízených knihovnou OpenGL vykreslovat pouze deset základních tvarů (grafických či též geometrických primitiv), mezi něž patří:

1. izolované body – GL_POINTS
2. úsečky – GL_LINES
3. lomené úsečky (polyčáry) – GL_LINE_STRIP
4. uzavřené lomené úsečky (uzavřené polyčáry) – GL_LINE_LOOP
5. samostatné trojúhelníky – GL_TRIANGLES
6. trs trojúhelníků – GL_TRIANGLE_FAN
7. pruh trojúhelníků – GL_TRIANGLE_STRIP
8. samostatné plošné konvexní čtyřúhelníky – GL_QUADS
9. pruh plošných konvexních čtyřúhelníků – GL_QUAD_STRIP
10. plošné konvexní polygony bez degenerovaných vrcholů a děr – GL_POLYGON

Tato grafická primitiva jsou, spolu se svými symbolickými jmény v grafické knihovně OpenGL, uvedena na následujících deseti ilustračních obrázcích. Symbolické jméno je použito například ve funkci glBegin(), kterým se specifikuje začátek vykreslování daného základního tvaru či tvarů.

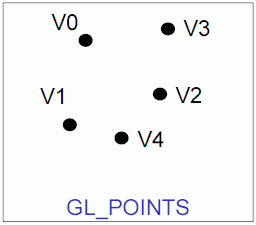
Obrázek 1: Grafická primitiva GL_POINTS

Obrázek 2: Grafická primitiva GL_LINES

Obrázek 3: Grafické primitivum GL_LINE_STRIP

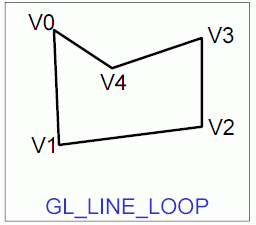
Obrázek 4: Grafická primitiva GL_LINE_LOOP

Obrázek 5: Grafická primitiva GL_TRIANGLES

Obrázek 6: Grafické primitivum GL_TRIANGLE_FAN

Obrázek 7: Grafické primitivum GL_TRIANGLE_STRIP

Obrázek 8: Grafická primitiva GL_QUADS

Obrázek 9: Grafické primitivum GL_QUAD_STRIP

Obrázek 10: Grafické primitivum GL_POLYGON

Jednoduchý příklad na vykreslení všech deseti primitiv je uveden také v dnešní demonstrační aplikaci.

Z výše uvedeného seznamu grafických primitiv OpenGL je patrné, že ani knihovna OpenGL ani samotný grafický akcelerátor nepodporují vykreslování obecných polygonů. Toto chování vyplývá z principu práce rasterizační jednotky grafického akcelerátoru, která provádí rasterizaci a následné vykreslování po jednotlivých řádcích (scanlines) framebufferu.

V některých aplikacích pro tvorbu komplikovaných modelů se však používají i složitější formy polygonálních stěn – buď se jedná o nekonvexní polygony, polygony s otvory, nebo o polygony, na kterých se nachází vícenásobné vrcholy (tj. polygony obsahují tzv. degenerované hrany). Na dalším obrázku jsou zobrazeny polygony, které lze v OpenGL přímo vykreslit, a současně i polygony, které vykreslit nelze. Korektně zadané polygony mají modrou hranici, nekorektní polygony mají hranici červenou.

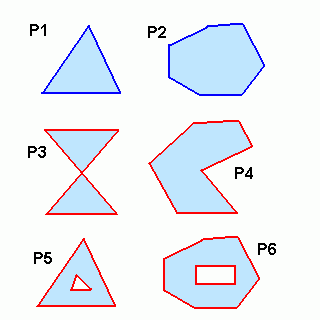
Obrázek 11: Korektně a nekorektně zadané polygony pro OpenGL

Z výše uvedených důvodů je vhodné, aby měli vývojáři grafických aplikací založených na OpenGL k dispozici vhodný nástroj pro převod obecných polygonů do formy vhodné pro vykreslování. Tento nástroj, který v OpenGL samozřejmě chybí, je dostupný až v nadstavbové knihovně GLU a nazývá se podle své funkce teselátor.

2. Základní funkce teselace a teselátorů

Teselace je proces, pomocí kterého se obecný polygon převádí na nepravidelnou trojúhelníkovou síť (TIN – triangular irregular network). Někdy se teselace chybně zaměňuje striangulací, oba procesy jsou však rozdílné, protože pomocí triangulace se trojúhelníková síť vytváří nad množinou původně izolovaných bodů v ploše či prostoru.

Teselátory pracují následujícím způsobem: pomocí specializovaných funkcí z knihovny GLU získají specifikaci takzvaného jednoduchého polygonu (u novějších verzí knihovny GLU však téměř jakéhokoli plošného polygonu) a po provedení teselace vrátí seznam grafických primitiv (trojúhelníků či trsů a pruhů trojúhelníků), které je již možné pomocí funkcí OpenGL přímo vykreslit.

Volba použitých výstupních grafických primitiv záleží na vývojářových preferencích. V jednoduchých aplikacích lze používat pouze trojúhelníky, použití trsů a pruhů trojúhelníků naopak zvyšuje výkonnost celé aplikace, protože se do grafického akcelerátoru přenáší menší počet vertexů.

Zbývá říci, co je to jednoduchý polygon. Polygon je, alespoň v podání knihovny GLU, jednoduchý v případě, že splňuje následující podmínky:

1. vrcholy a hrany polygonu leží v jedné rovině; před teselací se totiž všechny předávané vrcholy promítají do roviny
2. hrany polygonu se protínají pouze ve vrcholech a nikde jinde
3. polygon neobsahuje vícenásobné vrcholy (tzv. degenerované hrany)
4. vždy dvě hrany se setkávají v jednom vrcholu

Jednoduchý polygon nemusí být konvexní a může obsahovat i díry, které ovšem musí být vytvořeny tak, aby jejich specifikace neodporovala předchozím čtyřem podmínkám. Novější verze knihovny GLU už striktně nevyžadují pouze jednoduché polygony, zvládnou teselovat i polygony složitější, například s degenerovanými hranami apod.

3. Postup při použití teselátorů

Postup při teselaci polygonů je poměrně složitý, protože kromě vlastního zadávání jednotlivých polygonů je nutné správně reagovat na data poslaná do callback funkcí. Mimoto se každý polygon vytváří z několika kontur, takže celkový počet volaných funkcí je poměrně velký. Celý postup lze stručně shrnout do několika bodů:

1. vytvoření objektu pro teselaci
2. registrace callback funkce volané při automatickém vytvoření dalšího vrcholu, hrany či celého trojúhelníka
3. začátek zadávání nového polygonu
4. specifikace jedné nebo několika kontur, ze kterých se polygon skládá
5. konec zadávání polygonu
6. zrušení objektu pro teselaci

4. Funkce používané pro teselaci

V knihovně GLU je k dispozici několik funkcí, pomocí nichž se teselace provádí. V tomto dílu seriálu si používané funkce pouze vypíšeme, v dílech následujících bude uveden i jejich podrobnější popis.

gluBeginPolygon()
gluDeleteTess()
gluEndPolygon()
gluGetTessPro­perty()
gluNewTess()
gluNextContour()
gluTessBeginCon­tour()
gluTessBeginPo­lygon()
gluTessCallback()
gluTessEndContour()
gluTessEndPolygon()
gluTessNormal()
gluTessProperty()
gluTessVertex()

Některé výše zmíněné funkce jsou zastaralé, a proto jsou nahrazeny funkcemi novějšími. Příkladem může být například dvojice funkcí gluBeginPolygon() a gluTessBeginPo­lygon() nebogluEndPolygon() a gluTessEndPoly­gon().

Postup při teselaci popsaný v předchozí kapitole můžeme stručně zapsat pomocí funkcí knihovny GLU. V dalším pokračování bude zde uvedený příklad rozvinut do použitelné podoby.

// vytvoření nového objektu pro teselaci
gluNewTess();

    // registrace callback funkcí
    gluTessCallback();

    // začátek specifikace nového polygonu
    gluTessBeginPolygon();

        // začátek specifikace kontury,
        // jež je součástí polygonu
        gluTessBeginContour();

            // jeden vrchol kontury
            gluTessVertex();
            // další vrchol kontury
            gluTessVertex();
            // atd. až po zadání všech vrcholů

        // konec specifikace kontury
        gluTessEndContour();

        // začátek specifikace další kontury
        gluTessBeginContour();
            // opět následuje množina vrcholů
            gluTessVertex();
            gluTessVertex();
            ...
        gluTessEndContour();

    // konec specifikace nového polygonu
    gluTessEndPolygon();

// smazání objektu pro teselaci
gluDeleteTess();

Každý polygon musí obsahovat alespoň jednu konturu. Kontura musí tvořit hranici nenulové plochy, tj. musí být zadána alespoň trojicí vrcholů, které v tomto případě nemohou ležet v jedné přímce, ale musí tvořit trojúhelník. Maximální počet vrcholů kontury není normou OpenGL GLU omezen (v konkrétní implementaci však nějaké omezení může být aplikováno), stejně jako není obecně omezen počet kontur, ze kterých se polygon skládá.

V některých aplikacích se můžeme setkat i se staršími verzemi funkcí pro teselaci. Následuje příklad, který tyto funkce používá. V dalších textech se však budeme zabývat výhradně funkcemi, které nejsou zastaralé:

// vytvoření nového objektu pro teselaci
gluNewTess();

    // registrace callback funkcí
    gluTessCallback();

    // začátek specifikace nového polygonu
    gluTessBeginPolygon();

            // jeden vrchol kontury
            gluTessVertex();
            // další vrchol kontury
            gluTessVertex();
            // atd. až po zadání všech vrcholů

        // začátek specifikace další kontury
        gluNextContour();

            // jeden vrchol kontury
            gluTessVertex();
            // další vrchol kontury
            gluTessVertex();
            // atd. až po zadání všech vrcholů

        // začátek specifikace další kontury
        gluNextContour();
            gluTessVertex();
            gluTessVertex();
            gluTessVertex();

    // konec specifikace nového polygonu
    gluTessEndPolygon();

// smazání objektu pro teselaci
gluDeleteTess();

5. Obsah dalšího pokračování

V dalším pokračování tohoto seriálu si ukážeme postup, pomocí kterého lze provádět teselaci jednoduchých (konvexních i nekonvexních) polygonů.

6. Demonstrační příklad

Nyní ještě nemáme dostatek informací pro praktické provádění vlastní teselace, proto jsou v dnešním demonstračním příkladu připomenuta všechna grafická primitiva, se kterými může OpenGL pracovat. Po překladu a spuštění tohoto demonstračního příkladu se v okně aplikace nakreslí grafická primitiva OpenGL a program čeká na stisknutí klávesy ESC.

Zdrojový kód tohoto demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 12: Screenshot demonstračního příkladu

7. Zkomprimovaná verze článku i s přílohami

Zkomprimovaná verze tohoto článku i s přílohami, demonstračním příkladem a obrázky je uložena zde.