OpenGL a nadstavbová knihovna GLU (6)

Obsah

1. Co značí pojem kvadrika?
2. Podpora práce s kvadrikami v knihovně GLU
3. Rozdíl mezi podporou kvadrik v knihovnách GLU a GLUT
4. Postup pro vytvoření a zobrazení kvadrik
5. Kompatibilita se staršími verzemi knihovny GLU
6. Demonstrační příklady
7. Obsah dalšího pokračování
8. Seznam funkcí OpenGL a GLUT zmíněných v této části
9. Nové funkce z knihovny GLU popsané v této části
10. Zkomprimovaná verze článku i s přílohami
11. Literatura, od­kazy

1. Co značí pojem kvadrika?

Před popisem funkcí z knihovny GLU, které umožňují práci s kvadrikami si nejdříve řekněme, co to vlastně kvadrika je. Pojmem kvadrika se v matematice a přeneseně i v počítačové grafice označují trojrozměrná tělesa, jejichž povrch (plocha) je určena implicitní funkcí ve tvaru:

f(x, y, z)=0

kde implicitní funkce f(x, y, z) nabývá tvaru:

f(x, y, z) = a₁x² + a₂y² + a₃z² + a₄xy + a₅yz + a₆xz + a₇x + a₈y + a₉z + a₁₀

(jinými slovy – jedná se, podle nejvyšší použité mocniny, o algebraické plochy druhého stupně).

To znamená, že pro zadané parametry implicitní plochy a₁-a₁₀ je možné zjistit, zda bod P=[x, y, z] leží, či neleží na ploše kvadriky. Podle znaménka výsledku funkce f(x, y, z) lze dokonce zjistit, zda bod leží uvnitř, či vně kvadriky – to samozřejmě platí pouze pro uzavřené plochy, nikoli plochy nekonečné, jako jehyperboloid. Pro některé hodnoty parametrů je výše zmíněná rovnice v oboru reálných čísel neřešitelná (tj. neexistují takové hodnoty x, y, z, pro které by funkce f nabývala nuly), proto takovou kvadriku nelze sestrojit.

Mezi nejznámnější a nejpoužívanější kvadriky v matematice patří:

• Elipsoid: x²/a²+y²/b²+z­²/c²-1=0(uvádím nejpoužívanější tvar rovnice, převod na výše zmíněný formát je triviální).
• Hyperboloid: x²/a²+y²/b²-z²/c²=+-1.
• Paraboloid: x²/p+-y²/q=2z.

Speciálním případem elipsoidu je koule,válec lze získat dosazením vhodných hodnot do implicitní rovnice hyperboloidu. Takto získaný válec je nekonečný, tj. neobsahuje obě „víčka“, ale pouze plášť.

Kvadriky se často používají v CAD a CAM aplikacích, kde se z nich (a případně i z dalších tvarů – roviny, poloprostoru a toroidu) vytvářejí složitější tělesa pomocí konstruktivní geometrie těles – Constructive Solid Geometry – CSG.

Většina programů pro fotorealistické zobrazování scén pomocí raytracingu také CSG (a tím pádem i kvadriky, alespoň ty základní) využívá. Z této kategorie programů je pro Linux i pro další platformy – včetně Amigy, SGI a Sunu – dostupný volně šiřitelný raytracer POVRay, o kterém možná také napíšu nějaké informace. V tomto článku pouze ukážu obrázky kvadrik vykreslené pomocí POVRaye:

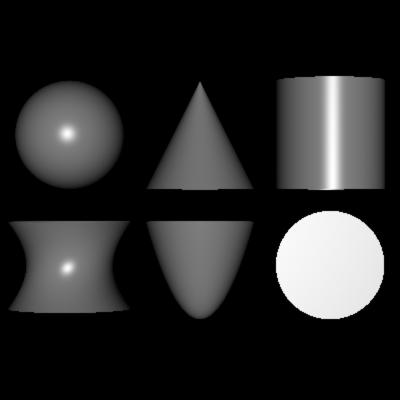
Obrázek 1: Základní typy kvadrik

Pokud se vrátíme zpět ke knihovnám GLU a OpenGL, je nutné říct, že GLU neumožňuje vytvářet všechny možné kvadriky, ale pouze ty nejzákladnější: koule a válce (resp. kužele, válce jsou v pojetí GLU speciálním případem kuželů). K tomu lze vytvářet i disky (plošné těleso) a jejich výřezy, což se hodí zejména pro uzavírání různých „děr“ ve vznikajícím modelu tělesa.

2. Podpora práce s kvadrikami v knihovně GLU

S kvadrikami lze za pomocí některých funkcí obsažených v nadstavbové knihovně GLU velmi jednoduše pracovat, protože jsou přímo podporovány objekty (z hlediska OOP), pomocí nichž je možné základní kvadriky vytvářet i vykreslovat. Mezi základní kvadriky jsou, jak jsem se již zmínil o odstavec výše, zahrnuta prostorová tělesa ve tvaru koule, válce a kužele. Taktéž je možné pracovat s plošným tělesem ve tvaru disku.

Složitější kvadriky, mezi něž patří různé hyperboloidy, paraboloidy, sedlové plochy atd., je možné vytvořit buď pomocí programově spočítané trojúhelníkové sítě, nebo pomocí NURBS ploch, kterými se v tomto seriálu budu v dalších částech také zabývat.

3. Rozdíl mezi podporou kvadrik v knihovnách GLU a GLUT

Pokud jste sledovali seriál o knihovně GLUT, který taktéž vycházel na Rootu (viz odkazy na konci článku), určitě jste si všimli, že i v této knihovně se vyskytují funkce, pomocí kterých je možné některé kvadriky vytvořit. Konkrétně se jedná o funkceglutSo­lidSphere(), glutWireSphere(), glutSolidCone() a glutWireCone(), pomocí nichž je možné vytvořit objekt koule či kužele (válec není podporován).

Tyto funkce z knihovny GLUT jsou sice jednoduché, ale neposkytují veškerou funkcionalitu funkcí z knihovny GLU – není například možné generovat texturovací souřadnice, pouze se používají normálové vektory. Z toho důvodu jsou funkce GLU mnohem použitelnější, i když poněkud složitější na použití, což bude patrné z dalšího textu a především z demonstračních příkladů uvedených v tomto a následujícím pokračování.

4. Postup pro vytvoření a zobrazení kvadrik

Pro vytvoření a následné vykreslení kvadrik ve vznikající scéně je nutné dodržet následující postup:

1. vytvořit nový objekt pro následné renderování kvadrik pomocí funkce gluNewQuadric().
2. nastavit atributy pro rendering (vykreslování) tohoto objektu, v některých případech je však možné ponechat původní nastavení. Změna atributů kvadrik se provádí pomocí funkcí gluQuadricDraw­Style(), gluQuadricOri­entation(), gluQuadricNor­mals() agluQuadricTex­ture().
3. zaregistrovat callback funkci, která je volána v případě výskytu chyby při renderování kvadriky. Registrace callback funkce se provede zavoláním funkce gluQuadricCallbac­k().
4. zavolat funkci pro vytvoření požadované kvadriky: gluSphere(), gluCylinder(), gluDisk() nebogluPartial­Disk().
5. po vykreslení požadované kvadriky je možné objekt pro renderování kvadrik smazat (tj. odstranit z paměti jeho atributy) pomocí funkce gluDeleteQuadric().

5. Kompatibilita se staršími verzemi knihovny GLU

Při práci s kvadrikami se ve všech funkcích pracuje s referencí na objekt typu GLUquadric. V dokumentaci ke knihovně GLU se sice stále mluví o objektu (má některé objektové vlastnosti, kromě polymorfismu a dědičnosti), ve skutečnosti ale jde o běžnou C-čkovou datovou strukturu, ostatně celá knihovna GLU je postavena na čistém jazyce C, což zjednodušuje volání jejích funkcí i z programů vytvořených v jiných programovacích jazycích.

Místo datového typu GLUquadric se v minulosti používal datový typ GLUquadricObj. V současných hlavičkových souborech glu.h je pomocí maker nebo klauzury typedef vytvořen jak datový typ GLUquadric, tak i starší verzeGLUquadri­cObj. Příklad z hlavičkového souboru přidávaného ke kompilátorům gcc:

#ifdef __cplusplusclass
    GLUquadric;
#else
    typedef struct GLUquadric GLUquadric;
#endif

typedef GLUquadric GLUquadricObj;

6. Demonstrační příklady

V dnešním pokračování jsme si konkrétně nepopsali žádné funkce, které je zapotřebí při zobrazování kvadrik použít. Proto zde neuvádím ani demonstrační příklady na vykreslování kvadrik vytvořených pomocí funkcí GLU, ale pro zopakování uvedu dva příklady, které demonstrují vytvoření kvadrik pomocí funkcí z nastavbové knihovny GLUT.

Všimněte si, že tělesa vytvořená pomocí funkcí GLUTu mohou být osvětlena, ale nikoli korektně otexturována. Je to z toho důvodu, že pro každý generovaný vrchol je vypočten pouze normálový vektor (použitý v osvětlovacím modelu), ale souřadnice do textury není vygenerována. Jak si ukážeme v dalším pokračování, je možné u kvadrik vytvářených pomocí funkcí z knihovny GLU texturovací souřadnice generovat, a vykreslovat tak kvadriky pokryté 2D texturou.

Po spuštění prvního demonstračního příkladu se zobrazí trojrozměrné těleso koule, které je zobrazeno s využitím funkce glutSolidSphere() resp. glutWireSphere() z nadstavbové knihovny GLUT. Koule může být vykreslena buď jako drátový model, nebo pomocí vyplněných plošek – přepnutí mezi těmito typy vykreslování se provádí klávesou Space. Pomocí kláves 1 a 2 je možné měnit poloměr koule, klávesami 3, 4,5 a 6 se mění počet dělení ideální koule na jednotlivé plošky – je tak možné vytvořit například osmistěn pouhým zmenšením počtu dělení.

Zdrojový kód prvního demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 2: Screenshot prvního demonstračního příkladu se zobrazeným drátovým modelem

Obrázek 3: Screenshot prvního demonstračního příkladu se zobrazeným vyplněným modelem – malý počet plošek, na který je model koule rozdělen, změní tvar modelu

Ve druhém demonstračním příkladu se vykresluje kužel pomocí funkce glutSolidCone() resp. glutWireCone() z knihovny GLUT. Vlastnosti tělesa se mění pomocí stejných kláves jako u prvního příkladu. Navíc přibylo ovládání klávesami 7 a 8, jimiž se zobrazovaný kužel snižuje a zvyšuje.

Zdrojový kód druhého demonstračního příkladu je dostupný zde, jeho HTML verze se zvýrazněním syntaxe zde.

Obrázek 4: Screenshot druhého demonstračního příkladu se zobrazeným vyplněným modelem kužele, který je rozdělen na malý počet plošek

Obrázek 4: Screenshot druhého demonstračního příkladu se zobrazeným drátovým modelem kužele

7. Obsah dalšího pokračování

V dalším pokračování tohoto seriálu si podrobně popíšeme celý postup, který je zapotřebí dodržet při vytváření a následném zobrazení kvadrik ve vykreslované scéně.

8. Seznam funkcí OpenGL a GLUT zmíněných v této části

glutSolidSphere()
glutWireSphere()
glutSolidCone()
glutWireCone()
 

9. Nové funkce z knihovny GLU popsané v této části

gluNewQuadric()
gluQuadricDraw­Style()
gluQuadricOri­entation()
gluQuadricNormals()
gluQuadricTexture()
gluQuadricCallbac­k()
gluDeleteQuadric()
gluSphere()
gluCylinder()
gluDisk()
gluPartialDisk()
 

10. Zkomprimovaná verze článku i s přílohami

Zkomprimovaná verze tohoto článku i s přílohami a demonstračními příklady je uložena zde.

11. Literatura, odkazy

GLUT I

Datum vydání: 29. 04. 2003
Odkaz: www.root.cz/cla­nek/1612

GLUT II

Datum vydání: 06. 05. 2003
Odkaz: www.root.cz/cla­nek/1622

GLUT III

Datum vydání: 13. 05. 2003
Odkaz: www.root.cz/cla­nek/1630

GLUT IV

Datum vydání: 20. 05. 2003
Odkaz: www.root.cz/cla­nek/1642

GLUT V

Datum vydání: 27. 05. 2003
Odkaz: www.root.cz/cla­nek/1655

GLUT VI

Datum vydání: 03. 06. 2003
Odkaz: www.root.cz/cla­nek/1666

GLUT VII

Datum vydání: 10. 06. 2003
Odkaz: www.root.cz/cla­nek/1677

GLUT VIII

Datum vydání: 17. 06. 2003
Odkaz: www.root.cz/cla­nek/1688

GLUT IX

Datum vydání: 24. 06. 2003
Odkaz: www.root.cz/cla­nek/1701