OpenGL evaluátory (9)

Obsah

Význam normálových vektorů Bézierových ploch

V předchozích částech tohoto seriálu jsme si řekli, jakým postupem je možné dosáhnout vykreslení Bézierových ploch pomocí OpenGL evaluátorů (část V a část VI). Dokonce již umíme automaticky vypočítat barvu na libovolném místě povrchu Bézierovy plochy (část VII), nebo Bézierovu plochu pokrýt texturou (část VIII).

K dokonalosti vykreslování Bézierových ploch tak schází pouze výpočet osvětlení, bez něj totiž vykreslené obrázky nepůsobí příliš věrohodně.

V grafické knihovně OpenGL se pro výpočet barvy osvětlených povrchů těles používá takzvaný Phongův osvětlovací model. Jedná se o empirický model, který je navržen tak, aby byl výpočet osvětlení jednoduchý, rychlý a aby současně výsledná scéna vypadala reálně či alespoň dostatečně věrohodně, což je patrné ze screenshotů demonstračních příkladů.

V seriálu, který se zabýval popisem grafické knihovny OpenGL, jsem způsob práce se světly a materiály těles popsal podrobněji. Informace o tomto tématu i demonstrační příklady lze nalézt zejména v částech OpenGL XVIII, OpenGL XIX, OpenGL XX aOpenGL XXI.

Při výpočtu osvětlení je bezpodmínečně nutné zadávat u každého vrcholu i jeho normálu (a.k.a. normálový vektor), jinak by nebylo možné spočítat barvu na povrchu tělesa – viz první obrázek s naznačeným normálovým vektorem, vektorem ke kameře a vektorem vedoucím ke zdroji světla. Pokud by normála nebyla explicitně nastavena či vypočtena, byla by použita implicitní hodnota normálového vektoru N=(0.0, 0.0, 1.0), tj. normála je orientována ve směru z-ové osy, což není ve většině případů korektní.

Obrázek 1: Význam normálového vektoru při výpočtu osvětlení plošky Phongovým osvětlovacím modelem

Ruční zadávání normálových vektorů v každém vypočteném bodě Bézierovy plochy však není ani jednoduché ani rychlé – každý vypočtený bod by se musel zkopírovat z grafického akcelerátoru zpět do operační paměti počítače, poté by se musel provést výpočet normály a výsledek by se opět zkopíroval do grafického akcelerátoru. Tím by se ztrácela veškerá elegance funkcí glMap2*() a glMapGrid().

Proto je nutné provést automatické generování normálových vektorů, které bude popsáno v následujícím odstavci.

Výpočet normálových vektorů ze znalosti lokálních parametrů povrchu

V OpenGL je podporováno automatické generování normálových vektorů, které je možné velmi jednoduše zapnout zavoláním funkce:

glEnable(GL_AUTO_NORMAL);

Pokud je automatické generování normál zapnuto, provádí se pro každý vrchol na Bézierově ploše analýza lokálního zakřivení povrchu. Nejprve se vyjádří dva tečné vektory ve směru růstu parametru u a v. Tyto vektory se znormalizují a provede se jejich vektorový součin.

Výsledkem je normálový vektor v daném místě povrchu Bézierovy plochy, jehož souřadnice se přenesou ve vykreslovacím řetězci do modulu, ve kterém se provádí výpočet osvětlení.

Zde musím upozornit na fakt, že vzhledem ke způsobu výpočtu normálových vektorů záleží na orientaci Bézierovy plochy, tj. zrcadlovým otočením indexů řídících bodů dojde i k otočení vypočtené normály, což samozřejmě při výpočtu osvětlení vede k chybám, protože odvrácená část Bézierovy plochy je neosvětlená.

Automatické generování normálových vektorů lze vypnout pomocí funkce:

glDisable(GL_AUTO_NORMAL);

a dotaz na aktuálně nastavené povolení či zákaz je možné provést příkazem:

glIsEnabled(GL_AUTO_NORMAL);

V dalším odstavci si popíšeme použití evaluátorů pro přímé vyjádření normálových vektorů bez jejich automatického výpočtu.

Výpočet normálových vektorů pomocí evaluátorů

Pokud je automatické generování normálových vektorů zakázáno pomocí výše zmíněné funkce glDisable(), mohou být pro výpočet normál použity evaluátory. Princip práce je obdobný výpočtům texturovacích souřadnic a barev bodů, které leží na Bézierových plochách – viz části VII a VIII tohoto seriálu.

Řídící body Bézierovy plochy, která reprezentuje normálové vektory, leží v prostoru, v němž každá souřadnice bodu odpovídá jedné souřadnici normálového vektoru. V krátkosti si popíšeme postup, který lze při práci s evaluátory a normálami použít:

Prvním příkazem je povolení práce evaluátoru, který se stará o generování normálových vektorů. Povolení se provede velmi jednoduše pomocí příkazu:

glEnable(GL_MAP2_NORMAL);

Opětovné zakázání výpočtu normálových vektorů se provede příkazem:

glDisable(GL_MAP2_NORMAL);

Dotaz na aktuálně nastavené povolení či zakázání výpočtu normál pomocí evaluátorů lze provést pomocí funkce:

glIsEnabled(GL_MAP2_NORMAL);

Druhým krokem je nastavení typu používaného evaluátoru. Pro tento účel se používají již dříve popsané funkce glMap2f() nebo glMap2d(), které mají hlavičku:

void glMap2d(
    GLenum   target,
    GLdouble u1,
    GLdouble u2,
    GLint    ustride,
    GLint    uorder,
    GLdouble v1,
    GLdouble v2,
    GLint    vstride,
    GLint    vorder,
    const    GLdouble *points
);

void glMap2f(
    GLenum   target,
    GLfloat  u1,
    GLfloat  u2,
    GLint    ustride,
    GLint    uorder,
    GLfloat  v1,
    GLfloat  v2,
    GLint    vstride,
    GLint    vorder,
    const    GLfloat *points
);

Význam argumentů těchto funkcí jsme si již popsali v předchozích částech, zde pouze připomenu, že hned v prvním parametru target je určeno, který evaluátor bude specifikován – může jít o výpočet pozic bodů v prostoru, jejich barev, souřadnic do textury, nebo právě o normálový vektor. Pokud má probíhat výpočet normálového vektoru, musí být první parametr nastaven na hodnotu GL_MAP2_NORMAL.

Pole, ve kterém jsou normálové vektory řídících bodů specifikovány, musí pro každou normálu obsahovat tři složky nx, ny, nz; princip funkce je tedy stejný jako při práci se souřadnicemi řídících bodů. Musíme však mít na paměti, že se normálové vektory bodů na ploše počítají pomocí interpolace, takže může docházet k nechtěným efektům, například pokud by se měnila orientace normály.

Poznámka: pokud není povoleno automatické generování normálových vektorů pomocí funkce glEnable(GL_A­UTO_NORMAL) ani výpočet normálových vektorů pomocí evaluátorů (funkce glEnable(GL_MAP2_­NORMAL)), nejsou normály při práci s Bézierovými plochami vytvářeny a výpočet osvětlení se neprovede.

Ukázka použití automaticky vygenerovaných normál při výpočtu osvětlení

V následující C-čkovské funkci je ukázáno, jakým způsobem je možné evaluátory použít pro vykreslení plochy, která je vystínovaná pomocí Phongova osvětlovacího modelu. Tato funkce je součástí níže uvedených demonstračních příkladů. Kromě výpočtů souřadnic bodů, jež leží na Bézierově ploše, se provádí výpočet souřadnic [u, v] do textury, což znamená, že vykreslovaná plocha je pokryta texturou a současně i osvětlena.

//-----------------------------------------------
// Tato funkce vykreslí Bézierovu plochu
// pomocí evaluátorů. Ke každé plošce je
// automaticky dopočítán i normálový vektor.
//-----------------------------------------------
void drawBezierSurfaceUsingEvaluators(
      GLfloat ctrlPoints[][4][3],
      GLfloat texturePoints[][2][2])
{
#define DELENI 20
  int i,j;

  // povolení 2D evaluátoru pro výpočet souřadnic
  // bodů na Bézierově ploše
  glEnable(GL_MAP2_VERTEX_3);

  // povolení mapování souřadnic do textury
  // pomocí evaluátorů
  glEnable(GL_MAP2_TEXTURE_COORD_2);

  // povolení automatického výpočtu normál
  glEnable(GL_AUTO_NORMAL);

  // předání řídících bodů Bézierovy plochy
  glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4,
                              0, 1,12, 4,
                            &ctrlPoints[0][0][0]);

  // předání řídících bodů pro výpočet
  // texturovacích souřadnic pomocí evaluátorů
  glMap2f(GL_MAP2_TEXTURE_COORD_2,
                            0, 1, 2, 2,
                            0, 1, 4, 2,
                            &texturePoints[0][0][0]);

  // vykreslení Bézierovy plochy
  glMapGrid2f(DELENI, 0.0f, 1.0f, DELENI, 0.0f, 1.0f);
  glEvalMesh2(GL_FILL, 0, DELENI, 0, DELENI);

  // zákaz aplikace obou typů evaluatorů
  glDisable(GL_MAP2_VERTEX_3);
  glDisable(GL_MAP2_TEXTURE_COORD_2);
}

Před použitím výše zmíněné funkce je zapotřebí nastavit všechny parametry materiálu a osvětlení. To je ukázáno na následujícím fragmentu kódu:

//---------------------------------------------
// Funkce pro inicializaci vykreslování
//---------------------------------------------
void onInit(void)
{
  // nastavení vlastností framebufferu
  glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
  glClearDepth(1.0f);
  glEnable(GL_DEPTH_TEST);
  glDepthFunc(GL_LESS);

  // nastavení stylu vykreslování
  glShadeModel(GL_SMOOTH);

  // nastavení vlastností materiálu a světel
  glPolygonMode(GL_FRONT, GL_FILL);
  glPolygonMode(GL_BACK, GL_FILL);
  glDisable(GL_CULL_FACE);
  glMaterialfv(GL_FRONT, GL_AMBIENT, materialAmbient);
  glMaterialfv(GL_FRONT, GL_DIFFUSE, materialDiffuse);
  glMaterialfv(GL_FRONT, GL_SPECULAR, materialSpecular);
  glMaterialfv(GL_FRONT, GL_SHININESS, materialShininess);
  glLightfv(GL_LIGHT0, GL_POSITION, light_position);
  glEnable(GL_LIGHTING);
  glEnable(GL_LIGHT0);
} 

Demonstrační příklady

Po překladu a spuštění prvního demonstračního příkladu se vykreslí Bézierova bikubická plocha, která je vypočtena pomocí evaluátorů. Výpočet probíhá ve funkci drawBezierSur­faceUsingEvalu­ators(). Bézierova plocha se zobrazí pomocí plošek vykreslovaných primitivou GL_QUADS.

Pro každou plošku je automaticky vyčíslen i její normálový vektor, který je použit při výpočtu osvětlení pomocí Phongova osvětlovacího modelu. Povolení a opětovné zakázání automatického výpočtu normálových vektorů je možné provést pomocí klávesy A. Při vypnutém automatickém výpočtu se pro každý vrchol dosazuje implicitní hodnota n=(0, 0, 1).

Pohled na Bézierovu plochu je animovaný, animaci lze spustit či zastavit pomocí klávesy S, klávesou Esc je možné program ukončit.

Zdrojový kód prvního demonstračního příkladu je dostupný zde, HTML verze se zvýrazněním syntaxe zde.

Obrázek 2: Screenshot prvního demonstračního příkladu s povoleným automatickým generováním normálových vektorů pro každý vypočtený vrchol Bézierovy plochy

Obrázek 3: Screenshot prvního demonstračního příkladu se zakázaným automatickým generováním normálových vektorů pro každý vypočtený vrchol Bézierovy plochy

Druhý demonstrační příklad je podobný příkladu prvnímu s tím rozdílem, že se kromě výpočtu osvětlení pokrývá zobrazovaný povrch rastrovou texturou, takže barva každého pixelu získaná z textury je modulována dopadajícím osvětlením. Pomocí klávesy A lze automatické generování normálových vektorů vypnout, podobně jako v prvním demonstračním příkladu.

Zdrojový kód druhého demonstračního příkladu je dostupný zde, HTML verze se zvýrazněním syntaxe zde.

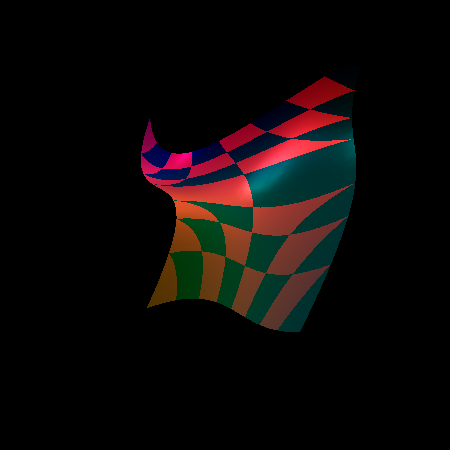
Obrázek 4: Screenshot druhého demonstračního příkladu s povoleným automatickým generováním normálových vektorů

Obrázek 5: Screenshot druhého demonstračního příkladu se zakázaným automatickým generováním normálových vektorů

Pokračování

Další díl seriálu o OpenGL evaluátorech bude již poslední. Proto bude věnován soupisu všech probraných témat a demonstračních příkladů uvedených ve všech devíti předchozích částech.

Seznam funkcí zmíněných v této části

Zkomprimovaná verze článku i s přílohami

Zkomprimovaná verze tohoto článku je umístěna zde.