OpenGL evaluátory (2)

Obsah

Teorie Bézierových křivek

Bézierovy křivky patří v počítačové grafice mezi jedny z nejpoužívanějších typů parametrických křivek. Jsou totiž velmi jednoduché jak na vytváření a editaci (tj. nepřinášejí žádné větší komplikace pro uživatele), tak i pro vykreslování (výhoda pro programátora nebo pro hardwarovou implementaci vykreslování). Bézierovy křivky stupně dvě a tři, tj. kvadriky a kubiky, jsou použity v mnoha aplikacích a technologiích, například v PostScriptu a postscriptových fontech, TrueType fontech, formátech aplikace Corel Draw, Adobe Illustrator,SVG – Scalable Vector Graphics, OpenOffice.or­g apod.

Bézierova křivka n-tého stupně je určena n+1 řídícími body P₀, P₁, … P_n a vztahem:

Kde index i probíhá přes interval i=0, …, n a Bⁿ_i(t) představuje Bernsteinův polynomn-tého řádu. Vyčíslení obecného Bernsteinova polynomu je poměrně složité a zdlouhavé, protože se ve vzorci používají faktoriály (resp. kombinační čísla) a mocniny. Bernsteinovy polynomy nízkých řádů, zejména druhého a třetího řádu, jsou však výpočetně jednoduché, protože použité mocniny a faktoriály jsou nízkého stupně.

Výpočet Bernsteinova polynomu třetího řádu (který je použit u Bézierových kubických křivek a bikubických ploch) je možné v programovacím jazyce C napsat následovně:

//--------------------------------------------------
// Tato funkce provede výpočet Bernsteinova polynomu
// třetího řádu. V parametru "ij" je předán index
// řídícího bodu, který musí nabývat celočíselných
// hodnot 0-3, v parametru "uv" je předána reálná
// hodnota z rozsahu 0.0-1.0.
//--------------------------------------------------
GLfloat B(GLint ij, GLfloat uv)
{
  // náhrada složitého výpočtu faktoriálu rozeskokem
    switch (ij) {
      case 0:
          return pow(1.0-uv, 3.0);
      case 1:
          return 3.0*uv*pow(1.0-uv, 2.0);
      case 2:
          return 3.0*uv*uv*(1.0-uv);
      case 3:
          return uv*uv*uv;
      default:
          return 0;
  }
}

Význam řídících bodů Bézierovy křivky

Bézierova křivka obecně prochází pouze svým prvním a posledním řídícím bodem, ostatní body pouze ovlivňují výsledný tvar křivky (ve speciálních případech však křivka může procházet i dalšími řídícími body). Pomocí prvního a druhého řídícího bodu P₀ a P₁ se určuje tečný vektor na začátku křivky. Předposlední a poslední řídící bodyP_n-1 a P_n zase určují tečný vektor na konci křivky. Této vlastnosti se často využívá při hladkém navazování Bézierových křivek (později uvidíme, že hladké navázání Bézierových plátů se provádí obdobně).

Pokud na sebe mají Bézierovy křivky hladce navazovat, tj. mají mít parametrickou spojitost alespoň C¹, musí být poslední řídící bod první křivky totožný s prvním řídícím bodem křivky druhé:

P_n=P'₀. Také tečný vektor na konci první křivky musí být stejný jako tečný vektor na začátku druhé (navazující) křivky. Na prvním obrázku jsou zobrazeny dvě Bézierovy kvadratické křivky, které jsou hladce navázány se spojitostí C¹.

Jednodušší je dosažení geometrické spojitosti G¹, kde je nutné, mimo totožnosti posledního řídícího bodu první křivky a prvního bodu druhé křivky, dodržet alespoň kolinearitu tečného vektoru na konci první křivky a na začátku křivky druhé. Geometrickou spojitost je snazší dodržet z toho důvodu, že volnost uživatele při zadávání řídících bodů je větší než v případě parametrické spojitosti, zejména při použití Bézierových kvadratických a kubických křivek.

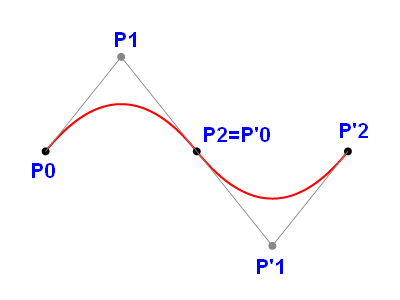
Obrázek 1: Dvě Bézierovy kvadratické křivky, které jsou navázány se spojitostí C¹

Bézierovy kubické křivky

V počítačové grafice patří mezi nejpoužívanější typ parametrických křivek Bézierovy kubické křivky, jejichž podporu nabízí téměř jakýkoli program pracující s vektorovou grafikou – jedná se opět o CorelDraw, Adobe Illustrator či OpenOffice. U systémů CAD a CAM je situace složitější, tam si své místo našly B-splajny a NURBS – těmi se budu podrobněji zabývat při popisu knihovny GLU v dalším seriálu. Nyní si zde však popíšeme základní vlastnosti Bézierovy kubické křivky.

Bézierovy kubické křivky jsou zadány pomocí čtyř řídících bodů v ploše či v prostoru. Křivka přitom prochází prvním a posledním řídícím bodem, druhý a třetí bod určují tečné vektory na začátku a na konci křivky. Křivka tedy druhým a třetím řídícím bodem obecně neprochází, což je patrné z druhého obrázku.

Obrázek 2: Bézierova kubická křivka zadaná čtyřmi řídícími body

Vykreslení Bézierovy kubické křivky lze provést postupným dosazováním hodnot do výše uvedeného vztahu a zobrazením či propojením bodů R(t) lomenou křivkou – viz též ilustrační funkce uvedená níže. Další možností, jak vykreslit Bézierovu křivku, je využití de Casteljau algoritmu pro postupné dělení křivky.

Mezi hlavní výhody Bézierových kubických křivek patří jejich intuitivní zadávání a snadné hladké navazování křivek na sebe. Také výpočet bodů, které leží na křivce, je velmi jednoduchý a rychlý. Pomocí Bézierových kubických křivek však nelze přesně modelovat kuželosečky, zejména kruh a elipsu, což omezuje použití těchto křivek v CAD systémech. Také nelze k obecné Bézierově kubice vytvořit offsetovou křivku, tj. křivku, která se od zadané křivky nachází v určité vzdálenosti.

V interaktivní grafice a designu však nejsou tato omezení Bézierových křivek kritická, viz například tento pěkný článek.

Programový výpočet Bézierovy kubické křivky je možné v programovacím jazyku C napsat následovně:

//-------------------------------------------------
// Tato funkce programově vykreslí Bézierovu
// kubickou křivku. Vstupem jsou čtyři řídící body
// s prostorovými souřadnicemi [x,y,z]. Při výpočtu
// se však využije pouze x-ová a y-ová souřadnice.
//-------------------------------------------------
void drawBezier(GLfloat points[][3])
{
    // váhy jednotlivých řídících bodů vypočtené
    // na základě Bernsteinova polynomu
    GLfloat mx,my,nx,ny,px,py,qx,qy;

    // souřadnice bodů, které se počítají
    GLfloat x, y;

    // parametr Bézierovy křivky, který probíhá
    // reálnými hodnotami od 0 do 1
    GLfloat t;

    // přejmenování řídících bodů pro větší
    // názornost dalších výpočtů
    GLfloat x0=points[0][0];
    GLfloat y0=points[0][1];
    GLfloat x1=points[1][0];
    GLfloat y1=points[1][1];
    GLfloat x2=points[2][0];
    GLfloat y2=points[2][1];
    GLfloat x3=points[3][0];
    GLfloat y3=points[3][1];

    // výpočet vah jednotlivých řídících bodů
    // na základě Bernsteinova polynomu
    mx = x0;
    my = y0;
    nx = 3.0 * (x1-x0);
    ny = 3.0 * (y1-y0);
    px = 3.0 * (x0+x2-2.0*x1);
    py = 3.0 * (y0+y2-2.0*y1);
    qx = x3-3.0*x2+3.0*x1-x0;
    qy = y3-3.0*y2+3.0*y1-y0;

    // křivku vykreslit jako 100 lineárních úseků
    glBegin(GL_LINE_STRIP);
    for (t=0; t<1.0; t+=0.01) {
        // výpočet souřadnic [x, y] bodu
        // na křivce na základě parametru t
        x = mx+nx*t+px*t*t+qx*t*t*t;
        y = my+ny*t+py*t*t+qy*t*t*t;
        glVertex2f(x, y);
    }
    glEnd();
}

Všimněte si, že jsme ve funkci drawBezier() nepoužili přímo výraz pro výpočet bodů na Bézierově křivce, ve kterém by se volala funkce pro vyčíslení Bernsteinova polynomu. Místo toho byl výpočet značně zjednodušen, takže se ve smyčce provádí pouze sčítání a násobení. Samozřejmě je možné provést další zjednodušení, například využít Hornerovo schéma nebo pomocí metody konečných diferencí nepřímo počítat výrazy tt a tt*t. Potom by se dala redukovat násobení ve smyčce na úkor aditivních operací – úpravu ponechávám na čtenáři, protože je celkem jednoduchá.

Bézierovy kvadratické křivky

V některých aplikacích, kde se pracuje s parametrickými křivkami (například tvorba fontů), jsou využity i jednodušší Bézierovy kvadratické křivky, které mají pouze tři řídící body. Křivka prochází prvním a třetím řídícím bodem, druhý řídící bod určuje současně oba tečné vektory. Ukázka Bézierovy kvadratické křivky spolu s jejími řídícími body je zobrazena na třetím obrázku.

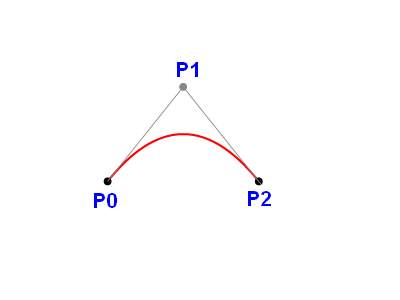
Obrázek 3: Bézierova kvadratická křivka zadaná třemi řídícími body

Rozdíl mezi Bézierovými kubickými křivkami (zadanými čtyřmi řídícími body) a kvadratickými křivkami (zadanými třemi řídícími body) je zobrazen na čtvrtém obrázku.

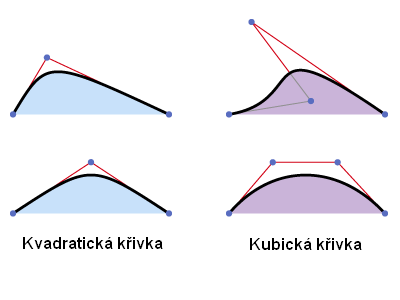
Obrázek 4: Rozdíl mezi kvadratickými a kubickými Bézierovými křivkami

Hladké napojení Bézierových kvadratických křivek lze zajistit zadáním identického koncového bodu první křivky a počátečního bodu křivky druhé. Současně musí být shodné tečné vektory v těchto bodech, tj. prostřední řídící body musí být středově symetrické okolo společného bodu obou křivek. Způsob hladkého napojení je patrný již z prvního obrázku.

Mnoho vektorových souborových formátů, zejména SVG, podporuje jak kvadratické Bézierovy křivky, tak i křivky kubické, protože každý typ křivek má jiný způsob použití. Při zadávání kvadratických křivek je možné povolit pouze specifikaci „prostředních“ řídících bodů s tím, že se krajní body dopočtou automaticky – musí ležet vždy v polovině vzdálenosti mezi dvěma prostředními řídícími body. Tento způsob práce s Bézierovými křivkami je použit například v TrueType fontech.

Demonstrační příklady

Po spuštění prvního demonstračního příkladu se vykreslí Bézierova kubická křivka, která je vypočtena programově, tj. bez použití evaluátorů. Výpočet bodů, které leží na Bézierově křivce, probíhá ve funkci drawBezier(). řídící body Bézierovy křivky lze měnit pouze programově, interaktivní editace je dostupná až ve druhém demonstračním příkladu. Pomocí klávesy F je možné provést přepnutí na celou obrazovku, klávesou W se zobrazení přepne zpět do okna. Ukončení aplikace se provádí buď pomocí klávesy Q, nebo ESC.

Zdrojový kód prvního demonstračního příkladu je dostupný zde, HTML verze se zvýrazněním syntaxe zde.

Obrázek 5: Screenshot prvního demonstračního příkladu s vykreslenou Bézierovou kubickou křivkou

Druhý demonstrační příklad navazuje na příklad první – je vykreslena Bézierova kubická křivka vypočtená programově, tj. bez použití evaluátorů. Výpočet probíhá opět ve funkci drawBezier(). Pomocí myši lze měnit polohu jednotlivých řídících bodů, a měnit tak tvar výsledné Bézierovy křivky. V horní části okna aplikace se vypisují souřadnice jednotlivých řídících bodů a číslo vybraného řídícího bodu. Řídící body jsou navzájem spojeny úsečkami, aby se zdůraznila vlastnost komplexní obálky a tečné vektory na začátku a na konci křivky. Ovládání této aplikace pomocí klávesnice je stejné jako u prvního demonstračního příkladu.

Zdrojový kód druhého demonstračního příkladu je dostupný zde, HTML verze se zvýrazněním syntaxe zde.

Obrázek 6: Screenshot druhého demonstračního příkladu s vykreslenou Bézierovou kubickou křivkou, u které byly přesunuty její řídící body.

Obsah dalších pokračování

V dalším pokračování seriálu o OpenGL evaluátorech si popíšeme základy Bézierových ploch, které mají v trojrozměrné počítačové grafice širší možnosti využití než zde popsané Bézierovy křivky.

Seznam funkcí zmíněných v této části

Zkomprimovaná verze článku i s přílohami

Zkomprimovaná verze tohoto článku je umístěna zde.