Obsah
1. Oslava 55 let od vzniku první implementace programovacího jazyka APL
2. Notace – osvobození z diktátu ASCII textu i důležitá myšlenková pomůcka
3. Malá odbočka – programovací jazyky s netradiční notací
4. První skutečný jazyk APL: APL\360
5. Základní vlastnosti programovacího jazyka APL
6. Ovšem je jazyk APL skutečně nečitelný?
7. Základní (primitivní) funkce a operátory programovacího jazyka APL
9. n-dimenzionální pole jako základní datový typ jazyka APL
10. Přístup k prvkům polí (použití indexů), funkce „take“ a „drop“
11. Šestice základních operátorů aplikovatelných na pole
12. Operátory „reduce“ a „scan“
15. Hierarchické datové struktury, komprese polí
16. Praktické vyzkoušení možností jazyka APL
17. Jak myslet v APL – výpočet prvočísel netradičním způsobem
18. Další programovací jazyky podporující práci s vektory a maticemi
1. Oslava 55 let od vzniku první implementace programovacího jazyka APL
Ve skutečnosti se ovšem historie programovacího jazyka APL začala psát nikoli v roce 1966, ale již v roce 1957. Právě tehdy Kenneth E. Iverson, který v té době pracoval na Harvardské universitě, vytvořil novou notaci určenou pro jednotný zápis matematických funkcí i pro tvorbu funkcí nových. Tato notace byla zcela odlišná od zavedené notace (resp. přesněji řečeno) notací, které se v matematice používaly. V roce 1962 byla tato notace popsána v knize nazvané „A Programming Language“ a (což původně nebylo plánováno) o několik let později se začaly objevovat skutečné interpretry i překladače programovacího jazyka používajícího stejné symboly, jaké popsal Iverson ve své knize. Konkrétně se jednalo o jazyk nazvaný IVSYS, který byl implementovaný v roce 1966 (což ovšem ještě nebyl skutečný APL, který byl následován jazykem APL\360 z roku 1966 a poté APL\1130 z roku 1968, jenž pracoval na počítači IBM 1130.

Obrázek 1: Přebal knihy K.E.Iversona o jeho revoluční notaci (ostatně název naznačuje, že až si IT projde současným vývojem programovacích jazyků, nakonec skončí stejně u APL :-).
Další implementace tohoto programovacího jazyka vznikly na mainframech IBM/370, později se různé (ve větší či menší míře modifikované) verze APL začaly používat i na minipočítačích a posléze i na mikropočítačích. Dnes existují implementace pro všechny rozšířené operační systémy mikropočítačů, takže APL je možné použít na Linuxu, Mac OS i Microsoft Windows (viz odkazy uvedené ve dvacáté kapitole). A nejjednodušší je použít webovou verzi APL dostupnou na adrese https://tryapl.org/, což je ostatně téma, kterému se budeme věnovat v navazujících kapitolách.

Obrázek 2: Rozložení znaků na klávesnici používané při programování v jazyku APL. Speciální znaky na klávesnici reprezentují základní (primitivní) funkce a operátory, z nichž mnohé si popíšeme.
Kenneth Iverson se rozvoji a propagaci jazyka APL aktivně věnoval více než 20 let, za což mu byla v roce 1979 udělena Turingova cena (Turing Award). Později Iverson navrhl programovací jazyk J, v němž se místo speciálních symbolů (viz následující kapitoly) používají pouze znaky obsažené v ASCII tabulce (v jazyku J se navíc ve velké míře podporuje tzv. tacit, což je téma na samostatný článek). Vraťme se však k APL. Specifikace tohoto jazyka se od poloviny šedesátých let minulého století několikrát změnila (rozšířila). Jedním z nejvíce důležitých rozšíření je APL2 od J. Browna z IBM, které do jazyka zavedlo podporu pro rekurzivní datové struktury (tedy, jak uvidíme dále, pro pole jako prvky jiných polí, což je mimochodem dále zobecněno v jazyku BQN). Většina dnešních implementací tohoto jazyka se snaží dodržovat specifikaci APL2, i když je jazyk dále rozšiřován (například v APLX verze 4 byla přidána podpora pro objektově orientované programování, i když v poněkud jiné podobě, než ji známe z mainstreamových programovacích jazyků). Z moderních implementací APL se pak musíme zmínit o komerčním Dyalog APL.
2. Notace – osvobození z diktátu ASCII textu i důležitá myšlenková pomůcka
„Notation as a tool of thought“
Kenneth Iverson si v průběhu svého působení na univerzitě uvědomil, jak důležitá je správně navržená notace pro popis složitějších matematických výrazů, funkcí i celých algoritmů. Notací se v tomto kontextu myslí systém, resp. přesněji řečeno pravidla určující vzájemné vztahy mezi symboly pro účely (strukturované) komunikace. Důležité je, že se prakticky vždy jedná o nějakou doménově specifickou oblast, ať již se jedná právě o matematiku (kde existuje hned několik vzájemně nekompatibilních notací), hudbu, chemii, ale například i o astrologii :-).

Obrázek 3: Hudební notace, resp. jedna z forem hudební notace.
Důležitost a možná i nezbytnost volby správné notace si můžeme ukázat na klasickém příkladu – způsobu zápisu čísel, konkrétně na dvou zcela odlišných notacích. Jedná se o římské číslice a o notaci, kterou dnes (nepřesně) označujeme jako arabské číslice. Způsob zápisu/notace římských číslic do značné míry komplikuje prakticky všechny aritmetické operace (zkuste si například vydělit DCCCCLXXXXVIIII hodnotou CXI – já to přímo nedokážu), ovšem komplikuje i další rozšiřování zápisu, například o nulu, o záporná čísla nebo o čísla s neceločíselnou částí. Pokud se ovšem má stejná operace provést s využitím zápisu hodnot arabskými číslicemi, jedná se o trivialitu, kterou prakticky kdokoli vypočte zpaměti. Ovšem ani klasická notace s arabskými číslicemi není všemocná, takže se musela pro výpočty s velmi malými nebo naopak velkými čísly rozšířit o „vědeckou“ notaci a×10b.
Obrázek 4: Dvě z mnoha notací používaných v chemii (a mimochodem popisujících stejnou strukturu).
S různými notacemi se setkáme především v matematice; jednotlivé notace se odlišují podle své domény. Známá je například Einsteinova notace nebo Einsteinova sumační konvence, která zajišťuje úsporný zápis (a manipulaci!) rovnic v obecné teorii relativity (ovšem je ji možné použít i obecně v rámci lineární algebry).
Obrázek 5: Matematická notace.
Obrázek 6: Další ukázka matematické notace.
Obrázek 7: A poslední ukázka matematické notace.
3. Malá odbočka – programovací jazyky s netradiční notací
Naprostá většina v současnosti používaných programovacích jazyků je založena na použití omezeného množství symbolů; typicky se jedná o znaky ASCII (s tím, že některé jazyky umožňují, aby uživatelské identifikátory obsahovaly i další znaky – mnohdy ovšem s omezeními). Ovšem nebylo tomu tak vždy, protože existuje poměrně velké množství programovacích jazyků, v nichž se používají i další symboly, popř. dokonce jazyky, v nichž se program nezapisuje lineárně zleva doprava a shora dolů, ale má složitější „2D“ strukturu.
Obrázek 8: I toto je forma notace.
Z historicky důležitých jazyků se jedná například o Algol; konkrétně si přiblížíme Algol 68. ALGOL je jedním z prvních jazyků, u nichž syntax existuje v několika rozdílných variantách. V případě Algolu se nazývají reference syntax, publication syntax a implementation syntax. Referenční syntax je použita především v oficiálním „Reportu“, publikační syntax je použita v článcích, při ukázce algoritmů na tabuli (slajdech) atd. A implementační syntax se liší podle použitého počítače a jeho schopností (znaková sada atd.). Kvůli této trojí syntaxi se zápis algoritmů v článcích a knihách mnohdy dosti podstatným způsobem odlišuje od zápisu pro konkrétní počítač. Navíc to umožňuje měnit (v článcích i konkrétní implementaci) klíčová slova a nahrazovat je za národní varianty, používat desetinnou čárku namísto desetinné tečky atd.
V „publikační“ syntaxi nalezneme kromě jiného i následující symboly:
- ∧, ∨
- ×, ÷, ÷×, ÷*, %×
- ≤, ≥, ≠, ¬=
- →, ○, ¢, ⏨, □
- ×:=, ÷:=, ÷×:=, ÷*:=, %×:=
- ¬, ↑, ↓, ⌊, ⌈, ⊥
- ⊂, ≡, , ⊃, ⎩, ⎧
Dalším příkladem může být programovací jazyk Fortress, který se sice zapisuje ve standardní textové podobě, která je ovšem následně transformována do tisknutelné podoby přes LaTex. Podívejme se na několik ukázek:

Obrázek 9: Výrazy a příkaz jazyka Fortress v prezentační formě.
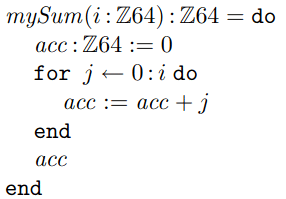
Obrázek 10: Zápis funkce v prezentační formě jazyka Fortress.
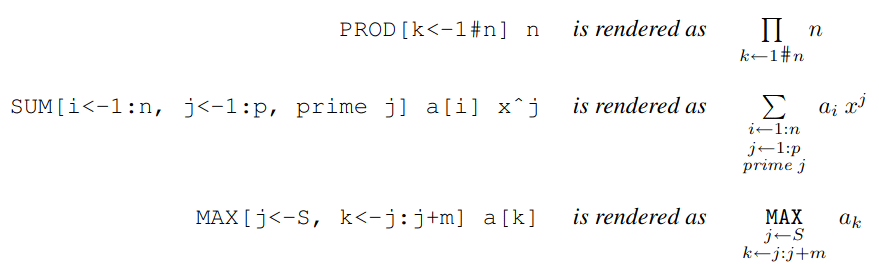
Obrázek 11: Vstupní a prezentační formy některých zápisů v jazyku Fortress (a toto má již velmi blízko v APL).
A konečně posledním příkladem je programovací jazyk Epigram, který taktéž podporuje vstupní formu zápisu a výstupní (prezentační) formu generovanou přes LaTeX. Uvedeme si dva příklady – prvním je definice datového typu, druhým pak definice funkce.
Definice datového typu:
( ! ( ! ( n : Nat !
data !---------! where !----------! ; !-----------!
! Nat : * ) !zero : Nat) !suc n : Nat)
Výsledek:
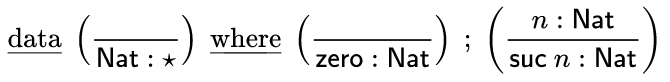
Obrázek 12: Datový typ v prezentační formě.
Definice funkce:
plus x y <= rec x {
plus x y <= case x {
plus zero y => y
plus (suc x) y => suc (plus x y)
}
}
Výsledek:
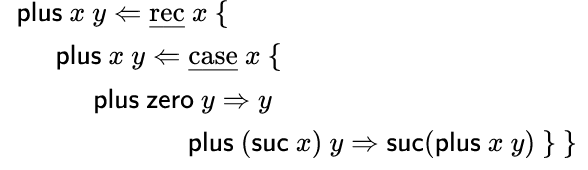
Obrázek 13: Rekurzivní definice funkce v prezentační formě.
4. První skutečný jazyk APL: APL\360
V úvodní kapitole jsme si řekli, že APL původně vznikl jako koncept nové unifikované notace zápisu matematických operací a algoritmů. Teprve později (a trvalo to ve skutečnosti celých devět let) byl na základě tohoto konceptu vytvořen prakticky použitelný programovací jazyk. První praktická implementace jazyka APL se nazývá APL\360. Toto poněkud podivné jméno vychází z toho, že tato verze APL byla provozována na slavných mainframech IBM System/360 (jak je patrné, lomítka a zpětná lomítka byla tehdy v IBM populární). APL\360 byl dokončen v listopadu 1966, což znamená, že slavíme (přesněji za tři týdny budeme slavit) 55. výročí tohoto neobvyklého programovacího jazyka. Mimochodem – tvůrci APL\360 získali cenu Grace Murray Hopperové za rok 1973, viz též https://en.wikipedia.org/wiki/Grace_Murray_Hopper_Award (z nějakého důvodu je zde však u každého roku uveden pouze jeden oceněný).

Obrázek 14: Zrekonstruovaný řídicí panel počítače IBM System/360 Model 30. Na dlaždici před panelem (zhruba pod čtveřicí bílých tlačítek) je pro porovnání velikostí umístěný současný mikrořadič PIC.

Obrázek 15: Moduly počítačů řady IBM System/360. Zpočátku měl každý modul podobu větší či menší skříně, později docházelo ke slučování některých funkcí do menšího počtu modulů i k celkovému zmenšování jak obsazeného prostoru, tak i spotřeby elektrické energie (to znamenalo i menší nároky na chlazení – klimatizaci).
5. Základní vlastnosti programovacího jazyka APL
„Real Programmers don't write in APL, unless the whole program can be written on one line“
Tento článek se nezabývá „pouze“ historií vzniku programovacího jazyka APL, popř. vlivem použité notace na způsob myšlení. Popíšeme si totiž i některé základní vlastnosti tohoto – jak uvidíme dále – zcela netradičně pojatého programovacího jazyka. V APL jsou přitom jednotlivé vlastnosti a operace nerozlučně spjaty právě s notací, tedy se způsobem jejich zápisu.
Prvním z typických rysů programovacího jazyka APL je jeho orientace na zpracování vektorů a matic (obecně polí téměř libovolné dimenze; většina implementací povoluje definovat až 63dimenzionální struktury, což je plně dostačující), a to bez nutnosti použití čítačů či programových smyček. Jazyk APL s těmito datovými strukturami pracuje z hlediska programátora prakticky stejným způsobem jako se skalárními hodnotami (čísly), takže například součet odpovídajících si položek dvou polí je zapisován s využitím stejné notace jako součet dvou číselných hodnot. Dalším typickým rysem je způsob aplikace funkcí na hodnoty (obecně pole) a vzájemné kombinace funkcí pomocí operátorů (slovem operátor jsou v programovacím jazyce APL označovány funkce vyššího řádu, tj. funkce vracející jiné funkce; s funkcemi vyššího řádu se dnes pochopitelně můžeme setkat i v mnoha dalších programovacích jazycích). S využitím funkcí a operátorů, které jsou přímo v APL definovány, je možné nahradit i řídicí struktury – podmíněné příkazy a programové smyčky – které dokonce v prvních verzích jazyka ani nebylo možné zapisovat (v pozdějších verzích se pro usnadnění programování tyto řídicí struktury do APL přidaly).
Každá základní (primitivní) funkce a operátor je v jazyce APL zapisována formou nějakého „jednoznakového“ symbolu, přičemž je nutné zdůraznit, že většina těchto symbolů (znaků) se nenachází v ASCII tabulce, ale jedná se buď o písmeno řecké abecedy nebo jiný (matematický) symbol zvolený Iversonem (některé symboly jsou zcela unikátní pro APL). Použití symbolů namísto kombinace alfanumerických znaků, tj. zápisu známého z většiny dalších vysokoúrovňových programovacích jazyků, je třetím a pro většinu programátorů nejtypičtějším (resp. nejviditelnějším) rysem programovacího jazyka APL. V podstatě se jedná o zcela opačný přístup než jaký jsme mohli vidět například při vývoji programovacího jazyka COBOL, jenž byl navržen takovým způsobem, aby bylo možné programy modifikovat i neprogramátory (což se pochopitelně v praxi prakticky nikdy nestalo). Zatímco v COBOLu se každá programová konstrukce popisovala jedním či několika klíčovými slovy (kterých existuje více než 300), jazyk APL ve skutečnosti žádná klíčová slova neobsahuje, ale nabízí programátorům sadu základních (primitivních) funkcí (cca 50) a operátorů (celkem šest v základní variantě), které je možné kombinovat a vytvářet tak nové uživatelské funkce i uživatelské operátory.

Obrázek 14: Základní funkce a operátory vypsané v nápovědě k prostředí TryAPL, s nímž se setkáme v dalším textu.
6. Ovšem je jazyk APL skutečně nečitelný?
Vzájemná kombinace (zřetězení) primitivních funkcí a operátorů bez vytváření a pojmenování funkcí vlastních vede k velmi úspornému zápisu kódu, což je ještě umocněno tím, že všechny základní funkce a operátory se zapisují jediným znakem. Výsledkem je sice stručný zápis, který je však pro většinu programátorů prakticky nečitelný (mnozí programátoři čtení podobných programů přirovnávají k luštění hieroglyfů), o čemž se můžete přesvědčit například z následujícího výpisu několika výrazů (vzhledem k tomu, že na některých systémech nemusí být všechny znaky zobrazeny korektně, byl z výpisu programu pořízen screenshot:

Obrázek 15: Užitečné a relativně často používané idiomy jazyka APL zapisované pomocí kombinace základních funkcí a operátorů.
Podobné programátorské praktiky, jaké byly ukázány na předchozím výpisu (ovšem vytvořené profesionálem, nejedná se o žádné nesmyslné demo, ale užitečné idiomy), vedly k tomu, že je jazyk APL považován, byť poněkud neoprávněně, za jazyk „write only“, podobně jako Forth (i když z poněkud jiného důvodu). Ve skutečnosti je však i v jazyku APL možné poměrně snadno psát přehledné a srozumitelné programy, ve kterých navíc programátoři mohou využívat všechny výhody tohoto jazyka (mezi něž patří jednoduchá práce s vektory, maticemi a poli, funkce vyššího řádu, velmi rychlé prototypování vhodné pro aplikace, ve kterých je důležitý co nejrychlejší nástup na trh atd.). V případě, že jsou například nadefinovány základní řídicí příkazy (mnoho moderních implementací APL je obsahuje), lze programy v APL zapisovat prakticky stejným způsobem, jako v jiných programovacích jazycích (symbol ← značí přiřazení a symbol ⎕ neboli quad je primitivní funkce pro načtení libovolné hodnoty z klávesnice či obecně ze standardního vstupu):
GUESS;VAL
'Hadej cislo'
:Repeat
VAL ← ⎕
:If VAL=42
'Uhodl jsi!'
:Leave
:EndIf
'Tesne vedle, zkus to znovu...'
:EndRepeat

Obrázek 16: Moderní fonty (OpenType, PostScriptové) obsahují buď část nebo dokonce všechny znaky používané jazykem APL pro zápis základních funkcí a operátorů.
Nicméně cesta k efektivní práci s APL vyžaduje, aby se programátor postupně naučil různé idiomy, tj. sekvence symbolů popisujících nějakou známou operaci. Tyto idiomy lze po určité době snadno rozeznat, a to bez toho, aby musel programátor program číst pomalým způsobem symbol po symbolu. Ostatně pokud lidský mozek něco umí skutečně efektivně, jde o rozeznávání vzorů (pattern) a idiomy lze za takové vzory považovat. Opět se nejedná o žádnou specialitu jazyka APL, protože rozeznání idiomů provádí i každý matematik, který například uvidí tento zápis:
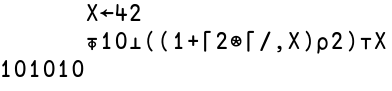
Obrázek 17: Vzor/idiom, který lze rozeznat jediným pohledem, pochopitelně až po náležitém tréninku. Prostřední řádek představuje převod hodnoty z dekadické soustavy do soustavy binární.
Každý matematik by měl ihned rozeznat, že se jedná o harmonickou řadu a automaticky si tento zápis spojit se všemi vlastnostmi této řady.
7. Základní (primitivní) funkce a operátory programovacího jazyka APL
V úvodním textu jsme si řekli, že programovací jazyk APL obsahuje přibližně padesát základních (primitivních) funkcí. V APL se můžeme setkat se třemi typy funkcí. Jedná se o funkce bez argumentů (takzvané niladické funkce), tj. ve skutečnosti o procedury, dále pak o funkce s jedním argumentem (takzvané monadické funkce) a konečně o funkce se dvěma argumenty (takzvané dyadické funkce). V jazyce APL je možné přímo ze zápisu zdrojového kódu určit, jakého typu je volaná funkce, což mj. Iversonovi umožnilo použít jeden symbol pro reprezentaci většího množství funkcí – podle toho, jakým způsobem je symbol v programu použit, je zavolána určitá primitivní funkce.
Na jednu stranu se může zdát, že toto „přetížení symbolů“ povede k větší nepřehlednosti programů, na stranu druhou jsou však symboly „přetížené“ s rozmyslem, takže například symbol - značí negaci (monadická funkce, resp. monadická forma) či rozdíl (dyadická funkce), podobně jako v mnoha dalších programovacích jazycích, kde se nad tímto dualismem symbolu „-“ nepozastavujeme. Symbol ÷ znamená v monadické formě výpočet převrácené hodnoty a ve formě dyadické podíl čísel, vektorů či korespondujících prvků polí (monadická forma je logická, pokud si uvědomíme, že pro násobení/dělení je jednotkovým prvkem jednička, kdežto pro součet/rozdíl je jím nula). V následující tabulce jsou vypsány některé primitivní funkce jazyka APL (pro korektní zobrazení symbolů v tabulce je nutné použít fonty s podporou Unicode, například některý z řezů fontu DejaVu):
| Symbol | Unicode (hex) | Jeden argument (monadická forma) | Dva argumenty (dyadická forma) |
|---|---|---|---|
| + | 002B | identita | součet |
| – | 002D | negace | rozdíl |
| × | 00D7 | znaménko | součin |
| ÷ | 00F7 | převrácená hodnota | podíl |
| ᒥ | 2308 | zaokrouhlení na celé číslo nahoru | vrátí větší argument |
| ᒪ | 230A | zaokrouhlení na celé číslo dolů | vrátí menší argument |
| | | 007C | absolutní hodnota | zbytek po dělení |
| ι | 2373 | čítač (generátor sekvence hodnot) | |
| * | 002A | ex | xy |
| < | 003C | menší než | |
| ≤ | 2264 | menší nebo rovno | |
| = | 003D | rovno | |
| ≥ | 2265 | větší nebo rovno | |
| > | 003E | větší než | |
| ≠ | 2260 | nerovno | |
| ∈ | 220A | obsahuje (dotaz na existenci prvku v poli) | |
| ∈ | 22F8 | nalezení hodnoty (prvku v poli) | |
| ○ | 25CB | π×hodnota | goniometrická funkce specifikovaná 2.argumentem |
| ! | 0021 | 1×2×3×.. (faktoriál) | kombinace |
| ⌹ | 2339 | inverze matice | podíl matic |
| ⍉ | 2349 | transpozice řádků za sloupce | transpozice specifikovaná 2.argumentem |
| ⌽ | 233D | obrácení pořadí položek | rotace položek (vektoru, matice) |
| ⍋ | 234B | setřídění položek vektoru vzestupně | setřídění podle zadaného argumentu |
| ⍒ | 2352 | setřídění položek vektoru sestupně | setřídění podle zadaného argumentu |
Obrázek 18: Programátorské textové editory a integrovaná vývojová prostředí pro programovací jazyk APL dnes většinou obsahují i dialog s nabídkou symbolů používaných při zápisu základních funkcí a operátorů.
8. Výrazy
Algoritmy zapisované v jazyce APL se skládají z výrazů, při jejichž zápisu se musí dodržovat jen minimální množství syntaktických pravidel. Nejdůležitějším pravidlem je, že se jednotlivé funkce vyhodnocují zprava doleva (což sice může vypadat zvláštně, ovšem jsou pro to praktické důvody), přičemž již vyhodnocená funkce (tj. její návratová hodnota) je použita jako argument funkce ležící nalevo od ní. Symboly monadických funkcí se zapisují vždy před svůj argument, naopak symboly funkcí dyadických jsou zapsány mezi oba argumenty (což je v matematice obvyklé, protože funkce v APL odpovídají v matematice operátorům – a je to jeden z důvodů, proč nejsou podporovány funkce s větším počtem parametrů). Při zápisu aritmetických výrazů je zapotřebí si dát pozor především na to, že všechny funkce mají stejné priority (bylo by totiž velmi složité definovat či zapamatovat si prioritu více než padesáti primitivních funkcí!). Interpret programovacího jazyka APL vypisuje hodnotu vyhodnoceného výrazu (tj. návratovou hodnotu nejlevější funkce) na výstup. Podívejme se nyní na několik jednoduchých příkladů.
Jednoduchý aritmetický výraz (povšimněte si zápisu násobení):
1+2×3 7
Vyhodnocení je prováděno zprava doleva, priority všech funkcí jsou stejné:
2×3+1 8
Argumentem funkce může být i vektor či pole (zde vektor šesti čísel) každá položka vektoru je vynásobena hodnotou 0.5:
2 4 6 8 × 0.5 1 2 3 4
Totéž pravidlo platí i pro monadickou funkci „převrácená hodnota“:
÷1 2 3 4 5 1 0.5 0.3333333333 0.25 0.2
Hodnota 10 je vydělena každou hodnotou z vektoru, výsledkem je též vektor:
10÷1 2 3 4 5 10 10 5 3.33333333 2.5 2.0 1
Ukázka kombinace více funkcí, vyhodnocování je stále prováděno zprava doleva:
ᒥ 10÷1 2 3 4 5 10 10 5 4 3 2 1
Dtto pro funkci provádějící zaokrouhlení na celá čísla směrem dolů:
ᒪ 10÷1 2 3 4 5 10 10 5 3 2 2 1
Mezery mezi funkcemi jsou zbytečné:
⌊10÷1 2 3 4 5 10 10 5 3 2 2 1

Obrázek 19: Ukázka obrazovky integrovaného vývojového prostředí jazyka APL se zvýrazněním syntaxe, automatickým číslováním řádků při zápisu funkcí atd.
9. n-dimenzionální pole jako základní datový typ jazyka APL
Již v předchozí kapitole jsme si na několika demonstračních příkladech ukázali základy práce s číselnými vektory. Jazyk APL podporuje i práci s vícedimenzionálními poli, kde hraje velkou roli monadická a dyadická funkce ρ (ró, reshape) a taktéž monadická funkce ι (jóta, index, též čítač).
Většina starších i současných překladačů a interpretrů programovacího jazyka APL podporuje tvorbu polí s maximálně 63 dimenzemi, ovšem v praxi se většinou můžeme setkat s 0-dimenzionálními poli (skalárními hodnotami, tj. čísly či znaky), jednodimenzionálními poli (vektory) a dvoudimenzionálními poli (maticemi). Při práci s poli hraje velkou roli již výše zmíněná monadická a dyadická funkce ρ (ró, reshape) a taktéž monadická funkce ι (jóta, index, též čítač). Monadická forma funkce ρ slouží ke zjištění prvků vektoru či velikosti matice (popř. vícerozměrného pole). Výsledkem této funkce je tedy vektor obsahující tolik prvků, kolik jich odpovídá dimenzi pole a hodnota každého prvku ve výsledku odpovídá velikosti pole v dané dimenzi (v případě vektoru se tedy vrátí jediné číslo reprezentující jeho délku, u matice dvojice číslic odpovídajících počtu řádků a sloupců, u trojrozměrných polí trojice číslic atd.).
V následujících ukázkách si povšimněte způsobu přiřazení hodnoty (čísla, vektoru nebo pole) do proměnné pomocí funkce ←.
Zjištění počtu prvků vektoru pomocí monadické funkce ρ:
ρ 1 2 3 4 4
Přiřazení vektoru do proměnné:
VECTOR ← 1 2 3 4 5 6
Zjištění počtu prvků vektoru pomocí monadické funkce ρ:
ρVECTOR 6
Použití funkce ι, která vygeneruje vektor s prvky 1..n (Pythonisté zde mohou vidět souvislost s voláním range()):
VECTOR ← ι10 VECTOR 1 2 3 4 5 6 7 8 9 10
Jeden ze způsobů vytvoření prázdného vektoru (seznamu) pomocí funkce ι:
EMPTY_LIST ← ι0 EMPTY_LIST *** zde se nic nezobrazilo :-) ***
Zjištění počtu prvků vektoru pomocí monadické funkce ρ:
ρEMPTY_LIST 0
Vytvoření dvourozměrného pole pomocí dyadické funkce ρ nejdříve se zadá rozměr jako první argument (4×3), druhým argumentem je seznam, který je transformován do požadovaného pole:
4 3 ρ 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
Dvourozměrné pole lze taktéž naplnit pomocí funkce ι:
4 3 ρ ι12 1 2 3 4 5 6 7 8 9 10 11 12
Pokud nemá seznam dostatečnou délku pro naplnění pole, jsou jeho položky do pole vloženy opakovaně za sebou:
4 3 ρ 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
Výše uvedené vlastnosti lze snadno využít pro vytvoření pole s prvky o stejné hodnotě:
4 3 ρ 0 0 0 0 0 0 0 0 0 0 0 0 0
Naplnění proměnné hodnotou matice:
MATICE ← 3 3 ρ ι 9 MATICE 1 2 3 4 5 6 7 8 9
Operace nad prvky matice:
MATICE × 10 10 20 30 40 50 60 70 80 90
Vytvoření matice se třemi řádky a dvěma sloupci:
CENY ← 3 2 ρ 1 2 3 4 5 6 CENY 1 2 3 4 5 6
Přeuspořádaní prvků v matici:
CENY ← 2 3 ρ CENY CENY 1 2 3 4 5 6
Vytvoření matice 2×2 se všemi prvky = 1:
M1 ← 2 2 ρ 1
Vytvoření matice 2×6 se všemi prvky = 5:
M2 ← 2 6 ρ 5
Spojení matic (musí mít stejný počet řádků):
VYSLEDEK ← M1,M2
Výpis obsahu všech tří matic:
M1 1 1 1 1 M2 5 5 5 5 5 5 5 5 5 5 5 5 VYSLEDEK 1 1 5 5 5 5 5 5 1 1 5 5 5 5 5 5
10. Přístup k prvkům polí (použití indexů), funkce „take“ a „drop“
V programovacím jazyku APL je možné, podobně jako v prakticky všech moderních programovacích jazycích, přistupovat k jednotlivým prvkům polí, tj. k prvkům vektorů, matic atd. Na následujícím demonstračním příkladu je ukázán způsob vytvoření jednorozměrného pole (vektoru) se sedmi prvky a přístup ke třetímu prvku tohoto pole s využitím indexu zapsaného do hranatých závorek. Posléze je vytvořeno dvourozměrné pole (tj. matice) velikosti 3×3 prvky a následně je proveden přístup k prvku ležícímu uprostřed této matice. Dvojice indexů je v tomto případě taktéž zapsána do závorek, přičemž indexy jsou od sebe odděleny středníkem (nikoli čárkou, ta má zcela jiný význam, protože v APL slouží ke spojování polí!). Povšimněte si, že prvky pole jsou číslovány od jedničky (na rozdíl od jazyků odvozených od céčka), což zjednodušuje poměrně velkou část algoritmů, především v těch případech, kdy se nepoužívají programové smyčky, kterým se v APL můžeme v mnoha případech velmi elegantně vyhnout:
Vektor ← 11 22 33 44 55 66 77
Vektor
11 22 33 44 55 66 77
Vektor[3]
33
Matice ← 3 3 ρ ι 9
Matice
1 2 3
4 5 6
7 8 9
Matice[2;2]
5
Výše uvedená dvojice demonstračních příkladů pravděpodobně žádného vývojáře nepřekvapila, protože přístup k jednomu prvku pole je v naprosté většině současných programovacích jazyků velmi podobný, samozřejmě pokud zanedbáme některé méně podstatné implementační detaily (způsob zápisu závorek, hodnota indexu prvního prvku, způsob oddělení indexů). Zajímavější je však to, že v programovacím jazyku APL je možné vybrat libovolný počet prvků pole, přičemž indexy prvků ve výběru se mohou opakovat nebo být různě zpřeházené. Výsledkem všech následujících operací je vektor, tj. nikoli pouze skalární hodnota. U posledního příkazu je navíc použita monadická varianta funkce ι, která v generuje indexy od jedničky až do zadané hodnoty (v tomto konkrétním případě se jedná o čísla 1 2 3 4 5, takže se vrátí hodnoty prvního až pátého prvku):
Pole ← 11 22 33 44 55 66 77
Pole
11 22 33 44 55 66 77
Pole[1 2 3]
11 22 33
Pole[3 2 1]
33 22 11
Pole[1 3 5 5 3]
11 33 55 55 33
Pole[ι5]
11 22 33 44 55
Ovšem všechny výše uvedené příklady jsou jen pouhým náznakem síly operací, které je možné s prvky polí provádět. Prvkům polí lze přiřazovat hodnoty (to samozřejmě nikoho neohromí), ovšem mnohem zajímavější je, že hodnoty lze přiřadit i více prvkům polí současně (v podstatě se jedná o opak výše ukázaných operací vrácení hodnot vybraných prvků polí). V některých případech je vhodné pracovat přímo s celým sloupcem či řádkem dvourozměrné i vícerozměrné matice. I tuto operaci programovací jazyk APL samozřejmě podporuje. Nejlépe se tato operace vysvětluje na dvourozměrných maticích: pokud je zapotřebí vybrat celý řádek matice, postačuje do hranatých závorek zadat číslo řádku, za nímž následuje pouze středník (bez dalších hodnot). Výběr sloupce je obdobný – do hranatých závorek se zapíše středník následovaný indexem sloupce (ve skutečnosti jsou hodnoty uložené ve sloupci převedeny na řádkový vektor, což je však v kontextu jazyka APL logické). Dokonce je možné jednotlivé způsoby zkombinovat, tj. například vybrat pouze několik hodnot na jednom řádku matice atd. – viz následující příklady:
Pole ← 11 22 33 44 55 66 77
Pole
11 22 33 44 55 66 77
Pole[7] ← 777
Pole
11 22 33 44 55 66 777
Pole[1 2 3] ← 0 42 6502
Pole
0 42 6502 44 55 66 777
Pole[7 6] ← 0 1
Pole
0 42 6502 44 55 1 0
Pole[ι5]
0 42 6502 44 55
10×Pole[ι5]
0 420 65020 440 550
Matice ← 3 3 ρ ι 9
Matice
1 2 3
4 5 6
7 8 9
Matice[2;2]
5
Matice[1;]
1 2 3
Matice[;1]
1 4 7
Matice[;1] + Matice[;3]
4 10 16
2×Matice[1;]
2 4 6
Matice[3;1 3]
7 9
Matice[;3] ← Matice[;1] + Matice[;2]
Matice[3;] ← Matice[2;] × Matice[3;]
Programovací jazyk APL obsahuje i dvojici funkcí, které se používají pro manipulaci se seznamy, jenž jsou reprezentovány pomocí vektorů, tj. jednodimenzionálních polí. Jedná se o funkce pojmenované „take“ a „drop“. Funkce „take“, která se zapisuje pomocí symbolu ↑, slouží k získání prvních n prvků seznamu. Pokud je použita monadická forma této funkce, vrátí se pouze první prvek (což v Lispu odpovídá funkci car), v případě použití dyadické formy se vrátí takový počet prvků, jaký udává hodnota prvního parametru této funkce (druhým parametrem je samotný seznam). Naproti tomu funkce „drop“ zapisovaná pomocí symbolu ↓ „zahodí“ prvních n prvků seznamu a následně vrátí jeho zbytek (takže 1↓ odpovídá v Lispu funkci cdr). U obou funkcí lze n zadat i jako záporné číslo. V tomto případě se prvky vybírají či zahazují z konce seznamu a nikoli z jeho začátku. Následuje jednoduchý příklad ukazující vlastnosti obou výše zmíněných funkcí „take“ a „drop“. V příkladu jsou použita záporná čísla, která jsou označena symbolem ¯ (overbar, high-minus) a nikoli funkcí – (minus):
Seznam ← ι10
Seznam
1 2 3 4 5 6 7 8 9 10
1 ↑ Seznam
1
1 ↓ Seznam
2 3 4 5 6 7 8 9 10
↑ Seznam
1
4 ↑ Seznam
1 2 3 4
5 ↓ Seznam
6 7 8 9 10
¯1 ↑ Seznam
10
¯1 ↓ Seznam
1 2 3 4 5 6 7 8 9
Funkce „take“ a „drop“ je možné použít i ke složitějším výpočtům s vektory, opět (jak je tomu v programovacím jazyce APL zvykem) bez použití programových smyček. Jedná se o výpočty, ve kterých je nutné provádět aritmetické či logické operace se sousedními hodnotami uloženými ve vektoru, a to tehdy, když není možné použít minule popsané operátory reduce a scan. Například budeme chtít vypočítat meziměsíční rozdíly mezi tržbami nějaké firmy (tržby jsou uloženy ve vektoru Trzby), a to jak v absolutních hodnotách, tak i rozdíly vyjádřené v procentech poklesu či naopak vzrůstu. Nejprve si vytvoříme dva pomocné vektory, z nichž jeden neobsahuje první prvek původního vektoru a druhý naopak neobsahuje jeho prvek poslední. Vytvoření pomocných vektorů zajistí funkce „drop“ (bylo by sice možné použít i funkci „take“, ale u té by se musela vypočítat délka vektoru, což je zbytečně komplikované):
Trzby ← 56 59 67 64 60 61 68 73 78 75 81 84
Trzby
56 59 67 64 60 61 68 73 78 75 81 84
1 ↓ Trzby
59 67 64 60 61 68 73 78 75 81 84
¯1 ↓ Trzby
56 59 67 64 60 61 68 73 78 75 81
Výpočet rozdílů mezi jednotlivými měsíčními tržbami je po získání pomocných vektorů triviální, neboť tyto vektory stačí od sebe odečíst:
(1 ↓ Trzby) - (¯1 ↓ Trzby) 3 8 ¯3 ¯4 1 7 5 5 ¯3 6 3
Následuje vzorec pro výpočet růstu či poklesu tržeb vyjádřeného v procentech, opět bez použití programových smyček a pomocných proměnných:
100 × ((1 ↓ Trzby) ÷ (¯1 ↓ Trzby)) - 1 5.35 13.56 ¯4.48 ...
V případě nejistoty, zda se nejdříve provede odečtení jedničky od mezivýsledku či vynásobení mezivýsledku hodnotou 100 si připomeňme, že v jazyku APL se parametry všech funkcí vyhodnocují zprava doleva, tj. nejdříve je od podílu odečtena jednička a teprve poté je proveden převod na procentní vyjádření výsledku celého výpočtu (pomocí závorek se samozřejmě dá pořadí vyhodnocování v případě potřeby upravit).
11. Šestice základních operátorů aplikovatelných na pole
Dalším zajímavým a přitom velmi důležitým nástrojem vývojářů v programovacím jazyce APL jsou vybrané operátory, pomocí nichž je možné například aplikovat nějakou funkci na všechny prvky pole, zkombinovat vzájemně všechny prvky v poli (z vektoru o n prvcích se aplikací operátoru inner product stane matice o rozměrech n×n prvků) atd. Právě díky těmto operátorům nemusí programátoři tvořící aplikace v jazyku APL vytvářet programové smyčky, protože například součet (sumu) či součin (produkt) všech prvků vektoru lze velmi jednoduše zapsat pomocí dyadické funkce + nebo × aplikované postupně na všechny prvky vstupního vektoru. Programovací jazyk APL obsahuje šest základních operátorů, ovšem některé jeho modernější implementace nabízí operátorů více (většinou osm). Šestice základních operátorů, se kterou se můžeme setkat ve většině dialektů jazyka APL, je vypsána v následující tabulce:
| Operátor | Unicode | Jméno |
|---|---|---|
| ¨ | 00a8 | each |
| / | 002f | slash, reduce |
| \ | 005c | backslash, scan |
| [] | 005b, 005d | axis |
| . | 002e | inner product |
| ◦. | 25e6, 002e | outer product |
12. Operátory „reduce“ a „scan“
Základním operátorem, využívaným v prakticky jakékoli aplikaci napsané v programovacím jazyku APL, je operátor pojmenovaný „reduce“, který je nazývaný také „slash“ (druhý název tohoto operátoru vznikl ze symbolu, kterým je operátor zapisovaný – /). Tento operátor se zapisuje za symbol dyadické funkce a má ten význam, že vybranou funkci postupně aplikuje (volá) na všechny prvky pole. Prvním argumentem každé aplikace funkce je mezivýsledek (většinou skalární hodnota, prvním mezivýsledkem je první prvek pole), druhým argumentem pak n-tý prvek pole. Operátor reduce tedy předané pole zpracovává postupně, prvek po prvku. Typickým příkladem může být výpočet sumy (součtu, v matematice zapisovaný symbolem Σ) všech prvků vektoru či součinu všech jeho prvků (v matematice se používá symbol Π). Tyto dvě často používané operace je možné s využitím operátoru reduce naprogramovat v jazyku APL velmi snadno bez použití programové smyčky a bez pomocných proměnných:
+/ 1 2 3 4
10
×/ 1 2 3 4
24
Při použití operátoru reduce samozřejmě můžeme použít jakoukoli dyadickou funkci, například i výše zmíněné funkce ᒥ a ᒪ, které vrací větší, popř. menší z obou předaných argumentů. Pokud se tyto funkce postupně aplikují na celý vektor, vrátí největší nebo nejmenší prvek celého tohoto vektoru:
ᒥ/ 75 72 78 90 69 77 81 88
90
ᒪ/ 75 72 78 90 69 77 81 88
69
Výpočet průměru řady čísel uložených ve vektoru je velmi jednoduchý když si uvědomíme, že počet čísel, tj. délku vektoru, lze zjistit pomocí funkce ρ. Nejprve se tedy všechna čísla sečtou a následně se mezivýsledek vydělí jejich počtem:
X ← 1 2 3 4 5
(+/X)÷ρX
3
Nyní si ukažme, jakým způsobem se používá operátor reduce při práci s maticemi. Při popisu tohoto operátoru jsme si řekli, že se postupně volá nějaká vybraná funkce na všechny prvky pole. V případě vektoru byla situace jednoduchá, protože prvkem vektoru byly přímo skalární hodnoty (tj. běžná čísla, popř. znaky). Pokud se však operátor reduce použije na dvourozměrné matice (podobně i na vícedimenzionální struktury), jsou v tomto případě prvkem pole myšlené celé vektory (řádky matice), na jejichž prvky je funkce aplikována (jinými slovy – operátor je uplatňován na nejnižší dimenzi, tj. sloupcích):
Matice ← 3 3 ρ ι 9
Matice
1 2 3
4 5 6
7 8 9
+/ Matice
6 15 24
Součet všech prvků dvourozměrné matice (například rastrového obrázku) lze zajistit dvojím použitím operátoru reduce. Jeho první aplikace zajistí součet všech hodnot na jednotlivých řádcích matice, druhá aplikace operátoru sečte vektor součtů (6 15 24) jednotlivých řádků:
+/ +/ Matice 45
Sumu lze samozřejmě spočítat i pro vybraný sloupec či řádek matice. Dokonce je možné v případě potřeby specifikovat dimenzi, ve které bude operátor uplatňován (v případě dvourozměrných matic tak lze operátor aplikovat buď na sloupce nebo na řádky bez nutnosti transpozice matice):
+/ Matice[;1]
12
+/[1] Matice
12 15 18
Dalším operátorem, se kterým se v tomto článku krátce seznámíme, je operátor nazvaný scan nebo také backslash. Tento operátor je v programech zapisovaných v jazyku APL reprezentován, jak již ostatně jeho druhé jméno napovídá, obráceným lomítkem – \. Operátor scan má chování podobné výše popsanému operátoru reduce, ovšem s jedním podstatným rozdílem – zatímco v případě použití operátoru reduce se dozvíme pouze celkový výsledek aplikace vybrané funkce na pole, je u operátoru scan vrácen vektor všech mezivýsledků, čehož je možné v některých případech využít a opět tak eliminovat potřebu tvorby programových smyček. Tento operátor lze použít spolu s jakoukoli dyadickou funkcí (tedy platí totéž, co o operátoru reduce). Na následujících demonstračních příkladech si povšimněte rozdílu v chování obou operátorů:
+/ 1 2 3 4 5
15
+\ 1 2 3 4 5
1 3 6 10 15
×/ ι4
24
× \ ι4
1 2 6 24
Poslední příklad počítá tabulku faktoriálů. Ostatně můžeme si to otestovat na delší řadě (tentokrát vynechám přebytečné mezery):
×\⍳10 1 2 6 24 120 720 5040 40320 362880 3628800
13. Operátor „inner product“
Další z doposud nepopsaných operátorů je operátor „inner product“ zapisovaný formou tečky okolo které se uvádí programátorem zvolená dvojice funkcí (může se jednat jak o uživatelské funkce, tak i o funkce primitivní). V podstatě se jedná o zobecněnou operaci skalárního součinu, ovšem s tím rozšířením, že obě aritmetické operace použité při násobení prvků vektorů (tj. součin a součet) je při použití operátoru „inner product“ možné zadat formou dvojice dyadických funkcí. To znamená, že pouze při použití cca dvaceti základních primitivních funkcí je možné vytvořit až 400 jejich kombinací a nahradit tak poměrně značnou část (nejenom maticových) algoritmů pouhou aplikací jednoho operátoru na dvojici funkcí. Kromě násobení matic lze například pomocí „inner productu“ vyjádřit hodnotu polynomu pro libovolné x (polynom je zadán vektorem koeficientů ai) atd.
Vstupní vektory:
v1 ← ⍳4
v2 ← 2 2 2 2
Klasický skalární součin dvou vektorů:
v1 +.× v2 20
Otočení pořadí operací – odpovídající si prvky se nejdříve sečtou a mezivýsledky se vynásobí:
v1 ×.+ v2 360
Součet všech součtů odpovídajících si prvků:
v1 +.+ v2 18
14. Operátor „outer product“
Jedním z prozatím nepopsaných operátorů je operátor nazvaný „outer product“ zapisovaný dvojicí symbolů ◦. (tj. jako kolečko+tečka) za níž následuje jméno či symbol nějaké dyadické funkce. Tento operátor je založen na principu aplikace zvolené dyadické funkce na dvojici vektorů x a y, přičemž vybraná funkce je aplikována na všechny možné kombinace složek prvního a druhého vektoru. Výsledkem je matice Z obsahující v prvku zij návratovou hodnotu funkce aplikované na prvky xi a yj. Nejlépe si význam i princip práce tohoto operátoru vysvětlíme na příkladu, ve kterém se pokusíme vypsat část tabulky malé násobilky. Budeme tedy chtít získat násobky všech možných kombinací vstupních vektorů:
1 2 3 4 5 ◦.× 1 2 3 4 5 1 2 3 4 5 2 4 6 8 10 3 6 9 12 15 4 8 12 16 20 5 10 15 20 25
Programátoři v APL by ale spíše napsali:
(ι5)◦.×(ι5) 1 2 3 4 5 2 4 6 8 10 3 6 9 12 15 4 8 12 16 20 5 10 15 20 25
Nebo jen:
(⍳10)∘.×⍳10 1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 100
Popř. si můžeme vytvořit pomocnou funkci f určenou pro výpočet tabulky součinů:
f ← {(⍳⍵) ∘.× (⍳⍵)}
f 10
1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
V úvodní části dnešního článku jsme si uvedli i primitivní funkci *, která slouží k umocnění dvou čísel, tj. provedení operace xy. Tabulku mocnin prvních čtyř přirozených čísel lze získat snadno:
(ι4)◦.*(ι4) 1 1 1 1 2 4 8 16 3 9 27 81 4 16 64 256
Tento operátor je samozřejmě možné použít i v kombinaci s dalšími funkcemi, nejenom s násobením a umocňováním. Poměrně často se používá například ke konstrukci jednotkové matice či trojúhelníkové matice obsahující pouze prvky s hodnotou 0 a 1. Konstrukce těchto matic je s využitím výše uvedených porovnávacích (relačních) funkcí velmi snadná a rychlá:
(ι5)◦.=(ι5)
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
(ι5)◦.<(ι5)
0 1 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
0 0 0 0 0
(ι5)◦.≤(ι5)
1 1 1 1 1
0 1 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
(ι5)◦.≥(ι5)
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
15. Hierarchické datové struktury, komprese polí
Ve všech předchozích demonstračních příkladech jsme používali buď skalární hodnoty, vektory (jednorozměrná pole) nebo pravidelné matice (dvourozměrná pole). Programovací jazyk APL však ve svých moderních implementacích podporuje i hierarchické datové struktury, které jsou ovšem stále reprezentovány pomocí polí. Jednou z nejpoužívanějších struktur jsou vnořené seznamy, na které se lze také dívat jako na „zubatá“ pole, resp. jako na matici s nestejně dlouhými řádky. Zápis takové struktury je velmi jednoduchý (povšimněte si, že při inicializaci není nutné uvádět dimenze ani velikost pole):
DATA ← (1 2 3) (4 5) (6 7) (8 9 10 11)
Předchozí datová struktura představuje vektor, jehož prvky jsou taktéž vektory. Podobnou strukturu lze vytvořit i z matic – prvkem matice totiž může být skalární hodnota, vektor, matice či pole o prakticky libovolné dimenzi (většinou jsme omezeni 63 dimenzemi, takže se o skutečné omezení ani nejedná). Následující příkaz vytvoří tabulku (matici) o dvou řádcích a třech sloupcích. První prvek matice je taktéž maticí, tentokrát o velikosti 2×2 prvky, druhý prvek je seznamem (vektorem) o pěti prvcích, třetí prvek je řetězcem (seznamem šesti znaků) atd. Povšimněte si nutnosti uzávorkování některých podvýrazů:
NEST ← 2 3ρ(2 2ρι4) (ι5) 'HELLO!' (2 4ρι8) 23 (3 2ρ 'APL')
NEST
1 2 1 2 3 4 5 HELLO!
3 4
1 2 3 4 23 APL APL
5 6 7 8 APL APL
APL APL
Rozměr pole lze zjistit, jak už víme z předchozího textu, pomocí monadické formy primitivní funkce ρ:
ρNEST 2 3
Při práci s hierarchickými strukturami je někdy nutné zjistit stupeň zanoření zpracovávané datové struktury. Pro zjištění stupně zanoření jakéhokoli objektu zpracovávaného jazykem APL je určena funkce depth zapisovaná pomocí symbolu ≡. Platí, že skalární hodnoty mají vždy stupeň zanoření roven nule, kdežto pole (vektory, matice, …) obsahující pouze skalární hodnoty mají stupeň zanoření 1. Výše uvedené pole NEST má stupeň zanoření roven dvěma, protože jako svůj prvek obsahuje matice. Vlastnosti funkce ≡ si můžeme snadno ověřit na několika hodnotách:
≡42 0 ≡1 2 3 1 ≡2 2ρ3 4 5 6 1 ≡NEST 2
S vektory či maticemi obsahujícími binární hodnoty úzce souvisí i funkce provádějící takzvanou kompresi polí. Jedná se o dyadickou primitivní funkci představovanou symbolem /, která na základě pole (vektoru, matice) obsahujícího pouze binární hodnoty 0 nebo 1 vybere z jiného pole o stejné dimenzi i velikosti ty prvky, u nichž je odpovídající binární hodnota rovna jedničce. Nejlépe si funkci komprese pole ukážeme na jednoduchém příkladu, ve kterém bude opět použit vektor Prodeje, s nímž jsme se již setkali v předchozí kapitole:
Prodeje ← 1100 1200 1300 900 850 930 1050 970
Prodeje
1100 1200 1300 900 850 930 1050 970
0 1 0 1 0 1 0 1 / Prodeje
1200 900 930 970
Binární vektor lze samozřejmě získat na základě jiného příkazu; například je možné vzít výsledek funkce porovnání (relace) popsané v předchozím odstavci a na základě hodnoty výsledného binárního vektoru vybrat z pole Prodeje jen hodnoty odpovídající zvolené podmínce:
Prodeje ← 1100 1200 1300 900 850 930 1050 970
(Prodeje > 1000) / Prodeje
1100 1200 1300 1050
V případě, že je zapotřebí získat indexy prvků a nikoli jejich hodnoty, můžeme si vypomoci vektorem zkonstruovaným pomocí funkce ι (jóta) se stejnou délkou, jako má původní vektor:
Prodeje ← 1100 1200 1300 900 850 930 1050 970
Prodeje
1100 1200 1300 900 850 930 1050 970
Prodeje > 1000
1 1 1 0 0 0 1 0
ρProdeje
8
ιρProdeje
1 2 3 4 5 6 7 8
Máme tedy dva mezivýsledky, oba ve formě vektoru o shodné délce (konkrétně vektor 1 1 1 0 0 0 1 0 a 1 2 3 4 5 6 7 8), které je možné zkonstruovat a současně i vzájemně zkombinovat v jednom příkazu a získat tak indexy prvků odpovídajících zapsané podmínce:
(Prodeje>1000)/ιρProdeje 1 2 3 7
16. Praktické vyzkoušení možností jazyka APL
V současnosti je pravděpodobně nejpoužívanější variantou APL Dyalog, což je komerční (a nutno podotknout, že velmi dobré) vývojové prostředí, které lze získat z adresy https://www.dyalog.com/. Ovšem pro otestování možností APL není nutné si Dyalog instalovat, protože je k dispozici webové prostředí dostupné na adrese https://tryapl.org/, které lze spustit přímo z prakticky jakéhokoli moderního webového prohlížeče. Toto prostředí mj. nabízí i trojí způsob zápisu základních funkcí a operátorů – buď se vybírají z horního pruhu se symboly, nebo je možné použít dvojznaku následovaného klávesou Tab, popř. prefixového znaku následovaného nějakým ASCII znakem. Obě poslední možnosti jsou uvedeny v tabulce pro často používaný symbol ι:
| Dvojznak následovaný TABem | iiTab |
| Prefixový znak | `i |
Obrázek 20: Prostředí TryAPL.
17. Jak myslet v APL – výpočet prvočísel netradičním způsobem
Ukažme si nyní, jakým způsobem by bylo možné s využitím programovacího jazyka APL napsat program pro výpočet prvočísel. Použijeme přitom pro jednoduchost neidiomatickou formu zápisu, v níž se několikrát vyskytuje mezivýsledek. Výsledný program pro výpočet prvočísel od 2 do hodnoty x může vypadat následovně:
(~R∊R∘.×R)/R←1↓⍳x
Pro jazyk APL je typické, že výsledný program nemusí být příliš čitelný, zatímco jeho tvorba je (pro autora) zcela logická. Bude tedy vhodnější si ukázat, jak vlastně tento program vznikl – protože myšlenkový postup se dosti podstatným způsobem odlišuje od „klasické“ implementace generátoru prvočísel, který bývá založen na algoritmu Eratosthenova síta. V APL lze využít odlišného postupu (ale když se nad programem zamyslíme, ve skutečnosti ne zcela odlišného – ve skutečnosti i zde obdobu Eratosthenova síta najdeme, ovšem v „maticové“ podobě).
Jednotlivé kroky si postupně rozepíšeme:
| Krok | Zápis | Význam |
|---|---|---|
| 1 | ⍳x | vytvoření sekvence čísel od 1 do x |
| 2 | 1↓⍳x | odstranění prvního čísla, tedy jedničky |
| 3 | R←1↓⍳x | uložení mezivýsledku do vektoru pojmenovaného R |
| 4 | R∘.×R | výpočet matice s násobky všech kombinací R (outer product) |
| 5 | R∊R∘.×R | test, která čísla jsou nalezena i v matici násobků |
| 6 | ~R∊R∘.×R | negace předchozího testu – vyberou se tedy čísla, která v matici nejsou |
| 7 | (~R∊R∘.×R)/R | použití předchozí matice pro výběr z mezivýsledku (vektoru čísel) |
Celý postup si ještě jednou postupně ukážeme a okomentujeme.
Budeme chtít získat prvočísla v rozsahu od 0 do 10. Nastavíme tedy hodnotu x na 10:
x ← 10
Pokračujeme zprava doleva. První funkce vrátí hodnoty od 1 do 10:
⍳x 1 2 3 4 5 6 7 8 9 10
V dalším kroku odstraníme jedničku ze začátku sekvence:
1↓⍳x 2 3 4 5 6 7 8 9 10
Mezivýsledek uložíme do pomocného vektoru R:
R←1↓⍳x R 2 3 4 5 6 7 8 9 10
Pomocí vnějšího násobení získáme tabulku s násobky všech kombinací prvků z R:
R∘.×R 4 6 8 10 12 14 16 18 20 6 9 12 15 18 21 24 27 30 8 12 16 20 24 28 32 36 40 10 15 20 25 30 35 40 45 50 12 18 24 30 36 42 48 54 60 14 21 28 35 42 49 56 63 70 16 24 32 40 48 56 64 72 80 18 27 36 45 54 63 72 81 90 20 30 40 50 60 70 80 90 100
Zde již máme nástin řešení – tato tabulku již z principu nemůže obsahovat žádné prvočíslo.
Zjistíme, které prvky z R jsou obsaženy v tabulce – tedy které prvky nejsou prvočísly:
R∊R∘.×R 0 0 1 0 1 0 1 1 1
Po negaci získáme masku těch prvků, které naopak prvočísly jsou:
~R∊R∘.×R 1 1 0 1 0 1 0 0 0
Nyní již zbývá použít výše uvedenou funkci / pro výběr prvků z R na základě vektoru binárních čísel (masky):
(~R∊R∘.×R)/R 2 3 5 7
Výpočet si můžeme uložit do funkce pojmenované p, kterou následně použijeme s různým horním limitem:
p←{(~R∊R∘.×R)/R←1↓⍳⍵}
p 10
2 3 5 7
p 100
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
18. Další programovací jazyky podporující práci s vektory a maticemi
Práce s vektory a maticemi ovšem nebyla pouze doménou programovacího jazyka APL. Objevila se již ve FORTRANu; ostatně překlad programů s orientací na paralelní výpočty proběhl právě s FORTRANem (konkrétně u superpočítačů vyráběných společností Cray). Nesmíme ale zapomenout ani na ideového následníka APL, jímž je programovací jazyk nazvaný J. Kromě dua APL a J (a na nich navazujících jazyků K, BQN apod.) byly maticové operace součástí programovacího jazyka BASIC, konkrétně jeho původní „originální a jediné pravé“ varianty nazvané Dartmouth BASIC, který ve své třetí verzi pocházející z roku 1966 obsahoval deklaraci MAT doplňující již dříve používanou deklaraci pole příkazem DIM. Zajímavé přitom je, že se v BASICu operace pro deklaraci a práci s maticemi objevily dříve než podpora řetězců, což bylo pravděpodobně způsobeno především tím, že oba autoři BASICu (tedy jak John Kemeny, tak i Thomas Kurtz) byli matematici a současně i vývojáři s velmi dobrou znalostí programovacího jazyka FORTRAN.
V současnosti je používáno relativně velké množství programovacích jazyků, popř. specializovaných knihoven orientovaných na práci s vektory a poli. Z komerčních nástrojů je zapotřebí jmenovat především známý MATLAB vydávaný společností MathWorks (ten má matici již ve svém názvu), nativní práci s maticemi a vektory ovšem velmi dobře podporuje také nástroj GNU Octave (https://gnu.org/software/octave/), jazyk R (http://www.r-project.org/) a také relativně nový jazyk Julia (http://julialang.org/, zajímavé výsledky benchmarků lze najít na adrese http://julialang.org/benchmarks/). Z knihoven jmenujme především oblíbenou a dnes dosti intenzivně využívanou Pythonovskou knihovnu NumPy (http://www.numpy.org/).
Programovací jazyk APL do vývoje některých typů aplikací (finančnictví, simulace, …) přinesl mnoho nových myšlenek (ostatně i proto se doposud používá), ale i několik nectností, ostatně jako každý programovací jazyk, který vznikl na samotném začátku vývoje interpretrů a překladačů, tj. v době, kdy ještě nebyla teorie překladačů tak rozvinutá jako v pozdějších letech (nejvíce byla neexistence teorie překladačů patrná u prvního překladače Fortranu firmou IBM, jehož vývoj by byl při uplatnění dnešních znalostí mnohem rychlejší i levnější). Už při letmém pohledu na programy napsané v programovacím jazyce APL je zřejmé, že se v něm používá velké množství symbolů, které se nenachází ve znakové sadě ASCII, což je sice velmi unikátní vlastnost (právě proto mnozí vývojáři v APL programují čistě pro radost), ale způsobuje poměrně velké problémy, a to jak při zápisu programů (rozložení znaků na klávesnici), tak i při jejich úpravách, prezentaci na Internetu, protože zdaleka ne všechny fonty obsahují všechny požadované symboly. Některé vlastnosti jazyka APL navíc nebyly navrženy zcela dokonale – typickým příkladem je podpora pro tacit programming, která ustrnula na půli cesty.
Z výše uvedených důvodů otec jazyka APL (již je v dnešním článku mnohokrát zmiňovaný Kenneth Iverson) na počátku devadesátých let minulého století navrhl nový programovací jazyk nazvaný jednoduše J, který některé výše zmíněné nedostatky jazyka APL odstranil a navíc jazyk rozšířil o některé důležité nové rysy, primitivní funkce i operátory. Programovací jazyk J je, podobně jako jeho ideový předchůdce APL, určen především pro tvorbu aplikací, v nichž se zpracovávají data uložená ve vektorech, maticích či polích s větším počtem dimenzí (může se jednat například o hierarchické mřížky atd.). Z tohoto důvodu je jazyk J vybaven jak jednoduchou syntaxí určenou pro zápis vektorů a matic, tak i sadou primitivních (základních) funkcí, pomocí nichž lze nad vektory i maticemi provádět různé operace. Tento jazyk dnes existuje jak v komerční, tak i volně dostupné variantě.
19. Literatura
O programovacím jazyku APL, resp. o Iversonově notaci vzniklo mnoho knih. V dnešním článku je udávám především z toho důvodu, že některé z nich je možné najít i v tuzemských univerzitních nebo technických knihovnách:
- Ajay Askoolum, „System Building with APL + WIN,“
Wiley, ISBN: 0–470–03020–8, August 2006. - Brown et. al. „APL2 at a Glance,“
Prentice Hall, ISBN 0–13–038670–7. - T. Budd, „An APL Compiler,“
Springer-Verlag. - Maurice Dalois, „Introduction to APL*PLUS PC,“
- J. Ever and C. Fair, „Guidelines for APL Systems,“
DPD 22 IBM 037301, March 1976. - Gilman and Rose, „APL – An Interactive Approach,“
Wiley, ISBN 220–471–30022–5. - Ulf Grenander, „Mathematical Experiments on the Computer,“
Academic Press, 1982, ISBN 0–12–301750–5. - Kent Haralson, „Useful APL Defined Functions“,
IBM Technical Report, TR 00.2409, Feb. 8 1973. - Timothy Holls, „APL Programming Guide,“
IBM G320–6103, 1978, and G320–6735, 1981. - IBM, „APL2 Programming: Language Reference“
(Version 2, SH21–1061; Version 1, SH20–9227). - IBM, „The APL Handbook of Techniques“,
IBM publication number S320–5996, April 1978. - IBM, „The IBM System Journal, V. 30, No. 4 (1991)“,
Special Issue Devoted to APL. - MicroAPL, „Learning APL with APLX“,
Version 5.0 July 2009 - A.D. Falkoff, K.E Iverson, E.H Sussenguth, „A formal description of System/360,“
The IBM System Journal, V. 3, No. 3 (1964) - K. E. Iverson, „A Programming Language“,
Wiley, 1962. - K. E. Iverson, „Algebra : an algorithmic treatment“,
APL Press 1977, Copyright 1972 by Addison Wesley,
Preliminary Edition entitled „Elementary Algebra“
Copyright 1971 by IBM Corporation. - K. E. Iverson, „Elementary analysis“,
APL press 1976, Preliminary Edition „Elementary Functions“
Copyright 1974 by IBM Corporation ISBN 0–917326–01–6 - K. E. Iverson, „An introduction to APL for Scientists and Engineers“,
APL Press 1976,
First published by IMB Corporation as Technical Report No 320–3019 March 1973 – ISBN 0–917326–04–0 - K. E. Iverson, „APL in exposition“,
APL Press 1976,
First published by IBM Corporation as Technical Report No 320–3010 March 1973 – ISBN 0–917326–02–4. - K. E. Iverson, „Introduction To APL“,
(1984-APL Press Palo Alto) ISBN 0–917326–14–8. - K. E. Iverson, „A personal view of APL,“
IBM Systems Journal, - K. E. Iverson, „Concrete Mathematics Companion“.
- S. Kamin, „Programming Languages: An Interpreter-Based Approach,“
contains (among other things) toy implementations of Lisp, APL, Scheme, SASL, CLU, Smalltalk, and Prolog, Addison-Wesley, 1990, ISBN 0–201–06824–9. - Bernard LEGRAND, „Les APL Etendus,“
Masson, Paris, 1994. An introduction to modern APL (French). - Jon McGrew, „An Introduction to APL2,“
IBM (SH20–9229). - James A. Mason, „Learning APL: An Array Processing Language,“
Harper & Row Publishers Inc., New York, 1986, ISBN 0–06–044243–3 260 pp. - Peelle, „APL an Introduction“,
Holt, Rinehart & Winston, ISBN 0–03–004953–9. - Reiter & Jones, „APL with a Mathematical Accent“,
Brooks/Cole ISBN 0–534–12864–5, (now being distributed by Chapman & Hall). - C. Reiter, „Fractuals Visualization and J“,
Iverson Software, Inc, 1995 ISBN 1–895721–11–3. - Adrian Smith, „APL, A Design Handbook for Commercial Systems,“
Wiley series in information processing, Wiley & Sons, 1982, ISBN 0–471–10092–7. - D. Stiers, M.J. Goovaerts, J. De Kerf, „APL – The Language and its Actuarial Applications“
- Norman D. Thomson, Raymond P. Polivka, „APL2 in Depth,“
Springer-Verlag, 1995, ISBN 0–387–94213–0. - Jerry R. Turner, „APL IS EASY!,“
Manugistics, 1993. - „SHARP APL Reference Manual,“
2nd ed., Soliton Associates Limited PC Version: Iverson Software, 1993, ISBN 1–895721–07–5. - „A Source Book in APL,“
APL Press, 1981, ISBN 0–917326–10–5. - „J Phrases,“
Iverson Software, 1996, ISBN 1–895721–12–1 - „Exploring Math“, Iverson Software, 1996, ISBN 1–895721–13-X
- „J Primer,“
Iverson Software, 1996, ISBN 1–895721–14–8 - Linda Alvord and Norman Thomson, „Easy-J: An Introduction to the World's most Remarkable Programming Language“
October 2002
20. Odkazy na Internetu
- APL Wiki
https://aplwiki.com/wiki/ - The Array Cast
https://www.arraycast.com/episodes/episode-03-what-is-an-array - EnthusiastiCon 2019 – An Introduction to APL
https://www.youtube.com/watch?v=UltnvW83_CQ - Dyalog
https://www.dyalog.com/ - Try APL!
https://tryapl.org/ - APL na replit
https://replit.com/languages/apl - Advent of Code 2020 in APL!
https://www.youtube.com/watch?v=0RQFW6P1Tt0 - Python vs APL (1 Problem)
https://www.youtube.com/watch?v=APdKFJkmBbM - APL Wins (vs C++, Java & Python)
https://www.youtube.com/watch?v=59vAjBS3yZM - A Tour de Force of APL in 16 Expressions by Roger Hui
https://www.youtube.com/watch?v=e0rywC7-i0U - Conway's Game Of Life in APL
https://www.youtube.com/watch?v=a9×AKttWgP4 - A List of companies that use Array Languages (J, K, APL, q)
https://github.com/interregna/arraylanguage-companies - APL – one of the greatest programming languages ever
http://www.vaxman.de/publications/apl_slides.pdf - „The J Programming Language“ by Tracy Harms (2013)
https://www.youtube.com/watch?v=RWYkx6-L04Q - Dyalog Modern Programming Language, Morten Kromberg, Talks at Google
https://www.youtube.com/watch?v=PlM9BXfu7UY - The J Language: Consistency, Adjacency, and Solution-Oriented Programming – Tracy Harms
https://www.youtube.com/watch?v=gLULrFY2-fI - Un-directed programming
https://www.sacrideo.us/un-structured-programming/









































