Ruční optimalizace kompilovaného kódu
Ačkoli překladače mají stále lepší podporu automatické vektorizace, někdy se jim vektorizovat kód nedaří, nebo výsledek není optimální. Proto se vyplatí kód profilovat, a pokud nějaká špatně zvektorizovaná smyčka zabírá většinu času, věnovat se její optimalizaci ručně. Ruční optimalizaci můžeme provést několika způsoby:
- Přeskupení příkazů přímo v jazyce C, například ruční eliminace podmíněných příkazů, přidání kvalifikátorů k proměnným (restrict) a napovídání překladači pomocí direktiv #pragma. To je nejjednodušší přístup, ale ne vždy pomůže.
- Použití nativních vektorů poskytovaných GCC. Výhodou tohoto řešení je, že kód je přenositelný mezi různými architekturami; nevýhodou je, že tímto způsobem nelze přistupovat k pokročilým instrukcím procesoru.
- Použití intrinsic funkcí. Tyto funkce přímo volají jednotlivé instrukce procesoru (kód tedy pak není přenositelný), ale překladač stále řeší například alokaci registrů. Některé tyto funkce nevolají přímo jednu instrukci, ale několik málo instrukcí, které vykonávají nějaký funkční celek; můžeme se však relativně spolehnout, že výběr těchto celků provedli vývojáři procesorů a překladačů tak, aby to bylo efektivní.
- Použití ručně psaného assembleru. Toto je nejsložitější, ale poskytuje absolutní kontrolu nad výsledkem.
My se v dnešním článku budeme věnovat třetí možnosti, použití intrinsics.
Vektorové instrukce a intrinsic funkce na architektuře x86–64
K dispozici máme následující rodiny instrukcí:
- MMX – 64bitové vektory, jen celá čísla. Poměrně zastaralé a omezené, dnes se nejspíš nevyplatí používat.
- SSE – 128bitové vektory, jen data typu float (v jednoduché přesnosti), konverze float-integer a jednoduché logické operace (AND, OR…).
- SSE2 – rozšiřuje SSE o doubly (dvojitou přesnost), 8, 16, 32 a 64bit integery a bitové posuny a rotace. Dále přidává streamové instrukce, též tzv. non-temporal memory hint, které obcházejí cache procesoru, což se hodí pokud zpracováváme dlouhé pole, které nebudeme v nejbližší době používat.
- SSE3 – přidává několik instrukcí pro operace v rámci jednoho vektoru
- SSSE3 – přidává saturační aritmetiku a instrukci
palignrvhodnou pro dynamické programování - SSE4.1 – několik dalších matematických instrukcí a blend – vyzobání výsledků z jednoho a druhého vektoru
- SSE4.2 – specializované instrukce pro práci s řetězci a CRC
- AVX – 256bitové vektory, data typu float a double.
- AVX2 – přidává 8, 16, 32 a 64bit integery a bitové posuny a rotace. Zajímavé jsou gather instrukce umožňující nahrání dat, která v paměti nejsou souvislá.
- AVX-512 – komplikovaná rodina instrukcí pracujícími s 512bitovými vektory, podporují je jen nejvyšší řady procesorů do superpočítačů.
Pokud vyvíjíte pro rozumně současné desktopové a notebookové procesory, můžete předpokládat, že máte k dispozici všechna SSE, AVX a AVX2. Pokud vyvíjíte pro starší počítače (před rokem 2014) a pro embedded systémy jako Intel Atom, pravděpodobně budete mít k dispozici jen SSE (všechny verze), ale nikoli AVX.
Před vymýšlením algoritmu doporučuji otevřít si Intel Intrinsics Guide, což je webová aplikace, kde si zaškrtnete, jaké instrukční sady můžete použít, a následně v tom můžete vyhledávat. U každé instrukce je stručný popis, pseudokód co dělá a většinou i orientačně uvedeno, jak dlouho ji trvá vykonat. Je dobré si v tom na začátek chvíli klikat, ať získáte cit pro to, jaké stavební bloky jsou dostupné.
Co se týče samotného výběru instrukčních sad, osobně mi přijde, že SSEx tvoří dohromady pěkně ucelený balíček a je radost v tom programovat. Oproti tomu AVX je tak trochu procházka minovým polem:
- Instrukční sada je navržena tak, že se 256bitové vektory zpracovávají jako dvě relativně izolované 128bit lanes, a pro míchání dat napříč těmito lanes existuje jen několik instrukcí. Některé operace tak nelze vyjádřit. Na některých levnějších procesorech se AVX zpracovává na dva takty po těchto 128bit komponentách, případně je 256bit vektorová jednotka vždy sdílená mezi dvěma jádry. Použití AVX tak nemusí přinést žádnou výkonnostní výhodu.
- Některé AVX instrukce jsou označené jako heavy. Typicky jednoduché bitové operace, sčítání atd. jsou light, ale násobení už je heavy. Pokud procesor vykonává heavy instrukce, tak se podtaktuje, a to mu vydrží i chvilku po tom co už tyto instrukce neprovádí, tedy ovlivní to i rychlost okolního kódu. Ve výsledku se tedy může vyplatit zpracovávat 128bit SSE vektory plnou rychlostí než 256bit vektory podtaktovaně.
- Kombinování SSE a AVX instrukcí může vést k zásadním výkonnostním problémům pokud se přepínání mezi nimi udělá nevhodně. Tohle kombinování navíc ani nemusíte dělat sami, stačí, že použijete nějakou knihovnu, která takové instrukce používá. Toto zpomalení se navíc chová na různých mikroarchitekturách různě, takže na jednom počítači to může skvěle fungovat a na jiném se to rozbije.
Jak uvidíme v tomto článku, zrovna mnou implementovaná funkce má velmi jednoduché rozšíření ze SSE na AVX instrukce. V některých případech ale zjistíte, že se AVX nevyplatí a program stačí napsat jen pomocí SSE instrukcí.
Multiplatformní kód s použitím intrinsics
Je vhodné vedle ruční implementace s intrinsics zachovat i původní implementaci napsanou bez speciálních technik. Jednak se to hodí pro testování, jestli obě implementace vrací stejná data (snadno se v tom udělá chyba), jednak můžeme program zkompilovat i na jiných architekturách, případně na procesorech, které například AVX nepodporují. Zjištění podporovaných instrukcí během kompilace lze udělat pomocí podmíněného překladu, například #ifdef __SSE3__.
Pokud distribuujete zkompilovaný program, potřebujete mít dostupné obě varianty a za běhu vyhodnotit, které instrukce procesor umí (například přečtením souboru /proc/cpuinfo). Buď můžete mít obě funkce a měnit například nějaký pointer na ně, nebo můžete zkompilovat několik dynamických knihoven ( .so) a nahrát při spuštění tu správnou.
Popis problému
V Meteopressu stavíme radar. Pro vytváření a digitalizaci rádiových signálů používáme softwarově definované rádio bladeRF. Radar vysílá a přijímá současně na dvou polarizacích (horizontální a vertikální), což zjednodušeně řečeno umožňuje identifikovat tvar cíle (jestli je cíl symetrický, nebo v jedné ose delší než ve druhé). Rádio má dva kanály, původně určené pro režim MIMO 2×2. Data z rádia jsou komplexní 16bit čísla se znaménkem ( int16_t), ovšem protože rádio je pouze 12bitové, je rozsah těchto čísel omezen na –2048 až 2047. Toho jsem využil k tomu, že do 13. bitu vkládám servisní informace, které kódují aktuální natočení antény (azimut a elevace) a vzdálenost měřeného cíle. Tímto změřené cíle geolokalizujeme a můžeme nakreslit do mapy. Zbylé tři bity (12 bitů data + 1 bit metadata + 3 bity zbydou = 16) obsahují původní znaménko (sign extend) resp. dvojkový doplněk. Data přijatá z rádia tedy vypadají takto:
Potřebujeme napsat program, který:
- Odstraní metadata (ta se zpracovávají v jiné části našeho softwaru) a opraví sign extend tak, aby to byl zase validní int16_t. Efektivně potřebujeme do 13. bitu zkopírovat znaménko z některého z bitů 14–16, čili děláme
result = (data & 0xEFFF) | ((data & 0xE000)>>1). - Výsledné 16bitové integery převede na floaty, protože veškeré další zpracování se dělá ve floatech.
- Výsledky rozhází (deinterleavuje) do dvou samostatných polí, jedno pro horizontální a jedno pro vertikální kanál.
Data se na nás valí rychlostí 80 milionů těchto 16bitových čísel za sekundu, pokud by procesor pracoval na 2.4 GHz, máme na zpracování jednoho čísla 30 taktů. Jenže tohle není ani zdaleka jediné, co se musí provést – z dat se dále musí spočítat Fourierova transformace, aplikovat filtry, zdecimovat a výsledek zapsat do socketu, kde si ho odebere klient pro další zpracování. Tohle „jednoduché“ rozbalení by tak nemělo spotřebovat více než pár procent času, tedy třeba 1 takt na číslo. Alternativně bychom mohli práci rozdělit mezi více vláken, ale na tom počítači neběží jenom tohle, takže si nemůžu jen tak sebrat více jader procesoru, a museli bychom řešit synchronizaci mezi vlákny, čímž by se kód zesložitil. Proto jsme se rozhodli optimalizovat jednovláknový výkon.
Implementace
Uvedené ukázky kódu naleznete v repozitáři, kde je též skript, který je zkompiluje, spustí nad ukázkovými daty a vyhodnotí výsledek.
Nejdříve jsme samozřejmě měli nejjednodušší implementaci:
for(int i = 0; i<4*SAMPLES; i++) {
// fix sign-extend
int16_t raw = inbuf[i];
raw = (raw & 0xEFFF) | ((raw & 0xE000)>>1);
// make float from int16
float raw_f = (float)raw;
// decide where to put it - horizontal or vertical buffer
int imod = i % 4;
if(imod < 2) {
int idx = i/2 + imod;
outbuf1[idx] = raw_f;
} else {
int idx = i/2 + imod - 3;
outbuf2[idx] = raw_f;
}
}
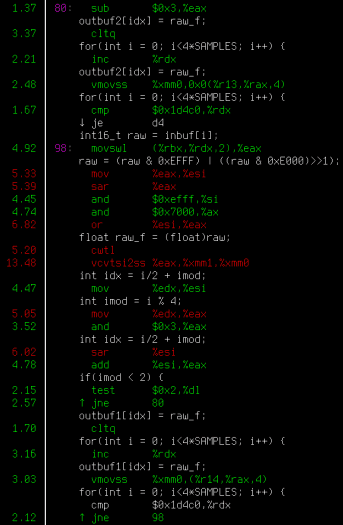
Software profiluji tak, že spustím perf record ./můj_program (vyrobí soubor perf.data) a následně perf report. Perf sleduje, na které instrukci tráví program kolik času, a zobrazí barevný přehled s anotovaným disassemblovaným programem. Čísla na boku říkají, kolik procent se na které instrukci trávilo, a díky proloženému assembleru s originálním kódem se v tom lze vyznat i když assembler příliš neumíte. Musím ovšem upozornit, že měření není „na instrukci přesné“ – dnešní procesory jsou superskalární a provádějí instrukce out-of-order, takže je možné, že se vám v perfu zobrazí červeně nějaká nevinná instrukce, která jenom, chudák, čeká na dokončení nějaké instrukce předcházející. Nicméně je to stejně nedocenitelný nástroj pro rychlou identifikaci míst v programu, kde se tráví nejvíc času (hotspotů) – přesnost identifikace „o několik instrukcí vedle“ je v praxi dostatečná.
Jak vidíme, překladač bohužel smyčku vykonává po jednotlivých 16bitových prvcích a používá 16bitové registry (si, ax…) jako kdyby byl rok 1985. Na embedded, ale mimořádně výkonném procesoru i9–10900TE to dává 860 milionů čísel za sekundu, což není zas tak špatné, ale současně to znamená, že to zabírá 20 % času zpracování signálu z radaru. Na jiném počítači s i7–9700TE to bylo více než dvakrát pomalejší a celé zpracování se už skoro nestíhalo.
Abych měl nějaký odhad, jestli je to dobrý nebo špatný výsledek, napsal jsem naprosto neoptimální implementaci v Pythonu pomocí NumPy:
def data2pol(d): pol = d[::2] # array is now not contiguous, so we cannot view pol = pol.copy() data = pol.view(np.uint16) pol = (data & 0xEFFF) | ((data & 0xE000)>>1) cfile = pol.view(np.int16).astype(np.float32).view(np.complex64) return cfile pol1 = data2pol(data) pol2 = data2pol(data[1:])
Ačkoli se provádí několikanásobné zbytečné kopírování pole a další neoptimality, běží to stejně rychle jako naivní céčková implementace. Hm.
Ruční rozbalení
Jako další krok jsem se rozhodl smyčku ručně rozbalit a zbavit se podmínek. Doufal jsem, že to překladač potom zvládne zvektorizovat automaticky, když mu ukážu, co přesně se s daty děje. Navíc jsem se mu pokusil napovědět, že se použité buffery nepřekrývají, a tedy je může zapisovat hromadně a v libovolném pořadí, to je pro vektorizaci důležité:
#pragma GCC ivdep
for(int i = 0; i<4*SAMPLES; i+=4) {
int16_t raw0 = inbuf[i+0];
int16_t raw1 = inbuf[i+1];
int16_t raw2 = inbuf[i+2];
int16_t raw3 = inbuf[i+3];
raw0 = (raw0 & 0xEFFF) | ((raw0 & 0xE000)>>1);
raw1 = (raw1 & 0xEFFF) | ((raw1 & 0xE000)>>1);
raw2 = (raw2 & 0xEFFF) | ((raw2 & 0xE000)>>1);
raw3 = (raw3 & 0xEFFF) | ((raw3 & 0xE000)>>1);
int i2 = i >> 1;
outbuf1[i2 ] = (float)raw0;
outbuf1[i2 + 1] = (float)raw1;
outbuf2[i2 ] = (float)raw2;
outbuf2[i2 + 1] = (float)raw3;
}
Kód se rozbalením smyčky trochu zrychlil, ale zvektorizovat se to bohužel nepodařilo. Pokud tohle čte nějaký expert na GCC, ocením, když mi poradí, na čem takový – dle mého názoru celkem jednoduchý – případ vázne.
Intrinsics
Nezbývá nám tedy než to zkusit napsat ručně. Jako první musíme vložit vhodný hlavičkový soubor. Můžeme vkládat jednotlivé soubory pro SSE a spol., ale soubor immintrin.h natáhne instrukce všechny a je pak na nás, které použijeme.
Vektorové instrukce často vyžadují načítání ze zarovnané paměti. Při alokaci paměti můžeme použít funkci aligned_alloc. Zarovnání je potřeba nastavit na 16 bajtů pro SSE nebo 32 pro AVX.
Před samotným zpracováním použiji funkci _mm_set1_epi16, která vytvoří vektor osmi 16bit intů a nastaví do všech zadanou hodnotu. Tím si připravím ty magické konstanty 0xEFFF a 0xE000, které jsme používali výše.
__m128i EFFF = _mm_set1_epi16(0xEFFF); __m128i E000 = _mm_set1_epi16(0xE000);
Následně začneme zpracovávat data. Načteme osm 16bit intů ze vstupu, používám výše zmíněné stream instrukce, které obchází cache, i když podle měření to nakonec nemá žádný přínos:
for(int i = 0; i<4*SAMPLES; i+=8) {
// load 8 items to r
__m128i r = _mm_stream_load_si128((void*)(inbuf + i));
Následně provedeme zmíněnou operaci se sign-extend všem osmi číslům současně. K tomu používám funkce, které jsem našel tím, že jsem v již zmíněné Intel Intrinsics Guide vyhledával funkce, které mají v názvu či popisu and, shift a or.
// fix meta/sign extend: perform r = (r & 0xEFFF) | ((r & 0xE000)>>1) __m128i rR = _mm_and_si128(EFFF, r); __m128i rL = _mm_and_si128(E000, r); rL = _mm_srai_epi16(rL, 1); r = _mm_or_si128(rR, rL);
Nyní máme validní int16_t a potřebujeme z nich udělat floaty. Na tohle jsem bohužel nenašel vhodnou funkci, ale našel jsem funkci na výrobu floatů z int32_t a funkci na konverzi int16_t na int32_t. Protože se ale do 128bitového vektoru vejdou 32bit inty jenom čtyři, funkce převede jenom spodní čtyři 16bit inty a zbytek zahodí. To budeme muset v dalším kroku ošetřit.
// convert low 4 elements (4xint16) to 4xint32 __m128i e = _mm_cvtepi16_epi32(r); // convert to 4xfloat __m128 f = _mm_cvtepi32_ps(e);
Všimněte si, že proměnná f je typu __m128, zatímco předchozí proměnné byly typu __m128i. To značí, že f je vektor floatů, zatímco předchozí proměnné byly inty. Toto je ovšem jen sémantika v jazyce C, procesoru je úplně jedno, jaká data zpracovává, a mezi typy lze převádět pomocí funkcí cast – ty žádné instrukce negenerují, jedná se jen o přetypování v C.
V proměnné f tedy máme 4 vzorky, z nichž spodní dva patří jedné polarizaci a horní dva patří druhé – je potřeba je zapsat do jednoho a druhého bufferu. Našel jsem funkce storel a storeh, které dělají přesně toto: ukládají spodní a horní polovinu vektoru na zadanou adresu.
int i2 = i >> 1; // store result _mm_storel_pi((void*)(outbuf1+i2), f); _mm_storeh_pi((void*)(outbuf2+i2), f);
Jako poslední nám zbývá vyřešit ta čtyři čísla, která jsme zahodili v kroku, kdy jsme převáděli 16bit na 32bit. Vezmu proto originální vektor, udělám bitový posun vpravo tak, aby horní čtyři čísla byla nyní spodní čtyři čísla, a konverzi provedu znovu. K tomu lze použít funkci bsrli. Všimněte si, že zatímco dříve uvedená funkce srai prováděla bitový posuv v rámci každého prvku vektoru, funkce bsrli provádí posun celého vektoru, napříč prvky. A má omezení, že lze posouvat pouze po celých bajtech. Na taková omezení narazíte často.
// do the same with high 4 elements e = _mm_cvtepi16_epi32(_mm_bsrli_si128(r,8)); f = _mm_cvtepi32_ps(e); i2 += 2; _mm_storel_pi((void*)(outbuf1+i2), f); _mm_storeh_pi((void*)(outbuf2+i2), f);
Kompilace programu s instrukcemi vyššími než SSE2
Pokud se nyní pokusíte program zkompilovat, pravděpodobně narazíte na to, že některé instrukce nejsou podporovány. GCC na běžném 64bitovém Linuxu totiž ve výchozím nastavení kompiluje pro nejnižší garantovanou podmnožinu x86–64 architektury: a tato podmnožina obsahuje jen SSE2 a nic vyššího. To lze nastavit přepínačem -m. Jedna možnost je použít -march=native, což při kompilaci zjistí, jaké instrukce počítač podporuje, a právě ty použije. Výsledný kód ale nebude přenositelný na počítače, které některé z instrukcí (které jste ani ručně nepoužili, stačí, že se použijí někde automaticky) nepodporují. Můžete proto ručně zadat, na jakou architekturu se má cílit: například -mssse3 nebo -mavx2. Nedávno též byly přidány jistým způsobem standardizované a doporučené „verze“ jako x86–64-v2. Můžete tak použít ty a rozumná podmnožina instrukcí se vybere.
Výsledný program je 4× až 9× rychlejší (na jednom a druhém testovaném počítači) než původní implementace.
Na závěr (ale i při samotném vývoji, pokud je to něco složitějšího) je vhodné napsat test, který spustí původní implementaci, novou ručně vektorizovanou implementaci, a data porovná – buď binárně, nebo pokud jde o výpočty v plovoucí řádové čárce a měnilo se zaokrouhlování, tak ověří maximální odchylku.
Rozšíření na instrukce AVX2
Můžeme to ještě nějak zlepšit? Pohled do perfu nám řekne, že se nejvíc času tráví jednak v konverzi intů na float ( _mm_cvtepi32_ps) a jednak tou taškařicí, kdy nedokážeme zkonvertovat všechna načtená čísla najednou, ale musíme udělat spodní čtyři, vektor posunout a udělat horní čtyři. Ale zrovna na obě tyto činnosti existují AVX instrukce: _mm256_cvtepi16_epi32 vezme 128bitový vektor 8×16bit intů a vyrobí z něj 256bitový vektor 8×32bit intů, a funkce _mm256_cvtepi32_ps, která konvertuje na floaty.
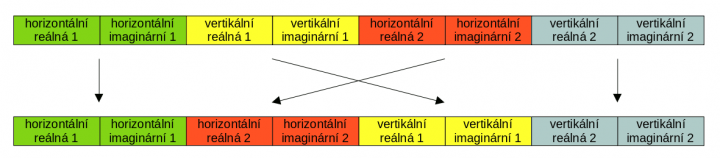
Registr už je ale tak široký, že se do něj vejde více vzorků, a ty jsou prokládané (horizontální a vertikální polarizace) – nemůžeme teď snadno uložit horní a spodní polovinu jako jsme to dělali předtím. Musíme provést následující permutaci:
To je navíc napříč 128bit lanes, což jak jsem psal výše, jde špatně. Existuje funkce, která něco takového umí, _mm256_permute4×64_epi64. Pracuje na 64bitových intech a my máme floaty (naštěstí po dvojcích, takže jsou to 64bitové kusy dat; s 32bit bychom měli v AVX smůlu), ale jak jsem psal, procesoru je jedno, jaká data zpracovává. Hned si tedy i vyzkoušíme funkci cast . Funkcipermute se dává tabulka, podle které permutaci provede; pro její zápis použijeme binární Cčkový literál. Například0b 11 01 10 00 (zde jsem to pro přehlednost napsal s mezerami) znamená, že první (nultý) prvek přeneseme na pozici 00, čili se jeho pozice nezmění. První prvek přeneseme na pozici 10 binárně, což je 2; naopak druhý prvek přeneseme na pozici 01 binárně, což je 1, takže si prohodí místo (přesně jak je naznačeno šipkami na obrázku). A poslední, třetí prvek, přeneseme na pozici 11 binárně, což je 3, takže se zase nezmění.
Nyní již můžeme uložit horní a spodní polovinu; na to slouží funkce _mm256_storeu2_m128i, které se zadají dvě adresy a ona to zařídí sama.
Celkový kód se zavedením AVX paradoxně zpřehlednil:
for(int i = 0; i<4*SAMPLES; i+=8) {
// load 8 items to r
__m128i r = _mm_stream_load_si128((void*)(inbuf + i));
// fix meta/sign extend: perform r = (r & 0xEFFF) | ((r & 0xE000)>>1)
__m128i rR = _mm_and_si128(EFFF, r);
__m128i rL = _mm_and_si128(E000, r);
rL = _mm_srai_epi16(rL, 1);
r = _mm_or_si128(rR, rL);
// convert 8xint16 to 8xint32
__m256i e = _mm256_cvtepi16_epi32(r);
// convert to 8xfloat, cast to 64bit ints for the next permute step
__m256i f = _mm256_castps_si256( _mm256_cvtepi32_ps(e) );
// deinterleave polarizations
f = _mm256_permute4x64_epi64(f, 0b11011000);
int i2 = i >> 1;
_mm256_storeu2_m128i((void*)(outbuf2+i2), (void*)(outbuf1+i2), f);
}
Oproti SSE implementaci je rychlejší, podle konkrétního počítače, o cca. 10–20 %, což už není pro moji aplikaci zásadní, zásadní bylo to mnohonásobné zrychlení při předchozím kroku.
Myslím si, že dalšího zrychlení by bylo možno dosáhnout, kdybychom 16bit čísla nekonvertovali na floaty pomocí obecných funkcí – bylo by možné nastudovat binární reprezentaci floatu a zjistit, zda nelze těch 16 bitů nějak šikovně přímo zapsat do mantissy. Tím bychom se zbavili posledního úzkého hrdla. Prezentovaná implementace je ovšem naprosto dostatečně rychlá.
Příště
Ukázali jsme si na příkladu reálného problému, jak pomocí použití intrinsic funkcí dosáhnout násobného zrychlení programu. V pokračování článku se podíváme, co se s takto vytvořenými daty děje dál – budeme optimalizovat počítání Fourierovy transformace, aplikaci filtrů a decimaci signálu.