Obsah
1. Použití MoviePy společně Matplotlibem pro tvorbu animovaných grafů (dokončení)
3. Zobrazení Lorenzova atraktoru (statický graf)
4. Animace Lorenzova atraktoru
5. Zobrazení dvou atraktorů s různými počátečními podmínkami
6. Aproximace funkcí Taylorovým polynomem
7. Skript pro vykreslení sinusovky aproximované Taylorovým polynomem
9. Reprezentace periodického průběhu pomocí funkcí sin a cos (Fourierova řada)
10. Statický graf – rekonstrukce obdélníkového signálu
11. Animace postupného zvyšování členů ve Fourierově řadě
12. Problematika vykreslení komplexních funkcí
13. Obarvení komplexních hodnot
14. Zobrazení 2D grafu s komplexní funkcí
15. Ukázky vytvořených grafů s komplexními funkcemi
16. Animace v grafech zobrazujících komplexní funkce
17. Vylepšení předchozího příkladu
18. Modul Animation dostupný v knihovně Matplotlib
19. Repositář s demonstračními příklady
1. Použití MoviePy společně Matplotlibem pro tvorbu animovaných grafů (dokončení)
Ve třetím článku o knihovně MoviePy se opět budeme zabývat způsobem kombinace MoviePy s Matplotlibem při tvorbě animovaných grafů, které je možné využít například při výuce. Z tohoto důvodu si ukážeme i některé poměrně typické příklady používané (nejenom) při výuce – aproximace průběhu funkce Taylorovým polynomem, reprezentace periodické funkce Fourierovou řadou, vykreslení komplexních funkcí atd. Taktéž si ukážeme, jak je možné animovat postupné vytváření stopy Lorenzova atraktoru pro různé počáteční podmínky. Z animace bude patrný takzvaný „motýlí efekt“ ve chvíli, kdy se budou souběžně vykreslovat dva atraktory s nepatrně odlišnými počátečními podmínkami. V závěru dnešního článku se alespoň ve stručnosti seznámíme s modulem nazvaným Animation, který je dostupný přímo v Matplotlibu. Tento modul umožňuje vytváření animací bez použití knihovny MoviePy.
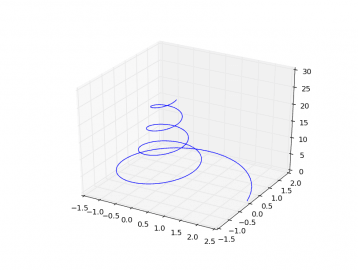
Obrázek 1: Spirála vykreslená posledním demonstračním příkladem popsaným minule. Podobný typ grafu použijeme i při zobrazení Lorenzova atraktoru.
2. Lorenzův atraktor
Poměrně vděčným příkladem funkce typu [x,y,z]=f(t) zobrazené v 3D prostoru je dynamický systém s takzvaným podivným atraktorem, který je nazvaný Lorenzův atraktor podle svého objevitele. Tento systém sestávající ze tří dynamických rovnic použil Edward Lorenz v roce 1963 při simulaci vývoje počasí (resp. ve velmi zjednodušeném modelu počasí). Na tomto systému byla také numericky a analyticky ověřena velká citlivost na počáteční podmínky (někdy také nazývaná „motýlí efekt“ neboli „butterfly effect“). Pro upřesnění je však nutné říci, že při simulaci na počítači vlastně získáme atraktor, jenž je periodický. Je to z toho důvodu, že pro zobrazení číselných hodnot je použito konečného počtu bitů, z toho nutně vyplývá, že se po určitém počtu kroků (který je však obrovský, takže tento jev mnohdy nezaregistrujeme) začne dráha Lorenzova atraktoru překrývat. V matematicky přesném modelu však tato situace nenastane, každá smyčka funkce bude mít unikátní tvar a dráhy se nebudou překrývat, pouze protínat.

Obrázek 2: Lorenzův atraktor vykreslený dnes již „starožitným“ programem Fractint.
Diferenciální rovnice Lorenzova atraktoru mají po převodu na diferenční tvar následující formát:
dx/dt = σ (y-x) dy/dt = x(ρ - z) - y dz/dt = xy - Βz
Takže pro iterativní (samozřejmě že nepřesný) výpočet můžeme pracovat s následujícími vztahy, které pro dostatečně malé dt vedou k výpočtu bodů ležících na Lorenzově atraktoru:
xn+1=xn+(σ (y-x)) dt
yn+1=yn+(x(ρ – z) – y) dt
zn+1=zn+(xy – Βz) dt
Podívejme se nyní na jeden ze způsobů implementace této funkce:
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
A výpočtu sekvence bodů ležících na atraktoru (zde použijeme možnosti knihovny Numpy):
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru (resp. bodů na něm ležících)
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt

Obrázek 3: Dynamických systémů s „podivným atraktorem“ existuje celá řada.
3. Zobrazení Lorenzova atraktoru (statický graf)
Vlastní zobrazení pak probíhá naprosto stejným způsobem, jako tomu bylo v předchozím demonstračním příkladu se spirálou. Nejprve vypočteme body tvořící atraktor. Jejich souřadnice jsou uloženy ve vektorech x, y a z. Následně z těchto bodů vytvoříme graf, a to následujícím postupem:
fig = plt.figure() ax = fig.gca(projection='3d') # vykreslení grafu ax.plot(x, y, z) # zobrazení grafu plt.show()
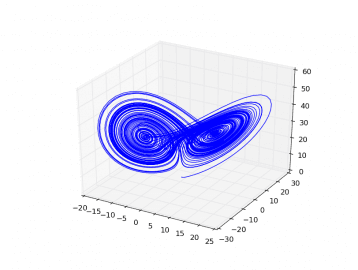
Obrázek 4: Lorenzův atraktor (resp. přesněji řečeno jeho hrubá aproximace) zobrazený knihovnou Matplotlib.
Úplný zdrojový kód demonstračního příkladu pro vykreslení interaktivního grafu s Lorenzovým atraktorem vypadá následovně:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - Lorenzův atraktor
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
fig = plt.figure()
ax = fig.gca(projection='3d')
# vykreslení grafu
ax.plot(x, y, z)
# zobrazení grafu
plt.show()
4. Animace Lorenzova atraktoru
Podívejme se nyní na způsob vytvoření animace postupného vzniku Lorenzova atraktoru. Právě z animace je (na rozdíl od statického obrázku) velmi dobře patrné, jak body tvořící atraktor přechází mezi několika „oblastmi přitažlivosti“, až se nakonec vytvoří ona charakteristická smyčka s atraktorem. Výsledek bude prozatím poměrně primitivní, protože například nenastavujeme limity grafu v osách x, y, z:

Obrázek 5: Velmi hrubá animace postupného vykreslování Lorenzova atraktoru (spíše se však podívejte na přiložené video).
Výsledné video:
https://tisnik.github.io/moviepy-videos/video5.htm
Výpočet bodů Lorenzova atraktoru se provádí stále stejně, ovšem pro každý snímek animace zvýšíme počet iterací, který je uložen v globální proměnné max. Ve skutečnosti by bylo možné výpočet optimalizovat, protože není nutné pro každý snímek začínat s prázdnými vektory x, y a z. Tuto jednoduchou úpravu ponechám na laskavém čtenáři:
max = 0
def make_frame(t):
axis.clear()
global max
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10 + max * 10
max += 1
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
ax = fig.gca(projection='3d')
ax.set_axis_off()
ax.plot(x, y, z)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
Samotné vytvoření animace již známe. Nejprve vytvoříme instanci třídy VideoClip, v níž zaregistrujeme callback funkci make_frame a následně vytvoříme jak animovaný GIF, tak i video ve formátu Ogg/Theora:
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('lorenz1.gif', fps=FPS)
animation.write_videofile('lorenz1.ogv', fps=FPS, progress_bar=True)
Úplný zdrojový kód demonstračního příkladu pro vytvoření animace vzniku Lorenzova atraktoru vypadá takto:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - Lorenzův atraktor
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 300
DPI = 100
# parametry animace
DURATION = 16
FPS = 8
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
axis = fig.add_subplot(111, projection="3d")
max = 0
def make_frame(t):
axis.clear()
global max
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10 + max * 10
max += 1
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
ax = fig.gca(projection='3d')
ax.set_axis_off()
ax.plot(x, y, z)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
# animation.write_gif('lorenz1.gif', fps=FPS)
animation.write_videofile('lorenz1.ogv', fps=FPS, progress_bar=True)
Předchozí příklad je možné vylepšit, a to hned v několika ohledech. První vylepšení spočívá v tom, že explicitně nastavíme limitní hodnoty ve všech třech osách, takže se zamezí nepříjemným změnám měřítka v počáteční fázi animace:
# rozměry grafu ve směru osy x
ax.set_xlim(-35, 35)
# rozměry grafu ve směru osy y
ax.set_ylim(-35, 35)
# rozměry grafu ve směru osy z
ax.set_zlim(0, 50)
Dále ponecháme zobrazení souřadných os a stěn v zadní části grafu. To zajistíme jednoduše smazáním nebo zakomentováním následujícího řádku kódu:
ax.set_axis_off()
Navíc zvětšíme hodnotu bitrate při vytváření videa ve formátu Ogg/Theora. Tím se zvýší dosti postatným způsobem zvýší kvalita animace, protože výchozí velikost bitového toku je nastavena pouze na 200000 kbps (kilobitů za sekundu):
animation.write_videofile('lorenz2.ogv', fps=FPS, progress_bar=True, bitrate="800000")
Výsledek již vypadá mnohem lépe:
Obrázek 6: Vylepšená animace postupného vykreslování Lorenzova atraktoru (spíše se však podívejte na přiložené video).
Výsledné video:
https://tisnik.github.io/moviepy-videos/video6.htm
Úplný zdrojový kód demonstračního příkladu pro vytvoření vylepšené animace vzniku Lorenzova atraktoru vypadá následovně:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - Lorenzův atraktor
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 600
HEIGHT = 450
DPI = 100
# parametry animace
DURATION = 16
FPS = 16
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
axis = fig.add_subplot(111, projection="3d")
max = 0
def make_frame(t):
axis.clear()
global max
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10 + max * 10
max += 1
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
ax = fig.gca(projection='3d')
# rozměry grafu ve směru osy x
ax.set_xlim(-35, 35)
# rozměry grafu ve směru osy y
ax.set_ylim(-35, 35)
# rozměry grafu ve směru osy z
ax.set_zlim(0, 50)
ax.plot(x, y, z)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
# animation.write_gif('lorenz2.gif', fps=FPS)
animation.write_videofile('lorenz2.ogv', fps=FPS, progress_bar=True, bitrate="800000")
5. Zobrazení dvou atraktorů s různými počátečními podmínkami
Velmi zajímavé bude zjistit, co se stane ve chvíli, kdy budeme sledovat vývoj dvou atraktorů, jejichž počáteční podmínky se nepatrně odlišují. Zpočátku se budou obě křivky zdánlivě překrývat (to kvůli omezenému rozlišení výsledných snímků), ovšem dříve či později (ale vždy) nastane situace, kdy dojde k úplnému oddělení křivek – každá se vydá po zcela odlišné trajektorii. Ostatně se podívejme na animaci a video:
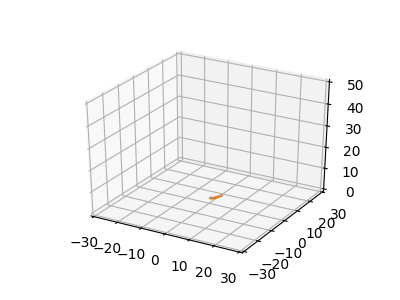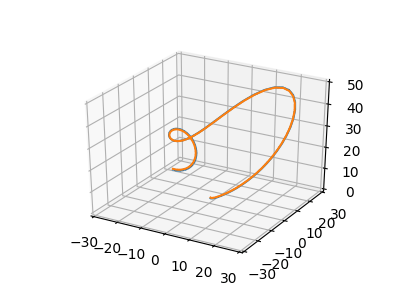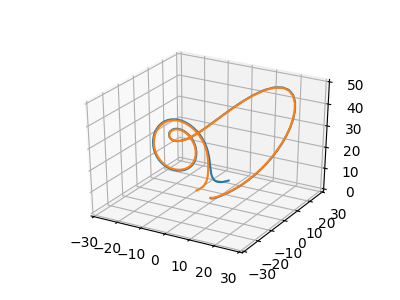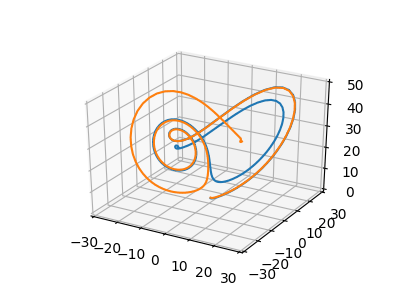
Obrázek 7: Zobrazení dvou divergujících atraktorů pro různé počáteční podmínky.
Výsledné video je kvalitnější, než výše uvedený animovaný GIF:
https://tisnik.github.io/moviepy-videos/video7.htm
Aby bylo možné vykreslit dva atraktory s různými počátečními podmínkami a různým počtem bodů, nepatrně pozměníme zdrojový kód – vytvoříme novou funkci nazvanou draw_attractor, které se předá maximální počet vykreslovaných bodů, počáteční podmínky a taktéž objekt typu Axes, který zajistí vlastní vykreslování (má metodu plot):
def draw_attractor(ax, n, x0, y0, z0):
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = x0, y0, z0
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
ax.plot(x, y, z)
Následuje úplný zdrojový kód tohoto demonstračního příkladu
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - Lorenzův atraktor
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 600
HEIGHT = 450
DPI = 100
# parametry animace
DURATION = 10
FPS = 20
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
axis = fig.add_subplot(111, projection="3d")
max = 0
def draw_attractor(ax, n, x0, y0, z0):
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = x0, y0, z0
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
ax.plot(x, y, z)
def make_frame(t):
axis.clear()
global max
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10 + max * 10
ax = fig.gca(projection='3d')
max += 1
# rozměry grafu ve směru osy x
ax.set_xlim(-30, 30)
# rozměry grafu ve směru osy y
ax.set_ylim(-30, 30)
# rozměry grafu ve směru osy z
ax.set_zlim(0, 50)
draw_attractor(ax, n, 0.0, 1.0, 0.95)
draw_attractor(ax, n, 0.0, 1.0, 1.25)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
# animation.write_gif('lorenz3.gif', fps=FPS)
animation.write_videofile('lorenz3.ogv', fps=FPS, progress_bar=True, bitrate="800000")
6. Aproximace funkcí Taylorovým polynomem
V další části dnešního článku si ukážeme, jak je možné vytvořit animovaný graf, v němž dochází ke stále přesnější aproximaci nějaké funkce ve vybraném bodě Taylorovým polynomem. Opět se jedná o oblast, v níž může být animace přehlednější než jediný statický graf s větším množstvím funkcí, jejichž průběhy se navíc v některých intervalech překrývají. Ostatně se můžeme podívat, jak vypadá graf, v níž je zobrazeno prvních pět aproximací sinusovky v bodě x=0 a následně prvních deset aproximací. Zejména druhý obrázek již není příliš přehledný:
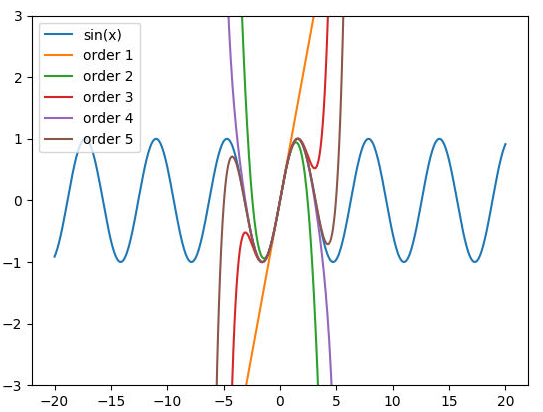
Obrázek 8: Aproximace sinusovky – prvních pět aproximací.
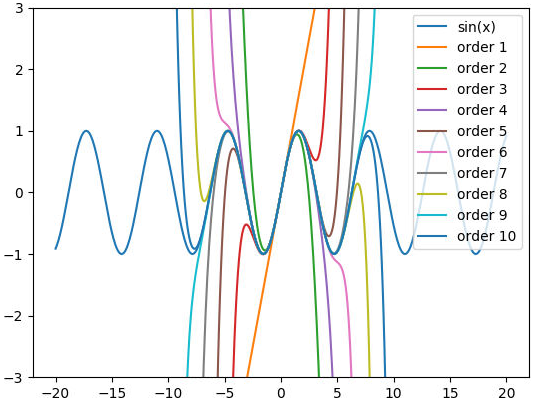
Obrázek 9: Aproximace sinusovky – prvních deset aproximací.
7. Skript pro vykreslení sinusovky aproximované Taylorovým polynomem
Nejprve si ukažme skript, který má vykreslit sinusovku a taktéž její aproximace ve zvoleném bodě pomocí Taylorova polynomu určitého stupně. Jak bod x, v jehož okolí bude funkce aproximována, tak i stupeň Taylorova polynomu jsou volitelné. Samotný výpočet přímo odpovídá Taylorovu rozvoji:
def taylor_series(x, order):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
Výše uvedenou funkci použijeme pro vykreslení několika aproximací s využitím polynomu různého stupně (maximální stupeň je uložen v proměnné N):
ys = np.vectorize(taylor_series)
# aproximace
N = 10
for order in range(1, N+1):
approx = ys(x, order)
plt.plot(x, approx, label='order {o}'.format(o=order))
Následuje výpis celého zdrojového kódu tohoto demonstračního příkladu:
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
def taylor_series(x, order):
"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-20, 20, 500)
# funkce kterou aproximujeme
y = np.sin(x)
# vykreslení původní funkce
plt.plot(x, y, label='sin(x)')
ys = np.vectorize(taylor_series)
# aproximace
N = 10
for order in range(1, N+1):
approx = ys(x, order)
plt.plot(x, approx, label='order {o}'.format(o=order))
# limity na ose y
plt.ylim([-3, 3])
# legenda grafu
plt.legend()
# zobrazení grafu
plt.show()
8. Animace vlivu postupného přidávání členů do Taylorova polynomu na tvar aproximované funkce (sinusovky)
Předchozí příklad můžeme velmi snadno upravit takovým způsobem, aby se postupné zlepšování přesnosti aproximace zvyšováním stupně Taylorova vykreslilo formou animace. Vykreslování stačí umístit do nám již známé funkce make_frame, přičemž stupeň Taylorova polynomu je uložen v globální proměnné order, která se postupně zvyšuje:
def make_frame(t):
axis.clear()
# vykreslení původní funkce
axis.plot(x, y, label='sin(x)')
# aproximace
global order
approx = ys(x, order)
axis.plot(x, approx, label='order {o}'.format(o=order))
order += 1
# limity na ose y
axis.set_ylim([-3, 3])
axis.legend()
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
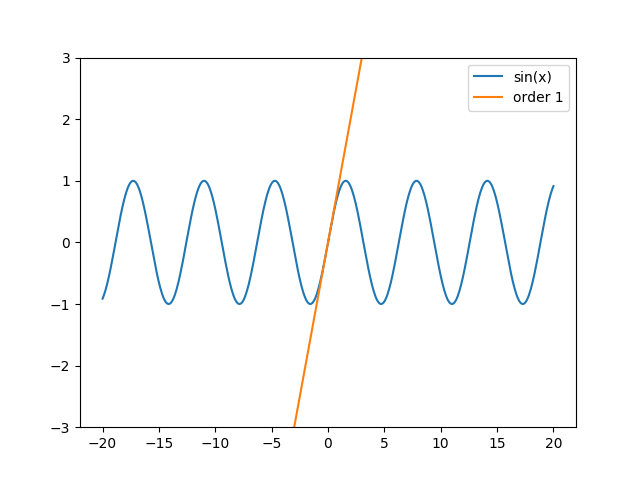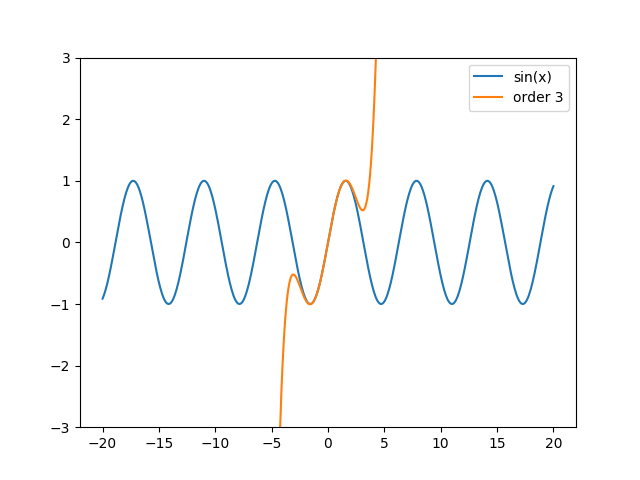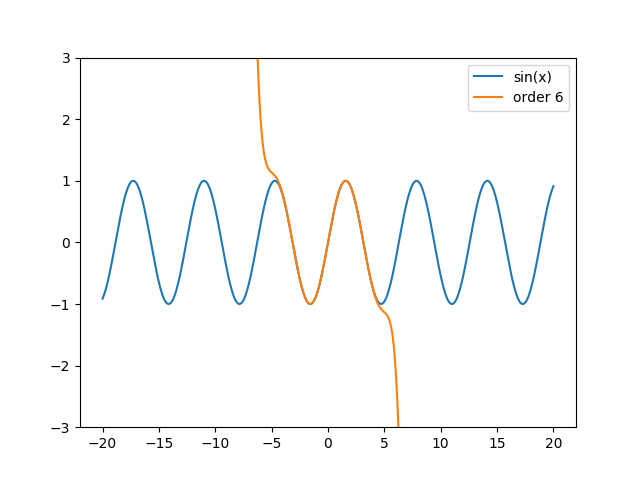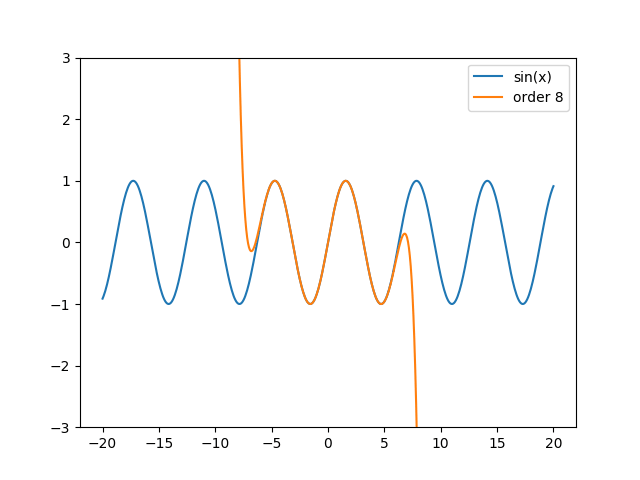
Obrázek 10: Postupně vylepšovaná aproximace sinusovky Taylorovým polynomem.
Následuje, jak již zajisté očekáváte, úplný zdrojový kód tohoto demonstračního příkladu
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
# Knihovny Numpy a matplotlib
#
# Demonstrační příklad:
# - vykreslení postupné aproximace funkce sin
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry animace
DURATION = 20
FPS = 0.8
def taylor_series(x, order):
u"""Výpočet aproximace hodnoty funkce pomocí Taylorovy řady."""
a = x
sum = a
for i in range(1, order):
a *= -1 * x**2 / ((2 * i) * (2 * i + 1))
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-20, 20, 500)
# funkce kterou aproximujeme
y = np.sin(x)
ys = np.vectorize(taylor_series)
# vytvoření objektu reprezentujícího průběh funkce
fig, axis = plt.subplots()
# zde začínáme od nuly!
# viz: https://github.com/Zulko/moviepy/issues/155
order = 0
def make_frame(t):
axis.clear()
# vykreslení původní funkce
axis.plot(x, y, label='sin(x)')
# aproximace
global order
approx = ys(x, order)
axis.plot(x, approx, label='order {o}'.format(o=order))
order += 1
# limity na ose y
axis.set_ylim([-3, 3])
axis.legend()
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('taylor_sinus.gif', fps=FPS)
# animation.write_videofile('taylor_sinus.ogv', fps=FPS)
9. Reprezentace periodického průběhu pomocí funkcí sin a cos (Fourierova řada)
Dalším příkladem použití kombinace knihoven Matplotlib a MoviePy, který si dnes popíšeme, bude skript, v němž budeme reprezentovat průběh nějaké periodické funkce s využitím základních goniometrických funkcí sin a cos. Použijeme přitom slavnou Fourierovu řadu. Opět se jedná o poměrně pěkný příklad situace, v níž může být použití animace výhodnější než zanesení průběhů několika funkcí do jediného grafu, což není příliš přehledné:
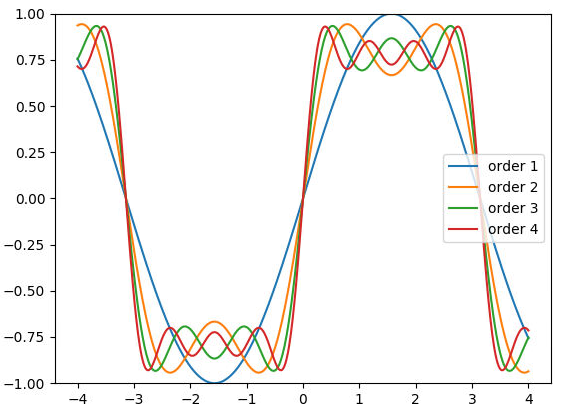
Obrázek 11: Aproximace obdélníkového signálu prvními max. čtyřmi členy Fourierovy řady. Nejpřesnější aproximací je zde červená křivka.
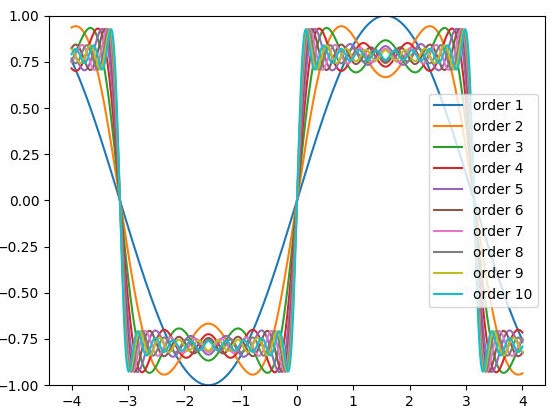
Obrázek 12: Aproximace obdélníkového signálu prvními max. deseti členy Fourierovy řady. Nejpřesnější aproximací je zde světle modrá křivka, která se však v grafu prakticky ztrácí.
10. Statický graf – rekonstrukce obdélníkového signálu
V případě, že budeme chtít rekonstruovat (či aproximovat) obdélníkový signál, budou nám k tomu stačit pouze liché členy Fourierovy řady (frekvence 1, 3, 5, 7, amplitudy 1/1, 1/3, 1/5, 1/7 atd., viz například tento text nebo ještě lépe přesný vzorec), takže výpočet bude relativně jednoduchý:
def fourier_serie(x, order):
sum = 0
for i in range(0, order):
n = 2 * i + 1
a = np.sin(x * n) / n
sum += a
return sum
Vykreslení aproximace obdélníkového signálu s využitím maximálně čtyř lichých členů:
# Fourierova syntéza
N = 4
for order in range(1, N+1):
approx = ys(x, order)
plt.plot(x, approx, label='order {o}'.format(o=order))
Samozřejmě si opět ukážeme úplný zdrojový kód tohoto skriptu:
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
def fourier_serie(x, order):
sum = 0
for i in range(0, order):
n = 2 * i + 1
a = np.sin(x * n) / n
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-4, 4, 500)
# funkce kterou aproximujeme
y = np.sin(x)
ys = np.vectorize(fourier_serie)
# Fourierova syntéza
N = 4
for order in range(1, N+1):
approx = ys(x, order)
plt.plot(x, approx, label='order {o}'.format(o=order))
# limity na ose y
plt.ylim([-1, 1])
# legenda grafu
plt.legend()
# zobrazení grafu
plt.show()
11. Animace postupného zvyšování členů ve Fourierově řadě
Prakticky stejným postupem, jakým jsme vytvořili animaci aproximace funkce pomocí Taylorova polynomu můžeme získat animaci zlepšující se aproximace periodického obdélníkového signály lichými členy Fourierovy řady. Opět použijeme globální proměnnou order, která se s každým snímkem zvýší o jedničku.
order = 0
def make_frame(t):
axis.clear()
# Fourierova syntéza
global order
approx = ys(x, order)
axis.plot(x, approx, label='order {o}'.format(o=order))
order += 1
# limity na ose y
axis.set_ylim([-1, 1])
axis.legend()
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
V animaci vidíme typické překmity na vzestupných i sestupných hranách aproximovaného signálu (souvisí s Gibbsovým jevem). Ty teoreticky vymizí při součtu všech členů Fourierovy řady (jichž je ovšem nekonečný počet).
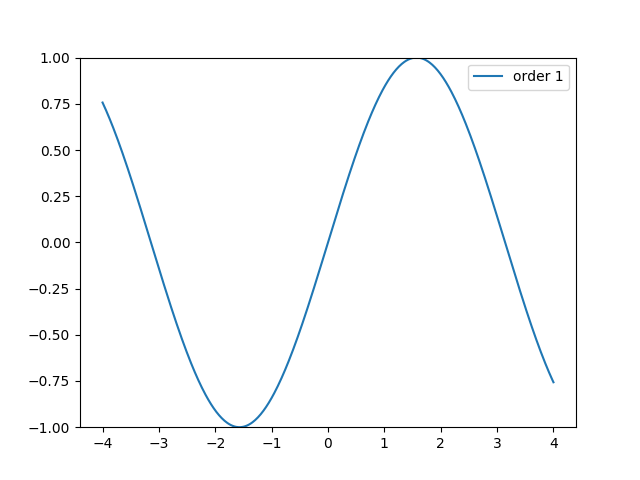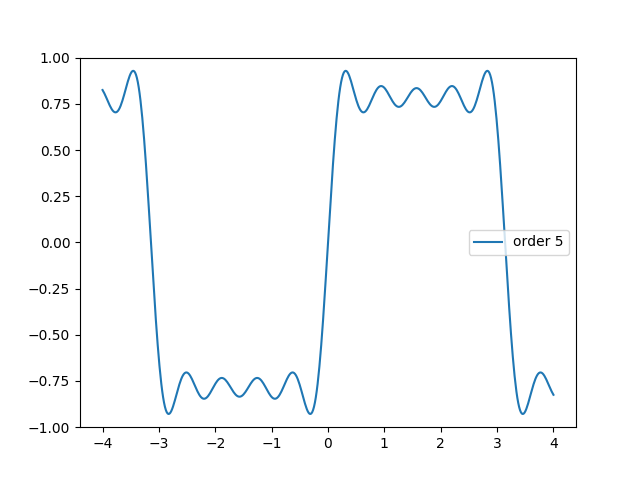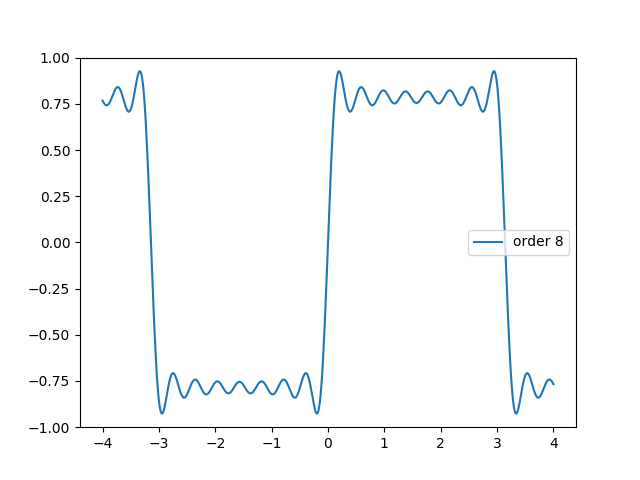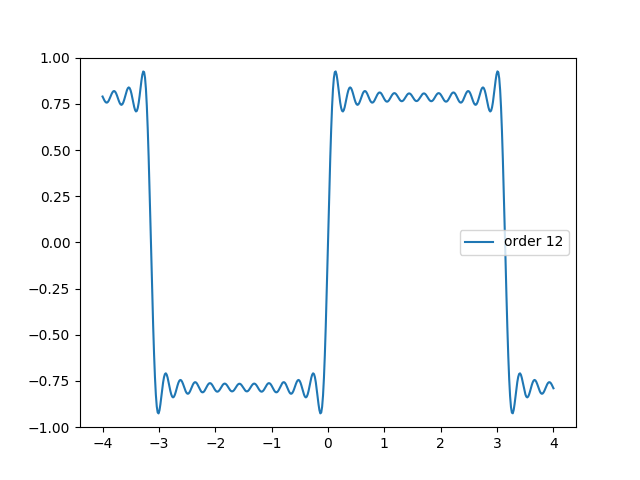
Obrázek 13: Postupné zlepšování aproximace (periodického) obdélníkového signálu s využitím lichých členů Fourierovy řady.
Následuje, jak již zajisté očekáváte, úplný zdrojový kód tohoto demonstračního příkladu
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
# Knihovny Numpy a matplotlib
#
# Demonstrační příklad:
# - vykreslení rozkladu obdélníkového signálu na sinusové průběhy
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry animace
DURATION = 20
FPS = 0.8
def fourier_serie(x, order):
sum = 0
for i in range(0, order):
n = 2 * i + 1
a = np.sin(x * n) / n
sum += a
return sum
# průběh nezávislé proměnné x
# (hodnoty na x-ové ose)
x = np.linspace(-4, 4, 500)
# funkce kterou aproximujeme
y = np.sin(x)
ys = np.vectorize(fourier_serie)
# vytvoření objektu reprezentujícího průběh funkce
fig, axis = plt.subplots()
# zde začínáme od nuly!
# viz: https://github.com/Zulko/moviepy/issues/155
order = 0
def make_frame(t):
axis.clear()
# Fourierova syntéza
global order
approx = ys(x, order)
axis.plot(x, approx, label='order {o}'.format(o=order))
order += 1
# limity na ose y
axis.set_ylim([-1, 1])
axis.legend()
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('fourier_square_wave.gif', fps=FPS)
12. Problematika vykreslení komplexních funkcí
V této kapitole se alespoň ve stručnosti seznámíme s problematikou vykreslování komplexních funkcí. Současná verze knihovny Matplotlib sice neobsahuje přímou podporu pro tvorbu 3D grafů zobrazujících komplexní funkce tak, jako je tomu v dalších nástrojích (například v Matlabu), ovšem i přesto je možné s komplexními funkcemi poměrně dobře pracovat a zobrazovat je – a to jak v 2D grafu, tak i v grafu trojrozměrném. Obě řešení samozřejmě mají své přednosti a zápory.
Nejjednodušší je zobrazení 2D grafu s „průběhem“ komplexní funkce. Princip je poměrně jednoduchý. Vstupem je matice komplexních čísel, které by při zobrazení v komplexní rovině tvořily mřížku. Čím hustší je mřížka, tím přesnější samozřejmě bude výsledný graf, ovšem i doba výpočtu se prodlouží (což bude patrné především při tvorbě animací). Vytvoření dvourozměrné matice komplexních čísel:
# rozmery mrizky N=1000 # mrizka realnych cisel # (zde má 1j speciální význam při tvorbě mřížky) x, y = np.ogrid[-5:5:N*1j, -5:5:N*1j] # prevod na komplexni cisla z = x + 1j*y
Příklad použití při vytvoření mřížky 3×3 komplexních čísel, přičemž reálná složka je rovna –5, 0, 5 a komplexní –5j, 0j a 5j:
x, y = np.ogrid[-5:5:3j, -5:5:3j]
x
array([[-5.],
[ 0.],
[ 5.]])
y
array([[-5., 0., 5.]])
z = x + 1j*y
z
array([[-5.-5.j, -5.+0.j, -5.+5.j],
[ 0.-5.j, 0.+0.j, 0.+5.j],
[ 5.-5.j, 5.+0.j, 5.+5.j]])
Následně je na každé komplexní číslo na vstupu (označme ho z) aplikovaná vybraná funkce, přičemž výsledkem je nové komplexní číslo w:
w = (z**2+4)/(z**2-4)
Nebo:
w=z**2
w
array([[ 0.+50.j, 25. -0.j, 0.-50.j],
[-25. -0.j, 0. +0.j, -25. +0.j],
[ 0.-50.j, 25. +0.j, 0.+50.j]])
A právě sérii těchto čísel budeme chtít nějakým způsobem vizualizovat. V 2D grafu je vizualizace založena na převodu hodnoty komplexního čísla na barevný kód, tj. vlastně na aplikaci další funkce z → RGB:
show_graph(w)
13. Obarvení komplexních hodnot
Pro obarvení komplexních hodnot provedeme dvě operace. Tou první je převod každého komplexního čísla na jeho goniometrický tvar, tj. na dvojici hodnot představujících velikost čísla (vzdálenost od středu komplexní roviny) a úhel. Primitivní (nevektorizovaná) varianta převodní funkce může vypadat následovně:
def to_polar_form(z):
"""Prevod komplexniho cisla na goniometricky tvar."""
r = np.abs(z)
phi = np.angle(z)
return r, phi
Ve druhém kroku provedeme převod z goniometrického tvaru na barvu reprezentovanou v barvovém prostoru HLS. Jedná se o jeden z barvových prostorů, kde má rotace význam změny barevného tónu:
def polar_to_hls(r, phi):
"""Prevod na HLS."""
h = (phi + pi) / (2 * pi) + 0.5
l = 1.0 - 1.0/(1.0 + r**0.3)
s = 0.8
return h, l, s
Dále je nutné výslednou trojici převést na vektor se složkami RGB, vložit ho do 2D pole a změnit tvar pole takovým způsobem, aby reprezentovalo rastrový obrázek:
def colorize(z):
"""Funkce pro prevod complex -> HLS -> RGB."""
r, phi = to_polar_form(z)
h, l, s = polar_to_hls(r, phi)
# prevod na n-tici
c = np.vectorize(hls_to_rgb) (h,l,s)
# zmena tvaru z (3,n,m) na (n,m,3)
c = np.array(c)
c = c.swapaxes(0,2)
return c
14. Zobrazení 2D grafu s komplexní funkcí
Celý zdrojový kód příkladu, který ve 2D grafu zobrazí několik komplexních funkcí, je vypsán pod tímto odstavcem:
import numpy as np
from numpy import pi
import pylab as plt
from colorsys import hls_to_rgb
# viz https://stackoverflow.com/a/20958684
def to_polar_form(z):
"""Prevod komplexniho cisla na goniometricky tvar."""
r = np.abs(z)
phi = np.angle(z)
return r, phi
def polar_to_hls(r, phi):
"""Prevod na HLS."""
h = (phi + pi) / (2 * pi) + 0.5
l = 1.0 - 1.0/(1.0 + r**0.3)
s = 0.8
return h, l, s
def colorize(z):
"""Funkce pro prevod complex -> HLS -> RGB."""
r, phi = to_polar_form(z)
h, l, s = polar_to_hls(r, phi)
# prevod na n-tici
c = np.vectorize(hls_to_rgb) (h,l,s)
# zmena tvaru z (3,n,m) na (n,m,3)
c = np.array(c)
c = c.swapaxes(0,2)
return c
def show_graph(w):
# obarveni vysledku
img = colorize(w)
# vykresleni grafu
plt.imshow(img)
plt.show()
# rozmery mrizky
N=1000
# mrizka realnych cisel
x, y = np.ogrid[-5:5:N*1j, -5:5:N*1j]
# prevod na komplexni cisla
z = x + 1j*y
w = z
show_graph(w)
w = 1/z
show_graph(w)
w = z**2
show_graph(w)
w = z**z+z
show_graph(w)
w = (z**2+4)/(z**2-4)
show_graph(w)
w = np.tan(z)
show_graph(w)
w = np.tan(10/z)
show_graph(w)
w = np.sin(z**2)
show_graph(w)
w = 1/(z+1j)**2 + 1/(z-2)**2
show_graph(w)
15. Ukázky vytvořených grafů s komplexními funkcemi
Podívejme se nyní na několik grafů zobrazujících „průběh“ komplexních funkcí. U každého grafu je zapsáno, o jakou funkci se jedná.
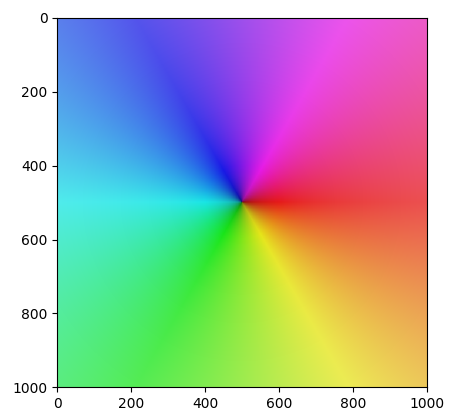
Obrázek 14: Graf komplexní funkce f=z.
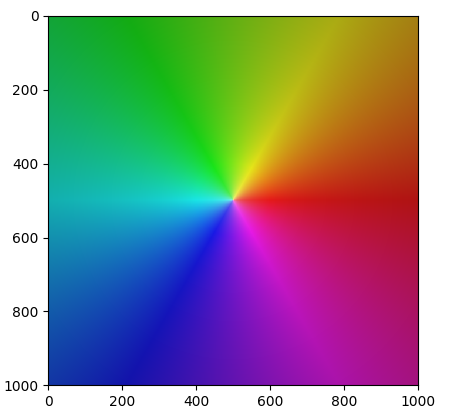
Obrázek 15: Graf komplexní funkce f=1/z.
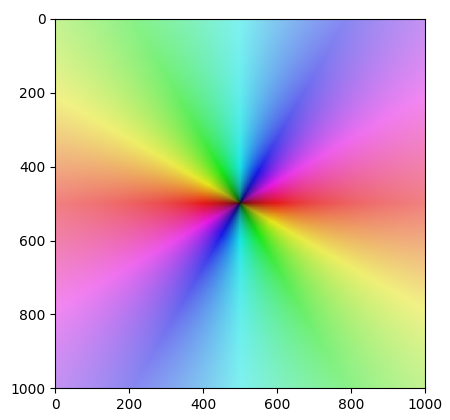
Obrázek 16: Graf komplexní funkce f=z2.
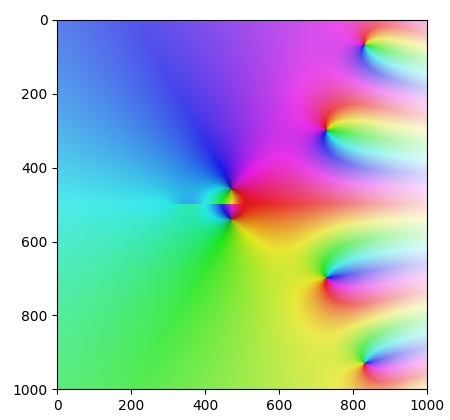
Obrázek 17: Graf komplexní funkce f=z*z=z.
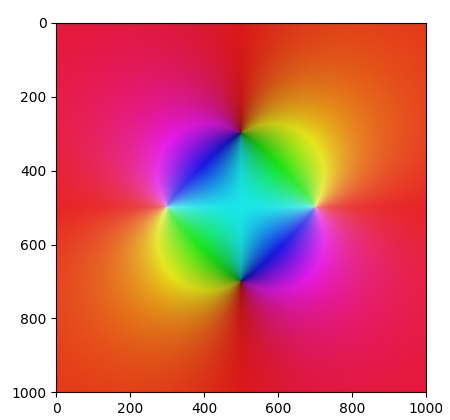
Obrázek 18: Graf komplexní funkce f=(z2+4) / (z2-4).
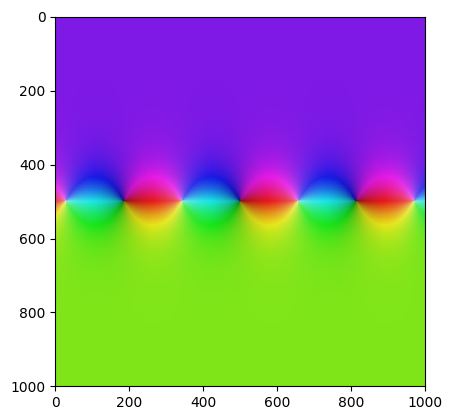
Obrázek 19: Graf komplexní funkce f=tan(z).
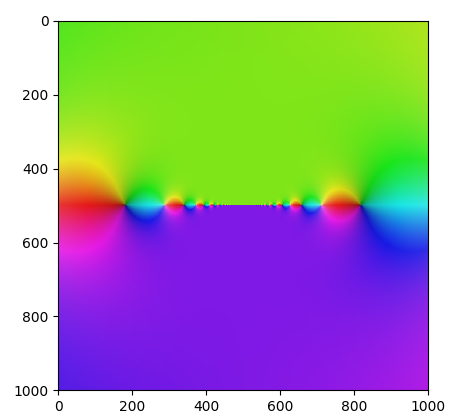
Obrázek 20: Graf komplexní funkce f=tan(10/z).
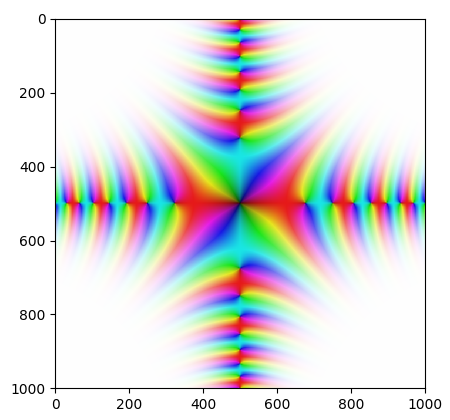
Obrázek 21: Graf komplexní funkce f=sin(z2).
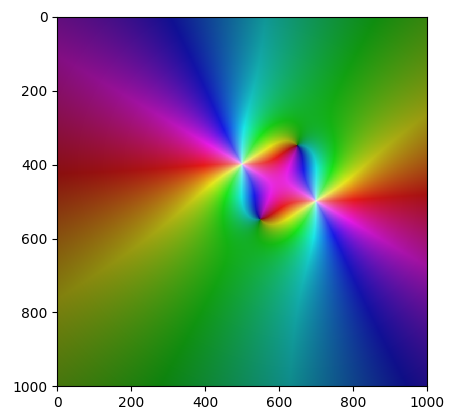
Obrázek 22: Graf komplexní funkce f=1/(z+j)2 + 1/(z-2)2.
16. Animace v grafech zobrazujících komplexní funkce
Nyní se podívejme na to, jak lze předchozí grafy s komplexními funkcemi „rozpohybovat“. Budeme postupně a v dostatečně malých krocích měnit nějaký parametr komplexní funkce, například následovně (měněná hodnota je uložena v globální proměnné offset):
def make_frame(t):
offset = 4 * t / DURATION - 2
print(offset)
w = 1/(z+2j)**2 + 1/(z-offset)**2
img = colorize(w)
fig = plt.figure(figsize=(20,20))
plt.subplot(111)
subplot = fig.add_subplot(111)
subplot.imshow(img)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
Výsledné video:
https://tisnik.github.io/moviepy-videos/video8.htm
Opět se podívejme, jak může vypadat úplný zdrojový kód tohoto příkladu:
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
import numpy as np
from numpy import pi
import pylab as plt
from colorsys import hls_to_rgb
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# viz https://stackoverflow.com/a/20958684
def to_polar_form(z):
"""Prevod komplexniho cisla na goniometricky tvar."""
r = np.abs(z)
phi = np.angle(z)
return r, phi
def polar_to_hls(r, phi):
"""Prevod na HLS."""
h = (phi + pi) / (2 * pi) + 0.5
l = 1.0 - 1.0/(1.0 + r**0.3)
s = 0.8
return h, l, s
def colorize(z):
"""Funkce pro prevod complex -> HLS -> RGB."""
r, phi = to_polar_form(z)
h, l, s = polar_to_hls(r, phi)
# prevod na n-tici
c = np.vectorize(hls_to_rgb) (h,l,s)
# zmena tvaru z (3,n,m) na (n,m,3)
c = np.array(c)
c = c.swapaxes(0,2)
return c
# parametry animace
DURATION = 10
FPS = 12
# rozmery mrizky
N=1000
# mrizka realnych cisel
x, y = np.ogrid[-4:4:N*1j, -4:4:N*1j]
# prevod na komplexni cisla
z = x + 1j*y
def make_frame(t):
offset = 4 * t / DURATION - 2
print(offset)
w = 1/(z+2j)**2 + 1/(z-offset)**2
img = colorize(w)
fig = plt.figure(figsize=(20,20))
plt.subplot(111)
subplot = fig.add_subplot(111)
subplot.imshow(img)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_videofile('complex.ogv', fps=FPS, progress_bar=False, bitrate="800000")
17. Vylepšení předchozího příkladu
V předchozím příkladu se po vykreslení snímku neuvolňovala paměť s grafem. To sice většinou nemusí vadit v případě, kdy je animace krátká, ovšem pro delší animace a animace s velkými snímky (v našem případě pro testovací účely dokonce 2000×2000 pixelů) to již začíná být problematické. Jedno řešení spočívá v tom, že se vykreslování provádí stále do stejného grafu, popř. se navíc graf před vytvořením nového snímku smaže:
fig = plt.figure(figsize=(20,20))
plt.subplot(111)
subplot = fig.add_subplot(111)
def make_frame(t):
power = 5 * t / DURATION - 2
w = 1/(z+2j)**power + 1/(z-2)**power
img = colorize(w)
subplot.imshow(img)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
Video vytvořené tímto příkladem je zajímavější (kdo přijde na to, proč nejsou barvové přechody v celé ploše plynulé?):
https://tisnik.github.io/moviepy-videos/video9.htm
Další řešení jsme si již naznačili na konci předchozí kapitoly – provádět vykreslování přímo s využitím možností knihovny MoviePy a Numpy. To si ukážeme příště.
Celý zdrojový kód příkladu vypadá takto:
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
import numpy as np
from numpy import pi
import pylab as plt
from colorsys import hls_to_rgb
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# viz https://stackoverflow.com/a/20958684
def to_polar_form(z):
"""Prevod komplexniho cisla na goniometricky tvar."""
r = np.abs(z)
phi = np.angle(z)
return r, phi
def polar_to_hls(r, phi):
"""Prevod na HLS."""
h = (phi + pi) / (2 * pi) + 0.5
l = 1.0 - 1.0/(1.0 + r**0.3)
s = 0.8
return h, l, s
def colorize(z):
"""Funkce pro prevod complex -> HLS -> RGB."""
r, phi = to_polar_form(z)
h, l, s = polar_to_hls(r, phi)
# prevod na n-tici
c = np.vectorize(hls_to_rgb) (h,l,s)
# zmena tvaru z (3,n,m) na (n,m,3)
c = np.array(c)
c = c.swapaxes(0,2)
return c
# parametry animace
DURATION = 10
FPS = 10
# rozmery mrizky
N = 400
# mrizka realnych cisel
x, y = np.ogrid[-4:4:N*1j, -4:4:N*1j]
# prevod na komplexni cisla
z = x + 1j*y
fig = plt.figure(figsize=(20,20))
plt.subplot(111)
subplot = fig.add_subplot(111)
def make_frame(t):
power = 5 * t / DURATION - 2
w = 1/(z+2j)**power + 1/(z-2)**power
img = colorize(w)
subplot.imshow(img)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_videofile('complex2.ogv', fps=FPS, progress_bar=True, bitrate="800000")
18. Modul Animation dostupný v knihovně Matplotlib
Prozatím jsme se zabývali především použitím knihovny Matplotlib společně s knihovnou MoviePy, přičemž knihovna Matplotlib sloužila k vytvoření snímků s 2D či 3D grafy a knihovna MoviePy z těchto snímků vytvářela buď animovaný GIF nebo plnohodnotné video používající zvolený kodek (například Ogg/Theora). Ve skutečnosti však v některých případech vůbec nemusíme knihovnu MoviePy použít, protože přímo v novějších verzích Matplotlibu existuje modul nazvaný Animation. Jméno tohoto modulu napovídá k čemu slouží – skutečně je možné s jeho využitím vytvářet různé animované grafy. V následujícím článku se seznámíme se základy použití tohoto modulu (i když osobně preferuji použití MoviePy, které je univerzálnější). Některé již hotové ukázky animovaných grafů naleznete na stránce https://matplotlib.org/gallery/index.html#animation a ukázkové skripty na https://matplotlib.org/examples/animation/index.html.
Jednoduchou animaci (obdobu animace z předchozího článku) můžeme vytvořit například takto (viz předchozí odkazy):
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig, ax = plt.subplots()
# nezávislá proměnná
x = np.arange(0, 2*np.pi, 0.01)
line, = ax.plot(x, np.sin(x))
def init():
line.set_ydata([np.nan] * len(x))
return line,
def animate(i):
line.set_ydata(np.sin(x + i / 100)) # update the data.
return line,
ani = animation.FuncAnimation(
fig, animate, init_func=init, interval=2, blit=True, save_count=50)
ani.save("movie.mp4")
19. Repositář s demonstračními příklady
Zdrojové kódy všech jedenácti dnes popsaných demonstračních příkladů určených pro Python 3 byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/moviepy-examples. V případě, že nebudete chtít klonovat celý repositář (ten je ovšem stále velmi malý, stále doslova několik kilobajtů), můžete namísto toho použít odkazy na jednotlivé příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- MoviePy 0.2.3.3 na PyPi
https://pypi.org/project/moviepy/ - MoviePy na GitHubu
https://github.com/Zulko/moviepy - MoviePy – dokumentace
http://zulko.github.io/moviepy/ - MoviePy – galerie
http://zulko.github.io/moviepy/gallery.html - Data Animations With Python and MoviePy
https://zulko.github.io/blog/2014/11/29/data-animations-with-python-and-moviepy/ - Porovnání formátů Ogg Theora a H.264
https://www.root.cz/zpravicky/porovnani-formatu-ogg-theora-a-h-264/ - Případ GIF
https://www.root.cz/clanky/pripad-gif/ - Pravda a mýty o GIFu
https://www.root.cz/clanky/pravda-a-myty-o-gifu/ - Anatomie grafického formátu GIF
https://www.root.cz/clanky/anatomie-grafickeho-formatu-gif/ - GIF: animace a konkurence
https://www.root.cz/clanky/gif-animace-a-konkurence/ - Two python modules : MoviePy and images2gif – part 001
http://free-tutorials.org/two-python-modules-moviepy-and-images2gif-part-001/ - images2gif
https://pypi.org/project/images2gif/ - Making GIFs from video files with Python
https://www.devbattles.com/en/sand/post-345-Making+GIFs+From+Video+Files+With+Python - GIF89a specification
https://www.w3.org/Graphics/GIF/spec-gif89a.txt - MPEG-4 Part 14
https://en.wikipedia.org/wiki/MPEG-4_Part14 - Theora video compression
https://www.theora.org/ - Theora
https://en.wikipedia.org/wiki/Theora - NumPy
http://www.numpy.org/ - numpy 1.14.2 (on PyPi)
https://pypi.org/project/numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
https://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy (2.část)
https://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy-2-cast/ - Non-linear editing system
https://en.wikipedia.org/wiki/Non-linear_editing_system - Lorenzův atraktor
http://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Lorenz system
https://en.wikipedia.org/wiki/Lorenz_system - Customising contour plots in matplotlib
https://philbull.wordpress.com/2012/12/27/customising-contour-plots-in-matplotlib/ - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - Taylorův polynom
https://algoritmy.net/article/1576/Tayloruv-polynom - Taylor series
https://en.wikipedia.org/wiki/Taylor_series - Taylor Series Approximation to Cosine
https://www.cut-the-knot.org/Curriculum/Calculus/TaylorSeries.shtml - Fourier series
https://en.wikipedia.org/wiki/Fourier_series - mpmath
http://mpmath.org/ - Gallery of mathematical functions
http://mpmath.org/gallery/ - 3D visualization of complex functions with matplotlib
http://fredrikj.net/blog/2009/08/3d-visualization-of-complex-functions-with-matplotlib/ - Animating the Lorenz System in 3D
https://jakevdp.github.io/blog/2013/02/16/animating-the-lorentz-system-in-3d/ - Lorenz example
http://docs.enthought.com/mayavi/mayavi/auto/example_lorenz.html - Color Graphs of Complex Functions
http://fs2.american.edu/lcrone/www/ComplexPlot.html