Obsah
1. Použití MoviePy společně s Matplotlibem pro tvorbu animovaných grafů
2. Vykreslení průběhu funkce sinus s využitím knihovny Matplotlib
4. Animovaná změna parametrů zobrazované funkce
5. Specifikace rozlišení výsledného videa nebo animovaného GIFu
6. Alternativní způsob vykreslení animace
7. Vykreslení průběhů dvou funkcí do jediného grafu
8. Animace předchozího příkladu
10. Postupná změna parametrů funkce vykreslené v polárním grafu
11. Použití funkce numpy.meshgrid()
12. Graf s konturami funkce z=f(x,y)
13. Animace funkce s proměnnými parametry vykreslená formou kontur
14. Jednoduchý trojrozměrný graf funkce z=f(x,y) – drátový model
15. Od drátového modelu k vyplněné ploše
16. Promítnutí grafu na plochy kolmé na osy
17. Animace „vlnek“ ve funkci sinc
18. Přidání dalšího rozměru – času
19. Repositář s demonstračními příklady
1. Použití MoviePy společně s Matplotlibem pro tvorbu animovaných grafů
V předchozím článku jsme si ukázali, jakým způsobem je možné použít knihovnu MoviePy pro programové vytváření videa v různých formátech. Dnes se zaměříme na další užitečné vlastnosti této knihovny, zejména na možnost zkombinovat ji s knihovnou Matplotlib. Díky kombinaci MoviePy + Matplotlib lze vytvářet animované grafy, ukazovat různé možnosti aproximace a interpolace funkcí, přidat do grafů funkcí čas jako další (třetí, čtvrtý) rozměr atd. Nejprve si ukážeme tvorbu klasických grafů funkcí jedné proměnné a následně do grafu přidáme průběh další funkce, popisky os, legendu apod. Dále si ukážeme další typy grafů, zejména polární grafy. Ve druhé části článku si pak ukážeme tvorbu grafů s konturami, 3D grafů funkcí se dvěma nezávislými proměnnými, 3D grafů funkcí typu x,y=f(t), x,y,z=f(t) apod. Všechny ukázky budou provedeny jak ve statické podobě, tak i v podobě animované.
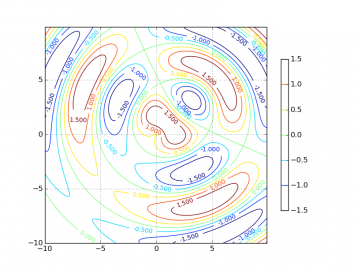
Obrázek 1: Ukázka možností knihovny Matplotlib.
2. Vykreslení průběhu funkce sinus s využitím knihovny Matplotlib
Na úvod si popíšeme velmi jednoduchý demonstrační příklad naprogramovaný v Pythonu 3, který po svém spuštění vykreslí graf s průběhem funkce sinus. V příkladu nalezneme pouze osm programových řádků. Nejprve je nutné naimportovat hlavní modul knihovny Numpy nazvaný přímočaře numpy, a následně i submodul pyplot z knihovny matplotlib. Většina aplikací, ale i demonstračních příkladů, s nimiž se setkáte, používá pro importované moduly zkratky np a plt, čehož se z důvodu zachování konzistence budeme držet i my:
import numpy as np import matplotlib.pyplot as plt
Následně je pomocí funkce numpy.linspace() (tu již dobře známe z předchozího článku) vytvořeno pole se sto prvky s hodnotami od 0 do 2π. Na toto pole je aplikována funkce pojmenovaná numpy.sin(), jejímž výsledkem je nové stoprvkové pole (hodnoty prvků leží v rozsahu od –1 do 1):
# hodnoty na x-ové ose x = np.linspace(0, 2*np.pi, 100) # hodnoty na y-ové ose y = np.sin(x)
Funkcí matplotlib.pyplot.plot() je vykreslen průběh funkce, ovšem graf ještě není zobrazen, takže do něj můžeme přidat popis obou os a graf následně zobrazit příkazem matplotlib.pyplot.show(). Způsob zobrazení závisí na nastavení Pythonu; implicitně se použije speciální prohlížeč naprogramovaný s použitím knihovny Tk (resp. Tkinter):
# vykreslit průběh funkce
plt.plot(x, y)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
# zobrazení grafu
plt.show()
Úplný zdrojový kód tohoto příkladu vypadá následovně:
# Knihovny Numpy a matplotlib
#
# První demonstrační příklad:
# - vykreslení průběhu funkce sin
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(x)
# vykreslit průběh funkce
plt.plot(x, y)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
# zobrazení grafu
plt.show()
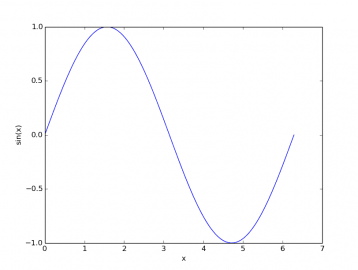
Obrázek 2: Průběh funkce sin(x) vykreslený prvním demonstračním příkladem.
3. Volba výstupního souboru
Implicitní prohlížeč, o němž jsme se zmínili v předchozí kapitole, sice dokáže uložit nakreslený graf do výstupního souboru, ovšem mnohdy je vyžadováno, aby knihovna Matplotlib graf vyexportovala automaticky (programově). Můžeme si například představit generátor výsledků spouštěný ze skriptu, pomocnou službu pro tvorbu grafů umisťovaných na webové stránky apod. Při takovýchto požadavcích, které jsou poměrně časté, je možné využít funkce matplotlib.pyplot.savefig(), které se v nejjednodušším případě předá pouze jméno výstupního souboru. Tato funkce se pak na základě analýzy přípony souboru dokáže rozhodnout o tom, který formát použije. K dispozici jsou mj. tyto formáty:
| # | Koncovka | Formát |
|---|---|---|
| 1 | png | rastrový formát PNG |
| 2 | dokument ve formátu PDF s vektorovým grafem | |
| 3 | eps | vektorový formát Encapsulated PostScript (varianta PostScriptu určená pro vložení do dalších dokumentů, včetně (La)TeXu) |
| 4 | ps | vektorový formát PostScript |
| 5 | svg | vektorový formát SVG |
Použití funkce matplotlib.pyplot.savefig() je v praxi velmi snadné, o čemž se ostatně můžete sami přesvědčit po porovnání zdrojového kódu prvního demonstračního příkladu popsaného v předchozí kapitole a příkladu druhého, do něhož jsme pouze vložili vytvoření pěti souborů s exportovaným grafem:
# Knihovny Numpy a matplotlib
#
# Druhý demonstrační příklad:
# - vykreslení průběhu funkce sin
# - uložení grafu do různých typů souboru
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(x)
# vykreslit průběh funkce
plt.plot(x, y)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
# vykreslení a uložení grafu do různých typů souborů
plt.savefig("example02.png")
plt.savefig("example02.pdf")
plt.savefig("example02.eps")
plt.savefig("example02.ps")
plt.savefig("example02.svg")
# zobrazení grafu
plt.show()
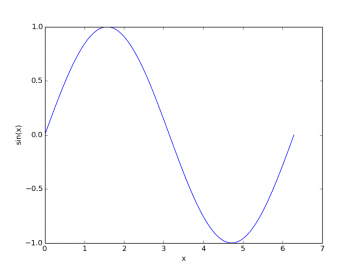
Obrázek 3: Průběh funkce sin(x) vykreslený druhým demonstračním příkladem (měl by být shodný s předchozím obrázkem).
4. Animovaná změna parametrů zobrazované funkce
Nyní si již můžeme ukázat, jak se vytvoří animovaný průběh funkce sinus. Animace bude spočívat v postupném přidávání offsetu k parametru této funkce. Pokud bude offset postupně nabývat hodnot od 0 do 2π, vznikne zdánlivě nekonečná smyčka. Nejprve je nutné naimportovat nám již známou třídu VideoClip a taktéž funkci mplfig_to_npimage, která provádí rasterizaci grafu do datové struktury ndarray:
from moviepy.editor import VideoClip from moviepy.video.io.bindings import mplfig_to_npimage
Dále nastavíme základní parametry animace, tj. její délku a počet snímků za sekundu:
DURATION = 10 FPS = 15
Vytvoření stoprvkového pole s hodnotami od 0 do 2π již známe:
# hodnoty na x-ové ose x = np.linspace(0, 2 * np.pi, 100)
Následuje změna – vytvoření objektu reprezentujícího vlastní graf (Figure) a jednotlivé elementy grafu (Axes):
# vytvoření objektu reprezentujícího průběh funkce fig, axis = plt.subplots()
Další část kódu je již vložena do funkce make_frame, protože právě tato funkce bude postupně volána pro vytvoření všech snímků. Ve funkci nejprve vymažeme z grafu všechny starší elementy, vypočítáme offset, vypočítáme pole hodnot funkce sinus, graf vykreslíme metodou plot a následně výsledný objekt Figure rasterizujeme do datové struktury typu ndarray:
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose
y = np.sin(x + offset)
# vykreslení průběhu funkce
axis.plot(x, y)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
Následuje část, kterou jsme si popsali minule – vytvoření video klipu, nastavení jeho parametrů, postupná tvorba snímků (volání callback funkce make_frame) a následné uložení video klipu do animovaného GIFu:
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('sinus_A.gif', fps=FPS)
Obrázek 4: Výsledná animace (zmenšená na poloviční rozlišení).
Původní animaci v plném rozlišení lze získat na této adrese.
Úplný zdrojový kód tohoto příkladu vypadá následovně:
# Knihovny Numpy a matplotlib
#
# První demonstrační příklad:
# - vykreslení animovaného průběhu funkce sin
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry animace
DURATION = 10
FPS = 15
# hodnoty na x-ové ose
x = np.linspace(0, 2 * np.pi, 100)
# vytvoření objektu reprezentujícího průběh funkce
fig, axis = plt.subplots()
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose
y = np.sin(x + offset)
# vykreslení průběhu funkce
axis.plot(x, y)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('sinus_A.gif', fps=FPS)
5. Specifikace rozlišení výsledného videa nebo animovaného GIFu
Při tvorbě animací je většinou nutné explicitně nastavit rozlišení výsledných snímků (rámců). Ovšem při použití knihovny Matplotlib je situace poněkud složitější, protože se rozlišení nenastavuje přímo v pixelech, ale je nutné specifikovat rozměry obrázku ve fyzických jednotkách (například v palcích). Malým trikem, konkrétně určením DPI (dot per inch), je však možné docílit toho, že rozlišení animace bude přepočteno z pixelů na délkové míry. Rozlišení snímků i DPI si nastavíme dopředu:
WIDTH = 400 HEIGHT = 300 DPI = 100
Dále nastavíme rozměr grafu, ovšem s přepočtem přes DPI. To znamená, že se šířka 400 pixelů přepočte na 4 palce při 100 DPI atd.:
fig, axis = plt.subplots(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
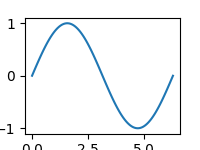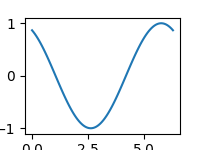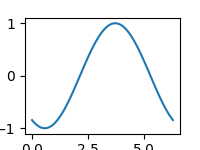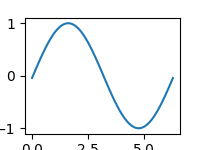
Obrázek 5: Výsledná animace (zmenšená na poloviční rozlišení).
Původní animaci v plném rozlišení lze získat na této adrese.
Opět se podívejme na úplný zdrojový kód tohoto demonstračního příkladu:
# Knihovny Numpy a matplotlib
#
# - vykreslení animovaného průběhu funkce sin
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 300
DPI = 100
# parametry animace
DURATION = 10
FPS = 15
# hodnoty na x-ové ose
x = np.linspace(0, 2 * np.pi, 100)
# vytvoření objektu reprezentujícího průběh funkce
# + nastavení rozlišení obrázku (resp. jednotlivých rámců)
fig, axis = plt.subplots(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose
y = np.sin(x + offset)
# vykreslení průběhu funkce
axis.plot(x, y)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('sinus_B.gif', fps=FPS)
6. Alternativní způsob vykreslení animace
Knihovna Matplotlib nabízí hned několik způsobů vykreslení grafů. Proto si ukažme ještě jednu variantu vytvoření animovaného průběhu funkce sinus. Tentokrát se bude každý snímek vytvářet takto (bez použití subplots):
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
plot = fig.add_subplot(111)
# vykreslení průběhu funkce
plot.plot(x, y)
Celý zdrojový kód této varianty vypadá následovně:
# Knihovny Numpy a matplotlib
#
# První demonstrační příklad:
# - vykreslení animovaného průběhu funkce sin
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 300
DPI = 100
# parametry animace
DURATION = 10
FPS = 15
# hodnoty na x-ové ose
x = np.linspace(0, 2 * np.pi, 100)
def make_frame(t):
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose
y = np.sin(x + offset)
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
plot = fig.add_subplot(111)
# vykreslení průběhu funkce
plot.plot(x, y)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('sinus_C.gif', fps=FPS)
7. Vykreslení průběhů dvou funkcí do jediného grafu
Velmi často se můžeme setkat s požadavkem vložení průběhů několika funkcí do jediného grafu. Zde knihovna matplotlib svým uživatelům nabízí větší množství řešení. Je například možné do jednoho obrázku či dokumentu vložit více grafů s totožnou x-ovou osou (a většinou odlišným měřítkem na y-ových osách), popř. lze skutečně sloučit větší množství průběhů v jediném grafu. Ukažme si nejdříve druhou zmiňovanou možnost, tj. vytvoření grafu s dvěma funkcemi, ovšem s totožnými x-ovými a y-ovými osami. I u takto vytvořeného grafu můžeme použít již zmíněnou funkci matplotlib.pyplot.plot(), které se ovšem předají čtyři pole: hodnoty na ose x, hodnoty první funkce, opět hodnoty na ose x (pro nás stejné pole) a hodnoty druhé funkce. Žádné další operace nejsou zapotřebí, což je ostatně patrné i při pohledu na zdrojový kód dnešního třetího demonstračního příkladu:
# Knihovny Numpy a matplotlib
#
# - vykreslení průběhů funkcí sin a cos
# do jediného grafu
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
# vykreslit průběh obou funkcí
plt.plot(x, y1, x, y2)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
# zobrazení grafu
plt.show()
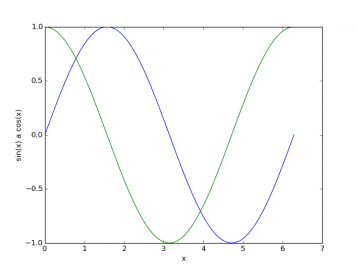
Obrázek 6: Graf, na němž jsou nakresleny průběhy dvou funkcí.
8. Animace předchozího příkladu
Předchozí příklady můžeme zkombinovat a vytvořit tak animovaný průběh většího množství funkcí. Aby byla situace ještě zajímavější, je u funkce sinus počítán kladný offset, u funkce kosinus offset záporný a navíc ještě zobrazíme součet obou funkcí. Aby se neměnilo měřítko na y-ové ose, nastavíme ho na fixní hodnotu:
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x + offset)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x - offset)
# hodnoty na y-ové ose: součet funkcí
y3 = y1 + y2
# vykreslení průběhu funkce
axis.plot(x, y1)
axis.plot(x, y2)
axis.plot(x, y3)
axis.set_ylim(-2, 2)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
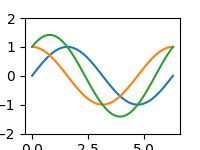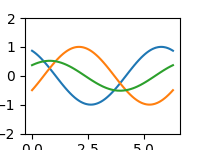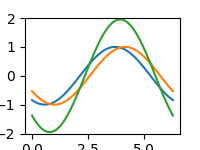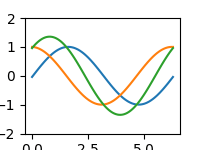
Obrázek 7: Výsledná animace (zmenšená na poloviční rozlišení).
Původní animaci v plném rozlišení lze získat na této adrese.
Úplný zdrojový kód příkladu:
# Knihovny Numpy a matplotlib
#
# Třetí demonstrační příklad:
# - vykreslení animovaného průběhů funkcí sin a cos
# do jediného grafu
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 300
DPI = 100
# parametry animace
DURATION = 10
FPS = 15
# hodnoty na x-ové ose
x = np.linspace(0, 2 * np.pi, 100)
# vytvoření objektu reprezentujícího průběh funkce
# + nastavení rozlišení obrázku (resp. jednotlivých rámců)
fig, axis = plt.subplots(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x + offset)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x - offset)
# hodnoty na y-ové ose: součet funkcí
y3 = y1 + y2
# vykreslení průběhu funkce
axis.plot(x, y1)
axis.plot(x, y2)
axis.plot(x, y3)
axis.set_ylim(-2, 2)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('sin_cos.gif', fps=FPS)
9. Základní polární graf
Pokud je zapotřebí vykreslit polární graf, je možné postupovat následujícím způsobem. Nejprve se plocha obrázku či dokumentu určená pro vykreslení grafu rozdělí do pomyslné mřížky o velikosti 1×1 buňka. Do této mřížky se funkcí matplotlib.pyplot.subplot() vloží „podgraf“, u něhož se pojmenovaným parametrem projection specifikuje použitá projekce. Magická konstanta 111 při volání této funkce značí, že se skutečně má vytvořit mřížka 1×1 buňka a podgraf se má vložit do této buňky (ta má index 1). Další vykreslování již vlastně známe, ovšem s tím nepatrným rozdílem, že se nevolá funkce matplotlib.pyplot.plot(), ale metoda objektu získaného výše zmíněnou funkcí matplotlib.pyplot.subplot(). Dále si povšimněte toho, že namísto polí pojmenovaných x a y používáme pole hodnot se jmény theta a radius, což se pro tento typ grafu hodí mnohem více:
# Knihovny Numpy a matplotlib # # - základní polární graf import numpy as np import matplotlib.pyplot as plt # úhel v polárním grafu theta = np.linspace(0.01, 2*np.pi, 150) # vzdálenost od středu radius = np.log(theta) ax=plt.subplot(111, projection="polar") # vykreslit průběh funkce # v polárním grafu ax.plot(theta, radius) # zobrazení grafu plt.show()
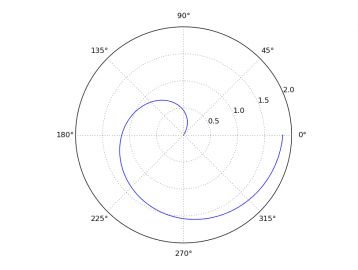
Obrázek 8: Polární graf se slavnou logaritmickou spirálou.
10. Postupná změna parametrů funkce vykreslené v polárním grafu
Postupné odvíjení logaritmické spirály lze vytvořit nepatrnou úpravou předchozího příkladu:
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# úhel v polárním grafu
theta = np.linspace(0.01 + offset, 2*np.pi + offset, 150)
# vzdálenost od středu
radius = np.log(theta)
# vykreslení průběhu funkce
# v polárním grafu
axis.plot(theta, radius)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
Na zmenšené animaci si povšimněte, jak se automaticky mění měřítko:
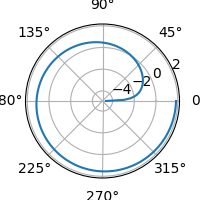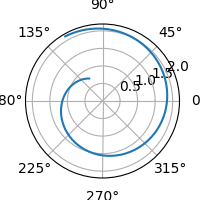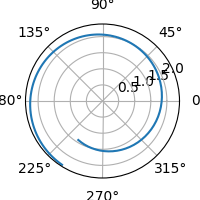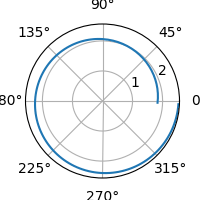
Obrázek 9: Postupné odvíjení logaritmické spirály.
Původní animaci v plném rozlišení lze získat na této adrese.
Úplný zdrojový kód příkladu:
# Knihovny Numpy a matplotlib
#
# - základní polární animovaný graf
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 400
DPI = 100
# parametry animace
DURATION = 10
FPS = 15
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
axis = fig.add_subplot(111, projection="polar")
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2 * np.pi * t / DURATION
# úhel v polárním grafu
theta = np.linspace(0.01 + offset, 2*np.pi + offset, 150)
# vzdálenost od středu
radius = np.log(theta)
# vykreslení průběhu funkce
# v polárním grafu
axis.plot(theta, radius)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('polar.gif', fps=FPS)
11. Použití funkce numpy.meshgrid()
Před popisem grafů zobrazujících drátové modely či kontury funkcí typu z=f(x,y) se musíme seznámit s užitečnou funkcí nazvanou numpy.meshgrid(). Tato funkce má sice poměrně univerzální možnosti použití, my se však v dnešním článku spokojíme s tím, že pokud se funkci numpy.meshgrid() předá dvojice jednorozměrných polí (vektorů) představujících hodnoty nezávislých x-ových a y-ových souřadnic, vytvoří se jako výsledek dvě dvourozměrné matice, které dohromady tvoří mřížku souřadnic [xi, yi]. Počet řádků těchto 2D matic odpovídá délce druhého pole, počet sloupců pak délce pole prvního. Podívejme se na jednoduchý příklad:
# vytvoření vektoru [1..10]
x=np.arange(1, 11, 1)
# vytvoření vektoru [101..105]
y=np.arange(101, 106, 1)
# zobrazení prvního vektoru
x
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# zobrazení druhého vektoru
y
array([101, 102, 103, 104, 105])
# zavolání funkce numpy.meshgrid
np.meshgrid(x,y)
[array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]),
array([[101, 101, 101, 101, 101, 101, 101, 101, 101, 101],
[102, 102, 102, 102, 102, 102, 102, 102, 102, 102],
[103, 103, 103, 103, 103, 103, 103, 103, 103, 103],
[104, 104, 104, 104, 104, 104, 104, 104, 104, 104],
[105, 105, 105, 105, 105, 105, 105, 105, 105, 105]])]
Většinou se první i druhá matice uloží do samostatné proměnné, a to následovně (povšimněte si, že výsledné matice jsou uloženy do proměnných označených verzálkami):
# uložení první matice do proměnné X
# uložení druhé matice do proměnné Y
X,Y=np.meshgrid(x,y)
# zobrazení první matice
X
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
# zobrazení druhé matice
Y
array([[101, 101, 101, 101, 101, 101, 101, 101, 101, 101],
[102, 102, 102, 102, 102, 102, 102, 102, 102, 102],
[103, 103, 103, 103, 103, 103, 103, 103, 103, 103],
[104, 104, 104, 104, 104, 104, 104, 104, 104, 104],
[105, 105, 105, 105, 105, 105, 105, 105, 105, 105]])
Z předchozího článku již víme, že s maticemi je možné mj. provádět i základní operace typu součet matic, rozdíl matic, maticový součin atd. Taktéž je možné na prvky matice aplikovat logaritmické či goniometrické funkce, takže například následující zápis je zcela korektní:
# součet matic a následně aplikace goniometrické funkce sin
# na každý prvek výsledné matice
Z=np.sin(X+Y)
# podívejme se na výslednou matici
Z
array([[ 0.99482679, 0.62298863, -0.3216224 , -0.97053528, -0.7271425 ,
0.18478174, 0.92681851, 0.81674261, -0.04424268, -0.86455145],
[ 0.62298863, -0.3216224 , -0.97053528, -0.7271425 , 0.18478174,
0.92681851, 0.81674261, -0.04424268, -0.86455145, -0.8899956 ],
[-0.3216224 , -0.97053528, -0.7271425 , 0.18478174, 0.92681851,
0.81674261, -0.04424268, -0.86455145, -0.8899956 , -0.09718191],
[-0.97053528, -0.7271425 , 0.18478174, 0.92681851, 0.81674261,
-0.04424268, -0.86455145, -0.8899956 , -0.09718191, 0.78498039],
[-0.7271425 , 0.18478174, 0.92681851, 0.81674261, -0.04424268,
-0.86455145, -0.8899956 , -0.09718191, 0.78498039, 0.94543533]])
12. Graf s konturami funkce z=f(x,y)
První způsob zobrazení funkce typu z=f(x,y) spočívá ve vykreslení takzvaných kontur, které si pro zjednodušení můžeme představit jako vrstevnice na mapě – body spojené konturou/vrstevnicí mají stejnou hodnotu funkce (tj. stejnou hodnotu z-ové souřadnice). Při vyhodnocování a následném vykreslení funkce budeme postupovat následovně:
- Vytvoříme vektor s hodnotami nezávislé proměnné x.
- Vytvoříme vektor s hodnotami nezávislé proměnné y.
- S využitím numpy.meshgrid necháme vygenerovat dvojici matic souřadnic.
- Necháme vypočítat body ležící na ploše funkce (z-ové souřadnice se uloží do matice Z).
- Vlastní vykreslení kontur zajistí funkce matplotlib.pyplot.contour(X, Y, Z).
Podívejme se na úplný příklad:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # - zobrazení kontur funkce typu z=f(x,y) import matplotlib import numpy as np import matplotlib.pyplot as plt delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R1 = np.sqrt(X*X+Y*Y) # vzdálenost od bodu [3,3] R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3)) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R1)-np.cos(R2) # povolení zobrazení mřížky plt.grid(True) # vytvoření grafu s konturami funkce z=f(x,y) plt.contour(X, Y, Z) # zobrazení grafu plt.show()
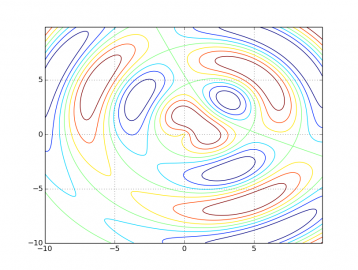
Obrázek 10: Zobrazení kontur funkce typu z=f(x,y).
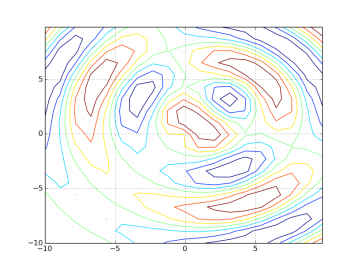
Obrázek 11: Pokud je hodnota „delta“ příliš vysoká, vypočte se menší počet bodů tvořících plochu funkce, takže i kontury budou vykresleny velmi nepřesně (knihovna bude mít k dispozici jen málo bodů, které bude moci spojit).
Další vylepšení, které může být výhodné zejména ve chvíli, kdy jsou plochy s konturami vybarveny (pro vybarvení použijte funkci matplotlib.pyplot.contourf namísto pouhého matplotlib.pyplot.countour) spočívá v přidání legendy, na níž se zobrazují výšky jednotlivých kontur/vrstevnic. Přidání je jednoduché, stačí pouze použít funkci nazvanou matplotlib.pyplot.colorbar(), které se opět předá datová struktura reprezentující graf funkce a několik nepovinných pojmenovaných parametrů. Z těchto parametrů dnes použijeme pouze parametr nazvaný shrink (relativní velikost popisku) a extend (způsob vykreslení popisků vedle grafu). Podívejme se na úplný zdrojový kód příkladu:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # - zobrazení kontur funkce typu z=f(x,y) # - zobrazení hodnot u jednotlivých "vrstevnic" # - přidání legendy import matplotlib import numpy as np import matplotlib.mlab as mlab import matplotlib.pyplot as plt delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R1 = np.sqrt(X*X+Y*Y) # vzdálenost od bodu [3,3] R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3)) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R1)-np.cos(R2) # povolení zobrazení mřížky plt.grid(True) # vytvoření grafu s konturami funkce z=f(x,y) CS = plt.contour(X, Y, Z) # přidání legendy (colorbar) CB = plt.colorbar(CS, shrink=0.7, extend='both') # popisky "vrstevnic" plt.clabel(CS, inline=1, fontsize=10) # zobrazení grafu plt.show()
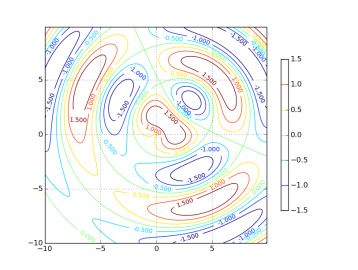
Obrázek 12: Kromě vrstevnic a jejich hodnot se napravo od grafu zobrazila i „mapa výšek“. Relativní velikost mapy vůči celému grafu se řídí hodnotou shrink. Zde konkrétně má celá legenda výšku jen 70% výšky celého grafu.
13. Animace funkce s proměnnými parametry vykreslená formou kontur
V následujícím demonstračním příkladu vykreslíme animovaný průběh funkce, která se vykreslí formou kontur (vrstevnic). Ve funkci počítáme vzdálenosti od dvou bodů [0, 0] a [3, 3]. Tyto vzdálenosti slouží jako vstup do funkcí sinus a kosinus, kde ovšem vypočtené hodnoty navíc posuneme o vypočtený offset, který je pro každý snímek odlišný:
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset1 = 3 * 2 * np.pi * t / DURATION
offset2 = 2 * 2 * np.pi * t / DURATION
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R1 = np.sqrt(X*X+Y*Y)
# vzdálenost od bodu [3,3]
R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3))
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R1 + offset1) - np.cos(R2 + offset2)
# povolení zobrazení mřížky
axis.grid(True)
# vytvoření grafu s konturami funkce z=f(x,y)
axis.contour(X, Y, Z)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
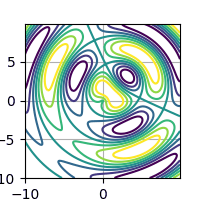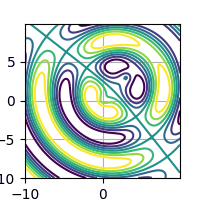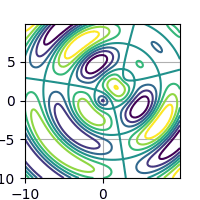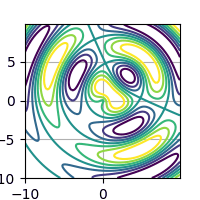
Obrázek 13: Animace funkce s proměnnými parametry vykreslená formou kontur.
Původní animaci v plném rozlišení lze získat na této adrese.
Úplný zdrojový kód příkladu:
# Knihovny Numpy a matplotlib
#
# - zobrazení kontur funkce typu z=f(x,y)
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 400
DPI = 100
# parametry animace
DURATION = 10
FPS = 15
# vytvoření objektu reprezentujícího průběh funkce
# + nastavení rozlišení obrázku (resp. jednotlivých rámců)
fig, axis = plt.subplots(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset1 = 3 * 2 * np.pi * t / DURATION
offset2 = 2 * 2 * np.pi * t / DURATION
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R1 = np.sqrt(X*X+Y*Y)
# vzdálenost od bodu [3,3]
R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3))
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R1 + offset1) - np.cos(R2 + offset2)
# povolení zobrazení mřížky
axis.grid(True)
# vytvoření grafu s konturami funkce z=f(x,y)
axis.contour(X, Y, Z)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('contour.gif', fps=FPS)
14. Jednoduchý trojrozměrný graf funkce z=f(x,y) – drátový model
Použití grafu s konturami sice může být v mnoha ohledech velmi užitečné (například při zjišťování lokálních minim a maxim), v praxi se však spíše setkáme s odlišným typem grafů zobrazujících funkce typu z=f(x,y). Jedná se o trojrozměrné grafy, v nichž se zobrazuje plocha funkce. Nejjednodušším typem tohoto grafu je takzvaný drátový model, který je spíše známý pod svým anglickým názvem wireframe. V tomto typu grafu je zobrazena série křivek či spíše lomených čar. Jedna série je vypočtena takovým způsobem, že x-ová souřadnice se postupně mění v nastaveném intervalu zatímco y-ová souřadnice je konstantní. Druhá série lomených čar se vykresluje kolmo na sérii první, tj. x-ová souřadnice je konstantní a postupně se mění hodnota y-ových souřadnic. Výsledkem je tedy plocha, která má při pohledu z osy z tvar pravidelné mřížky. Pro vykreslení tohoto typu grafu se používá funkce plot_wireframe(), které se předá trojice polí odpovídajících x-ovým, y-ovým a z-ovým souřadnicím bodů ležících na ploše představujících obraz funkce:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # - zobrazení 3D grafu funkce typu z=f(x,y) from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt import numpy as np fig = plt.figure() ax = fig.add_subplot(111, projection='3d') delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R = np.sqrt(X*X+Y*Y) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R)/R # zobrazení 3D grafu ax.plot_wireframe(X, Y, Z, rstride=7, cstride=7) # zobrazení grafu plt.show()
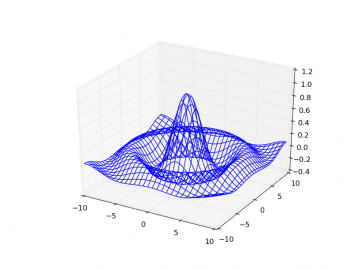
Obrázek 14: Drátový model vykreslený s využitím funkce plot_wireframe(X, Y, Z, rstride=7, cstride=7).
Pojmenované parametry rstride a cstride lze použít pro řízení hustoty vykreslované mřížky. Tyto parametry představují krok použitý při změně x-ových a y-ových souřadnic, což znamená, že čím menší hodnota se požije, tím bode vykreslená mřížka jemnější:
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3)
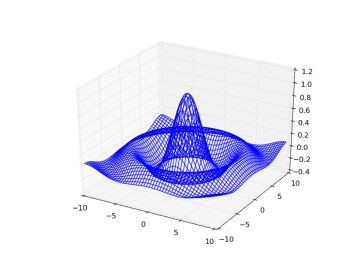
Obrázek 15: Drátový model vykreslený s využitím funkce plot_wireframe(X, Y, Z, rstride=3, cstride=3).
15. Od drátového modelu k vyplněné ploše
Drátový model je možné v případě potřeby nahradit vykreslením vyplněné plochy namísto pouhé mřížky. V tomto případě je nutné namísto funkce plot_wireframe() použít funkci pojmenovanou plot_surface(). První tři povinné parametry obou zmíněných funkcí jsou shodné, dokonce lze použít i stejně pojmenované parametry cstride a rstride, o jejichž významu jsme se taktéž zmiňovali. Kromě toho se však navíc většinou používá i další pojmenovaný parametr cmap, kterému se předá barvová paleta (či barvová mapa), která typicky definuje jeden gradientní přechod i větší množství gradientních přechodů mezi různými odstíny. Pro účely vytváření gradientních přechodů či pro použití již předem připravených barvových map se používá modul matplotlib.cm. Seznam všech předdefinovaných barvových map naleznete na adrese https://gist.github.com/endolith/2719900#id7, ukázky (palety) pak na adrese http://matplotlib.org/examples/color/colormaps_reference.html. My využijeme barvovou mapu pojmenovanou „coolwarm“:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - zobrazení 3D grafu funkce typu z=f(x,y)
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y)
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu formou plochy
ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# zobrazení grafu
plt.show()
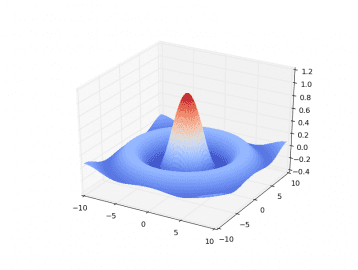
Obrázek 16: Plocha funkce z=f(x,y) používající barvovou mapu pojmenovanou „coolwarm“.
16. Promítnutí grafu na plochy kolmé na osy
Vzhledem k tomu, že se pro zobrazení trojrozměrného grafu na 2D obrazovce musí používat axonometrické promítání popř. promítání s perspektivou, nemusí být z obrázku na první pohled zřejmé, jak přesně vlastně průběh funkce vypadá. Knihovna Matplotlib nám však nabízí řešení – na plochy (které jsou kolmé na osy souřadného systému) se promítnou kontury průběhu funkce. Podívejme se, jak vypadá výsledek:
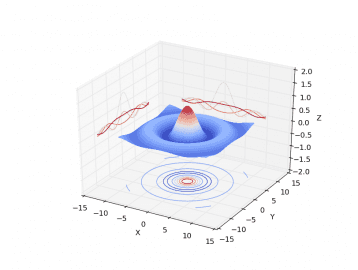
Obrázek 17: Promítnutí kontur průběhu funkce na plochy.
Samotná plocha představující funkci se vykreslí příkazem matplotlib.pyplot.plot_surface(), podobně jako v předchozím příkladu. Dále se metodou ax.contour() mohou vykreslit kontury grafu na jednotlivé plochy, ve skutečnosti je však ještě nutné korektně nastavit přesné umístění těchto kontur do grafu. K tomu slouží explicitní nastavení rozsahů na jednotlivých osách (set_xlim(), set_ylim(), set_zlim()) a vlastní posun reprezentovaný pojmenovaným parametrem offset předaným do metody ax.contour(). Podívejme se na odladěný příklad:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# - zobrazení 3D grafu funkce typu z=f(x,y)
# - pomocná legenda - colorbar
# - promítnutí grafu na ploch kolmých na osy
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y)
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu formou plochy
surface = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# kontutra: průmět na rovinu x-y
cset = ax.contour(X, Y, Z, zdir='z', offset=-5, cmap=cm.coolwarm)
# kontutra: průmět na rovinu y-z
cset = ax.contour(X, Y, Z, zdir='x', offset=-15, cmap=cm.coolwarm)
# kontutra: průmět na rovinu x-z
cset = ax.contour(X, Y, Z, zdir='y', offset= 15, cmap=cm.coolwarm)
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-15, 15)
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(-15, 15)
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(-5, 5)
# zobrazení grafu
plt.show()
17. Animace „vlnek“ ve funkci sinc
V dnešním předposledním příkladu je ukázána tvorba animovaných „vlnek“ s využitím funkce sinc. Postupovat budeme stejně jako v předchozím příkladu, ovšem do výpočtu navíc vložíme postupně měněný offset:
# offset v rozmezí 0 .. 2*Pi
offset = 2.0 * np.pi * t / DURATION
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y) + offset
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
Vykreslení grafu:
axis.plot_wireframe(X, Y, Z, rstride=7, cstride=7)
Následně musíme zakázat zobrazení všech další elementů v grafu, tj. souřadných os atd.:
axis.set_axis_off() axis.margins(0, 0, 0) axis.get_xaxis().set_visible(False)
Obrázek 18: Výsledná animace (zmenšená na poloviční rozlišení).
Původní animaci v plném rozlišení lze získat na této adrese.
Zdrojový kód příkladu:
# Knihovny Numpy a matplotlib
#
# - zobrazení 3D grafu funkce typu z=f(x,y)
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
# parametry obrázků / rámců
WIDTH = 400
HEIGHT = 300
DPI = 100
# parametry animace
DURATION = 4
FPS = 10
fig = plt.figure(figsize=(1.0 * WIDTH / DPI, 1.0 * HEIGHT / DPI), dpi=DPI)
axis = fig.add_subplot(111, projection="3d")
delta = 0.1
def make_frame(t):
axis.clear()
# offset v rozmezí 0 .. 2*Pi
offset = 2.0 * np.pi * t / DURATION
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y) + offset
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu
axis.set_axis_off()
axis.margins(0, 0, 0)
axis.plot_wireframe(X, Y, Z, rstride=7, cstride=7)
axis.get_xaxis().set_visible(False)
axis.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# konverze na objekt typu "frame"
return mplfig_to_npimage(fig)
animation = VideoClip(make_frame, duration=DURATION)
animation.write_gif('wireframe.gif', fps=FPS)
18. Zobrazení 3D grafu funkce typu [x,y,z]=f(t)
Poslední typ grafu, s nímž se dnes seznámíme, je trojrozměrný graf, v němž se zobrazuje funkce typu [x,y,z]=f(t) popř. složitější funkce [xn, yn, zn]=f(xn-1, yn-1, zn-1). Tento příkaz automaticky zjistí potřebné rozsahy na všech třech osách, což je dobře patrné z dalšího screenshotu. Podívejme se tedy, jakým způsobem je možné zobrazit trojrozměrnou spirálu (pokud budete potřebovat, aby se spirála nezužovala, postačuje proměnnou r nastavit na konstantní hodnotu):
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # - zobrazení 3D grafu funkce typu [x,y,z]=f(t) from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt import numpy as np # nezávislá proměnná t = np.arange(0, 8*np.pi, 0.1) # vzdálenost od osy spirály r = 10.0/(t+4) # výpočet souřadnic [x,y,z]) pro každé t x = r*np.cos(t) y = r*np.sin(t) z = t fig = plt.figure() ax = fig.gca(projection='3d') # vykreslení grafu ax.plot(x, y, z) # zobrazení grafu plt.show()
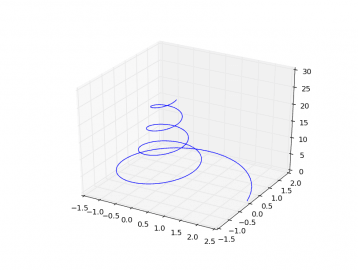
Obrázek 19: Spirála vykreslená předchozím demonstračním příkladem.
19. Repositář s demonstračními příklady
Zdrojové kódy všech dnes popsaných demonstračních příkladů určených pro Python 3 byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/moviepy-examples. V případě, že nebudete chtít klonovat celý repositář (ten je ovšem prozatím velmi malý, doslova několik kilobajtů), můžete namísto toho použít odkazy na jednotlivé příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- MoviePy 0.2.3.3 na PyPi
https://pypi.org/project/moviepy/ - MoviePy na GitHubu
https://github.com/Zulko/moviepy - MoviePy – dokumentace
http://zulko.github.io/moviepy/ - MoviePy – galerie
http://zulko.github.io/moviepy/gallery.html - Data Animations With Python and MoviePy
https://zulko.github.io/blog/2014/11/29/data-animations-with-python-and-moviepy/ - Porovnání formátů Ogg Theora a H.264
https://www.root.cz/zpravicky/porovnani-formatu-ogg-theora-a-h-264/ - Případ GIF
https://www.root.cz/clanky/pripad-gif/ - Pravda a mýty o GIFu
https://www.root.cz/clanky/pravda-a-myty-o-gifu/ - Anatomie grafického formátu GIF
https://www.root.cz/clanky/anatomie-grafickeho-formatu-gif/ - GIF: animace a konkurence
https://www.root.cz/clanky/gif-animace-a-konkurence/ - Two python modules : MoviePy and images2gif – part 001
http://free-tutorials.org/two-python-modules-moviepy-and-images2gif-part-001/ - images2gif
https://pypi.org/project/images2gif/ - Making GIFs from video files with Python
https://www.devbattles.com/en/sand/post-345-Making+GIFs+From+Video+Files+With+Python - GIF89a specification
https://www.w3.org/Graphics/GIF/spec-gif89a.txt - MPEG-4 Part 14
https://en.wikipedia.org/wiki/MPEG-4_Part14 - Theora video compression
https://www.theora.org/ - Theora
https://en.wikipedia.org/wiki/Theora - NumPy
http://www.numpy.org/ - numpy 1.14.2 (on PyPi)
https://pypi.org/project/numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
https://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy (2.část)
https://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy-2-cast/ - Non-linear editing system
https://en.wikipedia.org/wiki/Non-linear_editing_system - Lorenzův atraktor
http://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Lorenz system
https://en.wikipedia.org/wiki/Lorenz_system - Customising contour plots in matplotlib
https://philbull.wordpress.com/2012/12/27/customising-contour-plots-in-matplotlib/ - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb



































