Praktické ukázky možností aplikace Mandelbulber při tvorbě animací

Obsah

1. Praktické ukázky možností aplikace Mandelbulber při tvorbě animací

2. Řízení animace ve flight režimu

3. Záznam parametrů jednotlivých snímků

4. Vytvoření animace ve flight režimu

5. Druhý typ animace založené na klíčových snímcích (keyframes)

6. Algoritmus výpočtu mezisnímků vkládaných mezi klíčové snímky

7. Jednoduchá animace založená na změně pozice a orientace kamery mezi jednotlivými mezisnímky

8. Vybrané snímky ze druhé animace

9. Třetí animace: průlet IFS systémem (Sierpinského pyramida)

10. Čtvrtá animace: změna parametrů multifraktálu typu Mandelbulb

11. Pátá animace: úprava předchozího příkladu (změna pohledu a materiálu)

12. Šestá animace: postupná změna vybrané transformace IFS systému

13. Sedmá animace: postupná změna parametru fraktálu typu MandelBox

14. Vybrané snímky ze sedmé animace

15. Osmá animace: průlet multifraktálem typu MandelBox aneb výsledek deseti hodin renderingu

16. Vybrané snímky z osmé animace

17. Upravený skript pro vytvoření souboru s animací ze snímků typu PNG

18. Repositář s demonstračními příklady

19. Literatura

20. Odkazy na Internetu

1. Praktické ukázky možností aplikace Mandelbulber při tvorbě animací

Ve třetí části článku o aplikaci Mandelbulber si ukážeme tvorbu animací trojrozměrných fraktálů. Z předchozích dvou článků [1] [2] již víme, že existují dva způsoby tvorby animací. První z nich, který se jmenuje Flight Mode, spočívá v tom, že se myš použije pro okamžitou změnu souřadnic kamery, podobně jako v některých počítačových hrách při řízení letadla (FPS). Mandelbulber se v tomto případě snaží o rychlé (resp. většinou pouze „rychlé“) vygenerování snímků tak, aby vznikla plynulá animace. Ovšem výpočetní výkon většiny současných strojů dostačuje pouze pro vyrendrování animací s velmi nízkým rozlišením, například jen 320×240 pixelů nebo dokonce pouze 160×120 pixelů. Přesněji řečeno je pochopitelně možné vytvářet i animace s vyšším rozlišením, ovšem ovládání Mandelbulberu se v takovém případě stává velmi nepohodlné a taktéž nepřesné. Ostatně i dále ukázané animace trpí zásadním problémem – kvůli pomalému překreslování snímků bylo nutné při ovládání provádět korekce směru letu a orientace kamery, takže průběh letu není zcela plynulý (a to jsme pro rendering zvolili fraktál, jehož vykreslení není příliš náročné na výpočetní výkon, zejména v porovnání s ostatními typy fraktálů).

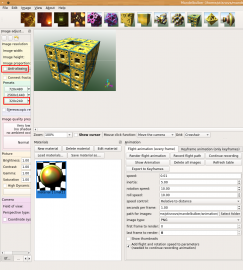
Obrázek 1: Při tvorbě animací s využitím Flight módu je vhodné vypnout antialiasing a nastavit malé rozlišení snímků (viz červeně označené oblasti). Po záznamu průletu se samozřejmě může celá animace přepočítat ve vyšší kvalitě.

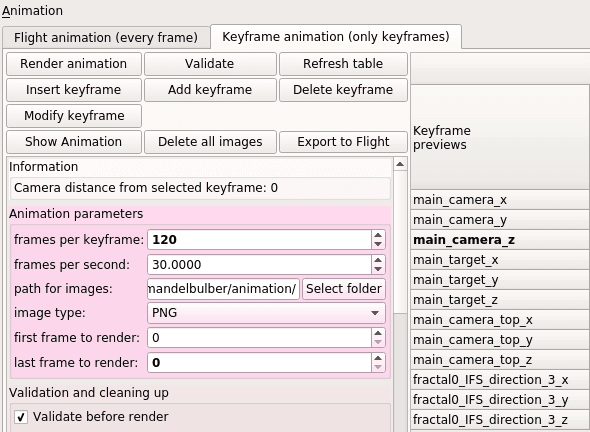
Obrázek 2: Takto vypadá ovládací panel Animation.

2. Řízení animace ve flight režimu

Při zapnutí flight režimu se směr letu řídí posunem myši (bez tlačítek), ovšem kurzorovými šipkami je navíc možné posunovat vlastní pozici kamery. Levé a pravé tlačítko myši v tomto režimu slouží k urychlení popř. naopak ke zpomalení letu. Jiné parametry není možné změnit – jinými slovy se flight režimu používá skutečně pro animaci průletu okolo fraktálu nebo do jeho vnitřních struktur.

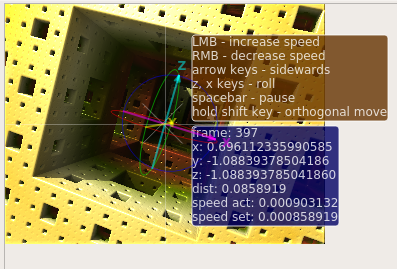
Obrázek 3: Řízení průletu fraktálem ve Flight režimu.

Samotná animace je na disk uložena ve formě jednotlivých snímků, přičemž každý snímek je reprezentován samostatným souborem obsahujícím rastrový obrázek ve volitelném formátu. Mezi dostupné formáty patří především PNG a JPEG. V případě formátu PNG se navíc může použít jak klasický osmibitový PNG (8 bitů na každý barvový kanál) nebo 16bitový PNG s prakticky neexistujícími limity grafické hloubky.

3. Záznam parametrů jednotlivých snímků

Ve flight režimu si program Mandelbulber zapamatuje parametry všech snímků. Tyto parametry je možné uložit do datového souboru (v čitelném textovém formátu) a v případě potřeby je později upravit. Výsledný soubor je poměrně velký, zejména v porovnání s druhým typem animace založené na takzvaných klíčových snímcích (keyframes).

Záznam o celé animaci v textové podobě vypadá následovně:

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
camera 0.6698412681641133 -1.006734812642523 0.8925065928012289;
camera_distance_to_target 0.0003269458059053389;
camera_rotation 42.59240267446317 9.484971255576303 -16.61404534485825;
camera_top -0.1036233068281728 -0.3097574898737641 0.9451521082604107;
flight_last_to_render 0;
flight_movement_speed_vector -0.0001793833208766696 0.0002724050449185366 2.259813473156575e-05;
flight_rotation_speed_vector -0.02544994188088445 -0.02768883180620245 1.066266961989842e-19;
formula_1 7;
image_proportion 2;
keyframe_last_to_render 0;
mat1_coloring_palette_offset 0.821;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 999 698403 1999 fff59b 2999 f5bd22 3999 0b5e87 5000 c68876 5999 a51c64 7000 3b9fee 7999 d4ffd4 9000 aba53c;
raytraced_reflections true;
target 0.6696230233293724 -1.006497409995474 0.8925604698397714;
view_distance_max 13.67068019813978;

Po globálních parametrech začíná sekce se záznamy snímků. Nejprve je uveden, které parametry se zapisují:

[frames]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z;main_flight_movement_speed_vector_x;main_flight_movement_speed_vector_y;main_flight_movement_speed_vector_z;main_flight_rotation_speed_vector_x;main_flight_rotation_speed_vector_y;main_flight_rotation_speed_vector_z

Následuje popis parametrů určujících jednotlivé snímky:

0;2.184320274477346;-3.78335369539757;2.52223579693171;2.181947883522066;-3.779283206204712;2.51949384638436;-0.2515020062654875;0.435614253057331;0.8642840756242927;-0.002360432187041097;0.004088388475776116;-0.002725592317184073;-0.003541666666666667;0.003472222222222221;0
1;2.179984801168247;-3.775882983629211;2.517227078372353;2.175599494455521;-3.768487793077087;2.512150133771537;-0.254267303519765;0.4403587981349881;0.8610646127125982;-0.004335473309099044;0.007470711768358814;-0.005008718559356938;-0.006493055555555557;0.00636574074074074;0
2;2.173989013214207;-3.765638982456678;2.510294429635929;2.167876905135092;-3.755574446731573;2.503202327889438;-0.2581123274041124;0.4468424334354252;0.856568658149211;-0.00599578795403969;0.01024400117253264;-0.006932648736423424;-0.008952546296296299;0.008777006172839504;0
...
...
...
576;0.6701932233994889;-1.007284512741679;0.8924665119947717;0.6699895522022018;-1.007032073109815;0.8925078714241756;-0.1386513581221036;-0.2680648250519875;0.9533714126513041;-0.0001657822991899907;0.000281559953000432;1.259161950593619e-05;-0.0242729163084736;-0.0270385844675982;1.535424425265372e-19
577;0.6700206514849899;-1.007007217687441;0.8924839946664973;0.6698095465534242;-1.006761975762592;0.8925316429902242;-0.1215387903450132;-0.2891098998409893;0.9495492553076982;-0.0001725719144990051;0.000277295054237456;1.748267172568313e-05;-0.02491493025706134;-0.02739326483410961;1.27952035438781e-19
578;0.6698412681641133;-1.006734812642523;0.8925065928012289;0.6696230233293724;-1.006497409995474;0.8925604698397714;-0.1036233068281728;-0.3097574898737641;0.9451521082604107;-0.0001793833208766696;0.0002724050449185366;2.259813473156575e-05;-0.02544994188088445;-0.02768883180620245;1.066266961989842e-19

4. Vytvoření animace ve flight režimu

V první animaci, kterou naleznete na adrese https://youtu.be/4PqqvcXOp5M?t=6, je ukázán průlet fraktálem, který se nazývá Mengerova houba. Animace byla vytvořena ve flight režimu a schválně neprošla žádnými dalšími úpravami, takže průlet je velmi „kostrbatý“. Ukazuje se zde základní nevýhoda tohoto režimu, který vyžaduje finální úpravy animace.

Obrázek 4: Vybraný snímek z animace průletu trojrozměrnou Mengerovou houbou.

Obrázek 5: Vybraný snímek z animace průletu trojrozměrnou Mengerovou houbou.

Obrázek 6: Vybraný snímek z animace průletu trojrozměrnou Mengerovou houbou.

Obrázek 7: Vybraný snímek z animace průletu trojrozměrnou Mengerovou houbou.

Obrázek 8: Vybraný snímek z animace průletu trojrozměrnou Mengerovou houbou.

5. Druhý typ animace založené na klíčových snímcích (keyframes)

Druhý režim tvorby animací je v porovnání s flight režimem mnohem pokročilejší i univerzálnější. Tento režim je založen na vytvoření takzvaných klíčových snímků (keyframes), mezi nimiž jsou automaticky dopočítány parametry mezisnímků, kterých může být libovolný počet (například třicet mezisnímků mezi každým klíčovým snímkem). Takový typ animací lze v případě potřeby vytvářet velmi precizním způsobem, protože pozice kamery a její orientaci, stejně jako další parametry vykreslovaného fraktálu, je možné nastavit bez nutnosti sledovat neustále se překreslující snímky, jak je tomu ve flight režimu. Ve výchozím stavu se zaznamenává pozice a orientace kamery, tj. i tento typ animace se (pokud neprovedeme žádné další úpravy) používá pro podobné účely jako výše popsaný režim flight.

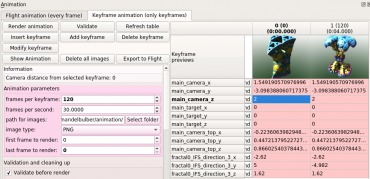
Obrázek 9: Animace, v níž se provádí interpolace mezi dvojicí klíčových snímků. Zbylých 120 snímků je dopočítáno automaticky.

6. Algoritmus výpočtu mezisnímků vkládaných mezi klíčové snímky

Při vytváření a úpravách animací je vhodné vědět, jak vlastně interně pracuje algoritmus výpočtu mezisnímků, které jsou vkládány mezi jednotlivé klíčové snímky. Nejprve si musíme uvědomit, jak je interně celá animace reprezentována. Zjednodušeně řečeno se jedná o sadu neměnných parametrů a dále o sadu parametrů, které se v čase (tj. mezi jednotlivými snímky) mohou měnit. Sadou neměnných parametrů se nemusíme dále zabývat, protože ty jsou pro všechny snímky shodné. U proměnných parametrů se většinou jedná o reálná čísla, ovšem v některých případech (pozice a orientace kamery) se taktéž může jednat o vektory různé délky. Tyto vektory se opět rozkládají na reálná čísla. Hodnoty všech parametrů jsou předem známé v jednotlivých klíčových snímcích, takže by se mohlo zdát, že postačuje mezihodnoty dopočítat tím nejprimitivnějším možným způsobem – lineární interpolací. To sice skutečně možné je, protože výsledkem bude animace, ve které nebude docházet ke skokové změně hodnot jednotlivých parametrů.

Výhodnější je však proložení hodnot nějakou křivkou, která mj. zajistí, aby nedocházelo ani ke skokovému rozdílu v rychlosti změny parametrů (takzvaná parametrická spojitost C1). V počítačové grafice, především právě při tvorbě animací (pohyb kamery), se k tomuto účelu používají křivky pojmenované podle svých tvůrců Edwina Catmulla a Raphaela Roma Catmull–Rom spline. Alternativní křivkou použitou v programu Mandelbulber je Akima spline (Akimova spline křivka), která je opět pojmenovaná podle svého tvůrce (Hiroshi Akima). U každého (!) parametru je možné z kontextového menu zvolit, který typ interpolace se použije, přičemž výchozí je Akimova spline křivka, ovšem zvolit lze i Catmull-Romovu spline křivku či běžnou lineární interpolaci.

Obrázek 10: Interpolační křivka je zobrazena i při prohlížení jednotlivých snímků animace (zelená křivka). Ve výsledné animaci samozřejmě tyto dodatečné informace již nejsou obsaženy.

Názorný popis teorie stojící za Catmull-Romovými spline křivkami naleznete na videu: https://www.youtube.com/wat­ch?v=yRGXJL9r9bs.

V navazujících kapitolách si ukážeme některé možnosti, které nám aplikace Mandelbulber poskytuje při tvorbě animací fraktálů a multifraktálů s využitím klíčových snímků. Popíšeme si celkem osm animací, z nichž některé budou založeny na „průletu“ kamery trojrozměrnou scénou a další na postupné změně dalšího parametru (či parametrů), které ovlivňují tvar a barvu vykreslovaného trojrozměrného objektu.

7. Jednoduchá animace založená na změně pozice a orientace kamery mezi jednotlivými mezisnímky

První animací založenou na interpolaci mezi jednotlivými mezisnímky je animace, ve které se mění pouze pozice a orientace kamery v 3D prostoru. Všechny ostatní parametry přitom zůstávají konstantní.

Výslednou animaci naleznete na adrese https://www.youtube.com/wat­ch?v=YElonk1qoOw. Povšimněte si, že v jednom místě kamera projde přímo tělesem fraktálu. Tento problém je sice možné detekovat, ale algoritmus detekce kolizí není ideální a 100% úspěšný.

Základní parametry animace:

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
antialiasing_enabled true;
camera 0.146880224016551 0.9824312030562514 -0.749819764737584;
camera_distance_to_target 0.01537383131265584;
camera_rotation -5.83998681940222 -3.735321559619328 0.0007354835459676367;
camera_top 0.006630655776514439 0.06470139509871728 0.997866797203131;
flight_last_to_render 0;
formula_1 7;
frames_per_keyframe 50;
image_proportion 2;
keyframe_last_to_render 0;
mat1_coloring_palette_offset 1.27697;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 999 698403 1999 fff59b 2999 f5bd22 3999 0b5e87 5000 c68876 5999 ffffff 7000 3b9fee 7999 d4ffd4 9000 aba53c;
raytraced_reflections true;
target 0.1484411974787843 0.9976927532930173 -0.750821331236061;

Ve druhé části konfiguračního souboru se nachází popis jedenácti klíčových snímků:

[keyframes]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z
0;1.536385357964839;-2.661097500000001;1.774064999999999;0;0;0;-0.2499999999999994;0.433012701892219;0.8660254037844389
1;0.08998520802143306;-1.352108442784274;0.02355372996525784;-0.4614006021377691;-1.004985377470033;-0.6762821378846748;-0.6193841855629544;0.3899312117547966;0.6814080134353806
2;-0.1206185580916745;-0.5392463964825122;-0.1976880450330409;-0.331222324204782;0.2736156498192495;-0.4189298200313397;-0.06390123311149226;0.2466379783556042;0.966998624631644
3;0.106074481344641;0.1476418112029654;-0.7070492455398547;0.1412285426420312;0.4591175733869118;-0.7981690762359502;0.03130596399437897;0.2773804401591648;0.9602499820544079
4;0.146576795116628;0.3128259795490299;-0.7336893447915228;0.1609067083388059;0.3571403375463972;-0.7375284592385013;0.02527684118868513;0.07816704624173214;0.9966197841611237
5;0.1546734915591849;0.5448900314303758;-0.745368174091708;0.1627701880017418;0.7769540833117217;-0.7570470033918931;0.001751517467621676;0.05020124483620785;0.9987375867581313
6;0.145639917566194;0.7713323533155919;-0.7443078900760406;0.1366063435732031;0.9977746752008079;-0.7432476060603733;0.0001864967390069002;-0.00467486674017504;0.9999890553600714
7;0.1534199995777104;0.873142063769607;-0.7440024225029764;0.1612000815892269;0.974951774223622;-0.7436969549299123;-0.0002279503019348791;-0.002982944678930413;0.9999955250298385
8;0.1402693162147516;0.9379744242544134;-0.7399069767735347;0.1384885666403564;0.9494048216975496;-0.7388523217261679;0.01397585795740999;-0.08970919513838463;0.995869939149675
9;0.1448069423026079;0.9675615732681002;-0.7466136038188748;0.1493445683904641;0.997148722281787;-0.7533202308642148;0.03314316084035036;0.2161067526459227;0.9758070518039643
10;0.1468817659228249;0.9824412763321352;-0.749821991751639;0.1484403604237604;0.9976930479973179;-0.7508185870775553;0.006594531308636691;0.06453140037248785;0.9978938874062638
interpolation;morphAkima;morphAkima;morphAkima

8. Vybrané snímky ze druhé animace

Obrázek 11: první snímek animace.

Obrázek 12: snímek číslo 67.

Obrázek 13: snímek číslo 102.

Obrázek 14: snímek číslo 137.

Obrázek 15: poslední snímek animace.

9. Třetí animace: průlet IFS systémem (Sierpinského pyramida)

V pořadí třetí animace, kterou lze nalézt na adrese https://www.youtube.com/watch?v=u-OFB8J1qZk zobrazuje průlet klasickým trojrozměrným fraktálem – 3D Sierpinského pyramidou, což je zobecnění známého dvourozměrného Sierpinského trojúhelníku.

Z výpisu konfiguračního souboru je patrné, že bylo použito pouze osmi klíčových snímků, mezi nimiž byly všechny mezisnímky automaticky dopočítány s využitím zvolené interpolační metody (Akimova spline):

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
camera 0.1435896286324866 -0.5017094597222777 0.1866890437413757;
camera_distance_to_target 0.00115271631227662;
camera_rotation 5.511998509862584 44.4281975115478 0.1871392018567766;
camera_top 0.07508952196018512 -0.7440161351845681 0.6716865622407544;
flight_last_to_render 0;
formula_1 10;
frames_per_keyframe 35;
keyframe_last_to_render 0;
mat1_coloring_palette_offset 0.16;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 725 d4ffd4 1428 698403 1999 fff59b 2999 f5bd22 3999 0b5e87 5000 ffffff 5999 a51c64 7000 000000 8185 ffff00;
raytraced_reflections true;
target 0.1435105580354893 -0.5008900787580178 0.1874959623077055;
[fractal_1]
IFS_abs_x true;
IFS_abs_y true;
IFS_abs_z true;
IFS_direction_5 1 -1 0;
IFS_direction_6 1 0 -1;
IFS_direction_7 0 1 -1;
IFS_enabled_5 true;
IFS_enabled_6 true;
IFS_enabled_7 true;
IFS_rotation_enabled true;
[keyframes]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z
0;0.454097650739787;-2.219072397550683;0.3993908086339395;0;0;0;-0.03481289900076248;0.1701227547102634;0.9848077530122081
1;0.2459340154355849;-0.9389220333985877;0.1589209231631789;0.1687795723214649;-0.5144079915117773;0.07554532048857852;-0.03392667317096217;0.1866690831307706;0.981836867433011
2;0.1657532821013686;-0.6131804035681236;0.1592296044725066;0.1358446799204512;-0.5060948700391179;0.17005454178142;0.02606692845974855;-0.09333070548364154;0.9952938735140492
3;0.1508343714034735;-0.5289307249655235;0.1748564528463116;0.1467713852727099;-0.5001861271674746;0.1810452522036345;0.0291807775395143;-0.2064466101561688;0.9780226374564222
4;0.144769086586466;-0.5082642430520836;0.1810663994316755;0.1423645743927419;-0.501914773877389;0.1832904041258494;0.11024362749722;-0.291114562166546;0.9503150289724112
5;0.1436877632536203;-0.5026707482858135;0.1855746973231235;0.1435487184274402;-0.5009695126190791;0.1874692318502007;0.06051973742425713;-0.7404686580299342;0.6693605365253074
6;0.1435456540800579;-0.5013130262215955;0.1870040407967709;0.1434917161978314;-0.5008469185083362;0.187481382928802;0.08197842076718341;-0.7084218486732237;0.7010121417286087
7;0.1434874442486439;-0.5008929641023905;0.187343583665591;0.143467684521936;-0.5007611638267184;0.1874369336987608;0.08506018617550182;-0.5673639191664941;0.8190622369245361
interpolation;morphAkima;morphAkima;morphAkima

Obrázek 16: první snímek.

Obrázek 17: snímek číslo 32.

Obrázek 18: snímek číslo 67.

Obrázek 19: snímek číslo 102.

Obrázek 20: poslední snímek.

10. Čtvrtá animace: změna parametrů multifraktálu typu Mandelbulb

V této kapitole si ukážeme animaci, která vznikla postupnou změnou jediného parametru multifraktálu typu Mandelbulb, podle kterého je vlastně celá aplikace pojmenována. Konkrétně se jedná o parametr, kterým se řídí rotace bodu provedená v každé iteraci. Tato rotace se postupně mění od 0° do 180°. Vytvořenou animaci naleznete na adrese https://www.youtube.com/wat­ch?v=mnlDuQa_pNM.

Obrázek 21: první snímek.

Obrázek 22: prostřední snímek.

Obrázek 23: poslední snímek.

11. Pátá animace: úprava předchozího příkladu (změna pohledu a materiálu)

Pátá animace vznikla podobným způsobem, jako animace předchozí, ovšem v tomto případě se díváme na detail celého fraktálu. Výpočet je ovšem v tomto případě velmi pomalý (průměrný čas renderingu jednoho snímku je dokonce nižší, než u poslední dnes uveřejněné animace). Na vytvořenou (v tomto případě ovšem velmi krátkou) animaci se můžete podívat na adrese https://www.youtube.com/wat­ch?v=QWz0vuEc0_k.

Obrázek 24: první snímek.

Obrázek 25: poslední snímek.

12. Šestá animace: postupná změna vybrané transformace IFS systému

Již v prvním článku o aplikaci Mandelbulber jsme se zmínili o tom, že mezi podporované typy fraktálů a multifraktálů patří i zobecněné systémy iterovaných funkcí (IFS). Připomeňme si, že klasické IFS jsou tvořeny sadou lineárních transformací, přičemž každá transformace je popsána jednou maticí (rotace, změna měřítka, zkosení) jedním vektorem (posun) a pravděpodobností, s níž je daná transformace použita při výpočtu bodů v rovině či prostoru. A samozřejmě nám nic nebrání v tom, aby se v animaci postupně měnily právě parametry jednotlivých transformací, z nichž se celý IFS skládá.

Tento postup je použit v následující animaci, v níž je použit následující IFS:

Obrázek 26: základní tvar IFS, který bude animován.

Výslednou animaci naleznete na adrese https://www.youtube.com/watch?v=NyxHHs-wrGk.

V animaci (mimochodem tvořené pouze dvěma klíčovými snímky), se postupně mění jediný parametr jediné transformace, což je ostatně patrné i z výpisu konfiguračního souboru (viz zvýrazněná část):

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
antialiasing_enabled true;
camera 1.549190570976996 -3.098388060717375 2;
camera_distance_to_target 4.000000000000001;
camera_rotation 26.565 -29.99999999999996 0;
camera_top -0.2236063982948991 0.4472137952272742 0.8660254037844389;
flight_last_to_render 0;
formula_1 10;
frames_per_keyframe 120;
image_proportion 2;
keyframe_last_to_render 0;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 999 698403 1999 fff59b 2999 f5bd22 3999 0b5e87 5000 c68876 5999 a51c64 7000 3b9fee 7999 d4ffd4 9000 aba53c;
raytraced_reflections true;
[fractal_1]
IFS_abs_x true;
IFS_abs_y true;
IFS_abs_z true;
IFS_direction_3 -2.62 -4.98 1.62;
IFS_direction_4 1.62 -2.62 1;
IFS_enabled_3 true;
IFS_enabled_4 true;
IFS_offset 1 0 1.62;
IFS_rotation 0 -7 -4;
IFS_rotation_enabled true;

Povšimněte si, že celá animace je definována pouze pomocí dvou klíčových snímků a automaticky dopočítaných mezisnímků:

[keyframes]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z;fractal0_IFS_direction_3_x;fractal0_IFS_direction_3_y;fractal0_IFS_direction_3_z
0;1.549190570976996;-3.098388060717375;2;0;0;0;-0.2236063982948991;0.4472137952272742;0.8660254037844389;-2.62;5;1.62
1;1.549190570976996;-3.098388060717375;2;0;0;0;-0.2236063982948991;0.4472137952272742;0.8660254037844389;-2.62;-4.982;1.62
interpolation;morphAkima;morphAkima;morphAkima;morphAkima

Obrázek 27: první snímek.

Obrázek 28: snímek číslo 21.

Obrázek 29: snímek číslo 44.

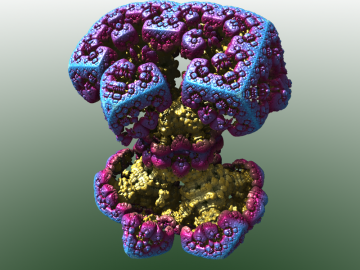
Obrázek 30: snímek číslo 79.

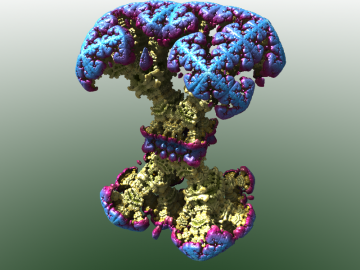
Obrázek 31: snímek číslo 89.

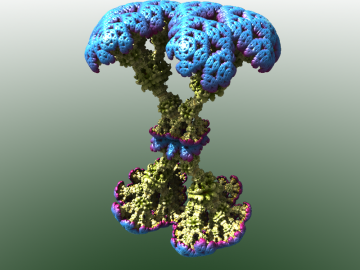
Obrázek 32: poslední snímek.

13. Sedmá animace: postupná změna parametru fraktálu typu MandelBox

V sedmé animaci je použit multifraktál nazvaný MandelBox se kterým jsme se již seznámili v úvodním článku. Jediným parametrem, který se v této animaci mění, je základní parametr (Folding)fixedRadius určující výsledný tvar objektu. Všechny ostatní parametry, a to včetně pozice a orientace kamery, zůstávají ve všech snímcích konstantní.

Výslednou animaci naleznete na adrese https://www.youtube.com/wat­ch?v=cNgXqCgmGUE.

Následuje výpis konfiguračního souboru:

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
antialiasing_enabled true;
camera 2.950124371652882 -5.109765300350009 1.803373307116767;
camera_distance_to_target 6.169691282203883;
camera_rotation 29.99999999999996 -20.99543734688988 0;
camera_top -0.1791468021504017 0.3102913633379855 0.9336089615664253;
flight_last_to_render 0;
formula_1 8;
frames_per_keyframe 180;
image_proportion 2;
keyframe_last_to_render 0;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 999 698403 1804 fff59b 2828 3b9fee 3985 d4ffd4 4988 0b5e87 6836 a51c64 7838 f5bd22 9000 aba53c;
raytraced_reflections true;
target 0.07008483607098773 -0.1213904969150865 -0.4071876198073064;
[fractal_1]
mandelbox_folding_fixed_radius 2.999769;
mandelbox_scale -2;

Opět si povšimněte, že se používají pouhé dva klíčové snímky:

[keyframes]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z;fractal0_mandelbox_folding_fixed_radius
0;2.950124371652882;-5.109765300350009;1.803373307116767;0.07008483607098773;-0.1213904969150865;-0.4071876198073064;-0.1791468021504017;0.3102913633379855;0.9336089615664253;0.5
1;2.950124371652882;-5.109765300350009;1.803373307116767;0.07008483607098773;-0.1213904969150865;-0.4071876198073064;-0.1791468021504017;0.3102913633379855;0.9336089615664253;3
interpolation;morphAkima;morphAkima;morphAkima;morphAkima

14. Vybrané snímky ze sedmé animace

Obrázek 33: první snímek.

Obrázek 34: snímek číslo 31.

Obrázek 35: snímek číslo 44.

Obrázek 36: snímek číslo 66.

Obrázek 37: snímek číslo 79.

Obrázek 38: snímek číslo 101.

Obrázek 39: poslední snímek.

15. Osmá animace: průlet multifraktálem typu MandelBox aneb výsledek deseti hodin renderingu

Poslední, v pořadí již osmá, animace ukazuje průlet kamery trojrozměrným modelem multifraktálu MandelBox, který ostatně tvořil základ i pro předchozí demonstrační příklad. Tato animace je založena na dvaceti klíčových snímcích, přičemž se mezi jednotlivými klíčovými snímky automaticky dopočítalo třicet mezisnímků. Rendering této animace trval nejdéle (cca deset hodin na stroji s osmi reálnými mikroprocesorovými jádry), protože kromě vyššího nastavení kvality snímků (800×600 pixelů s povoleným antialiasingem) se interní struktura objektu Mandelbox počítá poměrně pomalu.

Výslednou animaci naleznete na adrese https://www.youtube.com/wat­ch?v=PnJmjidWMjs.

Podobně jako tomu bylo i v předchozích případech následuje výpis konfiguračního souboru, který celou animaci popisuje:

# Mandelbulber settings file
# version 2.19
# only modified parameters
[main_parameters]
ambient_occlusion_enabled true;
antialiasing_enabled true;
camera 0.6605814562212847 0.05843283987467794 1.19804949480218;
camera_distance_to_target 0.01133855943936708;
camera_rotation -24.5515771530857 -2.85208291156551 0.008132234318936235;
camera_top 0.02074538646278866 0.04507162956535532 0.9987643123825091;
flight_last_to_render 0;
formula_1 8;
frames_per_keyframe 30;
image_proportion 2;
keyframe_last_to_render 0;
mat1_coloring_palette_offset 0.53;
mat1_is_defined true;
mat1_specular 4;
mat1_specular_width 0.063;
mat1_surface_color_gradient 0 fd6029 999 698403 1999 fff59b 2999 f5bd22 3999 0b5e87 5000 ffffff 5999 a51c64 7000 3b9fee 7999 d4ffd4 9000 aba53c;
raytraced_reflections true;
target 0.6652869303444912 0.06873347790665883 1.197485314361182;
[fractal_1]
mandelbox_folding_fixed_radius 1.5;
mandelbox_scale -2;
[keyframes]
frame;main_camera_x;main_camera_y;main_camera_z;main_target_x;main_target_y;main_target_z;main_camera_top_x;main_camera_top_y;main_camera_top_z
0;2.231831425504247;-5.476316072762058;1.532634206147215;0.3358449020068148;0.113711396788589;-0.2624638790442391;-0.09345413834390873;0.2755352920557527;0.9567374910905021
1;1.582902949716866;-3.536719449320143;1.281916149520598;0.9339744739294846;-1.597122825878227;1.031198092893982;-0.03860476745077607;0.1153866402694567;0.9925701965994136
2;1.411557647731036;-2.233897617033763;1.046875169801422;1.240212345745206;-0.9310757847473838;0.8118341900822461;-0.02295933539202468;0.174571015702484;0.9843768736591487
3;1.000662574621819;-0.2783909358907124;1.252725010946661;-0.6195501764144095;0.9492558221953091;0.9905775165441681;-0.1019422464494861;0.07724236726669188;0.991786970618121
4;0.8041926639459211;-0.1122908275096245;1.262208297315899;0.65170549477771;0.07601378534427967;1.163884416032277;-0.2366316150780143;0.2922136000643174;0.9266157189919787
5;0.7472780182634335;-0.06997176989652509;1.230936868217791;0.6818068717597969;-0.04301248954318098;1.199267748782276;-0.3775407529303775;0.1554612611296995;0.9128498102999896
6;0.7223935897082703;-0.05630159237549744;1.222451632475923;0.697509161153107;-0.04263141485446979;1.213966396734055;-0.2509694828514958;0.1378692452324204;0.9581264999447074
7;0.7005069290033393;-0.03907168448557996;1.208153665549771;0.6786202682984084;-0.02184177659566248;1.193855698623619;-0.3588116571340136;0.282468480943503;0.889643609530363
8;0.6733173416578581;-0.03024228434520128;1.196303774250392;0.6461277543123769;-0.02141288420482259;1.184453882951013;-0.3642004471052167;0.1182684914609862;0.9237806007142079
9;0.6504042248824585;-0.02309755023349599;1.195395081460824;0.627491108107059;-0.01595281612179071;1.194486388671255;-0.03611801648427193;0.01126226636698188;0.9992840688420489
10;0.6393316673237612;-0.0161441030069447;1.197999722707645;0.6282591097650639;-0.009190655780393414;1.200604363954466;0.1654516022384301;-0.1039018292399493;0.9807294107945008
11;0.6335064770548678;-0.01080029187746166;1.199751690523726;0.6276812867859745;-0.00545648074797862;1.201503658339807;0.1594480559088473;-0.1462716677754113;0.9763098466537601
12;0.630124158511137;-0.005715126649541305;1.200457305353725;0.6269534777270486;-0.0005744509089900006;1.198955603871742;-0.1266657107644721;0.205365153677497;0.9704539924033231
13;0.6275785992628951;0.002207752331324329;1.196917813432865;0.6250330400146531;0.01013063131218996;1.193378321512004;-0.1197250673154138;0.3726360798599076;0.9202218538173065
14;0.6260795154721805;0.007390188407257582;1.195752747667552;0.6245804316814662;0.01257262448319083;1.19458768190224;-0.05865596216451867;0.202777707472318;0.9774664595037651
15;0.6272443721472658;0.0145306129496766;1.196116993469315;0.628409228822351;0.02167103749209561;1.196481239271077;-0.008095849455333934;-0.0496265363619697;0.9987350319831134
16;0.6313689191830876;0.02399963909510161;1.199850151652071;0.6354934662189092;0.03346866524052662;1.203583309834827;-0.1357467800498201;-0.3116438722326125;0.9404525020467375
17;0.6430332801103015;0.03548946337227479;1.200926631922356;0.6546976410375154;0.04697928764944796;1.20200311219264;-0.04673870667717317;-0.0460393441195866;0.997845615359001
18;0.6558977340244686;0.04816142335515903;1.198607469472798;0.6687621879386358;0.06083338333804326;1.19628830702324;0.09075184025808875;0.0893938985515069;0.9918532322836546
19;0.6605847053817188;0.05845303569647171;1.198048540654687;0.6652716767389689;0.06874464803778441;1.197489611836576;0.02045970828999017;0.04492525562615294;0.9987808176690286
interpolation;morphAkima;morphAkima;morphAkima

16. Vybrané snímky z osmé animace

Obrázek 40: první snímek.

Obrázek 41: snímek číslo 35.

Obrázek 42: snímek číslo 70.

Obrázek 43: snímek číslo 100.

Obrázek 44: snímek číslo 200.

Obrázek 45: snímek číslo 300.

Obrázek 46: snímek číslo 400.

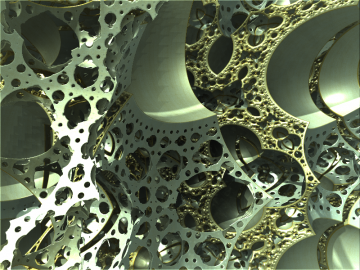
Obrázek 47: snímek číslo 500.

17. Upravený skript pro vytvoření souboru s animací ze snímků typu PNG

Na závěr si ještě ukažme upravený skript sloužící pro vytvoření souboru s animací ze snímků typu PNG, které jsou vygenerovány programem Mandelbulber. Předpokladem je, že snímky mají původní rozlišení 800×600 pixelů:

mencoder mf://*.png -mf w=800:h=600:fps=16:type=png -o output.avi -ovc xvid -xvidencopts pass=2:bitrate=3000

18. Repositář s demonstračními příklady

Konfigurační soubory všech dnes ukázaných animací byly uloženy do Git repositáře, který je dostupný na adrese https://github.com/tisnik/frac­tals.git (stále na GitHubu :-). V případě, že nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, můžete namísto toho použít odkazy na jednotlivé příklady, které naleznete v následující tabulce:

19. Literatura

Klasické knihy i vybrané články o fraktálech:

1. Barnsley Michael: „Fractals Everywhere“,
   Academic Press Inc., 1988, ISBN 0–12–079062–9
2. Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: „The Science of Fractal Images“,
   Springer-Verlag, New York, 1988
3. Barnsley Michael, Hurd Lyman P.: „Fractal Image Compression“,
   A. K. Peters, 1993
4. Bowman Richard L.: „Fractal Metamorfosis: A Brief Student Tutorial“
   Computer and Graphics, 19, strany 157–164, 1995
5. Bulín Jan: „Vykreslování výškových map“,
   Ročníkový projekt, VUT Brno, FEI, 1998
6. Cahalan R. F. a Joseph J. H.: „Fractal statistics of cloud fields“,
   Mon. Wea.Rev. 117, 261–272, 1989
7. Cahalan R. F., W. Ridgway, W. J. Wiscombe, T. L. Bell and J. B. Snider: „The albedo of fractal stratocumulus clouds“,
   Atmos. Sci. 51, 2434–2455, 1994
8. Devaney Robert L.: „A First Course In Chaotic Dynamical Systems“,
   Addison-Wesley, Reading, MA, 1992
9. Dewdney A. K: „Computer Recreations“,
   časopis Scientific American
10. Douady, A., Hubbard, J.: „Itération des polynomes quadratiques complexes“,
    C. R. Acad. Sci., Paris 1982
    
11. Etienne Martineau: „On a Bicomplex Distance Estimation for the Tetrabrot“
    June, 2004
12. Ewing, J. H., Schober, G.: „The area of the Mandelbrot Set“,
    Numer. Math. 1992
13. Fischer Yuval (editor): „Fractal Image Compression: Theory and Application“,
    Springer-Verlag, New York, 1995
14. Gleick James: „Chaos: Making a New Science“,
    Viking Press, Penguin, New York, 1987
15. Gleick James: „Chaos: Vznik nové vědy“ (český překlad předchozí knihy),
    Ando Publishing, Brno, 1996
16. Gröller Eduard: „Interactive design of Nonlinear Functions for Iterated Function System“,
    Technical University Vienna, 1995
17. Hill, F. S. jr.: „Computer Graphics using OpenGL“,
    Prentice Hall, 2001
18. Hook Brian: „An Introduction to Fixed Point Math“,
    Game Design and Review, 2003
19. Lauwerier Hans: „Fractals“,
    Princeton University Press, 1991
20. Makovský Dušan: „Stochastické fraktály“,
    Diplomová práce, VUT FIT Brno, 2003
    
21. Mandelbrot Benoit B.: „The Fractal Geometry of Nature“,
    W. H. Freeman, New York; San Francisco, 1982, ISBN 0–7167–1186–9
22. Mandelbrot Benoit B.: „Fractal Landscapes without creases and with rivers“,
    The Science of Fractal Images, ed. Heinz-Otto Peitgen, Dietmar Saupe; Springer-Verlag (1988) pp 243–260
23. Peitgen Heinz-Otto, D. Saupe: „The Science of Fractal Images“,
    Springer-Velag, 1988
24. Peitgen Heinz-Otto, Jurgens Hartmut, Saupe Dietmar: „Fractals For The Classroom“,
    Springer-Verlag, New York, 1988
25. Peitgen Heinz-Otto, Richter Peter: „The Beauty of Fractals“,
    Springer-Verlag, New York, 1986, ISBN 0–387–15851–0
26. Peitgen Heinz-Otto, Jurgens Hartmut, Saupe Dietmar: „Chaos and Fractals: New Frontiers of Science“,
    Springer-Verlag, New York, 1992
27. Perlin K. and Hoffert E. M.: „Hypertexture“,
    Computer graphics, Volume 23, Number 3, July 1989, pages 253–262
28. Perlin Ken: „An Image Synthesizer“,
    Computer Graphics, Volume 19, Number 3, 1985, pages 287–296
29. Pickover Clifford: „Computers, Pattern, Chaos and Beauty: Graphics from an Unseen World“,
    St. Martin's Press, New York, 1990
30. Pickover Clifford: „Chaos in Wonderland“,
    ISBN 0–312–10743–9 St. Martin's Press
    
31. Pritchard Joe: „The Chaos Cookbook: A Practical Programming Guide“,
    Butterworth-Heinemann, Oxford, 1992, ISBN 0–7506–0304–6
32. Prusinkiewicz Przemyslaw and Hanan James: „Lindenmayer Systems, Fractals, and Plants“,
    Springer-Verlag, New York, 1989.
33. Prusinkiewicz Przemyslaw and Lindenmayer Aristid: „The Algorithmic Beauty of Plants“,
    Springer-Verlag, NY, 1990. ISBN 0–387–97297–8
34. Sharman, J: „How to render landscapes“
35. Silverman B. W.: „Density Estimation for Statistics and Data Analysis“,
    Chapman and Hall, London, 1986.
36. Tišnovský Pavel: „Návrh editoru IFS“,
    Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1998
37. Tišnovský Pavel: „Interaktivní editor afinních transformací“,
    Vysoké učení technické v Brně, Fakulta elektrotechniky a informatiky, 1999
38. Tišnovský Pavel: „Výpočet plochy Mandelbrotovy množiny metodou součtu pixelů“,
    Elektrorevue, 2001
39. Tišnovský Pavel: „Fraktály: dynamické systémy v komplexní rovině“,
    Elektrorevue, 2001
40. Tumblin Jack, Holly Rushmeier: „Tone Reproduction for Realistic Images“,
    IEEE Computer Graphics and Applications, November/December 1993 (Vol. 13, No. 6) pp. 42–48.
    
41. Weber J., Penn J.: „Creation and Rendering of Realistic Trees“,
    Proceedings of SIGGRAPH '95, volume 22(4), ACM SIGGRAPH, New York, 1995
42. Wegner Timothy, Peterson Mark: „Fractal Creations, First Edition“,
    The Waite Group Press, 1991
43. Wegner Timothy, Tyler Bert: „Fractal Creations, Second Edition“,
    The Waite Group Press, 1993
44. Wegner Timothy, Tyler Bert, Peterson Mark, Branderhorst Pierer: „Fractals for Windows“,
    The Waite Group Press, 1992
45. Yates Randy: „Fixed-Point Arithmetic: An Introduction“
46. Žára J., Beneš B., Felkel P.: „Moderní počítačová grafika“,
    Computer Press, Praha, 1998, ISBN 80–7226–049–9
47. Žára J., Limpouch A., Beneš B., Werner T.: „Počítačová grafika – principy a algoritmy“,
    Grada, 1992
    

20. Odkazy na Internetu

1. Interpolation, approximation and extrapolation: Lecture 1
   https://www.youtube.com/wat­ch?v=yRGXJL9r9bs
2. Catmull-Rom splines
   http://graphics.cs.ucdavis­.edu/~joy/ecs278/notes/Cat­mull-Rom-Spline.pdf
3. Catmull-Rom spline
   https://en.wikipedia.org/wi­ki/Centripetal_Catmull%E2%80%93Rom_spli­ne
4. Interaktivní demo: Akimova spline křivka
   http://www.source-code.biz/snippets/typescript/akima/
5. Centripetal Catmull–Rom spline
   https://en.wikipedia.org/wi­ki/Centripetal_Catmull%E2%80%93Rom_spli­ne
6. Mandelbulber – creating animations
   https://sites.google.com/si­te/mandelbulber/getting-started
7. MandelbulberTutorial & User Manual Version: 0.9.1
   http://cdn.mandelbulber.or­g/doc/Mandelbulber_Manual_v091­.pdf
8. AppImage
   https://appimage.org/
9. Stránka aplikace Gnofract 4D
   http://edyoung.github.io/gnofract4d/
10. Repositář aplikace Gnofract 4D
    https://github.com/edyoung/gnofract4d
11. Multifractal system
    https://en.wikipedia.org/wi­ki/Multifractal_system
12. What are Multifractals?
    https://imagej.nih.gov/ij/plu­gins/fraclac/FLHelp/Multi­fractals.htm
13. Multifractal vs Fractal – What's the difference?
    https://wikidiff.com/multi­fractal/fractal
14. Mandelbulb
    http://www.mandelbulb.com/
15. Mandelbulber Fractal Rendering Software
    http://www.mandelbulb.com/2012/3d-fractal-rendering-mandelbulber/
16. Mandelbulber na Sourceforge
    https://sourceforge.net/pro­jects/mandelbulber/
17. Mandelbulb 3D (MB3D) Fractal Rendering Software
    http://www.mandelbulb.com/2014/man­delbulb-3d-mb3d-fractal-rendering-software/
18. Mandelbox (Wikipedia)
    https://en.wikipedia.org/wi­ki/Mandelbox
19. Gallery of Mandelbox fractals
    https://sites.google.com/si­te/mandelbox/
20. Mandelbulb (Wikipedia)
    https://en.wikipedia.org/wi­ki/Mandelbulb
21. Cygnus software: „Fractal eXtreme (fractal generator for Windows)“,
    http://www.cygnus-software.com
    We think that if you give Fractal eXtreme a try, you will soon decide that Fractal eXtreme's unique combination of speed, power, and intuitive interface make it your best choice for exploring the wonders of fractals.
22. Devaney Bob: „Dynamical systems and Iterated Function Systems“,
    http://math.bu.edu/people/bob/
    Bob Devaney's Home Page
23. Gintz Terry W.: „Zplot (fractal generator)“,
    http://www.mysticfractal.com/Frac­talZplot.html
    Fractal Zplot is an interactive program for generating fractal images. Originally named Zplot, this program has been in continuous development since 1989. Fractal Zplot currently supports the Mandelbrot set, Julia sets, Newton's method, and Phoenix curves, with millions of mapping variations. 3D fractal types include quaternion, hypercomplex, orbital fractals and lsystems, in addition to the original height field and landscape types.
24. Hubička Jan: „Stránky programu XaoS“,
    http://xaos.sourceforge.net/en­glish.php
    Welcome to the redesigned web portal of XaoS. Here we offer up-to-date information about the XaoS project, the development issues and others.
25. Hubička Jan: „Starší (a IMHO hezčí) verze stránek programu XaoS“,
    http://xaos.sourceforge.net/blac­k/index.php
    XaoS is a fast portable real-time interactive fractal zoomer. It displays the Mandelbrot set (among other escape time fractals) and allows you zoom smoothly into the fractal. Various coloring modes are provided for both the points inside and outside the selected set. In addition, switching between Julia and Mandelbrot fractal types and on-the-fly plane switching is provided. The first version was a minimal X Window Mandelbrot viewer by Thomas later modified by Jan to support high frame-rate zooming. Other additions were later made by both Thomas and Jan including autopilot (for those of you without drivers licenses), palette changing, GIF saving, and fractal inversion.
26. Chardonnet David: „IFS Fractals Digital Encyclopedy“,
    http://www.chez.com/fractal­s/galeries/gb_index.html
27. Jones Damien M. a kol.:„Fractalus“,
    http://www.fractalus.com
    fractalus.com exists to showcase fractal art, provide information about fractals, and promote fractals in general. We (the artists who build and maintain this site) want to show you our very best; we create this art because we love to do it. We're happy to share this with you, but we would appreciate it if you would respect our wishes regarding image re-use and copyrights.
28. Kolka Milan: „Spojování želv v jazyce založeném na L-systémech“,
    http://www.elektrorevue.cz/clan­ky/01010/index.html
    Článek představuje programovací jazyk Fraktálovač, který je určen ke generování fraktálů. Jazyk je založen na Lindenmayerových systémech (L-systémech). Zejména je zde ukázán princip spojování želv, který rozšiřuje možnosti klasických L-systémů.
29. Lartigue Ghislain: „Hydrodynamical Instabilities: The Iterative Function System“,
    http://www.enseeiht.fr/hmf/tra­vaux/CD9900/travaux/optmfn/hi/00pa/mfn11/pa01­.htm
    The aim of this hands-on was to study a dynamical system. I have choosen to deal with a particular class of these systems which are the Iterative Function System (IFS). These systems are not really what one could call a „pure“ dynamical system. Actually, all the systems we have studied so far can be written X'=F(X,t), that is to say that the derivative of a given set of variables X=(x1,…,xn) can be expressed as a function of this set X and of the time (for the non-autonomous systems). Thus, the whole evolution of the system is perfectly deterministic and actually, is totally determined by the initial condition X(0). However, it is well known that in many cases, the evolution of a system can become chaotic and then, the sensibility to the initial conditions can give the impression that the system follows a random trajectory. But one should still remember that this is just an illusion which is the consequence of our finite precision knowing of the initial condition.
30. Pulcini Giovambattista, Verrando, Meloni Rossi: „IFS: Fractal Image Compression“,
    http://mathforum.org/libra­ry/view/6165.html
    Download IFS Application Framework, a freeware educational program for fractal image coding. Note: It needs 486DX2/66, 8MB RAM, Windows 3.1 with a 11MB swapfile and a 32000 SVGA driver (at least). Download IFSDOC, an introduction to IFS and IFSAF (in Postscript format). A more detailed description of IFSAF is also available.
31. Pulcini Giovambattista: „Fractal Image Compression Software (for Windows)“,
    http://www.verrando.com/pulcini/gp-ifs1.html
    IFSAF: IFS Application Framework is a software running under Windows 3.x for fractal image encoding. It has some bugs, makes no control on what you are doing, so it crashes frequently, is not a well-behaved window application: it monopolizes the CPU until the enc/dec is over, but shows graphically each step of the computation, so may be a valuable choise for the beginners in this field.Besides, it is a powerful framework, for testing several different algorithms, andoptions.
32. Scott Draves: „The Fractal Flame Algorithm“,
    http://flam3.com/flame_draves.pdf, May 18, 2005
33. Slijkerman Frederik: „Ultra Fractal (fractal generator for Windows)“,
    http://www.ultrafractal.com
    Ultra Fractal is the best tool to create fractal artwork and fractal animations. Whether you are a graphics designer, a professional fractal artist, a video producer, or a complete beginner, Ultra Fractal 4 makes it easy to create beautiful fractal pictures, animated textures, and moving fractal backgrounds.
34. Thornton Sterling: „XenoDream (Interactive IFS Editor)“,
    http://xenodream.com
    XenoDream is a 3-D graphics program that combines standard shapes with 3-D IFS fractal methods for interactive modeling with a difference. Browse through our galleries for some examples, and the XenoDream pages to learn more.
35. Tyler Bert, Wegner Tim a kol.:
    „Fractint (fractal generator for DOS, Windows and Unix)“,
    http://www.fractint.org
    Fractint is a freeware fractal generator created for IBMPC's and compatible computers to run under DOS and ported to Linux. This page is for developers who wish to keep up with the latest source changes and users who would like to try the current developer's version. This page is under development by a one-finger typist entering html in a text editor, so it may not get much fancier than this for a while.
36. Mandelbrot Explorer (prohlížeč Mandelbrotovy množiny jako jednoduchá webová aplikace):
    http://www.softlab.ece.ntu­a.gr/miscellaneous/mandel/man­del.html