Teorie chaosu je plná sofistikovaných matematických termínů jako nelineární dynamické systémy, bifurkace, fraktály, Poincarého mapy, Lyapunovovy exponenty, orbity, atraktory, Feigenbaumova konstanta, turbulence. Fíkový stromeček a mandlový chlebíček. Ale nikde jsem ještě neviděl s pomocí těchto pojmů vysvětlené, proč je chaos nepředvídatelný, citlivý na počáteční podmínky (tzv. motýlí efekt).
Na počítači si můžeme toto snadno odsimulovat, např. prográmkem v C s použitím long double přesnosti floating point čísel. To nám ale stále neřekne, proč se tohle všude ve všech chaotických systémech děje.
Na vysvětlení nic z toho potřebovat nebudeme. Stačí nám můj open-source chleba Twibright Quickbread.
Ten chleba rozhodně doporučuji. S majonézou, sýrem, chilli papričkami a nakládanými okurkami.

Twibright Quickbread, jednoduchý a levný open-source chleba, při jehož výrobě se používá metoda překládání vrstev, která demonstruje důvod, proč je chaos nepředvídatelný.
Já jsem vídával lidi, jak se namáhali při míchání těsta v díži. Do Quickbreadu jsem se proto rozhodl dát metodu, která tolik energie na promíchání těsta nepotřebuje.
Jak míchání funguje? U těsta potřebujeme, aby nasáknutí mouky vodou bylo všude rovnoměrné. Nechceme, aby po zmáčknutí chleba z jedné půlky vystříkla voda a druhá půlka se nám v prstech rozpadla na prach. Jediné, co za nás příroda udělá, je difúze vody. Ta je ale pomalá a funguje v rozumném čase jen na krátké vzdálenosti, například 1 mm.
Proto musíme přidat spojitou transformaci prostoru, která nám vytvoří vrstvy nebo jiné jemné tvary, kde se bude střídat mokrá hmota se suchou na škále 1 milimetru. Difúze pak míchání za nás dokončí.
Je jedno zda mícháme hmotu těsta nebo nějaký kontinuální stavový prostor chaotického systému. V obou případech se jedná o spojitý vícerozměrný prostor (v případě těsta 3 dimenze).
Pro vysvětlení, proč je chaos chaotický je kritický jeden řádek ve výrobních instrukcích chleba:
8 times flatten to about 5 cm (2 in) and fold.
Představme si, že naše těleso těsta má tloušťku 128 mm a jednu část mokrou a druhou suchou. Rozmáčknutím a přeložením získáme dvě vrstvy o tloušťce 64 mm: suchou a mokrou. A teď přijde kouzlo iterace: Pokud to uděláme 8krát, máme 128 mm tlusté těsto, které obsahuje 256 vrstev o tloušťce 0,5 mm, různě se střídajících mokrých a suchých. Někdy jsou dvě mokré nebo dvě suché vedle sebe, ale nikdy ne víc, takže efektivní tloušťka vrstev je max. 1 mm a voda může už do mouky prosáknout difúzí.
Co když neiterujeme 8krát, ale 113krát? Tloušťka vrstvy bude menší než Planckova délka vesmíru 1,6 × 10-35 m, čili už bude fyzikálně nerozlišitelná. Stačí, abychom se v dimenzi tloušťky těsta posunuli zcela neměřitelně, a původní místo odkud částice mouky a vody přišly, bude skákat přes celou šířku těsta: mezi mokrou a suchou částí. Nepředvídatelnost.
Pro vysvětlení co se děje postup nepodstatně modifikujeme: rozmáčkneme, přeřízneme a dáme na sebe. Představme si, že souřadnice částic mají formu reálných binárních čísel od .00000… do .11111… . Operace rozmáčknutí v X – přeříznutí – složení v Z posune registr X o 1 bit doleva, a vypadlý bit nacpe do nejvyššího bitu registru Z a ten posune doprava. V assembleru Z80:
SLA X RR Z
V assembleru 80×86:
SHL X,X RCR Z,Z
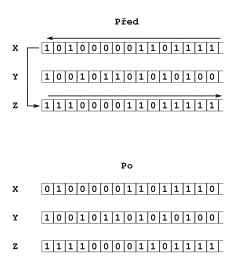
V průběhu jednoho cyklu našeho modelového chaotického systému se souřadnice X částice mouky nebo vody posune o bit doleva a vypadlý bit se nacpe shora do registru Z, který se současně posune doprava.
V reálných systémech jako různá dvojitá kyvadla, atmosféra atd. bod stavu systému běhá v krychli stavového prostoru po drahách, které jsou dané fyzikálními zákony. Tyto dráhy jsou u chaotického systému tak tvarované, že v nich nastává stejné rozmačkávání jako v našem chlebu, a tak vzniká stejný efekt vyčítání binárních číslic reálného čísla doleva a cpaní jich do binárních číslic jiného čísla. Jeden cyklus odpovídá jednomu přeložení.
Takže i kdybychom pozici kyvadla změřili s přesností na kdoví kolikátou binární číslici za binární tečkou, po dostatečném počtu cyklů se nám vyposouvá kdoví kolikátá plus první číslice za binární tečkou do nejvyšší číslice (značící půlky tedy s hodnotou 0,5) a tu už nebudeme schopni předvídat, protože jsme ji již nedokázali změřit. Nebudeme vědět, za bude horko nebo zima, sucho nebo pršet, vítr nebo ne, nebudeme vědět, zda kyvadlo bude vlevo nebo vpravo, zda bude nahoře nebo dole.
My to těsto protahujeme ve směru X a smršťujeme ve směru Z. Kdyby se ale dělalo jenom tohle, dosáhneme velmi nepřirozeného tvaru dlouhého tenkého proužku, který se nám nakonec nevejde do vesmíru.
A já si myslím, že ta úplně základní převratná idea toho chaotického systému je v tom přeložení. To přeložení nám umožňuje neomezené natažení v omezených rozměrech.
Chaotické systémy mohou běžet rychle nebo pomalu. Odpovídá to tomu, že bychom cykly rozmačkávání a skládání těsta dělali rychle nebo pomalu. Není proto podstatné, kolik sekund nebo hodin uběhlo v chaotickém systému. Podstatné je, kolik uběhlo cyklů, které mají charakter nebo tvar natažení a přeložení.
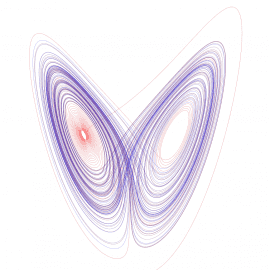
I v Lorenzově chaotickém systému se v každém cyklu masa bodů natáhne, rozdělí a pak zase složí přes sebe dohromady, podobně jako při našem míchání těsta překládáním.
Také vlastně vidíme, že ač je chaotický cyklus spojitý, o co v něm skutečně jde, jsou zřejmě diskrétní věci – diskrétní počet uběhlých cyklů, diskrétní bity které se posouvají v reálných číslech. I operace přeložení má diskrétní charakter – má dvě ramena, a bod se nachází jen v jednom z nich.
V reálném systému je šum a deformace. Tvar cyklu není tak modelový jako u chleba, aby se nám bity hezky zachovaly. Bity reálného čísla se nám v průběhu cyklu tedy různě manglují do sebe nelineárními transformacemi a šumí do nich. Nic to ale nemění na základním principu, že se titěrné bity nakonec vyposouvají až úplně nahoru a nebudeme je schopni předvídat.
Dalo by se říci, že analogový, spojitý chaotický systém je analogová implementace posuvného registru nad reálnými čísly?
Neustálé bitové posouvání reálného čísla doleva. To je ten důvod, proč je chaotický systém nepředvídatelný.




































