Obsah
1. Programovací jazyk J – od hieroglyfů k ASCII znakům
2. Vývojové prostředí programovacího jazyka J
3. Zápis programů v jazyku J, primitivní funkce
4. Způsob pojmenování primitivních funkcí
5. Vyhodnocování aritmetických výrazů
7. Obsah následující části seriálu
1. Programovací jazyk J – od hieroglyfů k ASCII znakům
V předchozích třech částech seriálu o historii výpočetní techniky jsme se zabývali popisem netradičního a v mnoha ohledech i výjimečného programovacího jazyka nazvaného APL („A Programming Language“). Tento jazyk vychází z notace pro jednotný zápis matematických funkcí, který již v roce 1957 navrhl a zveřejnil Kenneth Iverson z Harvardské university. Na základě jeho návrhu vznikly v polovině šedesátých let minulého století první implementace tohoto programovacího jazyka. APL je jazyk umožňující rychlou tvorbu i změnu programů, které provádí i komplikované matematické (numerické) výpočty. Právě z tohoto důvodu je v několika oborech (například finančnictví či výzkum orientovaný na různé simulace), ve kterých je vyžadován rychlý vývoj, tento programovací jazyk dodnes používaný, většinou lidmi, kteří se sami nepovažují za skutečné programátory, což možná vyplývá z naší (mnohdy nepřiznané) konzervativnosti (skutečně – dnes nejvíce rozšířené programovací jazyky jsou v mnoha ohledech velmi konzervativní, což s sebou nese jak zápory, tak i mnohé klady).

Obrázek 1: Při zápisu programů v jazyku APL se pro primitivní (základní) funkce i operátory používá velké množství symbolů, které je nutné zapisovat buď na klávesnici s upravenou znakovou sadou nebo pomocí speciální sekvence kláves (dvojznaky – digraphs, trojznaky – trigraphs, viz též možnosti textového editoru Vim, příkaz :dig). Na tomto obrázku je ukázáno typické umístění symbolů na klávesnici upravené pro potřeby programovacího jazyka APL.
Ovšem programovací jazyk APL má i několik nectností, ostatně jako každý programovací jazyk, který vznikl na samotném začátku vývoje interpretrů a překladačů, tj. v době, kdy ještě nebyla teorie překladačů tak rozvinutá jako v pozdějších letech (nejvíce byla neexistence teorie překladačů patrná u prvního překladače Fortranu firmou IBM, jehož vývoj by byl při uplatnění dnešních znalostí mnohem rychlejší i levnější). Už při letmém pohledu na programy napsané v programovacím jazyce APL je zřejmé, že se v něm používá velké množství symbolů, které se nenachází ve znakové sadě ASCII, což je sice velmi unikátní vlastnost (právě proto mnozí v APL programují čistě pro radost), ale způsobuje poměrně velké problémy, jak při zápisu programů (rozložení znaků na klávesnici), tak i při jejich úpravách, prezentaci na Internetu (zdaleka ne všechny fonty obsahují všechny požadované symboly, viz též druhý obrázek umístěný pod tímto odstavcem) atd.

Obrázek 2: Tento font, zobrazený v aplikaci Mapa znaků (Character Map), sice obsahuje některé znaky používané a vyžadované programovacím jazykem APL, ale zdaleka ne znaky všechny. Chybějící znaky jsou označeny červenou výplní. Právě neexistence všech potřebných znaků v nějakém fontu způsobuje problémy při zveřejňování zdrojových kódů programů v APL na webu.
Některé nedostatky programovacího jazyka APL jsou obsaženy i v jeho samotné sémantice; jmenujme například zápis řídicích struktur s využitím čísel řádků (podobně jako v BASICu, i když čísla řádků jsou v APL pro každou funkci lokální, což například znemožňuje provádět skoky dovnitř funkcí o odstraňuje vzájemnou závislost jednotlivých funkcí). Z výše uvedených důvodů otec jazyka APL (již zmiňovaný Kenneth Iverson) na počátku devadesátých let minulého století navrhl nový programovací jazyk nazvaný jednoduše J, který některé výše zmíněné nedostatky jazyka APL odstranil a navíc jazyk rozšířil o některé důležité nové rysy, primitivní funkce i operátory. V dalších kapitolách i navazující části tohoto seriálu si jazyk J stručně popíšeme a taktéž si řekneme, které vlastnosti se oproti APL změnily a které naopak zůstaly shodné.

Obrázek 3: Zápis idiomů (krátkých, v daném kontextu ustálených výrazů) v jazyku APL se skutečně odlišuje od naprosté většiny ostatních programovacích jazyků. Zajímavé je, že programátoři mající dlouhodobější zkušenosti s APL tyto idiomy nečtou po jednotlivých symbolech, ale po jejich větších skupinách či dokonce celý idiom jako celek, tj. podobným způsobem, jakým lidé čtou běžné texty (v nich taktéž mají pro mozek smysl skupiny symbolů, nikoli jednotlivé znaky, což lidem umožňuje plynule přečíst i text, v němž jsou některé znaky zpřeházené či nahrazené jinými písmeny).
2. Vývojové prostředí programovacího jazyka J
V následujících kapitolách bude uvedeno větší množství demonstračních příkladů (spíše jen jednořádkových výrazů) odzkoušených v jedné z nejznámějších implementací programovacího jazyka J, která je volně dostupná na adrese http://www.jsoftware.com. Na uvedené stránce jsou nabízeny balíčky s interpretrem jazyka J pro všechny tři nejrozšířenější desktopové systémy. Po instalaci (která v případě Linuxu spočívá v prostém spuštění staženého skriptu s parametrem -install) se nainstaluje jak interpret jazyka (knihovna libj.so popř. j.dll), tak i konzolové (řádkové) rozhraní k interpretru (jconsole) a vývojové prostředí naprogramované v Javě (jwd). Pro odzkoušení demonstračních programů postačuje spustit řádkové rozhraní interpretru jazyka J z konzole – jedná se o program jconsole (pozor – tento program je nutné spustit s uvedením cesty, například ./jconsole, v opačném případě by se mohla spustit stejnojmenná utilita dodávaná spolu s JDK).

Obrázek 4: Vývojové prostředí (vytvořené v Javě) dodávané spolu s interpretrem programovacího jazyka J.
3. Zápis programů v jazyku J, primitivní funkce
Způsob zápisu programů v programovacím jazyku J se v mnoha ohledech podobá zápisu používaném v minule popisovaném jazyku APL. Na každém řádku je (většinou) zapsán jeden výraz, který je interpretrem ihned po svém zápisu zpracován a vyhodnocen. Pokud je výraz zapsaný v interaktivním režimu (například z aplikace jconsole), je výsledek výrazu ihned po jeho vyhodnocení zapsán na terminál – právě tento způsob práce, který je ostatně společný většině interpretovaných programovacích jazyků, budeme používat ve všech následujících demonstračních příkladech (příkazy zadávané uživatelem jsou pro odlišení zpráv interpretru odsazeny od levého okraje). V mnoha programovacích jazycích se pro označení začátku řádkových komentářů používá speciální znak či znaky. Například v C++, Javě či JavaScriptu se jedná o dvojici znaků „//“ a v shellu o jeden znak „#“. V programovacím jazyku J se začátek komentáře označuje trojicí znaků „NB.“. Veškerý text na řádku zapsaný za těmito znaky je interpretrem ignorován:
NB. komentar umisteny na zacatku programoveho radku 1+2*3 NB. komentar umisteny za vyrazem, samotny vyraz se vykona a vypise se jeho vysledek 7 NB. tento vyraz se nevykona, nebot je soucasti komentare: 1+2*3
Podobně jako v programovacím jazyk APL, obsahuje i jazyk J velké množství primitivních (základních) funkcí. Ty však nejsou reprezentovány speciálními symboly, ale jedním nebo více nealfanumerickými ASCII znaky, takže jejich zápis i editace je jednodušší, než tomu bylo v případě APL (na druhou stranu nevypadají zapsané algoritmy tak efektně :-). Primitivní funkce mohou akceptovat buď jeden parametr (monadické funkce) nebo parametry dva (funkce dyadické). Název monadických funkcí je uveden v prefixové podobě, tj. vždy před svým parametrem, zatímco dyadické funkce jsou zapisovány v podobě infixové – mezi oba parametry, čímž se efektivně v mnoha případech eliminuje nutnost použití závorek. Znaky, kterými jsou primitivní funkce pojmenovány, jsou většinou použity minimálně dvakrát – jednou pro zápis monadické funkce, podruhé pro zápis funkce dyadické, jejíž význam bývá v menší či větší míře podobný příslušné monadické funkci.

Obrázek 5: Interpret jazyka J je vybaven i možností práce s různými typy grafů, což je (spolu s podporou snadné práce s vektory a maticemi) jeden z důvodů poměrně velké oblíbenosti tohoto jazyka mezi inženýry (určitá podobnost s Maple jistě není náhodná).
4. Způsob pojmenování primitivních funkcí
Kromě použití stejného znaku pro pojmenování nějaké primitivní monadické a současně i dyadické funkce může být navíc za znakem představujícím jméno primitivní funkce uveden symbol „:“ (dvojtečka) nebo „.“ (tečka), což v praxi znamená, že tentýž znak může být ve skutečnosti použit pro pojmenování až šesti různých primitivních funkcí. Například pro znak „<“ existuje celkem pět různých forem, které byly Iversonem a jeho kolegy při návrhu jazyka J zvoleny tak, aby buď přímo odpovídaly významu tohoto znaku v matematickém zápisu, nebo měly alespoň podobný význam. Zmíněný znak je (nejenom) v matematice spojen se slovem „menší“, takže je použit i pro implementaci funkce vyhledání minima či dekrementaci/zmenšení operandu o jedničku, jak je ostatně patrné z následujících výrazů a jejich výsledku po vyhodnocení interpretrem programovacího jazyka J (v příkladech jsou jako parametry použity i vektory, které budou popsány v navazující kapitole):
NB. dyadicka funkce NB. porovnani dvou hodnot na relaci "mensi nez" 1 < 2 1 2 < 2 NB. porovnavat lze i slozky vektoru 1 2 3 < 3 2 1 1 0 0 NB. Dyadicka funkce ukoncena dvojteckou NB. porovnani dvou hodnot na relaci "mensi nebo rovno" 1 <: 2 1 2 <: 2 1 NB. opet lze porovnavat i slozky vektoru 1 2 3 <: 3 2 1 1 1 0 NB. dyadicka funkce ukoncena teckou NB. vrati mensi operand (parametr) = odpovida funkci min 1 <. 2 1 2 <. 1 1 NB. porovnani prislusnych slozek vektoru a vraceni mensi z nich 1 2 1 <: 3 2 1 1 2 1 NB. monadicka funkce ukoncena teckou NB. zaokrouhleni smerem dolu (obdoba ceckove funkce floor) <. 2.5 2 <. 2.9 2 NB. tuto funkci lze samozrejme volat i na vektory <. 1.9 2.0 2.1 2.9 1 2 2 2 NB. monadicka funkce ukoncena dvojteckou NB. operace dekrementace (obdoba ceckoveho operatoru --) <: 1 <: 10 9 <: 1 2 3 0 1 2 <: 0 1 2 _1 0 1
5. Vyhodnocování aritmetických a logických výrazů
Aritmetické a logické výrazy, které tvoří nejdůležitější součást všech programů zapisovaných v jazyku J, se vyhodnocují stejným způsobem, jako v již popsaném programovacím jazyku APL, tj. zprava doleva bez toho, aby některé funkce měly vyšší prioritu než funkce jiné. Funkce se zapisují stejným způsobem jako v jiných jazycích prefixové a infixové operátory, tj. buď mezi oba argumenty (operandy) při volání dyadických funkcí nebo před jediný argument v případě, že se volá funkce monadická. Pokud je zapotřebí změnit pořadí volání funkcí, lze k tomuto účelu použít obligátní kulaté závorky. V jazyku J je k dispozici pět základních aritmetických funkcí, které jsou vypsány v tabulce pod odstavcem (povšimněte si především odlišného způsobu zápisu funkce podílu dvou hodnot). Způsob použití těchto funkcí i způsob úpravy priority (pořadí volání) je patrný z demonstračních příkladů uvedených pod tabulkou.
| Znak funkce | Monadická funkce | Dyadická funkce |
|---|---|---|
| + | negace imaginární složky komplexního čísla | součet (skalárů, vektorů, matic…) |
| – | negace | rozdíl |
| * | vrací znaménko | součin |
| % | převrácená hodnota | podíl |
| | | absolutní hodnota | zbytek |
| ^ | umocnění xy | |
| *: | druhá mocnina x2 | |
| %: | druhá odmocnina x1/2 | |
| ! | faktoriál |
1+2*3 7 1+(2*3) 7 (1+2)*3 9 NB. funkce jsou vyhodnocovany zprava doleva, NB. tj. zde nejdrive soucet a teprve pote soucin 3*2+1 9 3*(2+1) 9 NB. zmena poradi vyhodnoceni funkci pomoci zavorek (3*2)+1 7 NB. zaporna cisla jsou zapisovana se symbolem _ 10-20 _10 42%3 14 NB. druha mocnina je zapisovana pomoci monadicke funkce *: *: 10 100 NB. vypocet prevracene (reciproke) hodnoty % 3 0.33333 NB. vypocet desate mocniny 2^10 1024 2^(_10) 0.000976562 NB. aritmeticke funkce lze pouzit i pro soucet vektoru 1 2 3 + 4 5 6 5 7 9 NB. vydeleni skalarni hodnoty postupne vsemi slozkami vektoru 42 % 2 3 4 21 14 10.5 NB. kazda slozka vektoru je umocnena na desatou 2 3 4 ^ 10 1024 59049 1.04858e6 NB. vypocet druhych mocnin vsech slozek vektoru *: 1 2 3 4 1 4 9 16 NB. vypocet faktorialu (samozrejme je pouzit prefixovy zapis) !6 720 !170 7.25742e306 NB. tento zapis si podrobneji vysvetlime priste !i.10 1 1 2 6 24 120 720 5040 40320 362880
6. Proměnné
V programovacím jazyku J se používají proměnné způsobem, který se příliš neliší od jiných jazyků. Jediná odlišnost spočívá v tom, že proměnné mohou obsahovat buď skalární hodnotu (celé číslo či číslo uložené v systému plovoucí řádové tečky/čárky, možné je i použití čísel komplexních), vektor čísel, matici čísel nebo pole o prakticky libovolné dimenzi – v tomto ohledu jsou si jazyky J a APL velmi podobné. Přiřazení hodnoty do proměnné je zapisováno pomocí znaků =:, což v jazyce APL odpovídá symbolu ↓ (pozor – skutečně se jedná o dvojici znaků =: a nikoli :=; to vyplývá ze způsobu zápisu primitivních funkcí a operátorů popsaného ve třetí a čtvrté kapitole). Způsob pojmenování proměnných i jejich využití v aritmetických a logických výrazech se příliš neliší od jiných programovacích jazyků, což je ostatně patrné i z následujících ukázek kódu:
NB. prirazeni hodnoty do promennych x =: 3 y =: 4 NB. vypocet s promennymi x+y^2 19 NB. prirazeni hodnoty do promenne a soucasne vypocet 100 * (z =: 42) 4200 NB. promenna z skutecne obsahuje prirazenou hodnotu z 42 NB. monadickou funkci + lze pouzit k prirazeni a soucasne NB. tisku hodnoty promenne (nefunguje vsak v pripade prirazeni NB. komplexniho cisla, protoze funkce + zmeni znamenko imaginarni slozky) +z=:6502 6502 z 6502
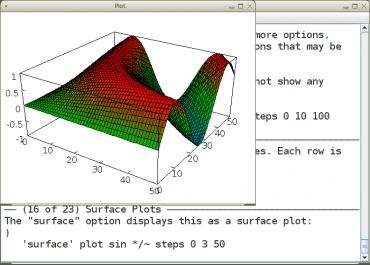
Obrázek 6: Ukázka tvorby 3D grafu, v tomto případě zobrazení průběhu funkce dvou nezávislých proměnných.
7. Obsah následující části seriálu
V následující části seriálu o historii výpočetní techniky si popíšeme další vlastnosti poněkud netradičního programovacího jazyka J. Budeme se zabývat způsobem práce s vektory, maticemi i poli o vyšším počtu dimenzí. Taktéž si řekneme, jakým způsobem lze použít funkce pro porovnávání hodnot, konstrukce / a ~ (obdoba operátorů známých z programovacího jazyka APL), funkce pro pokročilejší operace s maticemi a v neposlední řadě taktéž způsob využití řídicích konstrukcí, tj. příkazů pro tvorbu podmínek a cyklů (programových smyček).

Obrázek 7: Parametrické křivky a další typy grafů, se kterými se seznámíme v některém z dalších pokračování tohoto seriálu.
8. Literatura
- Ulf Grenander, „Mathematical Experiments on the Computer,“
Academic Press, 1982, ISBN 0–12–301750–5. - K. E. Iverson, „A Programming Language“,
Wiley, 1962. - K. E. Iverson, „Algebra : an algorithmic treatment“,
APL Press 1977, Copyright 1972 by Addison Wesley,
Preliminary Edition entitled „Elementary Algebra“
Copyright 1971 by IBM Corporation.
- K. E. Iverson, „Elementary analysis“,
APL press 1976, Preliminary Edition „Elementary Functions“
Copyright 1974 by IBM Corporation ISBN 0–917326–01–6
- K. E. Iverson, „A personal view of APL,“
IBM Systems Journal, - C. Reiter, „Fractuals Visualization and J“,
Iverson Software, Inc, 1995 ISBN 1–895721–11–3. - „J Phrases,“
Iverson Software, 1996, ISBN 1–895721–12–1 - „Exploring Math“, Iverson Software, 1996, ISBN 1–895721–13-X
- „J Primer,“
Iverson Software, 1996, ISBN 1–895721–14–8 - Linda Alvord and Norman Thomson, „Easy-J: An Introduction to the World's most Remarkable Programming Language“
October 2002
9. Odkazy na Internetu
- Learning J (Roger Stokes)
http://www.jsoftware.com/…contents.htm - J: a modern, high-level, general-purpose, high-performance programming language
http://www.jsoftware.com/ - K, Kdb: an APL derivative for Solaris, Linux, Windows
http://www.kx.com - Vector (obsahuje odkazy na články, knihy a blogy o programovacích jazycích APL, J a K)
http://www.vector.org.uk/ - APL – A Glimpse of Heaven
http://www.vector.org.uk/…/legrand.htm - APL Interpreters
http://www.vector.org.uk/?… - APL_(programming_language
http://en.wikipedia.org/wiki/APL_(programming_language - APL FAQ
http://www.faqs.org/faqs/apl-faq/ - APL FAQ (nejnovější verze)
http://home.earthlink.net/…apl.faq.html - A+
http://www.aplusdev.org/ - Rosetta Code
http://rosettacode.org/wiki/Main_Page