Obsah
1. Programovací jazyky odvozené od APL
2. Programovací jazyk BQN – Big Questions Notation
3. Webová a terminálová varianta BQN
4. Základní vlastnosti jazyka BQN
5. Ilustrace pořadí vykonávání operací funkcí Explain
6. Porušení mantry „vše je pole“
7. Seznamy, konstrukce polí, způsob zobrazení polí
8. Tabulka se všemi základními funkcemi jazyka BQN
10. Další modifikátory jazyka BQN
12. Výpočet tabulky faktoriálu s využitím modifikátoru scan
18. První seznámení s možnostmi jazyka ivy
19. Výpočet prvočísel v jazyku ivy
1. Programovací jazyky odvozené od APL
Joel Moses: “APL is like a beautiful diamond – flawless, beautifully symmetrical. But you can’t add anything to it. If you try to glue on another diamond, you don’t get a bigger diamond. Lisp is like a ball of mud. Add more and it’s still a ball of mud – it still looks like Lisp.”
Na úvodní dvojici článků [1] [2] o programovacích jazycích určených a mnohdy i přímo optimalizovaných pro provádění operací s N-dimenzionálními poli dnes navážeme. Připomeňme si, že v úvodním článku jsme se zabývali především univerzálními programovacími jazyky podporujícími (kromě dalších operací) i „nativní“ zpracování vícerozměrných polí, v článku druhém jsme se pak podrobněji věnovali programovacímu jazyku nazvanému J, jenž je přímo odvozen od v mnoha ohledech přelomového programovacího jazyka APL (i když to na první pohled nemusí být patrné kvůli zcela odlišné sadě symbolů, z nichž se programy skládají). Do této série článků ovšem nepřímo patří i článek o historii vzniku a dalšího vývoje programovacího jazyka APL.
Na všechny tři výše zmíněné články dnes navážeme, protože si popíšeme další dva zajímavé programovací jazyky, které jsou do značné míry inspirovány právě programovacím jazykem APL. Nejdříve se budeme zabývat jazykem nazvaným poněkud neobvykle BQN, za jehož vývojem stojí programátor, který se APL jazykům věnuje již velmi dlouho a tudíž poměrně do hloubky zná i jejich limity a pochopitelně i jejich nedokonalosti (ostatně který programovací jazyk je dokonalý?). Druhým jazykem, na který se dnes zaměříme, je jazyk nazvaný ivy. Ten je zajímavý mj. i kvůli tomu, že je naprogramován v Go a za jeho vývojem stojí přímo Rob Pike, tedy jeden ze spoluautorů Go. Současně dnes již téma programovacích jazyků odvozených od APL opustíme, a to mj. i z toho důvodu, že práce s vícerozměrnými poli (a zejména pak s jednorozměrnými vektory a dvourozměrnými maticemi) je dobře rozpracována i v dalších jazycích, které jsou přece jen více mainstreamové – jedná se v první řadě o Fortran, ale taktéž o programovací jazyk C++.
2. Programovací jazyk BQN – Big Questions Notation
„BQN: finally, an APL for your flying saucer“
Nejprve se budeme zabývat programovacím jazykem, který se jmenuje BQN a za jehož vývojem stojí především Marshall Lochbaum. Tento autor se dlouhodobě zabývá programovacími jazyky z rodiny APL (a částečně i Scheme) a před BQN vytvořil programovací jazyk pojmenovaný jednoduše I, který je do značné míry inspirován jazykem J, jímž jsme se zabývali minule. Vraťme se ovšem k jazyku BQN. Jedná se o programovací jazyk, jenž je do značné míry inspirován jazykem APL, ovšem některé (i poměrně základní) operace jsou v BQN prováděny odlišně. Odlišnosti nalezneme již u způsobu implementace n-dimenzionálních polí, kde se BQN vrací k původnímu APL (a nikoli k APL modernímu). Liší se ovšem i základní symboly, z nichž se skládají větší celky a z nich pak ucelené algoritmy i celé programy.

Obrázek 1: Logo programovacího jazyka BQN.
3. Webová a terminálová varianta BQN
Programovací jazyk BQN v současnosti existuje ve dvou variantách. První variantu lze spustit přímo ve webovém prohlížeči. Tuto variantu můžeme najít na stránce https://mlochbaum.github.io/BQN/ a její výhodou je, že obsahuje volbu Explain, kterou si ukážeme dále. Navíc dostaneme „zadarmo“ podporu všech potřebných znaků Unicode, na nichž je jazyk BQN postaven. Druhá varianta se jmenuje CBQN. Tato varianta, jejíž repositář je umístěn na adrese https://github.com/dzaima/CBQN, je naprogramována v čistém C (což ostatně naznačuje již její název) a lze ji přeložit a spustit přímo z terminálu.
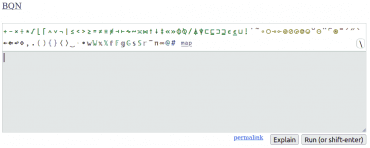
Obrázek 2: Webové rozhraní programovacího jazyka BQN.
Překlad a slinkování CBQN je snadný a rychlý. Nejprve je nutné naklonovat repositář s touto variantou jazyka BQN:
$ git clone git@github.com:dzaima/CBQN.git Cloning into 'CBQN'... remote: Enumerating objects: 5753, done. remote: Counting objects: 100% (4177/4177), done. remote: Compressing objects: 100% (3078/3078), done. remote: Total 5753 (delta 3342), reused 1905 (delta 1084), pack-reused 1576 Receiving objects: 100% (5753/5753), 1.07 MiB | 3.77 MiB/s, done. Resolving deltas: 100% (4592/4592), done.
Ve druhém kroku provedeme překlad s volbou překladače, který se má použít:
$ cd CBQN/ $ make CC=gcc
Výsledkem překladu je spustitelný soubor „BQN“, který se v případě potřeby vejde na disketu:
$ ls -l -rwxrwxr-x. 1 ptisnovs ptisnovs 1027984 Dec 25 20:13 BQN -rwxrwxr-x. 1 ptisnovs ptisnovs 2779 Dec 25 20:12 cc.bqn -rwxrwxr-x. 1 ptisnovs ptisnovs 442 Dec 25 20:12 genRuntime -rwxrwxr-x. 1 ptisnovs ptisnovs 354 Dec 25 20:12 genRuntimeSrc -rw-rw-r--. 1 ptisnovs ptisnovs 35148 Dec 25 20:12 LICENSE -rw-rw-r--. 1 ptisnovs ptisnovs 4665 Dec 25 20:12 makefile drwxrwxr-x. 3 ptisnovs ptisnovs 60 Dec 25 20:13 obj -rwxrwxr-x. 1 ptisnovs ptisnovs 1120 Dec 25 20:12 precompiled.bqn -rw-rw-r--. 1 ptisnovs ptisnovs 2283 Dec 25 20:12 README.md drwxrwxr-x. 2 ptisnovs ptisnovs 40 Dec 25 20:12 SingeliClone -rwxrwxr-x. 1 ptisnovs ptisnovs 688 Dec 25 20:12 SingeliMake.bqn drwxrwxr-x. 9 ptisnovs ptisnovs 440 Dec 25 20:12 src -rwxrwxr-x. 1 ptisnovs ptisnovs 1188 Dec 25 20:12 test.bqn
Otestujeme, zda je možné BQN spustit:
$ ./BQN --help Usage: ./BQN [options] [file.bqn [arguments]] Options: -f file: execute the contents of the file with all further arguments as •args -e code: execute the argument as BQN -p code: execute the argument as BQN and print its result pretty-printed -o code: execute the argument as BQN and print its raw result -M num : set maximum heap size to num megabytes -r : start the REPL after executing all arguments -s : start a silent REPL
Spuštění v režimu interpretru:
$ ./BQN 1+1 2 π 3.141592653589793 ∞ ∞
4. Základní vlastnosti jazyka BQN
Jazyk BQN, podobně jako jeho ideový předchůdce APL, podporuje infixovou notaci zápisu výrazů. To znamená, že jméno či symbol funkce (nebo, chcete-li, operátoru) se zapisuje mezi oba operandy. Příkladem může být funkce/operátor pro podíl dvou hodnot:
10 ÷ 4 2.5
Mnoho funkcí akceptuje pouze jediný operand. Příkladem může být opět funkce zapisovaná znakem „÷“, jejíž jednooperandová podoba slouží pro výpočet převrácené hodnoty:
÷ 4 0.25
Operátory/funkce nemají stanovenou prioritu (přesněji řečeno mají shodnou prioritu) a vyhodnocují se zprava doleva, tedy stejně, jako je tomu v APL:
7 × 4 + 2 42 4 + 5 × 6 34
Pořadí výpočtů lze ovlivnit závorkami:
(4 + 5) × 6 54 (1 + (2 + 3) × 4) × 2 42
Popř.:
(((10 ÷ 9) ÷ 8) ÷ 7) + (100 ÷ ((4 + 3) ÷ (2 + 1)))
Existuje i mnoho dalších funkcí majících monadickou a současně i dyadickou podobu reprezentovanou jediným symbolem. Příkladem může být funkce pro výpočet druhé odmocniny (monadická podoba) nebo n-té odmocniny (dyadická podoba):
√2 1.4142135623730951 4√81 3 8√65536 4
Popř. výpočet ex nebo xy:
⋆1 2.718281828459045 2⋆8 256
5. Ilustrace pořadí vykonávání operací funkcí Explain
V některých případech nemusí být jednoduché pravidlo „funkce mají shodné priority a vyhodnocují se zprava doleva“ zcela zřejmé v případě složitějších výrazů, zejména při použití takzvaných manipulátorů. V takových případech lze použít funkci Explain dostupnou z webového prostředí, která kromě vlastního výpočtu zobrazí i pořadí vyhodnocování jednotlivých částí výrazů. Podívejme se na několik jednoduchých ukázek, v nichž budeme používat základní funkce:
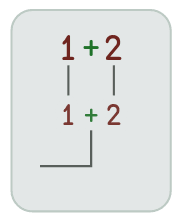
Obrázek 3: Ukázka vyhodnocení výrazu 1+2.
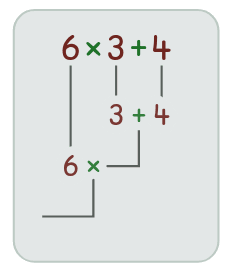
Obrázek 4: Ukázka vyhodnocení výrazu 6×3+4 (3+4 se vyhodnotí dříve).
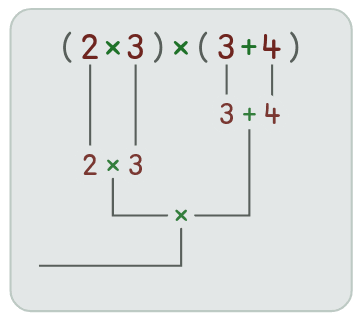
Obrázek 5: Ukázka vyhodnocení výrazu s několika podvýrazy v závorkách.
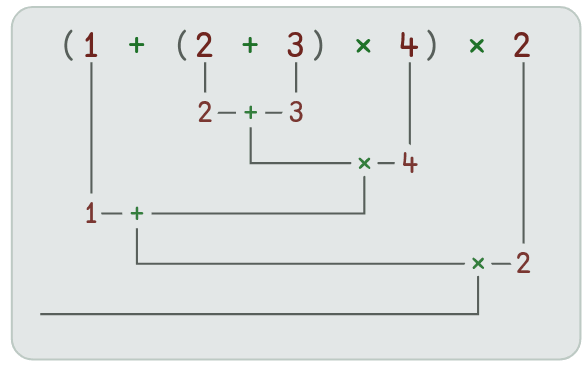
Obrázek 6: Ukázka vyhodnocení výrazu s několika podvýrazy v závorkách.
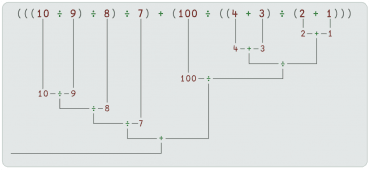
Obrázek 7: Ukázka vyhodnocení výrazu s několika podvýrazy v závorkách.
6. Porušení mantry „vše je pole“
V prvních variantách programovacího jazyka APL se používala takzvaná „plochá“ pole neboli flat arrays. Jednalo se (poněkud zjednodušeně řečeno) o pole, jejichž prvky mohly být skalární hodnoty (skaláry), tj. typicky buď hodnoty typu float nebo znaky. Okolo roku 1981 však došlo k rozšíření sémantiky datového typu pole – nyní mohla pole obsahovat jako své prvky další pole. První komerčně dostupná varianta APL, která tato rozšířená pole implementovala, se jmenovala APL*PLUS a nová vlastnost se označovala zkratkou NARS neboli Nested Array Research System.
Později se tento koncept „vše je pole“ začal používat i v dalších variantách programovacího jazyka APL. Kromě několika výhod se ovšem ukázalo, že tento koncept může mít i nevýhody. Ty vyplývají z „podivné“, přesněji řečeno neintuitivní sémantiky některých operací, kdy se skalární hodnota někdy považuje za pole 1×1 prvek a jindy nikoli (navíc se zde objevuje nová vlastnost „hloubka“ pole; dále se jednoprvkové pole rovná tomuto prvku při porovnávání). Z tohoto důvodu se BQN vrací k myšlence původní varianty APL – pole zde pochopitelně stále existují, mohou mít libovolný počet dimenzí i libovolný tvar, ovšem prvky polí jsou skalární hodnoty a nikoli další pole.
V BQN se hodnoty rozdělují do dvou hlavních kategorií:
- atomy: čísla, znaky, funkce, modifikátory, jmenné prostory
- pole
Přitom platí, že atomy mají vždy hloubku (depth) rovnou nule a nemají tvar (shape). Pole naproti tomu mají tvar a jejich identita je odvozena právě z tvaru a navíc z typu elementů.
Rozdíl mezi atomem a jednotkovým polem je vidět ihned na výstupu:
Atom:
3 3
Pole s jediným prvkem:
<3
┌·
· 3
┘
Mezi další vlastnosti polí v BQN patří, že pole jsou neměnná (immutable) v tom smyslu, že nelze měnit jejich tvar ani typ elementů. Ovšem hodnoty elementů (prvků) již měnit lze.
7. Seznamy, konstrukce polí, způsob zobrazení polí
Na rozdíl od jazyka APL či J, v němž existuje způsob konstrukce literálu představujícího pole, je nutné v BQN pole vytvářet nepřímo; typicky přes seznamy. Literál představující celý seznam totiž existuje – jedná se o hodnoty prvků, které jsou propojeny znakem „‿“. Následuje příklad seznamu se třemi prvky s hodnotami 1, 2 a 3:
1‿2‿3 ⟨ 1 2 3 ⟩
Existuje taktéž funkce nazvaná range, která vrací seznam (ne vektor!) s prvky od 0 omezené zadanou hodnotou. Jedná se tedy o obdobu funkce iota z klasického APL:
↕ 6 ⟨ 0 1 2 3 4 5 ⟩
Další užitečná funkce se jmenuje reshape a slouží k vytvoření pole o zadaném tvaru. Prvky pole lze získat například z vektoru, samotný tvar pak taktéž typicky bývá představován seznamem:
1‿12 ⥊ ↕ 12
┌─
╵ 0 1 2 3 4 5 6 7 8 9 10 11
┘
Konstrukce sloupcového vektoru:
12‿1 ⥊ ↕ 12
┌─
╵ 0
1
2
3
4
5
6
7
8
9
10
11
┘
Konstrukce pole 2×6 prvků:
2‿6 ⥊ ↕ 12
┌─
╵ 0 1 2 3 4 5
6 7 8 9 10 11
┘
Konstrukce pole 3×4 prvků:
3‿4 ⥊ ↕ 12
┌─
╵ 0 1 2 3
4 5 6 7
8 9 10 11
┘
Konstrukce pole 2×3×4 prvků:
2‿3‿4 ⥊ ↕ 12
┌─
╎ 0 1 2 3
4 5 6 7
8 9 10 11
0 1 2 3
4 5 6 7
8 9 10 11
┘
Čtyřrozměrné pole:
2‿2‿2‿3 ⥊ ↕ 12
┌─
┆ 0 1 2
3 4 5
6 7 8
9 10 11
0 1 2
3 4 5
6 7 8
9 10 11
┘
Šestirozměrné pole:
2‿2‿2‿2‿2‿2 ⥊ ↕ 32 ┌6 ┊ 0 1 2 3 4 5 6 7 ... ... ...
Povšimněte si, že počet rozměrů pole je zakódován tvarem levého horního rohu pole. Pouze u polí s šesti a více rozměry už musí být zapsán počet dimenzí číselně:
0 1 2 3 4 5 ┌· ┌─ ┌─ ┌─ ┌─ ┌─ ┌6 ┌7 … · · ╵ ╎ ┆ ┊ ┊ ┊ …
Boxing atomu do pole:
<3
┌·
· 3
┘
Konstrukce pole, jehož všechny prvky mají shodnou hodnotu:
5‿5 ⥊ <1
┌─
╵ 1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
┘
V tomto konkrétním případě však můžeme boxing vynechat:
5‿5 ⥊ 1
┌─
╵ 1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
┘
8. Tabulka se všemi základními funkcemi jazyka BQN
V této kapitole je uvedena tabulka obsahující všechny základní funkce jazyka BQN. Originál tabulky je dostupný na adrese https://pastebin.com/raw/ynsghrHM:
| Funkce/modifikátor | Alternativní zápis | Popis | Funkce/modifikátor | Alternativní zápis | Popis |
|---|---|---|---|---|---|
| + | + | conjugate / add | ⥊ | \z | deshape / reshape |
| – | – | negate / subtract | ∾ | \, | join / join to |
| × | \= | sign / multiply | ≍ | \. | solo / couple |
| ÷ | \- | reciprocal / divide | ↑ | \r | prefixes / take |
| ⋆ | \+ | exponential / power | ↓ | \c | sufixes / drop |
| √ | \_ | square root / nth root | ↕ | \d | range / windows |
| ⌊ | \b | floor / minimum | « | \H | nudge / shift before |
| ⌈ | \B | ceiling / maximum | » | \L | nudge after / shift after |
| ∧ | \t | sort up / and | ⌽ | \q | reverse / rotate |
| ∨ | \v | sort down / or | ⍉ | \a | transpose / reorder axes |
| ¬ | \~ | not / span | / | / | indices / replicate |
| | | | | absolute value / modulus | ⊏ | \i | first cell / select |
| ≤ | \< | less than or equal to | ⊑ | \I | first / pick |
| <; | < | enclose / less than | ⊐ | \o | classify / index of |
| > | > | merge / greater than | ⊒ | \O | occurence count / progressive index of |
| ≥ | \> | greater than or equal to | ⍋ | \T | grade up / bins up |
| = | = | rank / equals | ⍒ | \V | grade down / bins down |
| ≠ | \/ | length / not equals | ∊ | \e | mark first / member of |
| ≡ | \m | depth / match | ⍷ | \E | deduplicate / find |
| ≢ | \M | shape / not match | ⊔ | \u | group indices / group |
| ⊣ | \{ | identity / left | ! | ! | assert / assert with message |
| ⊢ | \} | identity / right |
9. Modifikátor table
V článku o programovacím jazyku APL jsme se zmínili o operátoru nazvaném „outer product“. Podobný koncept existuje i v jazyku BQN, ovšem namísto pojmu „operátor“ se zde používá pojem „modifikátor“ a z „outer product“ se stal modifikátor „table“. Tento modifikátor dokáže aplikovat zvolenou dyadickou funkci (například +) na všechny kombinace prvků vstupních vektorů nebo polí. Můžeme si například vytvořit pole s malou násobilkou (prozatím v nedokonalé podobě):
(↕ 10) ×⌜ (↕ 10)
┌─
╵ 0 0 0 0 0 0 0 0 0 0
0 1 2 3 4 5 6 7 8 9
0 2 4 6 8 10 12 14 16 18
0 3 6 9 12 15 18 21 24 27
0 4 8 12 16 20 24 28 32 36
0 5 10 15 20 25 30 35 40 45
0 6 12 18 24 30 36 42 48 54
0 7 14 21 28 35 42 49 56 63
0 8 16 24 32 40 48 56 64 72
0 9 18 27 36 45 54 63 72 81
┘
Funkcí drop odstraníme ze vstupních vektorů nuly:
(1↓ (↕ 10)) ×⌜ (1↓ (↕ 10))
┌─
╵ 1 2 3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
┘
Ještě lepší je však vytvořit vektory s hodnotami od 1 do 10 (včetně):
(1 + (↕ 10)) ×⌜ (1 + (↕ 10))
┌─
╵ 1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
┘
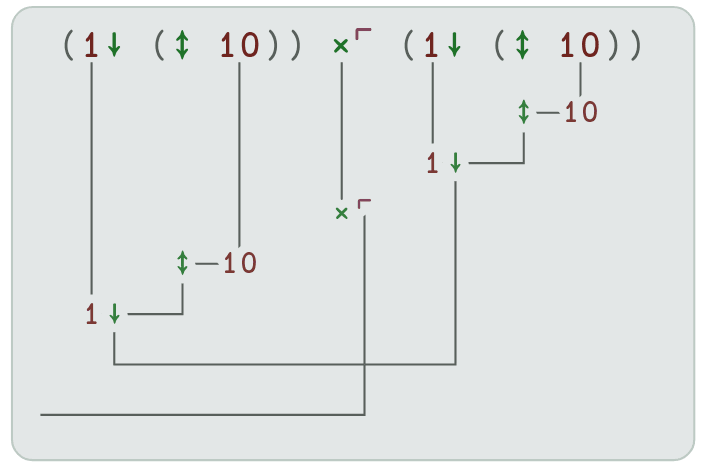
Obrázek 8: Postup provádění výpočtu.
Většina závorek je zbytečná, pochopitelně za předpokladu, že dodržíme pravidlo vyhodnocování funkcí zprava doleva:
(1+↕10)×⌜1+↕10
┌─
╵ 1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
┘
10. Další modifikátory jazyka BQN
Operátor table popsaný v předchozí kapitole je ve skutečnosti pouze jedním z mnoha modifikátorů, které programovací jazyk BQN programátorům nabízí. Obecně je možné říci, že modifikátory umožňují určit způsob iterace nad prvky seznamů nebo polí i to, jaký má být výsledek aplikace tohoto manipulátoru. Modifikátorů existuje v jazyce BQN větší množství. Kromě vykonávané operace se liší i tím, kolik funkcí dokážou na prvky seznamu či polí aplikovat a jakým způsobem. Poměrně dobrým příkladem může být modifikátor nazvaný scan, který postupně prochází všemi prvky, aplikuje zvolenou funkci na aktuální prvek a akumulátor a na vstup posílá výsledek zvolené funkce. Jedná se tedy o obdobu funkce reduction z jazyka APL.
11. Modifikátor scan
Podívejme se na jednoduchý příklad použití tohoto modifikátoru. Nejprve si řekněme, že funkce maximum vrací větší z obou předaných prvků:
2 ⌈ 3 3 3 ⌈ 2 3
Nyní můžeme tuto funkci postupně aplikovat na prvky seznamu. Výsledkem bude seznam o stejné délce, který ovšem bude na i-té pozici obsahovat maximální hodnotu prvních i prvků seznamu:
⌈` 1‿3‿0‿5‿3‿2‿1‿0‿9 ⟨ 1 3 3 5 5 5 5 5 9 ⟩
Postupný součet prvků seznamu se všemi mezivýsledky:
+` 1‿3‿0‿5‿3‿2‿1‿0‿9 ⟨ 1 4 4 9 12 14 15 15 24 ⟩
12. Výpočet tabulky faktoriálu s využitím modifikátoru scan
Modifikátor scan můžeme využít například při výpočtu tabulky faktoriálů. Předpokládejme, že budeme chtít vypočítat tabulku faktoriálů pro vstupy 1 až 10. Tento výpočet je možné zapsat pouhými deseti znaky (sémantická síla APL i BQN je v těchto oblastech obrovská), ovšem my si celý výpočet rozdělíme na víc částí. Nejprve získáme vstupní vektor:
↕10 ⟨ 0 1 2 3 4 5 6 7 8 9 ⟩
Tento vektor ještě neodpovídá požadovanému vstupu, protože budeme muset zvýšit všechny hodnoty o jedničku:
1+↕10 ⟨ 1 2 3 4 5 6 7 8 9 10 ⟩
Nyní již můžeme přistoupit k použití modifikátoru scan a postupně násobit prvky vstupního vektoru s akumulátorem, jehož počáteční hodnota je nastavena na hodnotu prvního prvku:
×`1+↕10 ⟨ 1 2 6 24 120 720 5040 40320 362880 3628800 ⟩
Graf s vizualizací způsobu výpočtu bude vypadat následovně:
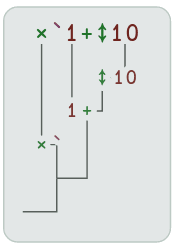
Obrázek 9: Způsob vyhodnocení výrazů při výpočtu tabulky faktoriálů.
V případě potřeby můžeme na začátek přidat chybějící jedničku pro 0!, a to operací join:
1~×`1+↕10 ⟨ 1 1 2 6 24 120 720 5040 40320 362880 3628800 ⟩
×´1+↕10 3628800
13. Kombinátory
Dalším důležitým prvkem programovacího jazyka BQN jsou takzvané kombinátory. Kombinátory nějakým způsobem modifikují výraz zapsaný programátorem; teprve poté je daný výraz skutečně vykonán. To je velmi silná programovací technika, která odpovídá lepším makrosystémům (ne ovšem tomu céčkovému – ten je totiž realizován ještě před lexikální analýzou a nikoli až po konstrukci AST), protože manipulací se zapsaným výrazem je možné dosáhnout užitečných efektů. Právě kombinátory umožňují i v jazyce BQN realizovat tacit programming, což je technika, které jsme se již na stránkách Roota (prozatím jen ve stručnosti) věnovali v článku Programovací technika nazvaná tacit programming.
Kombinátor swap přehazuje operandy předané funkci. Výpočet 1–2 je triviální:
1 - 2 ¯1
Přidáním kombinátoru swap otočíme operandy a budeme tedy počítat 2–1:
1 ˜- 2 1
Vyzkoušejme si nyní jeden z nejjednodušších kombinátorů nazvaný atop. Ten se zapisuje následujícím způsobem:
f∘g
Kde f a g jsou libovolné funkce, přičemž f je funkce monadická a g funkce dyadická. Společně s parametry x a y vypadá zápis takto:
x f∘g y
Kombinátor atop tento zápis ztransformuje na:
f x g y
což díky asociativitě operací vlastně znamená:
f (x g y)
14. Tacit programming
Nyní si ukažme poněkud praktičtější příklad, který byl získán modifikací příkladu z oficiální dokumentace k programovacímu jazyku BQN. Vytvoříme v něm novou funkci, která vypočte absolutní odchylku ze dvou zadaných hodnot. To vlastně znamená, že se hodnoty od sebe odečtou a posléze se vypočte absolutní hodnota tohoto rozdílu.
Samotný výpočet rozdílu je v BQN až trapně jednoduchý:
1 - 2 ¯1
Triviální je i výpočet absolutní hodnoty:
|-10 10
Celý výpočet by tedy vypadal takto:
|1-2 1
Nyní se pokusíme obě funkce zkombinovat, a to právě s využitím kombinátoru atop, kterým vlastně vytvoříme novou dyadickou funkci nazvanou například „absolutní odchylka“. Využijeme toho, že platí ekvivalence mezi:
x f∘g y
a:
f (x g y)
V našem konkrétním případě tedy:
1 |∘- 10 9
Verze s opačnými parametry:
10 |∘- 1 9
Nyní se již dostáváme k závěrečné části. Definujeme novou funkci, která ovšem bude obsahovat pouze kombinátor a dvě další funkce – nevyskytuje se zde tedy žádný parametr (resp. dva parametry, protože výsledkem je dyadická funkce). Jedná se o typický příklad použití tacit programmingu:
ABS_DIFF ← |∘-
Nově definovanou funkci už můžeme snadno otestovat na dvojici vstupů:
10 ABS_DIFF 4 6
15. Shrnutí
V předchozím textu jsme si přiblížili pouze relativně malé množství technik, které v jazyku BQN nalezneme. BQN nijak nezastírá, že je založen na APL, ovšem přináší některá zjednodušení (plochá pole), odděluje funkce od operátorů a kombinátorů, nabízí možnost zvýraznění operací technikou explain atd. Nejedná se však o APL, protože sada symbolů je zcela odlišná a zejména sémantika kombinátorů se od APL v mnoha ohledech odlišuje. Taktéž se v mnohem větší míře používají seznamy namísto vektorů.
16. Programovací jazyk ivy
V závěrečné části dnešního článku si ve stručnosti popíšeme další programovací jazyk inspirovaný původním APL. Tento jazyk se jmenuje ivy a zajímavé na něm je, že jeho autorem je Rob Pike a naprogramován je v jazyce Go. Na rozdíl od klasického APL je ivy založen na znakové sadě ASCII a nikoli na specializovaných znacích. Taktéž umožňuje práci se zlomky (typ rational) a celočíselné hodnoty nemají (prakticky) omezený rozsah. Dnes si představíme pouze základy tohoto jazyka, ovšem někdy se k němu vrátíme, protože i způsob jeho implementace je velmi zajímavý, efektivní a navíc Rob Pike díky elegantnímu návrhu obešel nutnost použití generik (které v jazyce Go v té době ještě neexistovaly). V dalších třech kapitolách ukážeme jen několik příkladů použití ivy, ale k tomuto jazyku se ještě vrátíme v souvislosti s články o lexikální a syntaktické analýze.
17. Instalace jazyka ivy
Pro instalaci jazyka ivy je vyžadováno Go verze 1.17. Pokud je Go této verze dostupné, je instalace snadná:
$ go install robpike.io/ivy@latest go: downloading robpike.io/ivy v0.1.10
Výsledný spustitelný soubor je umístěn do $GOPATH/bin, typicky do ~/go/bin.
18. První seznámení s možnostmi jazyka ivy
Nejprve spustíme interpret jazyka ivy:
$ ivy
Funkce se zapisují v běžné infixové podobě:
1+2 3 2*3 6
Priorita funkcí je stejná, asociativita zprava:
1+2*3 7 2*3+1 8
Výpočty nad vektory:
1 2 3 + 3 4 5 4 6 8
Výpočty se zlomky:
1/3 + 1/4 7/12
Operace reduce převzatá z APL:
*/+ 1 2 3 4 5 120
Výpočet faktoriálu 10:
*/ iota 10 3628800
Prakticky neomezený rozsah celých čísel:
*/ iota 100 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
Převod na zlomek (se zjednodušením):
3 / */ iota 10 1/1209600
atd.
19. Výpočet prvočísel v jazyku ivy
V článku o programovacím jazyku APL jsme si ukázali, jakým způsobem je možné vypočítat prvočísla od 2 do zadané hodnoty x. Celý výpočet lze zapsat na jediný řádek, a to následovně:
(~R∊R∘.×R)/R←1↓⍳x
Jednotlivé kroky si postupně rozepíšeme:
| Krok | Zápis | Význam |
|---|---|---|
| 1 | ⍳x | vytvoření sekvence čísel od 1 do x |
| 2 | 1↓⍳x | odstranění prvního čísla, tedy jedničky |
| 3 | R←1↓⍳x | uložení mezivýsledku do vektoru pojmenovaného R |
| 4 | R∘.×R | výpočet matice s násobky všech kombinací R (outer product) |
| 5 | R∊R∘.×R | test, která čísla jsou nalezena i v matici násobků |
| 6 | ~R∊R∘.×R | negace předchozího testu – vyberou se tedy čísla, která v matici nejsou |
| 7 | (~R∊R∘.×R)/R | použití předchozí matice pro výběr z mezivýsledku (vektoru čísel) |
Tento algoritmus lze přepsat do jazyka ivy relativně jednoduše – náhradou speciálních symbolů APL za názvy funkcí. Nejprve celý výpočet postupně provedeme v interaktivním prostředí:
Určíme meze výpočtu:
x=10
Vytvoření sekvence hodnot:
iota x 1 2 3 4 5 6 7 8 9 10
Odstranění prvního čísla, tedy jedničky:
1 drop iota x 2 3 4 5 6 7 8 9 10
Uložení mezivýsledku do proměnné R:
R = 1 drop iota x R 2 3 4 5 6 7 8 9 10
Výpočet matice s násobky všech kombinací R:
R o.* R 4 6 8 10 12 14 16 18 20 6 9 12 15 18 21 24 27 30 8 12 16 20 24 28 32 36 40 10 15 20 25 30 35 40 45 50 12 18 24 30 36 42 48 54 60 14 21 28 35 42 49 56 63 70 16 24 32 40 48 56 64 72 80 18 27 36 45 54 63 72 81 90 20 30 40 50 60 70 80 90 100
Test, která čísla jsou nalezena v matici násobků:
R in R o.* R 0 0 1 0 1 0 1 1 1
Negace předchozího testu – vyberou se tedy čísla, která v matici nejsou:
not R in R o.* R 1 1 0 1 0 1 0 0 0
Použití předchozího vektoru s 0/1 pro výběr z mezivýsledku (vektoru čísel):
(not R in R o.* R) sel R 2 3 5 7
Dostali jsme tedy kýžený výsledek.
Vše si můžeme zapsat na jediný řádek a vypočítat tak prvočísla od 2 do 100:
(not R in R o.* R) sel R = 1 drop iota 100 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
Porovnání verze v APL a v ivy ukazuje pouze syntaktické rozdíly, nikoli rozdíly v sémantice:
| Krok | APL | Ivy |
|---|---|---|
| 1 | ⍳x | iota x |
| 2 | 1↓⍳x | 1 drop iota x |
| 3 | R←1↓⍳x | R = 1 drop iota x |
| 4 | R∘.×R | R o.* R |
| 5 | R∊R∘.×R | R in R o.* R |
| 6 | ~R∊R∘.×R | not R in R o.* R |
| 7 | (~R∊R∘.×R)/R | (not R in R o.* R) sel R |
20. Odkazy na Internetu
- BQN: An APL Variant from Marshall Lochbaum (mlochbaum.github.io)
https://news.ycombinator.com/item?id=24167804 - Marshall Lochbaum
https://www.aplwiki.com/wiki/Marshall_Lochbaum - BQN
https://www.aplwiki.com/wiki/BQN - Co-dfns
https://www.aplwiki.com/wiki/Co-dfns - Array model
https://www.aplwiki.com/wiki/Array_model#Based_array_theory - Fonts for BQN
https://mlochbaum.github.io/BQN/fonts.html - Leading axis theory
https://www.aplwiki.com/wiki/Leading_axis_theory - A based system for general arrays
https://dl.acm.org/doi/abs/10.1145/586656.586663 - APL – A Glimpse of Heaven (2006)
https://news.ycombinator.com/item?id=19325361 - APL and J
https://crypto.stanford.edu/~blynn/c/apl.html - ivy (dokumentace)
https://pkg.go.dev/robpike.io/ivy#section-readme - ivy na GitHubu
https://github.com/robpike/ivy/ - Ivy na APL wiki
https://aplwiki.com/wiki/Ivy - Implementing a bignum calculator (slajdy)
https://talks.godoc.org/github.com/robpike/ivy/talks/ivy.slide#1 - Implementing a bignum calculator – Rob Pike – golang-syd November 2014
https://www.youtube.com/watch?v=PXoG0WX0r_E - Rob Pike na Wikipedii
https://en.wikipedia.org/wiki/Rob_Pike - Rob Pike na cat-v
http://genius.cat-v.org/rob-pike/ - Jazyky umožňující operace s poli aneb rozsáhlý svět „array programmingu“
https://www.root.cz/clanky/jazyky-umoznujici-operace-s-poli-aneb-rozsahly-svet-bdquo-array-programmingu-ldquo/ - Programovací technika nazvaná tacit programming
https://www.root.cz/clanky/programovaci-technika-nazvana-tacit-programming/ - Oslava 55 let od vzniku první implementace jazyka APL
https://www.root.cz/clanky/oslava-55-let-od-vzniku-prvni-implementace-programovaciho-jazyka-apl/ - NuVoc
https://code.jsoftware.com/wiki/NuVoc - J (programming language) [Wikipedia]
https://en.wikipedia.org/wiki/J_%28programming_language%29 - J – Absolutely Essential Terms
https://code.jsoftware.com/wiki/Vocabulary/AET - J – Atoms and Arrays
https://code.jsoftware.com/wiki/Vocabulary/Nouns#Atom - Why J
https://www.jsoftware.com/help/primer/why_j.htm - What is an Array?
https://vector.org.uk/what-is-an-array/ - Comments
http://www.gavilan.edu/csis/languages/comments.html - Vector (Wolfram MathWorld)
https://mathworld.wolfram.com/Vector.html - n-Tuple (Wolfram MathWorld)
https://mathworld.wolfram.com/n-Tuple.html - n-Vector (Wolfram MathWorld)
https://mathworld.wolfram.com/n-Vector.html - Matrix (Wolfram MathWorld)
https://mathworld.wolfram.com/Matrix.html - Array (Wolfram MathWorld)
https://mathworld.wolfram.com/Array.html - ND Arrays (Tensors) in different languages
https://www.youtube.com/watch?v=WbpbEilgQBc - Extending APL to Infinity\
https://www.jsoftware.com/papers/eem/infinity.htm - Vector Library (R7RS-compatible)
https://srfi.schemers.org/srfi-133/srfi-133.html - Vectors (pro Gauche)
https://practical-scheme.net/gauche/man/gauche-refe/Vectors.html - Kawa: Compiling Scheme to Java
https://www.mit.edu/afs.new/sipb/project/kawa/doc/kawa-tour.html - Kawa in Languages shootout
http://per.bothner.com/blog/2010/Kawa-in-shootout/ - Kawa 2.0 Supports Scheme R7RS
https://developers.slashdot.org/story/14/12/13/2259225/kawa-20-supports-scheme-r7rs/ - Kawa — fast scripting on the Java platform
https://lwn.net/Articles/623349/ - Incanter is a Clojure-based, R-like platform for statistical computing and graphics.
http://incanter.org/ - Evolution of incanter (Gource Visualization)
https://www.youtube.com/watch?v=TVfL5nPELr4 - Questions tagged [incanter] (na Stack Overflow)
https://stackoverflow.com/questions/tagged/incanter?sort=active - Data Sorcery with Clojure
https://data-sorcery.org/contents/ - Back to the Future: Lisp as a Base for a Statistical Computing System
https://rd.springer.com/chapter/10.1007/978–3–7908–2084–3_2 - Incanter Cheat Sheet
http://incanter.org/docs/incanter-cheat-sheet.pdf - Back to the Future: Lisp as a Base for a Statistical Computing System (celá verze článku)
https://www.researchgate.net/publication/227019917_Back_to_the_Future_Lisp_as_a_Base_for_a_Statistical_Computing_System - BQN: finally, an APL for your flying saucer
https://mlochbaum.github.io/BQN/ - Is BQN stable?
https://mlochbaum.github.io/BQN/commentary/stability.html - Specification: BQN system-provided values
https://mlochbaum.github.io/BQN/spec/system.html - Tutorial: BQN expressions
https://mlochbaum.github.io/BQN/tutorial/expression.html - BQN primitives
https://mlochbaum.github.io/BQN/doc/primitive.html - Function trains
https://mlochbaum.github.io/BQN/doc/train.html - BQN community links
https://mlochbaum.github.io/BQN/community/index.html - BQN UV
https://observablehq.com/@lsh/bqn-uv - APL Wiki
https://aplwiki.com/wiki/ - The Array Cast
https://www.arraycast.com/episodes/episode-03-what-is-an-array - EnthusiastiCon 2019 – An Introduction to APL
https://www.youtube.com/watch?v=UltnvW83_CQ - Dyalog
https://www.dyalog.com/ - Try APL!
https://tryapl.org/ - Lisp-Stat Information
http://homepage.cs.uiowa.edu/~luke/xls/xlsinfo/ - Sample Plots in Incanter
https://github.com/incanter/incanter/wiki/Sample-Plots-in-Incanter#line - vectorz-clj
https://github.com/mikera/vectorz-clj - vectorz – Examples
https://github.com/mikera/vectorz-clj/wiki/Examples - Basic Vector and Matrix Operations in Julia: Quick Reference and Examples
https://queirozf.com/entries/basic-vector-and-matrix-operations-in-julia-quick-reference-and-examples - Vectors and matrices in Julia
https://fncbook.github.io/v1.0/linsys/demos/matrices-julia.html - Array vs Matrix in R Programming
https://www.geeksforgeeks.org/array-vs-matrix-in-r-programming/ - Concurrency (computer science)
https://en.wikipedia.org/wiki/Category:Concurrency_%28computer_science%29 - Koprogram
https://cs.wikipedia.org/wiki/Koprogram - Coroutine
https://en.wikipedia.org/wiki/Coroutine - Coroutines in C
http://www.chiark.greenend.org.uk/~sgtatham/coroutines.html - S-expression (Wikipedia)
https://en.wikipedia.org/wiki/S-expression - S-Expressions (Rosetta Code)
http://rosettacode.org/wiki/S-Expressions - Introducing Julia/Metaprogramming
https://en.wikibooks.org/wiki/Introducing_Julia/Metaprogramming - Tutorial for the Common Lisp Loop Macro
http://www.ai.sri.com/pkarp/loop.html - Clojure Macro Tutorial (Part I, Getting the Compiler to Write Your Code For You)
http://www.learningclojure.com/2010/09/clojure-macro-tutorial-part-i-getting.html - Clojure Macro Tutorial (Part II: The Compiler Strikes Back)
http://www.learningclojure.com/2010/09/clojure-macro-tutorial-part-ii-compiler.html - Clojure Macro Tutorial (Part III: Syntax Quote)
http://www.learningclojure.com/2010/09/clojure-macro-tutorial-part-ii-syntax.html - Clojure Macros and Metaprogramming
http://clojure-doc.org/articles/language/macros.html - Fatvat – Exploring functional programming: Clojure Macros
http://www.fatvat.co.uk/2009/02/clojure-macros.html - CS 2101 Parallel Computing with Julia
https://www.coursehero.com/file/11508091/CS-2101-Parallel-Computing-with-Julia/ - Julia By Example
https://samuelcolvin.github.io/JuliaByExample/ - Array Programming
https://en.wikipedia.org/wiki/Array_programming - Discovering Array Languages
http://archive.vector.org.uk/art10008110 - no stinking loops – Kalothi
http://www.nsl.com/ - Vector (obsahuje odkazy na články, knihy a blogy o programovacích jazycích APL, J a K)
http://www.vector.org.uk/ - APL Interpreters
http://www.vector.org.uk/?area=interpreters - APL_(programming_language
http://en.wikipedia.org/wiki/APL_(programming_language - APL FAQ
http://www.faqs.org/faqs/apl-faq/ - APL FAQ (nejnovější verze)
http://home.earthlink.net/~swsirlin/apl.faq.html - A+
http://www.aplusdev.org/ - APLX
http://www.microapl.co.uk/ - FreeAPL
http://www.pyr.fi/apl/index.htm - Learning J (Roger Stokes)
http://www.jsoftware.com/help/learning/contents.htm - J: a modern, high-level, general-purpose, high-performance programming language
http://www.jsoftware.com/ - K, Kdb: an APL derivative for Solaris, Linux, Windows
http://www.kx.com - openAPL (GPL)
http://sourceforge.net/projects/openapl - Parrot APL (GPL)
http://www.parrotcode.org/ - Learning J (Roger Stokes)
http://www.jsoftware.com/help/learning/contents.htm - Rosetta Code
http://rosettacode.org/wiki/Main_Page - Why APL
http://www.acm.org/sigapl/whyapl.htm - Introducing Julia/Functions
https://en.wikibooks.org/wiki/Introducing_Julia/Functions - Functions (Julia documentation)
https://docs.julialang.org/en/v1/manual/functions/ - Evaluate binomial coefficients
http://rosettacode.org/wiki/Evaluate_binomial_coefficients - Ackermann function
http://rosettacode.org/wiki/Ackermann_function - Julia (front page)
http://julialang.org/ - Julia – dokumentace
http://docs.julialang.org/ - Julia – repositář na GitHubu
https://github.com/JuliaLang/julia - Julia (programming language)
https://en.wikipedia.org/wiki/Julia_%28programming_language%29 - IJulia
https://github.com/JuliaLang/IJulia.jl - Introducing Julia
https://en.wikibooks.org/wiki/Introducing_Julia - Julia: the REPL
https://en.wikibooks.org/wiki/Introducing_Julia/The_REPL - Month of Julia
https://github.com/DataWookie/MonthOfJulia - Learn X in Y minutes (where X=Julia)
https://learnxinyminutes.com/docs/julia/ - New Julia language seeks to be the C for scientists
http://www.infoworld.com/article/2616709/application-development/new-julia-language-seeks-to-be-the-c-for-scientists.html - Julia: A Fast Dynamic Language for Technical Computing
http://karpinski.org/publications/2012/julia-a-fast-dynamic-language - The LLVM Compiler Infrastructure
http://llvm.org/ - Julia: benchmarks
http://julialang.org/benchmarks/ - Type system
https://en.wikipedia.org/wiki/Type_system - Half-precision floating-point format
https://en.wikipedia.org/wiki/Half-precision_floating-point_format - Dartmouth BASIC
https://en.wikipedia.org/wiki/Dartmouth_BASIC - BASIC 4th Edition
http://www.bitsavers.org/pdf/dartmouth/BASIC_4th_Edition_Jan68.pdf - VECTRAN
https://encyclopedia2.thefreedictionary.com/VECTRAN - Comparison of programming languages (array)
https://en.wikipedia.org/wiki/Comparison_of_programming_languages_(array) - BASIC at 50
https://www.dartmouth.edu/basicfifty/commands.html - BBC Basic – arrays
http://www.riscos.com/support/developers/bbcbasic/part2/arrays.html - Datová struktura
https://cs.wikipedia.org/wiki/Datov%C3%A1_struktura - SIMD instrukce využívané v moderních mikroprocesorech řady x86
https://www.root.cz/clanky/simd-instrukce-vyuzivane-v-modernich-mikroprocesorech-rady-x86/ - SIMD instrukce v moderních mikroprocesorech řady x86 (2.část: SSE)
https://www.root.cz/clanky/simd-instrukce-v-modernich-mikroprocesorech-rady-x86–2-cast-sse/ - SIMD instrukce v moderních mikroprocesorech řady x86 (3.část: SSE2)
https://www.root.cz/clanky/simd-instrukce-v-modernich-mikroprocesorech-rady-x86–3-cast-sse2/ - Inductive type
https://en.wikipedia.org/wiki/Inductive_type - JuliaMono, a font for programming
https://github.com/cormullion/juliamono - It’s arrays all the way down
https://xpqz.github.io/learnapl/array.html





































