Rekurzivní datové typy v jazyku OCaml

Obsah

1. Definice výčtového typu s osmi základními barvami

2. Nový unifikovaný typ color a funkce pro převod barvy na trojici složek RGB

3. Realizace převodu všech základních barev na RGB

4. Přidání podpory pro stupně šedi

5. Úplný zdrojový kód druhé varianty příkladu

6. Reprezentace obecné barvy v barvovém prostoru RGB

7. Detekce chybějící větve ve funkci to_rgb

8. Doplnění funkce pro převod jakékoli barvy do barvového prostoru RGB

9. Přidání možnosti modifikace základních barev o atribut světlost

10. Zjednodušení výpočtu tmavší varianty základních barev

11. Malá odbočka: převod mezi barvovými modely HSV a RGB

12. Realizace algoritmu převodu HSV do RGB v jazyku Python

13. Realizace algoritmu převodu HSV do RGB v jazyku OCaml

14. Přidání barev v prostoru HSV do našeho typového systému

15. Důsledné využití zjednodušeného zápisu funkcí obsahujících jen pattern matching

16. Poslední typ barvy: mix dvou barev (rekurzivní datový typ)

17. Definice dvojice vzájemně rekurzivních funkcí pro rekurzivní datový typ

18. Výsledná podoba projektu s typovým systémem barev

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

1. Definice výčtového typu s osmi základními barvami

V dnešním článku o programovacím jazyku OCaml se ještě jednou vrátíme k typovému systému tohoto zajímavého jazyka. Ukážeme si, jakým způsobem lze realizovat datový typ pro reprezentaci barvy, a to v různých barvových modelech. Řešení bude založeno na „neobjektovém“ OCamlu (což zní poněkud divně, protože „O“ ve jménu „OCaml“ znamená „objektový“). Ukážeme a zopakujeme si jak vlastnosti typového systému OCamlu, tak i pattern matching (s jeho možným zkráceným zápisem) a v neposlední řadě se zmíníme o rekurzivních datových typech.

Začněme datovým typem, který bychom již měli dobře znát. Jedná se o takzvané disjunktní zobrazení, které obsahuje pouze výčet jmen. Tento datový typ použijeme pro reprezentaci základních osmi barev v barvové paletě:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;

V případě potřeby ovšem můžeme celou definici datového typu zapsat i na jediný řádek:

type basic_color = Black | Red | Green | Yellow | Blue | Magenta | Cyan | White;;

2. Nový unifikovaný typ color a funkce pro převod barvy na trojici složek RGB

V dalším textu budeme postupně budovat datový typ, který bude možné využít pro uložení barvy v jakékoli reprezentaci. První verze tohoto typu bude obsahovat jen jedinou možnost – již výše definovaný typ basic_color:

type color =
  | BasicColor of basic_color
;;

Postupně budeme přidávat i další možnosti.

Dále se pokusme definovat funkci, která převede barvu ze základní palety osmi barev na tři složky RGB. Tyto složky můžeme reprezentovat trojicí celočíselných hodnot a samotný převod lze realizovat funkcí (nazvěme ji basic_color_to_rgb) s pattern matchingem. Prozatím se pokusme v pattern matcheru zapsat jen jedinou barvu:

let basic_color_to_rgb c =
  match c with
  | Black -> (0, 0, 0)
;;

Ovšem funkci, která má jen jediný parametr a jejím tělem je jen blok s pattern matchingem, můžeme zapsat i jednodušším způsobem. Ten je založen na použití klíčového slova function:

let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
;;

Povšimněte si, že takovou funkci lze sice vytvořit (a bude mít i korektní typ), ovšem OCaml vypíše varování o tom, že jsme nepoužili všech osm barev:

let basic_color_to_rgb = function
  | Black -> (0, 0, 0);;
 
val basic_color_to_rgb : basic_color -> int * int * int =
 
1 Warning : this pattern-matching is not exhaustive.
Here is an example of a case that is not matched:
(Red|Green|Yellow|Blue|Magenta|Cyan|White)

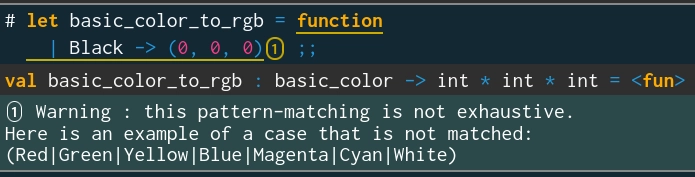
Obrázek 1: Varování OCamlu.

První varianta příkladu, který budeme postupně vyvíjet, tedy bude vypadat následovně:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type color =
  | BasicColor of basic_color
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
;;
 
 
let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
;;

3. Realizace převodu všech základních barev na RGB

V další variantě odstraníme korektní varování OCamlu. Rozšíříme totiž funkci pro převod základních barev na RGB složky tak, že budou použity všechny základní barvy:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type color =
  | BasicColor of basic_color
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255);;
 
 
let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
;;

Vše si otestujeme:

let c1 = BasicColor(Black);;
to_rgb c1;;
 
let c2 = BasicColor(Red);;
to_rgb c2;;

S výsledky (černá a červená barva reprezentovaná RGB složkami):

- : int * int * int = (0, 0, 0)
- : int * int * int = (255, 0, 0)

val basic_color_to_rgb : basic_color -> int * int * int = <fun>
val to_rgb : color -> int * int * int = <fun>

4. Přidání podpory pro stupně šedi

Podporu barev rozšíříme o možnost reprezentace barvy ve stupních šedi. Pro jednoduchost budeme předpokládat, že taková barva bude specifikována jednou celočíselnou hodnotou v rozsahu 0..255 (prozatím nebudeme kontrolovat meze). Datový typ „barva“ tedy bude muset být rozšířen o další pojmenovaný prvek:

type color =
  | BasicColor of basic_color
  | Gray of int
;;

A rozšířit budeme muset i funkce to_rgb pro převod barvy na trojici složek RGB. Pro jednoduchost bude převod ze stupňů šedi realizován tak, že se vstupní hodnota rozkopíruje do všech třech složek RGB (což ale nemusí být přesné – záleží na konkrétním barvovém prostoru):

let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
  | Gray g -> (g, g, g)

Popř. můžeme použít kratší zápis založený na klíčovém slově function:

let to_rgb = function
  | BasicColor (c, b) -> basic_color_to_rgb c
  | Gray g -> (g, g, g)

Vše si opět otestujeme:

let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;

S výsledky:

- : int * int * int = (0, 0, 0)
- : int * int * int = (255, 255, 255)

5. Úplný zdrojový kód druhé varianty příkladu

Shrnutí, jak nyní vypadá celý zdrojový kód:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type color =
  | BasicColor of basic_color
  | Gray of int
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let to_rgb = function
  | BasicColor (c, b) -> basic_color_to_rgb c
  | Gray g -> (g, g, g)
;;
 
 
let c1 = BasicColor(Black);;
to_rgb c1;;
 
let c2 = BasicColor(Red);;
to_rgb c2;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;

6. Reprezentace obecné barvy v barvovém prostoru RGB

Barvu je možné pochopitelně reprezentovat i přímo v barvovém prostoru RGB specifikací tří složek R, G a B. Přidání tohoto typu barvy do našeho obecného datového typu color je v tomto případě triviální – přidáme specifikaci pro trojici hodnot typu int:

type color =
  | BasicColor of basic_color
  | Gray of int
  | RGB of int * int * int
;;

Zbytek příkladu zůstane prozatím nezměněn:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type color =
  | BasicColor of basic_color
  | Gray of int
  | RGB of int * int * int
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
  | Gray g -> (g, g, g)
;;
 
 
let c1 = BasicColor(Black);;
to_rgb c1;;
 
let c2 = BasicColor(Red);;
to_rgb c2;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;

7. Detekce chybějící větve ve funkci to_rgb

Aby byl datový typ color plně funkční, je nutné rozšířit funkci to_rgb takovým způsobem, aby akceptovala i hodnoty typu RGB. Pokud totiž funkci nerozšíříme, bude si OCaml zcela oprávněně stěžovat, že funkce nebude korektně pracovat pro všechny možné varianty vstupních dat (ale přeloží ji):

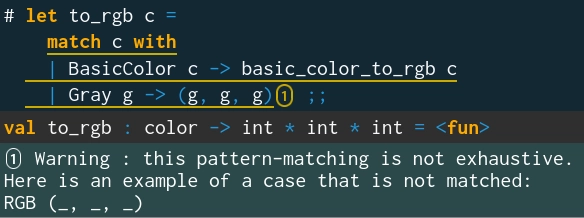
Obrázek 2: Detekce potenciálního problému v kódu – jedna z možných variant vstupních dat není v kódu zmíněna.

Ovšem problém nastane při volání této funkce, pokud jí předáme barvu typu RGB:

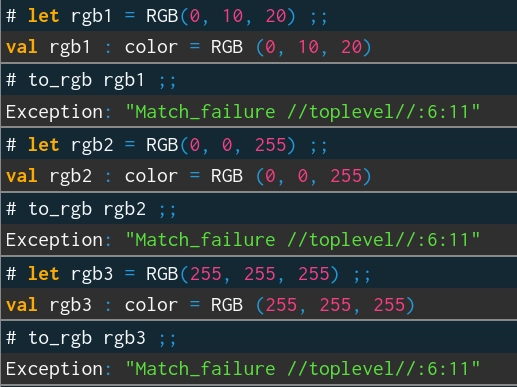
Obrázek 3: Pokus o předání barvy typu RGB do funkce to_rgb nebude úspěšný.

8. Doplnění funkce pro převod jakékoli barvy do barvového prostoru RGB

Do funkce to_rgb přidáme větev pro barvu typu RGB. Můžeme přitom ve vzorku (pattern) barvu nejprve rozložit na složky R, G a B a ve výrazu (za šipkou) z nich zase složit trojici (asi je zřejmé, že podpora například formátu BGR atd. by byla triviální):

let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)

Alternativní způsob zápisu s využitím klíčového slova function:

let to_rgb = function
  | BasicColor c -> basic_color_to_rgb c
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)

Novou funkcionalitu to_rgb si snadno ověříme:

let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let rgb2 = RGB(0, 0, 255);;
to_rgb rgb2;;
 
let rgb3 = RGB(255, 255, 255);;
to_rgb rgb3;;

Výše uvedených šest řádků kódu bude interpretováno následujícím způsobem:

let rgb1 = RGB(0, 10, 20) ;;
val rgb1 : color = RGB (0, 10, 20)
 
to_rgb rgb1 ;;
- : int * int * int = (0, 10, 20)
 
let rgb2 = RGB(0, 0, 255) ;;
val rgb2 : color = RGB (0, 0, 255)
 
to_rgb rgb2 ;;
- : int * int * int = (0, 0, 255)
 
let rgb3 = RGB(255, 255, 255) ;;
val rgb3 : color = RGB (255, 255, 255)
 
to_rgb rgb3 ;;
- : int * int * int = (255, 255, 255)

A pro úplnost si opět uvedeme úplný zdrojový kód upraveného příkladu:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type color =
  | BasicColor of basic_color
  | Gray of int
  | RGB  of int * int * int
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let to_rgb c =
  match c with
  | BasicColor c -> basic_color_to_rgb c
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
;;
 
 
let c1 = BasicColor(Black);;
to_rgb c1;;
 
let c2 = BasicColor(Red);;
to_rgb c2;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;
 
let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let rgb2 = RGB(0, 0, 255);;
to_rgb rgb2;;
 
let rgb3 = RGB(255, 255, 255);;
to_rgb rgb3;;

9. Přidání možnosti modifikace základních barev o atribut světlost

Nyní provedeme další rozšíření našeho systému barev. Přidáme možnost určit u základních osmi barev jejich světlost, tj. atribut Dark či Bright. Typ tohoto atributu je triviální:

type brightness =
  | Dark
  | Bright
;;

Důležitější ovšem je, že se změní i konstruktor pro základní barvy. Kromě jména barvy (Red atd.) se musí specifikovat i její světlost, takže výsledkem je (typově bezpečná) dvojice:

type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
;;

A pochopitelně musíme modifikovat i přepočet základních barev na RGB. Pokud má být základní barva světlá, neprovedeme žádnou změnu, ale pokud má být tmavá, podělíme všechny její barvové složky dvěma (to pro jednoduchost – v praxi se spíše násobí konstantou 2/3):

let brightness rgb brightess =
  match brightess with
  | Dark -> (match rgb with
      | (r, g, b) -> (r/2, g/2, b/2))
  | Bright -> rgb
;;
 
 
let to_rgb c =
  match c with
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
;;

Výpočet si ověříme:

let c1 = BasicColor(Black, Dark);;
to_rgb c1;;
 
let c2 = BasicColor(Black, Bright);;
to_rgb c2;;
 
let c3 = BasicColor(Red, Dark);;
to_rgb c3;;
 
let c4 = BasicColor(Red, Bright);;
to_rgb c4;;

Pro tyto čtyři řádky bychom měli získat následující RGB složky (nejdůležitější je tmavě červená, tedy barva c3):

to_rgb c1 ;;
- : int * int * int = (0, 0, 0)
 
to_rgb c2 ;;
- : int * int * int = (0, 0, 0)
 
to_rgb c3 ;;
- : int * int * int = (127, 0, 0)
 
to_rgb c4 ;;
- : int * int * int = (255, 0, 0)

A pro úplnost si opět uvedeme úplný zdrojový kód upraveného příkladu:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type brightness =
  | Dark
  | Bright
;;
 
 
type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let brightness rgb brightess =
  match brightess with
  | Dark -> (match rgb with
      | (r, g, b) -> (r/2, g/2, b/2))
  | Bright -> rgb
;;
 
 
let to_rgb c =
  match c with
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
;;
 
 
let c1 = BasicColor(Black, Dark);;
to_rgb c1;;
 
let c2 = BasicColor(Black, Bright);;
to_rgb c2;;
 
let c3 = BasicColor(Red, Dark);;
to_rgb c3;;
 
let c4 = BasicColor(Red, Bright);;
to_rgb c4;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;
 
let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let rgb2 = RGB(0, 0, 255);;
to_rgb rgb2;;
 
let rgb3 = RGB(255, 255, 255);;
to_rgb rgb3;;

10. Zjednodušení výpočtu tmavší varianty základních barev

V demonstračním příkladu z předchozí kapitoly jsme použili poněkud nešikovné řešení založené na vnořených konstrukcích match. Tento koncept sice programovací jazyk OCaml podporuje, ale výsledek není příliš čitelný, o čem se můžeme snadno přesvědčit:

let brightness rgb brightess =
  match brightess with
  | Dark -> (match rgb with
      | (r, g, b) -> (r/2, g/2, b/2))
  | Bright -> rgb
;;

Lepší bude, když si vnitřní blok match převedeme do lokální či globální funkce. Potom se předchozí kód změní na:

let darker rgb =
  match rgb with
  | (r, g, b) -> (r/2, g/2, b/2)
;;
 
 
let brightness rgb brightess =
  match brightess with
  | Dark -> darker rgb
  | Bright -> rgb
;;

A úplný kód příkladu bude nyní vypadat následovně:

type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type brightness =
  | Dark
  | Bright
;;
 
 
type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let darker rgb =
  match rgb with
  | (r, g, b) -> (r/2, g/2, b/2)
;;
 
 
let brightness rgb brightess =
  match brightess with
  | Dark -> darker rgb
  | Bright -> rgb
;;
 
 
let to_rgb c =
  match c with
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
;;
 
 
let c1 = BasicColor(Black, Dark);;
to_rgb c1;;
 
let c2 = BasicColor(Black, Bright);;
to_rgb c2;;
 
let c3 = BasicColor(Red, Dark);;
to_rgb c3;;
 
let c4 = BasicColor(Red, Bright);;
to_rgb c4;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;
 
let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let rgb2 = RGB(0, 0, 255);;
to_rgb rgb2;;
 
let rgb3 = RGB(255, 255, 255);;
to_rgb rgb3;;

11. Malá odbočka: převod mezi barvovými modely HSV a RGB

V dalších kapitolách přidáme do našeho systému barev možnost specifikace barvy v barvovém prostoru (modelu) HSV neboli Hue, Saturation, Value. Taková barva je reprezentována trojicí složek v rozsahu 0,0 až 1,0 (někdy jsou provedeny přepočty hue na úhly a ostatních složek na hodnoty 0% až 100%). Složka hue určuje odstín barvy v kruhu nebo šestiúhelníku, složka saturation pak čistotu barvy a složka value její světlost. Barvový prostor HSV tedy zhruba vypadá následovně (ve skutečnosti jsou ale barvy umístěny v kuželi, ne v celém válci, protože na špičce kužele je černá barva bez sytosti a odstínu).

12. Realizace algoritmu převodu HSV do RGB v jazyku Python

Nejdříve se podívejme na to, jak může vypadat realizace algoritmu pro převod barvy z barvového prostoru HSV do prostoru RGB ve vysokoúrovňovém pseudokódu, který je (čistě náhodou :-) i korektním Pythonovským zdrojovým kódem. Na základě odstínu barvy (hue) je zjištěno, ve které šestině HSV kužele se barva nachází a posléze je proveden přepočet pouze v rámci této šestiny. Z tohoto důvodu je i v Pythonovském kódu použita konstrukce pro pattern matching, i když se v ní ve skutečnosti nerozpoznávají žádné složité vzory, ale pouze celočíselné konstanty 0 až 5:

def scale_rgb(r, g, b):
    return (int(255*r), int(255*g), int(255*b))
 
 
def hsv_to_rgb(h, s, v):
    if s==0:
        return scale_rgb(v, v, v)
    else:
        return hsv_to_rgb_(h, s, v)
 
 
def hsv_to_rgb_(h, s, v):
    if h == 1.0:
        h = 0.0
    i = int(h*6.0)
    f = h*6.0 - i
 
    w = v * (1.0 - s)
    q = v * (1.0 - s * f)
    t = v * (1.0 - s * (1.0 - f))
 
    match i:
        case 0:
            return scale_rgb(v, t, w)
        case 1:
            return scale_rgb(q, v, w)
        case 2:
            return scale_rgb(w, v, t)
        case 3:
            return scale_rgb(w, q, v)
        case 4:
            return scale_rgb(t, w, v)
        case 5:
            return scale_rgb(v, w, q)
 
 
print(hsv_to_rgb(0.0, 0.0, 1.0))
print(hsv_to_rgb(0.0, 0.0, 0.5))
 
print(hsv_to_rgb(0.0, 1.0, 1.0))
print(hsv_to_rgb(0.3333, 1.0, 1.0))
print(hsv_to_rgb(0.6666, 1.0, 1.0))
print(hsv_to_rgb(1, 1.0, 1.0))
print(hsv_to_rgb(1.0, 0.5, 0.5))

13. Realizace algoritmu převodu HSV do RGB v jazyku OCaml

Zajímavé bude porovnání pythonovského (typově nezabezpečeného) kódu do jazyka OCaml. Snažil jsem se o zachování stejné struktury kódu, takže se sémantika nebude lišit. Na druhou stranu je syntaxe odlišná a současně je kód typově bezpečný:

let scale_component x =
  int_of_float (255.*.x)
;;
 
 
let scale_rgb r g b =
  (scale_component r,
   scale_component g,
   scale_component b)
;;
 
 
let hsv_to_rgb_ h s v =
  let h =
    match h with
    | 1.0 -> 0.0
    | _ -> h
  in
  let i = int_of_float (h*.6.0) in
  let f = h *. 6.0 -. (float i) in
  let w = v *. (1.0 -. s) in
  let q = v *. (1.0 -. s*.f) in
  let t = v *. (1.0 -. s*.(1.0 -. f)) in
  match i with
  | 0 -> scale_rgb v t w
  | 1 -> scale_rgb q v w
  | 2 -> scale_rgb w v t
  | 3 -> scale_rgb w q v
  | 4 -> scale_rgb t w v
  | 5 -> scale_rgb v w q
  | _ -> (0, 0, 0)
;;
 
 
let hsv_to_rgb h s v =
  match s with
  | 0.0 -> (scale_rgb v v v)
  | _ -> (hsv_to_rgb_ h s v)
;;

Jednotlivé převody barev si otestujeme:

hsv_to_rgb 0.0 0.0 1.0;;
hsv_to_rgb 0.0 0.0 0.5;;
hsv_to_rgb 0.0 1.0 1.0;;
hsv_to_rgb 0.3333 1.0 1.0;;
hsv_to_rgb 0.6666 1.0 1.0;;
hsv_to_rgb 1.0 1.0 1.0;;
hsv_to_rgb 1.0 0.5 0.5;;

S výsledky:

čistě bílá barva
hsv_to_rgb 0.0 0.0 1.0 ;;
- : int * int * int = (255, 255, 255)
 
šedá barva (50%)
hsv_to_rgb 0.0 0.0 0.5 ;;
- : int * int * int = (127, 127, 127)
 
čistě červená barva (hue=0)
hsv_to_rgb 0.0 1.0 1.0 ;;
- : int * int * int = (255, 0, 0)
 
čistě zelená barva (hue=1/3)
hsv_to_rgb 0.3333 1.0 1.0 ;;
- : int * int * int = (0, 255, 0)
 
čistě modrá barva (hue=2/3)
hsv_to_rgb 0.6666 1.0 1.0 ;;
- : int * int * int = (0, 0, 255)
 
čistě červená barva (hue=0 == hue=1)
hsv_to_rgb 1.0 1.0 1.0 ;;
- : int * int * int = (255, 0, 0)
 
modifikace saturace
hsv_to_rgb 1.0 0.5 0.5 ;;
- : int * int * int = (127, 63, 63)

14. Přidání barev v prostoru HSV do našeho typového systému

Nyní, když již víme, jakým způsobem je možné převést barvu z prostoru HSV do prostoru RGB, bude rozšíření našeho typového systému barev o možnost specifikace barvy v HSV ve skutečnosti dosti triviální. Nejdříve musíme deklarovat novou variantu barvy HSV reprezentované trojicí hodnot typu float. Úprava bude vypadat následovně:

type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
  | HSV of float * float * float
;;

A druhá změna se týká funkce pro převod jakékoli barvy na RGB. Zde opět postačuje přidání jediného řádku:

let to_rgb c =
  match c with
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
;;

15. Důsledné využití zjednodušeného zápisu funkcí obsahujících jen pattern matching

Náš postupně vznikající projekt ještě dále upravíme. Změníme všechny funkce, které obsahují pouze blok match, na jejich jednodušší variantu založenou na použití klíčového slova function. To je snadné, protože se tento „problém“ týká jen dvou funkcí:

let darker = function
  | (r, g, b) -> (r/2, g/2, b/2)
;;

a:

let to_rgb = function
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
;;

Předposlední verze projektu bude nyní vypadat takto:

let scale_component x =
  int_of_float (255.*.x)
;;
 
 
let scale_rgb r g b =
  (scale_component r,
   scale_component g,
   scale_component b)
;;
 
 
let hsv_to_rgb_ h s v =
  let h =
    match h with
    | 1.0 -> 0.0
    | _ -> h
  in
  let i = int_of_float (h*.6.0) in
  let f = h *. 6.0 -. (float i) in
  let w = v *. (1.0 -. s) in
  let q = v *. (1.0 -. s*.f) in
  let t = v *. (1.0 -. s*.(1.0 -. f)) in
  match i with
  | 0 -> scale_rgb v t w
  | 1 -> scale_rgb q v w
  | 2 -> scale_rgb w v t
  | 3 -> scale_rgb w q v
  | 4 -> scale_rgb t w v
  | 5 -> scale_rgb v w q
  | _ -> (0, 0, 0)
;;
 
 
let hsv_to_rgb h s v =
  match s with
  | 0.0 -> (scale_rgb v v v)
  | _ -> (hsv_to_rgb_ h s v)
;;
 
 
type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type brightness =
  | Dark
  | Bright
;;
 
 
type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
  | HSV of float * float * float
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255);;
;;
 
 
let darker = function
  | (r, g, b) -> (r/2, g/2, b/2)
;;
 
 
let brightness rgb brightess =
  match brightess with
  | Dark -> darker rgb
  | Bright -> rgb
;;
 
 
let to_rgb = function
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
;;
 
 
let c1 = BasicColor(Black, Dark);;
to_rgb c1;;
 
let c2 = BasicColor(Black, Bright);;
to_rgb c2;;
 
let c3 = BasicColor(Red, Dark);;
to_rgb c3;;
 
let c4 = BasicColor(Red, Bright);;
to_rgb c4;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;
 
let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let rgb2 = RGB(0, 0, 255);;
to_rgb rgb2;;
 
let rgb3 = RGB(255, 255, 255);;
to_rgb rgb3;;
 
let hsv1 = HSV(0.0, 0.0, 1.0);;
to_rgb hsv1;;
 
let hsv2 = HSV(0.0, 0.0, 0.5);;
to_rgb hsv2;;
 
let hsv3 = HSV(0.0, 1.0, 1.0);;
to_rgb hsv3;;
 
let hsv4 = HSV(0.3333, 1.0, 1.0);;
to_rgb hsv4;;
 
let hsv5 = HSV(0.6666, 1.0, 1.0);;
to_rgb hsv5;;
 
let hsv6 = HSV(1.0, 1.0, 1.0);;
to_rgb hsv6;;
 
let hsv7 = HSV(1.0, 0.5, 0.5);;
to_rgb hsv7;;

16. Poslední typ barvy: mix dvou barev (rekurzivní datový typ)

Nyní se dostáváme k nejzajímavější části námi vytvářeného typového systému barev. Přidáme do něj možnost definovat novou barvu mixem dvou jiných barev, přičemž bude možné specifikovat poměr obou barev. Například tedy budeme moci říci: „nová barva je z 10% tvořena základní červenou barvou a z 90% je tvořena HSV barvou (1.0, 0.5, 0.5)“ atd. Nebo samozřejmě můžeme novou barvu vytvořit mixem barev, které vznikly mixem jiných barev. Výsledkem je rekurzivní datový typ:

type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
  | HSV of float * float * float
  | Mix of float * color * color
;;

Samozřejmě budeme muset přidat novou větev do funkce to_rgb. V případě, že budeme chtít použít novou variantu Mix, je nutné z obou barev vypočítat jejich smíchané RGB složky:

let to_rgb = function
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
  | Mix(ratio, color1, color2) -> mix_colors ratio color1 color2
;;

Samotný výpočet smíchané barvy není nijak komplikovaný, ovšem má jeden problém – voláme v něm opět funkci to_rgb, protože míchané barvy je nejprve nutné převést na jejich RGB složky:

let mix_components ratio c1 c2 =
  int_of_float ((float c1) *. ratio +. (float c2) *. (1.0 -. ratio))
;;
 
 
 
let mix_colors ratio color1 color2 =
  let (r1, g1, b1) = to_rgb color1 in
  let (r2, g2, b2) = to_rgb color2 in
  (mix_components ratio r1 r2, mix_components ratio g1 g2, mix_components ratio b1 b2)
;;

Takto strukturovaný programový kód nebude možné přeložit, protože z funkce to_rgb voláme funkci mix_colors a z mix_colors voláme opět to_rgb.

17. Definice dvojice vzájemně rekurzivních funkcí pro rekurzivní datový typ

Při řešení problému s rekurzivní datovou strukturou a z ní plynoucí rekurzí v programovém kódu musíme obě vzájemně rekurzivní funkce definovat přes let rec a navíc je musíme definovat současně – se spojkou and (což již známe):

let rec mix_colors ratio color1 color2 =
  let (r1, g1, b1) = to_rgb color1 in
  let (r2, g2, b2) = to_rgb color2 in
  (mix_components ratio r1 r2, mix_components ratio g1 g2, mix_components ratio b1 b2)
and
  to_rgb = function
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
  | Mix(ratio, color1, color2) -> mix_colors ratio color1 color2
;;

Nyní již bude možné kód bez problémů přeložit a spustit.

18. Výsledná podoba projektu s typovým systémem barev

Celý projekt s realizací poměrně komplikovaného datového typu color byl vytvořen pouze s využitím typového systému jazyka OCaml (rekurzivní typy + n-tice + disjunktní zobrazení) a pattern matchingu. Jak je patrné, je celé řešení vlastně řešeno ortogonálně v porovnání s objektovým přístupem. V OO řešení by se vytvořila hierarchie tříd, každá třída by měla vlastní realizaci to_rgb a stav i vlastní hodnota barvy by byla zapouzdřena a dostupná přes nějaké metody. Řešení na úrovni typů je odlišné – typ je jeden (i když rekurzivní) a i to_rgb je řešeno na jediném místě. Každý z použitých přístupů má pochopitelně své přednosti a zápory, které se týkají rozšiřitelnosti, čitelnosti, testovatelnosti apod.

Dále si povšimněte, že se v celém kódu setkáme jen s jedním místem, v němž musíme konkrétně specifikovat datové typy. Jedná se o samotnu definici typu color. Ostatní kód je již zcela založen na automaticky prováděné typové inferenci jazyka OCaml:

let scale_component x =
  int_of_float (255.*.x)
;;
 
 
let scale_rgb r g b =
  (scale_component r,
   scale_component g,
   scale_component b)
;;
 
 
let hsv_to_rgb_ h s v =
  let h =
    match h with
    | 1.0 -> 0.0
    | _ -> h
  in
  let i = int_of_float (h*.6.0) in
  let f = h *. 6.0 -. (float i) in
  let w = v *. (1.0 -. s) in
  let q = v *. (1.0 -. s*.f) in
  let t = v *. (1.0 -. s*.(1.0 -. f)) in
  match i with
  | 0 -> scale_rgb v t w
  | 1 -> scale_rgb q v w
  | 2 -> scale_rgb w v t
  | 3 -> scale_rgb w q v
  | 4 -> scale_rgb t w v
  | 5 -> scale_rgb v w q
  | _ -> (0, 0, 0)
;;
 
 
let hsv_to_rgb h s v =
  match s with
  | 0.0 -> (scale_rgb v v v)
  | _ -> (hsv_to_rgb_ h s v)
;;
 
 
type basic_color =
  | Black
  | Red
  | Green
  | Yellow
  | Blue
  | Magenta
  | Cyan
  | White
;;
 
 
type brightness =
  | Dark
  | Bright
;;
 
 
type color =
  | BasicColor of basic_color * brightness
  | Gray of int
  | RGB of int * int * int
  | HSV of float * float * float
  | Mix of float * color * color;;
;;
 
 
let basic_color_to_rgb = function
  | Black -> (0, 0, 0)
  | Red -> (255, 0,0)
  | Green -> (0, 255, 0)
  | Yellow -> (255, 255, 0)
  | Blue -> (0, 0, 255)
  | Magenta -> (255, 0, 255)
  | Cyan -> (0, 255, 255)
  | White -> (255, 255, 255)
;;
 
 
let darker = function
  | (r, g, b) -> (r/2, g/2, b/2)
;;
 
 
let brightness rgb brightess =
  match brightess with
  | Dark -> darker rgb
  | Bright -> rgb
;;
 
 
let mix_components ratio c1 c2 =
  int_of_float ((float c1) *. ratio +. (float c2) *. (1.0 -. ratio))
;;
 
 
let rec mix_colors ratio color1 color2 =
  let (r1, g1, b1) = to_rgb color1 in
  let (r2, g2, b2) = to_rgb color2 in
  (mix_components ratio r1 r2, mix_components ratio g1 g2, mix_components ratio b1 b2)
and
  to_rgb = function
  | BasicColor (c, b) -> brightness (basic_color_to_rgb c) b
  | Gray g -> (g, g, g)
  | RGB(r,g,b) -> (r, g, b)
  | HSV(h,s,v) -> hsv_to_rgb h s v
  | Mix(ratio, color1, color2) -> mix_colors ratio color1 color2
;;
 
 
let c1 = BasicColor(Black, Dark);;
to_rgb c1;;
 
let c2 = BasicColor(Black, Bright);;
to_rgb c2;;
 
let c3 = BasicColor(Red, Dark);;
to_rgb c3;;
 
let c4 = BasicColor(Red, Bright);;
to_rgb c4;;
 
let g1 = Gray(0);;
to_rgb g1;;
 
let g2 = Gray(255);;
to_rgb g2;;
 
let rgb1 = RGB(0, 10, 20);;
to_rgb rgb1;;
 
let hsv1 = HSV(0.0, 0.0, 1.0);;
to_rgb hsv1;;
 
let hsv2 = HSV(0.0, 0.0, 0.5);;
to_rgb hsv2;;
 
let hsv3 = HSV(0.0, 1.0, 1.0);;
to_rgb hsv3;;
 
let hsv4 = HSV(0.3333, 1.0, 1.0);;
to_rgb hsv4;;
 
let hsv5 = HSV(0.6666, 1.0, 1.0);;
to_rgb hsv5;;
 
let hsv6 = HSV(1.0, 1.0, 1.0);;
to_rgb hsv6;;
 
let hsv7 = HSV(1.0, 0.5, 0.5);;
to_rgb hsv7;;
 
let mixed1 = Mix(0.0, BasicColor(Red, Bright), BasicColor(Blue, Bright));;
to_rgb mixed1;;
 
let mixed2 = Mix(0.5, BasicColor(Red, Bright), BasicColor(Blue, Bright));;
to_rgb mixed2;;
 
let mixed3 = Mix(1.0, BasicColor(Red, Bright), BasicColor(Blue, Bright));;
to_rgb mixed3;;

19. Repositář s demonstračními příklady

Všechny výše popsané demonstrační příklady byly uloženy do repositáře dostupného na adrese https://github.com/tisnik/ocaml-examples/. V tabulce umístěné pod tímto odstavcem jsou uvedeny odkazy na tyto příklady:

20. Odkazy na Internetu

1. General-Purpose, Industrial-Strength, Expressive, and Safe
   https://ocaml.org/
2. OCaml playground
   https://ocaml.org/play
3. Online Ocaml Compiler IDE
   https://www.jdoodle.com/compile-ocaml-online/
4. Get Started – OCaml
   https://www.ocaml.org/docs
5. Get Up and Running With OCaml
   https://www.ocaml.org/docs/up-and-running
6. Better OCaml (Online prostředí)
   https://betterocaml.ml/?ver­sion=4.14.0
7. OCaml file extensions
   https://blog.waleedkhan.name/ocaml-file-extensions/
8. First thoughts on Rust vs OCaml
   https://blog.darklang.com/first-thoughts-on-rust-vs-ocaml/
9. Standard ML of New Jersey
   https://www.smlnj.org/
10. Programming Languages: Standard ML – 1 (a navazující videa)
    https://www.youtube.com/wat­ch?v=2sqjUWGGzTo
11. 6 Excellent Free Books to Learn Standard ML
    https://www.linuxlinks.com/excellent-free-books-learn-standard-ml/
12. SOSML: The Online Interpreter for Standard ML
    https://sosml.org/
13. ML (Computer program language)
    https://www.barnesandnoble­.com/b/books/other-programming-languages/ml-computer-program-language/_/N-29Z8q8Zvy7
14. Strong Typing
    https://perl.plover.com/y­ak/typing/notes.html
15. What to know before debating type systems
    http://blogs.perl.org/user­s/ovid/2010/08/what-to-know-before-debating-type-systems.html
16. Types, and Why You Should Care (Youtube)
    https://www.youtube.com/wat­ch?v=0arFPIQatCU
17. DynamicTyping (Martin Fowler)
    https://www.martinfowler.com/bli­ki/DynamicTyping.html
18. DomainSpecificLanguage (Martin Fowler)
    https://www.martinfowler.com/bli­ki/DomainSpecificLanguage­.html
19. Language Workbenches: The Killer-App for Domain Specific Languages?
    https://www.martinfowler.com/ar­ticles/languageWorkbench.html
20. Effective ML (Youtube)
    https://www.youtube.com/watch?v=-J8YyfrSwTk
21. Why OCaml (Youtube)
    https://www.youtube.com/wat­ch?v=v1CmGbOGb2I
22. Try OCaml
    https://try.ocaml.pro/
23. CSE 341: Functions and patterns
    https://courses.cs.washin­gton.edu/courses/cse341/04wi/lec­tures/03-ml-functions.html
24. Comparing Objective Caml and Standard ML
    http://adam.chlipala.net/mlcomp/
25. What are the key differences between Standard ML and OCaml?
    https://www.quora.com/What-are-the-key-differences-between-Standard-ML-and-OCaml?share=1
26. Cheat Sheets (pro OCaml)
    https://www.ocaml.org/doc­s/cheat_sheets.html
27. Think OCaml: How to Think Like a (Functional) Programmer
    https://www.greenteapress­.com/thinkocaml/thinkocam­l.pdf
28. The OCaml Language Cheat Sheet
    https://ocamlpro.github.io/ocaml-cheat-sheets/ocaml-lang.pdf
29. Syllabus (FAS CS51)
    https://cs51.io/college/syllabus/
30. Abstraction and Design In Computation
    http://book.cs51.io/
31. Learn X in Y minutes Where X=Standard ML
    https://learnxinyminutes.com/doc­s/standard-ml/
32. CSE307 Online – Summer 2018: Principles of Programing Languages course
    https://www3.cs.stonybrook­.edu/~pfodor/courses/summer/cse307­.html
33. CSE307 Principles of Programming Languages course: SML part 1
    https://www.youtube.com/wat­ch?v=p1n0_PsM6hw
34. CSE 307 – Principles of Programming Languages – SML
    https://www3.cs.stonybrook­.edu/~pfodor/courses/summer/CSE307/L01_SML­.pdf
35. SML, Some Basic Examples
    https://cs.fit.edu/~ryan/sml/in­tro.html
36. History of programming languages
    https://devskiller.com/history-of-programming-languages/
37. History of programming languages (Wikipedia)
    https://en.wikipedia.org/wi­ki/History_of_programming_lan­guages
38. Jemný úvod do rozsáhlého světa jazyků LISP a Scheme
    https://www.root.cz/clanky/jemny-uvod-do-rozsahleho-sveta-jazyku-lisp-a-scheme/
39. The Evolution Of Programming Languages
    https://www.i-programmer.info/news/98-languages/8809-the-evolution-of-programming-languages.html
40. Evoluce programovacích jazyků
    https://ccrma.stanford.edu/cou­rses/250a-fall-2005/docs/ComputerLanguagesChart.png
41. Poly/ML Homepage
    https://polyml.org/
42. PolyConf 16: A brief history of F# / Rachel Reese
    https://www.youtube.com/wat­ch?v=cbDjpi727aY
43. Programovací jazyk Clojure 18: základní techniky optimalizace aplikací
    https://www.root.cz/clanky/pro­gramovaci-jazyk-clojure-18-zakladni-techniky-optimalizace-aplikaci/
44. Moscow ML Language Overview
    https://itu.dk/people/ses­toft/mosml/mosmlref.pdf
45. ForLoops
    http://mlton.org/ForLoops
46. Funkcionální dobrodružství v JavaScriptu
    https://blog.kolman.cz/2015/12/fun­kcionalni-dobrodruzstvi-v-javascriptu.html
47. Recenze knihy Functional Thinking (Paradigm over syntax)
    https://www.root.cz/clanky/recenze-knihy-functional-thinking-paradigm-over-syntax/
48. Currying
    https://sw-samuraj.cz/2011/02/currying/
49. Používání funkcí v F#
    https://docs.microsoft.com/cs-cz/dotnet/fsharp/tutorials/using-functions
50. Funkce vyššího řádu
    http://naucte-se.haskell.cz/funkce-vyssiho-radu
51. Currying (Wikipedia)
    https://en.wikipedia.org/wi­ki/Currying
52. Currying (Haskell wiki)
    https://wiki.haskell.org/Currying
53. Haskell Curry
    https://en.wikipedia.org/wi­ki/Haskell_Curry
54. Moses Schönfinkel
    https://en.wikipedia.org/wi­ki/Moses_Sch%C3%B6nfinkel
55. .NET framework
    https://dotnet.microsoft.com/en-us/
56. F# – .NET Blog
    https://devblogs.microsof­t.com/dotnet/category/fshar­p/
57. Playground: OCaml
    https://ocaml.org/play
58. The F# Survival Guide
    https://web.archive.org/web/20110715231625/htt­p://www.ctocorner.com/fshar­p/book/default.aspx
59. Object-Oriented Programming — The Trillion Dollar Disaster
    https://betterprogramming.pub/object-oriented-programming-the-trillion-dollar-disaster-92a4b666c7c7
60. Goodbye, Object Oriented Programming
    https://cscalfani.medium.com/goodbye-object-oriented-programming-a59cda4c0e53
61. So You Want to be a Functional Programmer (Part 1)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-1–1f15e387e536
62. So You Want to be a Functional Programmer (Part 2)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-2–7005682cec4a
63. So You Want to be a Functional Programmer (Part 3)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-3–1b0fd14eb1a7
64. So You Want to be a Functional Programmer (Part 4)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-4–18fbe3ea9e49
65. So You Want to be a Functional Programmer (Part 5)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-5-c70adc9cf56a
66. So You Want to be a Functional Programmer (Part 6)
    https://cscalfani.medium.com/so-you-want-to-be-a-functional-programmer-part-6-db502830403
67. Don Syme
    https://en.wikipedia.org/wi­ki/Don_Syme
68. Python to OCaml: Retrospective
    http://roscidus.com/blog/blog/2014/06/0­6/python-to-ocaml-retrospective/
69. Why does Cambridge teach OCaml as the first programming language?
    https://www.youtube.com/wat­ch?v=6APBx0WsgeQ
70. OCaml and 7 Things You Need To Know About It In 2021 | Functional Programming | Caml
    https://www.youtube.com/wat­ch?v=s0itOsgcf9Q
71. OCaml 2021 – 25 years of OCaml
    https://www.youtube.com/watch?v=-u_zKPXj6mw
72. Introduction | OCaml Programming | Chapter 1 Video 1
    https://www.youtube.com/wat­ch?v=MUcka_SvhLw&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU
73. Functional Programming – What | OCaml Programming | Chapter 1 Video 2
    https://www.youtube.com/wat­ch?v=JTEwC3HihFc&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=2
74. Functional Programming – Why Part 1 | OCaml Programming | Chapter 1 Video 3
    https://www.youtube.com/wat­ch?v=SKr3ItChPSI&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=3
75. Functional Programming – Why Part 2 | OCaml Programming | Chapter 1 Video 4
    https://www.youtube.com/wat­ch?v=eNLm5Xbgmd0&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=4
76. OCaml | OCaml Programming | Chapter 1 Video 5
    https://www.youtube.com/watch?v=T-DIW1dhYzo&list=PLre5AT9JnKShBOPeuiD9b-I4XROIJhkIU&index=5
77. Five Aspects of Learning a Programming Language | OCaml Programming | Chapter 2 Video 1
    https://www.youtube.com/wat­ch?v=A5IHFZtRfBs&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=6
78. Expressions | OCaml Programming | Chapter 2 Video 2
    https://www.youtube.com/watch?v=3fzrFY-2ZQ8&list=PLre5AT9JnKShBOPeuiD9b-I4XROIJhkIU&index=7
79. If Expressions | OCaml Programming | Chapter 2 Video 3
    https://www.youtube.com/wat­ch?v=XJ6QPtlPD7s&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=8
80. Let Definitions | OCaml Programming | Chapter 2 Video 4
    https://www.youtube.com/wat­ch?v=eRnG4gwOTlI&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=10
81. Let Expressions | OCaml Programming | Chapter 2 Video 5
    https://www.youtube.com/wat­ch?v=ug3L97FXC6A&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=10
82. Variable Expressions and Scope | OCaml Programming | Chapter 2 Video 6
    https://www.youtube.com/wat­ch?v=_TpTC6eo34M&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=11
83. Scope and the Toplevel | OCaml Programming | Chapter 2 Video 7
    https://www.youtube.com/wat­ch?v=4SqMkUwakEA&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=12
84. Anonymous Functions | OCaml Programming | Chapter 2 Video 8
    https://www.youtube.com/wat­ch?v=JwoIIrj0bcM&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=13
85. Lambdas | OCaml Programming | Chapter 2 Video 9
    https://www.youtube.com/wat­ch?v=zHHCD7MOjmw&list=PLre5AT9JnKShBO­PeuiD9b-I4XROIJhkIU&index=15
86. Operators
    https://ocaml.org/docs/operators
87. Operator overloading
    https://en.wikipedia.org/wi­ki/Operator_overloading
88. Generalized algebraic data type
    https://en.wikipedia.org/wi­ki/Generalized_algebraic_da­ta_type