Obsah
1. Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
2. Řešený problém: rozpoznání ručně nakreslených číslic
3. Instalace všech potřebných balíčků
4. Kooperace mezi knihovnami Matplotlib a NumPy: vizualizace obsahu 2D matice
5. Datová množina obsahující naskenované ručně napsané číslice
6. Další atributy datové množiny, které použijeme při trénování
7. Přečtení a následné vykreslení jednotlivých ručně nakreslených číslic
8. Odstranění umělé aplikované barvové palety (obrázky ve stupních šedi)
9. Vykreslení ručně nakreslených číslic ve formě obrázků ve stupních šedi
10. Obrázky s jejich ohodnocením
11. Rozdělení plochy grafu do oblastí; vykreslení více obrázků do jediného grafu
15. Vykreslení obrázků společně s jejich klasifikací
16. Změna poměru rozdělení dat na tréninkovou a verifikační množinu
18. Repositář s demonstračními příklady
19. Seriály a články s relevantní tématikou vydané na Rootu
1. Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
Na stránkách Roota jsme se již v minulosti zabývali problematikou rozpoznávání rastrových obrazů. Pro tento účel jsme použili knihovnu nazvanou Torch (viz též příslušný seriál), s jejímž využitím jsme realizovali rozpoznávání obrázků pomocí ručně vytvořených neuronových sítí (včetně konvolučních sítí). Ovšem vývoj v této oblasti informatiky je velmi rychlý a dnes se v praxi setkáme spíše s knihovnami určenými pro použití společně s programovacím jazykem Python.

Obrázek 1: Logo projektu NumPy.
I z tohoto důvodu se dnes zaměříme na odlišné nástroje, konkrétně na Scikit-learn, jenž je navržen tak, aby velmi dobře kooperoval s knihovnami NumPy, Pandas (pravděpodobně i Polars), Xarray a Matplotlib. O těchto technologiích jsme si na stránkách Roota již psali (kromě samotného Scikit-learn), takže bude zajímavé zjistit, jak lze tyto nástroje a knihovny použít společně.

Obrázek 2: Logo projektu Pandas.
Ve stručnosti: Pandas či Polars (popř. Xarray) použijeme pro načítání vstupních dat a jejich prvotní filtraci, transformaci, popř. normalizaci. Matplotlib bude použit pro vizualizaci jak vstupních dat, tak i výsledků modelů. Knihovna Scikit-learn nabízí prakticky veškerou funkcionalitu při tvorbě modelů (ovšem například i clustering) a NumPy se používá interně, protože prakticky všechna data jsou uložena ve formě n-dimenzionálních polí.

Obrázek 3: Logo projektu Matplotlib.

Obrázek 4: Logo projektu Scikit-learn.
2. Řešený problém: rozpoznání ručně nakreslených číslic
V dnešním článku si – prozatím ovšem ve stručnosti – ukážeme jeden ze způsobů realizace rozpoznávání ručně nakreslených číslic. Naše řešení by mělo pro vstupní obrázek (z testovací nebo verifikační množiny) k tomuto obrázku přiřadit číslici 0 až 9, která byla na obrázku rozpoznána (a pro jednoduchost budeme zjišťovat přesnost tohoto přiřazení). Tyto číslice byly získány a digitalizovány v rámci projektu MNIST (Modified National Institute of Standards and Technology database). Tato databáze, která obsahuje 60000 trénovacích obrázků a 10000 testovacích obrázků, se používá pro testování různých algoritmů pro rozpoznání obrazů, což jsou dnes většinou algoritmy postavené na strojovém učení (ML – Machine Learning). Některé obrázky z této databáze jsou přímo součástí knihovny Scikit-learn, což náš problém zjednoduší – po instalaci všech knihoven již nebude nutné stahovat trénovací a testovací data (ovšem pochopitelně i tento problém je v praxi nutné řešit a proto se k tomu problému vrátíme).

Obrázek 5: Ručně nakreslené číslice, které byly po naskenování uloženy do databáze MNIST. Jen na okraj – povšimněte si, jaký tvar mají číslice 1 a 7. Jedná se o styl používaný ve „státech“, kde mohou být lidé zmateni, pokud číslici 1 zapíšete i s horní úhlopříčkou (což se mi stalo – a zrovna u čísla účtu :-). Poučením je, že trénovací množinu je nutné vybírat pečlivě a s ohledem na kontext použití.
3. Instalace všech potřebných balíčků
Nejdříve si nainstalujeme všechny potřebné balíčky a samozřejmě i jejich tranzitivní závislosti. Použijeme přitom nástroj PDM, který byl na Rootu již popsán. Ukažme si pro úplnost, jak by mohl vypadat výsledný projekt.
Nejprve si necháme vytvořit kostru nového projektu, a to konkrétně příkazem:
$ pdm init
Poctivě odpovíme na položené otázky (většinou jen potvrzením klávesou Enter):
Creating a pyproject.toml for PDM...
Please enter the Python interpreter to use
0. /usr/bin/python (3.11)
1. /usr/bin/python3.11 (3.11)
2. /usr/bin/python3 (3.11)
Please select (0): 0
Would you like to create a virtualenv with /usr/bin/python? [y/n] (y): Enter
Virtualenv is created successfully at /home/ptisnovs/test1/.venv
Is the project a library that is installable?
If yes, we will need to ask a few more questions to include the project name and
build backend [y/n] (n): Enter
License(SPDX name) (MIT): Enter
Author name (): Enter
Author email (): Enter
Python requires('*' to allow any) (>=3.11): Enter
Project is initialized successfully
Do projektu přidáme všechny potřebné závislosti příkazem pdm add balíček. Jedná se o numpy, matplotlib, sklearn a scikit-learn. Ovšem vývoj můžeme chtít provádět v Jupyter Notebooku, takže si nainstalujeme i balíček notebook. Výsledný projektový soubor pyproject.toml by měl vypadat zhruba následovně (konkrétní verze knihoven však mohou být o desetinky či setinky vyšší):
[project]
name = ""
version = ""
description = ""
authors = [
{name = "", email = ""},
]
dependencies = [
"notebook>=7.0.6",
"numpy>=1.25.2",
"matplotlib>=3.8.1",
"sklearn>=0.0.post11",
"scikit-learn>=1.3.2",
]
requires-python = ">=3.11"
readme = "README.md"
license = {text = "MIT"}
V praxi se (později) setkáme i s dalšími knihovnami, které je nutné mít nainstalovány. Jde o pomocný nástroj nbmerge (spojování notebooků) a taktéž o knihovny xarray, plotnine a seaborn. A takto může vypadat projektový soubor popisující všechny přímé závislosti:
[project]
name = ""
version = ""
description = ""
authors = [
{name = "", email = ""},
]
dependencies = [
"notebook>=7.0.6",
"nbmerge>=0.0.4",
"numpy>=1.25.2",
"matplotlib>=3.8.1",
"xarray>=2023.10.1",
"scipy>=1.9.3",
"plotnine>=0.12.4",
"seaborn>=0.13.0",
"sklearn>=0.0.post11",
"scikit-learn>=1.3.2",
]
requires-python = ">=3.11"
readme = "README.md"
license = {text = "MIT"}
4. Kooperace mezi knihovnami Matplotlib a NumPy: vizualizace obsahu 2D matice
Začněme jednoduchou a možná i triviální ukázkou kooperace mezi knihovnami Matplotlib a NumPy. Konkrétně si ukážeme vizualizaci obsahu dvourozměrné matice (NumPy podporuje obecná n-rozměrná pole a matice jsou tedy pouze podtypem). Vytvoříme si matici o rozměrech 10×10 prvků a naplníme ji náhodnými hodnotami. Výsledek si necháme zobrazit na grafu a tento graf taktéž uložíme do souboru (formát PNG):
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
import numpy as np
# vytvoření matice, kterou budeme vizualizovat
array = np.random.rand(10, 10)
# vykreslení
plt.matshow(array)
# uložení vizualizované matice
plt.savefig("random.png")
# vizualizace na obrazovku
plt.show()
# finito
Výsledek bude vypadat následovně:
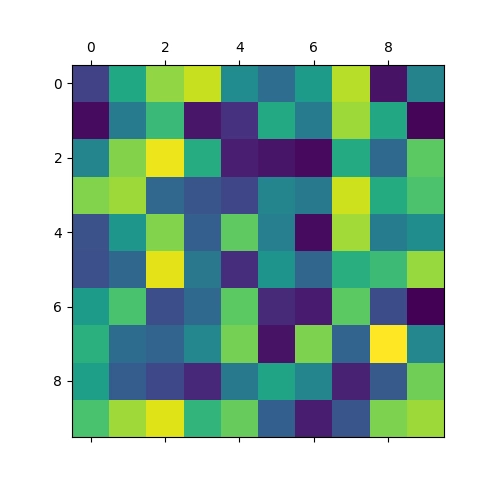
Obrázek 6: Vizualizace pole s náhodným obsahem.
Povšimněte si, že se při vizualizaci použily nepravé barvy. Těch se později zbavíme, protože nás budou spíše mást.
5. Datová množina obsahující naskenované ručně napsané číslice
Víme již, že trénovací i testovací (či verifikační) množina s ručně nakreslenými obrázky je součástí balíčku Scikit-learn. Přečíst ji můžeme funkcí load_digits z podbalíčku sklearn.datasets. Výsledkem je datová struktura s metadaty, vektory s obrázkem (viz další text) i maticemi představujícími obrázky. V dalším skriptu si ukážeme, jak lze některá vrácená metadata a data zpracovat:
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits_data.DESCR)
print("Data:", digits_data.data.shape)
print("Obrázky:", digits_data.images.shape)
# výpis informací o obrázcích
for i in range(0, 10):
print(f"Image #{i}:")
print("Data:\n", digits_data.data[i])
print("Image:\n", digits_data.images[i])
print("Target:\n", digits_data.target[i])
print()
# finito
Nejprve si necháme zobrazit popis dat a metadat – atribut DESCR:
Description: .. _digits_dataset:
Optical recognition of handwritten digits dataset
--------------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 1797
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
|details-start|
**References**
|details-split|
- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
Graduate Studies in Science and Engineering, Bogazici University.
- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
Linear dimensionalityreduction using relevance weighted LDA. School of
Electrical and Electronic Engineering Nanyang Technological University.
2005.
- Claudio Gentile. A New Approximate Maximal Margin Classification
Algorithm. NIPS. 2000.
|details-end|
Dále jsou zobrazeny rozměry (resp. tvar) n-rozměrných polí uložených v atributech data a images:
Data: (1797, 64) Obrázky: (1797, 8, 8)
Vidíme, že se vlastně (jedna z možných interpretací) jedná o 1797 64prvkových vektorů, resp. o 1797 dvourozměrných matic 8×8 prvků.
Dále si necháme zobrazit prvních 10 vektorů i prvních 10 dvourozměrných matic:
Image #0: Data: [ 0. 0. 5. 13. 9. 1. 0. 0. 0. 0. 13. 15. 10. 15. 5. 0. 0. 3. 15. 2. 0. 11. 8. 0. 0. 4. 12. 0. 0. 8. 8. 0. 0. 5. 8. 0. 0. 9. 8. 0. 0. 4. 11. 0. 1. 12. 7. 0. 0. 2. 14. 5. 10. 12. 0. 0. 0. 0. 6. 13. 10. 0. 0. 0.] Image: [[ 0. 0. 5. 13. 9. 1. 0. 0.] [ 0. 0. 13. 15. 10. 15. 5. 0.] [ 0. 3. 15. 2. 0. 11. 8. 0.] [ 0. 4. 12. 0. 0. 8. 8. 0.] [ 0. 5. 8. 0. 0. 9. 8. 0.] [ 0. 4. 11. 0. 1. 12. 7. 0.] [ 0. 2. 14. 5. 10. 12. 0. 0.] [ 0. 0. 6. 13. 10. 0. 0. 0.]] Target: 0 Image #1: Data: [ 0. 0. 0. 12. 13. 5. 0. 0. 0. 0. 0. 11. 16. 9. 0. 0. 0. 0. 3. 15. 16. 6. 0. 0. 0. 7. 15. 16. 16. 2. 0. 0. 0. 0. 1. 16. 16. 3. 0. 0. 0. 0. 1. 16. 16. 6. 0. 0. 0. 0. 1. 16. 16. 6. 0. 0. 0. 0. 0. 11. 16. 10. 0. 0.] Image: [[ 0. 0. 0. 12. 13. 5. 0. 0.] [ 0. 0. 0. 11. 16. 9. 0. 0.] [ 0. 0. 3. 15. 16. 6. 0. 0.] [ 0. 7. 15. 16. 16. 2. 0. 0.] [ 0. 0. 1. 16. 16. 3. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 0. 11. 16. 10. 0. 0.]] Target: 1 Image #2: Data: [ 0. 0. 0. 4. 15. 12. 0. 0. 0. 0. 3. 16. 15. 14. 0. 0. 0. 0. 8. 13. 8. 16. 0. 0. 0. 0. 1. 6. 15. 11. 0. 0. 0. 1. 8. 13. 15. 1. 0. 0. 0. 9. 16. 16. 5. 0. 0. 0. 0. 3. 13. 16. 16. 11. 5. 0. 0. 0. 0. 3. 11. 16. 9. 0.] Image: [[ 0. 0. 0. 4. 15. 12. 0. 0.] [ 0. 0. 3. 16. 15. 14. 0. 0.] [ 0. 0. 8. 13. 8. 16. 0. 0.] [ 0. 0. 1. 6. 15. 11. 0. 0.] [ 0. 1. 8. 13. 15. 1. 0. 0.] [ 0. 9. 16. 16. 5. 0. 0. 0.] [ 0. 3. 13. 16. 16. 11. 5. 0.] [ 0. 0. 0. 3. 11. 16. 9. 0.]] Target: 2 Image #3: Data: [ 0. 0. 7. 15. 13. 1. 0. 0. 0. 8. 13. 6. 15. 4. 0. 0. 0. 2. 1. 13. 13. 0. 0. 0. 0. 0. 2. 15. 11. 1. 0. 0. 0. 0. 0. 1. 12. 12. 1. 0. 0. 0. 0. 0. 1. 10. 8. 0. 0. 0. 8. 4. 5. 14. 9. 0. 0. 0. 7. 13. 13. 9. 0. 0.] Image: [[ 0. 0. 7. 15. 13. 1. 0. 0.] [ 0. 8. 13. 6. 15. 4. 0. 0.] [ 0. 2. 1. 13. 13. 0. 0. 0.] [ 0. 0. 2. 15. 11. 1. 0. 0.] [ 0. 0. 0. 1. 12. 12. 1. 0.] [ 0. 0. 0. 0. 1. 10. 8. 0.] [ 0. 0. 8. 4. 5. 14. 9. 0.] [ 0. 0. 7. 13. 13. 9. 0. 0.]] Target: 3 Image #4: Data: [ 0. 0. 0. 1. 11. 0. 0. 0. 0. 0. 0. 7. 8. 0. 0. 0. 0. 0. 1. 13. 6. 2. 2. 0. 0. 0. 7. 15. 0. 9. 8. 0. 0. 5. 16. 10. 0. 16. 6. 0. 0. 4. 15. 16. 13. 16. 1. 0. 0. 0. 0. 3. 15. 10. 0. 0. 0. 0. 0. 2. 16. 4. 0. 0.] Image: [[ 0. 0. 0. 1. 11. 0. 0. 0.] [ 0. 0. 0. 7. 8. 0. 0. 0.] [ 0. 0. 1. 13. 6. 2. 2. 0.] [ 0. 0. 7. 15. 0. 9. 8. 0.] [ 0. 5. 16. 10. 0. 16. 6. 0.] [ 0. 4. 15. 16. 13. 16. 1. 0.] [ 0. 0. 0. 3. 15. 10. 0. 0.] [ 0. 0. 0. 2. 16. 4. 0. 0.]] Target: 4 Image #5: Data: [ 0. 0. 12. 10. 0. 0. 0. 0. 0. 0. 14. 16. 16. 14. 0. 0. 0. 0. 13. 16. 15. 10. 1. 0. 0. 0. 11. 16. 16. 7. 0. 0. 0. 0. 0. 4. 7. 16. 7. 0. 0. 0. 0. 0. 4. 16. 9. 0. 0. 0. 5. 4. 12. 16. 4. 0. 0. 0. 9. 16. 16. 10. 0. 0.] Image: [[ 0. 0. 12. 10. 0. 0. 0. 0.] [ 0. 0. 14. 16. 16. 14. 0. 0.] [ 0. 0. 13. 16. 15. 10. 1. 0.] [ 0. 0. 11. 16. 16. 7. 0. 0.] [ 0. 0. 0. 4. 7. 16. 7. 0.] [ 0. 0. 0. 0. 4. 16. 9. 0.] [ 0. 0. 5. 4. 12. 16. 4. 0.] [ 0. 0. 9. 16. 16. 10. 0. 0.]] Target: 5 Image #6: Data: [ 0. 0. 0. 12. 13. 0. 0. 0. 0. 0. 5. 16. 8. 0. 0. 0. 0. 0. 13. 16. 3. 0. 0. 0. 0. 0. 14. 13. 0. 0. 0. 0. 0. 0. 15. 12. 7. 2. 0. 0. 0. 0. 13. 16. 13. 16. 3. 0. 0. 0. 7. 16. 11. 15. 8. 0. 0. 0. 1. 9. 15. 11. 3. 0.] Image: [[ 0. 0. 0. 12. 13. 0. 0. 0.] [ 0. 0. 5. 16. 8. 0. 0. 0.] [ 0. 0. 13. 16. 3. 0. 0. 0.] [ 0. 0. 14. 13. 0. 0. 0. 0.] [ 0. 0. 15. 12. 7. 2. 0. 0.] [ 0. 0. 13. 16. 13. 16. 3. 0.] [ 0. 0. 7. 16. 11. 15. 8. 0.] [ 0. 0. 1. 9. 15. 11. 3. 0.]] Target: 6 Image #7: Data: [ 0. 0. 7. 8. 13. 16. 15. 1. 0. 0. 7. 7. 4. 11. 12. 0. 0. 0. 0. 0. 8. 13. 1. 0. 0. 4. 8. 8. 15. 15. 6. 0. 0. 2. 11. 15. 15. 4. 0. 0. 0. 0. 0. 16. 5. 0. 0. 0. 0. 0. 9. 15. 1. 0. 0. 0. 0. 0. 13. 5. 0. 0. 0. 0.] Image: [[ 0. 0. 7. 8. 13. 16. 15. 1.] [ 0. 0. 7. 7. 4. 11. 12. 0.] [ 0. 0. 0. 0. 8. 13. 1. 0.] [ 0. 4. 8. 8. 15. 15. 6. 0.] [ 0. 2. 11. 15. 15. 4. 0. 0.] [ 0. 0. 0. 16. 5. 0. 0. 0.] [ 0. 0. 9. 15. 1. 0. 0. 0.] [ 0. 0. 13. 5. 0. 0. 0. 0.]] Target: 7 Image #8: Data: [ 0. 0. 9. 14. 8. 1. 0. 0. 0. 0. 12. 14. 14. 12. 0. 0. 0. 0. 9. 10. 0. 15. 4. 0. 0. 0. 3. 16. 12. 14. 2. 0. 0. 0. 4. 16. 16. 2. 0. 0. 0. 3. 16. 8. 10. 13. 2. 0. 0. 1. 15. 1. 3. 16. 8. 0. 0. 0. 11. 16. 15. 11. 1. 0.] Image: [[ 0. 0. 9. 14. 8. 1. 0. 0.] [ 0. 0. 12. 14. 14. 12. 0. 0.] [ 0. 0. 9. 10. 0. 15. 4. 0.] [ 0. 0. 3. 16. 12. 14. 2. 0.] [ 0. 0. 4. 16. 16. 2. 0. 0.] [ 0. 3. 16. 8. 10. 13. 2. 0.] [ 0. 1. 15. 1. 3. 16. 8. 0.] [ 0. 0. 11. 16. 15. 11. 1. 0.]] Target: 8 Image #9: Data: [ 0. 0. 11. 12. 0. 0. 0. 0. 0. 2. 16. 16. 16. 13. 0. 0. 0. 3. 16. 12. 10. 14. 0. 0. 0. 1. 16. 1. 12. 15. 0. 0. 0. 0. 13. 16. 9. 15. 2. 0. 0. 0. 0. 3. 0. 9. 11. 0. 0. 0. 0. 0. 9. 15. 4. 0. 0. 0. 9. 12. 13. 3. 0. 0.] Image: [[ 0. 0. 11. 12. 0. 0. 0. 0.] [ 0. 2. 16. 16. 16. 13. 0. 0.] [ 0. 3. 16. 12. 10. 14. 0. 0.] [ 0. 1. 16. 1. 12. 15. 0. 0.] [ 0. 0. 13. 16. 9. 15. 2. 0.] [ 0. 0. 0. 3. 0. 9. 11. 0.] [ 0. 0. 0. 0. 9. 15. 4. 0.] [ 0. 0. 9. 12. 13. 3. 0. 0.]] Target: 9
Ve výpisu se objevuje i atribut nazvaný target. Je to výsledná hodnota, na kterou by měl být natrénován model.
6. Další atributy datové množiny, které použijeme při trénování
V datové množině získané zavoláním funkce load_digits() nalezneme i další potenciálně užitečné informace. Jedná se o názvy sloupců v případě, že budeme pole uložené v atributu data chápat jako tabulku (v tomto konkrétním případě o tabulku s 1797 řádky a 64 sloupci). Názvy sloupců takového pole jsou uloženy v atributu feature_names. A konečně v atributu target_names nalezneme jména tříd, které dohromady představují obor hodnot pro hodnoty target (tedy pro hodnoty, na které budeme model trénovat):
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits_data.DESCR)
print("Data:", digits_data.data.shape)
print("Obrázky:", digits_data.images.shape)
print("Feature names")
for feature_name in digits_data.feature_names:
print(feature_name)
print()
print("Target names")
for target_name in digits_data.target_names:
print(target_name)
# finito
Po spuštění tohoto skriptu se nejprve opět vypíšou informace o dvou n-rozměrných polích s trénovacími a verifikačními daty:
Data: (1797, 64) Obrázky: (1797, 8, 8)
Dále se vypíšou názvy všech 64 sloupců pole data. Zde se prozrazuje to, co již vlastně víme z předchozí kapitoly – že v tomto poli jsou uloženy vektory s 64 hodnotami pixelů, které tvoří logický obrázek 8×8 pixelů:
Feature names pixel_0_0 pixel_0_1 pixel_0_2 pixel_0_3 pixel_0_4 pixel_0_5 pixel_0_6 pixel_0_7 pixel_1_0 pixel_1_1 pixel_1_2 pixel_1_3 pixel_1_4 pixel_1_5 pixel_1_6 pixel_1_7 pixel_2_0 pixel_2_1 pixel_2_2 pixel_2_3 pixel_2_4 pixel_2_5 pixel_2_6 pixel_2_7 pixel_3_0 pixel_3_1 pixel_3_2 pixel_3_3 pixel_3_4 pixel_3_5 pixel_3_6 pixel_3_7 pixel_4_0 pixel_4_1 pixel_4_2 pixel_4_3 pixel_4_4 pixel_4_5 pixel_4_6 pixel_4_7 pixel_5_0 pixel_5_1 pixel_5_2 pixel_5_3 pixel_5_4 pixel_5_5 pixel_5_6 pixel_5_7 pixel_6_0 pixel_6_1 pixel_6_2 pixel_6_3 pixel_6_4 pixel_6_5 pixel_6_6 pixel_6_7 pixel_7_0 pixel_7_1 pixel_7_2 pixel_7_3 pixel_7_4 pixel_7_5 pixel_7_6 pixel_7_7
Obsah pole target_names obsahuje u této datové množiny hodnoty „0“ až „9“, ovšem u jiných množin se může jednat o zcela odlišné informace (například „zapni kotel“/„vyplni kotel“, „před autem je chodec“ atd.):
Target names 0 1 2 3 4 5 6 7 8 9
7. Přečtení a následné vykreslení jednotlivých ručně nakreslených číslic
V datové množině, kterou dokážeme přečíst funkcí load_digits, nalezneme (jak již víme) i atribut nazvaný images. Jedná se o n-rozměrné pole, konkrétně o trojrozměrné pole s velikostí 1797×8×8. Toto pole obsahuje 1797 matic velikosti 8×8 reprezentujících malé rastrové obrázky 8×8 pixelů, jejichž hodnoty jsou normalizovány do rozsahu 0..16 (to je důležité pro trénink modelu). Takové obrázky lze snadno zobrazit metodou, kterou jsme si již popsali ve čtvrté kapitole. Podívejme se tedy, co je vlastně uloženo v prvních deseti obrázcích z datové množiny:
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print(digits_data.data.shape)
# vykreslení a uložení prvních deseti obrázků
for i in range(0, 10):
plt.matshow(digits_data.images[i])
plt.savefig(f"Image #{i}.png")
plt.show()
# finito
Výsledkem by mělo být následujících deset grafů s vizualizací ručně psaných číslic 0 až 9 (nepoužíváme zde přitom žádnou interpolaci ani žádné další „vylepšení“ výsledků, které by mohl mozek špatně interpretovat):
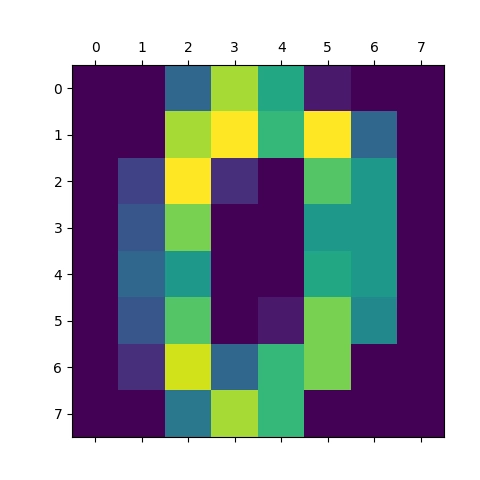
Obrázek 7: Vizualizace pole s číslicí 0.
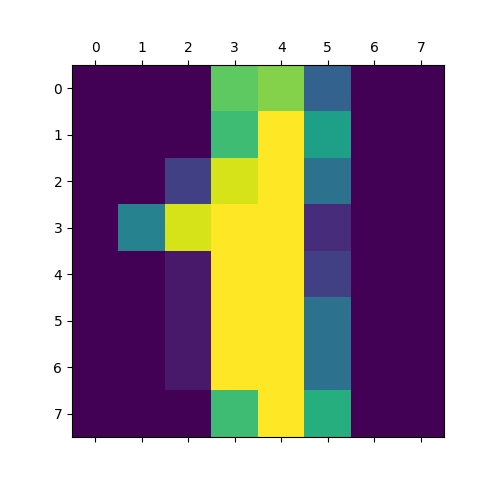
Obrázek 8: Vizualizace pole s číslicí 1.
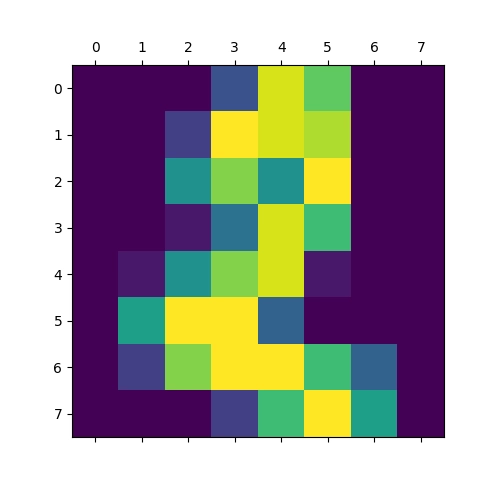
Obrázek 9: Vizualizace pole s číslicí 2.
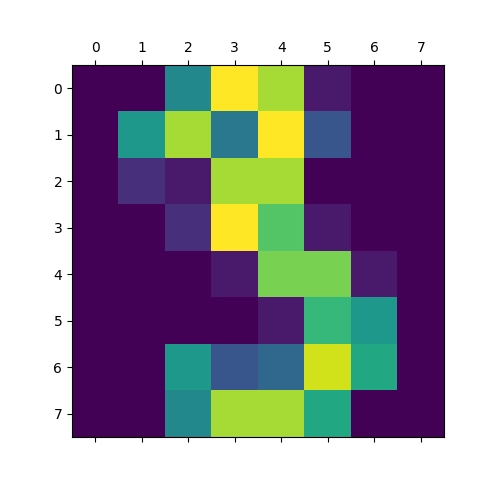
Obrázek 10: Vizualizace pole s číslicí 3.
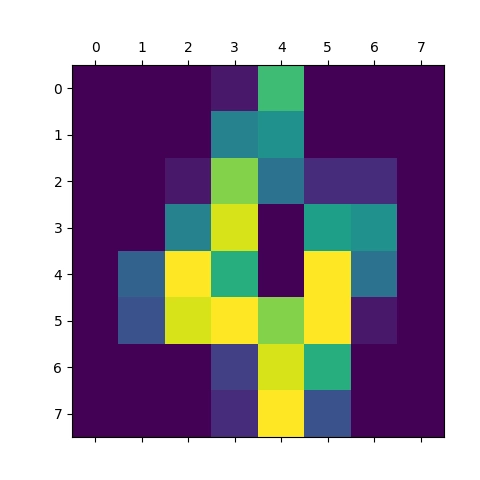
Obrázek 11: Vizualizace pole s číslicí 4.
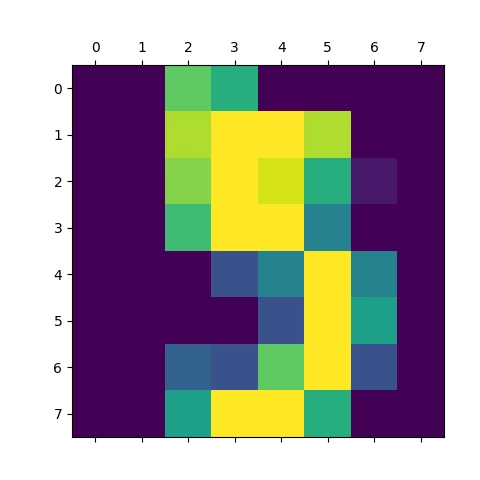
Obrázek 12: Vizualizace pole s číslicí 5.
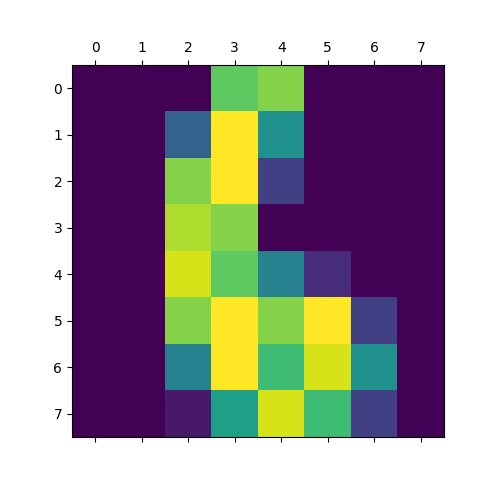
Obrázek 13: Vizualizace pole s číslicí 6.
Obrázek 14: Vizualizace pole s číslicí 7.
Obrázek 15: Vizualizace pole s číslicí 8.
Obrázek 16: Vizualizace pole s číslicí 9.
8. Odstranění umělé aplikované barvové palety (obrázky ve stupních šedi)
Vraťme se nyní na okamžik k příkladu uvedeném ve čtvrté kapitole. Tam jsme si ukázali zobrazení obsahu matice ve formě grafu, ovšem knihovna Matplotlib v takovém případě použila nepravé barvy. Ty jsou někdy vhodné, ovšem zrovna v případě naskenovaných obrázků spíše matoucí. Z tohoto důvodu si ukažme, jak lze graf vykreslit ve stupních šedi. Jedno z možných řešení vypadá následovně:
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
import numpy as np
# vytvoření matice, kterou budeme vizualizovat
array = np.random.rand(10, 10)
# vykreslení
plt.matshow(array)
# použití stupňů šedi
plt.gray()
# uložení vizualizované matice
plt.savefig("random_grayscale.png")
# vizualizace na obrazovku
plt.show()
# finito
Výsledek bude po této malé úpravě vypadat následovně:
Obrázek 17: Vizualizace pole s náhodným obsahem při použití stupňů šedi.
9. Vykreslení ručně nakreslených číslic ve formě obrázků ve stupních šedi
Stejný princip, tj. zavolání plt.gray() samozřejmě můžeme využít i pro vykreslení číslic vzniklých naskenováním. Skript pro jejich načtení a vykreslení tedy nepatrně upravíme:
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print(digits_data.data.shape)
# vykreslení a uložení prvních deseti obrázků
for i in range(0, 10):
plt.matshow(digits_data.images[i])
# převod na stupně šedi
plt.gray()
plt.savefig(f"Grayscale image #{i}.png")
# vykreslení na obrazovku
plt.show()
# finito
A takto vypadají výsledky:
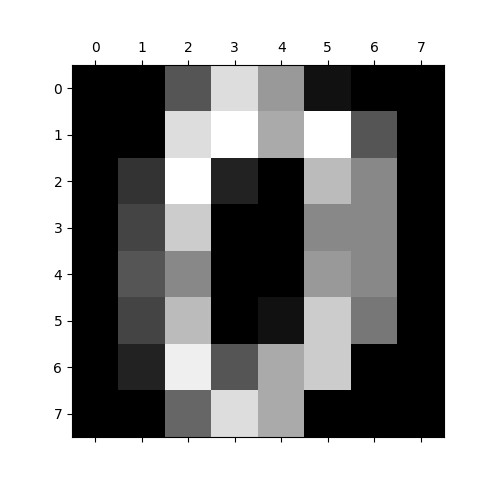
Obrázek 18: Vizualizace pole s číslicí 0 ve stupních šedi.
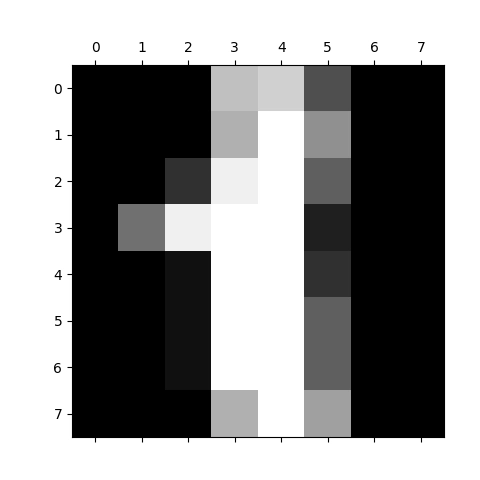
Obrázek 19: Vizualizace pole s číslicí 1 ve stupních šedi.
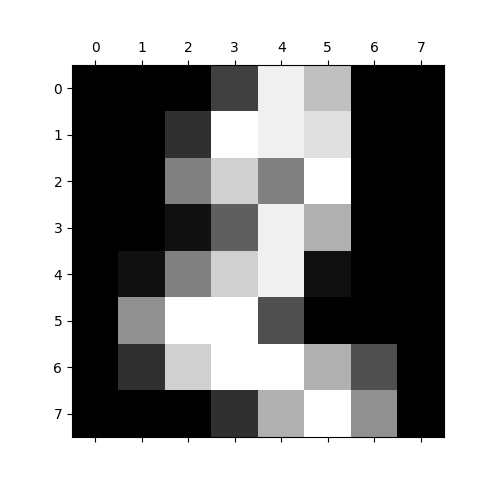
Obrázek 20: Vizualizace pole s číslicí 2 ve stupních šedi.
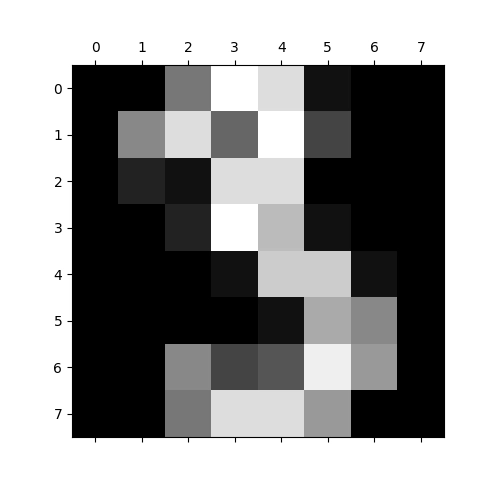
Obrázek 21: Vizualizace pole s číslicí 3 ve stupních šedi.
Obrázek 22: Vizualizace pole s číslicí 4 ve stupních šedi.
Obrázek 23: Vizualizace pole s číslicí 5 ve stupních šedi.
Obrázek 24: Vizualizace pole s číslicí 6 ve stupních šedi.
Obrázek 25: Vizualizace pole s číslicí 7 ve stupních šedi.
Obrázek 26: Vizualizace pole s číslicí 8 ve stupních šedi.
Obrázek 27: Vizualizace pole s číslicí 9 ve stupních šedi.
Pokud preferujete, aby se použilo inverzní zobrazení (tedy bílý papír a černé číslice), lze odstranit volání plt.gray() a namísto toho číslice vykreslit s explicitní specifikací barvové palety (gray_r = stupně šedi, ovšem obrácené, „reversed“):
plt.matshow(digits_data.images[i], cmap=plt.cm.gray_r)
10. Obrázky s jejich ohodnocením
Nyní, když již víme, jak využijeme knihovnu Matplotlib i jak načteme množinu trénovacích a testovacích nebo verifikačních dat, se znovu podívejme na atribut targets, jenž obsahuje hodnoty přiřazené ke všem obrázkům. Pro náš konkrétní případ je touto hodnotou pouze informace o číslici (0–9), která má být v obrázku uložena. Model, který vytvoříme v navazujících krocích, bude trénován právě tak, aby pro daný vstupní obrázek (nebo obrázek podobný) vrátil právě hodnotu, která je uložena v targets. Pro trénovací množinu budeme modelu konkrétní předpověď předávat (na čem jiném by se model mohl učit?) a pro testovací množinu naopak nikoli (je úkolem modelu nám vrátit, o jakou číslici se jedná):
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# vytvoření seznamu, které použijeme
images = list(zip(digits_data.target, digits_data.images))
# nebudeme vypisovat tisíce údajů - postačí prvních dvacet
shortened = images[:20]
# výpis dat použitých pro tvorbu modelu
for i, (label, image) in enumerate(shortened):
print(f"i={i} label={label}\n", image, "\n")
# finito
Zatímco i obsahuje jen počitadlo smyčky, je v label uložena konkrétní číslice reprezentovaná obrázkem (nikde totiž není zaručeno, že obrázky budou uspořádány v pořadí 0, 1, 2, … 9, 0, 1, 2):
i=0 label=0 [[ 0. 0. 5. 13. 9. 1. 0. 0.] [ 0. 0. 13. 15. 10. 15. 5. 0.] [ 0. 3. 15. 2. 0. 11. 8. 0.] [ 0. 4. 12. 0. 0. 8. 8. 0.] [ 0. 5. 8. 0. 0. 9. 8. 0.] [ 0. 4. 11. 0. 1. 12. 7. 0.] [ 0. 2. 14. 5. 10. 12. 0. 0.] [ 0. 0. 6. 13. 10. 0. 0. 0.]] i=1 label=1 [[ 0. 0. 0. 12. 13. 5. 0. 0.] [ 0. 0. 0. 11. 16. 9. 0. 0.] [ 0. 0. 3. 15. 16. 6. 0. 0.] [ 0. 7. 15. 16. 16. 2. 0. 0.] [ 0. 0. 1. 16. 16. 3. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 0. 11. 16. 10. 0. 0.]] i=2 label=2 [[ 0. 0. 0. 4. 15. 12. 0. 0.] [ 0. 0. 3. 16. 15. 14. 0. 0.] [ 0. 0. 8. 13. 8. 16. 0. 0.] [ 0. 0. 1. 6. 15. 11. 0. 0.] [ 0. 1. 8. 13. 15. 1. 0. 0.] [ 0. 9. 16. 16. 5. 0. 0. 0.] [ 0. 3. 13. 16. 16. 11. 5. 0.] [ 0. 0. 0. 3. 11. 16. 9. 0.]] i=3 label=3 [[ 0. 0. 7. 15. 13. 1. 0. 0.] [ 0. 8. 13. 6. 15. 4. 0. 0.] [ 0. 2. 1. 13. 13. 0. 0. 0.] [ 0. 0. 2. 15. 11. 1. 0. 0.] [ 0. 0. 0. 1. 12. 12. 1. 0.] [ 0. 0. 0. 0. 1. 10. 8. 0.] [ 0. 0. 8. 4. 5. 14. 9. 0.] [ 0. 0. 7. 13. 13. 9. 0. 0.]] i=4 label=4 [[ 0. 0. 0. 1. 11. 0. 0. 0.] [ 0. 0. 0. 7. 8. 0. 0. 0.] [ 0. 0. 1. 13. 6. 2. 2. 0.] [ 0. 0. 7. 15. 0. 9. 8. 0.] [ 0. 5. 16. 10. 0. 16. 6. 0.] [ 0. 4. 15. 16. 13. 16. 1. 0.] [ 0. 0. 0. 3. 15. 10. 0. 0.] [ 0. 0. 0. 2. 16. 4. 0. 0.]] i=5 label=5 [[ 0. 0. 12. 10. 0. 0. 0. 0.] [ 0. 0. 14. 16. 16. 14. 0. 0.] [ 0. 0. 13. 16. 15. 10. 1. 0.] [ 0. 0. 11. 16. 16. 7. 0. 0.] [ 0. 0. 0. 4. 7. 16. 7. 0.] [ 0. 0. 0. 0. 4. 16. 9. 0.] [ 0. 0. 5. 4. 12. 16. 4. 0.] [ 0. 0. 9. 16. 16. 10. 0. 0.]] i=6 label=6 [[ 0. 0. 0. 12. 13. 0. 0. 0.] [ 0. 0. 5. 16. 8. 0. 0. 0.] [ 0. 0. 13. 16. 3. 0. 0. 0.] [ 0. 0. 14. 13. 0. 0. 0. 0.] [ 0. 0. 15. 12. 7. 2. 0. 0.] [ 0. 0. 13. 16. 13. 16. 3. 0.] [ 0. 0. 7. 16. 11. 15. 8. 0.] [ 0. 0. 1. 9. 15. 11. 3. 0.]] i=7 label=7 [[ 0. 0. 7. 8. 13. 16. 15. 1.] [ 0. 0. 7. 7. 4. 11. 12. 0.] [ 0. 0. 0. 0. 8. 13. 1. 0.] [ 0. 4. 8. 8. 15. 15. 6. 0.] [ 0. 2. 11. 15. 15. 4. 0. 0.] [ 0. 0. 0. 16. 5. 0. 0. 0.] [ 0. 0. 9. 15. 1. 0. 0. 0.] [ 0. 0. 13. 5. 0. 0. 0. 0.]] i=8 label=8 [[ 0. 0. 9. 14. 8. 1. 0. 0.] [ 0. 0. 12. 14. 14. 12. 0. 0.] [ 0. 0. 9. 10. 0. 15. 4. 0.] [ 0. 0. 3. 16. 12. 14. 2. 0.] [ 0. 0. 4. 16. 16. 2. 0. 0.] [ 0. 3. 16. 8. 10. 13. 2. 0.] [ 0. 1. 15. 1. 3. 16. 8. 0.] [ 0. 0. 11. 16. 15. 11. 1. 0.]] i=9 label=9 [[ 0. 0. 11. 12. 0. 0. 0. 0.] [ 0. 2. 16. 16. 16. 13. 0. 0.] [ 0. 3. 16. 12. 10. 14. 0. 0.] [ 0. 1. 16. 1. 12. 15. 0. 0.] [ 0. 0. 13. 16. 9. 15. 2. 0.] [ 0. 0. 0. 3. 0. 9. 11. 0.] [ 0. 0. 0. 0. 9. 15. 4. 0.] [ 0. 0. 9. 12. 13. 3. 0. 0.]] i=10 label=0 [[ 0. 0. 1. 9. 15. 11. 0. 0.] [ 0. 0. 11. 16. 8. 14. 6. 0.] [ 0. 2. 16. 10. 0. 9. 9. 0.] [ 0. 1. 16. 4. 0. 8. 8. 0.] [ 0. 4. 16. 4. 0. 8. 8. 0.] [ 0. 1. 16. 5. 1. 11. 3. 0.] [ 0. 0. 12. 12. 10. 10. 0. 0.] [ 0. 0. 1. 10. 13. 3. 0. 0.]] i=11 label=1 [[ 0. 0. 0. 0. 14. 13. 1. 0.] [ 0. 0. 0. 5. 16. 16. 2. 0.] [ 0. 0. 0. 14. 16. 12. 0. 0.] [ 0. 1. 10. 16. 16. 12. 0. 0.] [ 0. 3. 12. 14. 16. 9. 0. 0.] [ 0. 0. 0. 5. 16. 15. 0. 0.] [ 0. 0. 0. 4. 16. 14. 0. 0.] [ 0. 0. 0. 1. 13. 16. 1. 0.]] i=12 label=2 [[ 0. 0. 5. 12. 1. 0. 0. 0.] [ 0. 0. 15. 14. 7. 0. 0. 0.] [ 0. 0. 13. 1. 12. 0. 0. 0.] [ 0. 2. 10. 0. 14. 0. 0. 0.] [ 0. 0. 2. 0. 16. 1. 0. 0.] [ 0. 0. 0. 6. 15. 0. 0. 0.] [ 0. 0. 9. 16. 15. 9. 8. 2.] [ 0. 0. 3. 11. 8. 13. 12. 4.]] i=13 label=3 [[ 0. 2. 9. 15. 14. 9. 3. 0.] [ 0. 4. 13. 8. 9. 16. 8. 0.] [ 0. 0. 0. 6. 14. 15. 3. 0.] [ 0. 0. 0. 11. 14. 2. 0. 0.] [ 0. 0. 0. 2. 15. 11. 0. 0.] [ 0. 0. 0. 0. 2. 15. 4. 0.] [ 0. 1. 5. 6. 13. 16. 6. 0.] [ 0. 2. 12. 12. 13. 11. 0. 0.]] i=14 label=4 [[ 0. 0. 0. 8. 15. 1. 0. 0.] [ 0. 0. 1. 14. 13. 1. 1. 0.] [ 0. 0. 10. 15. 3. 15. 11. 0.] [ 0. 7. 16. 7. 1. 16. 8. 0.] [ 0. 9. 16. 13. 14. 16. 5. 0.] [ 0. 1. 10. 15. 16. 14. 0. 0.] [ 0. 0. 0. 1. 16. 10. 0. 0.] [ 0. 0. 0. 10. 15. 4. 0. 0.]] i=15 label=5 [[ 0. 5. 12. 13. 16. 16. 2. 0.] [ 0. 11. 16. 15. 8. 4. 0. 0.] [ 0. 8. 14. 11. 1. 0. 0. 0.] [ 0. 8. 16. 16. 14. 0. 0. 0.] [ 0. 1. 6. 6. 16. 0. 0. 0.] [ 0. 0. 0. 5. 16. 3. 0. 0.] [ 0. 1. 5. 15. 13. 0. 0. 0.] [ 0. 4. 15. 16. 2. 0. 0. 0.]] i=16 label=6 [[ 0. 0. 0. 8. 15. 1. 0. 0.] [ 0. 0. 0. 12. 14. 0. 0. 0.] [ 0. 0. 3. 16. 7. 0. 0. 0.] [ 0. 0. 6. 16. 2. 0. 0. 0.] [ 0. 0. 7. 16. 16. 13. 5. 0.] [ 0. 0. 15. 16. 9. 9. 14. 0.] [ 0. 0. 3. 14. 9. 2. 16. 2.] [ 0. 0. 0. 7. 15. 16. 11. 0.]] i=17 label=7 [[ 0. 0. 1. 8. 15. 10. 0. 0.] [ 0. 3. 13. 15. 14. 14. 0. 0.] [ 0. 5. 10. 0. 10. 12. 0. 0.] [ 0. 0. 3. 5. 15. 10. 2. 0.] [ 0. 0. 16. 16. 16. 16. 12. 0.] [ 0. 1. 8. 12. 14. 8. 3. 0.] [ 0. 0. 0. 10. 13. 0. 0. 0.] [ 0. 0. 0. 11. 9. 0. 0. 0.]] i=18 label=8 [[ 0. 0. 10. 7. 13. 9. 0. 0.] [ 0. 0. 9. 10. 12. 15. 2. 0.] [ 0. 0. 4. 11. 10. 11. 0. 0.] [ 0. 0. 1. 16. 10. 1. 0. 0.] [ 0. 0. 12. 13. 4. 0. 0. 0.] [ 0. 0. 12. 1. 12. 0. 0. 0.] [ 0. 1. 10. 2. 14. 0. 0. 0.] [ 0. 0. 11. 14. 5. 0. 0. 0.]] i=19 label=9 [[ 0. 0. 6. 14. 4. 0. 0. 0.] [ 0. 0. 11. 16. 10. 0. 0. 0.] [ 0. 0. 8. 14. 16. 2. 0. 0.] [ 0. 0. 1. 12. 12. 11. 0. 0.] [ 0. 0. 0. 0. 0. 11. 3. 0.] [ 0. 0. 0. 0. 0. 5. 11. 0.] [ 0. 0. 1. 4. 4. 7. 16. 2.] [ 0. 0. 7. 16. 16. 13. 11. 1.]]
11. Rozdělení plochy grafu do oblastí; vykreslení více obrázků do jediného grafu
V praxi budeme při analýze a/nebo rozpoznávání obrazů chtít zobrazit velké množství různých obrázků (a to nikoli pod sebou – ideální je využít celou plochu monitoru). Knihovna Matplotlib nám v tomto případě nabízí poměrně elegantní řešení, které je založeno na tom, že se větší množství obrázků vloží do jediného grafu do pomyslné mřížky. Ve skutečnosti se nejedná o nijak přelomové řešení, protože je používáno již delší dobu například knihovnou Lattice určené pro programovací jazyk R nebo knihovnou ggplot pro Python.
Pro tento účel použijeme příkaz subplot, kterému se předá jak velikost pomyslné mřížky, tak i (jednorozměrný) index buňky mřížky, do které se má vykreslit následující graf. Řešení je tedy v praxi poměrně jednoduché, což je ukázáno na následujícím kódu, který vytvoří a vykreslí graf s celkem 5×3 obrázky (povšimněte si, že každému grafu navíc můžeme přiřadit i titulek):
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# vytvoření seznamu, které použijeme
images = list(zip(digits_data.target, digits_data.images))
# vykreslení tréninkových číslic
for i, (label, image) in enumerate(images[:15]):
plt.subplot(3, 5, i+1)
plt.imshow(image, cmap=plt.cm.gray_r) #, interpolation='nearest')
plt.title(f"číslice {label}")
# uložení a vykreslení výsledku
plt.savefig("training_set.png")
plt.show()
# finito
Výsledek může vypadat takto:

Obrázek 28: Prvních patnáct číslic, které použijeme pro trénink modelu.
12. Příprava dat pro trénink
Pro trénink modelu je nutné použít nějakou část ze vstupní množiny obrázků. Pro jednoduchost se v první iteraci pokusíme o použití první poloviny obrázků pro trénink a druhé polovinu obrázků pro validaci modelu. Toto rozdělení je v praxi snadné, protože knihovna NumPy podporuje (přetěžuje) operátor indexování i operátor výběru řezu z nějaké kolekce. Ostatně způsob získání obrázků a jejich ohodnocení pro testování je ukázán na dalším demonstračním příkladu:
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# celkový počet vzorků
samples = len(digits_data.images)
print("Vzorků celkem:", samples)
# počet vzorků pro trénink
for_training = samples // 2
print("Vzorků pro trénink:", for_training)
# obrázky (ve formě vektoru) a jejich označení
training_images = digits_data.data[:for_training]
training_labels = digits_data.target[:for_training]
# finito
Vstupní množina je rozdělena na (nepřesné) poloviny:
Vzorků celkem: 1797 Vzorků pro trénink: 898
13. Klasifikace obrázků
Nyní nastává to nejzajímavější část. Budeme totiž trénovat model s využitím 898 obrázků se známými číslicemi, které jsme si připravili v rámci předchozí kapitoly. Scikit-learn podporuje velké množství tréninkových metod a navíc i možností, jak ovlivnit jejich konfiguraci, ovšem dnes pro jednoduchost použijeme SVM neboli Support Vector Machines. Tréninkovému algoritmu postupně předáme jednotlivé obrázky (resp. přesněji řečeno jejich 64prvkové vektory) i očekávaný výsledek, tj. číslici, která je na obrázku napsána. Model následně použijeme pro klasifikaci zbývajících 899 obrázků (tedy těch obrázků, o nichž model neví, jaké číslice jsou na nich zapsány):
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# celkový počet vzorků
samples = len(digits_data.images)
print("Vzorků celkem:", samples)
# vytvoření seznamu, které použijeme
images = list(zip(digits_data.target, digits_data.images))
# počet vzorků pro trénink
for_training = samples // 2
print("Vzorků pro trénink:", for_training)
# obrázky (ve formě vektoru) a jejich označení
training_images = digits_data.data[:for_training]
training_labels = digits_data.target[:for_training]
# provést klasifikaci
from sklearn import svm
classify = svm.SVC(gamma=0.001)
classify.fit(training_images, training_labels)
# očekávané výsledky vs. výsledky modelu
expexted_labels = digits_data.target[for_training:]
predicted_labels = classify.predict(digits_data.data[for_training:])
# jak je náš model úspěšný?
total = 0
same = 0
for (expected, predicted) in zip(expexted_labels, predicted_labels):
print(expected, predicted)
# finito
O každém obrázku, který jsme použili pro verifikaci, si vypíšeme, jakou číslici představuje i jakou číslici na něm „vidí“ náš model:
8 8 ... ... ... 8 8 9 9 8 8 1 1 ... ... ... 5 9 ... ... ... 5 6 2 2 8 8 2 3 ... ... ... 7 7 8 8 4 4 9 9 0 0 8 8 9 9 8 8
14. Výpočet přesnosti modelu
Dobré je si ověřit, jak je model přesný. V tom nejjednodušším případě můžeme například zjistit, u kolika obrázků se model spletl a podílem s celkovým počtem verifikačních obrázků pak můžeme vypočítat přesnost či naopak nepřesnost modelu:
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# celkový počet vzorků
samples = len(digits_data.images)
print("Vzorků celkem:", samples)
# vytvoření seznamu, které použijeme
images = list(zip(digits_data.target, digits_data.images))
# počet vzorků pro trénink
for_training = samples // 2
print("Vzorků pro trénink:", for_training)
# obrázky (ve formě vektoru) a jejich označení
training_images = digits_data.data[:for_training]
training_labels = digits_data.target[:for_training]
# provést klasifikaci
from sklearn import svm
classify = svm.SVC(gamma=0.001)
classify.fit(training_images, training_labels)
# očekávané výsledky vs. výsledky modelu
expexted_labels = digits_data.target[for_training:]
predicted_labels = classify.predict(digits_data.data[for_training:])
# jak je náš model úspěšný?
total = 0
same = 0
for (expected, predicted) in zip(expexted_labels, predicted_labels):
print(expected, predicted)
if expected==predicted:
same+=1
total+=1
print("Total:", total)
print("Same:", same)
print("Precision:", 100.0*same/total)
# finito
Podívejme se na vypočtené výsledky:
Total: 899 Same: 871 Precision: 96.88542825361513
15. Vykreslení obrázků společně s jejich klasifikací
Kromě numerického vyjádření přesnosti modelu bude zajímavé zjistit, u jakých obrázků se model spletl a kde naopak provedl správné rozpoznání číslice. To je snadná úloha, protože již víme, jakým způsobem můžeme vložit víc obrázků (i s jejich rozpoznanou číslicí) do grafu rozděleného do pomyslné mřížky:
#!/usr/bin/env python
# vykreslování budeme provádět s využitím knihovny Matplotlib
import matplotlib.pyplot as plt
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# celkový počet vzorků
samples = len(digits_data.images)
print("Vzorků celkem:", samples)
# vytvoření seznamu, které použijeme
images = list(zip(digits_data.target, digits_data.images))
# počet vzorků pro trénink
for_training = samples // 2
print("Vzorků pro trénink:", for_training)
# obrázky (ve formě vektoru) a jejich označení
training_images = digits_data.data[:for_training]
training_labels = digits_data.target[:for_training]
# provést klasifikaci
from sklearn import svm
classify = svm.SVC(gamma=0.001)
classify.fit(training_images, training_labels)
# očekávané výsledky vs. výsledky modelu
expexted_labels = digits_data.target[for_training:]
predicted_labels = classify.predict(digits_data.data[for_training:])
# získat predikce modelu
predictions = list(zip(predicted_labels, digits_data.images[for_training:]))
def show_predictions(predictions, from_index, filename):
# zobrazit patnáct výsledků
for i, (predicted_digit, image) in enumerate(predictions[from_index:from_index+15]):
plt.subplot(3,5, i+1)
plt.axis('off')
# zobrazení obrázku
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
# a přidání predikce - o jakou číslici se jedná
plt.title("Predict: %i" % predicted_digit)
# nakonec vše uložíme a zobrazíme
plt.savefig(filename)
plt.show()
show_predictions(predictions, 0, "predictions_1.png")
show_predictions(predictions, 15, "predictions_2.png")
# finito
A takto bude vypadat výsledek činnosti skriptu. Sami se můžete přesvědčit, že model měl u některých obrázků skutečně těžkou pozici:

Obrázek 29: Prvních patnáct výsledků.

Obrázek 30: Dalších patnáct výsledků.
16. Změna poměru rozdělení dat na tréninkovou a verifikační množinu
Vzhledem k tomu, že máme k dispozici 1797 obrázků, můžeme se sami rozhodnout, kolik z těchto obrázků použít pro trénink a kolik pro verifikaci. Příliš malé množství trénovacích dat bude mít negativní efekt (malá natrénovanost), ovšem i druhý extrém nemusí být vhodný (přetrénovanost). Zkusme si tedy udělat malý pokus: budeme postupně zvětšovat množinu trénovacích obrázků a zjišťovat, jak dobře či naopak špatně bude takto natrénovaný model rozpoznávat zbylé obrázky:
def train_and_predict(training_set_size):
# počet vzorků pro trénink
for_training = training_set_size
# obrázky (ve formě vektoru) a jejich označení
training_images = digits_data.data[:for_training]
training_labels = digits_data.target[:for_training]
# provést klasifikaci
from sklearn import svm
classify = svm.SVC(gamma=0.001)
classify.fit(training_images, training_labels)
# očekávané výsledky vs. výsledky modelu
expexted_labels = digits_data.target[for_training:]
predicted_labels = classify.predict(digits_data.data[for_training:])
# jak je náš model úspěšný?
total = 0
same = 0
for (expected, predicted) in zip(expexted_labels, predicted_labels):
if expected==predicted:
same+=1
total+=1
return 100.0*same/total
Výsledek si můžeme zobrazit ve formě tabulky, z níž je patrné, že přibližně u 500 obrázků jsme již dosáhli poměrně dobrých výsledků a poté se kvalita modelu zvyšuje jen málo:
Vzorků celkem: 1797
Pro trénink Odhadů Korektních Přesnost
10 1787 1065 59.6%
130 1667 1340 80.4%
251 1546 1264 81.8%
371 1426 1287 90.3%
492 1305 1239 94.9%
612 1185 1135 95.8%
733 1064 1021 96.0%
853 944 912 96.6%
974 823 799 97.1%
1094 703 678 96.4%
1215 582 566 97.3%
1335 462 447 96.8%
1456 341 327 95.9%
1576 221 208 94.1%
1697 100 98 98.0%
Ještě lepší je grafické zobrazení závislosti počtu trénovacích obrázků na přesnosti odhadu modelu:
training_sizes = np.linspace(10, samples-100, 15, dtype=int)
vectorised = np.vectorize(train_and_predict)
precisions = vectorised(training_sizes)
plt.plot(training_sizes, precisions)
plt.savefig("precisions.png")
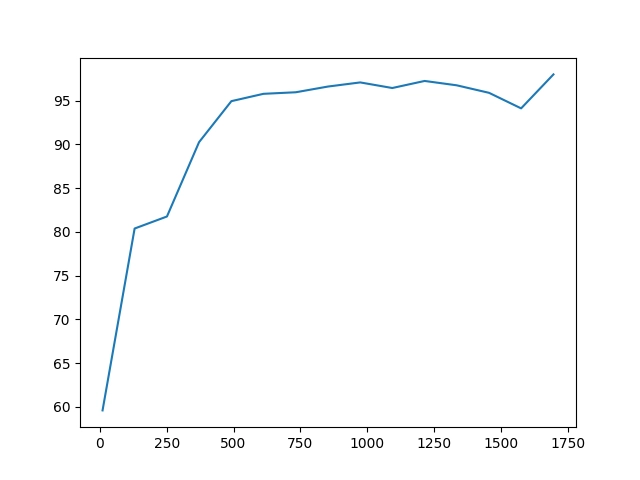
Obrázek 31: Závislost počtu trénovacích obrázků na přesnosti odhadu modelu.
17. Další kroky a vylepšení
I přesto, že výsledky odhadů našim modelem nejsou až tak špatné, je nutné si uvědomit všechna jeho omezení. Zejména model nedokáže zareagovat na posun obrázku, změnu jeho celkové světlosti atd. Jinými slovy – dostali jsme model odpovídající natrénovaným datům a nic víc. Proto bude nutné model vylepšit a například se pokusit o využití konvolučních neuronových sítí atd. To je však téma na samostatný článek.
18. Repositář s demonstračními příklady
Všechny skripty s postupnými kroky vedoucími k rozpoznání obrazů, které byly uvedeny v předchozích kapitolách, lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady a taktéž na notebook s celým postupem (včetně poznámek, co každý příkaz znamená):
19. Seriály a články s relevantní tématikou vydané na Rootu
- Seriál Knihovna Pandas
https://www.root.cz/serialy/knihovna-pandas/ - Seriál Torch: framework pro strojové učení
https://www.root.cz/serialy/torch-framework-pro-strojove-uceni/ - JupyterLite: nová alternativní architektura Jupyter Notebooku
https://www.root.cz/clanky/jupyterlite-nova-alternativni-architektura-jupyter-notebooku/ - Jupyter Notebook – operace s rastrovými obrázky a UML diagramy, literate programming
https://www.root.cz/clanky/jupyter-notebook-operace-s-rastrovymi-obrazky-a-uml-diagramy-literate-programming/ - Jupyter Notebook – nástroj pro programátory, výzkumníky i lektory
https://www.root.cz/clanky/jupyter-notebook-nastroj-pro-programatory-vyzkumniky-i-lektory/ - Tvorba grafů v Jupyter Notebooku s využitím knihovny Matplotlib (dokončení)
https://www.root.cz/clanky/tvorba-grafu-v-jupyter-notebooku-s-vyuzitim-knihovny-matplotlib-dokonceni/ - Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook
https://www.root.cz/clanky/knihovna-ipycanvas-aneb-kreslici-platno-pro-jupyter-notebook/ - Knihovna ipycanvas aneb kreslicí plátno pro Jupyter Notebook (2. část)
https://www.root.cz/clanky/knihovna-ipycanvas-aneb-kreslici-platno-pro-jupyter-notebook-2-cast/ - Interaktivní ovládací prvky v Jupyter Notebooku
https://www.root.cz/clanky/interaktivni-ovladaci-prvky-v-jupyter-notebooku/ - Xarray: sémantické rozšíření n-rozměrných polí z knihovny NumPy
https://www.root.cz/clanky/xarray-semanticke-rozsireni-n-rozmernych-poli-z-knihovny-numpy/ - Xarray: sémantické rozšíření n-rozměrných polí z knihovny NumPy (dokončení)
https://www.root.cz/clanky/xarray-semanticke-rozsireni-n-rozmernych-poli-z-knihovny-numpy-dokonceni/
20. Odkazy na Internetu
- scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/







































